1

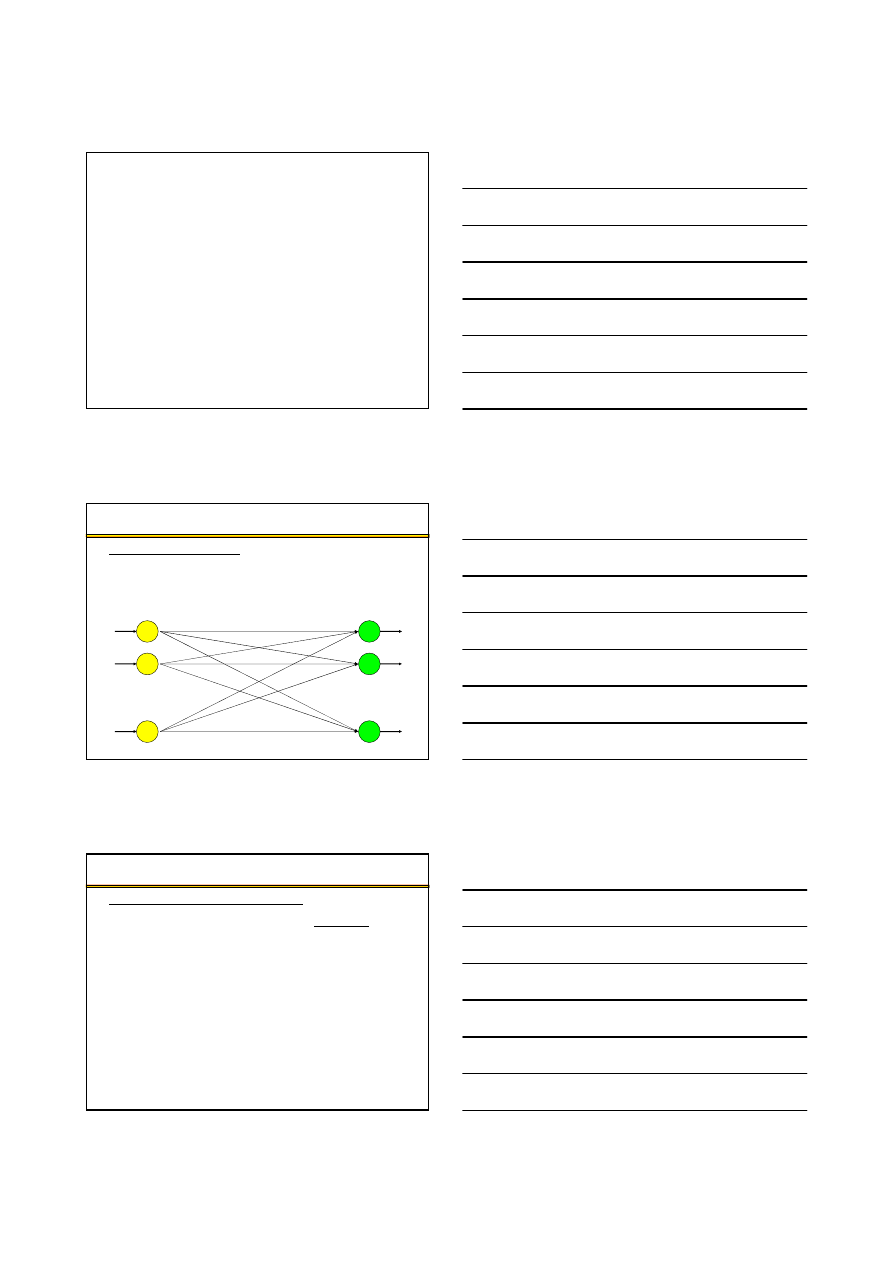
Zagadnienia transportowe

Klasyczne zadanie transportowe – definicja (1)

Klasyczne zadanie transportowe – problem najta

ń

szego przewozu

jednorodnego dobra pomi

ę

dzy punktami nadania (dostawcy) a punktami

odbioru (odbiorcy).

D

1

D

2

D

m

●
●
●

O

1

O

2

O

n

●
●
●

a

1

a

2

a

m

b

1

b

2

b

n

poda

ż

popyt

punkty

nadania

(i)

punkty

odbioru

(j)

x

11

c

11

x

12

c

12

x

1n

c

1n

x

21

c

21

x

22

c

22

x

2n

c

2n

x

m1

c

m1

x

m2

c

m2

x

mn

c

mn

Klasyczne zadanie transportowe – definicja (2)

∑

∑

=

=

≥

n

j

j

m

i

i

b

a

1

1

Zało

ż

enia klasycznego zadania transportowego:

x

ij

- zmienne decyzyjne; ilo

ść

przewo

ż

onego jednorodnego dobra

na trasie pomi

ę

dzy i-tym dostawc

ą

a j-tym odbiorc

ą

[i=1,2,…,m;

j=1,2,…,n;]

a

i

- parametr problemu; zasób dobra u i-tego dostawcy (poda

ż

)

[i=1,2,…,m]

a = [a

1

,a

2

,…,a

m

]

b

j

- parametr problemu; zapotrzebowanie na dobro j-tego odbiorcy
(popyt) [j=1,2,…,n]

b = [b

1

,b

2

,…,b

n

]

c

ij

- parametr problemu; koszt przewozu jednostki dobra na trasie
pomi

ę

dzy i-tym dostawc

ą

a j-tym odbiorc

ą

[i=1,2,…,m;

j=1,2,…,n;]

























=

mn

m

m

n

n

c

c

c

c

c

c

c

c

c

L

M

O

M

M

L

L

2

1

2

22

21

1

12

11

C

2

Klasyczne zadanie transportowe – definicja (3)

Klasyfikacja zada

ń

transportowych:

1. Zamkni

ę

te

∑

∑

=

=

=

n

j

j

m

i

i

b

a

1

1

2. Otwarte

∑

∑

=

=

>

n

j

j

m

i

i

b

a

1

1

Otwarte

⇒

Zamkni

ę

te:

a) doda

ć

n+1 punkt odbioru

b) zapotrzebowanie b

n+1

dodanego punktu odbioru – ró

ż

nica mi

ę

dzy

całkowit

ą

poda

żą

a całkowitym popytem:

∑

∑

=

=

+

−

=

n

j

j

m

i

i

n

b

a

b

1

1

1

Klasyczne zadanie transportowe – model decyzyjny

Funkcja celu: (ł

ą

czny koszt transportu)

min

)

(

1

1

→

=

∑ ∑

= =

m

i

n

j

ij

ij

x

c

F x

Ograniczenia:

i

n

i

ij

a

x

=

∑

=

1

Warunki brzegowe:

0

≥

ij

x

i = 1,2,…,m

(bilanse dla punktów nadania)

j

m

i

ij

b

x

=

∑

=

1

j = 1,2,…,n

(bilanse dla punktów odbioru)

i = 1,2,…,m

j = 1,2,…,n

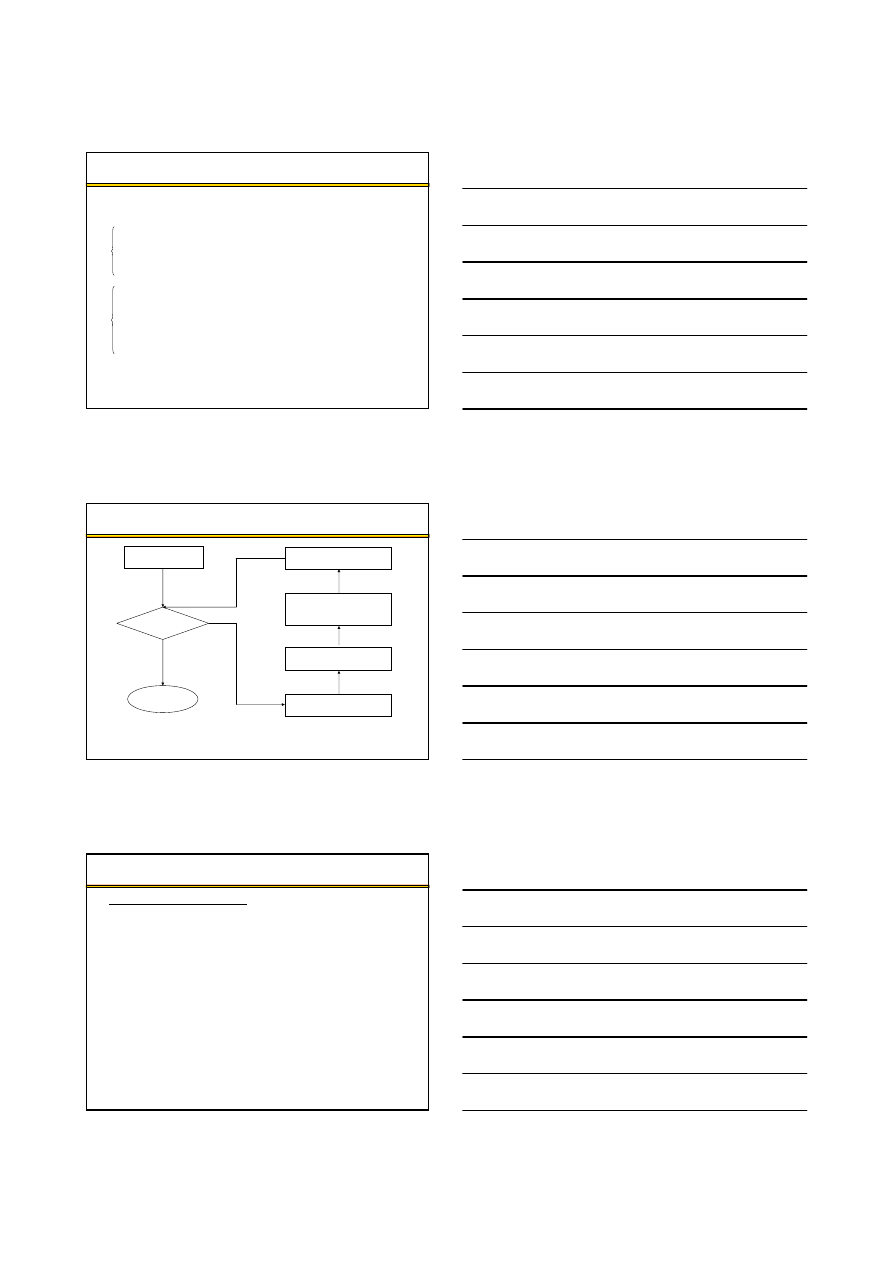
Klasyczne zadanie transportowe – przykład (1)

350

120

70

110

50

zapotrzebowanie

odbiorców

130

4

4

4

2

D3

80

2

1

1

3

D2

140

5

3

2

2

D1

O4

O3

O2

O1

poda

ż

dostawców

jednostkowe koszty transportu

3

Klasyczne zadanie transportowe – przykład (2)

x

34

≥

0

x

33

≥

0

x

32

≥

0

x

31

≥

0

x

24

≥

0

x

23

≥

0

x

22

≥

0

x

21

≥

0

x

14

≥

0

x

13

≥

0

x

12

≥

0

x

11

≥

0

120

=

+x

34

+x

24

x

14

70

=

+x

33

+x

23

x

13

110

=

+x

32

+x

22

x

12

50

=

+x

31

+x

21

x

11

130

=

+x

34

+x

33

+x

32

+x

31

80

=

+x

24

+x

23

+x

22

+x

21

140

=

+x

14

+x

13

+x

12

x

11

min

→

+4x

34

+4x

33

+4x

32

+2x

31

+2x

24

+x

23

+x

22

+3x

21

+5x

14

+3x

13

+2x

12

2x

11

F(

χχχχ

) =

p

o

d

a

ż

p

o

p

y

t

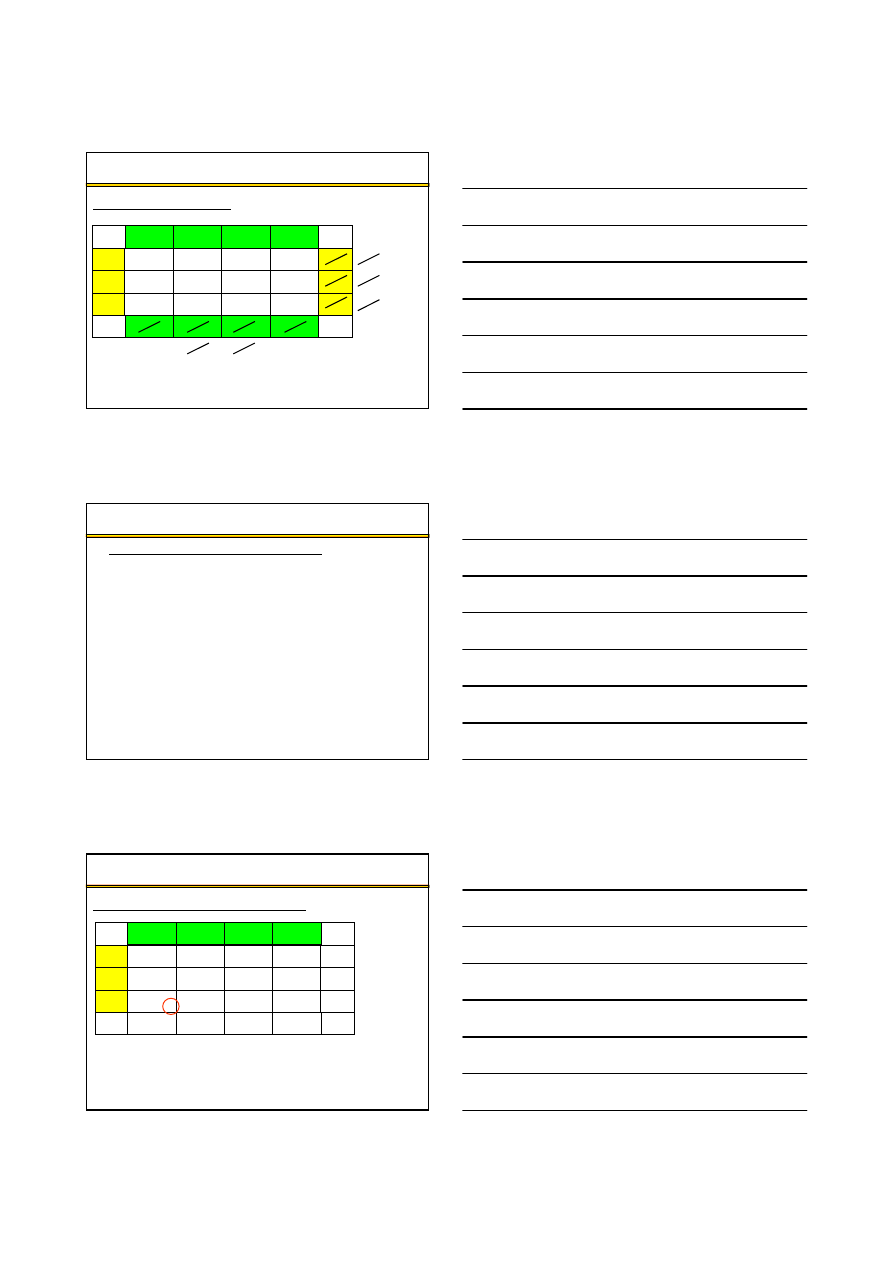
Klasyczne zadanie transportowe – algorytm transportowy (1)

Pocz

ą

tkowy

program przewozowy

Program

optymalny?

KONIEC

Wybierz tras

ę

daj

ą

c

ą

najwi

ę

ksz

ą

obni

ż

k

ę

kosztów

Zbuduj cykl

Koryguj

ą

cy przewozy

1

2

3

4

Ustal maksymalny

przewóz na trasie

ustalonej w [3]

5

Skoryguj program

przewozowy

6

TAK

NIE

Klasyczne zadanie transportowe – algorytm transportowy (2)

Pocz

ą

tkowy program przewozowy – Metoda k

ą

ta północno-zachodniego

1. wprowad

ź

maksymalny przewóz na trasie (i,j): x

ij

= min(a

i

,b

j

)

2. skoryguj poda

ż

w i-tym punkcie nadania: a

i

= a

i

– x

ij

i popyt w j-tym

punkcie odbioru: b

i

= b

i

– x

ij

4

Klasyczne zadanie transportowe – algorytm transportowy (3)

350

120

70

110

50

popyt

130

D3

80

D2

140

D1

poda

ż

O4

O3

O2

O1

Pocz

ą

tkowy program przewozowy – Metoda k

ą

ta północno-zachodniego

50

90

0

90

0

20

20

60

0

60

0

10

10

120

0

120

0

0

Koszt = 2

××××

50 + 2

××××

90 + 1

××××

20 + 1

××××

60 + 4

××××

10 + 4

××××

120 = 880

Klasyczne zadanie transportowe – algorytm transportowy (4)

Sprawdzenie optymalno

ś

ci programu przewozowego - tabela wska

ź

ników

optymalno

ś

ci

1. pola tabeli wska

ź

ników optymalno

ś

ci, dla których x

ij

>0 zawieraj

ą

jedn

ą

liczb

ę

: jednostkowy koszt transportu c

ij

2. pozostałe pola tabeli wska

ź

ników optymalno

ś

ci zawieraj

ą

dwie liczby:

(u

i

+v

j

) oraz wska

ź

nik optymalno

ś

ci

∆

ij

= c

ij

–(u

i

+v

j

)

3. program przewozowy jest optymalny, je

ż

eli wszystkie

∆

ij

≥

0

4. wyznaczenie trasy daj

ą

cej najwi

ę

ksz

ą

obni

ż

k

ę

kosztów (je

ż

eli uzyskany

program przewozowy nie jest optymalny):
dla wszystkich

∆

ij

<0

∆

kl

= min{

∆

ij

}

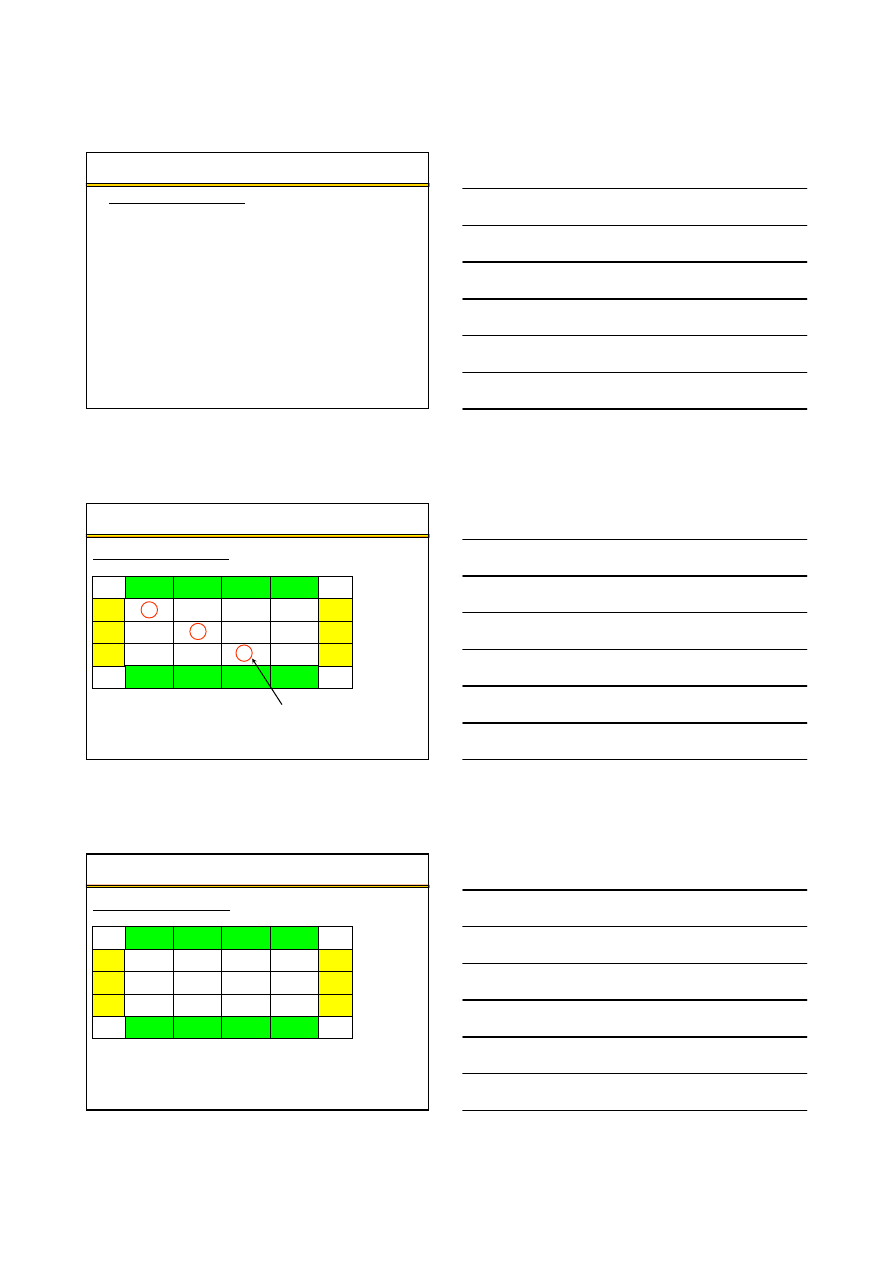
Klasyczne zadanie transportowe – algorytm transportowy (5)

Sprawdzenie optymalno

ś

ci programu przewozowego

××××

v

j

D3

D2

D1

u

i

O4

O3

O2

O1

2

2

1

1

4

4

2

-1

0

2

2

2

2

2

2

1

1

4

4

1

3

2

1

-2

0

5

Klasyczne zadanie transportowe – algorytm transportowy (6)

Korekta programu przewozowego

1. postaw znak „+” na wytypowanej trasie daj

ą

cej najwi

ę

ksz

ą

obni

ż

k

ę

kosztów

2. w rozpatrywanym programie przewozowym znakuj trasy o przewozie

niezerowym znakami „+” i „-” w taki sposób, aby w ka

ż

dym wierszu i

ka

ż

dej kolumnie była para „+” „-” lub nie było ich w ogóle

3. wyznacz wielko

ść

korekty

δδδδ

poprzez wybór warto

ś

ci najmniejszej oznaczonej

znakiem „-”:

δδδδ

= min(x

ij”

-”

)

4. skoryguj rozpatrywany program przewozowy poprzez:

x

ij

*

= x

ij

+

δ

dla tras oznaczonych znakiem „+”

x

ij

*

= x

ij

+

δ

dla tras oznaczonych znakiem „-”

x

ij

*

= x

ij

dla tras nieoznaczonych

Klasyczne zadanie transportowe – algorytm transportowy (7)

350

120

70

110

50

popyt

130

D3

80

D2

140

D1

poda

ż

O4

O3

O2

O1

Korekta programu przewozowego

50

90

20

60

10

120

–

+

+

–

+

–

min{50,20,10} = 10

-10

-10

-10

+10

+10

+10

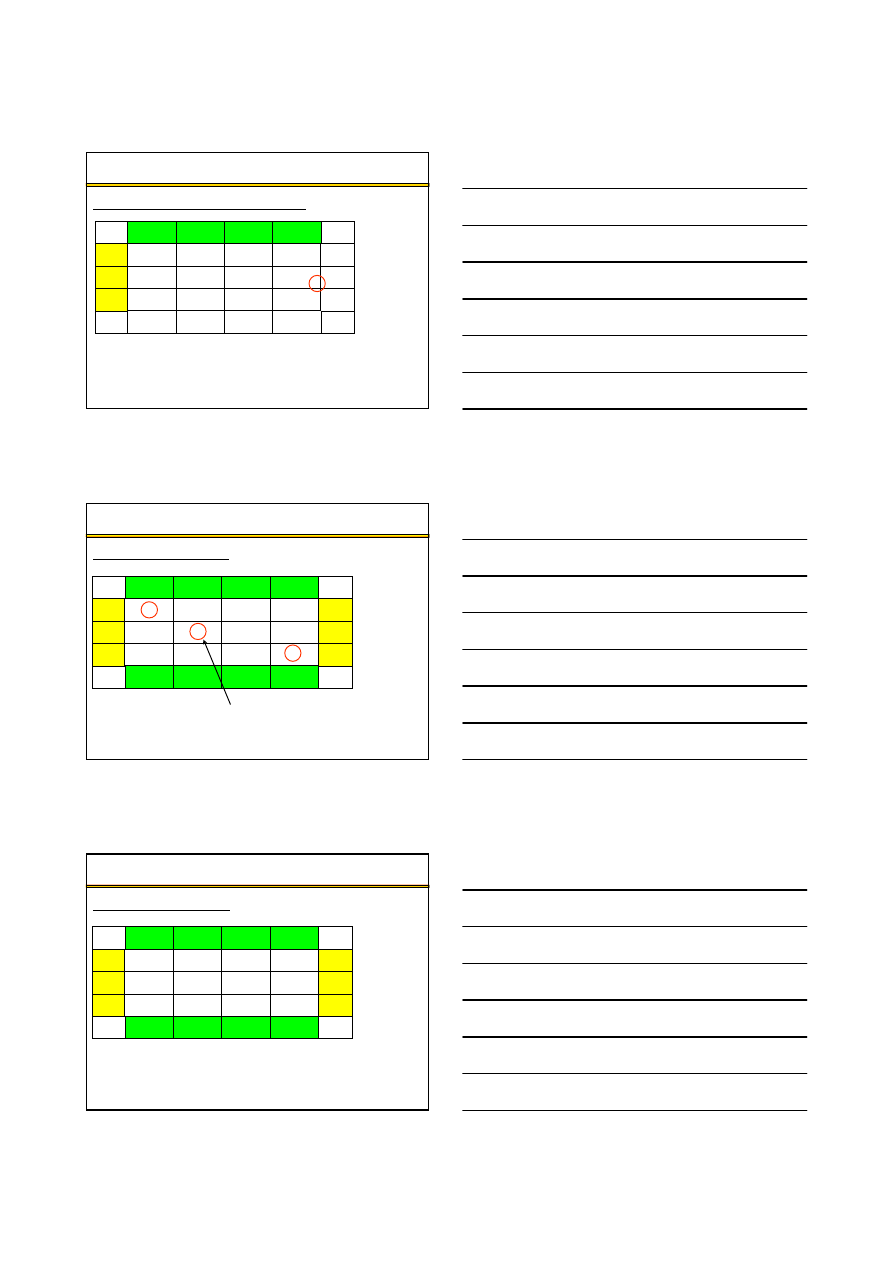
Klasyczne zadanie transportowe – algorytm transportowy (8)

350

120

70

110

50

popyt

130

D3

80

D2

140

D1

poda

ż

O4

O3

O2

O1

Poprawiony program przewozowy

40

100

10

70

10

120

Koszt = 2

××××

40 + 2

××××

100 + 1

××××

10 + 1

××××

70 + 2

××××

10 + 4

××××

120 = 860

lub

Koszt = 880 + 10

××××

(–2) = 880 – 20 = 860

6

Klasyczne zadanie transportowe – algorytm transportowy (9)

Sprawdzenie optymalno

ś

ci programu przewozowego – iteracja 2

××××

v

j

D3

D2

D1

u

i

O4

O3

O2

O1

2

2

1

1

2

4

0

-1

0

2

4

2

2

2

4

1

1

2

2

1

1

2

-1

2

2

Klasyczne zadanie transportowe – algorytm transportowy (10)

350

120

70

110

50

popyt

130

D3

80

D2

140

D1

poda

ż

O4

O3

O2

O1

Korekta programu przewozowego

40

100

10

70

120

–

+

+

–

+

–

min{40,10,120} = 10

-10

-10

-10

+10

+10

+10

10

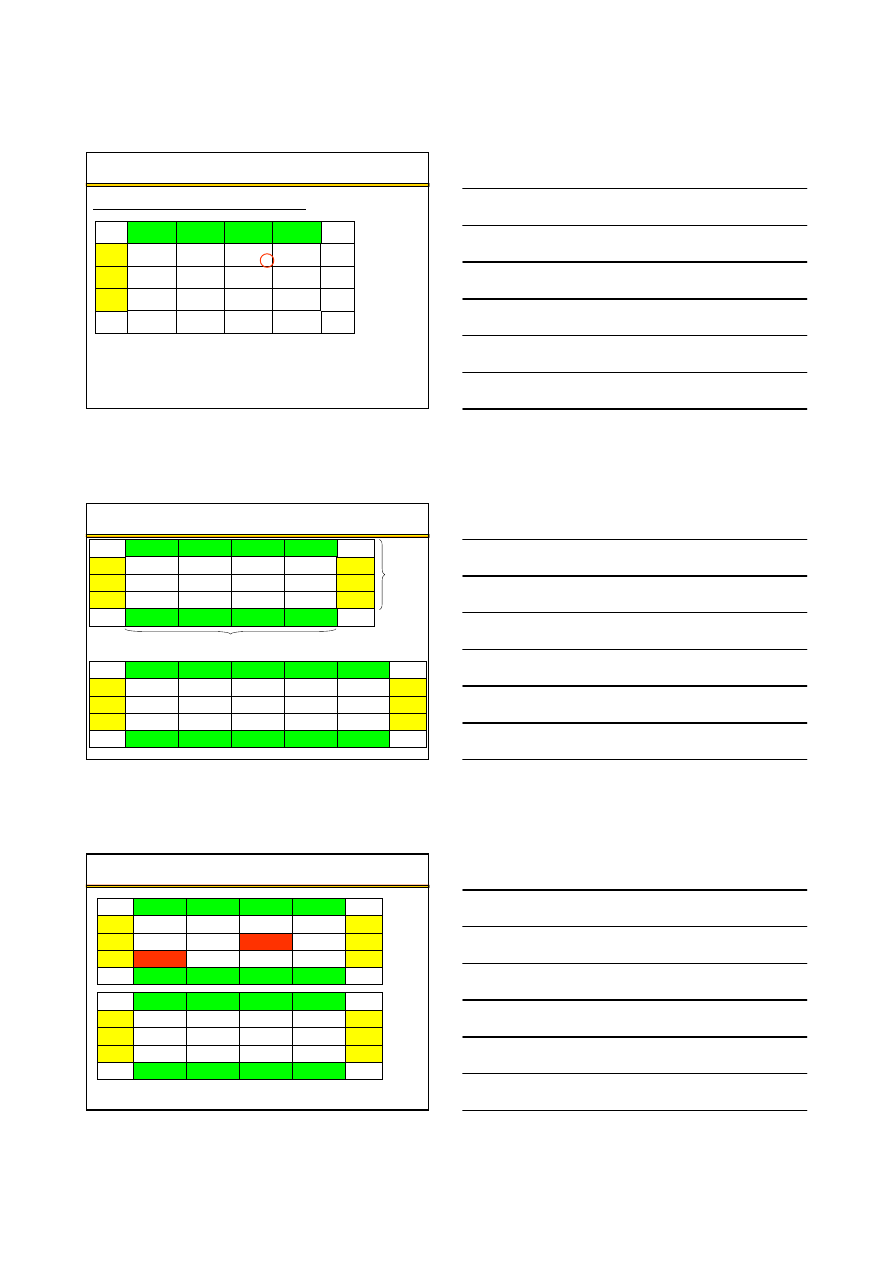
Klasyczne zadanie transportowe – algorytm transportowy (11)

350

120

70

110

50

popyt

130

D3

80

D2

140

D1

poda

ż

O4

O3

O2

O1

Poprawiony program przewozowy

30

110

10

70

20

110

Koszt = 2

××××

30 + 2

××××

110 + 1

××××

70 + 2

××××

10 + 2

××××

20 + 4

××××

110 = 850

lub

Koszt = 860 + 10

××××

(–1) = 860 – 10 = 850

7

Klasyczne zadanie transportowe – algorytm transportowy (12)

Sprawdzenie optymalno

ś

ci programu przewozowego – iteracja 3

××××

v

j

D3

D2

D1

u

i

O4

O3

O2

O1

2

2

2

1

2

4

0

-2

0

3

4

2

2

3

4

0

0

3

2

0

1

3

1

1

2

Rozwi

ą

zanie optymalne

Klasyczne zadanie transportowe – zadanie otwarte

120

70

110

50

popyt

130

4

4

4

2

D3

130

2

1

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3

O2

O1

50

0

0

0

M

400

120

70

110

50

popyt

130

4

4

4

2

D3

130

2

1

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3

O2

O1

400

350

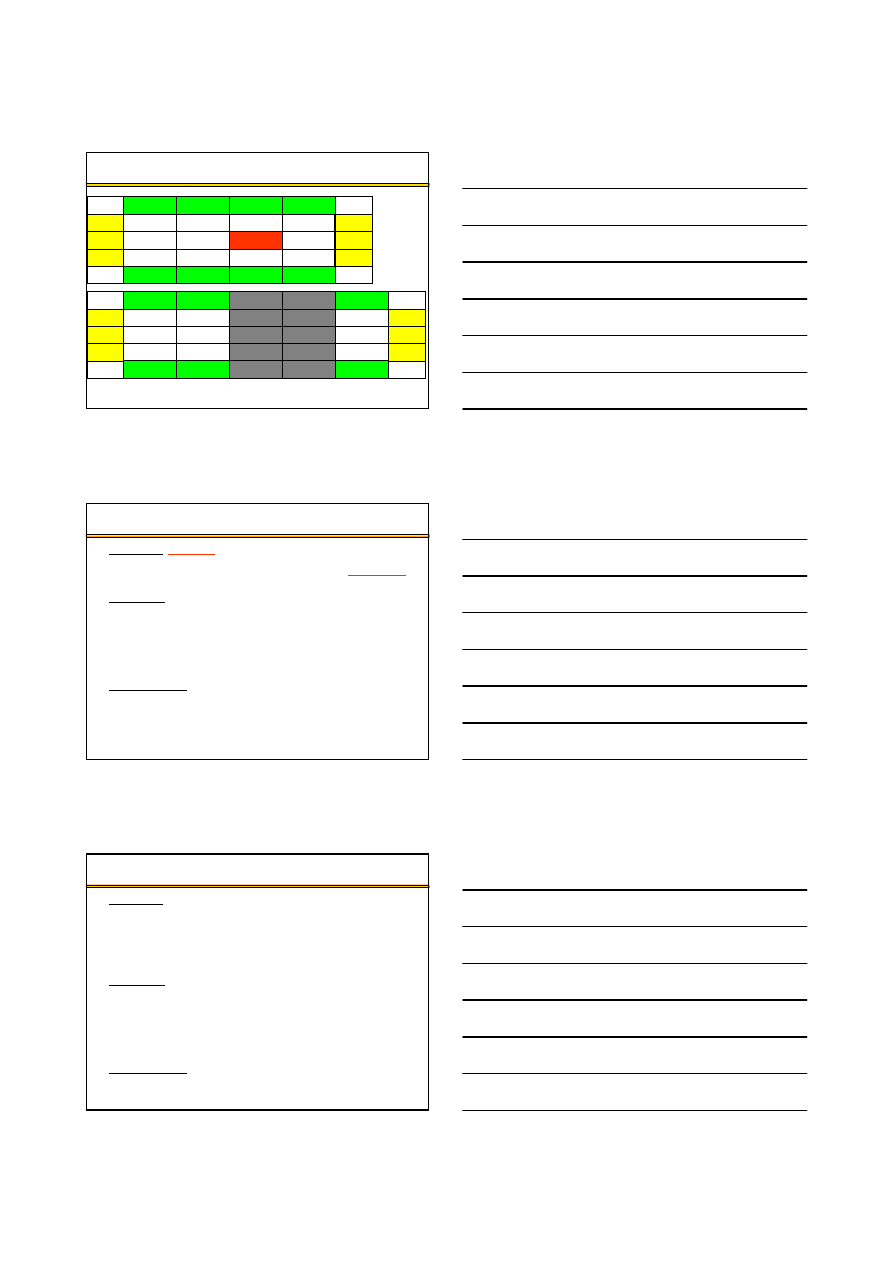
Klasyczne zadanie transportowe – całkowita blokada trasy lub tras

350

120

70

110

50

popyt

130

4

4

4

2

D3

80

2

1

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3

O2

O1

350

120

70

110

50

popyt

130

4

4

4

M

D3

80

2

M

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3

O2

O1

M

→

∞

8

Klasyczne zadanie transportowe – cz

ęś

ciowa blokada trasy

350

120

70

110

50

popyt

130

4

4

4

2

D3

80

2

1 (max. 50)

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3

O2

O1

20

4

M

3

O3(b)

350

120

50

110

50

popyt

130

4

4

4

2

D3

80

2

1

1

3

D2

140

5

3

2

2

D1

poda

ż

O4

O3(a)

O2

O1

Zadanie transportowe – kryterium czasu I rodzaju

Funkcja celu: (

ł

ą

czny czas

transportu)

min

)

(

1

1

→

=

∑ ∑

= =

m

i

n

j

ij

ij

x

t

F

x

Ograniczenia:

i

n

i

ij

a

x

=

∑

=

1

Warunki brzegowe:

0

≥

ij

x

i = 1,2,…,m

(bilanse dla punktów nadania)

j

m

i

ij

b

x

=

∑

=

1

j = 1,2,…,n

(bilanse dla punktów odbioru)

i = 1,2,…,m

j = 1,2,…,n

t

ij

– czas transportu

jednostki dobra

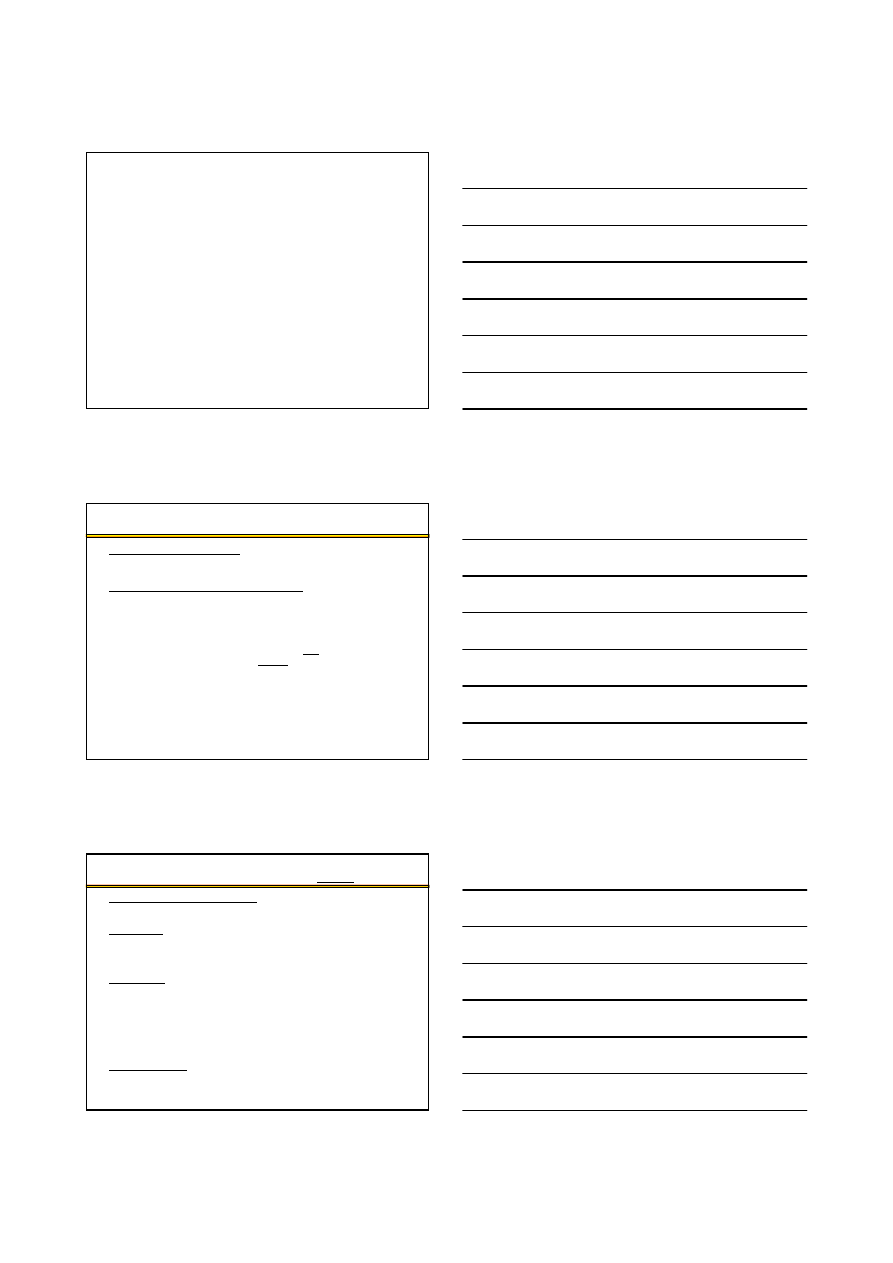
Zadanie transportowe – kryterium czasu II rodzaju

Funkcja celu: (najdłu

ż

szy czas przewozu w optymalnym programie

przewozowym jest najkrótszy spo

ś

ród wszystkich

dopuszczalnych programów przewozowych – program
przewozu zako

ń

czy si

ę

najszybciej)

}

{

max

min

)

(

0

ij

x

X

t

F

ij

>

∈

=

x

x

Ograniczenia:

i

n

i

ij

a

x

=

∑

=

1

Warunki brzegowe:

0

≥

ij

x

i = 1,2,…,m

(bilanse dla punktów nadania)

j

m

i

ij

b

x

=

∑

=

1

j = 1,2,…,n

(bilanse dla punktów odbioru)

i = 1,2,…,m

j = 1,2,…,n

t

ij

– czas przejazdu pomi

ę

dzy punktem

nadania i a punktem odbioru j

9

Zagadnienie przydziału

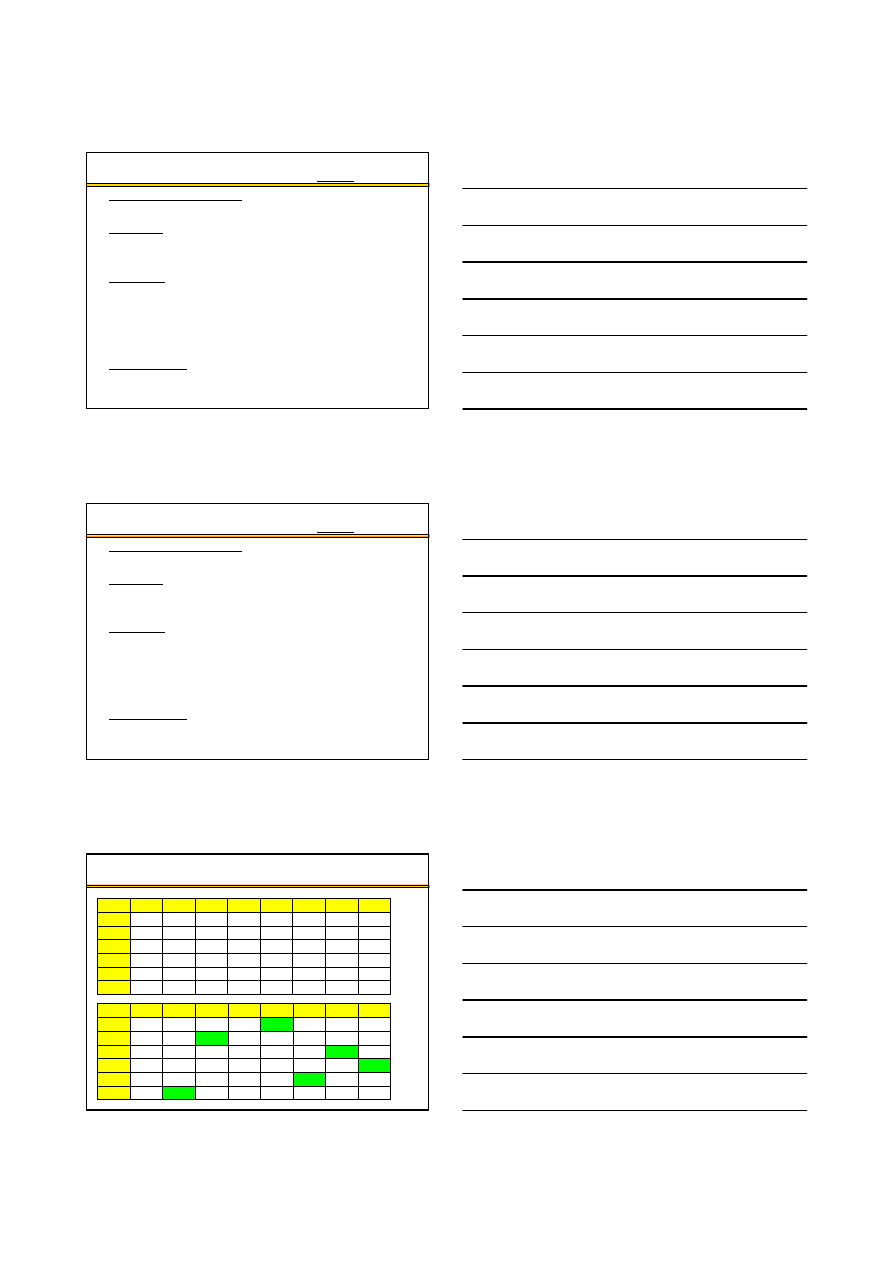
Zadanie przydziału – definicja (1)

Zadanie optymalnego przydziału – problem najkorzystniejszego
skojarzenia n

ś

rodków z m celami, przy czym ka

ż

dy

ś

rodek mo

ż

e by

ć

u

ż

yty tylko jeden raz.

Zało

ż

enia klasycznego zadania transportowego:

n

- liczba

ś

rodków

m

- liczba celów

x

ij

- zmienne decyzyjne; x

ij

=1 je

ż

eli i-ty cel jest realizowany przez

j-ty

ś

rodek; x

ij

=0 je

ż

eli i-ty cel nie jest realizowany przez

j-ty

ś

rodek;

[i=1,2,…,m; j=1,2,…,n;]

c

ij

- parametr problemu; korzy

ść

zwi

ą

zana z realizacj

ą

i-tego celu

przez j-ty

ś

rodek [i=1,2,…,m; j=1,2,…,n;]

Zadanie przydziału – model decyzyjny (n = m)

Liczba celów = liczba

ś

rodków = n

Funkcja celu: (ł

ą

czna korzy

ść

)

(min)

max

)

(

1

1

→

=

∑ ∑

= =

n

i

n

j

ij

ij

x

c

U x

Ograniczenia:

1

1

=

∑

=

n

i

ij

x

Warunki brzegowe:

}

1

,

0

{

∈

ij

x

i = 1,2,…,n

(bilanse dla celów)

1

1

=

∑

=

n

i

ij

x

j = 1,2,…,n

(bilanse dla

ś

rodków)

i = 1,2,…,n

j = 1,2,…,n

10

Zadanie przydziału – model decyzyjny (n > m)

Nadwy

ż

ka

ś

rodków nad celami

Funkcja celu: (ł

ą

czna korzy

ść

)

(min)

max

)

(

1

1

→

=

∑ ∑

= =

m

i

n

j

ij

ij

x

c

U x

Ograniczenia:

1

1

=

∑

=

n

i

ij

x

Warunki brzegowe:

}

1

,

0

{

∈

ij

x

i = 1,2,…,m

(bilanse dla celów)

1

1

≤

∑

=

m

i

ij

x

j = 1,2,…,n

(bilanse dla

ś

rodków)

i = 1,2,…,m

j = 1,2,…,n

Zadanie przydziału – model decyzyjny (n < m)

Nadwy

ż

ka celów nad

ś

rodkami

Funkcja celu: (ł

ą

czna korzy

ść

)

(min)

max

)

(

1

1

→

=

∑ ∑

= =

m

i

n

j

ij

ij

x

c

U x

Ograniczenia:

1

1

≤

∑

=

n

i

ij

x

Warunki brzegowe:

}

1

,

0

{

∈

ij

x

i = 1,2,…,m

(bilanse dla celów)

1

1

=

∑

=

m

i

ij

x

j = 1,2,…,n

(bilanse dla

ś

rodków)

i = 1,2,…,m

j = 1,2,…,n

Zadanie przydziału – przykład

Kooperant (

ś

rodki)

12

12

7

7

11

10

8

10

F

20

16

10

10

16

14

12

16

E

15

15

13

13

15

12

14

15

D

9

9

8

8

9

9

10

10

C

9

12

9

15

12

6

15

12

B

12

10

8

6

12

8

8

10

A

VIII

VII

VI

V

IV

III

II

I

0

0

0

0

0

0

1

0

F

0

0

1

0

0

0

0

0

E

1

0

0

0

0

0

0

0

D

0

1

0

0

0

0

0

0

C

0

0

0

0

0

1

0

0

B

0

0

0

1

0

0

0

0

A

VIII

VII

VI

V

IV

III

II

I

U

k

ła

d

(

c

e

le

)

U

min

= 54

U

→

min