Opis doświadczeń na maturę z fizyki

rok szkolny 2003/2004

II Liceum Ogólnokształcące im. Stanisława Wyspiańskiego w Będzinie

Spis treści

1 Wyznaczanie współczynnika tarcia.................................................................................................. 3
2 Badanie zależności siły sprężystości od wydłużenia........................................................................ 4
3 Wyznaczanie gęstości ciała stałego na podstawie prawa Archimedesa........................................... 5
4 Wyznaczanie gęstości cieczy na podstawie prawa Archimedesa..................................................... 6
5 Wyznaczanie przyśpieszenia ziemskiego z wykorzystaniem wahadła matematycznego.................7
6 Tworzenie obrazów rzeczywistych przez soczewkę skupiającą.......................................................8
7 Badanie gęstości ciał stałych............................................................................................................ 9
8 Zależność napięcia od natężenia (prawo Ohma)............................................................................ 10
9 Prawo zachowania ładunku............................................................................................................ 11
10 Indukcja pola magnetycznego wokół przewodnika z prądem...................................................... 12
11 Naczynia połączone i u-rurka....................................................................................................... 13
12 Kalorymetr – bilans cieplny..........................................................................................................14
13 Wyznaczyć ciepło topnienia......................................................................................................... 15
14 Prawo Kirchhoffa......................................................................................................................... 16
15 Prawo Ampere'a............................................................................................................................17
16 Rozszerzalność cieplna.................................................................................................................18
17 Badanie ruchu jednostajnie zmiennego........................................................................................ 19
18 Badanie ruchu drgającego.............................................................................................................20
19 Badanie gęstości wybranych cieczy..............................................................................................21
20 Badanie zasady działania maszyn prostych.................................................................................. 22

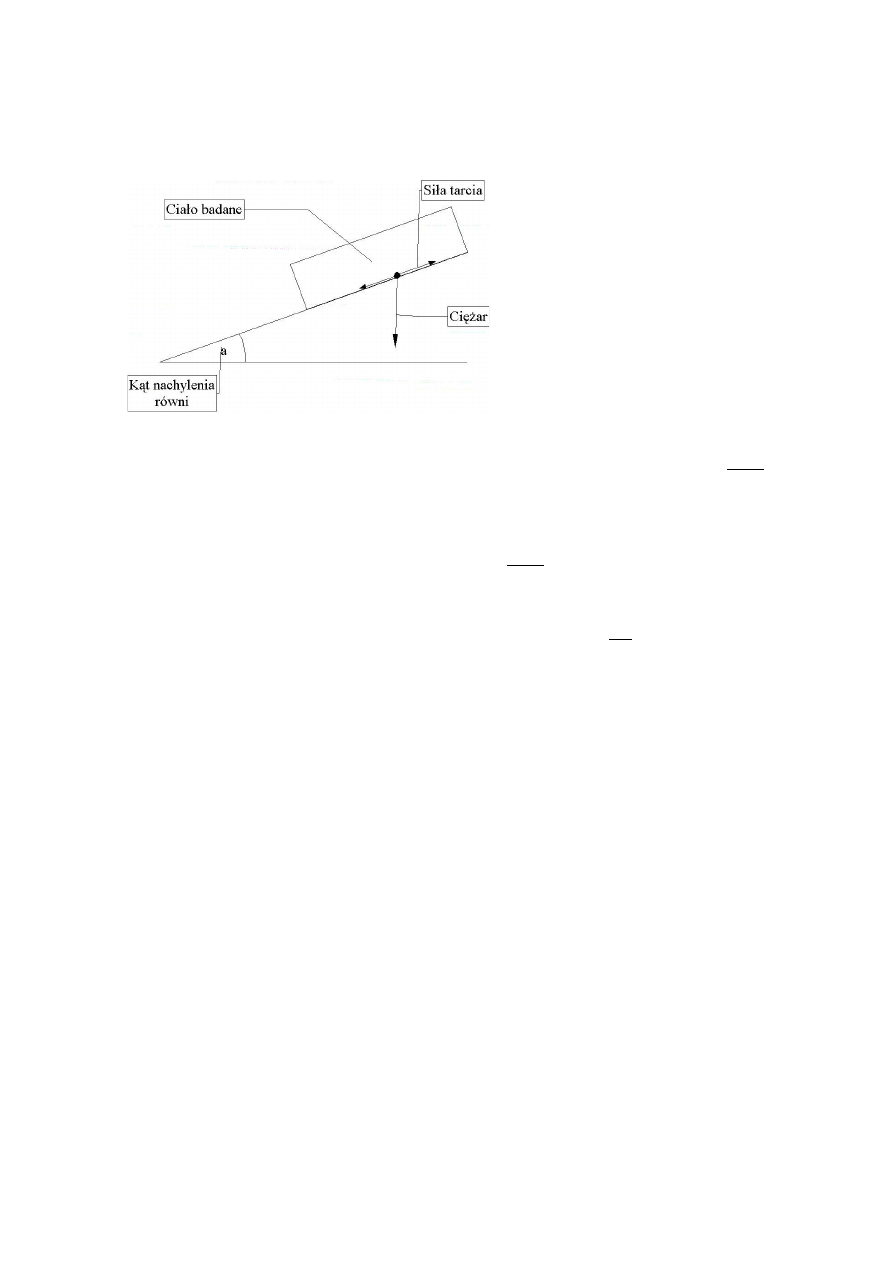
1 Wyznaczanie współczynnika tarcia

1.1 Do doświadczenia potrzebna jest waga laboratoryjna, równia pochyła, stoper i ciało, które nie może się

toczyć. Ustawiamy ciało na szczycie równi pochyłej, po czym dostosowujemy kąt nachylenia



równi

tak, że po minimalnym zwiększeniu tego kąta ciało zacznie się zsuwać:

Badamy również masę m badanego ciała (za pomocą wagi laboratoryjnej). Przy znanej wartości
przyśpieszenia ziemskiego g(=9,81 N/kg) stwierdzamy, że maksymalna wartość siły tarcia statycznego,

które może działać między materiałami, z których jest wykonane ciało i równia wynosi

F

t

=

mg

sin



.

1.2 W kwestii tarcia dynamicznego postępujemy następująco: ustawiamy ciało na szczycie równi, po czym

zmieniamy kąt nachylenia tak, aby był większy niż %alfa. Dla danej wartości



kąta nachylenia równi

pochyłej wiemy, jaka siła powinna działać na ciało:

F

p

=

mg

sin



. Mając znaną długość s równi pochyłej

badamy, w jakim czasie ciało pokona drogę s pod wpływem siły

F

=F

p

−F

t

. Stąd już tylko krok do

określenia współczynnika tarcia dynamicznego między substancjami:

=

F

t

F

p

1.3 Zagadnienia dodatkowe do tematu:

1.3.1 Tarcie – zjawisko występujące między ciałami, których powierzchnie się stykają. Polega na zamianie

pewnej ilości energii, dostarczonej do ciała w celu nadania mu prędkości, w ciepło. Zjawisko tarcia
można rozpatrywać zarówno pozytywnie, jak i negatywnie. Pozytywnie, gdyż, gdyby nie istniało tarcie,
to nie istniałaby żadna siła powstrzymująca przedmioty „na miejscu”. Z drugiej jednak strony tarcie
stanowi duży problem technologiczny, gdyż z jego powodu maszyny pracują mało wydajnie.

1.3.2 Zjawisko tarcia jest wykorzystane na przykład przy produkcji samochodów. Opona wykonana jest z

materiału, który ma duże współczynniki tarcia z materiałami, z których zbudowane są drogi. Wobec
tego w momencie, gdy zostanie przyłożona do koła pewna siła (moc z silnika), to koło potoczy się, a nie
– poślizgnie. Jednocześnie bieżnik opony ma za zadanie odprowadzić substancje trzecie spomiędzy
opony a nawierzchni, gdyż to mogłoby spowodować spadek współczynnika tarcia (a zatem i
przyczepności ==> spadek bezpieczeństwa jazdy )

1.3.3 W celu zmniejszenia tarcia stosuje się substancje, zwane smarami, które mają mniejszy

współczynnik tarcia z oboma substancjami trącymi, niż one ze sobą nawzajem. Dzięki temu straty
energii spowodowane tarciem zostają zmniejszone.

1.4 Źródła błędów pomiarowych:

1.4.1 Niedokładność pomiarów: masy ciała, kąta nachylenia równi, czasu drogi ciała. (Za każdym razem

najmniejsza jednostka na skali)

1.4.2 Błąd człowieka

1.4.3 Błąd paralaksy

2 Badanie zależności siły sprężystości od wydłużenia

2.1 Do wykonania doświadczenia potrzebne są: linijka, sprężyna, stojak, pewna ilość ciężarków o znanej

masie. Sprężynę wieszamy na stojaku, i obciążmy ciężarkiem o masie m (w celu wytłumienia drgań i
usunięcia ewentualnych mikro nierówności). Mierzymy jej długość w takim stanie i oznaczamy przez

l

0

. Po kolei powtarzamy:

2.1.1 Zawieszenie kolejnego ciężarka

2.1.2 Zmierzenie długości i zaznaczenie jej na wykresie

l

m

2.1.3 odwieszenie ciężarka i kontrola, czy sprężyna wróciła do długości początkowej

2.2 Powyższe możemy powtarzać aż do trwałego odkształcenia sprężyny – kiedy po zdjęciu ciężarka nie

wróci do swojego stanu początkowego. Punkty na wykresie powinny układać się mniej więcej w linię
prostą. Zauważamy wobec tego liniową zależność wydłużenia sprężyny w zależności od siły rozciągającej.
Korzystając z dowolnych metod aproksymacji wyznaczamy wzór tej prostej, przy czym zerowej sile
obciążającej odpowiada pewne wydłużenie

l

0

, gdyż za zerowe obciążenie uznaliśmy jeden odważnik.

Współczynnik proporcjonalności wydłużenia sprężyny – kąt jej nachylenia - to moduł Younga.

2.3 Źródła błędu pomiarowego:

2.3.1 Niemożliwe do wytłumienia oscylacje układu

2.3.2 Mikro nierówności sprężyny, nawet po zawieszeniu zerującego odważnika

2.3.3 Błędy pomiaru masy wieszanych odważników

2.3.4 Błąd pomiaru długości sprężyny – najmniejsza podziałka na linijce

2.3.5 Błąd paralaksy

2.3.6 Mała ilość powtórzeń doświadczenia

2.3.7 Jeżeli ostatni odważnik trwale odkształcił sprężynę, a wynik ten nie został odrzucony, to fałszuje on

wynik całego eksperymentu,

3 Wyznaczanie gęstości ciała stałego na podstawie prawa

Archimedesa

3.1 Do wyznaczania gęstości ciała stałego na podstawie prawa Archimedesa potrzebne są: badane ciało,

naczynie z podziałką, waga laboratoryjna, siłomierz, ciecz o znanej gęstości.

3.2 Badane ciało wieszamy na siłomierzu i odczytujemy siłę grawitacji, która na nie działa:

F

g

=m

c

g

.

Następnie nalewamy do naczynia pewną ilość

V

1

cieczy o gęstości



f

. Zanurzamy ciało

zawieszone na siłomierzu w naczyniu z cieczą tak, aby całe ciało było zanurzone. Z siłomierza
odczytujemy siłę

F

2

=F

g

−F

w

, gdzie

F

w

jest to siła ciężkości, która działa na wypartą część

cieczy. Z podziałki na naczyniu odczytujemy nową objętość

V

2

cieczy. Wobec tego:

F

2

=F

g

– V



c

g ,V

=V

2

−V

1

. Z czego

V

=

F

2

– F

g



c

g

. Ponieważ



s

=

F

g

gV

, to mamy:



s

=

F

g



c

F

2

−F

g

.

3.3 Prawo Archimedesa: na ciało zanurzone w cieczy działa, oprócz siły ciężkości, siła wyporu równa

ciężarowi cieczy o objętości badanego ciała.

3.4 Źródła błędu pomiarowego:

3.4.1 Błąd odczytu:

3.4.1.1 Siły ciężkości działającej na ciało niezanurzone – najmniejsza skala

3.4.1.2 Siły działającej na ciało zanurzone – najmniejsza skala

3.4.1.3 Zmiany objętości cieczy – najmniejsza skala

3.4.2 Mały błąd przy uznaniu gęstości cieczy z tablic fizyko-chemicznych (nie można podać dokładnej

gęstości)

3.4.3 Nieuwzględnienie wpływu temperatury otoczenia i ciśnienia atmosferycznego na wyniki pomiarów

3.4.4 Jeżeli ciało jest wyjątkowo nieregularnej budowy, to istnieje możliwość przeoczenia np. bąbelków

powietrza przy zanurzaniu ciała, co bardzo wpływa na pomiar.

4 Wyznaczanie gęstości cieczy na podstawie prawa

Archimedesa

4.1 Do wykonania doświadczenia są potrzebne: ciało stałe, siłomierz, zlewka ze skalą.

4.2 Zawieszamy ciało na siłomierzu i odczytujemy wartość

F

g

siły przyciągania ziemskiego. W dowolny

sposób badamy jego objętość. Nalewamy do zlewki pewną ilość badanej cieczy, oznaczamy jej poziom
przez

V

1

, następnie zanurzamy ciało w badanej cieczy i odczytujemy nowy poziom

V

2

cieczy.

Podstawiamy znane wartości do wzoru:

F

2

=F

g

−V

2

−V

1

 g 

c

. Z tego po prostych

przekształceniach otrzymujemy badane



c

4.3 Przyczyny błędu pomiarowego:

4.3.1 Błąd pomiaru F_g – najmniejsza podziałka na skali siłomierza

4.3.2 Błąd pomiaru objętości ciała – w zależności od metody pomiaru.

5 Wyznaczanie przyśpieszenia ziemskiego z wykorzystaniem

wahadła matematycznego

5.1

6 Tworzenie obrazów rzeczywistych przez soczewkę

skupiającą

6.1

7 Badanie gęstości ciał stałych

7.1 Badanie gęstości ciał stałych sprowadza się do pomiaru ich masy oraz objętości.

7.2 Pomiaru masy można dokonać na dwa sposoby

7.2.1 Pomiar na wadze laboratoryjnej

7.2.1.1 Ustawienie wagi w pionie

7.2.1.2 Wyskalowanie wagi przed pomiarem

7.2.1.3 Przy zablokowanej wadze: ułożenie ciała badanego na jednej szalce (nie wolno dotykać go gołą

skórą, najlepsza jest pęseta lub inne narzędzie) oraz odważnika na drugiej szalce – również nie
należy go dotykać.

7.2.1.4 Zwolnienie blokady wagi. Jeżeli widać, że ramiona wagi są niezrównoważone, to należy

zaobserwować, w którą stronę wychylają się ramiona wagi, po czym ją zablokować. Następnie
należy odpowiednio zmodyfikować zawartość szalki z odważnikami (jeśli była zbyt ciężka, to ulżyć
jej, dołożyć w przeciwnym przypadku), i zwolnić blokadę. Czynność należy powtarzać do momentu
uzyskania równowagi ramion.

7.2.1.5 Zablokować wagę. Odczytać z odważników ich masy nominalne i je zsumować. Jest to masa

badanego ciała.

7.2.1.6 Przyczyny błędu pomiarowego masy:

7.2.1.6.1 Zatłuszczenie badanego ciała, odważników, lub obu naraz.

7.2.1.6.2 Złe wyskalowanie ramion wagi

7.2.1.6.3 Nie ustawienie wagi w pionie przed dokonaniem pomiaru

7.2.1.6.4 Drgania podłoża

7.2.1.6.5 Ponadto niedopuszczalne jest, aby cokolwiek robić przy wadze (np. dokładać

odważników) przy zluzowanej blokadzie!

7.2.2 Pomiar za pomocą siłomierza:

7.2.2.1 Wieszamy badane ciało na siłomierzu. Odczytujemy z niego wartość siły ciężkości działającej

na ciało. Po podzieleniu tej liczby przez wartość przyspieszenia ziemskiego otrzymujemy masę ciała.

7.2.2.2 Przyczyny błędu pomiarowego:

7.2.2.2.1 Kumulatywny błąd paralaksy (kąta odczytu) i drgań przyrządu mierniczego, równy

najmniejszej podziałce na skali siłomierza.

7.2.2.2.2 Ewentualne trwałe odkształcenie sprężyny w siłomierzu, tudzież inne mankamenty

techniczne

7.2.2.2.3 Nieuwzględnienie wpływu położenia geograficznego miejsca pomiaru na wartość

przyśpieszenia ziemskiego (w porównaniu do wartości tablicowej)

7.3 Pomiaru objętości cieczy można dokonać na dwa sposoby:

7.3.1 Jeżeli ciało jest kształtem bliskie matematycznej bryle, to można zmierzyć za pomocą

linijki/suwmiarki/śruby mikrometrycznej odpowiednie wymiary ciała i skorzystać ze wzoru na objętość.

7.3.1.1 Przyczyny błędu pomiarowego:

7.3.1.1.1 Ciało fizyczne nigdy nie ma idealnego kształtu matematycznego, a trudno jest ocenić, jak

duża jest różnica objętości np. geoidy i kuli

7.3.1.1.2 Błąd pomiaru odpowiednich wymiarów bryły, równy najmniejszej podziałce na skali

przyrządu mierniczego

7.3.1.1.3 Błąd paralaksy

7.3.2 Objętość ciała można też wyznaczyć korzystając z prawa Archimedesa przez zanurzenie w cieczy.

Ciało zanurzone wypiera taką objętość cieczy, jaką samo posiada.

7.3.2.1 Przyczyny błędu pomiarowego:

7.3.2.1.1 Kumulatywny błąd odczytu objętości cieczy – pomiaru trzeba dokonać przed i po

zanurzeniu ciała w cieczy, za każdym razem za błąd przyjmując najmniejszą podziałkę na skali
za wielkość błędu pomiarowego.

7.4 Otrzymane wartości należy podstawić do wzoru:

=

m

V

7.4.1 Przyczyny błędu pomiarowego:

7.4.1.1 Kumulatywnie wszystkie powyższe

7.4.1.2 Mała ilość dokonanych pomiarów, co źle wpływa na ich wiarygodność.

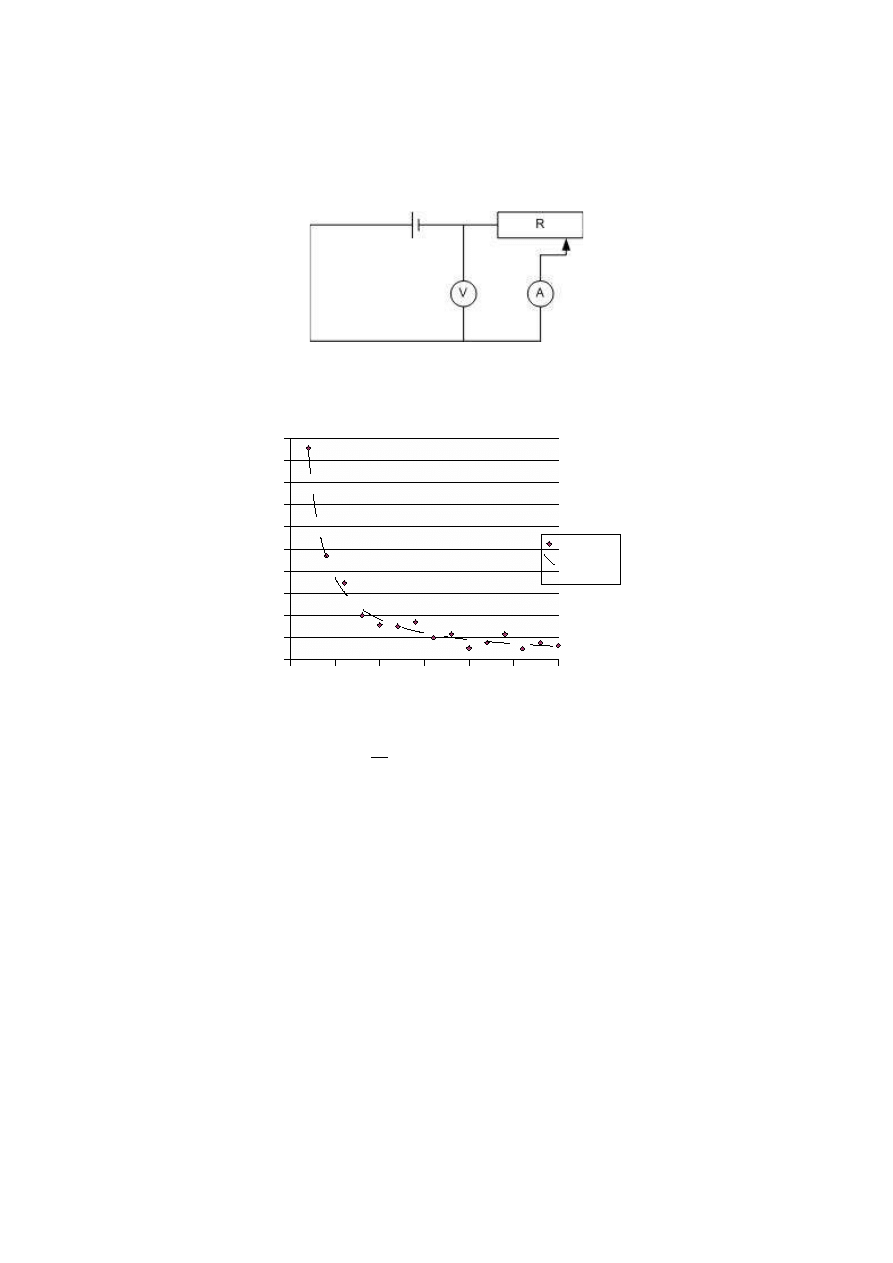
8 Zależność napięcia od natężenia (prawo Ohma)

8.1 Metoda I

8.1.1 Potrzebne: bateria, potencjometr, amperomierz, woltomierz.

8.1.2 Podłączyć następujący układ:

8.1.3 Dokonujemy kilkukrotnego pomiaru napięcia i natężenia prądu przy różnych ustawieniach

potencjometru. Zaznaczamy na wykresie zależność I(R):

8.1.4 Zauważamy, że im większy opór – tym mniejsze natężenie prądu, natomiast napięcie pozostaje stałe.

Zgadza się to z prawem Ohma –

U

I

=R

8.1.5 Źródła błędów:

8.1.5.1 Niedoskonałość użytych materiałów i przyrządów pomiarowych

8.1.5.1.1 Różny materiał, z którego są wykonane przewody

8.1.5.1.2 Różne styki, w tym niektóre mogą być zaśniedziałe

8.1.5.1.3 Bateria nie musi dawać nominalnego napięcia!

8.1.5.1.4 Rozregulowane/uszkodzone amperomierze i woltomierze

8.1.5.1.5 Niemożność dokładnego określenia oporu potencjometra.

8.1.5.2 Błąd paralaksy

8.1.5.3 Mała ilość powtórzenie doświadczenia

8.2 Metoda II

8.2.1 Potrzebne: kilka baterii o takiej samej sile elektromotorycznej, rezystor, amperomierz, woltomierz.

8.2.2 Łączymy podany układ:

0

2,5

5

7,5

10

12,5

15

0

1

2

3

4

5

6

7

8

9

10

Natężenie od oporu przy stałym napięciu

I

Regresja po-
tęgowa, I

Opór

N

at

ęż

en

ie

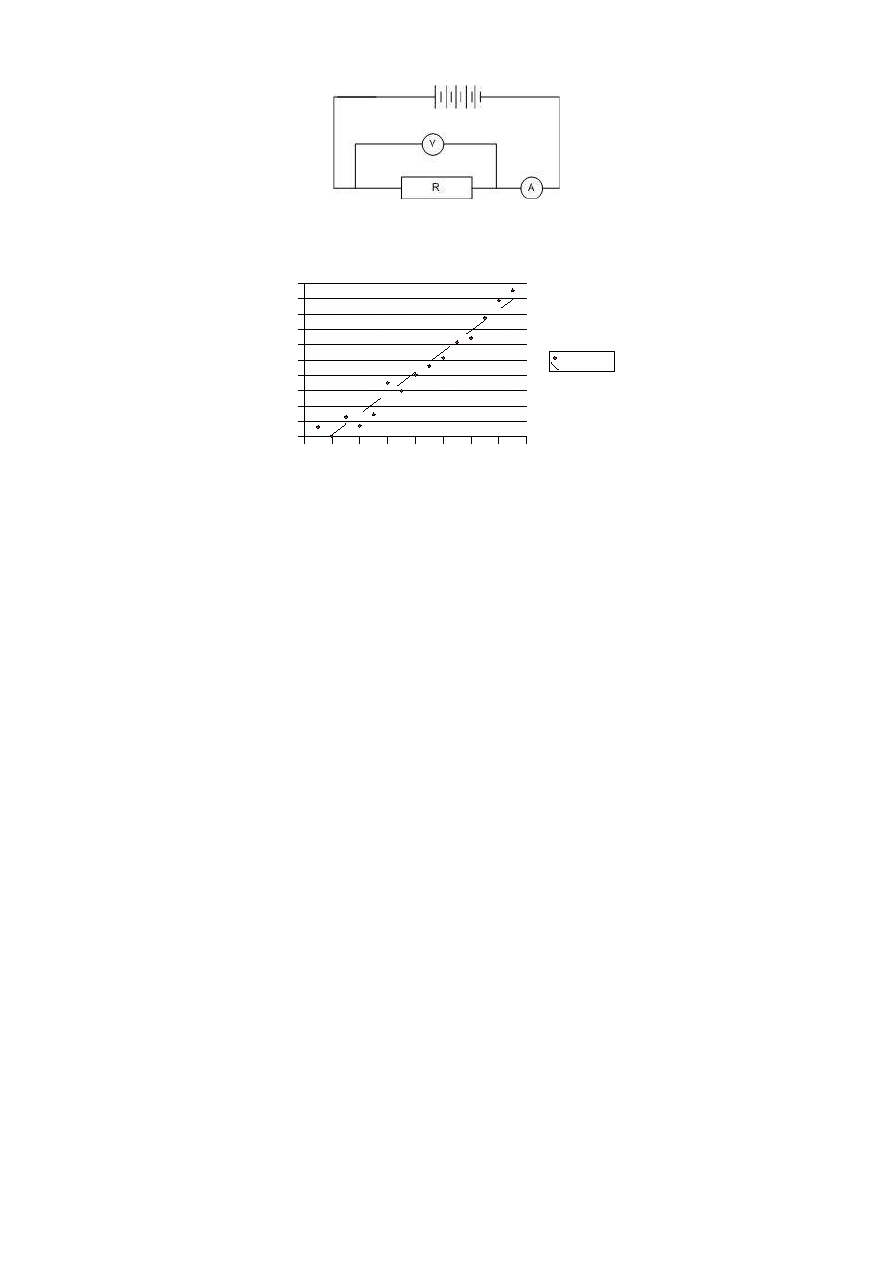
8.2.3 Kolejno dokładamy baterie do układu i odczytujemy wyniki pomiaru. Zauważamy, że przy wzroście

napięcia wzrasta natężenie, a ich stosunek pozostaje stały, co jest potwierdzeniem prawa Ohma:

8.2.4 Przyczyny błędów pomiarowych:

8.2.4.1 Takie same jak w metodzie 1, z wyjątkiem określania oporu potencjometru

0

2

4

6

8

10

12

14

16

0,5

1

1,5

2

2,5

3

3,5

4

4,5

5

5,5

Natężenie od napięcia przy stałym oporze

I
Regresja liniowa, I

Napięcie

N

a

tę

że

n

ie

9 Prawo zachowania ładunku

9.1 Do wykonania doświadczenie potrzebne są: pałka szklana lub ebonitowa, albo elektrofor, elektroskop.

9.2 Prawo zachowania ładunku: W każdym odizolowanym układzie całkowity ładunek jest stały.

9.3 Traktujemy elektroskop jako „układ odizolowany”. Elektryzujemy pałkę lub elektrofor, po czym zbliżamy

ją do elektroskopu. Tym samym powodujemy elektryzację elektroskopu przez indukcję – ładunki ujemne
przesuwają się wewnątrz elektroskopu względem dodatnich, efektem czego jest wychylenie się wskazówki.

9.4 Odsuwamy naelektryzowany przedmiot od elektroskopu, którego listki wracają do pozycji wyjściowej.

9.5 Wniosek – ponieważ nie miał miejsca przepływ ładunku między ciałem naelektryzowanym a

elektroskopem, to suma wszystkich ładunków w tym ostatnim nie uległa zmianie – prawo zachowania
ładunku zostało zachowane.

9.6 Przyczyny błędów pomiarowych:

9.6.1 Doświadczenie nie polega na wyliczeniu konkretnej wartości, a jedynie na udowodnieniu istnienia

danego zjawiska. Nie odbywają się pomiary, nie ma też ich błędów.

10 Indukcja pola magnetycznego wokół przewodnika z

prądem

11 Naczynia połączone i u-rurka

12 Kalorymetr – bilans cieplny

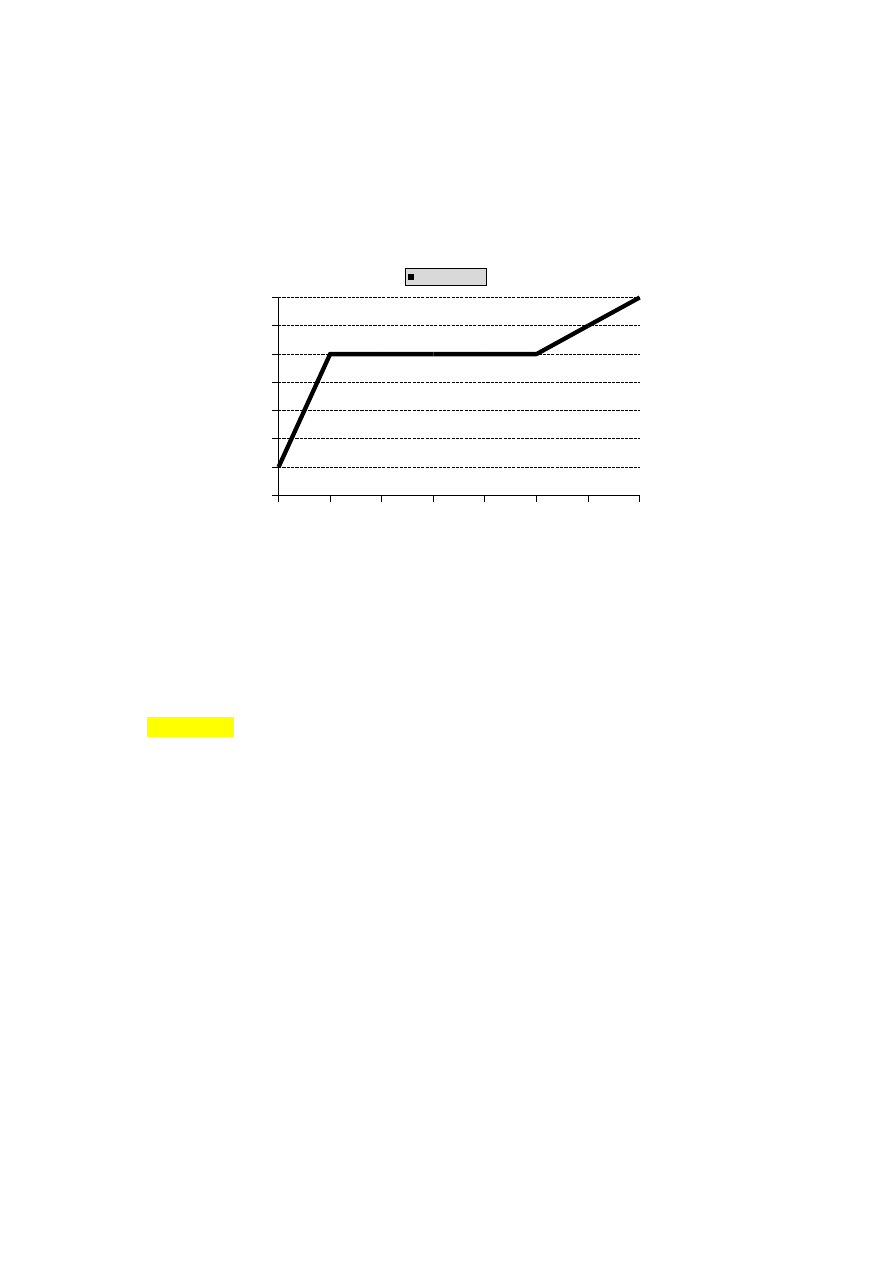
13 Wyznaczyć ciepło topnienia

13.1 Ciało krystaliczne ogrzewamy do temperatury topnienia t

t

. Dalsze ogrzewanie nie

podnosi temperatury ciała, ale powoduje stopniowe topnienie. Dzieje się tak do chwili, kiedy
cała masa zostanie przekształcona w ciecz. Od tej chwili ponownie wzrasta temperatura (już
cieczy).

13.2

13.3 Poziomy fragment krzywej ogrzewania substancji krystalicznej to próg topnienia.

Odpowiada mu pewna ilość ciepła (ciepła topnienia) potrzebna na przeprowadzenie ciała ze
stanu stałego w stan ciekły. Ciepło topnienia q

t

jest to ilość energii, jaką trzeba

doprowadzić do ciała, aby doprowadzić do stopienia jednostki masy substancji stałej o
temperaturze topnienia na ciecz o tej samej temperaturze. Ponieważ podczas topnienia, mimo
doprowadzania ciepła do ciała, jego temperatura nie wzrasta, czasem nazywa się ciepło
topnienia ciepłem utajnionym. Zużyte ono zostaje nie na wzrost energii kinetycznej cząsteczek
(temperatura), ale wykonuje prace związaną z rozluźnianiem wiązań międzycząsteczkowych –
zwiększa energię potencjalną cząstek.

13.4 <równania>
13.5 Przebieg doświadczenia:

13.5.1 Wyznaczyć pojemność cieplną W kalorymetru
13.5.2 Zważyć naczynie środkowe kalorymetru=> m

k

13.5.3 Napełnić naczynie wodą o temperaturze około 30

0

C i zważyć je powtórnie:

m

w

=m−m

k

, m

w

– masa wody,

m

– masa wody i kalorymetru, m

k

– masa

kalorymetru

13.5.4 Odczytać temperaturę t

1

wody, po czym wrzucić starannie osuszone kawałki lodu.

13.5.5 Mieszać do rozpuszczenia całego lodu. Odczytać temperaturę końcową t

2

mieszaniny.

13.5.6 Zważyć całość jeszcze raz. W ten sposób odczytamy wagę lodu: m

2

−m

13.5.7 Podstawić do wzoru i przeprowadzić obliczenia.

Krzywa ogrzewania substancji krystalicznej

temperatura ciała

Q

t

14 Prawo Kirchhoffa

15 Prawo Ampere'a

16 Rozszerzalność cieplna

16.1 Do wykonania doświadczenia potrzebne są: odpowiedni przyrząd z prętem miedzianym, rynienką, skalą i

wskazówką, nafta lub inna płynna substancja palna, iskra.

16.2 Kalibrujemy przyrząd – upewniamy się, że w danej temperaturze wskazówka wskazuje na początek

skali.

16.3 Nalewamy do rynienki substancję palną i zapalamy ją.

16.4 Obserwujemy jak, w miarę spalania się paliwa, wskazówka podnosi się, wskazując na coraz większą

wartość.

16.5 Wniosek z doświadczenia: na wskutek podgrzania pręta metalowego jego długość wzrosła.

16.6 Przyczyny błędu pomiarowego:

16.6.1 W doświadczeniu wykazywane było istnienie zjawiska rozszerzalności cieplnej. Brak błędów

pomiarowych.

16.7 Praktyczne zastosowania zjawiska rozszerzalności cieplnej:

16.7.1 Szyny bezstykowe – kiedy temperatura rośnie, odległości miedzy końcówkami szyn zmniejszają

się. Gdyby szyny były ułożone „na styk”, to latem szyny byłyby wyrywane z łożysk przez naprężenia
wewnętrzne.

16.7.2 Wieszanie przewodów wysokiego napięcia: przewody te są wieszane na dużych wysokościach,

gdyż działa na nie podwójnie wysoka temperatura – raz, energia cieplna otrzymywana w ciepłe dni,
dwa, część energii elektrycznej przesyłanej za ich pomocą jest tracona w postaci ciepła.

17 Badanie ruchu jednostajnie zmiennego

18 Badanie ruchu drgającego

18.1 Przykłady: oscylator harmoniczny (siła sprężyny), wahadło matematyczne (siła grawitacji), wahadło

torsyjne (siła sprężystości materiału)

18.2 Bierzemy wahadło na znanej długości nierozciągliwej liny i o znanej masie. Wychylamy je o niewielki

kąt i badamy okres/częstotliwość. Następnie kolejno zmieniamy długość liny, amplitudy, masę i badamy
jaki ma to wpływ na wynik pomiaru częstotliwości. Wyciągamy właściwe wnioski:

18.2.1 Długość liny rośnie – częstotliwość maleje, okres rośnie

18.2.2 Amplituda rośnie – częstotliwość maleje

18.2.3 Masa rośnie – częstotliwość rośnie

18.3 Opisanie ruchu drgającego: zależność położenia od czasu i sił od czasu

18.4 Opis ruchu drgającego tłumionego (coraz mniejsza amplituda), wymuszonego, zjawiska rezonansu

(pokrycie się częstości siły wymuszającej z częstości drgań wahadła – amplituda rośnie w niekontrolowany
sposób prowadząc ewentualnie do zniszczenia badanego obiektu)

18.5 BONUS: opis złożeń ruchów drgających – można rozpatrywać jako różne oscylatory drgające w różnych

płaszczyznach, np. x(t), y(t), z(t).

19 Badanie gęstości wybranych cieczy

19.1 Patrz: metoda Archimedesa

19.2 ??? Wykorzystanie u-rurki

19.3 Metoda najprostsza:

19.3.1 Ważymy pustą zlewkę. Nalewamy do niej znaną objętość badanej cieczy. Różnica to masa danej

objętości cieczy. Gęstość to masa przez objętość.

19.3.2 Błąd pomiarowy:

19.3.2.1 Błędy przy ważeniu

19.3.2.2 Błąd przy wyznaczaniu objętości cieczy

19.3.2.3 Mała ilość wykonania doświadczenia

20 Badanie zasady działania maszyn prostych

20.1 Proponowane doświadczenia:

20.2 Równia pochyła

20.2.1 Potrzebne: trzy lub cztery równie o różnym kącie nachylenia. Na każdej należy przeprowadzić

badanie ruchu jednostajnie przyśpieszonego z wózkiem kołowym. Zauważyć zależność przyśpieszenia
działającego na ciało w zależności od kąta nachylenia równi (tak, jak cosinus kąta).

20.2.2 Błędy pomiarowe:

20.2.2.1 Tak, jak przy badaniu ruchu jednostajnie zmiennego:

20.2.2.1.1 Błąd pomiaru czasu drogi – najmniejsza podziałka na stoperze+czas reakcji obserwatora

20.2.2.1.2 Błąd pomiaru długości drogi – najmniejsza podziałka na skali linijki

20.2.2.2 Błąd pomiaru kąta nachylenia równi.

20.2.2.3 Mała ilość powtórzeń doświadczenia.

20.3 Dźwignia jednostronna

20.3.1 Potrzebne: siłomierz, odważnik o znanej masie, dźwignia o zmiennej długości ramienia. Za pomocą

siłomierza będziemy unosili ramię dźwigni i odczytywali przyłożoną siłę.

20.3.2 Metoda I

20.3.2.1 Przy stałym punkcie przyłożenia siły ustawiamy odważnik w różnych punktach ramienia i

sprawdzamy, jaka jest potrzebna siła do uniesienia ciała – im dalej od punktu podparcia dźwigni,
tym siła ta jest większa (może być za punktem przyłożenia siłomierza!).

20.3.3 Metoda II

20.3.3.1 Przy stałym punkcie przyłożenia ciężaru ciała – przesuwamy punkt przyłożenia siły. Im dalej

od punktu w którym znajduje się ciało (i od punktu podparcia), tym mniejsza musi być przyłożona
siła.

20.3.4 Various:

20.3.4.1 „Dajcie mi punkt podparcia, a poruszę Ziemię”

20.3.4.2 Zastosowanie: taczka

20.4 Dźwignia dwustronna

20.4.1 Postępowanie identyczne, jak przy dźwignie jednostronnej, tylko, ze siłę należy przyłożyć w dół i

na ramię, na którym nie ma badanego ciała.

20.5 Blok nieruchomy

20.5.1 Bierzemy odważnik i wieszamy na siłomierzu. Otrzymujemy jakąś siłę F. Następnie wieszamy ten

odważnik na bloku nieruchomym i za pomocą siłomierza badamy, jaką siłę trzeba przeciwstawić
grawitacji, aby ciało pozostało w spoczynku. Jest ona równa w przybliżeniu 0,5 F.

20.6 Przekładnia duży blok – mały blok

20.6.1 Na przykład przerzutka w rowerze.

20.6.2 Zasada działania: podczas jednego obrotu dużego bloku, mały wykonuje odpowiednio więcej

obrotów (zależne od stosunku obwodów->promieni).

20.6.3 Cel: w zależności od tego, na które koło działamy siłą, możemy odpowiednio ułatwić, lub utrudnić

wykonanie pewnej zadanej pracy.

20.7 Przyczyny błędów pomiarowych: brak. Doświadczenia polegały na wykazaniu zasady działania.