2008-10-07

1

Pojęcia podstawowe. 

Abstrakcyjne typy danych

Algorytmy i struktury danych

Wykład 1.

Rok akademicki: 2008/2009

2

Ramowy plan wykładów

•

Pojęcie podstawowe. Poprawność i złożoność algorytmów

•

Rekurencja

•

Algorytmy tablicowe

•

Zbiory

•

Tablice asocjacyjne

•

Struktury listowe

•

Drzewa

•

Grafy

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

2

3

Literatura

•

Cormen T., Leiserson C., Rivest R., Stein C., Wprowadzenie do algorytmów, 
Wydawnictwo Naukowo-Techniczne, 2004

•

Lafore R., Java. Algorytmy i struktury danych, Helion, 2004

•

Koffman E., Wolfgang P., Struktury danych i techniki obiektowe na 
przykładzie Javy 5.0, Helion, 2006

•

Wirth N., Algorytmy + struktury danych = programy, dowolne wydanie

•

Sysło M., Algorytmy, Wydawnictwo Szkolne i Pedagogiczne, Warszawa, 
1997

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

4

Informacje organizacyjne

•

Osoby prowadzące: Paweł Lula (wykład), Janusz Sztorc i Wit 
Urban (ćwiczenia)

•

Wymiar godzinowy: 30 + 30

•

Egzamin: pisemny (nie ma zwolnień z egzaminu)

•

Materiały do wykładu: 

http://www.ae.krakow.pl/~lulap

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

3

5

Algorytm

•

sposób postępowania umożliwiający rozwiązanie zadania 
określonego typu

•

podany w postaci zestawu kolejnych czynności do wykonania

•

wykonawcą algorytmu może być człowiek lub urządzenie (np. 
komputer)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

6

Struktura danych

•

Zestaw powiązanych ze sobą danych wraz z mechanizmami
określającymi sposób tworzenia, likwidowania i wykorzystania
zdefiniowanego zestawu jako całości oraz poszczególnych jego
elementów.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

4

7

Program komputerowy

•

zrozumiały dla komputera sposób zapisu algorytmu i opisu 
struktur danych

•

zapisywany przy użyciu języków programowania.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Ewolucja metod programowania (1)

•

Programowanie w języku maszynowym

–

Programista posługuje się pojęciami 
charakterystycznymi dla systemu 
komputerowego, a nie dla dziedziny 
zastosowań (operuje rozkazami 
wchodzącymi w skład listy rozkazów 
procesora)

–

Rozkazy składające się na program 
programista zapisu w postaci binarnych 
kodów

–

Programista operuje bezpośrednio na 
komórkach pamięci operacyjnej. 
Odpowiedzialny jest za określenie sposobu 
binarnej reprezentacji informacji.

8

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

5

Ewolucja metod programowania (2)

•

Programowanie w języku 
symbolicznym (asemblerze)

–

Programista posługuje się rozkazami 
pochodzącymi z listy rozkazów procesora 
(ale są one zapisywane w postaci 
instrukcji, a nie w postaci binarnych 
kodów). 

–

Języki symboliczne wprowadziły zmiany 
w sposobie notacji programu, ale nie 
spowodowały zasadniczych zmian w 
zestawie pojęć wykorzystywanych do 
opisu algorytmów.

–

Pojawiła się możliwość przypisywania 
nazw komórkom pamięci (definiowanie 
zmiennych)

9

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Ewolucja metod programowania (3)

•

Programowanie w językach wysokiego 

poziomu I generacji

–

Pojawiła się możliwość stosowania instrukcji:

•

podstawienia (przypisania), 

•

warunkowej, 

•

pętli (iteracji), 

•

skoku. 

–

Przy opisie algorytmy następuje rezygnacja ze 

stosowania rozkazów z listy rozkazów 

procesora i pojawia się możliwość stosowania 

pojęć o znacznie większym stopniu ogólności. 

–

Wprowadzenie mechanizmu deklarowania 
zmiennych

–

Ułatwione zostało operowanie na 
wartościach tekstowych

–

Pojawiła się możliwość korzystania ze 
złożonych typów danych (tablice, pliki)

10

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

6

Ewolucja metod programowania (4)

•

Programowanie proceduralne

–

Możliwość definiowania podprogramów.

–

Zdefiniowanie nowego podprogramu 
pozwala na rozszerzenie zbioru instrukcji 
dostępnych w stosowanym języku 
programowania.

–

Mechanizm parametrów zwiększył 
uniwersalność definiowanych instrukcji.

–

Pojawiła się możliwość definiowania danych 
lokalnych (dostępnych tylko w 
podprogramie) oraz danych globalnych 
(dostępnych w całym programie)

11

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Ewolucja metod programowania (5)

•

Programowanie strukturalne

–

Zwiększenie liczby instrukcji sterujących 
(np.: różne postaci pętli, instrukcji 
warunkowych, wyboru, podstawienia) –
dzięki czemu można było wyeliminować 
instrukcję skoku bezwarunkowego

–

Podział programu na dwie części: opis 
struktur danych i opis algorytmu

–

Zwiększenie liczby dostępnych typów 
danych (tablice, rekordy, zbiory, pliki),

–

Możliwość stosowania dynamicznych 
struktur danych (stos, kolejka, listy, drzewa),

–

Możliwość definiowania własnych struktur 
danych.

12

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

7

Ewolucja metod programowania (6)

Programowanie obiektowe

•

Równoległe definiowanie algorytmów i 
struktur danych i ich połączenie w jedną całość
(klasę):

–

reprezentuje w programie fragment rzeczywistości 
(jego cechy, jego zachowania),

–

pozwala programiście posługiwać się pojęciami 
charakterystycznymi dla dziedziny problemu 
(oderwać się od pojęć związanych ze sprzętem 
komputerowym),

–

pozwala ukryć szczegóły implementacji

•

klasa – abstrakcyjny typ danych 
(ABSTRAHOWANIE  - operacja myślowa 
polegająca na uwzględnianiu tylko wybranych 
cech sytuacji (przedmiotu, osoby), z 
pominięciem cech uznanych za nieistotne) 

13

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Interfejs jako kolejny poziom abstrahowania

•

Klasa:

–

reprezentuje obiekt rzeczywisty (koło, kwadrat, prostokąt),

–

charakteryzuje jego cechy (pola),

–

opisuje czynności (metody)

•

Interfejs:

–

reprezentuje obiekt abstrakcyjny (figura posiadająca środek symetrii),

–

wskazuje czynności charakterystyczne dla obiektu (ale ich nie 
implementuje)

•

interfejs – abstrakcyjny typ danych, poziom abstrakcji wyższy 
niż w przypadku klasy.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

14

2008-10-07

8

15

Interfejsy (1)

•

Interfejs - zbiór nagłówków metod i definicji stałych.

–

nagłówki metod - określają sposób ich wywoływania, nie określają 
sposobu ich implementacji (określamy co można zrobić, ale nie 
mówimy jak to zrobić),

–

stałe - określają wartości cech, które nie ulegają zmianie (stałe są 
definiowane jako pola publiczne, statyczne i finalne).

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

16

Interfejsy (2)

•

Definicja interfejsu:

interface NazwaInterfejsu [extends
nazwyInterfejsów] {

nagłówki metod

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

9

17

Przykład interfejsu

interface OperacjeGraficzne {

void rysowanie();

void usuwanie();

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

18

Implementacja interfejsu

•

Definicja metod umieszczonych w interfejsach umieszczana 
jest w klasach implementujących dany interfejs.

•

... class nazwaKlasy extends ... implements ListaInterfejsów

•

klasa implementująca interfejs musi zawierać definicje 
wszystkich metod zadeklarowanych w interfejsie (w 
przeciwnym przypadku staje się klasą abstrakcyjną)

•

klasa może implementować wiele interfejsów

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

10

19

Zastosowanie interfejsów

•

wskazuje na właściwości pewnego abstrakcyjnego pojęcia

•

definiowanie związków pomiędzy klasami - wszystkie klasy 
implementujące interfejs posiadają wspólne właściwości 
(mogą realizować operacje określone w interfejsie)

•

nazwa interfejsu może funkcjonować jako nazwa typu

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

20

Przykład (1)

interface ZdolnyDoLotu {

void jestemWPowietrzu();

}

abstract class Zwierze {
}

class ZwierzeLadowe extends Zwierze {
}

class ZwierzeWodne extends Zwierze {
}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

11

21

Przykład (2)

class Ptak extends Zwierze implements ZdolnyDoLotu {

public void jestemWPowietrzu()

{

System.out.println("Lecacy ptak");

}

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

22

Przykład (3)

abstract class Pojazd {

}

class Statek extends Pojazd {

}

class Samochod extends Pojazd {

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

12

23

Przykład (4)

class Samolot extends Pojazd implements ZdolnyDoLotu {

public void jestemWPowietrzu()

{

System.out.println("Lecacy samolot");

}

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

24

Przykład (5)

public class Lot {

public static void wzbijaSieWPowietrze(ZdolnyDoLotu obiektLatajacy) {

obiektLatajacy.jestemWPowietrzu();

}

public static void main(String [] args)
{

Ptak p = new Ptak();
Samolot s = new Samolot();

wzbijaSieWPowietrze(p);
wzbijaSieWPowietrze(s);

}

} 

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

13

Wymagania wobec algorytmów

•

poprawność – algorytm generuje prawidłowe rezultaty (nie 
zawiera błędów),

•

wydajność – realizacja algorytmu wymaga użycia 
akceptowalnej ilości zasobów:

–

czasu,

–

pamięci.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

25

26

Pojęcie błędu

•

niezgodność z obowiązującymi regułami pisania, liczenia, 
wymowy itp.; odstępstwo od normy; pomyłka

•

postępek, działanie, które przynosi komuś złe skutki; 
niewłaściwe posunięcie, przedsięwzięcie

•

mylne, fałszywe mniemanie o czymś (przestarz.)

Źródło: Słownik języka polskiego PWN

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

14

27

Błędy w programowaniu

•

błędy logiczne – na etapie projektowania algorytmu (środki 
zaradcze: stosowanie sprawdzonych algorytmów, formalne 
dowodzenie poprawności algorytmu, testowanie programu)

•

błędy wykonania programu – ujawniające się w trakcie 
realizacji algorytmu zapisanego w postaci programu 
(ujawniające się w postaci wyjątków)

•

błędy syntaktyczne – polegające na niezgodności tekstu 
programu z gramatyką języka programowania (wykrywane 
przez kompilator)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

28

Złożoność obliczeniowa

•

Złożoność obliczeniowa algorytmu – ilość zasobów systemu 
komputerowego niezbędnych do jego realizacji.

•

Zasoby systemu komputerowego niezbędne do realizacji 
algorytmu:

–

czas pracy procesora (złożoność czasowa algorytmu),

–

pamięć operacyjna (złożoność pamięciowa algorytmu).

•

Złożoność obliczeniowa jest uzależniona od wielkości zadania.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

15

29

Sortowania przez wybieranie (1)

import java.io.*;

public class SortowaniePrzezWybieranie {

static void sortuj(int [] liczby) {

int k, pomoc;
for (int i = 0; i < liczby.length - 1; i++) {

k = i;
for (int j = i; j < liczby.length; j++)

if (liczby[k] > liczby[j])

k = j;

pomoc = liczby[i];
liczby[i] = liczby[k];
liczby[k] = pomoc;

}

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

30

Sortowania przez wybieranie (2)

static int czytajLiczbe() throws IOException 

{

BufferedReader klaw = new BufferedReader (new 

InputStreamReader (System.in));

return Integer.parseInt(klaw.readLine());

}

static void drukujWektor(int [] tab) {

for (int i = 0; i < tab.length; i++)

System.out.print(tab[i] + "  ");

System.out.print("\n");

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

16

31

Sortowania przez wybieranie (3)

public static void main(String [] args) throws IOException {

System.out.print("Liczba elementow w wektorze: ");
int n = czytajLiczbe();

int [] wektor = new int[n];

for (int i = 0; i < wektor.length; i++)

wektor[i] = (int) (100 * Math.random());

long czas1, czas2;
czas1 = System.currentTimeMillis();
// czas w milisekundach, jaki upłynął od 
// 1 stycznia 1970 roku, godz. 0:00

sortuj(wektor);
czas2 = System.currentTimeMillis();
System.out.println("Czas realizacji obliczen: " + (czas2 - czas1));

}

}

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

32

Sortowania przez wybieranie (4)

Rezultat działania programu:

Liczba elementow w wektorze: 10000

Czas realizacji obliczen: 250

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

17

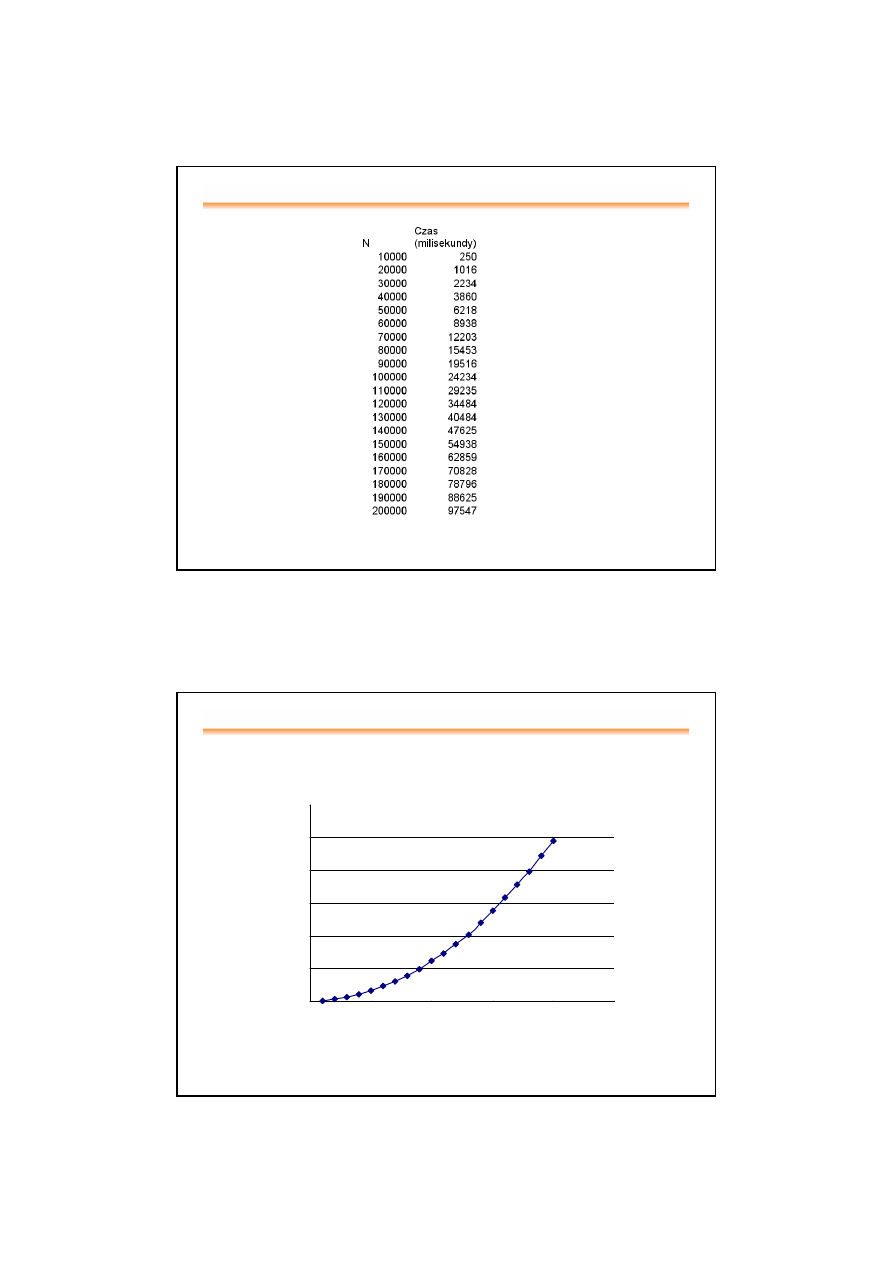
33

Czas realizacji algorytmu (1)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

34

Czas realizacji algorytmu (2)

Czas (milisekundy)

0

20000

40000

60000

80000

100000

120000

0

50000

100000

150000

200000

250000

y = 0,000002 n

2

– 0,0094 n + 286,41

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

18

Oszacowanie czasu realizacji algorytmu (1)

35

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Oszacowanie czasu realizacji algorytmu (2)

•

Analiza powyższych danych pozwala stwierdzić, że czas 
obliczeń uzależniony jest przede wszystkim od składnika:

0,000002 n

2

Składnik ten nazywany jest składnikiem dominującym.

•

Po pominięciu stałych współczynników można stwierdzić, że 
zależność pomiędzy czasem wykonania a wielkością zadania 
ma charakter funkcji kwadratowej. Kwadratowy charakter 
zależności uwidacznia się w coraz większym stopniu wraz ze 
wzrostem wielkości zadania.

36

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

19

Cechy empirycznego określania złożoności

•

Zalety:

–

otrzymane czasy obliczeń są proste w interpretacji

•

Wady:

–

konieczność wielokrotnego uruchamiania programu (dla złożonych algorytmów 
może to być bardzo czasochłonne),

–

uzyskane wyniki dotyczą zastosowanego w obliczeniach zestawu danych (trudno 
jest określić czas realizacji dla przypadku „najlepszego”, najgorszego” oraz 
„przeciętnego”),

–

wyniki dotyczą zwykle stosunkowo niewielkich zbiorów danych – nie wiadomo, czy 
dla zbiorów o większym rozmiarze charakter zależności się nie zmieni,

–

czas jest uzależniony od szybkości i architektury komputera, języka programowanie, 
techniki translacji, systemu operacyjnego – trudna porównywalność wyników

–

z uwagi na wielozadaniowy charakter systemów operacyjnych trudno jest określić, 
jaka część czasu była rzeczywiście przeznaczona na realizację analizowanego 
programu.

37

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

38

Bezpośrednia analiza algorytmów

Analiza dotyczy:

•

charakteru zależności (np. zależność liniowa lub kwadratowa), a nie jej 
dokładnej postaci (wzór funkcji) – uwzględniany jest element dominujący, 
pomijane są współczynniki stałe

•

górnego i dolnego ograniczenia czasu realizacji algorytmu (a nie czasu 
realizacji algorytmu)

–

górne ograniczenie – czas realizacji algorytmu jest nie większy niż ... 
(ale może być krótszy) – przypadek pesymistyczny,

–

dolne ograniczenie – czas realizacji algorytmu jest nie mniejszy niż ... 
(ale może być dłuższy) – przypadek optymistyczny,

•

zachowania się algorytmu dla zbiorów danych o dużej wielkości (czyli dla 
wszystkich n większych od pewnej wartości n

0

)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

20

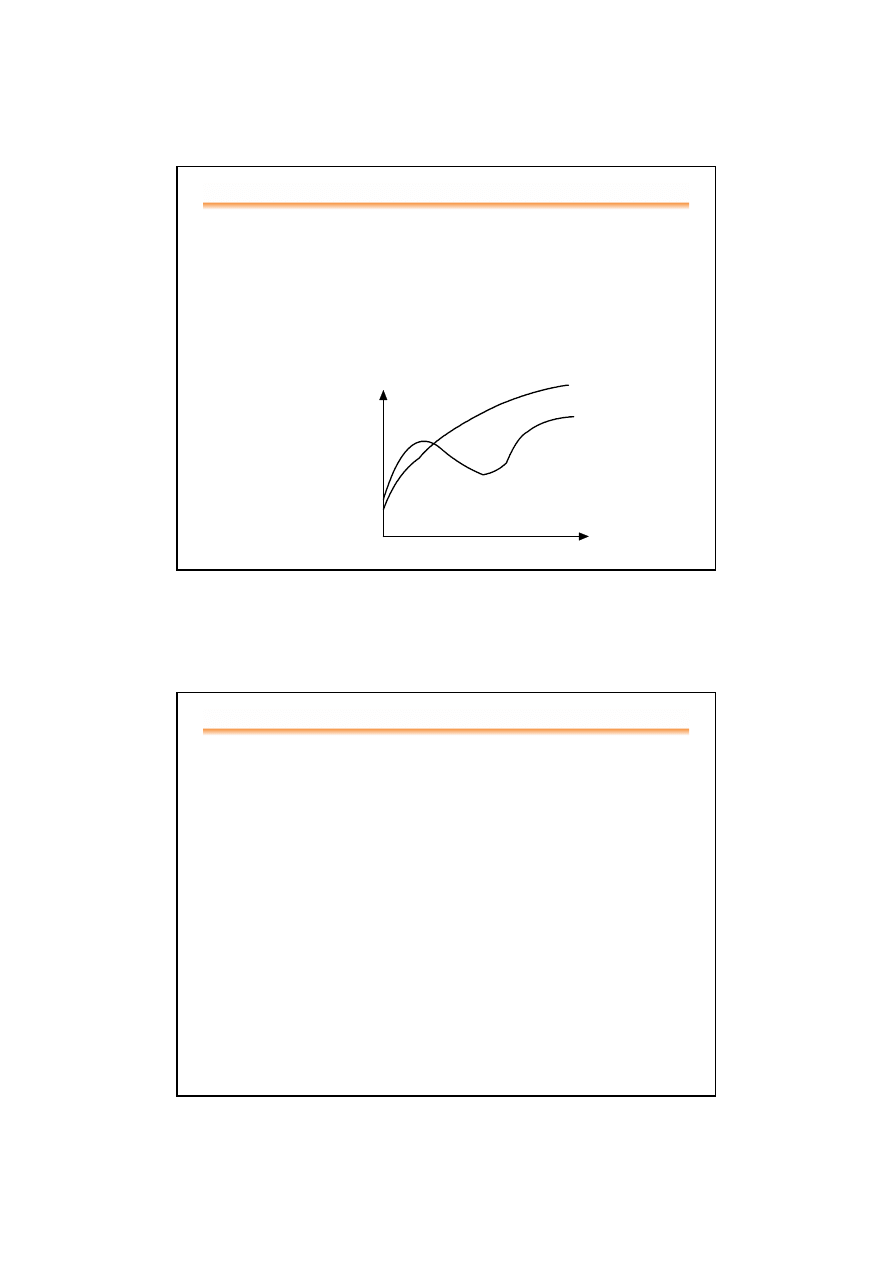
Górne ograniczenie czasu realizacji algorytmu (1)

•

f(n) – czas realizacji algorytmu (zależny od n)

•

f(n) zależy od wielu czynników i podanie dokładnego 
charakteru zależności jest trudne

•

łatwiej jest zdefiniować ograniczenie górne dla f(n).

39

f(n)

n

c g(n)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Górne ograniczenie czasu realizacji algorytmu (2)

•

Czas realizacji algorytmu jest rzędu co najwyżej g(n), jeśli 
istnieją stała rzeczywista c > 0 i stała naturalna n

0

takie, że 

nierówność f(n) ≤ c g(n) zachodzi dla każdego n ≥ n

0

.

•

Zbiór wszystkich funkcji f(n) spełniających powyższe 
ograniczenie określany jest jako O(g(n)).

•

O(g(n)) = {f(n): istnieją dodatnie stałe c oraz n

0

takie, że 0 ≤ 

f(n) ≤ c g(n) dla wszystkich n ≥ n

0

}

40

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

21

Górne ograniczenie czasu realizacji algorytmu (3)

Stwierdzenie:

czas realizacji algorytmu wynosi O(g(n))

lub

czas realizacji algorytmu jest rzędu co najwyżej g(n)

lub

algorytm jest klasy O(g(n))

oznacza: że istnieje taka stała c, że dla n ≥ n

0

czas realizacji 

algorytmu wynosi co najwyżej c g(n).

41

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Dolne ograniczenie czasu realizacji algorytmu (4)

•

Czas realizacji algorytmu jest rzędu co najmniej g(n), jeśli istnieją stała 
rzeczywista c > 0 i stała naturalna n

0

takie, że nierówność f(n) ≥ c g(n)

zachodzi dla każdego n ≥ n

0

.

•

Zbiór wszystkich funkcji spełniających to ograniczenie określany jest jako 
Ω(g(n))

•

Ω(g(n)) = {f(n): istnieją dodatnie stałe c i n

0

takie, że 0 ≤ cg(n) ≤ f(n) dla 

wszystkich n ≥ n

0

}

42

f(n)

n

c g(n)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

22

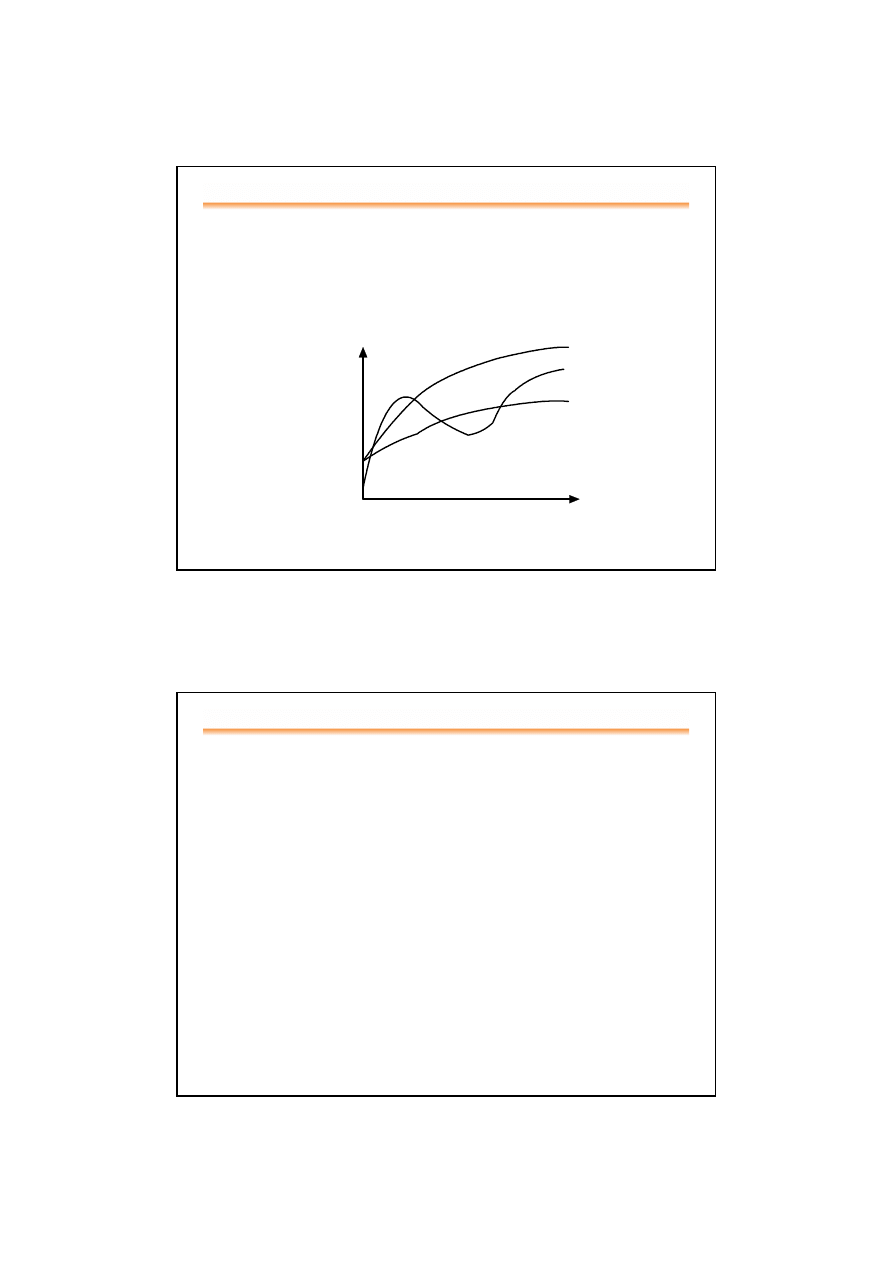
Dolne i górne ograniczenie czasu realizacji algorytmu (1) 

•

Czas realizacji algorytmu jest dokładnie rzędu g(n) jeśli istnieją 
stała rzeczywista c

1

> 0, c

2

> 0 i stała naturalna n

0

takie, że 

nierówność  c

1

g(n) ≤ f(n) ≤ c

2

g(n) zachodzi dla każdego n ≥ n

0

.

43

f(n)

n

c

1

g(n)

c

2

g(n)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Dolne i górne ograniczenie czasu realizacji algorytmu (2)

•

Zbiór wszystkich funkcji spełniających to ograniczenie 
określany jest jako Θ(g(n))

•

Θ(g(n)) = {f(n); istnieją dodatnie stałe c

1

, c

2

i n

0

takie, że 0 ≤ c

1

g(n) ≤ f(n) ≤ c

2

g(n) dla wszystkich n ≥ n

0

}

44

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

23

45

Średnia złożoność obliczeniowa

•

Średnia złożoność czasowa uwzględnia prawdopodobieństwa 
pojawienia się każdego możliwego zestawu danych 
wejściowych

•

Z

i

(n) – i-ty możliwy zestaw danych n-elementowy

•

p

i

– prawdopodobieństwo wystąpienia i-tego zestawu

•

T

i

(n) – złożoność czasowa algorytmu dla i-tego zestawu 

danych

•

Średnia złożoność czasowa algorytmu dana jest formułą:

( )

( )

∑

=

i

i

i

ś

r

n

T

p

n

T

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Złożoność obliczenia sortowania przez wybieranie (1)

static void sortuj(int [] liczby) {

int k, pomoc;
for (int i = 0; i < liczby.length - 1; i++) {

//koszt K1
k = i;

for (int j = i; j < liczby.length; j++)

//koszt K2
if (liczby[k] > liczby[j])

k = j;

//koszt K3
pomoc = liczby[i];
liczby[i] = liczby[k];
liczby[k] = pomoc;

}

}

46

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

24

Złożoność obliczenia sortowania przez wybieranie (2)

for (int i = 0; i < n - 1; i++)
{

K1

for (int j = i; j < n; j++)
{

K2

}

K3

}

47

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

Złożoność obliczenia sortowania przez wybieranie (3)

for (int i = 0; i < n - 1; i++)

{

K1

(n – 1) * K2

K3

}

48

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

25

Złożoność obliczenia sortowania przez wybieranie (4)

(n – 1) * K1 + (n – 1) [n * K2 + (n-1) * K2 + ... + 2 * K2] + (n – 1) 
* K3 =

= n * K1 – K1 + [½ * (2 + n) * (n – 1) * K2] + n * K3 – K3 =

= n * K1 – K1 + n * K2 – K2 + ½ * n

2

* K2 – ½ * n * K2 + n * K3 –

K3 =

= ½ * K2 * n

2

+ (K1 + ½ * K2 + K3) * n – (K1 + K2 + K3) = O(n

2

)

49

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

50

Rodzaje złożoności (1)

•

Złożoność logarytmiczna – log n

•

W każdym kroku algorytmu zadanie o rozmiarze n jest 
sprowadzane do zadania o rozmiarze n / 2

•

Przykład:

•

algorytm wyszukiwania binarnego jest klasy O(log n)

•

Przykładowa realizacja wyszukiwania binarnego: Mamy 
odszukać wartość 11 w ciągu liczb:

1, 2, 7, 9, 9, 11, 12, 15, 22, 34, 52, 67, 87, 90, 99

1, 2, 7, 9, 9, 11, 12

9, 11, 12

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

26

51

Rodzaje złożoności (2)

•

Złożoność liniowa – n

•

gdy dla każdego elementu pochodzącego z n – elementowego 
zbioru danych wykonywana jest stała liczba operacji

•

Przykłady:

–

wyszukiwanie sekwencyjne

–

sumowanie liczb w wektorze

–

wyznaczanie minimum, maksimum

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

52

Rodzaje złożoności (3)

•

złożoność liniowo – logarytmiczna – n log n

•

gdy w każdym kroku zadanie o rozmiarze n jest sprowadzane 
do dwóch zadań o rozmiarze n/2, a uzyskane wyniki są 
ponownie scalane 

•

Przykład:

–

sortowanie przez łączenie jest klasy O(n log n)

–

sortowanie szybkie – jest klasy O(n

2

), ale przeciętny czas 

realizacji algorytmu jest rzędu n log n

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

27

53

Rodzaje złożoności (4)

•

złożoność kwadratowa – n

2

•

gdy dla każdej pary elementów realizowana jest pewna, stała 
liczba operacji (zwykle algorytmy takie są zapisywane za 
pomocą dwóch zagnieżdżonych pętli for)

•

Przykłady:

–

proste metody sortowania (przez wstawianie, wybieranie, bąbelkowe) 
są klasy O(n

2

), również średni czas realizacji tych metod jest rzędu 

O(n

2

)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

54

Rodzaje złożoności (5)

•

złożoność wielomianowa stopnia wyższego niż dwa (n

3

, n

4

, 

...)

•

Przykład:

•

mnożenie macierzy w sposób tradycyjny jest algorytmem 
klasy O(n

3

)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

28

55

Rodzaje złożoności (6)

•

Złożoność wykładnicza postaci 2

n

•

gdy realizowanych jest n kroków, a liczba operacji w każdym z 
nich wzrasta w sposób geometryczny

•

Przykład:

–

wieże Hanoi

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

56

Rodzaje złożoności (7)

•

Złożoność wykładnicza typu n!

•

gdy pewna, stała liczba operacji realizowana jest dla każdej 
permutacji n elementów 

•

Przykład:

•

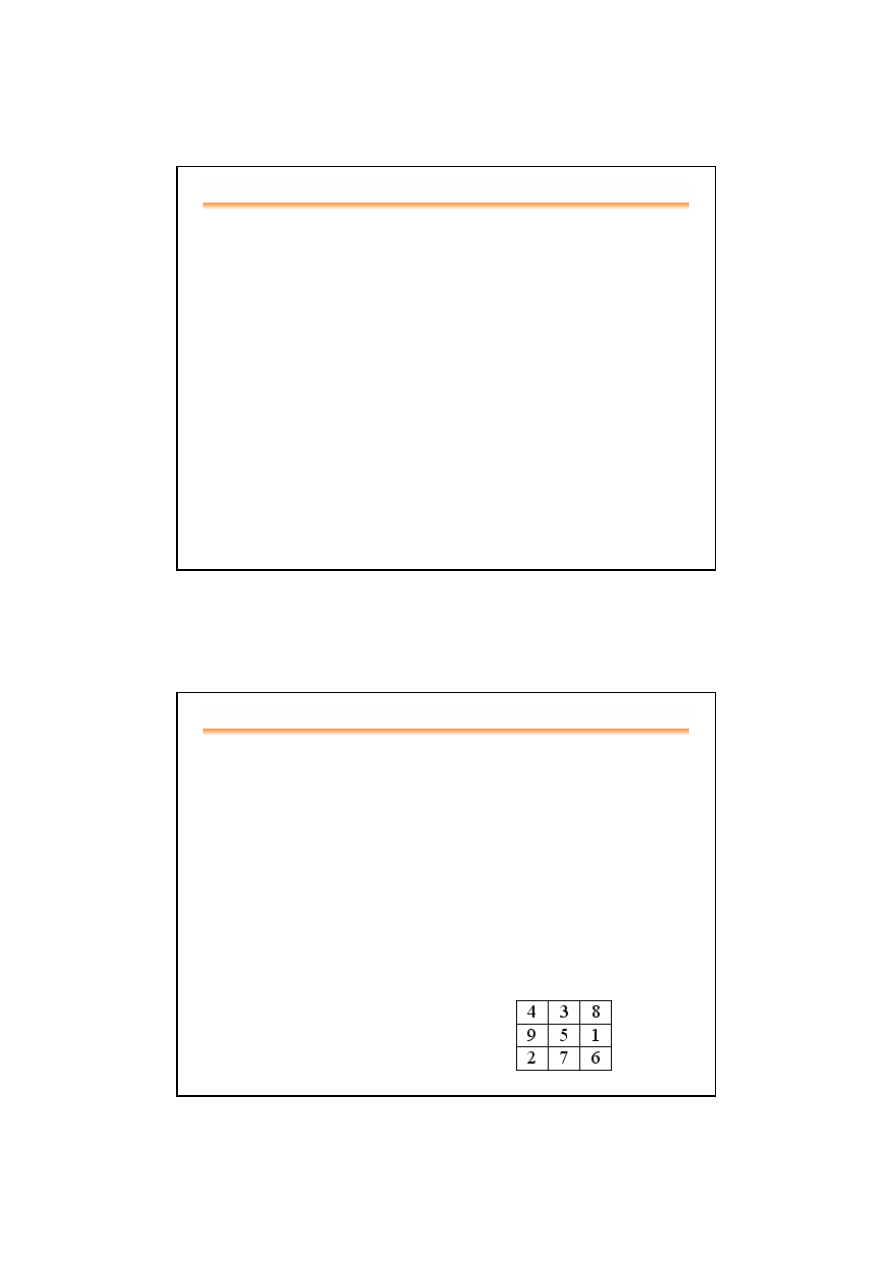
Tworzenie magicznych kwadratów z n elementów (pierwiastek 
z n musi być wartością całkowitą)

•

Algorytm postępowania: tworzymy kolejną permutację, 
wpisujemy do kwadratu i sprawdzamy, czy spełnia konieczne 
warunki.

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie

2008-10-07

29

57

Rodzaje złożoności (8)

Paweł Lula, Katedra Systemów Obliczeniowych, Uniwersytet Ekonomiczny w Krakowie