Podstawowe struktury danych

1) Listy

Lista to skończony ciąg elementów: q=[x

1

, x

2

, ... , x

n

].

Skrajne elementy x

1

i x

n

nazywamy końcami listy, a

wielkość |q| = n długością (rozmiarem) listy.
Szczególnym przypadkiem jest lista pusta: q = [ ].

Podstawowe abstrakcyjne operacje na listach
q =[x

1

, x

2

, ... , x

n

] i r =[y

1

, y

2

, ... , y

m

] dla 1

≤ i ≤ j ≤ n to:

• dostęp do elementu listy - q[i] = x

i

;

• podlista - q[i..j] = [x

i

, x

i+1

, ... , x

j

] ;

• złożenie - q&r = [x

1

, ... , x

n

, y

1

, ... ,y

m

] ;

Na podstawie operacji podstawowych można zdefiniować
inne operacje, np. wstawianie elementu x za element x

i

, na

liście q: q[1..i] & [x] & q[i+1 .. |q| ].

W operacjach na listach ograniczamy się zwykle do zmian
ich końców:
a)

front(q)

= q[1] - pobierz lewy koniec listy

b)

push(q,x)

= [x]&q - wstaw element na lewy koniec

c)

pop(q)

=q[2..|q| ] - usuń bieżący lewy koniec

d)

rear(q)

= q[|q|] - pobierz prawy koniec listy

e)

inject(q,x)

=q&[x] -wstaw element na prawy koniec

f)

eject(q)

=q[1..|q|-1 ] - usuń bieżący prawy koniec

W zależności od możliwości wykonania różnych operacji
wyróżniemy:
•

kolejkę podwójną

- wszystkie sześć operacji

•

stos

- tylko operacje front, push, pop

•

kolejkę

- tylko operacje front, pop , inject

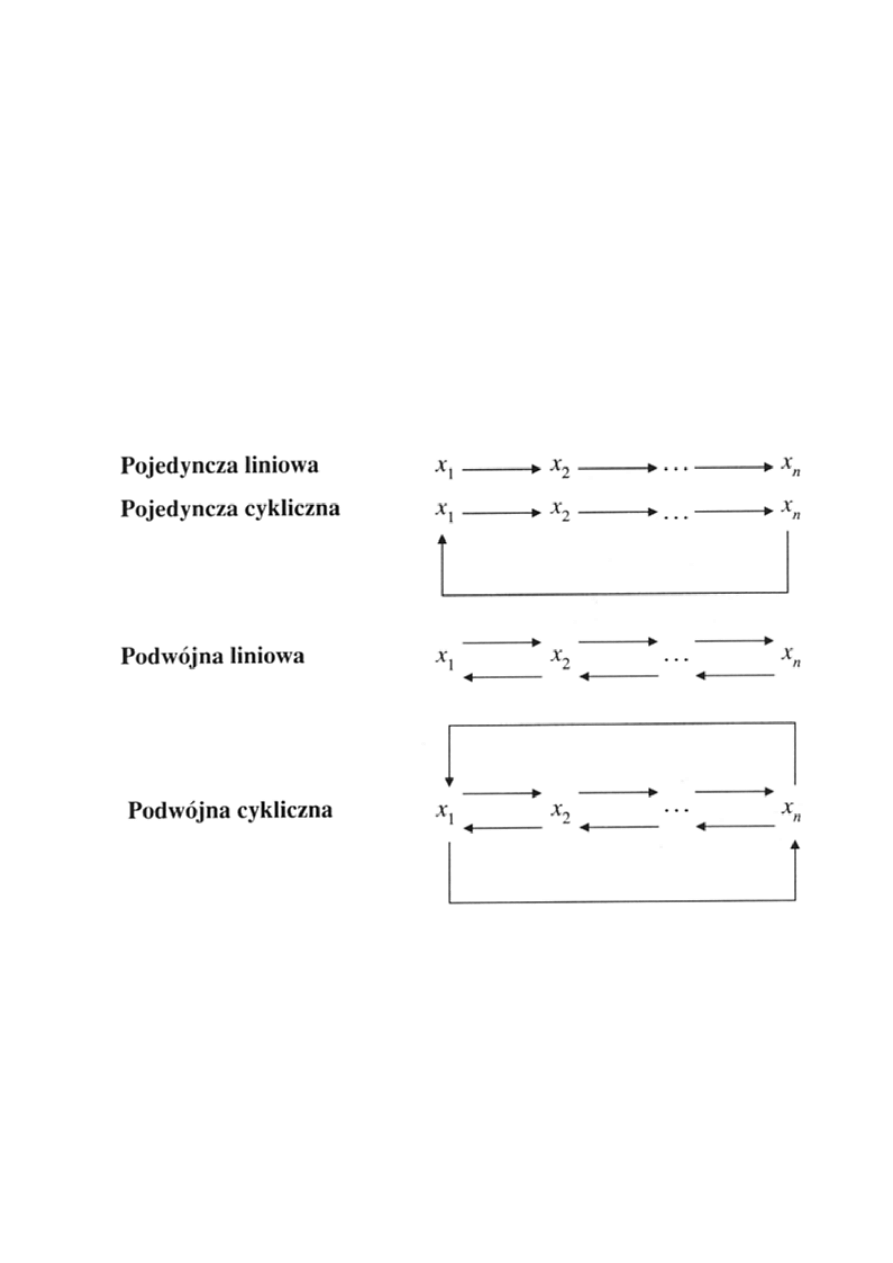
Dwie podstawowe implementacje (reprezentacje) listy
q =[x

1

, x

2

, ... , x

n

] to:

• tablicowa - q[i] = x

i

, gdzie 1

≤

i

≤

n,

• dowiązaniowa

W implementacjach pojedynczej liniowej i podwójnej
liniowej dowiązanie prowadzące do listy wskazuje na
pierwszy element na liście.

W implementacji pojedynczej cyklicznej i podwójnej
cyklicznej dowiązanie prowadzące do listy wskazuje na
element ostatni.

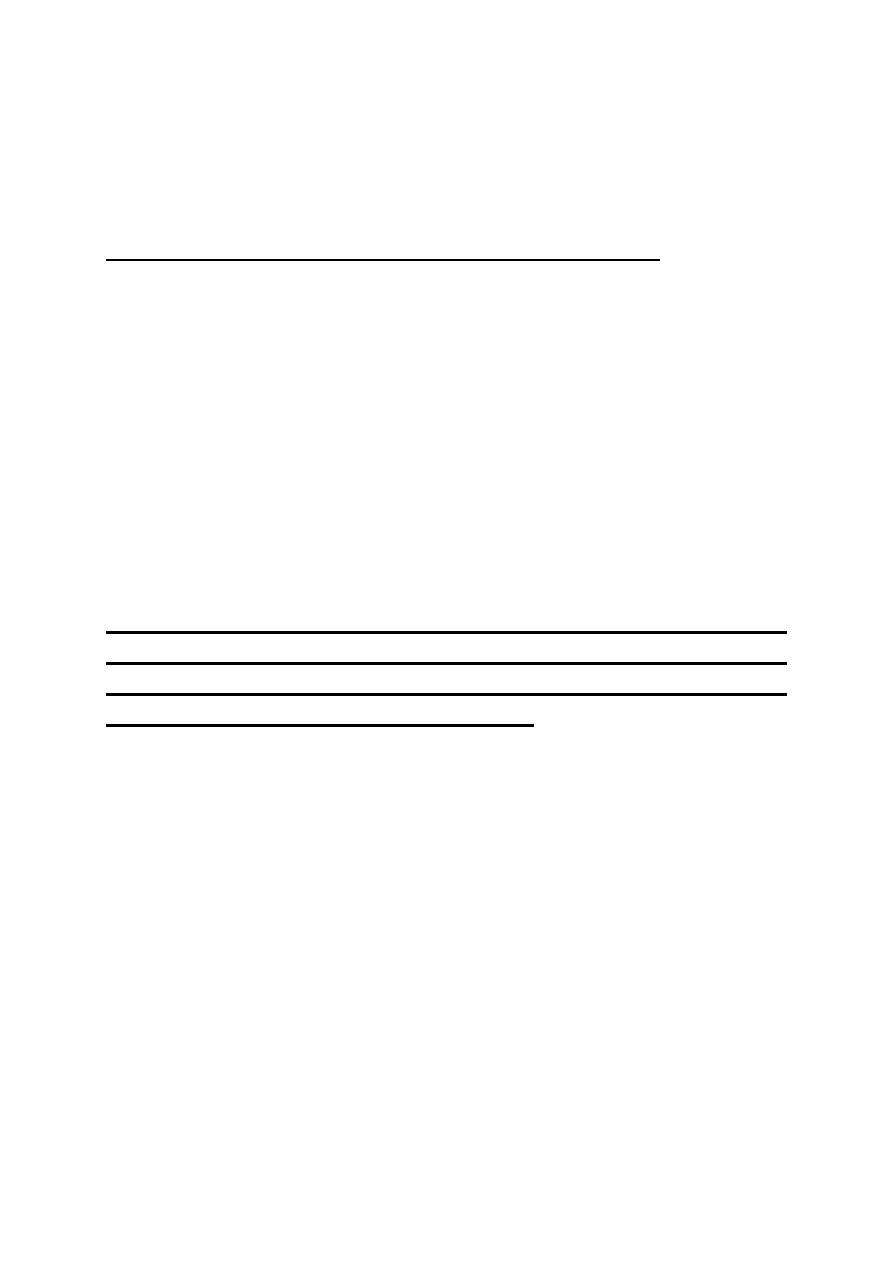
Aby dowiązana struktura nigdy nie była pusta dodaje się
na początku listy element pusty zwany

GŁOWĄ

lub

WARTOWNIKIEM

listy.

Operacje na listach o stałej złożoności czasowej:
a) w implementacji pojedynczej liniowej: operacje stosu,

wstawianie jednego elementu za drugi, usuwanie
następnego elementu,

b) w implementacji pojedynczej cyklicznej: te co w a) oraz

złożenie i operacje rear i inject,

c) w implementacji podwójnej cyklicznej: te co w b) oraz

eject, wstawianie jednego elementu przed drugim,
wstawianie danego elementu, odwracanie listy.

LISTY JEDNOKIERUNKOWE

Lista jednokierunkowa jest oszczędną pamięciowo
strukturą danych, pozwalającą grupować dowolną -
ograniczoną tylko ilością dostępnej pamięci - liczbę
elementów: liczb, znaków, rekordów.

Do budowy listy używane są dwa typy rekordów:
-

informacyjny

- wskaźniki, dowiązania do początku listy

(głowa) i końca listy (ogon)

-

robocze

- pole wartości i wskaźnik do następnego

elementu listy

Dzięki rekordowi informacyjnemu mamy ciągły dostęp do
niektórych operacji, np. dołączanie elementu na koniec
listy.

Głowa, ogon i następny

to wskaźniki,

wartość

to dowolna

wielkość (znanego typu).

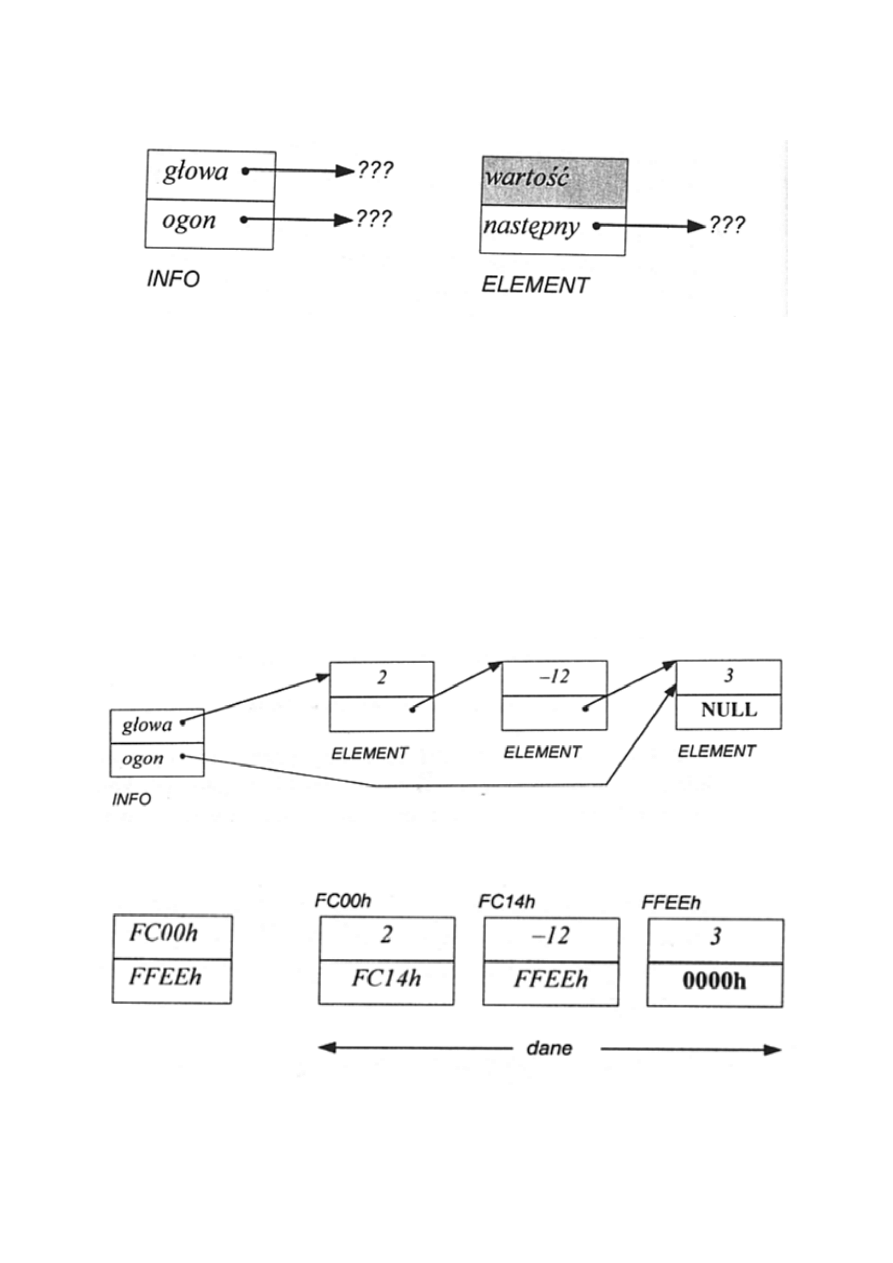
Wskaźniki NULL oznaczają adresy pamięci pod którymi
nie ma żadnej zmiennej.

Przykład listy jednokierunkowej:

Pola głowa i ogon pozwalają na przeglądanie elementów
listy i dołączanie nowych elementów.

Przykład (pseudokod) przeglądania elementów listy:
_________________________________________________
adres_tmp=info.głowa;
while

(adres_tmp <> NULL )

{
if(adres_tmp.wartość == x)
{
Wypisz "Znalazłem szukany element"
opuść procedurę
}

else

adres_tmp=adres_tmp.następny

}
Wypisz

"Nie znalazłem elementu"

_________________________________________

Dokładanie nowych elementów (dwa podejścia):
1)potraktowanie listy jak worek nie-uporządkowanych
elementów i umieszczanie nowych elementów na
początku

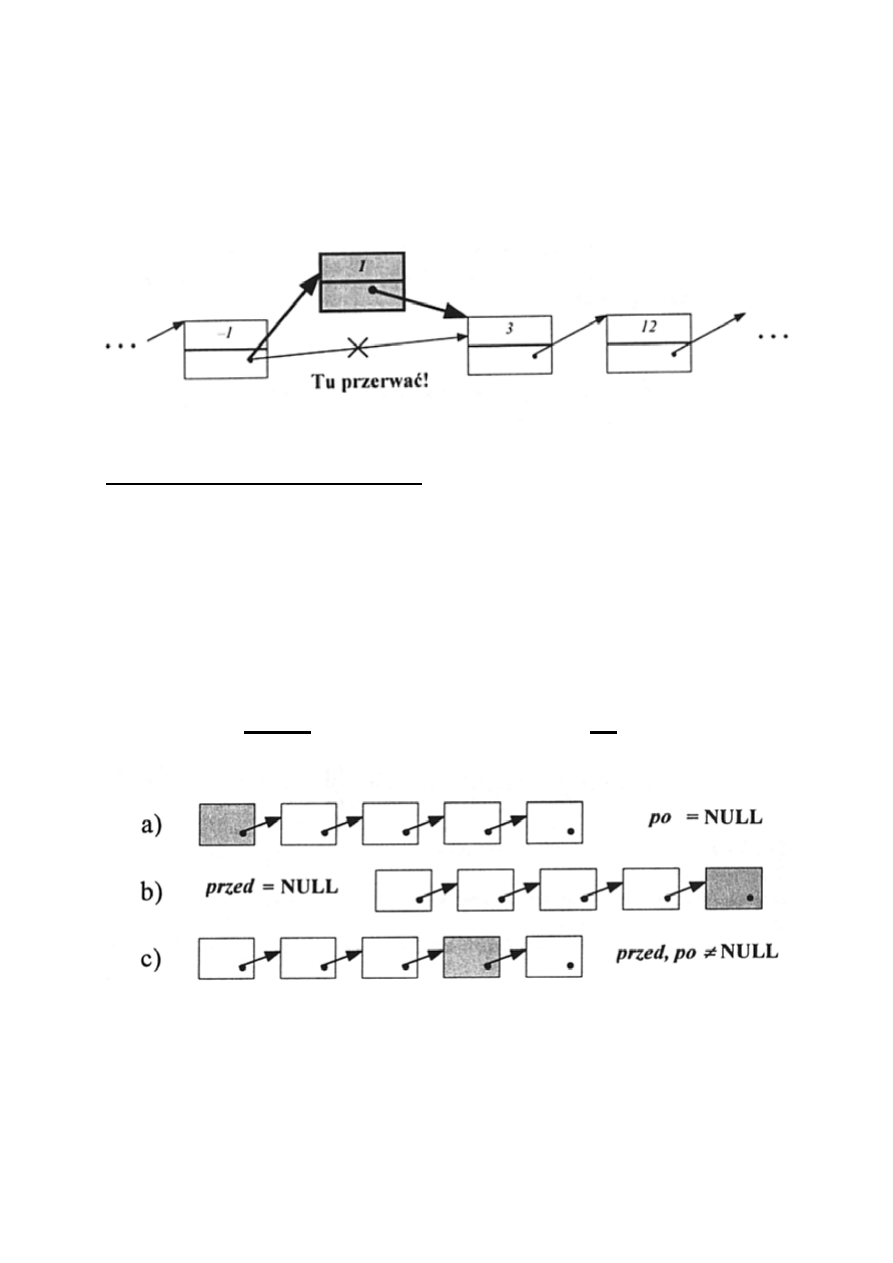
2) dokładanie elementów we właściwym ustalonym przez

użytkownika porządku (całość listy musi być widziana
jako posortowana)

Możliwe są trzy przypadki:

a) wstawiamy element na początek listy

b) wstawiamy element na koniec listy

c) wstawiamy element gdzieś w środku

W każdym z przypadków musimy zapamietywać dwa
wskaźniki - przed który element wstawić i po którym
mamy to zrobić.

Podobnie postępujemy przy fuzji (łączeniu) list tak by
wypadkowa lista pozostała uporządkowana.

Podsumowując wady i zalety list jednokierunkowych:

Wady Zalety

nienaturalny dostęp do

elementów

małe zużycie pamięci

niełatwe sortowanie

elastyczność

Lista w której elementy są już na samym początku
wstawiane w określonym porządku, służy obok
gromadzenia danych, także do ich porządkowania.

W sytuacji, gdy jest tylko jedno kryterium sortowania
struktura działa bardzo dobrze "sama" dbając o
sortowanie.

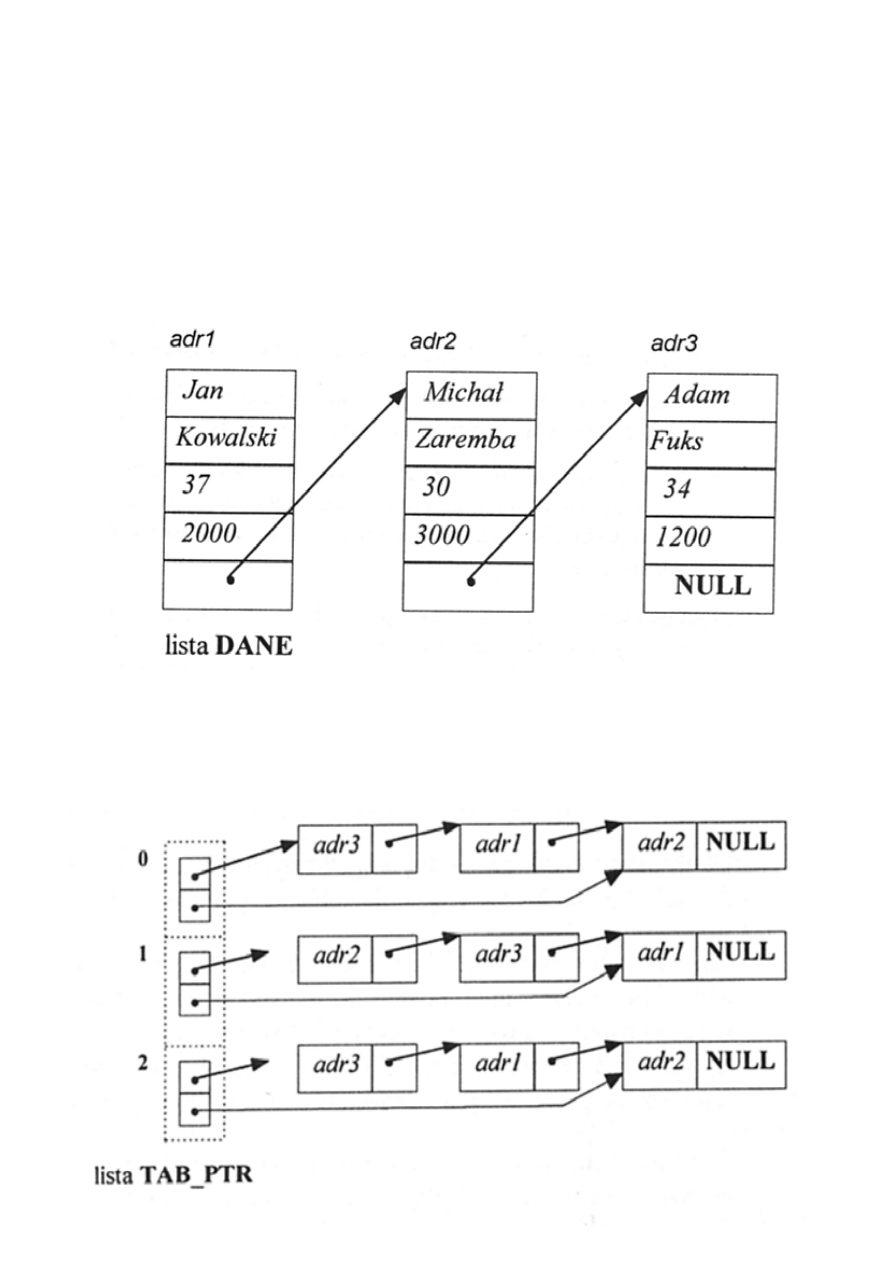
Dla kilku kryteriów sortowania należy wprowadzić obok
listy danych, także kilka list z wskaźnikami do danych - list
tych powinno byś tyle ile kryteriów sortowania.
Sortowanie w takich wypadku polega na porządkowaniu
wskaźników bez ruszania listy danych.

Nieposortowaną listę DANE można uporządkować według

zech kryteriów:

tr

- imienia i nazwiska (Adam Fuks, Jan Kowalski, Michał

Zaremba)

- kodów ( 30, 34, 37)
- kwot ( 1200, 2000, 3000 )

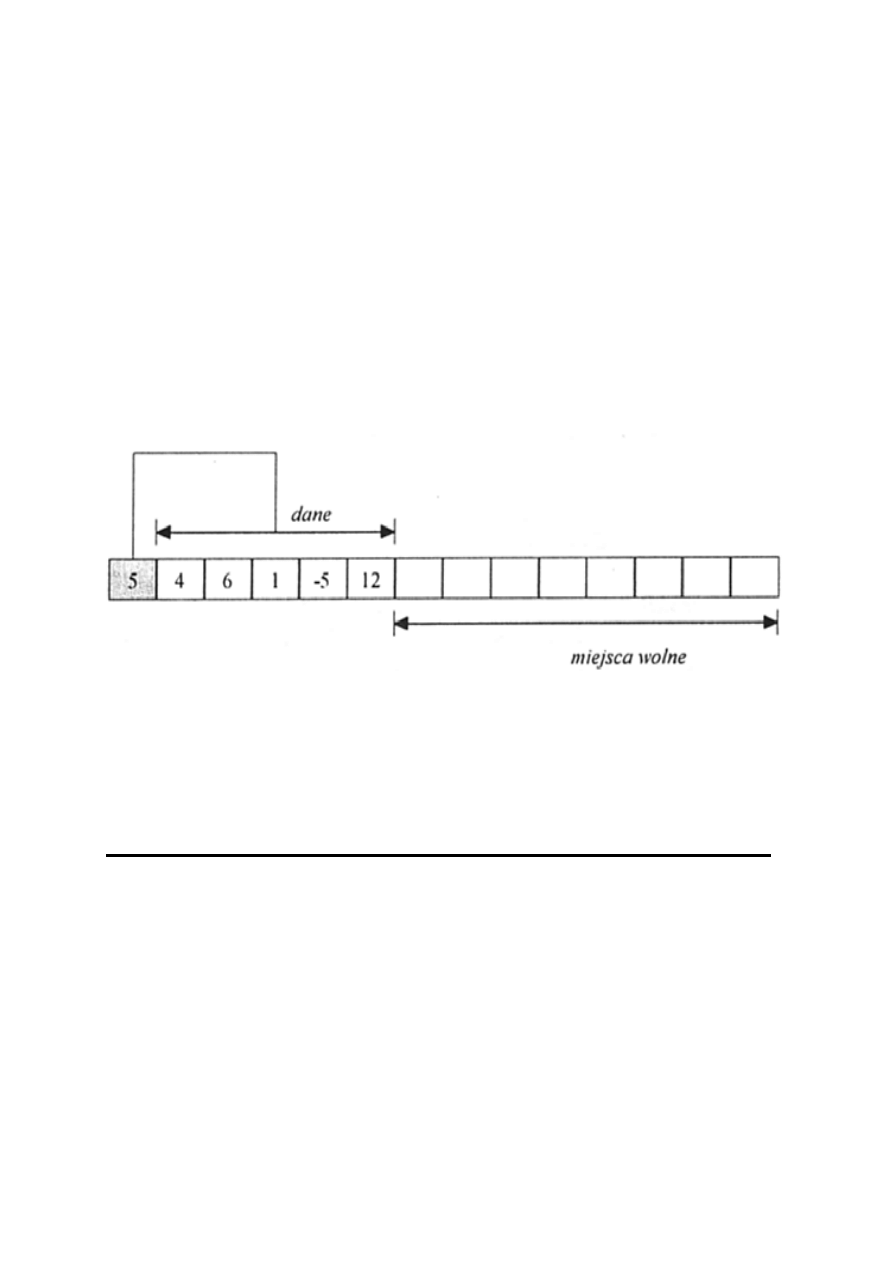
Tablicowa implemantacja list jest niezwykle prosta jeśli
umówimy się, że i-temu indeksowi tablicy odpowiada i-ty
element listy. Wymagana jest dodatkowa informacja
wskazująca jak wiele elementów liczy lista (jak duża musi
być tablica).

Wadą jest marnotrawstwo pamięci bo najczęściej
przydzielamy na tablicę większy obszar pamięci niż to
zwykle potrzeba.

Operacje na listach są w implementacji tablicowej proste:
1)

front(q)

, x=q[1]

- pobierz lewy koniec listy

2)

push(q,x)

- przesuń wszystkie elementy tablicy o jeden w

prawo i

q[1]=x

- wstaw element na lewy koniec

3)

pop(q)

, przesuń wszystkie elementy tablicy poza

pierwszym o jeden w lewo - usuń bieżący lewy koniec

4)

rear(q), x=q[n]

- pobierz prawy koniec listy

5)

inject(q,x), q[n+1]=x

-wstaw element na prawy koniec

6)

eject(q), n=n-1

- usuń bieżący prawy koniec

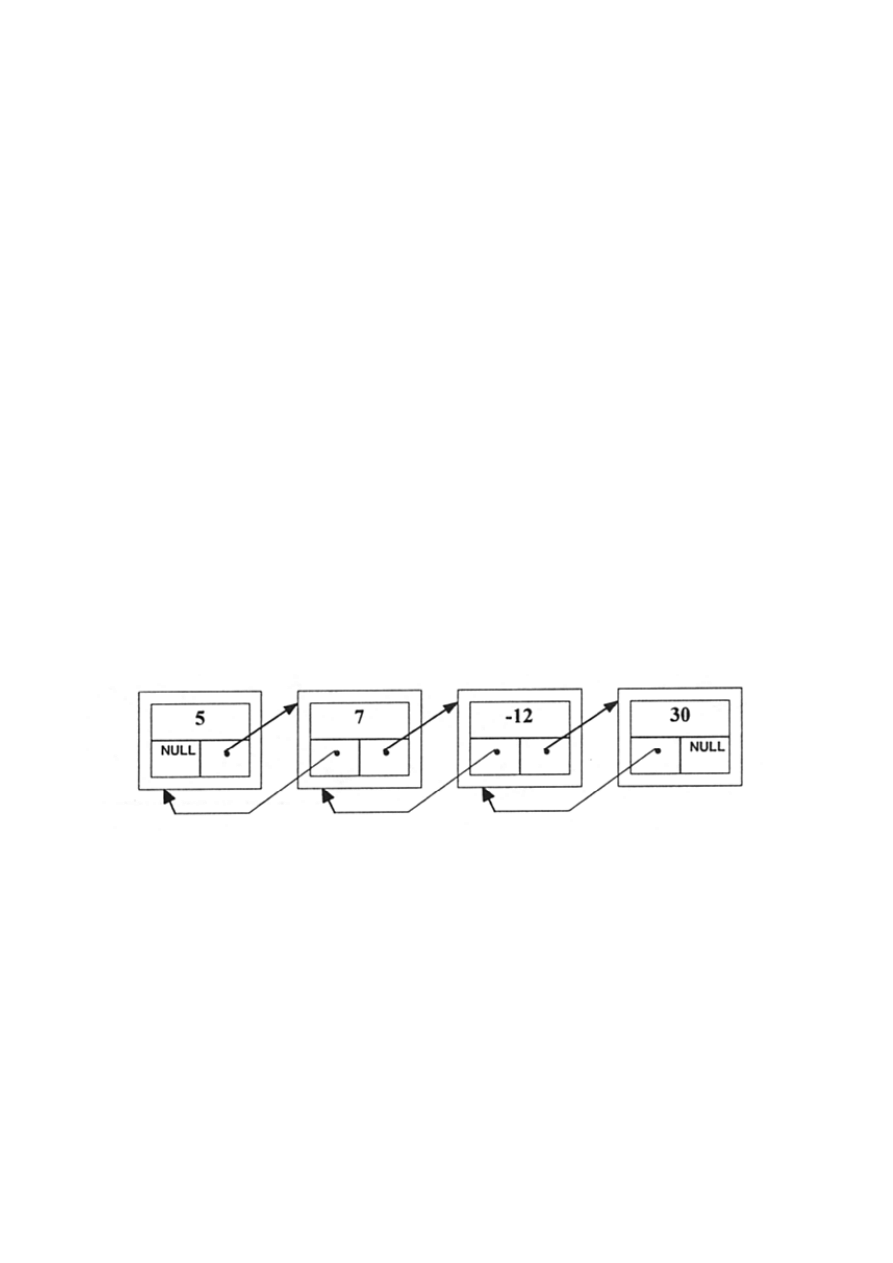
Dodatkowo:

A) usunięcie k-tego elementu to - przesunąć w lewo

elementy tablicy q[k+1]...q[n], n=n-1

B) wstawienie elementu na pozycję k to - przesunąć w

prawo elementy tablicy q[k]...q[n], n=n+1

LISTY DWUKIERUNKOWE

Listy jednokierunkowe są wygodne i zajmują mało
pamięci. Operacje na nich zajmują dużo czasu.

W liście dwukierunkowej komórka robocza zawiera
wskaźniki do elementów: poprzedniego i następnego .
• pierwsza komórka na liście nie posiada swojego

poprzednika (pole poprzedni zawiera NULL wskaźnik
pokazujący pusty element pamięci)

• ostatnia komórka na liście nie posiada swojego

następnika (pole następny zawiera NULL wskaźnik
pokazujący pusty element pamięci)

Lista dwukierunkowa jest kosztowna jeśli chodzi o pamięć,
ale wygodna gdy chodzi o szybkość.

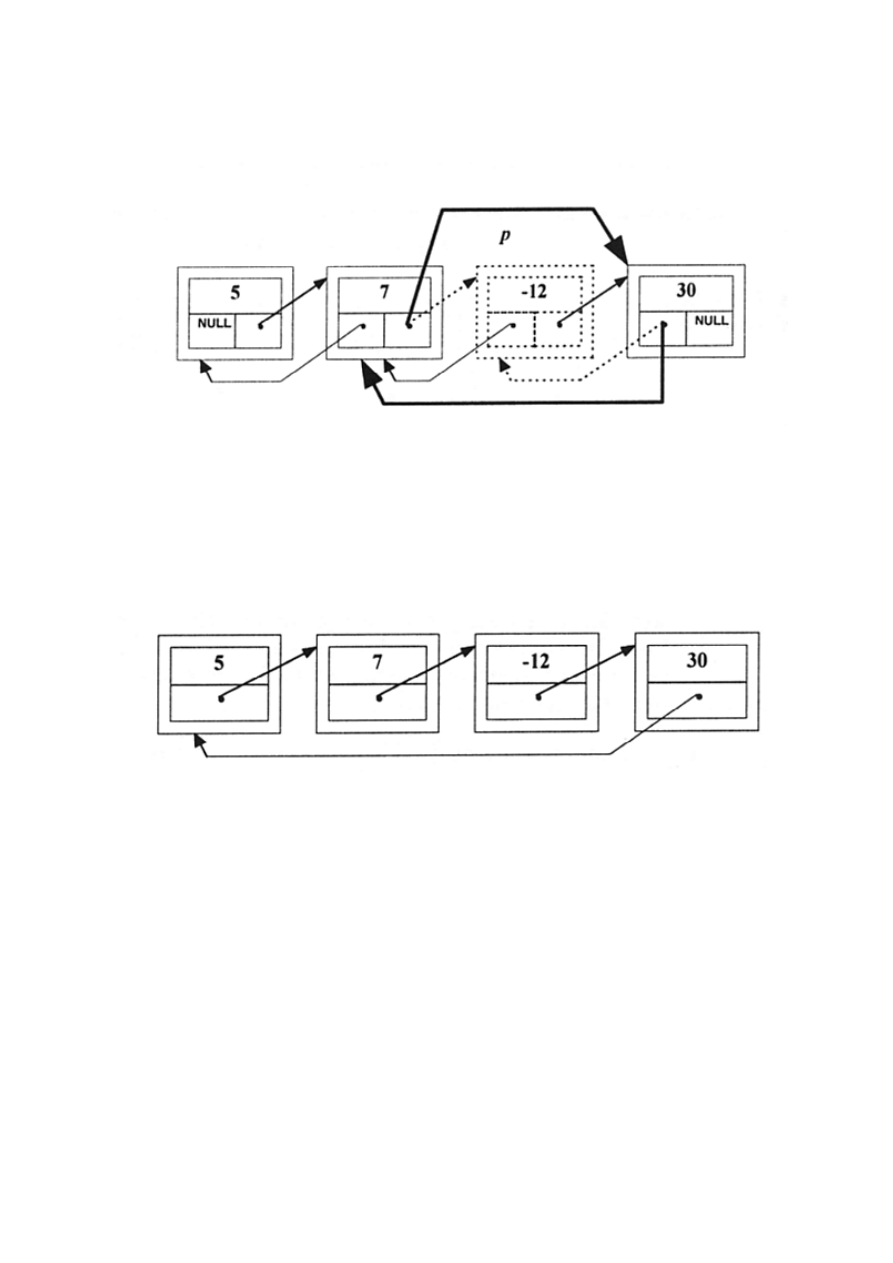
Usunięcie elementu listy dwukierunkowej:

Lista cykliczna jest zamknięta w pierścień , wskaźnik
„ostatniego” elementu wskazuje na „pierwszy” element.

Elementy „pierwszy” i „ostatni” są umowne.

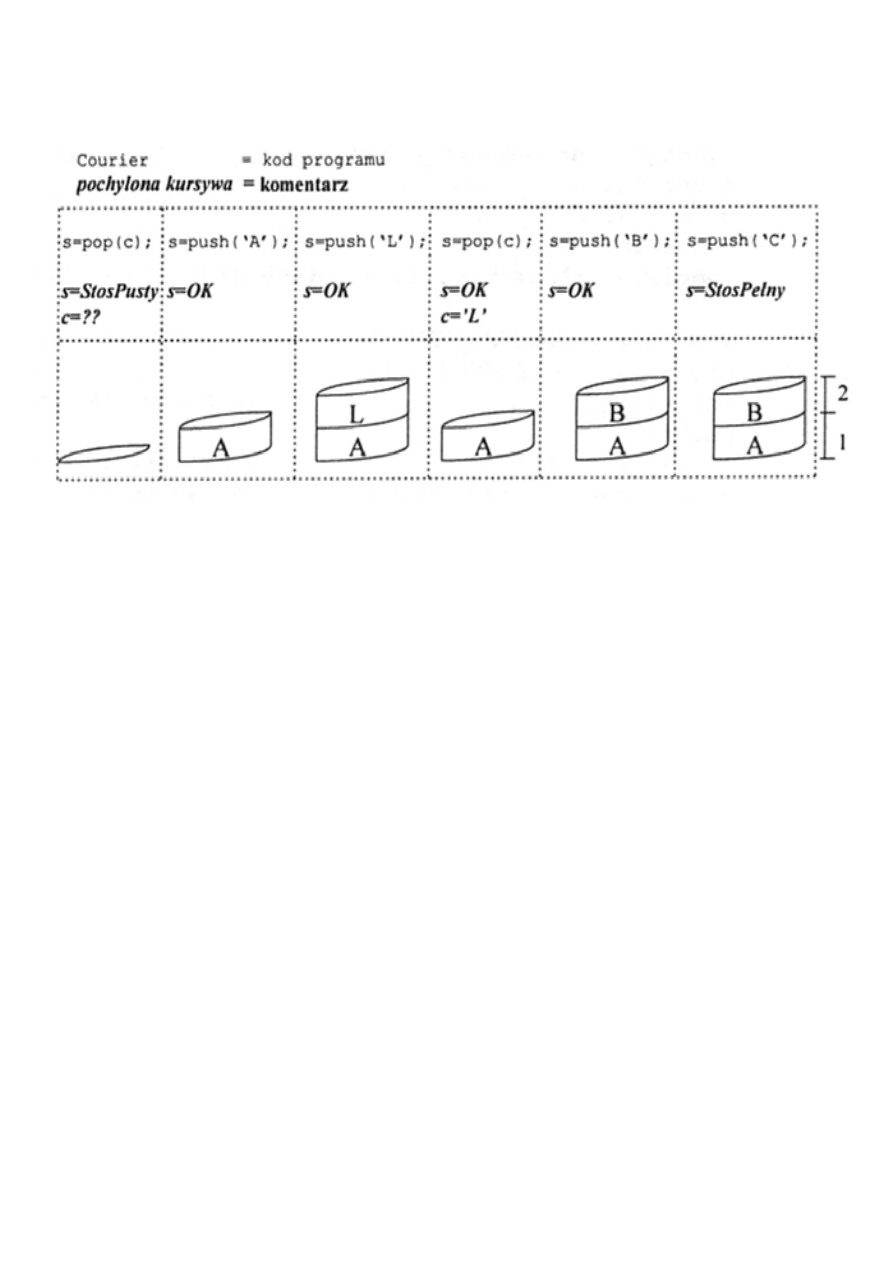
STOSY

Stos jest struktura danych, do której dostęp jest możliwy
tylko od strony tzw. wierzchołka, czyli pierwszego wolnego
miejsca znajdującego się na nim.

Funkcje odkładania elementu X na stos (

push(X)

) i

pobieranie go ze stosu (

pop(X)

) można opisać

symbolicznie (wraz z kodem błędu s wprowadzonym przez
użytkownika):

Tablicowa implementacja stosu wygląda analogicznie jak
dla listy, ale z dostępnymi jedynie operacjami

front

,

push

,

pop

.