Krótki opis programu pandor.exe

1. Budowa panelu głównego

Po uruchomieniu programu oba pola są puste. Lewe służy do wprowadzania badanej
funkcji w postaci tablicy prawdy, w prawym natomiast prezentowane są wyniki
obliczeń. Lewe okno służy dodatkowo jako źródło, z którego pobierane są dane do
zapisywania plików – zarówno w formacie PAN, jak i po konwersji w formatach AHDL
oraz VHDL.

Przcisk „Reset fields” czyści oba pola.
Działanie przycisku „Convert to PAN” omówię w dziale 4.2.

W menu

Files

dostępne są funkcje drukowania zawartości lewego i prawego pola.

W menu

Tools

można wybrać jedną z dostępnych funkcji programu – redukcję liczby

argumentów funkcji oraz minimalizację funkcji metodą ekspansji.

Podczas obliczeń metodą ekspansji budowana jest macierz implikantów prostych
funkcji, która nawet przy niewielkich funkcjach potrafi osiągać dużą liczbę kolumn.
Wąskim gardłem metody ze względu na czasochłonność algorytmu jest szukanie
minimalnych pokryć kolumnowych macierzy. Dlatego w celu ewentualnego
zmniejszenia tej macierzy i zwiększenia szybkości obliczeń zaleca się wcześniejsze
przeprowadzenie redukcji argumentów.

2. Format danych wejściowych

Program odczytując z lewego okna tabelę funkcji działa następująco:

a. Wyszukiwane są wszystkie wiersze rozpoczynające się znakiem ‘0’,’1’ lub ‘-‘.
b. Począwszy od lewej strony wiersza wczytywane są wszystkie znaki aż do

momentu napotkania znaku innego niż ‘0’,’1’ lub ‘-‘. Będą one tworzyć blok
argumentów funkcji.

c. Przeszukując analizowany wiersz program posuwa się w prawo, by po

napotkaniu pierwszego znaku ‘0’,’1’ lub ‘-‘ rozpocząć wczytywanie wiersza,
który będzie tworzyć blok wartości funkcji. Naturalnym ograniczeniem
wczytywania jest oczywiście również koniec wiersza.

d. Wszystkie wiersze z wyjątkiem bloku:

Variable names:
x1,x2,x3,x4,x5
Function names:
y1,y2

będą ignorowane i mogą służyć jako komentarz.

Minimalna i wystarczająca postać danych wejściowych może być następująca:

00111000 01
11000101 01
11110011 01
11010011 00
01110100 01
11101010 00
11101101 01
00111001 00
00110001 00
11101100 11
11000001 10
11000010 10

lub też w przypadku funkcji niezupełnych:

0-111000 01
11000101 01
11110011 01
11010011 0-
0111--00 01
11101010 00
11101101 -1
00111001 -0
001-0001 00
11101100 11
11000001 10
11000010 10

Uruchomienie przycisku „Convert to PAN” powoduje, że program po sprawdzeniu
poprawności tablicy funkcyjnej przedstawia ją w standardowym formacie Pandora. W
przypadku drugiego przykładu będzie to:

Variables = 8
Functions = 2
Data lines = 16

2

Variable names:
x1,x2,x3,x4,x5,x6,x7,x8
Function names:
y1,y2

11000101 01
11110011 01
11010011 0-
11101010 00
11101101 -1
00111001 -0
11101100 11
11000001 10
11000010 10
00111000 01
00100001 00
00110001 00
01110000 01
01110100 01
01111000 01
01111100 01

Zauważmy, że przy okazji Pandor rozwinął wszystkie znaki ‘-‘ po stronie argumentów
– raz zastępując każdy z nich znakiem ‘0’, a następnie znakiem ‘1’.
Jeśli istniał wiersz, w którym po stronie wartości funkcji istnieją same znaki ‘-‘, to w
czasie sprawdzania poprawności funkcji będzie on usunięty.

Warto zwrócić uwagę na fakt, iż w podanym przykładzie program sam wygenerował
nazwy argumentów oraz wartości funkcji.
Nazwy te możemy poprawić w lewym oknie w tym momencie zanim zostanie
uruchomiona procedura redukcji lub ekspansji.
Możemy też wprowadzić je od razu budując właściwie wejściowy plik danych.
Bardzo ważne jest, aby wiersze zapowiadające wystąpienie w wierszu kolejnym
definicji nazw brzmiały dokładnie tak: „Variable names:” oraz „Function names:”. W
przeciwnym razie będą one zignorowane jako komentarz.
Nazwy muszą być oddzielone przecinkami i podawane bez żadnej spasji. Oczywiście
ich liczba musi odpowiadać podanej tablicy. W przypadku nieprawidłowości program
sam wygeneruje nowe nazwy.

3. Pliki wejściowe w formacie PAN i PLA

Typowym standardem zapisu funkcji boolowskich dla obliczeń w komputerowych
systemach syntezy na poziomie akademickim jest tzw. standard espresso, w którym
funkcje są zapisywane w plikach z rozszerzeniem *.pla.

Przykładowy zapis funkcji w standardzie espresso:

3

.type fr
.i 9
.o 6
.p 12
000111000 0000-0
101000000 00-101
101110000 011011
111101000 011110
101010000 000-01
001110000 110100
111000000 10-010
101101000 1100-1
101101100 -101-1
111000010 10101-
000111001 0010-1
000110001 --1000
.e

Pandor będzie je oczywiście akceptować i dalej przetwarzać, choć przy pierwszej
nadarzającej się okazji przekonwertuje je na format *.pan, jeśli użytkownik nie uczyni
tego wcześniej przy pomocy przycisku „Convert to PAN”.

4. Redukcja argumentów

Program liczy metodą opisaną w rozdziale III.

Działanie procedury pokażę na przykładzie następującego pliku wejściowego:

Variables = 9
Functions = 6
Data lines = 12

Variable names:
x1,x2,x3,x4,x5,x6,x7,x8,x9
Function names:
y1,y2,y3,y4,y5,y6

000111000 0000-0
101000000 00-101
101110000 011011
111101000 011110
101010000 000-01
001110000 110100
111000000 10-010
101101000 1100-1
101101100 -101-1
111000010 10101-
000111001 0010-1
000110001 --1000

W przypadku funkcji wielowartościowej pojawi się zapytanie, czy redukcja ma być
przeprowadzona dla wszystkich funkcji łącznie, czy też dla każdej oddzielnie.

4

Przeprowadzenie redukcji dla wszystich funkcji łącznie:

Wyniki obliczeń:

Input data OK!

REDUCTION

Computing for function y1,y2,y3,y4,y5,y6

Essential variables

x1,x2,x4,x6,x7,x9

Status of all variables

++-+-++-+

Table C full size

Table C is empty.

All results as status lines

++-+-++-+

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x4,x6,x7,x9}

Istnieje zatem tylko jedna minimalna realizacja przy użyciu argumentów
x1, x2, x4, x6, x7 oraz x9.
Możliwe jest uzyskanie kilku minimalnych realizacji przy różnych doborach
argumentów. Liczba argumentów będzie w każdej takiej realizacji jednakowa.



Przeprowadzenie redukcji dla wszystich funkcji oddzielnie:

Wyniki obliczeń:

Input data OK!

REDUCTION

Computing for function y1

Essential variables

x1,x2

Status of all variables

++-------

Table C full size

5

1001000
0101000
0011000
0101000
0101010
0111000
1001001

Table C reduced

1001
0101
0011

New status of all variables

++----xxx

All results as status lines

++---cxxx

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x6}

Computing for function y2

Essential variables

x4

Status of all variables

---+-----

Table C full size

10101000
11110000
00101000
10110000
10110100
10101001
11110001
00101001
10110001
10110101

Table C reduced

0101
1110

New status of all variables

-x-+--xxx

All results as status lines

-xc+--xxx

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables

6

"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x3,x4}

Computing for function y3

Essential variables

x1,x2,x4,x9

Status of all variables

++-+----+

Table C full size

01100
01110

Table C reduced

11

New status of all variables

++x+--xx+

All results as status lines

++x+c-xx+
++x+-cxx+

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x4,x5,x9}
R2 = {x1,x2,x4,x6,x9}

Computing for function y4

Essential variables

x1,x2,x7

Status of all variables

++----+--

Table C full size

100100
011000
010100
010100
010110
100101
100001

Table C reduced

10010
01100
01010
10001

New status of all variables

7

++----+x-

All results as status lines

++cc--+x-

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x3,x4,x7}

Computing for function y5

Essential variables

x1,x2,x4

Status of all variables

++-+-----

Table C full size

Table C is empty.

All results as status lines

++-+-----

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x4}

Computing for function y6

Essential variables

x1,x2,x6,x9

Status of all variables

++---+--+

Table C full size

Table C is empty.

All results as status lines

++---+--+

Explanation od status lines
"+" essential variables
"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

All results

R1 = {x1,x2,x6,x9}

8

Results for all functions

Results for function y1:
R1 = {x1,x2,x6}

Results for function y2:
R1 = {x3,x4}

Results for function y3:
R1 = {x1,x2,x4,x5,x9}
R2 = {x1,x2,x4,x6,x9}

Results for function y4:
R1 = {x1,x2,x3,x4,x7}

Results for function y5:
R1 = {x1,x2,x4}

Results for function y6:
R1 = {x1,x2,x6,x9}

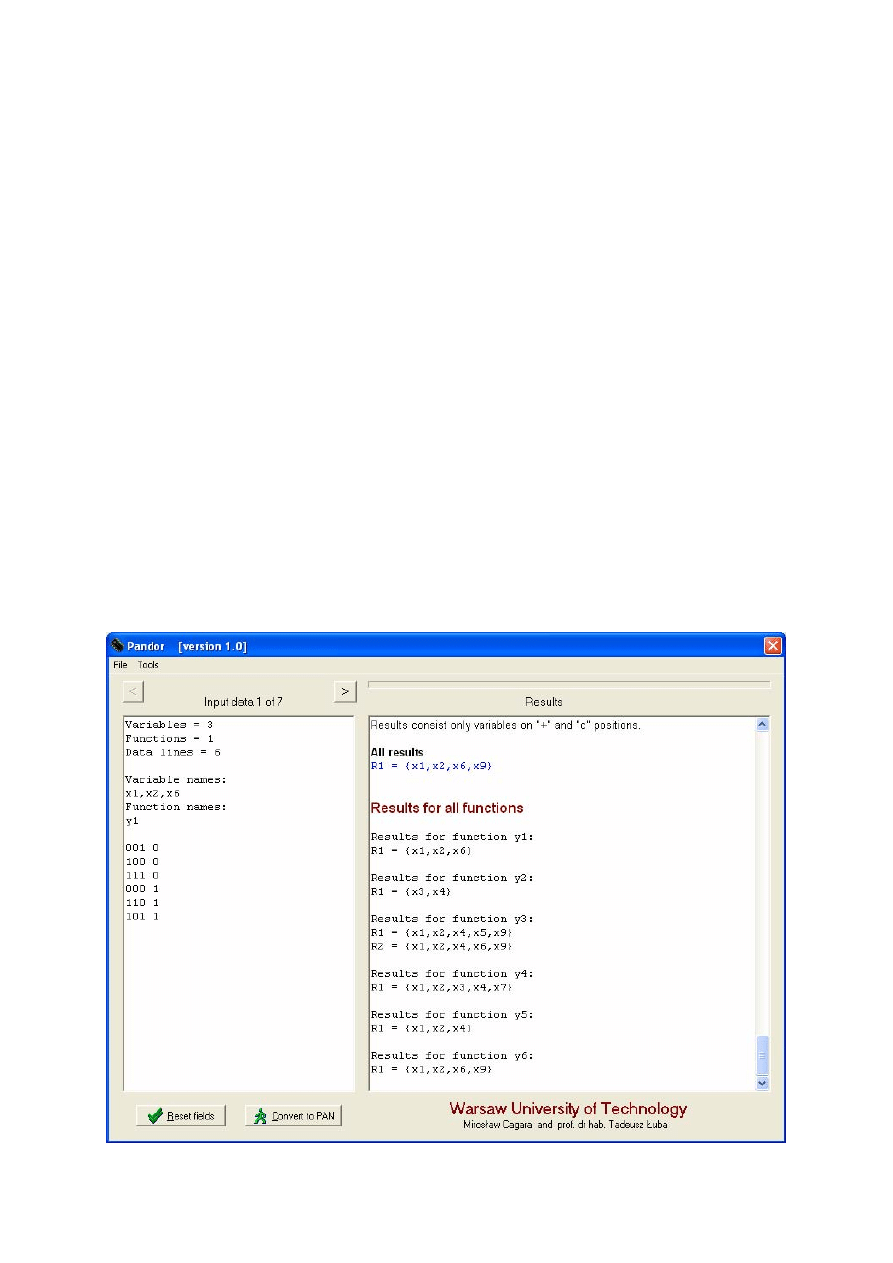
Widzimy, że dla każdej funkcji minimalna liczba argumentów może być różna.
Każda z funkcji może również posiadać kilka różnych minimalnych realizacji, tak jak
w przypadku funkcji y3.

Zwróćmy uwagę na to, jak wygląda teraz panel programu.
Aktywne stały się przyciski ‘<’ oraz ‘>’ służące do przewijania wyświetlanych w lewym
oknie w postaci pliku w formacie *.pan kolejnych realizacji funkcji.
Oczywiście każdy z wyświetlanych plików możemy teraz poddać metodzie ekspansji.

9

5. Ekspansja

Program liczy metodą opisaną w dziale II.
Ze względu na specyfikę metody ekspansji obliczenia możliwe są tylko dla
wszystkich funkcji oddzielnie.

Aby nie przytaczać tu bardzo obszernych wyników obliczeń, jakie powstaną w
poprzednim przykładzie, wybiorę na potrzeby ekspansji inny plik:

Variables = 8
Functions = 1
Data lines = 12

Variable names:
x1,x2,x3,x4,x5,x6,x7,x8
Function names:
y1

00111000 0
11000101 0
11110011 0
11010011 0
01110100 0
11101010 0
11101101 0
00111001 0
00110001 0
11101100 1
11000001 1
11000010 1

Celowo wybrałem tabelę jednofunkcyjną, bo w przypadku tabeli wielofunkcyjnej
metoda obliczeń będzie taka sama. Program wykona wtedy w pętli kolejne obliczenia
dla każdej funkcji oddzielnie.

Wyniki obliczeń:

Input data OK!

New variable names generated.
New function names generated.

EXPANSION

Computing for function y1

Table F of function y1

11101100
11000001
11000010

Table R of function y1

00111000
11000101
11110011
11010011
01110100
11101010
11101101
00111001
00110001

10

Table B1 of function y1

11010100
00101001
00011111
00111111
10011000
00000110
00000001
11010101
11011101

All minimal cover columns in table B1 of function y1:

c-x--c-+
c-x---c+
--xc-c-+
--xc--c+
--x-cc-+

Current cube:

k1 = (11101100)

All cube expansions of table B1:

1****1*0
1*****00
***0*1*0
***0**00
****11*0

Table B2 of function y1

11111001
00000100
00110010
00010010
10110101
00101011
00101100
11111000
11110000

All minimal cover columns in table B2 of function y1:

c----+c-
-c---+c-
--cc-+--
--c--+c-
---cc+--
---c-+c-
---c-+-c

Current cube:

k2 = (11000001)

All cube expansions of table B2:

1****00*
*1***00*
**00*0**
**0**00*
***000**
***0*00*
***0*0*1

Table B3 of function y1

11111010
00000111

11

00110001
00010001
10110110
00101000
00101111
11111011
11110011

All minimal cover columns in table B3 of function y1:

-xc----c

Current cube:

k3 = (11000010)

All cube expansions of table B3:

**0****0

All cube expansions of function y1 and their implicants

1****1*0 ==> x1x6!x8
1*****00 ==> x1!x7!x8
***0*1*0 ==> !x4x6!x8
***0**00 ==> !x4!x7!x8
****11*0 ==> x5x6!x8
1****00* ==> x1!x6!x7
*1***00* ==> x2!x6!x7
**00*0** ==> !x3!x4!x6
**0**00* ==> !x3!x6!x7
***000** ==> !x4!x5!x6
***0*00* ==> !x4!x6!x7
***0*0*1 ==> !x4!x6x8
**0****0 ==> !x3!x8

Implicants table of function y1

1111100000000
0000011111110
0000000101001

All minimal cover columns:

c------c-----
c--------c---
-c-----c-----
-c-------c---
--c----c-----
--c------c---
---c---c-----
---c-----c---
----c--c-----
----c----c---

All results of function y1

y1 = x1x6!x8 + !x3!x4!x6
y1 = x1x6!x8 + !x4!x5!x6
y1 = x1!x7!x8 + !x3!x4!x6
y1 = x1!x7!x8 + !x4!x5!x6
y1 = !x4x6!x8 + !x3!x4!x6
y1 = !x4x6!x8 + !x4!x5!x6
y1 = !x4!x7!x8 + !x3!x4!x6
y1 = !x4!x7!x8 + !x4!x5!x6
y1 = x5x6!x8 + !x3!x4!x6
y1 = x5x6!x8 + !x4!x5!x6

Explanation od status lines
"+" essential variables

12

"-" non-essential variables
"x" needless variables
"c" cover variables
Results consist only variables on "+" and "c" positions.

Podaną funkcję można zatem uprościć do postaci minimalnej składającej się tylko z
dwóch implikantów prostych. W podanym przykładzie takich minimalnych rozwiązań
jest aż 10.

Bardzo ważne jest, że przeprowadzenie ekspansji nie ingeruje w zawartość lewego
okna, jeśli jest ono podane w poprawnym formacie Pandora.
Dzięki temu po przeprowadzeniu wcześniejszej redukcji zachowana zostaje
możliwość przewijania kolejnych realizacji funkcji i wielokrotnego wykonywania
ekspansji dla dowolnie wybranej realizacji.

6. Zapisywanie plików w formacie PAN

Przed zapisaniem pliku program wykona szereg czynności sprawdzających
poprawność tabeli funkcji.
Jeśli nie jest ona podana w formacie Pandora, będzie przed zapisem do tego formatu
przekonwertowana.

7. Zapisywanie plików w formacie PLA

Jest to format flików wejściowych dla programu Espresso.
Tabela będzie najpierw poddana procedurze sprawdzającej jej poprawność.
Następnie konwerter na podstawie podanej tabeli stworzy plik, który powinien być
zapisany z rozszerzeniem *.pla.

Przykład:

Zawartość lewego okna:

.type fr
.i 8
.o 1
.p 12
00111000 0
11000101 0
11110011 0
11010011 0
01110100 0
11101010 0
11101101 0
00111001 0
00110001 0
11101100 1
11000001 1
11000010 1
.e

13

8. Zapisywanie plików w formacie AHDL

Podobnie jak w przypadku zapisu w formacie PAN tabela będzie najpierw poddana
procedurze sprawdzającej jej poprawność.
Następnie konwerter na podstawie podanej tabeli stworzy plik, który powinien być
zapisany z rozszerzeniem *.tdf.

Przykład:

Zawartość lewego okna:

Variables = 5
Functions = 2
Data lines = 8

Variable names:
x1,x2,x3,x4,x5
Function names:
y1,y2

00000 01
00111 01
01010 00
01111 01
01100 01
00011 10
01000 10
01101 11

Otrzymany plik *.tdf

Zapisując plik nadałem mu nazwę ahdl1.tdf.
Taka sama nazwa pojawia się wtedy automatycznie wewnątrz pliku.

TITLE "Project Pandor ahdl1";

SUBDESIGN ahdl1
(
-- input signals
in[4..0] : INPUT;
-- output signals
out[1..0] : OUTPUT;
)

BEGIN
TABLE (in[4..0]) => (out[1..0]);
B"00000" => B"01";
B"00111" => B"01";
B"01010" => B"00";
B"01111" => B"01";
B"01100" => B"01";
B"00011" => B"10";
B"01000" => B"10";
B"01101" => B"11";
END TABLE;
END;

14

9. Zapisywanie plików w formacie VHDL

Podobnie jak w przy konwersji na format AHDL tabela będzie najpierw poddana
procedurze sprawdzającej jej poprawność.
Następnie konwerter na podstawie podanej tabeli stworzy plik, który powinien być
zapisany z rozszerzeniem *.vhd.

Przykład:

Zawartość lewego okna:

Variables = 5
Functions = 2
Data lines = 8

Variable names:
x1,x2,x3,x4,x5
Function names:
y1,y2

00000 01
00111 01
01010 00
01111 01
01100 01
00011 10
01000 10
01101 11

Otrzymany plik *.vhd

LIBRARY ieee;
USE ieee.std_logic_1164.ALL;

ENTITY vhdl1 IS
PORT (
in: IN STD_LOGIC_VECTOR(4 DOWNTO 0);
out: OUT STD_LOGIC_VECTOR(1 DOWNTO 0)
);
END vhdl1;

ARCHITECTURE vhdl1_arch OF vhdl1 IS
BEGIN
pandor: PROCESS (in)
BEGIN
CASE in IS
WHEN "00000" => out <= "01";
WHEN "00111" => out <= "01";
WHEN "01010" => out <= "00";
WHEN "01111" => out <= "01";
WHEN "01100" => out <= "01";
WHEN "00011" => out <= "10";
WHEN "01000" => out <= "10";
WHEN "01101" => out <= "11";
WHEN OTHERS => out <= "00";
END CASE;
END PROCESS pandor;
END vhdl1_arch;

15

10. Drukowanie danych wejściowych i wyjściowych

Zawartość obu okien można wydrukować bezpośrednio korzystając z menu

Files/Print left panel

oraz

Files/Print righ panel

.

t

11. Granice możliwości programu

Jedynym ograniczeniem programu jest procedura szukająca minimalne pokrycia
kolumnowe macierzy. Problem jest NP-zupełny, a w związku z tym bardzo
czasochłonny.
Procedura sprawdza kolejno możliwość pokrycia dla 1, 2 , 3 … kolumn. W skrajnie
niekorzystnym przypadku pokrycie może być znalezione dopiero dla kombinacji
wszystkich kolumn. Nastąpi to przykładowo w przypadku tabeli:

100000
010000
001000
000100
000010
000001

Aby nie dopuścić do takiej sytuacji oraz zmniejszyć czasochłonność procedury
wbudowałem w nią mechanizm redukujący tablicę według metody opisanej w dziale
1.2.
Przy poszukiwaniu k-kolumnowego pokrycia n-kolumnowej macierzy trzeba wykonać

obliczenia sprawdzające dla

(

)

!

!

!

n

k n

k

−

kombinacji.

Najbardziej czasochłone jest przeszukiwanie kombinacji, gdzie n = 2 k.
Już w przypadku tablicy 30 kolumnowej przeszukanie tylko kombinacji 15
kolumnowych wymaga 155 117 520 obliczeń.

12. Podsumowanie

Minimalizacja funkcji boolowskich jest podstawową procedurą syntezy logicznej w
komputerowych systemach projektowania układów cyfrowych. Skuteczność i
szybkość działania tej procedury może być decydująca o jakości implementacji
sprzętowych wielu systemów cyfrowych o różnorodnych zastosowaniach. Typowymi
układami cyfrowymi wymagającymi stosowania w procesie ich optymalizacji
procedur minimalizacji funkcji boolowskich są m.in. S-boxy układów
kryptograficznych lub struktury arytmetyki rozproszonej filtrów cyfrowych [16].
Z tych powodów zagadnieniu temu poświęcano specjalne zadania badawcze
niejednokrotnie sponsorowane przez renomowane instytucje, jak np. IBM. Miały one
na celu opracowanie metod i algorytmów minimalizacji odpowiednich do ogromnej
złożoności układów wykonywanych w zaawansowanych technologiach. Jednym z
najważniejszych rezultatów tych badań jest program Espresso, opracowany na
początku lat osiemdziesiątych na Uniwersytecie kalifornijskim w Berkeley.

Rozbudowane procedury programu ESPRESSO weszły już dzisiaj do kanonów syntezy
logicznej, a ich różnorodność i obszerność uprawnia do stosowania hasłowej nazwy:
metoda espresso. W skład metody espresso wchodzą przede wszystkim procedury
ekspansji, pokrycia, uzupełnienia i tautologii. Procedury te operując na zbiorach kostek

16

funkcji boolowskiej

f

= (

F

,

R

) umożliwiają obliczenie zminimalizowanego zbioru

F

M

wg

następującego schematu.

Najpierw procedura

ekspansji

(Expand) oblicza zbiór

F

E

= EXPAND((

F

,

R

). Następnie

obliczany jest zbiór nieokreśloności

D,

jako uzupełnienie sumy zbiorów

F

i

R

. Obliczenia

te realizuje procedura

uzupełnienie

(COMPLEMENT), czyli

D

= COMPLEMENT(

F

,

R

).

Wreszcie w procedurze

pokrycie

(IRREDUNDANT-COVER) zbiory

F

E

i

D

transformowane są do zbioru

F

M

= IRREDUNDANT_ COVER(

F

E

,

D

),

uznawanego za

minimalne pokrycie funkcji

f

.

Niestety ze względu na heurystyczny sposób obliczeń uzyskany wynik

F

M

może nie

być pokryciem minimalnym, co przy wzrastającej złożoności układów realizowanych
w nowoczesnych technologiach może okazać się istotną barierą.

Niniejsza praca prezentuje oryginalną metodę zmniejszania złożoności obliczeniowej
algorytmów minimalizacji funkcji boolowskich. Istotą tej metody jest zastosowanie
algorytmu redukcji argumentów, jako oddzielnej procedury poprzedzającej właściwą
minimalizację. Redukcja argumentów jest procedurą do tej pory rzadko stosowaną w
komputerowych systemach syntezy logicznej. Jedną z przyczyn takiej sytuacji jest
brak świadomości, że złożone układy cyfrowe są – od strony pojedynczych wyjść –
reprezentowane funkcjami boolowskimi o znacznie nadmiarowych zależnościach
wejściowych. Dodatkowo okazuje się, że redukcja tych zależności po procesie
klasycznej minimalizacji jest mało skuteczna.

Program Pandor opracowany w ramach niniejszej pracy pozwalając na wykonanie

procesu redukcji argumentów dla pojedynczych i grupowych funkcji boolowskich
przed procesem minimalizacji umożliwia efektywne wykorzystanie tego zjawiska dla
wszystkich następnych procesów syntezy.

Uzasadnienie skuteczności takiej strategii omówione jest w poniższych
eksperymentach.





Wiele funkcji nie da się zminimalizować poprzez bezpośrednie zastosowanie
systematycznej procedury minimalizacji np. zmodyfikowanej

ekspansji

.

Przykład

Variables = 21
Functions = 1
Data lines = 31

Variable names:
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21
Function names:
y1

100110010110011111101 1
111011111011110111100 1
001010101000111100000 1
001001101100110110001 1
100110010011011001101 1
100101100100110110011 1

17

001100100111010011011 1
001101100011011011001 1
110110010011001001101 1
100110110011010010011 1
110011011011010001100 1
010001010000001100111 0
100110101011111110100 0
111001111011110011000 0
101101011100010111100 0
110110000001010100000 0
110110110111100010111 0
110000100011110010001 0
001001000101111101101 0
100100011111100110110 0
100011000110011011110 0
110101000110101100001 0
110110001101101100111 0
010000111001000000001 0
001001100101111110000 0

Procedura ekspansji generuje 416 implikantów prostych, co oznacza, że macierz
implikantów zawiera 416 kolumn.
Systematyczne szukanie minimalnego pokrycia kolumnowego jest praktycznie
niewykonalne. Przykładowo sprawdzenie, czy istnieją pokrycia 3-kolumnowe

wymaga

416!

3! 413!

⋅

czyli prawie 12 milionów uruchomień procedury sprawdzającej, czy

dla danej kombinacji kolumn istnieje pokrycie kolumnowe.
Trzeba koniecznie zdawać sobie sprawę z tego jak szybko rośnie ta liczba wraz ze
zwiększeniem się liczby sprawdzanych kolumn.
W naszym 416-kolumnowym przykładzie:

n

k

(

)

!

!

!

n

k n

k

−

416 1

416

416 2

86320

416 3

11912160

416 4

1229930520

416 5

101346274848

416 6

6942219827088

416 7

406615732729440

416 8

20788229335792620

416 9

942399729889265440

416 10

38355669006493103408

416 11

1415672874239654543968

416 12

47778959505588340858920

416 13

1484823049250591515923360

Najbardziej czasochłonne jest sprawdzenie połowy spośród całkowitej liczby kolumn.
W naszym przykładzie w celu sprawdzenia pokrycia wszystkich kombinacji
208-kolumnowych trzeba wykaonać następującą liczbę operacji sprawdzających:

6616230063578456454088151537337222572939614651059079377712426254170
976447903825456241212171286045820096024918596033164779400

18

Jest to w przybliżeniu

.

123

6, 6 10

⋅

Procedura reducji zmniejsza w podanym przykładzie liczbę argumentów z 21 do 5-
ciu.
Dla każdej z pięcioargumentowych realizacji funkcji z osobna można teraz bez
problemu przeprowadzić minimalizację metodą ekspansji.

Porównanie wyników programów Espresso i Pandor

Przykład 1 (funkcja TL27.pla)

.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e

Wyniki obliczeń programu Espresso:

.i 10
.o 1
.p 6
----00-1-- 1
00------0- 1
----10-0-0 1
---1--0--1 1
------1-0- 1
-----11--1 1
.e

19

Jak widać, program Espresso potrafił zredukować zadaną funkcję do liczby 9
argumentów. Funkcja ta składa się z 6 termów.

y = !x5!x6x8 + !x1!x2!x9 + x5!x6!x8!x9 + x4!x7x10 + x7!x9 + x6x7x10

Wyniki obliczeń programu Pandor:

All results

R1 = {x1,x2,x4,x5,x6,x7,x10}
R2 = {x1,x2,x4,x6,x7,x8,x10}
R3 = {x1,x2,x4,x6,x7,x9,x10}
R4 = {x1,x4,x5,x6,x7,x9,x10}
R5 = {x1,x4,x6,x7,x8,x9,x10}
R6 = {x1,x5,x6,x7,x8,x9,x10}
R7 = {x2,x3,x4,x5,x6,x7,x10}
R8 = {x2,x3,x5,x6,x7,x8,x10}
R9 = {x3,x4,x5,x6,x7,x9,x10}
R10 = {x3,x5,x6,x7,x8,x9,x10}

Jak widać, program Pandor potrafił zredukować zadaną funkcję do liczby 7
argumentów.

Każdą z otrzymanych realizacji możemy poddać procedurze ekspansji.
Dla kilku różnych realizacji otrzymujemy rozwiązania składające się tylko z 5 termów,
a każdy z nich wykorzystuje tylko 7 argumentów.

Przykładowo dla realizacji R3 otrzymamy 5 bardzo prostych termów:

y1 = !x1x10 + !x1!x2!x7 + !x1!x4!x6 + x7!x9 + x1x2x4
y1 = !x1x10 + !x1!x2!x9 + !x1!x4!x6 + x7!x9 + x1x2x4

Przykład 2 (funkcja KAZ.pla)

.type fr
.i 21
.o 1
.p 31
100110010110011111101 1
111011111011110111100 1
001010101000111100000 1
001001101100110110001 1
100110010011011001101 1
100101100100110110011 1
001100100111010011011 1
001101100011011011001 1
110110010011001001101 1
100110110011010010011 1
110011011011010001100 1
010001010000001100111 0
100110101011111110100 0
111001111011110011000 0
101101011100010111100 0
110110000001010100000 0

20

110110110111100010111 0
110000100011110010001 0
001001000101111101101 0
100100011111100110110 0
100011000110011011110 0
110101000110101100001 0
110110001101101100111 0
010000111001000000001 0
001001100101111110000 0
100100111111001110010 0
000010001110001101101 0
101000010100001110000 0
101000110101010011111 0
101010000001100011001 0
011100111110111101111 0
.end

Wyniki obliczeń programu Espresso:

.i 21
.o 1
.p 3
-0-----------1----0-1 1
-------0--00--------- 1
----1--1-----------0- 1
.e

Jak widać, program Espresso potrafił zredukować zadaną funkcję do liczby 9
argumentów, na którą składają się łącznie 3 termy:

y = !x2x14!x19x21 + !x8!x11!x12 + x5x8!x20

Wyniki obliczeń programu Pandor:

All results

R1 = {x1,x5,x8,x10,x15}
R2 = {x2,x4,x5,x9,x18}
R3 = {x2,x4,x5,x18,x21}
R4 = {x2,x4,x7,x9,x16}
R5 = {x2,x4,x7,x9,x19}
R6 = {x2,x4,x9,x10,x19}
R7 = {x2,x4,x9,x13,x19}
R8 = {x2,x4,x9,x15,x19}
R9 = {x2,x4,x9,x17,x19}
R10 = {x2,x4,x9,x18,x19}
R11 = {x2,x4,x9,x19,x20}
R12 = {x2,x4,x10,x19,x21}
R13 = {x2,x4,x16,x17,x21}
R14 = {x2,x5,x8,x17,x21}
R15 = {x2,x9,x11,x19,x20}
R16 = {x2,x11,x16,x17,x21}
R17 = {x3,x5,x8,x10,x15}
R18 = {x4,x5,x8,x10,x15}
R19 = {x4,x7,x8,x9,x19}
R20 = {x4,x7,x9,x12,x19}
R21 = {x4,x7,x9,x16,x19}
R22 = {x4,x9,x11,x13,x16}
R23 = {x4,x9,x12,x17,x19}
R24 = {x4,x9,x14,x16,x17}
R25 = {x4,x9,x16,x17,x19}
R26 = {x4,x10,x15,x17,x19}
R27 = {x4,x11,x12,x13,x16}

21

R28 = {x4,x16,x17,x19,x21}
R29 = {x5,x8,x10,x11,x15}
R30 = {x5,x8,x10,x12,x15}
R31 = {x5,x8,x10,x15,x17}
R32 = {x5,x8,x10,x15,x19}
R33 = {x5,x8,x12,x13,x14}
R34 = {x8,x10,x15,x19,x20}
R35 = {x10,x15,x17,x19,x20}

Jak widać, program Pandor potrafił zredukować zadaną funkcję do liczby 5
argumentów, przy czym znalazł wszystkie 35 minimalnych realizacji funkcji.

Poddanie procedurze ekspancji realizacji R11 daje w wyniku tylko 3 termy, a
wykorzystują one łącznie tylko 5 argumentów.

y1 = !x2x4!x9 + x2x19!x20 + !x2!x4x9!x19
y1 = !x2x4!x9 + x2x19!x20 + !x2x9!x19!x20

Przykład 3 (funkcja LeI20.pla)

Variables = 20
Functions = 1
Data lines = 40

Variable names:
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20
Function names:
y1

11101101100011000111 1
00010010111100111000 1
00100100000100110001 1
01001011110110100111 1
11110111100111010111 1
00001000011110101000 1
11000010000100010000 1
11010110000100011100 1
10001100001011111010 1
01110111110100000101 1
00110111111100110000 1
00010101000101100000 1
10000101110000010100 1
10001001100001111111 1
10101010010101111001 1
01010001101010110111 1
11101001000101111010 1
00000110111000100101 1
01110000110010011010 1
01010110010011110101 1
11011000111101100010 0
11010001111000011110 0
11000111001001010101 0
11011001000000111111 0
00010001000100101000 0
11100110111011000111 0
01111110110101001100 0
10010001011010110001 0
10100110110011000011 0

22

11001011100011111110 0
00110100101110001100 0
01100101000000111100 0
10110100101011110011 0
01001011010010001100 0
11011111111001010101 0
10110100000111101100 0
00001011000000101000 0
00010011010010101000 0
00011010111010010111 0
11000100010011000011 0

Program espresso daje następujący wynik:

.i 20
.o 1
.p 5
----------0---01---- 1
----------0-----01-- 1
1--0-0------0------- 1
-------0--------10-- 1
0-------------1-0--- 1
.e

Zminimalizowana funkcja używa 10 argumentów, które składają się na 5 termów
funkcji:

y1 = !x11!x15x16 + !x11!x17x18 + x1!x4!x6!x13 + !x8x17!x18 + !x1x15!x17

Program Pandor daje następujące wyniki:

Po redukcji argumentów:

Program generuje wszystkie możliwe minimalne ze względu na liczbę agrumentów
realizacje funkcji, które są funkcjami tylko 6-argumentowymi:

R1 = {x1,x2,x3,x6,x11,x17}
R2 = {x1,x2,x4,x8,x13,x17}
R3 = {x1,x2,x6,x11,x17,x18}
R4 = {x1,x2,x8,x17,x18,x19}
R5 = {x1,x2,x11,x17,x18,x19}
R6 = {x1,x3,x4,x6,x8,x20}
R7 = {x1,x3,x6,x8,x9,x20}
R8 = {x1,x4,x5,x7,x12,x14}
R9 = {x1,x4,x6,x8,x13,x20}
R10 = {x1,x4,x8,x11,x13,x17}
R11 = {x1,x5,x6,x9,x12,x13}
R12 = {x1,x5,x9,x12,x13,x17}
R13 = {x1,x8,x13,x14,x17,x18}
R14 = {x2,x3,x6,x8,x17,x19}
R15 = {x2,x3,x8,x13,x14,x15}
R16 = {x2,x3,x8,x13,x17,x19}
R17 = {x2,x3,x8,x17,x19,x20}
R18 = {x2,x4,x7,x9,x13,x14}
R19 = {x2,x4,x8,x13,x14,x17}
R20 = {x2,x5,x6,x12,x13,x16}
R21 = {x2,x5,x12,x13,x14,x16}
R22 = {x2,x5,x12,x13,x16,x17}
R23 = {x2,x8,x13,x16,x17,x18}
R24 = {x2,x10,x12,x13,x17,x19}
R25 = {x3,x4,x7,x9,x12,x17}
R26 = {x3,x4,x8,x17,x19,x20}

23

R27 = {x3,x6,x7,x8,x9,x20}
R28 = {x3,x6,x8,x9,x16,x20}
R29 = {x3,x6,x8,x9,x19,x20}
R30 = {x3,x8,x9,x14,x19,x20}
R31 = {x3,x8,x9,x17,x19,x20}
R32 = {x3,x8,x13,x14,x17,x18}
R33 = {x3,x8,x14,x17,x19,x20}
R34 = {x4,x7,x8,x10,x14,x17}
R35 = {x4,x7,x8,x14,x17,x19}
R36 = {x4,x7,x10,x13,x14,x17}
R37 = {x4,x8,x10,x13,x14,x17}
R38 = {x4,x8,x13,x14,x17,x18}
R39 = {x5,x6,x7,x9,x12,x13}
R40 = {x5,x6,x9,x12,x13,x16}
R41 = {x6,x7,x8,x14,x17,x19}
R42 = {x6,x7,x9,x13,x16,x20}
R43 = {x6,x8,x9,x13,x16,x20}
R44 = {x6,x8,x9,x14,x19,x20}
R45 = {x6,x8,x9,x16,x19,x20}
R46 = {x7,x8,x9,x11,x14,x15}
R47 = {x7,x8,x9,x14,x15,x19}
R48 = {x7,x8,x9,x14,x17,x19}
R49 = {x7,x8,x9,x14,x19,x20}
R50 = {x7,x8,x14,x15,x17,x19}
R51 = {x7,x8,x14,x17,x18,x19}
R52 = {x7,x9,x13,x14,x16,x17}
R53 = {x7,x10,x13,x14,x16,x17}
R54 = {x7,x11,x13,x14,x17,x18}
R55 = {x8,x9,x10,x14,x19,x20}
R56 = {x8,x9,x11,x14,x15,x20}
R57 = {x8,x9,x13,x14,x16,x17}
R58 = {x8,x9,x13,x14,x17,x18}
R59 = {x8,x9,x13,x14,x19,x20}
R60 = {x8,x9,x14,x15,x19,x20}
R61 = {x8,x9,x14,x16,x19,x20}
R62 = {x8,x9,x14,x18,x19,x20}
R63 = {x8,x10,x13,x14,x16,x17}
R64 = {x8,x10,x13,x14,x19,x20}
R65 = {x8,x11,x13,x14,x17,x18}
R66 = {x8,x13,x14,x15,x17,x18}
R67 = {x8,x13,x14,x15,x17,x19}
R68 = {x8,x13,x14,x16,x17,x18}
R69 = {x8,x13,x14,x17,x18,x19}
R70 = {x11,x13,x14,x15,x17,x18}
R71 = {x11,x13,x14,x15,x18,x20}
R72 = {x11,x14,x15,x16,x18,x20}

Każdą z powyższych realizacji możemy poddać procedurze ekspansji.

Wniosek:

Program Pandor znalazł szereg minimalizacji funkcji, które mają 6 argumentów
(Espresso ma ich 10).



W przypadku używania programu Pandor do projektowania wszelkiego rodzaju
układów sekwencyjnych lub kombinacyjnych jesteśmy w stanie utworzyć rozwiązanie
o strukturze najprostszej ze wszystkich możliwych.

24

Bardzo często ma to zdecydowany wpływ na koszty produkcji, zwłaszcza gdy mamy
do czynienia z elementami produkowanymi masowo jak na przykład układy scalone.

I jakkolwiek celem niniejszej pracy nie były realizacje praktycznych układów, to już
można przewidywać zastosowania Pandora w zadaniach o charakterze aplikacyjnym.
Typowym przykładem takich zastosowań może być redukcja argumentów bloków
kombinacyjnych filtrów cyfrowych.

Filtr cyfrowy 4-rzędu jest opisany tablicą prawdy o 7 wejściach i 8 wyjściach.
Programem Pandor szybko można obliczyć, że w rzeczywistości poszczególne
wyjścia są zależne od następujących argumentów:

Results for function y1:
R1 = {x1,x3,x4,x5,x7}

Results for function y2:
R1 = {x1,x3,x4,x5,x7}

Results for function y3:
R1 = {x1,x3,x4,x5,x7}

Results for function y4:
R1 = {x1,x3,x5,x7}

Results for function y5:
R1 = {x1,x3,x5,x7}

Results for function y6:
R1 = {x1,x3,x5,x7}

Results for function y7:
R1 = {x1,x3,x5,x7}

Results for function y8:
R1 = {x1,x3,x5,x7}

Można przypuszczać, że uwzględnienie tej redukcji w dalszych zabiegach
optymalizacyjnych istotnie wpłynie na realizację całego filtru.


Filtr cyfrowy 7-rzędu jest opisany tablicą prawdy o 11 wejściach i 12 wyjściach.
Tabela prawdy składa się z 2048 rzędów, jest to więc funkcja pełna.
Programem Pandor można obliczyć, że w rzeczywistości poszczególne wyjścia są
zależne od następujących argumentów:

Results for function y1:
R1 = {x3,x5,x6,x7,x9}

Results for function y2:
R1 = {x1,x3,x5,x6,x7,x9,x11}

Results for function y3:
R1 = {x1,x3,x5,x6,x7,x9,x11}

Results for function y4:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y5:
R1 = {x1,x3,x5,x7,x9,x11}

25

Results for function y6:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y7:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y8:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y9:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y10:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y11:
R1 = {x1,x3,x5,x7,x9,x11}

Results for function y12:
R1 = {x1,x3,x9,x11}

Uwzględnienie tej redukcji w dalszych zabiegach optymalizacyjnych istotnie wpłynie
na realizację całego filtru.

Przeprowadzenie redukcji dla wszystkich wyjść funkcji łącznie daje wynik:

R1 = {x1,x3,x5,x6,x7,x9,x11}

Program Pandor pozwala stwierdzić, że funkcja jest niezależna od argumentów
x2, x4, x8 oraz x10, co wpłynie na znaczne uproszczenie dalszych obliczeń.
Z 11 argumentów funkcja redukuje się do 7-miu. Oznacza to jednocześnie redukcję
liczby wierszy w tabeli prawdy z 2048 do 128.

26