MECHANIKA BUDOWLI

Architektura sem. II letni

GEOMETRIA MAS

dr inż. Marek BARTOSZEK

KTKB p.126 WB

[e-mail]

http://kateko.rb.polsl.pl/

11-3-22

Za wszystkie uwagi odnośnie poniższych wykładów z góry dziękuję.

Jeśli ktoś chciałby wykorzystać te materiały to proszę o kontakt.

www.rb.polsl.pl

22.03.11

dr inż. Marek Bartoszek

2

Geometria mas

Geometria figur płaskich (pól przekrojów)

Wprowadzenie

22.03.11

dr inż. Marek Bartoszek

3

Geometria mas a geometria figur

płaskich (przekrojów)

Masa

m

dowolnego elementu

konstrukcji zależy od jego
objętości

V

:

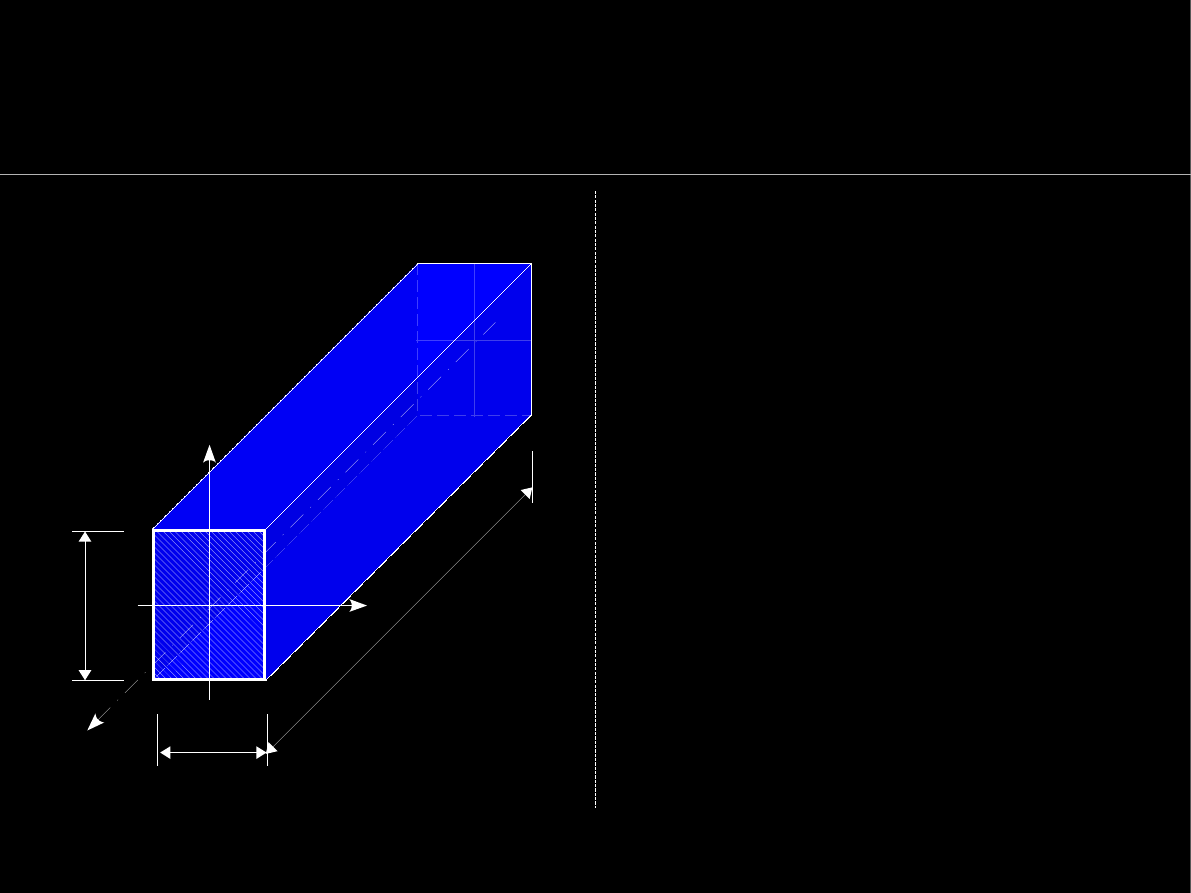
Objętość

V

pręta o stałym

przekroju na całej długości

L

(

pręt pryzmatyczny

) zależy

głównie od pola

A

jego

przekroju poprzecznego:

Tak więc

geometria mas

w przypadku elementów
prętowych zwykle sprowadza

się do

geometrii pól

przekroju

.

b

h

y

x

z

L

m=∗V

m=∗L∗A

A=b*h
V=L*A

22.03.11

dr inż. Marek Bartoszek

4

Geometria mas

Charakterystyka geometryczna przekroju

Wielkości charakteryzujące

geometrię pola przekroju:

●

Wymiary [m]: b, h, t, a

●

Pole powierzchni [m

2

]:A lub F

●

Momenty statyczne pola

[m

3

]:

S

x

, S

y

●

Momenty bezwładności i
dewiacji pola

[m

4

]: I

x

, I

y

, D

xy

●

Promienie bezwładności

[m]:

i

x

, i

y

●

Wskaźniki zginania

[m

3

]:

W

x

, W

y

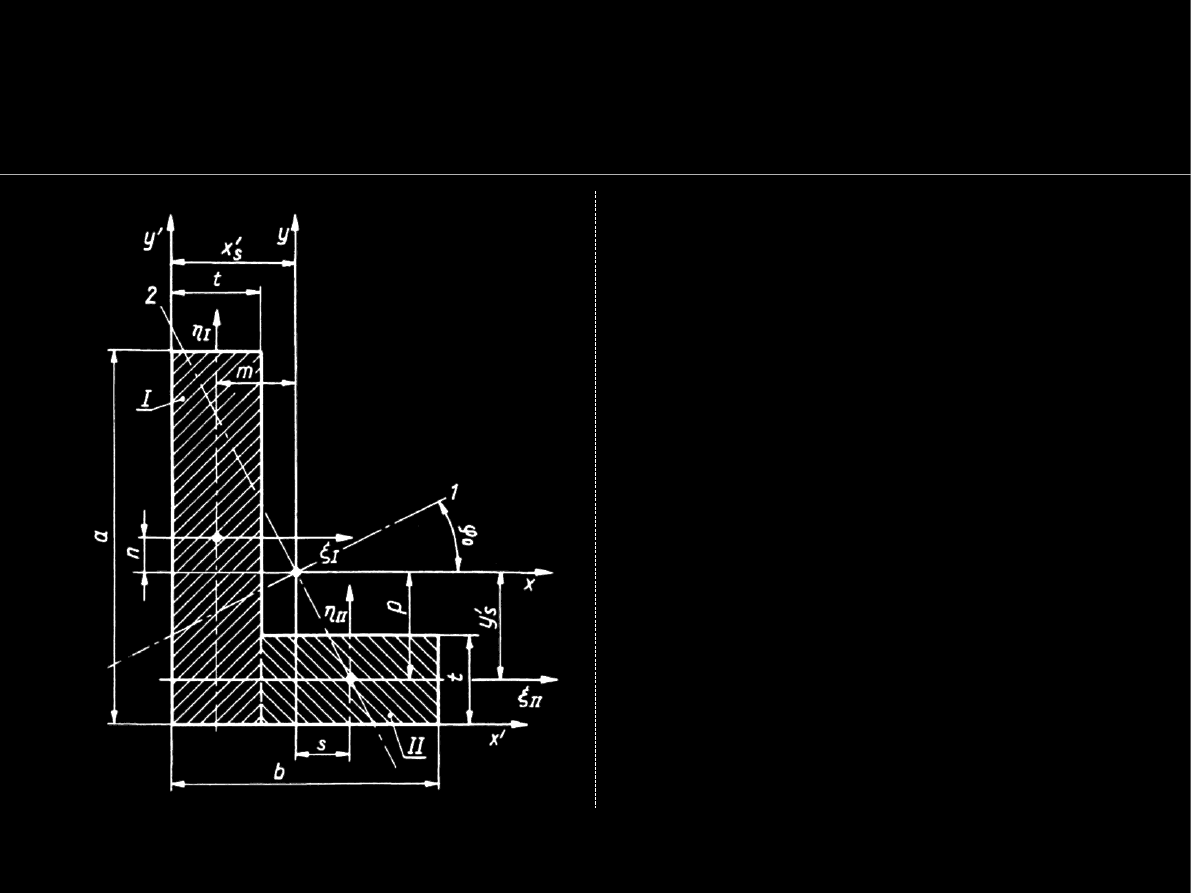
Z. Dyląg i in. str.174 rys 8.12

22.03.11

dr inż. Marek Bartoszek

5

Geometria mas

Przekrój złożony z figur prostych

Figury proste

– znane są ich

charakterystyczne wielkości
geometryczne (m.in.: pole
powierzchni, położenie

środka ciężkości i momenty
bezwładności).

Dane geometryczne różnych

podstawowych figur

zestawiono w tablicach.

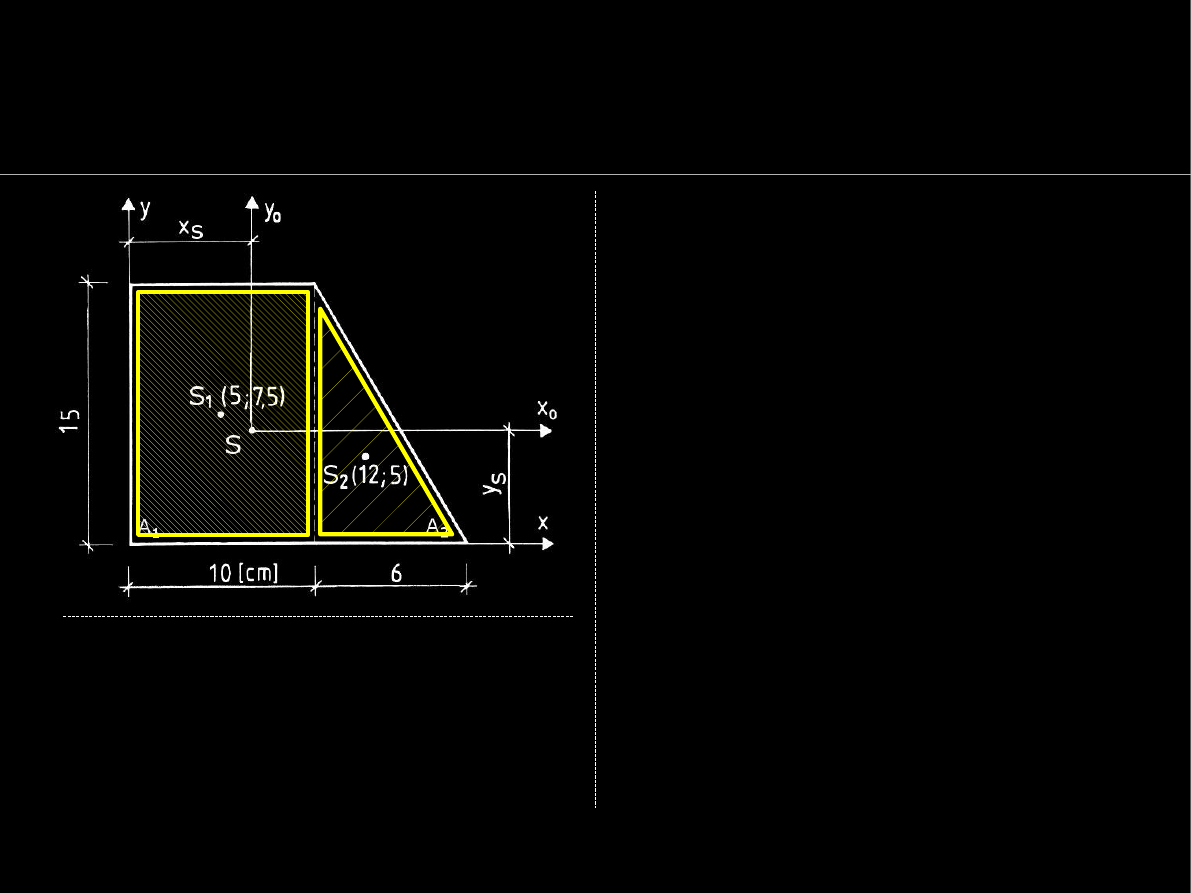
Jeżeli

pole przekroju A

składa

się z kilku

figur prostych

A

i

(jak na rysunku), to mówimy

o złożonym przekroju

poprzecznym pręta

.

A=

∑

i=1

2

A

i

Przekrój dzielimy na figury proste

w taki sposób, aby ułatwić dalsze
obliczenia.

Również układ współrzędnych dobiera

się kierując prostotą dalszych obliczeń.

22.03.11

dr inż. Marek Bartoszek

6

Geometria mas

Geometria przekroju złożonego

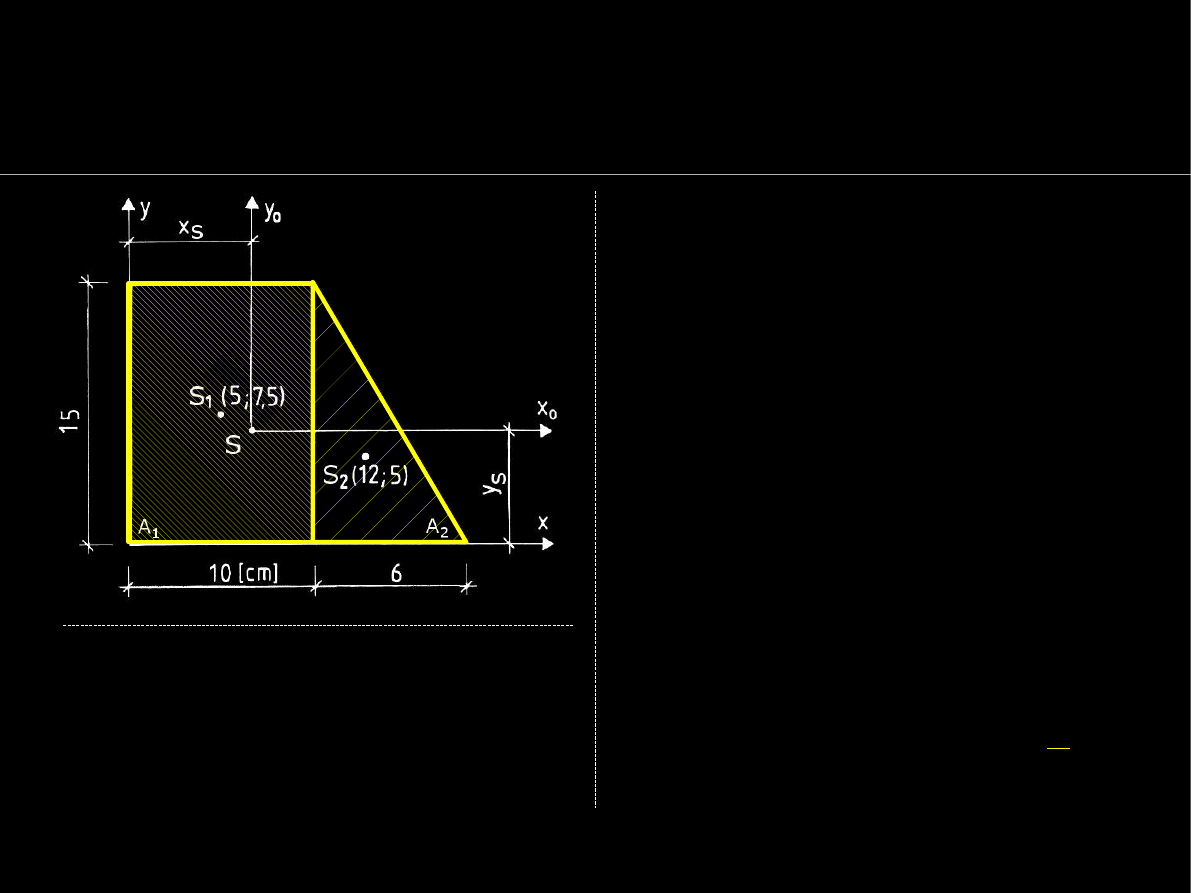
Złożony przekrój

A

dzieli się na

figury proste

A

i

.

Pole złożonego przekroju A

jest oczywiście sumą

pól

figur składowych A

i

:

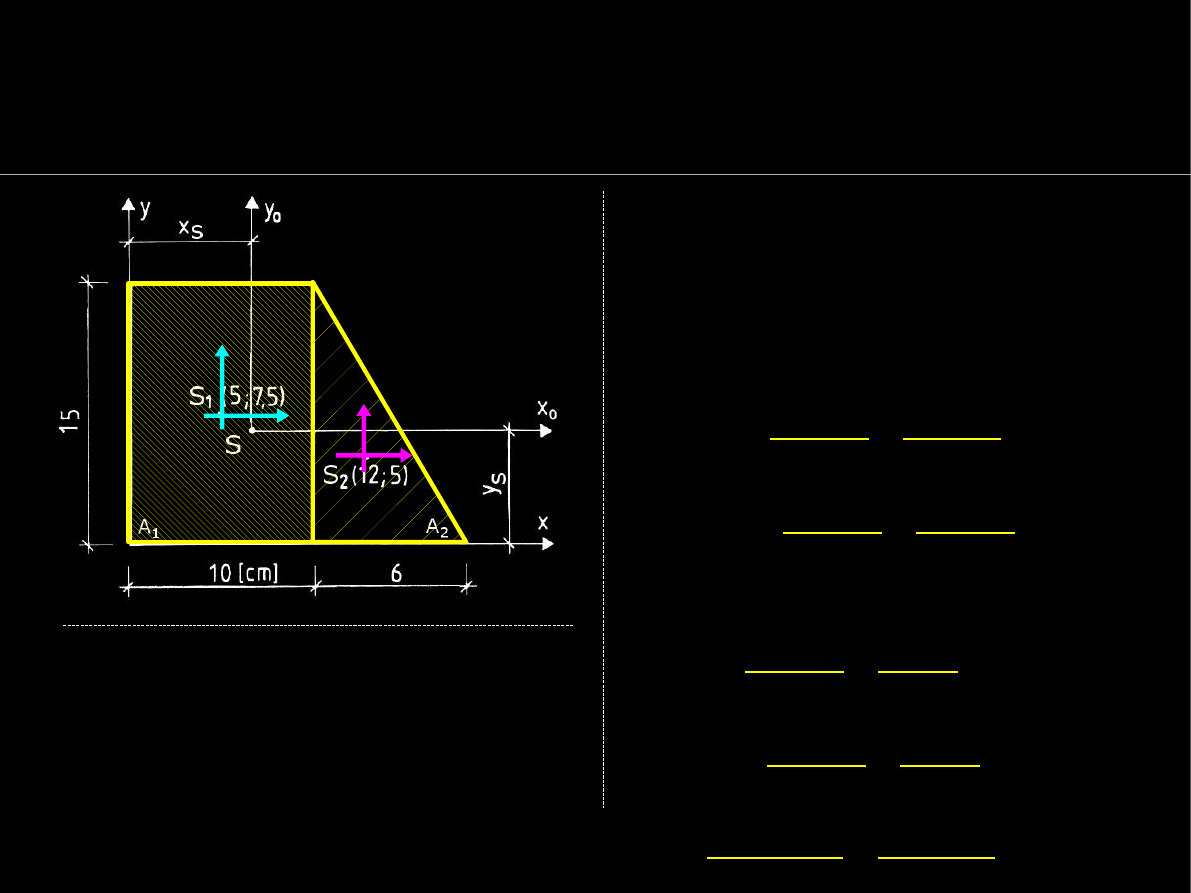
Dla przekroju z rysunku obok

otrzymamy sumę pól:

A=

∑

i=1

2

A

i

=

A

1



A

2

=

150

1

2

⋅

90=

=

195 cm

2

Pola, momenty statyczne

i momenty bezwładności

przekroju

złożonego A

oblicza się sumując

odpowiednie wielkości dla figur
składowych

A

i

.

A=

∑

i=1

n

A

i

=

A

1



A

i



A

n

22.03.11

dr inż. Marek Bartoszek

7

Geometria mas

Figury proste – bierzemy wzory z tablic

Na podst. tablic dla prostokąta i

trójkąta jako figur prostych:

I

x

1



1

=

dx⋅dy

3

12

=

10⋅15

3

12

=

2812,5 cm

4

I

y

1



1

=

dy⋅dx

3

12

=

15⋅10

3

12

=

1250 cm

4

D

x

1

y

1



1

=

0 cm

4

W tablicach matematycznych znajdziemy

wzory dla figur geometrycznych

Gotowe wartości liczbowe dla profili

walcowanych (dwuteowników,
kątowników, itp) zestawiono
w tablicach konstrukcji metalowych

I

x

2



2

=

dx⋅dy

3

36

=

6⋅15

3

36

=

562,5 cm

4

I

y

2



2

=

dy⋅dx

3

36

=

15⋅6

3

36

=

90 cm

4

D

x

2

y

2



2

=

−

dx

2

⋅

dy

2

72

=

−

6

2

⋅

15

3

72

=−

112,5cm

4

A

1

=

dx⋅dy=10⋅15=150 cm

2

A

2

=

1/2⋅dx⋅dy=1/ 2⋅6⋅15=45 cm

2

y

2

x

2

x

1

y

1

dx

1

dx

2

dy

22.03.11

dr inż. Marek Bartoszek

8

Geometria mas

Momenty statyczne

– środek ciężkości przekroju

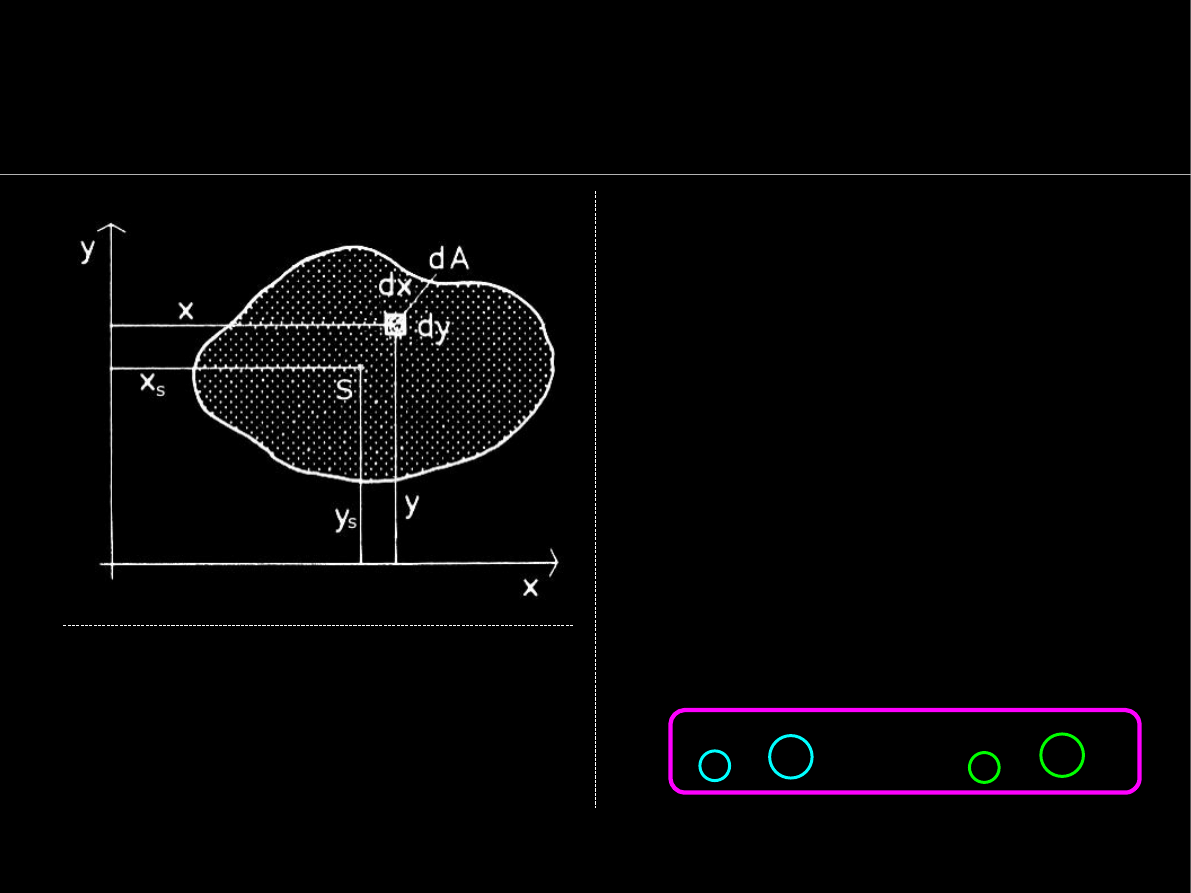
Jeśli pole przekroju

A

ma

środek ciężkości w punkcie

S(x

s

,y

s

)

w układzie

OXY

, to

momenty statyczne S

x

, S

y

pola

A względem osi

OX i OY

tego

układu

oblicza się jako:

Momenty statyczne

dowolnego

pola

A

względem osi układu

OXY

definiuje się jako sumy:

S

x

=

A∗y

s

oraz

S

y

=

A∗x

s

S

x

=

∫

y dA

oraz

S

y

=

∫

x dA

Aby uniknąć pracochłonnego całkowania

pole przekroju dzieli się na figury
proste – o znanych charakterystykach
geometrycznych.

O

(x

s

,y

s

)

A

22.03.11

dr inż. Marek Bartoszek

9

Geometria mas

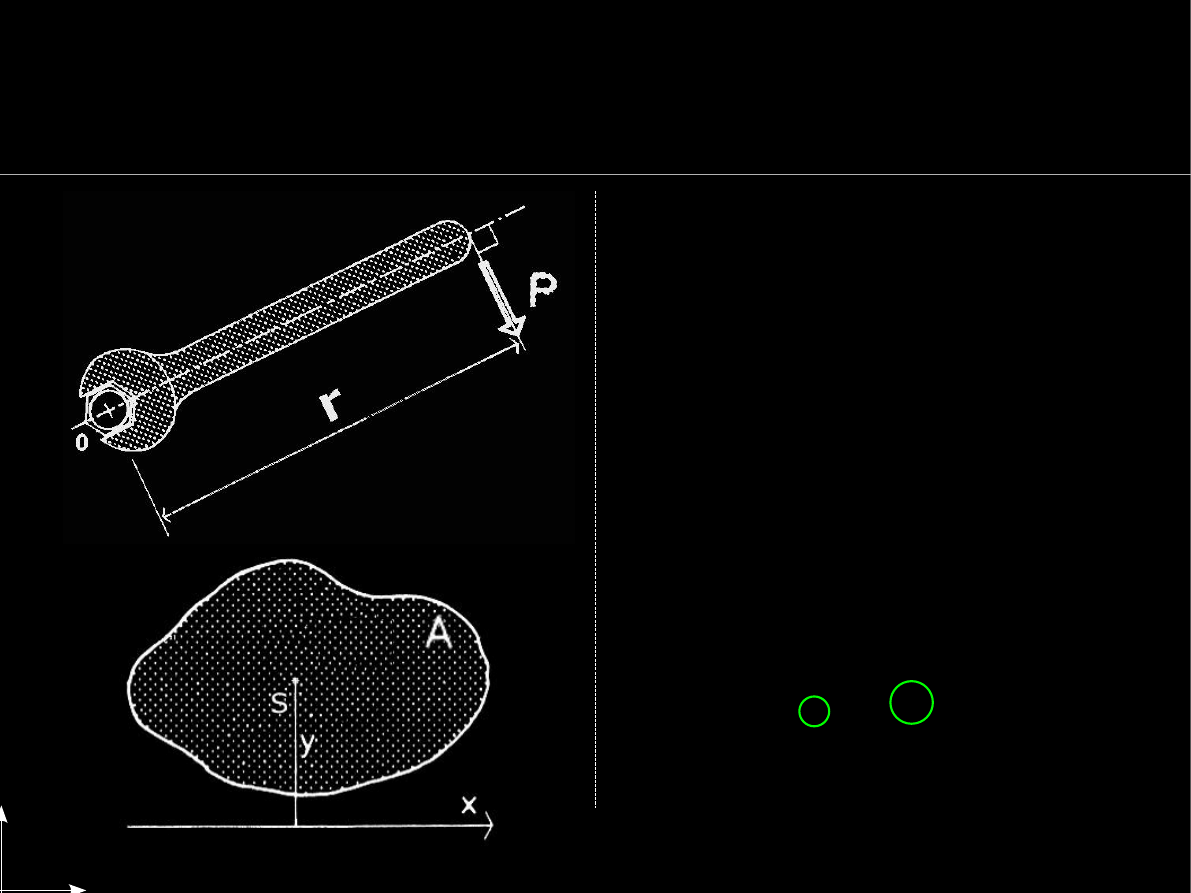
Moment statyczny pola a moment siły

Moment statyczny pola

jest

analogią do

momentu siły

skupionej w statyce

:

Moment M siły P w statyce to:

r

– jest

odległością

osi obrotu

O od kierunku działania siły

P

.

Moment statyczny pola

A

względem osi OX – czyli

S

x

:

y

– jest

współrzędną

środka

ciężkości pola

A

wzgl. osi OX.

S

x

=

A∗y

M=P∗r

x

y

22.03.11

dr inż. Marek Bartoszek

10

Geometria mas

Momenty statyczne przekroju złożonego

Momenty statyczne pola

wzgl.

osi OX i OY układu współrz.
dla

przekroju złożonego

są

sumą tychże dla fig. skład.:

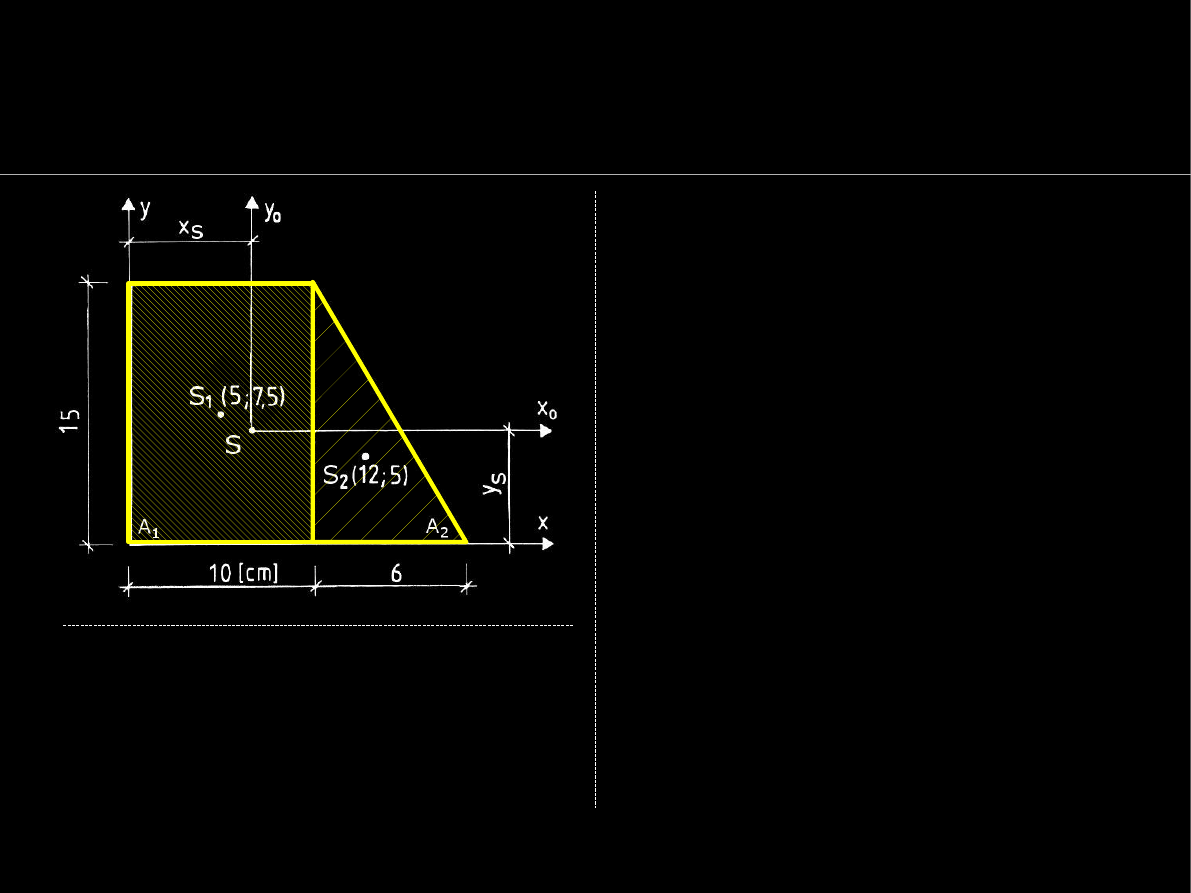
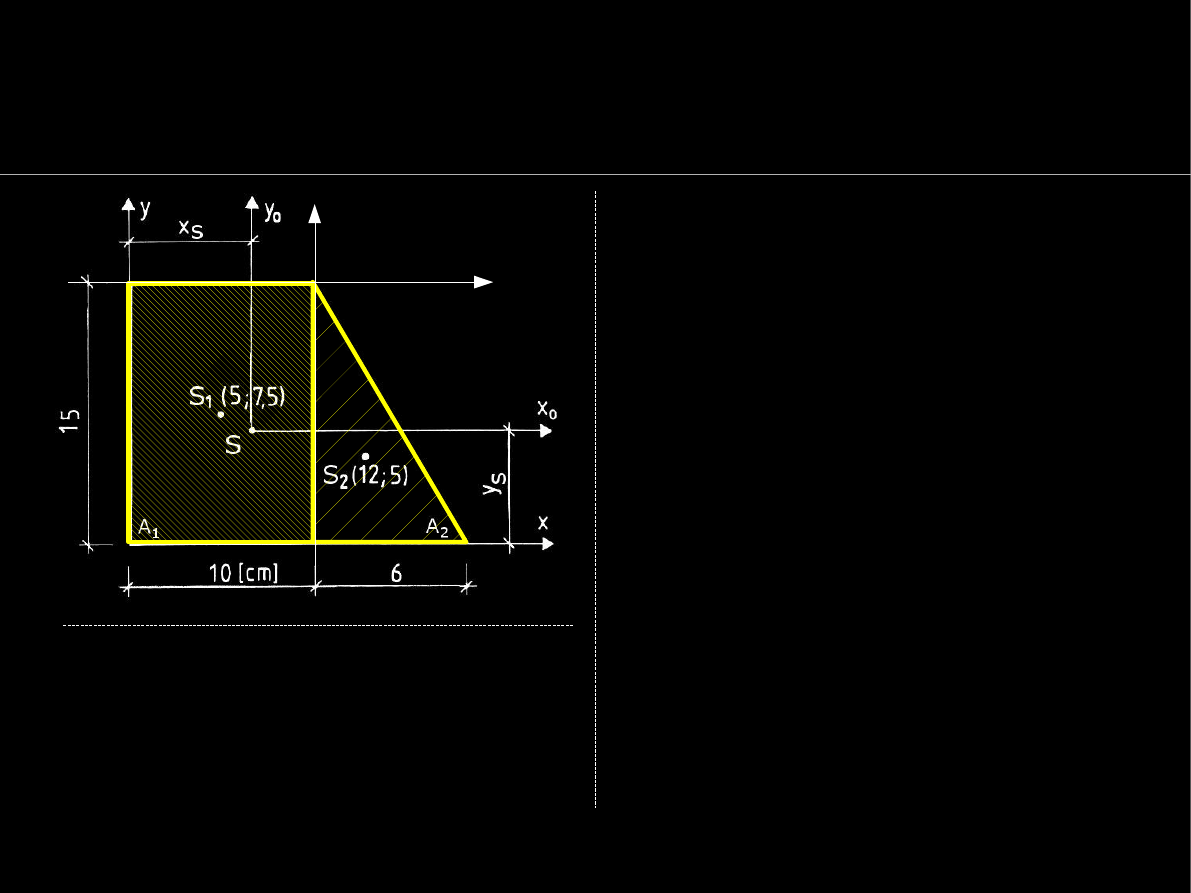
Dla przekroju obok otrzymamy:

S

x

=

∑

i=1

2

S

x



i

=

y

1

A

1



y

2

A

2

=

7.5⋅150



5⋅45=1350 cm

3

S

y

=

x

1

A

1



x

2

A

2

=

5⋅150102⋅45=

=

1290 cm

3

Dodawać można tylko te momenty

statyczne

S

x

(i)

(lub

S

y

(i)

), które są

obliczone względem tej samej osi OX
(lub OY) lub osi pokrywających się –
leżących na jednej linii.

S

x

=

∑

i=1

n

S

x



i

=

∑

i=1

n

y

i

A

i

S

y

=

∑

i=1

n

S

y



i

=

∑

i=1

n

x

i

A

i

22.03.11

dr inż. Marek Bartoszek

11

Geometria mas

Momenty statyczne – przykład c.d.

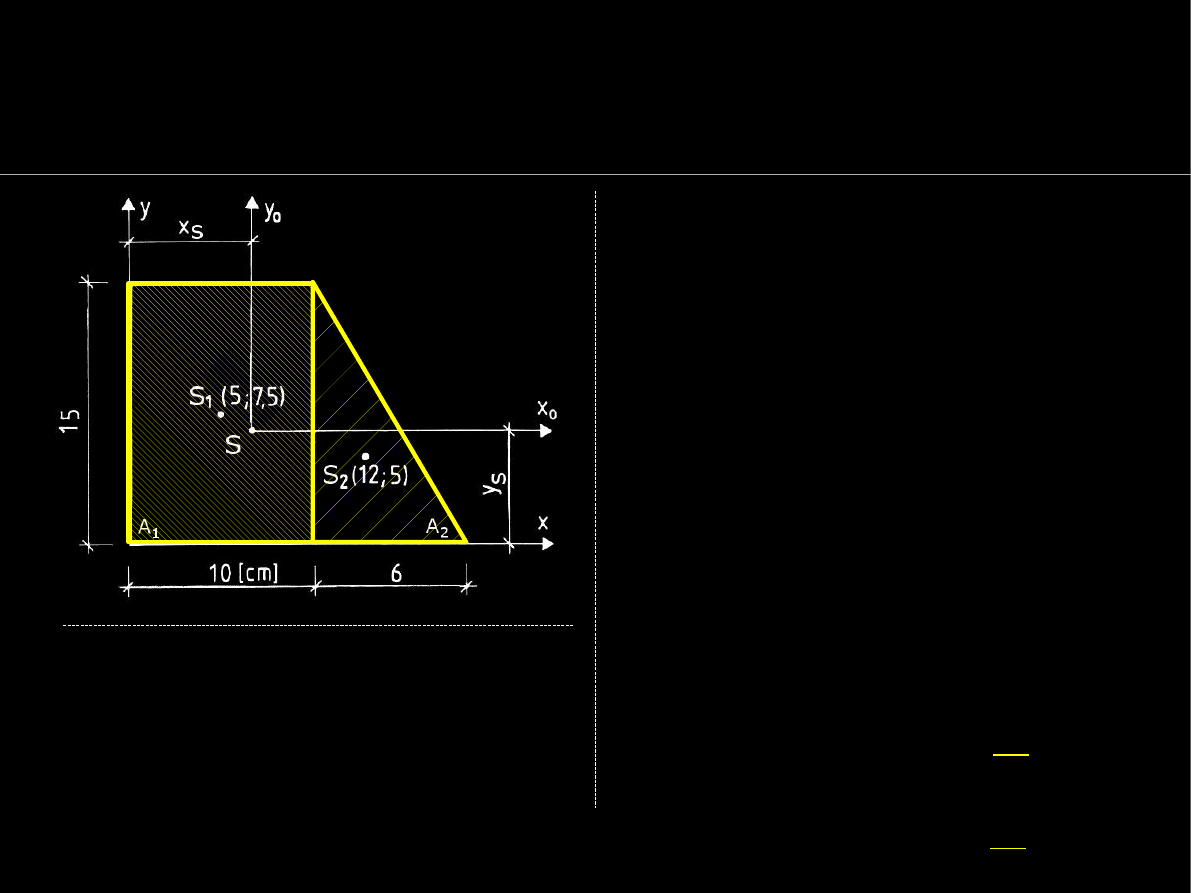
Natomiast względem OX'Y'

momenty statyczne pola
przekroju obok obliczymy:

Momenty statyczne figur

obliczone względem różnych

osi nie sumuje się (

!

) :

S

x '

=

y '

1

A

1



y '

2

A

2

=−

7.5⋅150−

−

10⋅45=1575 cm

3

S

y '

=

x '

1

A

1



x '

2

A

2

=−

5⋅1502⋅45=

=−

660 cm

3

Sumować można tylko te momenty

statyczne

S

x

(i)

(lub

S

y

(i)

), które są

obliczone względem tej samej osi OX
(lub OY) lub osi pokrywających się –
leżących na jednej linii.

y'

x'

S

y

0



1



S

y '



2

=

błąd !

−

różne osie OY

0

i OY '

S

x

0



1



S

x



2

=

błąd !

−

różne osie OX

0

i OX

22.03.11

dr inż. Marek Bartoszek

12

Wzory na momenty statyczne

dla całego pola przekroju
wymagają znajomości

współrzędnych

jego

środka

ciężkości

x

s

i

y

s

:

Znając

pole powierzchni A

całego przekroju oraz jego

momenty statyczne

S

x

, S

y

wyznaczymy

współrzędne

jego

środka ciężkości x

s

i

y

s

:

Geometria mas

Środek ciężkości przekroju – momenty statyczne

S

x

=

A

∗

y

s

⇒

y

s

=

S

x

A

S

y

=

A

∗

x

s

⇒

x

s

=

S

y

A

S

x

=

A

∗

y

s

lub

S

y

=

A

∗

x

s

Momenty statyczne

S

x

(i)

i

S

y

(i)

) oraz pola

powierzchni

A

i

przekroju złożonego

obliczymy jako sumy odpowiednich
wielkości dla figur składowych.

22.03.11

dr inż. Marek Bartoszek

13

Geometria mas

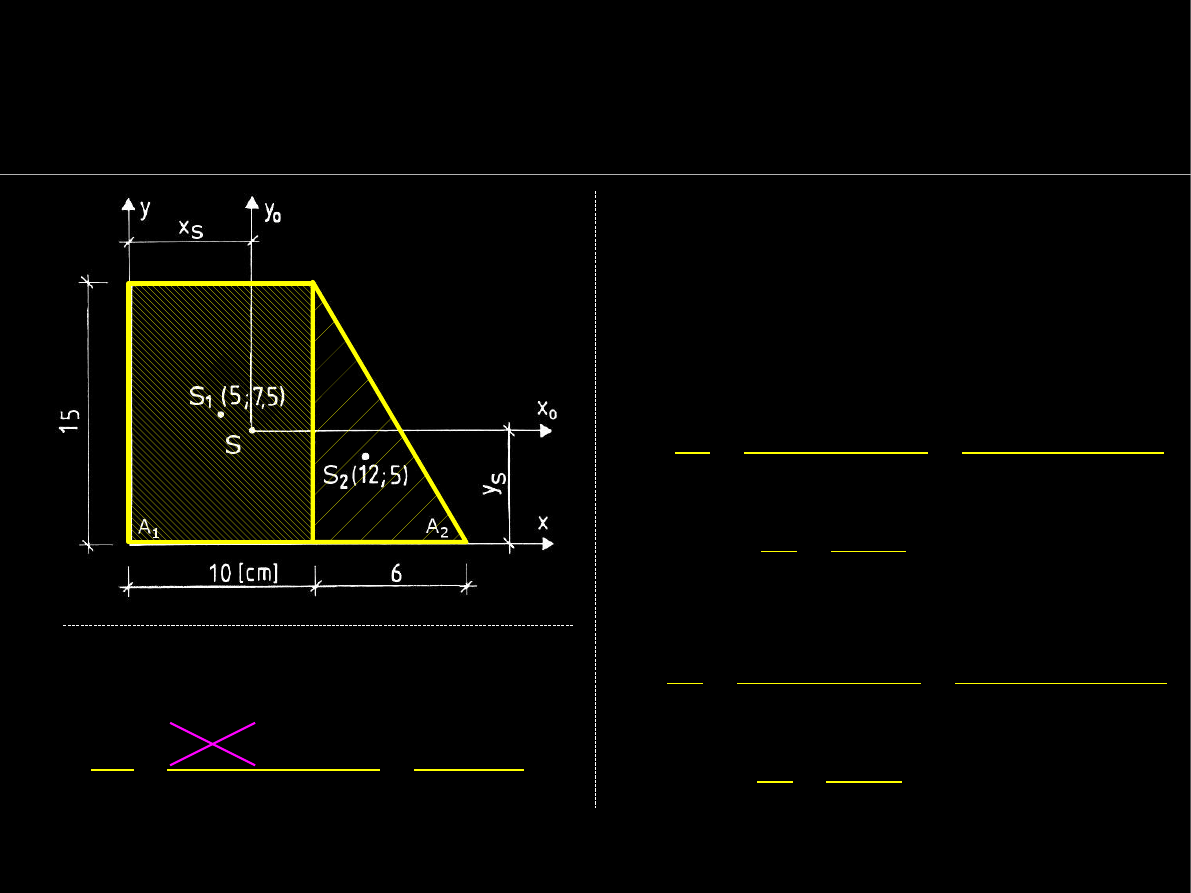
Środek ciężkości przekroju – przykład

Podstawiając odpowiednie

wielkości do wzorów
otrzymamy

współrzędne

x

s

i

y

s

w układzie OXY:

x

s

=

S

y

A

=

A

1

x

1



A

2

x

2

A

1



A

2

=

150⋅545⋅12

15045

=

=

S

y

A

=

1290

195

=

6,62 cm

y

s

=

S

x

A

=

A

1

y

1



A

2

y

2

A

1



A

2

=

150⋅7,545⋅5

15045

=

=

S

x

A

=

1350

195

=

6,92 cm

Dobrze dobrany układ współrzędnych

upraszcza obliczenia, np :

y

s1

=

S

x

1

A

=

150⋅0−45⋅2,5

15045

=

−

112,5
195

=

=−

0,577cm

22.03.11

dr inż. Marek Bartoszek

14

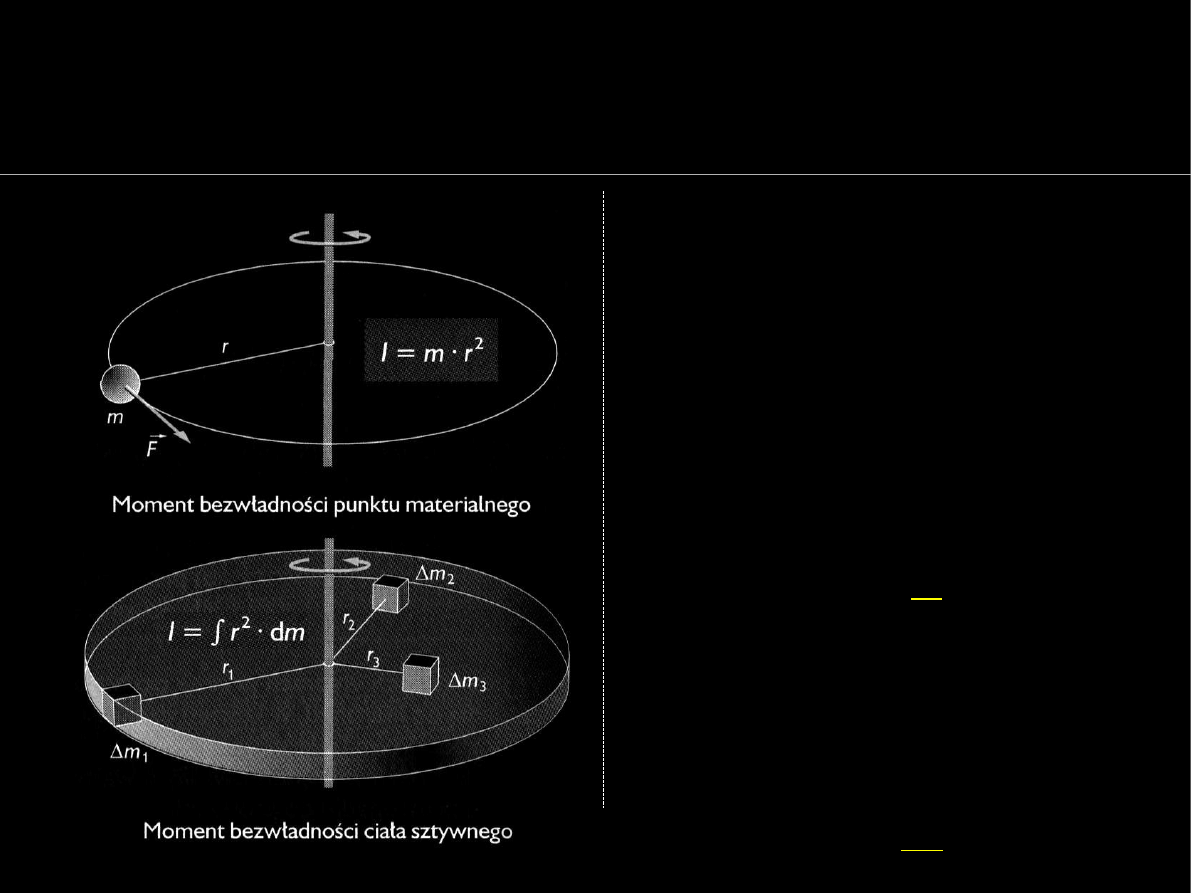
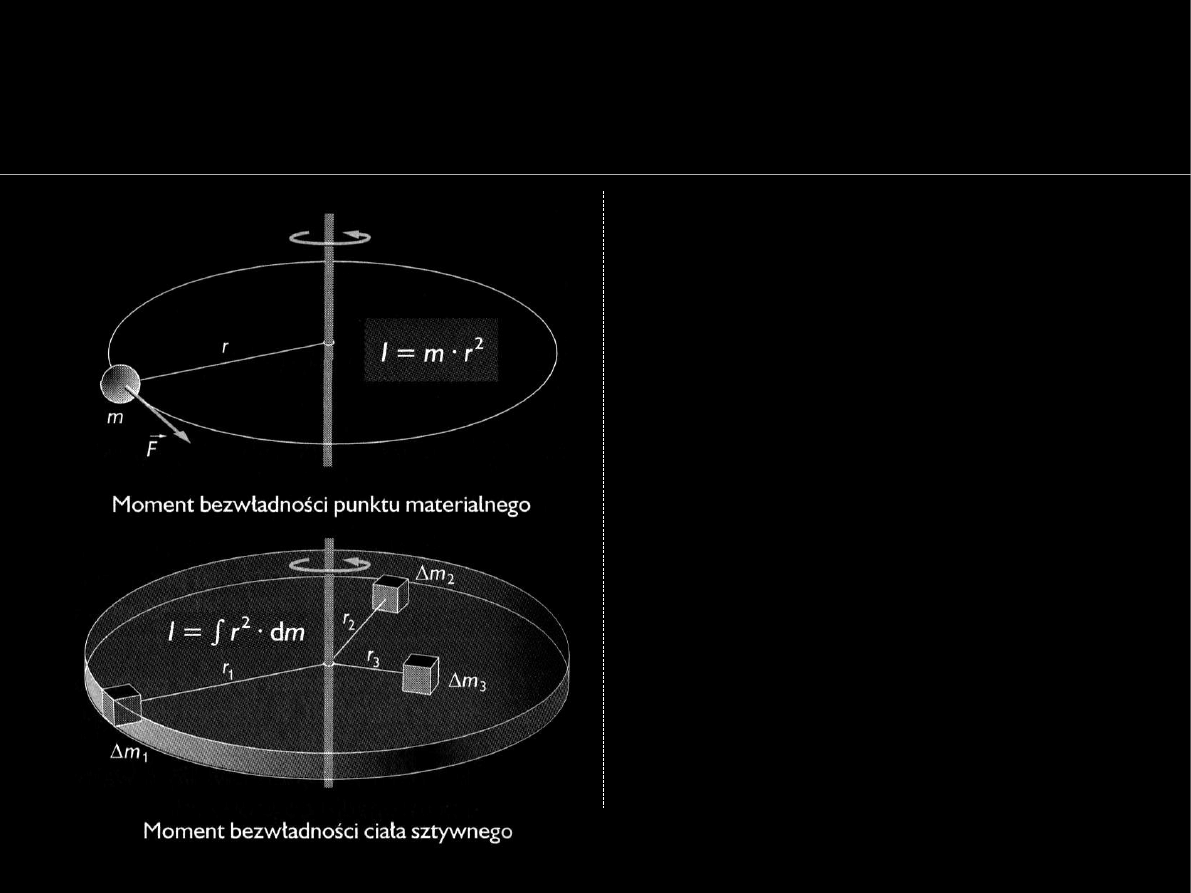
Geometria mas

Pojęcie momentu bezwładności

W fizyce moment bezwładności

masy wykorzystywany jest

w analizie ciał obracających
się wokół osi.

Tak jak przyśpieszenie ciała

a

jest proporcjonalne do

przyłożonej siły

F

oraz

odwrotnie prop. do jego
masy

m

:

tak przyśp. kątowe

ε

jest prop.

do przyłożonego momentu
siły

M

i odwrotnie prop. do

momentu bezwładności

I

:

a=

F
m

=

M

I

M=F*r

M=I*

ε

22.03.11

dr inż. Marek Bartoszek

15

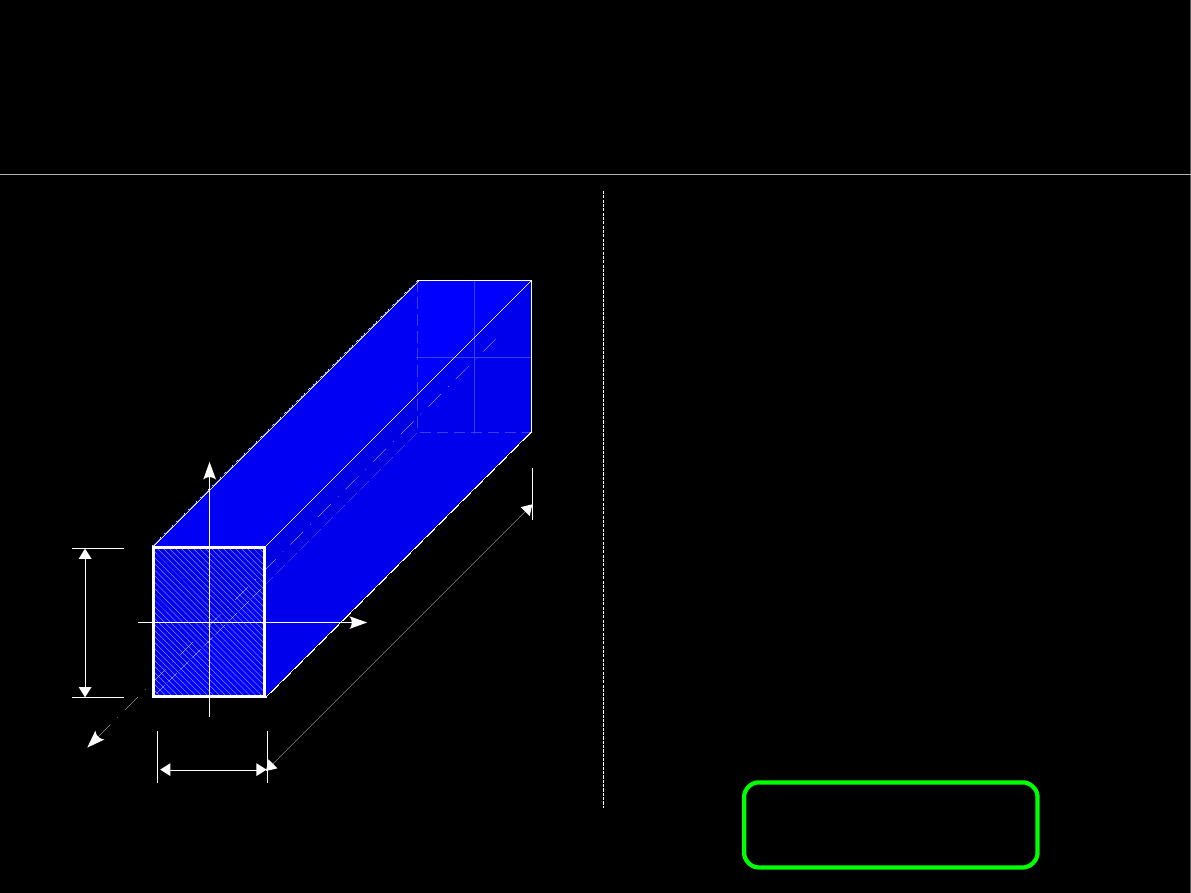
Geometria mas

Pojęcie momentu bezwładności

Moment bezwładności masy

m

to iloczyn tej masy i kwadratu

promienia

r

jej środka

ciężkości względem osi
obrotu:

Dla kilku mas

∆

m

i

wykonuje się

sumowanie odp. iloczynów:

a w przypadku ciągłego

obszaru całkowanie:

M=F*r

I =m⋅r

2

I =

∫

r

2

dm

I =

∑

i=1

n

r

i

2

∗

m

i

M=I*

ε

22.03.11

dr inż. Marek Bartoszek

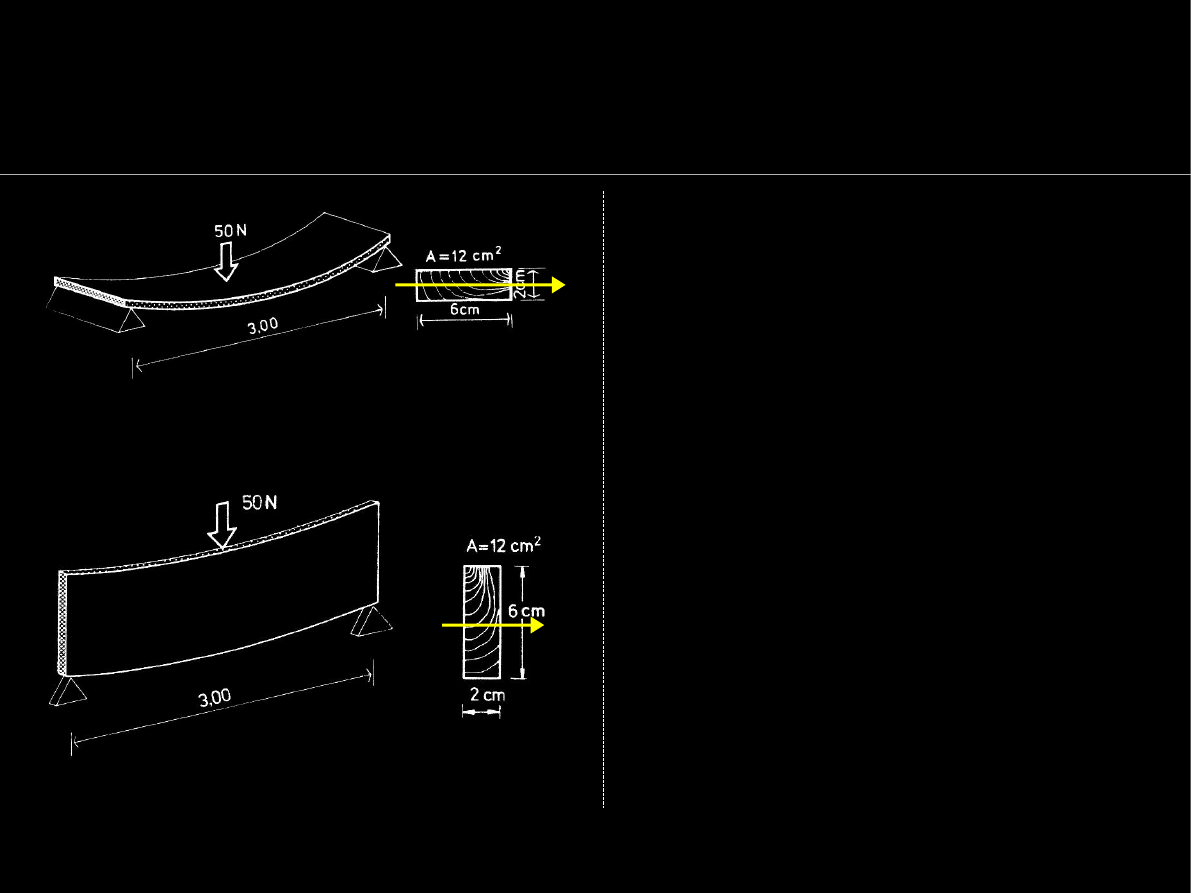
16

Geometria mas

Pojęcie momentu bezwładności

Masa

pręta pryzmatycznego

to

iloczyn długości

L

pola,

stałego przekroju

A

i ciężaru

objętościowego

ρ

materiału:

Moment bezwładności pręta

I

jest wówczas proporcjonalny
do

momentu bezwładności

pola przekroju pręta

, np.

I

x

– wzgl. osi OX:

m=

ρ

*V=

ρ

*L*A

A=b*h

I =

∫

r

2

dm=

∫

r

2

d  L A= L

∫

r

2

dA

I = L

∫

y

2

dA= L

∗

I

x

gdzie : I

x

=

∫

y

2

dA

b

h

y

x

z

L

22.03.11

dr inż. Marek Bartoszek

17

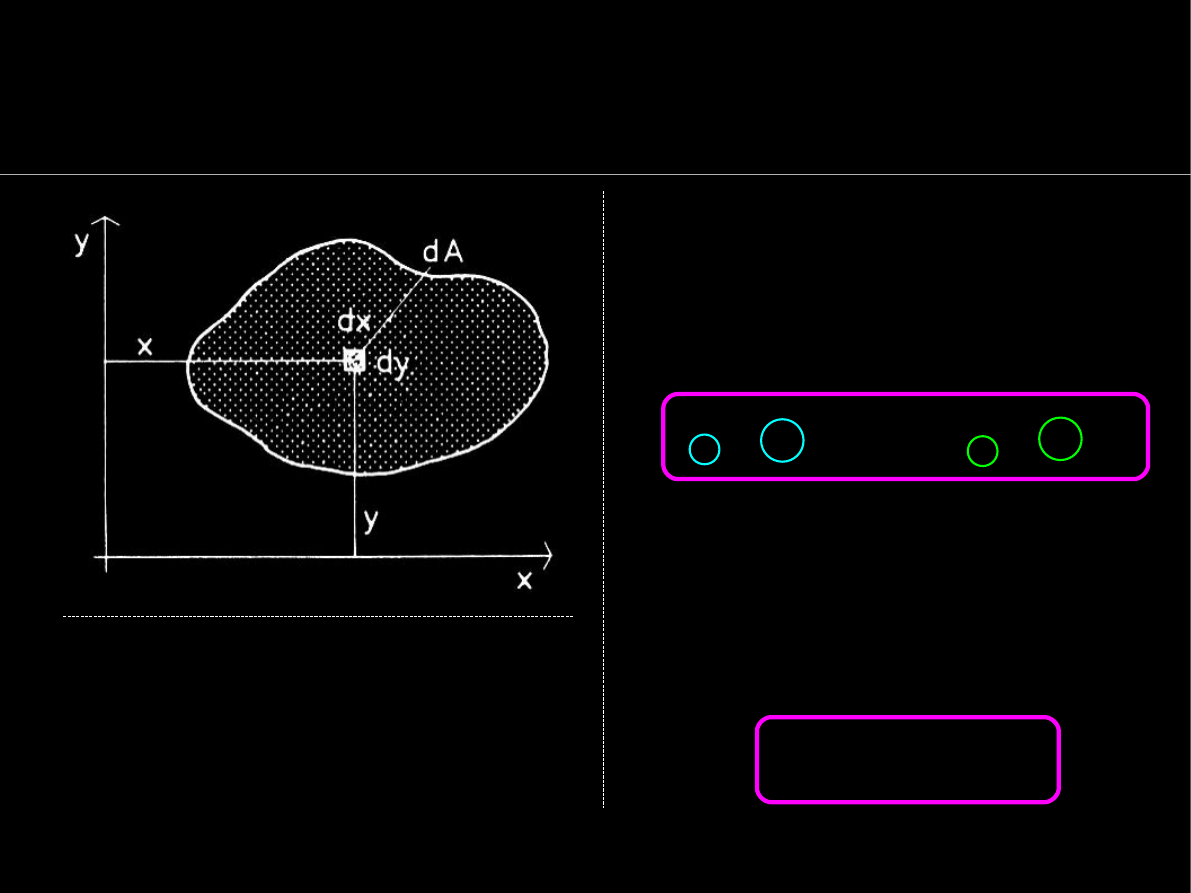
Geometria mas

Znaczenie momentu bezwładności pola przekroju

Prostokątny przekrój deski ma

dwie osie symetrii, które

przyjmujemy jako osie OXY.

Momenty bezwładności

I

x

i

I

y

wyznaczone względem osi
symetrii prostokąta różnią się
– jeden jest mniejszy od

drugiego

I

x

<

I

y

.

Ugięcie deski

u

jest odwrotnie

proporcjonalne do momentu
bezwładności obliczonego
względem osi poziomej.

Moment dewiacji

w układzie współrz. OXY,

którego oś (jedna lub obie) jest osią
symetrii, jest zerowy:

D

xy

=0.

x

I

x

=4 cm

4

u

=7 cm

y

I

y

=36 cm

4

u

=0.8 cm

22.03.11

dr inż. Marek Bartoszek

18

Geometria mas

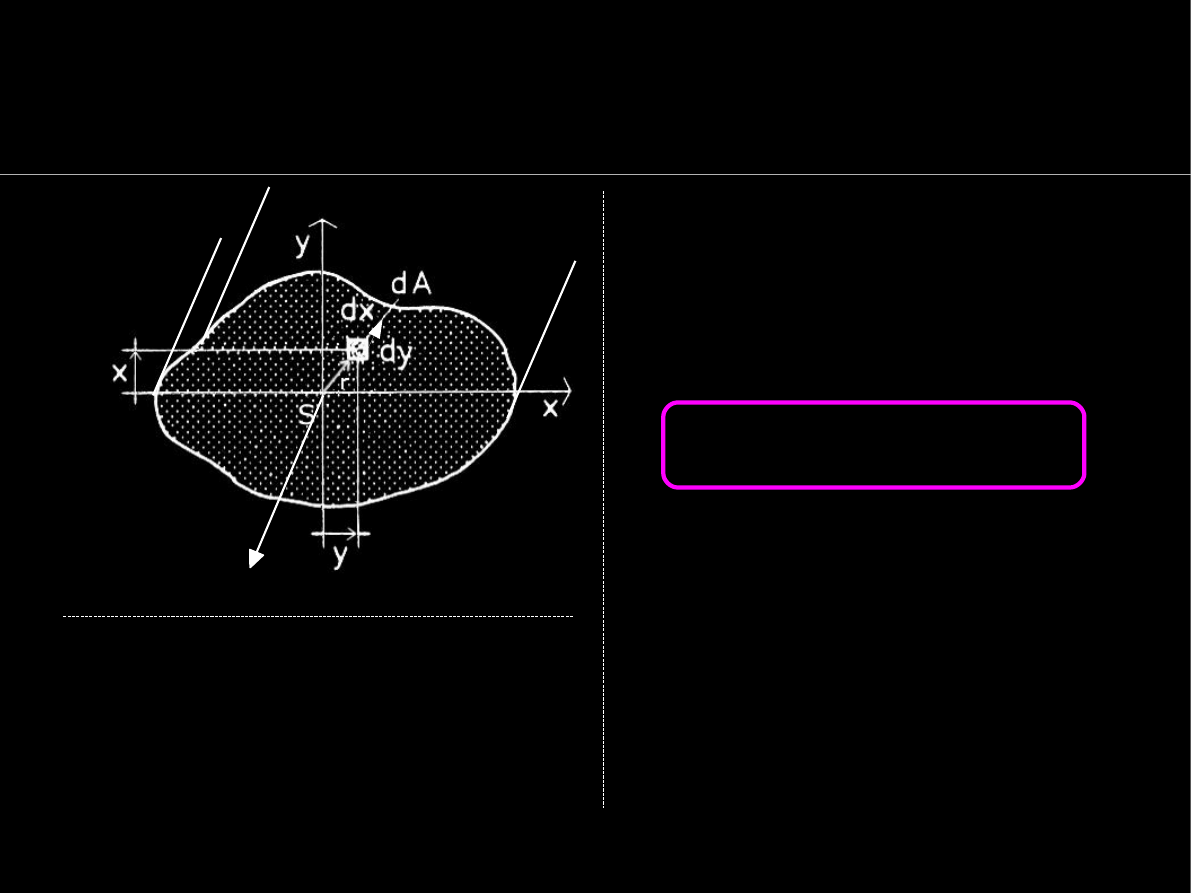
Momenty bezwładności i dewiacji pola przekroju

Moment bezwładności pola

A

przekroju pręta względem osi

układu OXY definiuje się
jako:

natomiast

moment dewiacji

pola

A

przekroju pręta

w układzie współrzędnych
OXY definiuje się:

I

x

=

∫

y

2

dA

oraz

I

y

=

∫

x

2

dA

I

xy

=

D

xy

=

∫

xy dA

Moment bezwładności

(

I

x

lub

I

y

) może być

tylko dodatni

(współrzędna w

kwadracie),

moment dewiacji

(

D

xy

)

może mieć

dowolny znak lub być równy

zeru

(iloczyn współrzędnych).

22.03.11

dr inż. Marek Bartoszek

19

Geometria mas

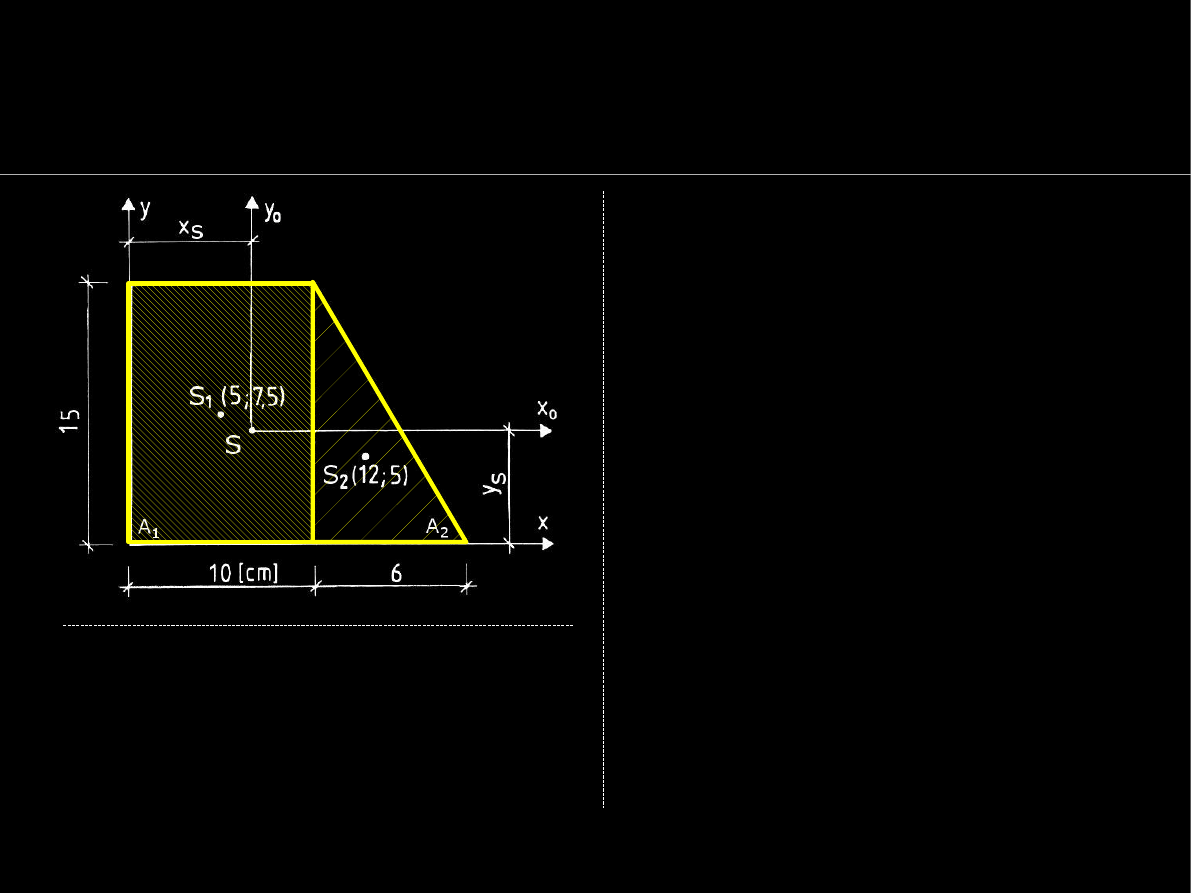
Biegunowy moment bezwładności pola przekroju

Biegunowy moment

bezwładności I

0

pola

przekroju pręta oblicza się

względem osi pręta OZ jako:

Biegunowy

moment

bezwładności

potrzebny jest

w przypadku elementów
prętowych skręcanych (wokół

osi pręta OZ) natomiast

momenty bezwładności

w

przypadku elementów

zginanych względem osi OX
lub OY.

I

0

=

∫

r

2

dA=

∫

x

2



y

2

dA

Biegunowy moment bezwładności

I

0

jest

wielkością

dodatnią, gdyż

promień r

jest nieujemny i w dodatku w drugiej
potędze.

z

22.03.11

dr inż. Marek Bartoszek

20

Geometria mas

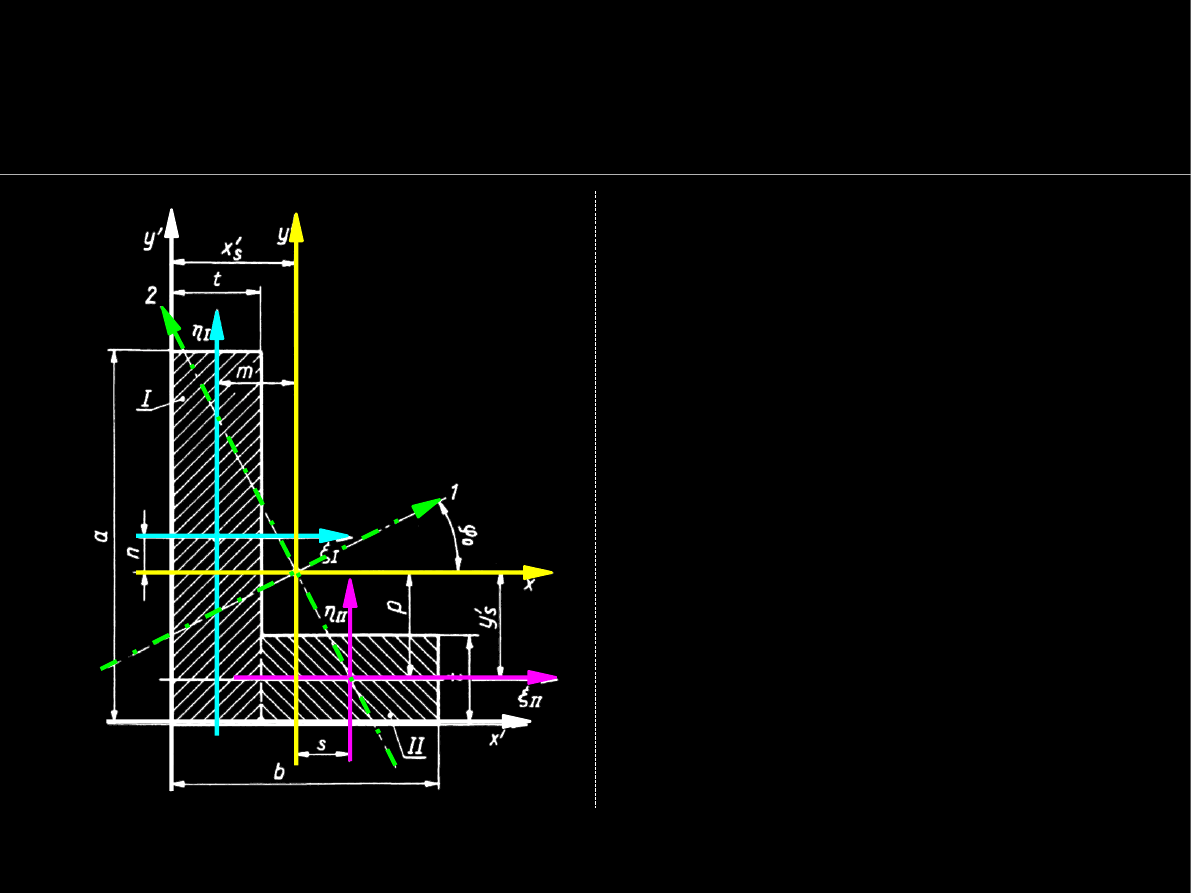
Momenty bezwładności przekroju złożonego

Dla przekroju podzielonego na

figury proste

moment bezwł.

względem jakiejś osi

jest

równy

sumie momentów

bezwł.

figur składowych

obl.

względem tej samej osi

:

Podobnie

moment dewiacji

przekroju złożonego

względem osi układu OXY

jest

sumą momentów

dewiacji

figur składowych

obliczonych

w tym samym

układzie wsp

.:

I

x

=

∑

i

I

x



i

lub

I

y

=

∑

i

I

y



i

I

xy

=

D

xy

=

∑

i

D

x y



i

Moment bezwładności

(

I

x

lub

I

y

) może być

tylko dodatni.

Moment dewiacji

(

D

xy

) może mieć

dowolny znak lub być równy zeru.

22.03.11

dr inż. Marek Bartoszek

21

Geometria mas

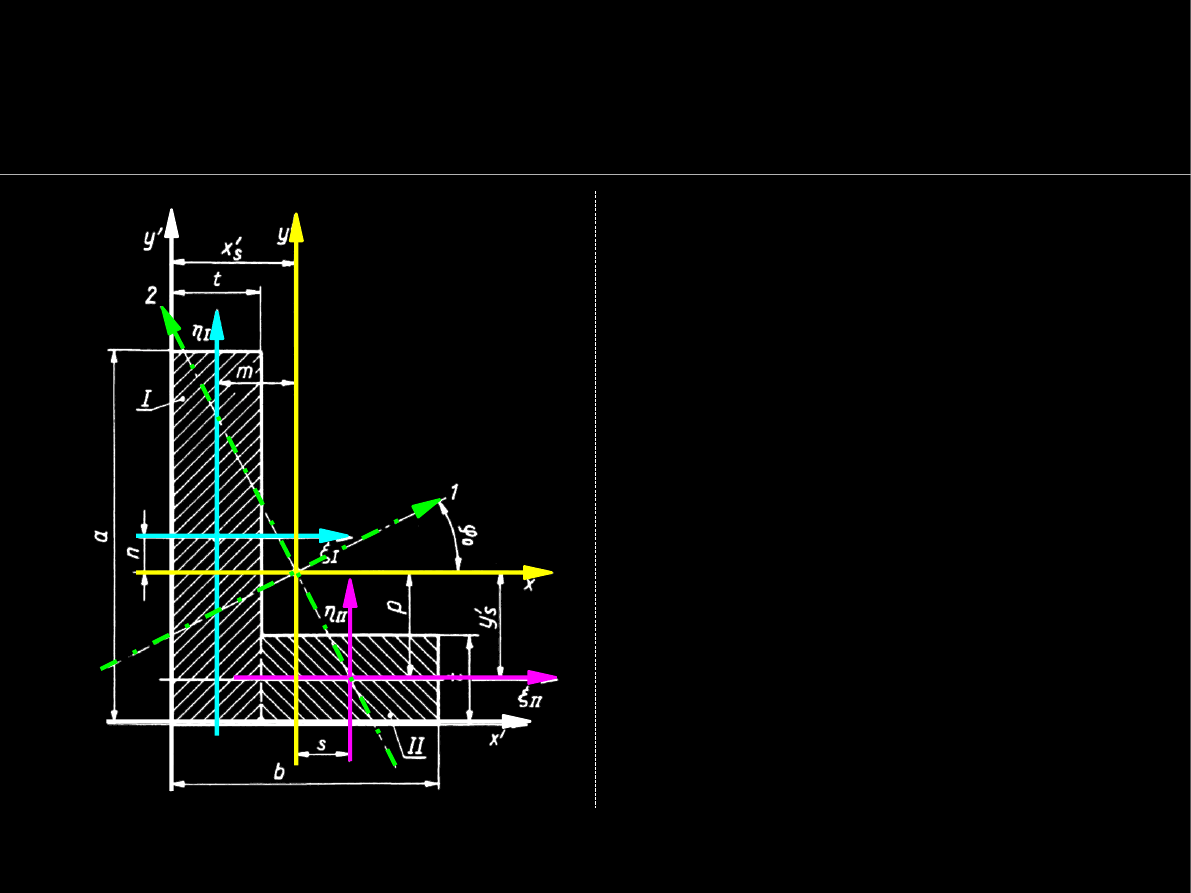
Układy współrzędnych w geometrii mas

Wykorzystuje się różne układy

współrzędnych – na rysunku
obok mamy pięć układów :

O

I

ξ

Ι

η

Ι

– centralny układ (i główny)

figury prostej I (lokalny figury I)

O

II

ξ

ΙΙ

η

ΙΙ

– centralny układ (i główny)

figury prostej II (lokalny figury II)

O'X'Y' – wyjściowy układ

współrzędnych do obliczeń

OXY – centralny układ całego

przekroju (globalny)

O12 – główny centralny układ całego

przekroju

(gł. centr. osie bezwładności)

I

II

Z. Dyląg i in. str.174 rys 8.12

22.03.11

dr inż. Marek Bartoszek

22

Geometria mas

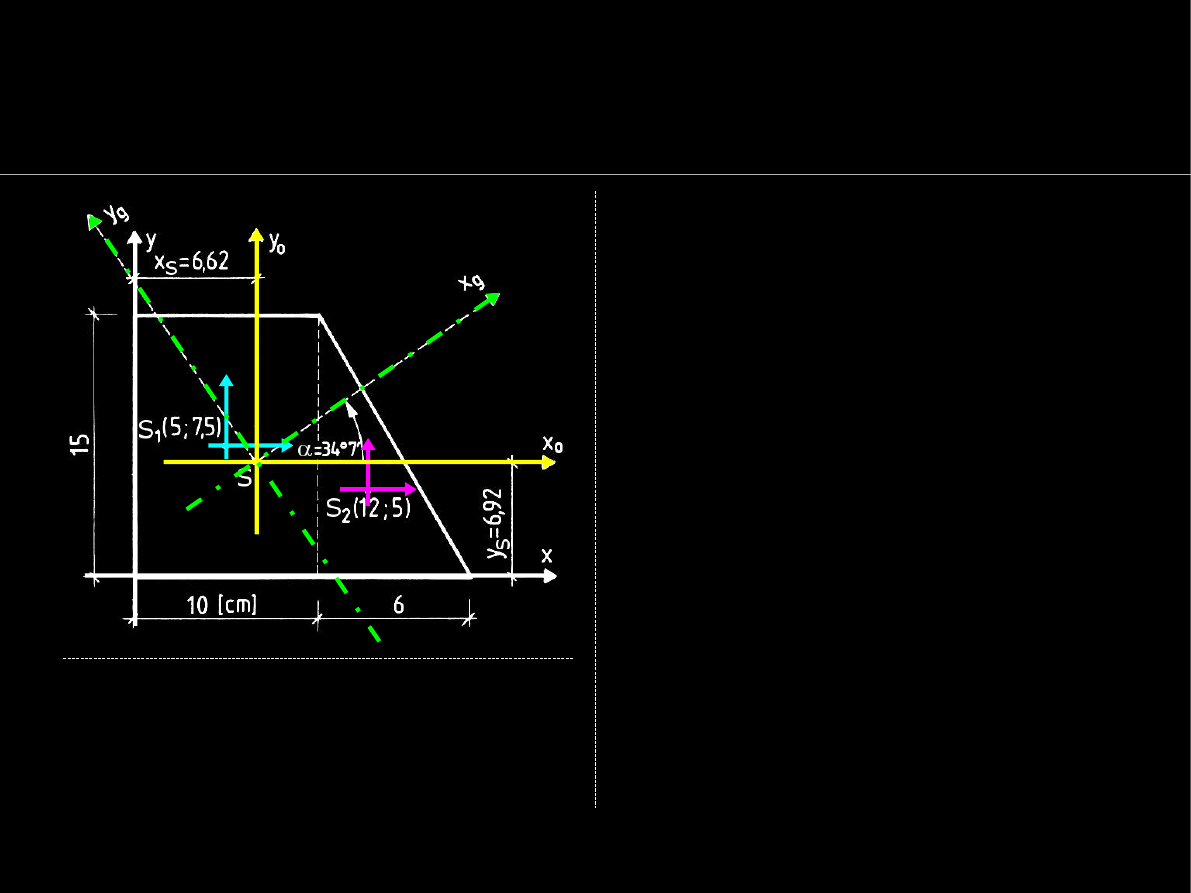
Centralne układy współrzędnych

Centralny układ współrzędn.

ma początek

w środku

ciężkości figury

.

Główny centralny układ

współrzędnych

jest to

taki

układ centralny,

w którym

momenty bezwładności
przyjmują

ekstremalne dla

tego przekroju

wartości:

(

I

x

,

I

y

)==>(

I

min

,

I

max

)

a

moment dewiacji jest

równy zeru

D

xy

=0

.

Osią główną centralną

jest

zawsze

oś symetrii

figury.

22.03.11

dr inż. Marek Bartoszek

23

Geometria mas

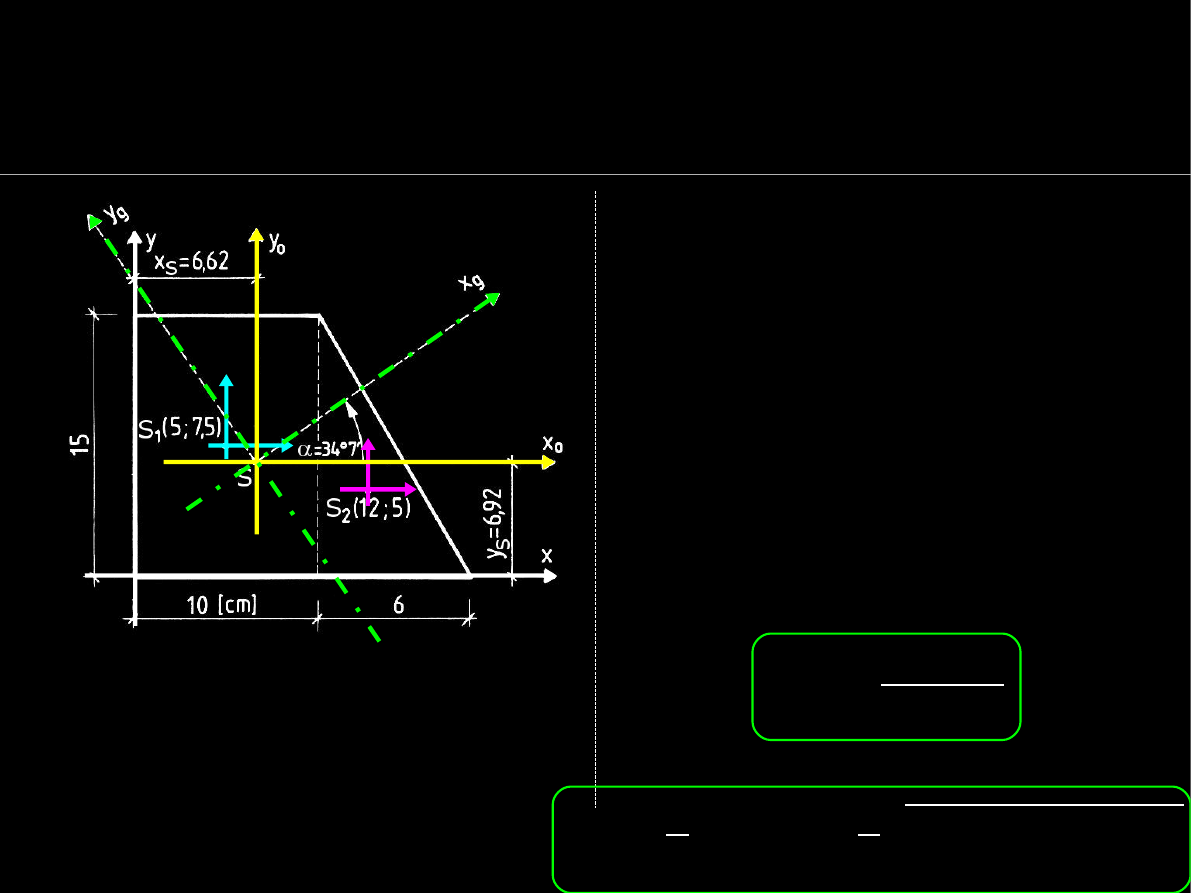
Główny centralny układ współrzędnych

Do projektowania potrzebne są

główne centralne momenty
bezwładności

przekroju.

Najpierw wyznacza się

mom.

bezwł.

I

x

,

I

y

i

dewiacji D

xy

w układzie centralnym

.

Jeśli

D

xy

<>0

, to oblicza się kąt

α

o jaki należy obrócić

aktualny układ centralny

aby

otrzymać

układ główny

.

Następnie wyznacza się

centralne momenty bezwł.

w układzie głównym

:

I

min

i

I

max

.

Jeśli

D

xy

=0

, to aktualny układ centralny

jest jednocześnie układem głównym.

Jeśli oś układu centr. jest osią symetrii to

D

xy

=0

– i jest to jedna z osi głównych.

22.03.11

dr inż. Marek Bartoszek

24

Geometria mas

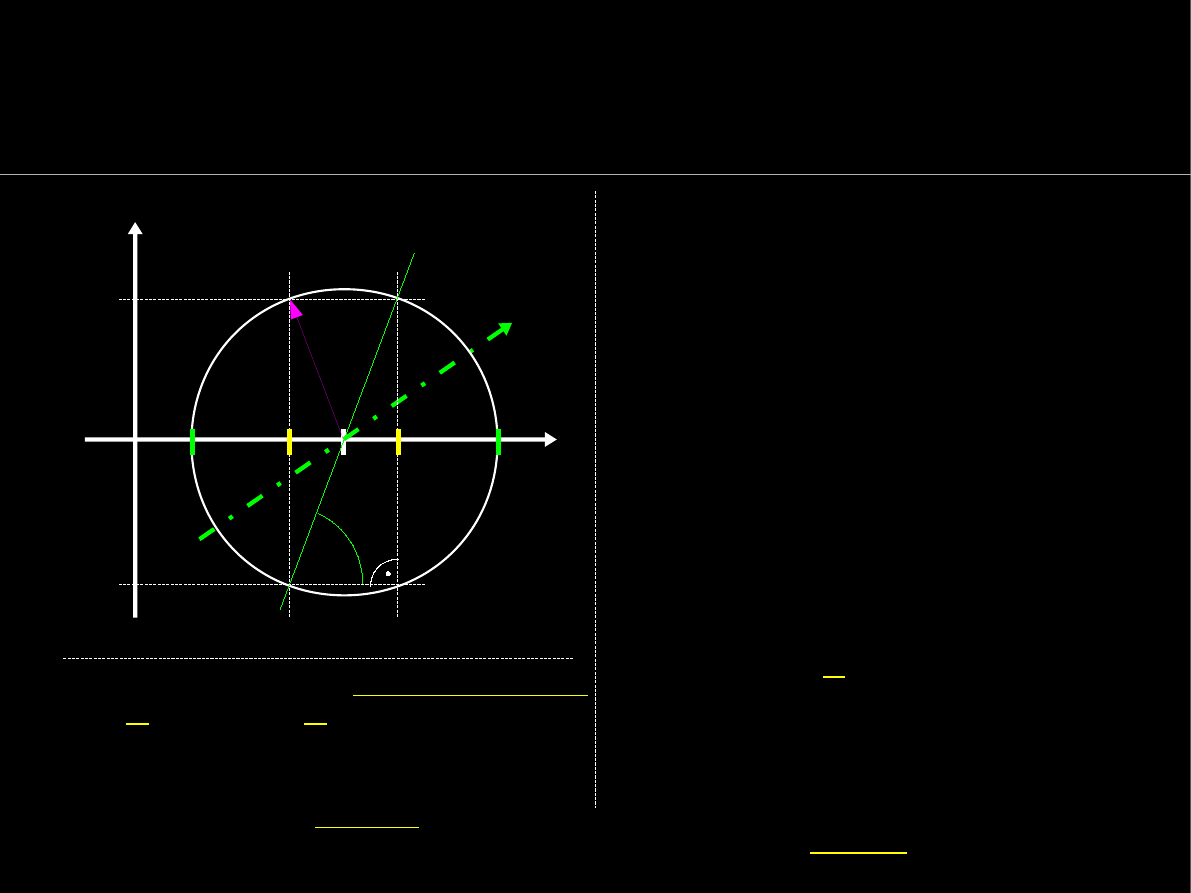
Główne centralne momenty bezwładności - wzory

Centralne momenty bezwł. i dewiacji:

I

x0

=3591.35 cm

4

,

I

y0

=3054.61 cm

4

,

D

x0y0

= -718.27 cm

4

=> D

xy

<>0.

Załóżmy, że :

●

znamy

centralne

momenty

bezwł. i dewiacji

przekroju:

I

x0

, I

y0

, D

x0y0

w układzie

SX

0

Y

0

.

●

jest to układ

centralny

ale

nie

główny

, gdyż

D

x0y0

<>0

.

Kąt obrotu

α

układu głównego

względem

centralnego

:

Gł. centr. momenty bezwł.:

tg 2=

−

2

D

x

0

y

0

I

x

0

−

I

y

0

I

max

min

=

1

2



I

x

0



I

y

0

±

1
2





I

x

0

−

I

y

0



2



4

D

x

0

y

0

2

22.03.11

dr inż. Marek Bartoszek

25

Geometria mas

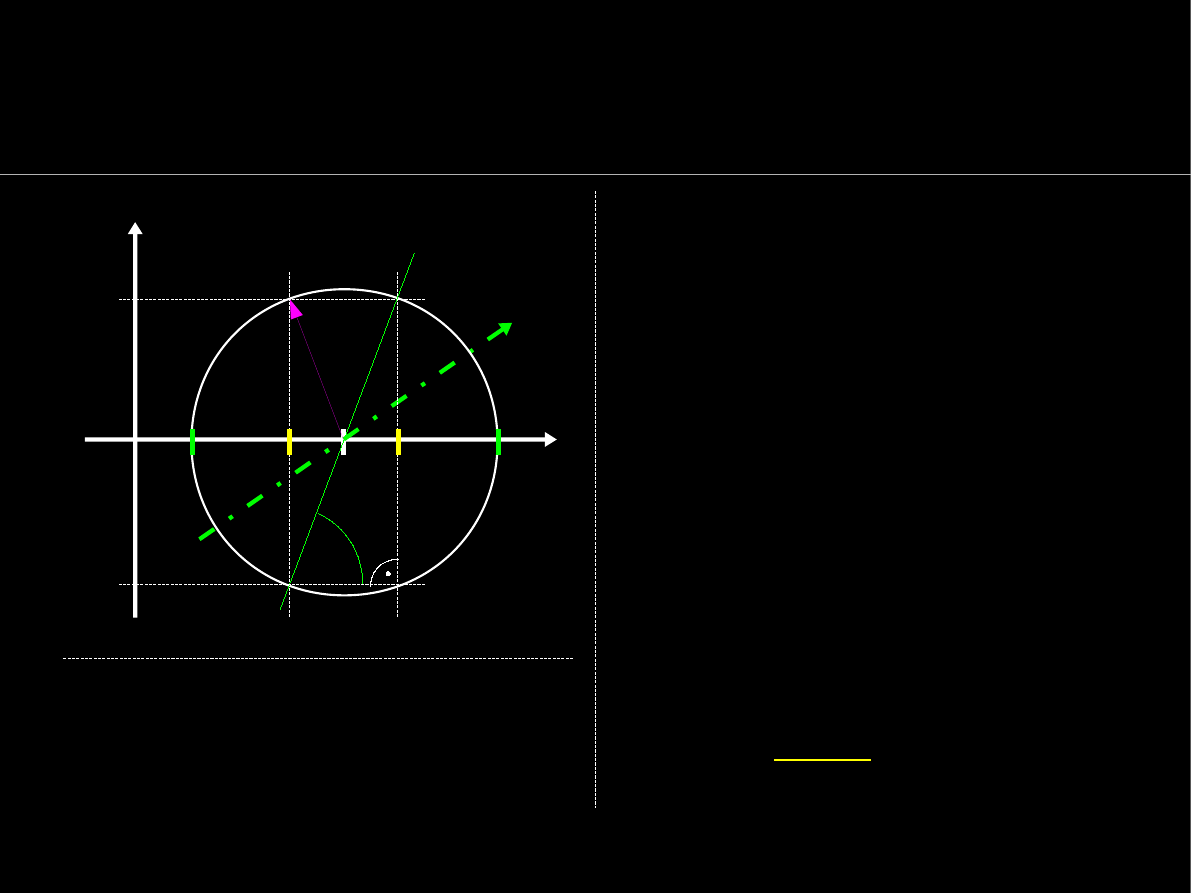
Interpretacja graficzna – koło Mohra

Momenty bezwł. i dewiacji

przekroju w układzie

centralnym

:

I

x

, I

y

i

D

xy

<>0.

Główne centr. momenty bezwł.

otrzymuje się w miejscach

przecięcia się koła Mohra z
osią poziomą OI.

Średnia arytmetyczna

I

x

i

I

y

jest

środkiem koła Mohra:

Promień koła oblicza się z

twierdzenia Pitagorasa:

tg 2=

−

2 D

xy

I

x

−

I

y

r

2

=



I

x

−

I

y

2



2



D

xy

2

I

max

s=

1

2



I

x



I

y



I

max

min

=

1

2



I

x



I

y

±

1
2





I

x

−

I

y



2



4 D

xy

2

I

D

D

xy

I

x

I

y

I

min

2

α

r

s

22.03.11

dr inż. Marek Bartoszek

26

Geometria mas

Interpretacja graficzna – koło Mohra

W miejscu przecięcia się koła

z osią OI zeruje się

moment

dewiacji D=0

,

a

główne

centralne momenty bezwł.

I

min

i

I

max

oblicza się:

co

odpowiada

Z proporcji boków 2

D

xy

do

I

y

-I

x

oblicza się tan(2

α

) kąta

α

o jaki należy obrócić

układ

centralny

aby był

głównym

:

D

xy

=0

<=>

α

=0

<=>

centr.

=

główny

I

D

D

xy

I

x

I

y

I

min

I

max

2

α

r

s

2 D

xy

I

y

−

I

x

=

tg 2

I

max

=

sr

oraz

I

min

=

s−r

Momenty bezwładności w układzie

centralnym

i obróconym

głównym

mają

tę samą średnią arytmetyczną

s

a więc

i sumę:

I

x0

+

I

y0

=

I

min

+

I

max

22.03.11

dr inż. Marek Bartoszek

27

Geometria mas

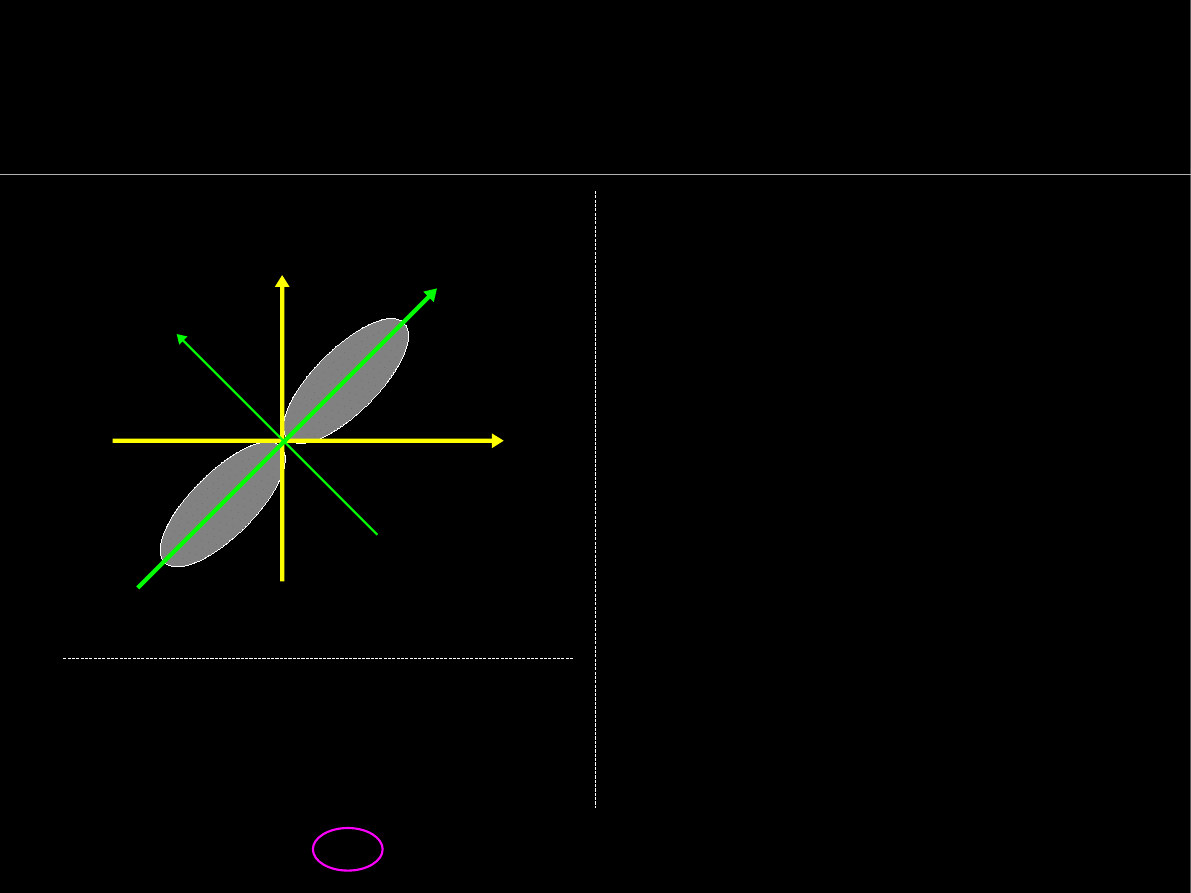
Główne centralne osie bezwładności

Podane wzory nie pozwalają

określić, względem której
z obróconych o kąt

α

osi

kładu głównego

otrzymamy

wartość

Ι

min

, a dla której

Ι

max

.

Poznaje się to po znaku

momentu dewiacji D

xy

:

D

xy

>0

=> większość masy leży

w ćwiartkach I i III i przez nie

przechodzi oś

I

min

D

xy

<0

=> oś

I

min

leży w II i IV

D

xy

=0

=>

ukł. centr

. =

główny

x

0

y

0

min

max

ćw.I

ćw.II

ćw.III

ćw.IV

D

x

0

y

0

=

∫

x y dA

Moment dewiacji informuje

o nierównomierności rozkładu „masy” w
przekroju, a jego znak zależy od
iloczynu x*y we wzorze:

D

x

0

y

0



0

22.03.11

dr inż. Marek Bartoszek

28

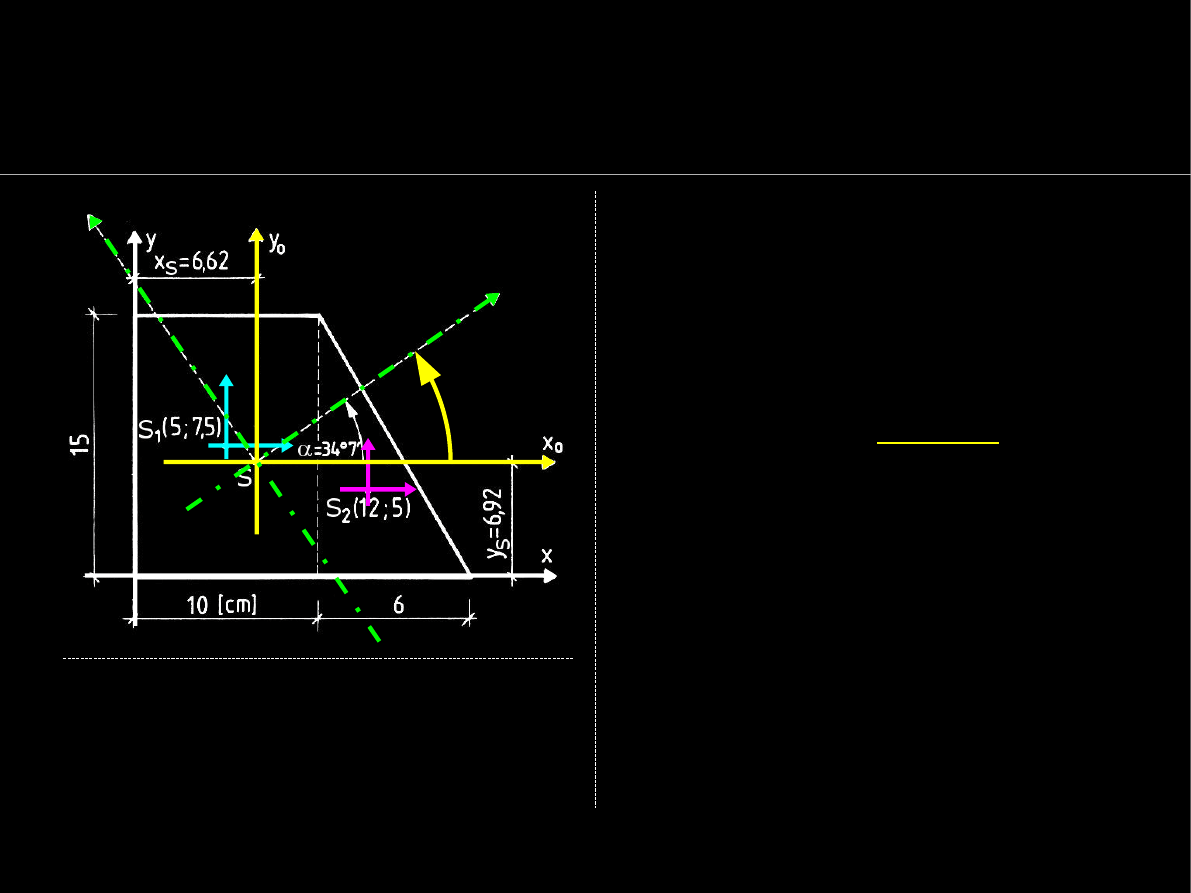
Geometria mas

Transformacja momentów bezwładności przy

obrocie układu o dowolny kąt

φ

Załóżmy, że mamy kąt

φ

o jaki

należy obrócić

układ

centralny,

np. do

układu

głównego

wg wzoru:

Transformujemy momenty

bezwładności z układu

centralnego SXY

do

obróconego o kąt

φ

układu

SX'Y'

(podręcznik S.Pyrak)

:

I

x '

=

I

x

0

⋅

cos

2



I

y

0

⋅

sin

2

−

D

x

0

y

2

⋅

sin2 

I

y '

=

I

x

0

⋅

sin

2



I

y

0

⋅

cos

2



D

x

0

y

0

⋅

sin2 

tg 2=

−

2 D

x

0

y

0

I

x

0

−

I

y

0

Momenty bezwładności w układzie

centralnym

i obróconym, (np.

głównym

)

mają tę samą średnią arytmetyczną

s

a więc i sumę:

I

x0

+

I

y0

=

I

min

+

I

max

φ

x'

y'

22.03.11

dr inż. Marek Bartoszek

29

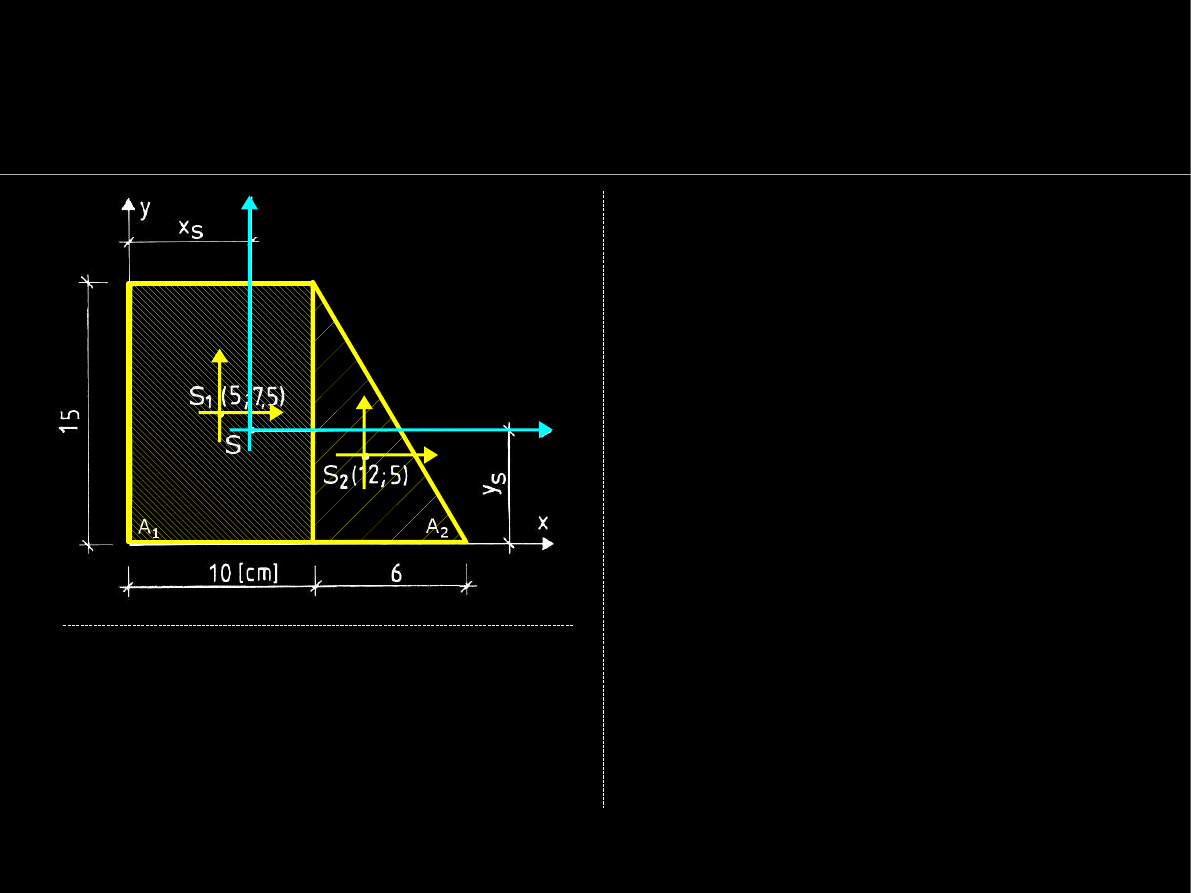
Geometria mas

Momenty bezwładności względem osi

równoległych

Momenty bezwładności (lub

statyczne) pola można

dodawać ale tylko jeśli są
obliczone względem tych
samych osi:

Przykład wartości

I

x

[cm

4

] wzgl.

różnych osi na rysunku:

I

x

1



1

=

2812.5

Momenty bezwładności

figur składowych

można dodać tylko jeśli są obliczone
względem tej samej osi

– np.

względem osi OX

0

dla przekroju

powyżej :

y

0

x

0

x

2

y

2

y

1

x

1

I

x

0



1

=

2862.43

I

x



1

=

10001.85

I

x

2



2

=

562.5

I

x

0



2

=

1853.92

I

x

0

=

I

x

0



1



I

x

0



2

oraz

I

y

0

=

I

y

0



1



I

y

0



2

I

x

=

I

x



1



I

x



2

oraz

I

y

=

I

y



1



I

y



2

I

x

0

=

I

x

0



1



I

x

0



2

=

2862.431853.92

22.03.11

dr inż. Marek Bartoszek

30

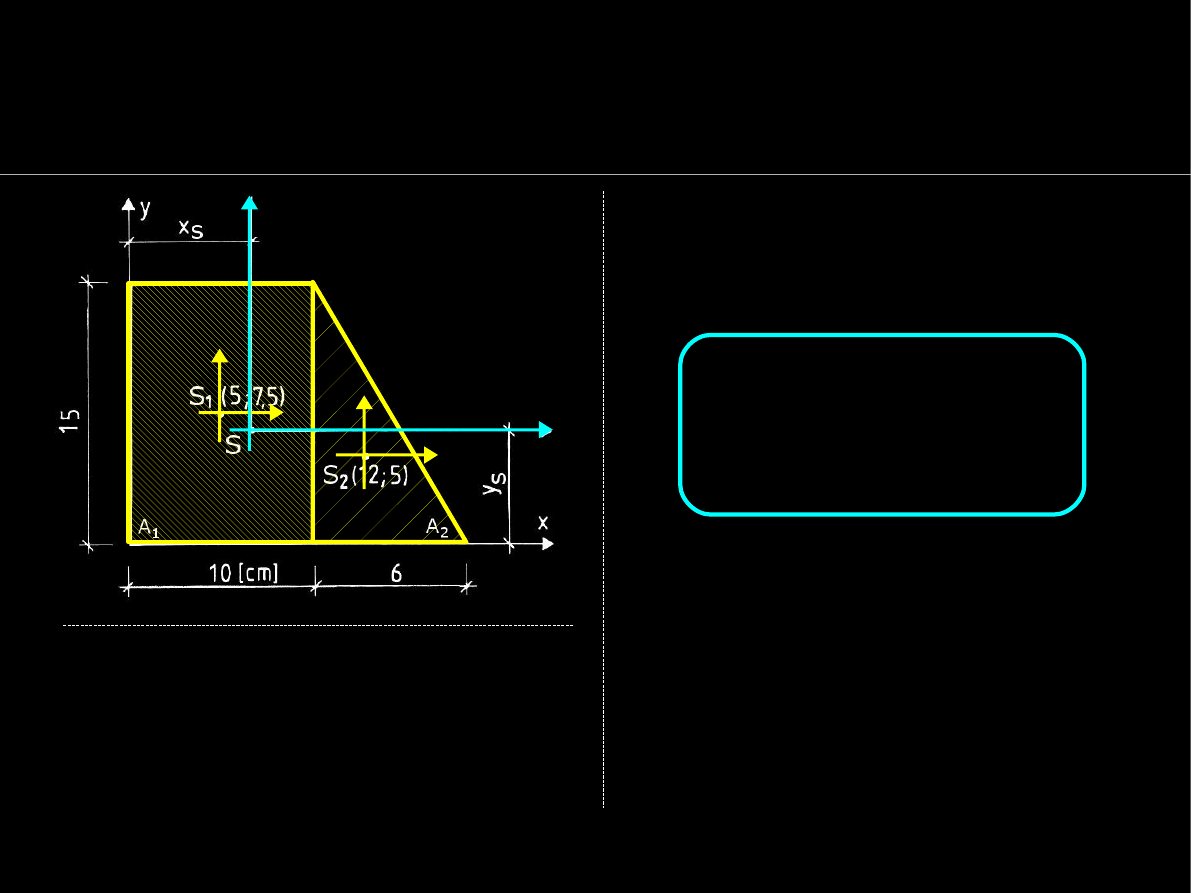
Geometria mas

Transformacja momentów bezwł. przy

przesunięciu układu współ. – wzór Steinera

Do przeliczania momentów

bezwładności z układu OX

i

Y

i

do OXY służy

wzór Steiner'a

:

gdzie:

– to momenty

bezwł. względem osi układu
OX

i

Y

i

przech. przez środek

ciężkości figury

i

oraz

||

do

osi układu OXY,

– to współrzędne

środków cieżk. figury

i

Wzór Steinera wiąże momenty

bezwładności figury obliczone
względem osi centralnych, z
momentami OX

i

Y

i

bezwładności

obliczonymi względem osi do nich
równoległych, np. OX

0

Y

0

.

y

0

x

0

x

2

y

2

y

1

x

1

I

x

i

=

I

x

i



i 



A



i

⋅

y

i



2

I

y

i

=

I

y

i



i



A



i

⋅

x

i



2

D

xy

i

=

D

x

i

y

i



i



A



i

⋅

x

i

⋅

y

i



I

x

i



i

, I

y

i



i

, D

x

i

y

i



i

x

i

, y

i

22.03.11

dr inż. Marek Bartoszek

31

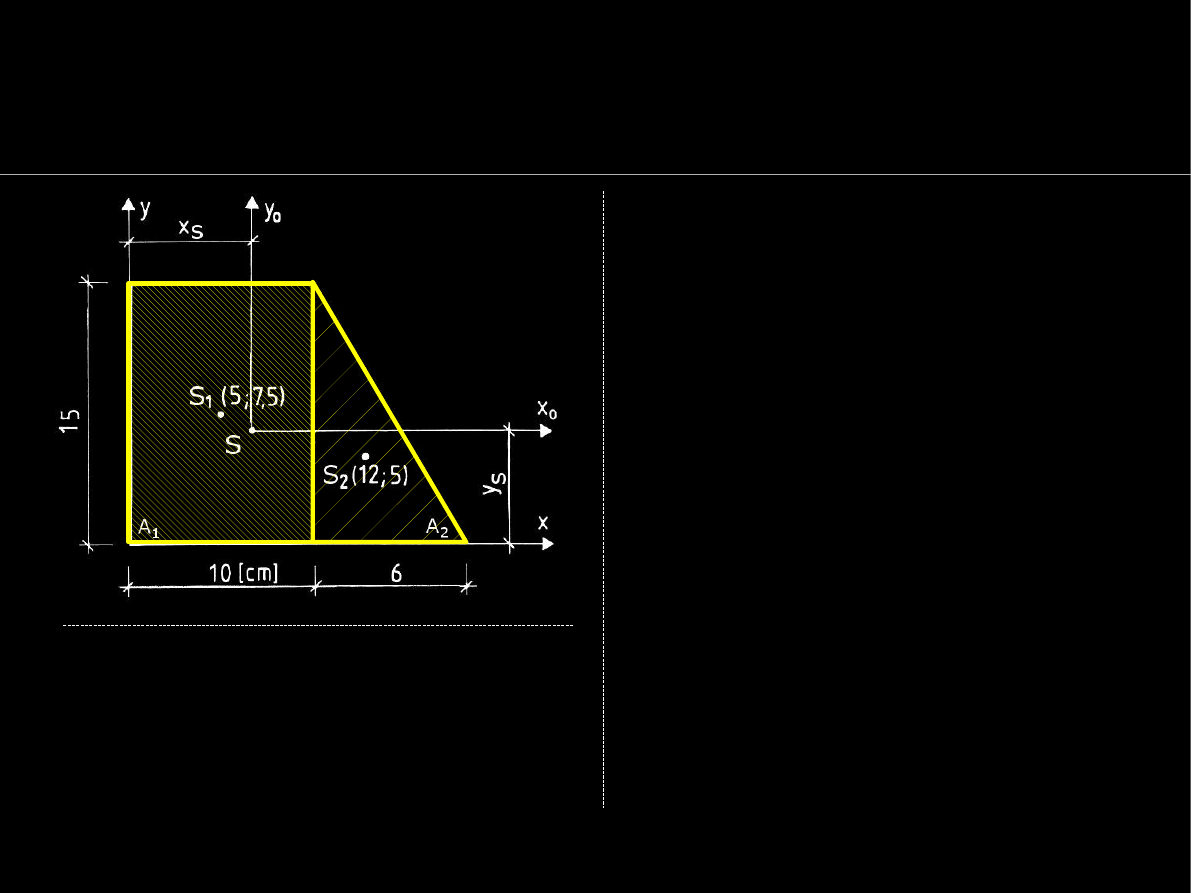
Geometria mas

Momenty bezwładności - przykład

Momenty bezwł. i dewiacji

z układów lokalnych

przeliczamy do układu
centralnego SXY za pomocą

wz. Steiner'a, np.:

Suma momentów bezwładności

figur skład. np. wzgl. osi OX

to

centr. moment bezwł. I

x

:

Moment bezwładności

(

I

x

lub

I

y

) może być

tylko dodatni.

Moment dewiacji

(

D

xy

) może mieć

dowolny znak lub być równy zeru.

I

x



1

=

I

x

1



1



A

1

⋅

y

0



1



2

=

2812,5



150⋅7,5− y

s



2

=

2862,43 cm

4

I

x



2

=

I

x

2



2



A

2

⋅

y

0



2



2

=

562,5



45⋅5− y

s



2

=

728,92 cm

4

I

x

=

I

x



1



I

x



2

=

2862,43728,92=

=

3591,35 cm

4

22.03.11

dr inż. Marek Bartoszek

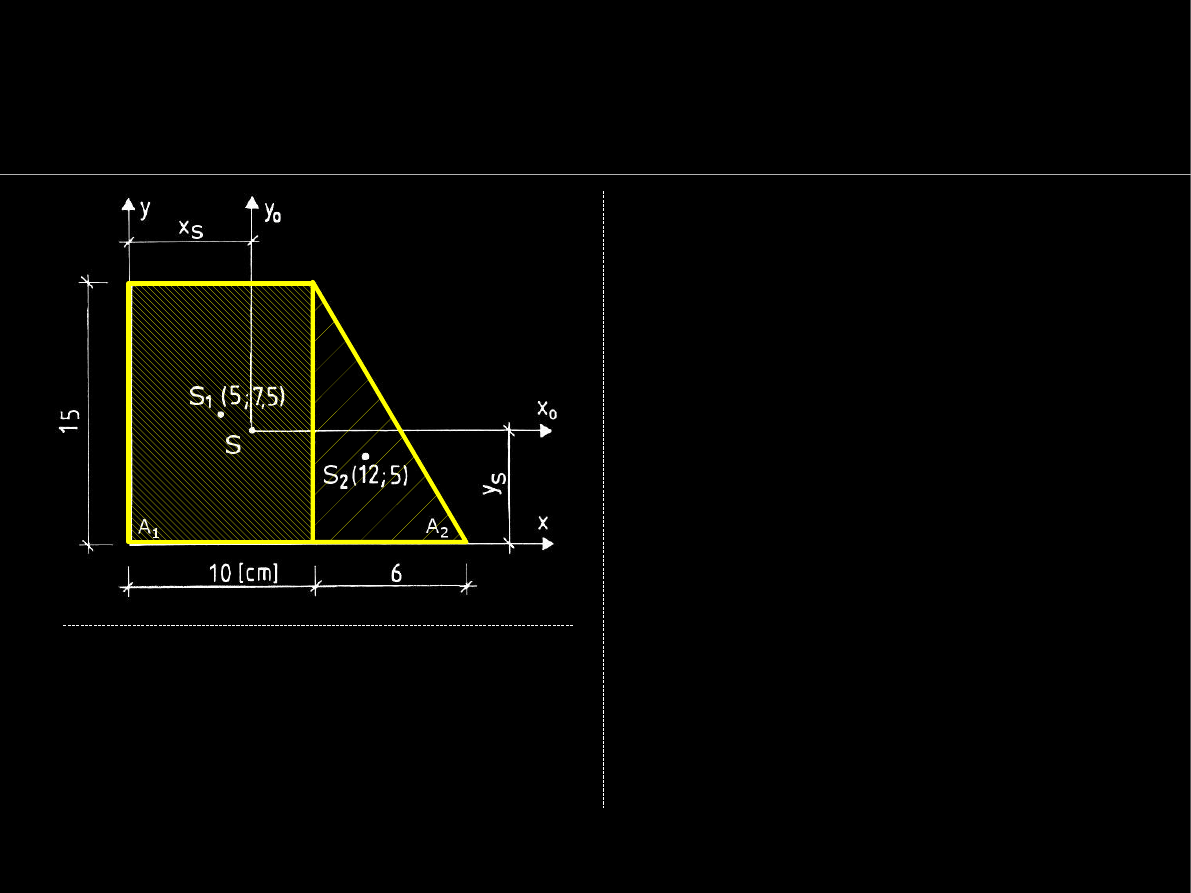
32

Geometria mas

Momenty bezwładności - przykład

Podobnie przeliczymy (Steiner)

pozostałe

momenty bezwł.

I

(i)

yi

do centralnego układu

OXY całego przekroju :

następnie obliczymy

centralny

moment bezwładności

całego

przekroju względem osi OY:

Moment bezwładności

(

I

x

lub

I

y

) może być

tylko dodatni.

Moment dewiacji

(

D

xy

) może mieć

dowolny znak lub być równy zeru.

I

y



1

=

I

y

1



1



A

1

⋅

x

0



1



2

=

1250



150⋅5−x

s



2

=

1804,73cm

4

I

y



2

=

I

y

2



2



A

2

⋅

x

0



2



2

=

90



45⋅12−x

s



2

=

1249,88 cm

4

I

y

=

I

y



1



I

y



2

=

1804,731249,88=

=

3054.61 cm

4

22.03.11

dr inż. Marek Bartoszek

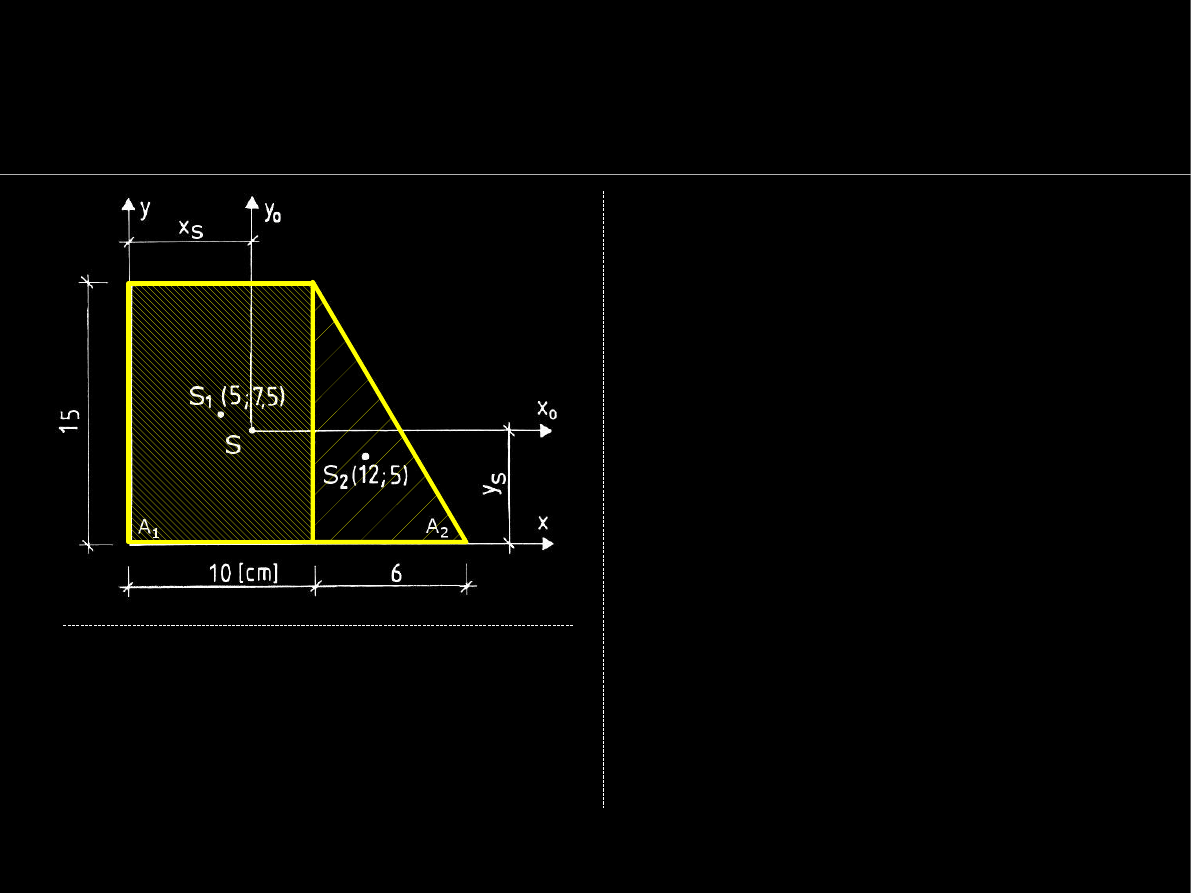
33

Geometria mas

Moment dewiacji - przykład

Ostatecznie te same operacje

wykonamy dla

momentów

dewiacji D

(i)

xiyi

(w.Steiner'a) :

następnie obliczymy

centralny

moment bezwładności

całego

przekroju względem osi OY:

Moment bezwładności

(

I

x

lub

I

y

) może być

tylko dodatni.

Moment dewiacji

(

D

xy

) może mieć

dowolny znak lub być równy zeru.

D

xy



1

=

D

x

1

y

1



1



A

1

⋅

x

0



1

y



1

0

=

0



150⋅5− x

s



7,5− y

s

=−

166,42 cm

4

D

xy



2

=

I

x

2

y

2



2



A

2

⋅

x

0



2

y



2

0

=−

112,5



45⋅12−x

s



5− y

s

=−

551,85 cm

4

D

xy

=

D

xy



1



D

xy



2

=−

166,42−551,85=

=−

718,27 cm

4

22.03.11

dr inż. Marek Bartoszek

34

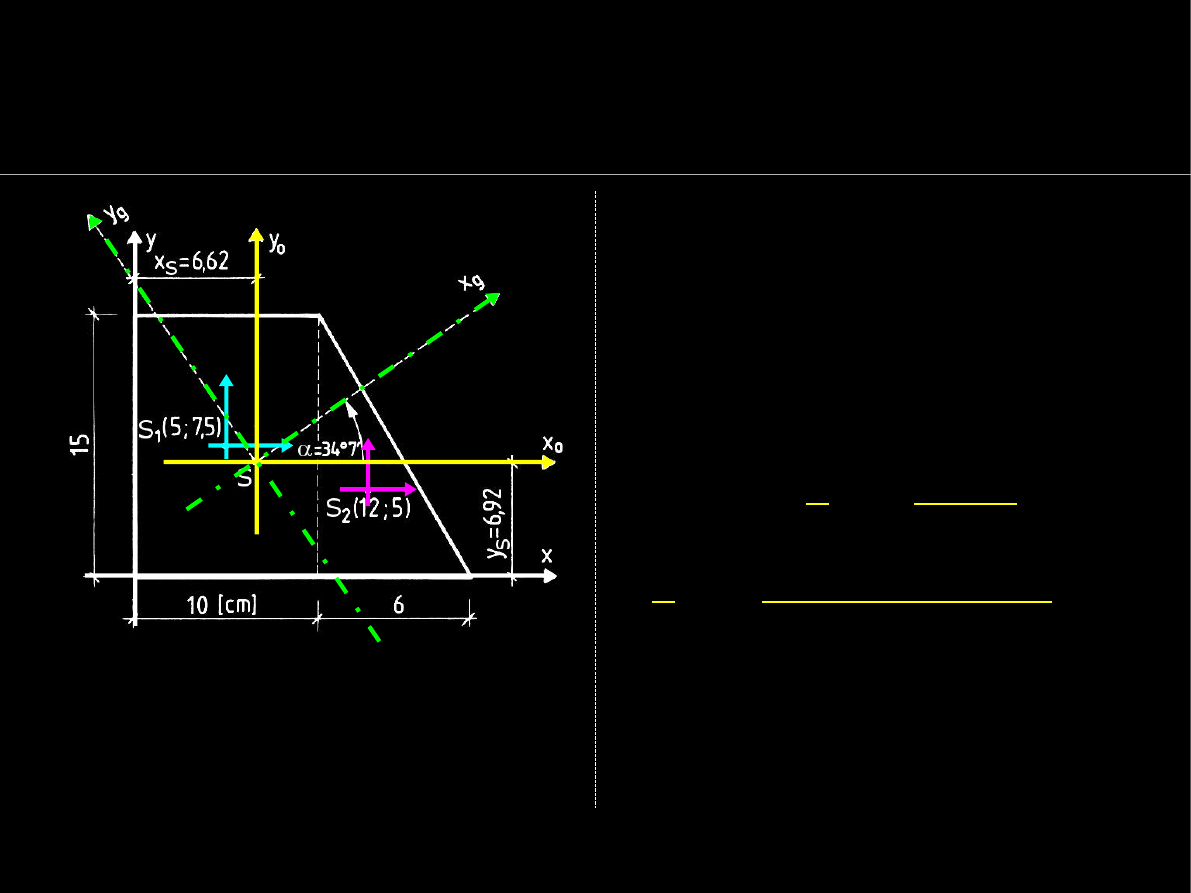
Geometria mas

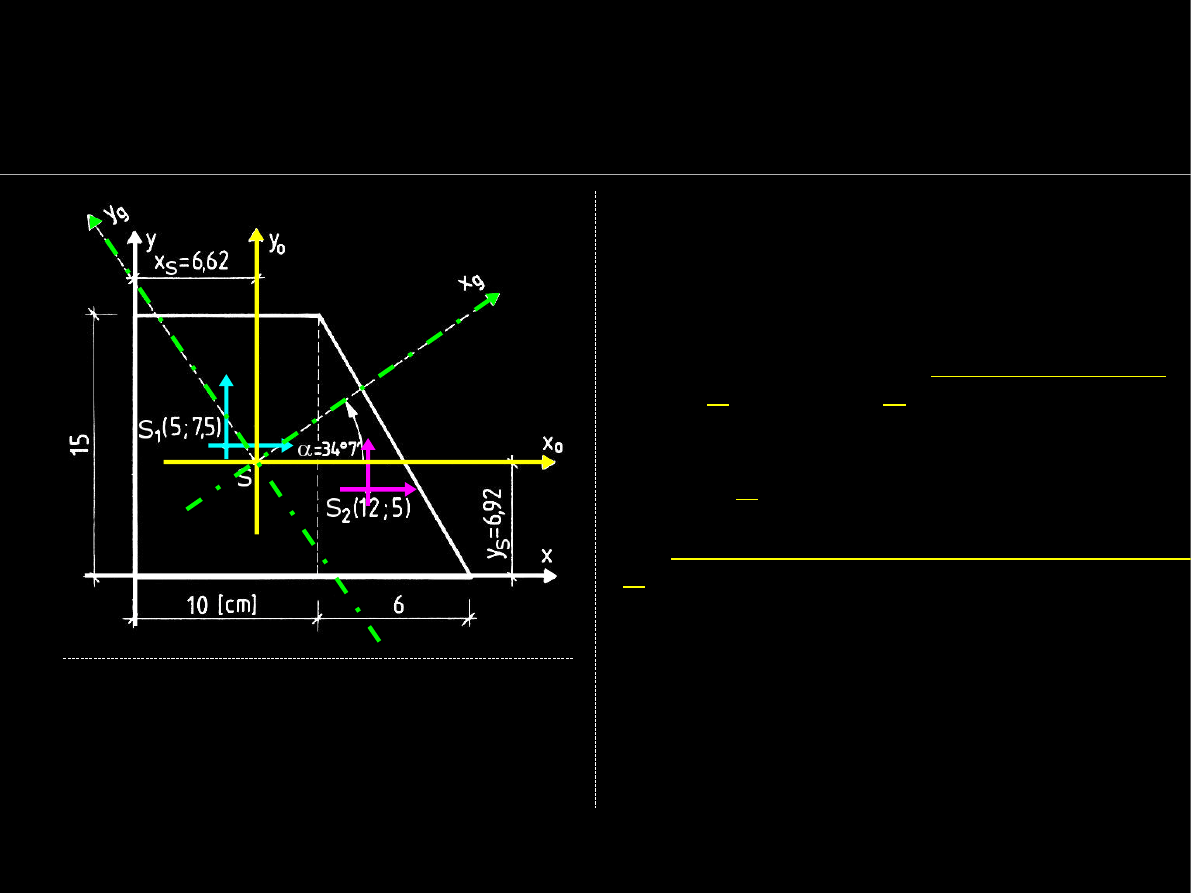
Główne centralne momenty bezwł. - przykład

Na podstawie c

entralnych

momentów bezwł. i dewiacji
I

x

, I

y

, D

xy

obliczamy kąt

α

obrotu

układu głównego

względem

centralnego

:

a następnie ...

Centralne momenty bezwł. i dewiacji:

I

x

=3591.35 cm

4

,

I

y

=3054.61 cm

4

,

D

xy

= -718.27 cm

4

=> D

xy

<0.

=

1

2

atan 

−

2 D

xy

I

x

−

I

y

=

=

1

2

atan



−

2⋅−718,27



3591,35−3054,61



=

34 ° 7'

22.03.11

dr inż. Marek Bartoszek

35

Geometria mas

Główne centralne momenty bezwł. - przykład

następnie z

I

x

, I

y

, D

xy

obliczamy

główne centralne momenty

bezwładności

przekroju:

Oznaczyć osie

I

min

i

I

max

;

Dxy<0

Centralne momenty bezwł. i dewiacji:

I

x

=3591.35 cm

4

,

I

y

=3054.61 cm

4

,

D

xy

= -718.27 cm

4

=> D

xy

<0.

I

max

min

=

1
2



I

x



I

y

±

1

2





I

x

−

I

y



2



4 D

xy

2

=

1
2



3591.353054.61±

±

1

2





3591.35−3054.61

2



4⋅−718.27

2

=

3322,98±766,77

I

max

=

3322,98766,77=4089,75cm

4

I

min

=

3322,98−766,77=2556,21cm

4

I

max

I

min

D

xy

<0

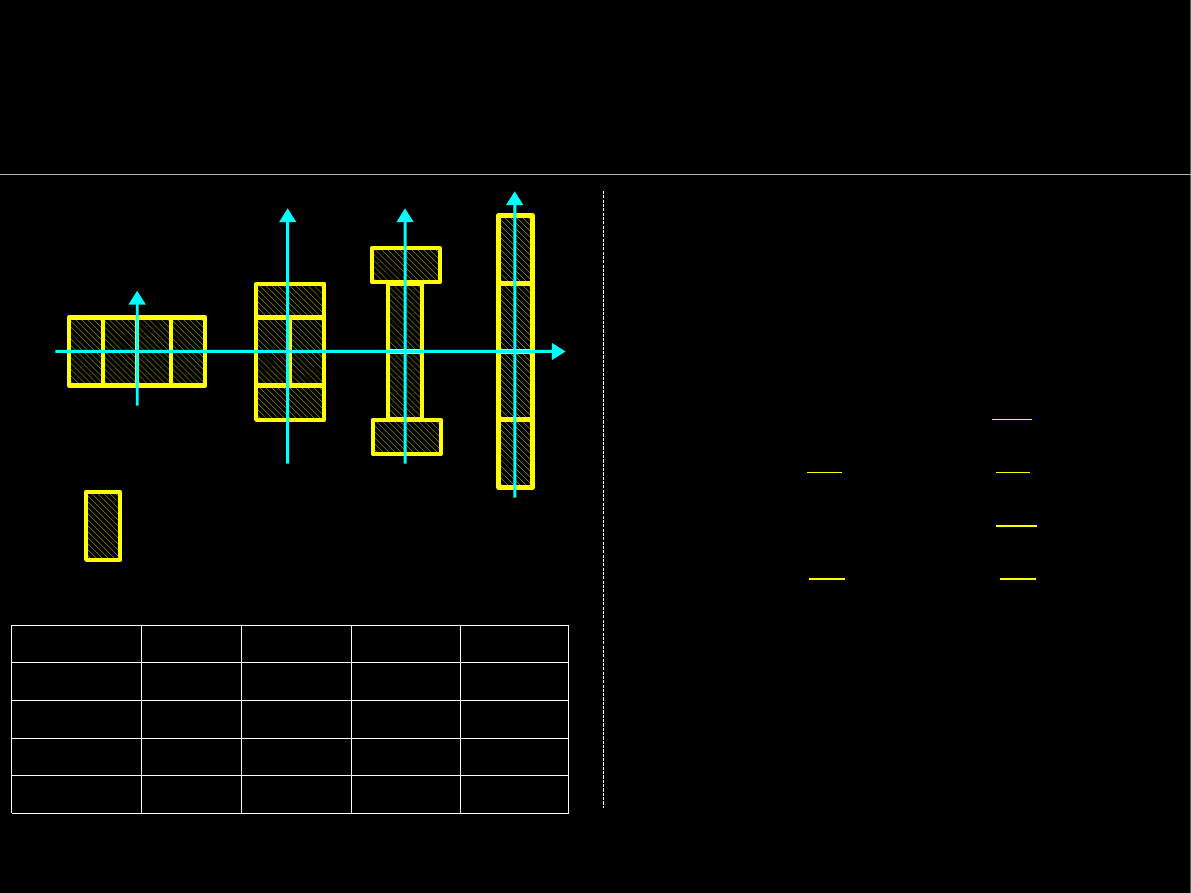
22.03.11

dr inż. Marek Bartoszek

36

Geometria mas

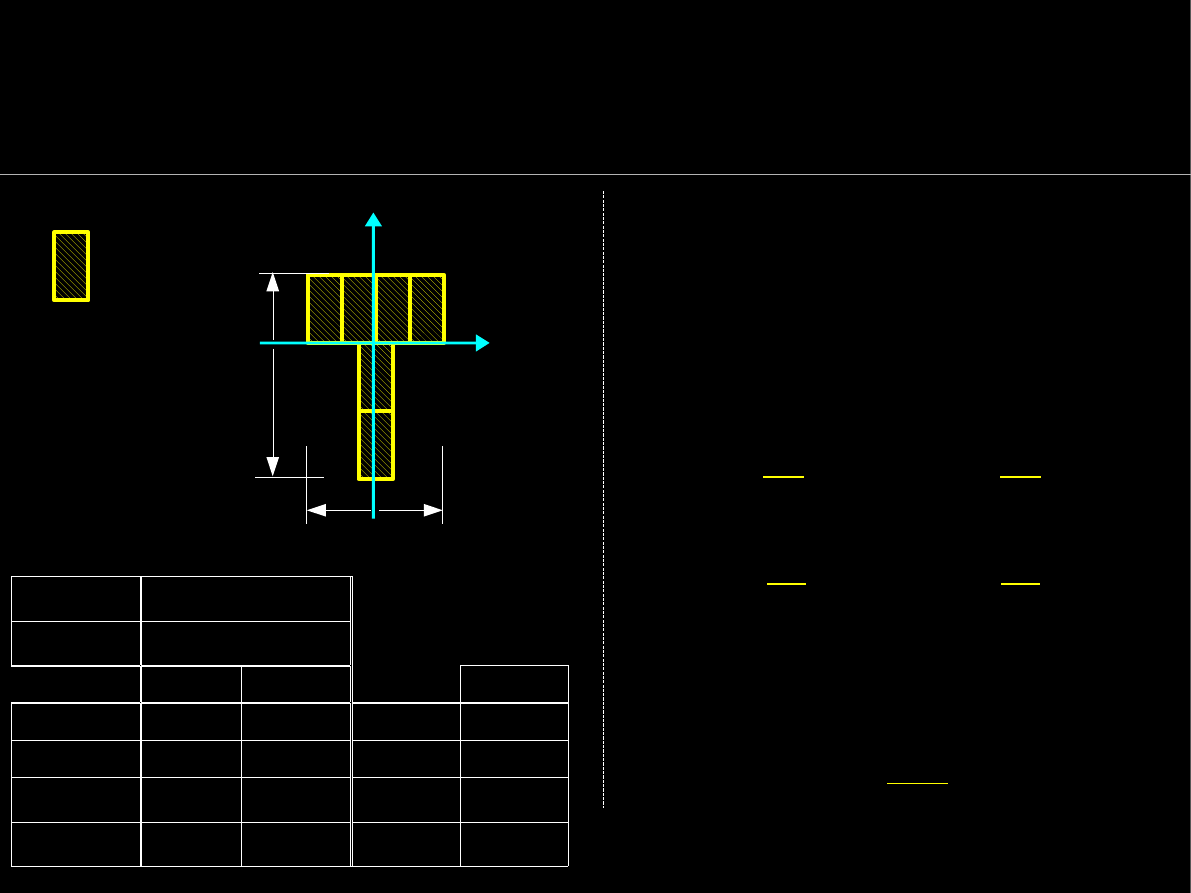
Promienie bezwładności przekroju

Mając

pole powierzchni A

całego przekroju oraz jego

momenty bezwładności

I

x

,

I

y

można obliczyć

promienie

bezwładności i

x

i

i

y

:

Promienie bezwładności

są

miarą tego jak daleko od

danej osi jest rozłożone pole
przekroju – jak duży jest

moment bezwładności

I

x

i

I

y

w stosunku

do pola pow.

A

.

y

x

i

x

2

=

I

x

A

⇒

i

x

=



I

x

A

i

y

2

=

I

y

A

⇒

i

y

=



I

y

A

4A=32 cm

2

A [cm2]

32

32

32

32

42,67 170,67 490,67 682,67

ix2 [cm2] 1,33

5,33

15,33 21,33

1,15

2,31

3,92

4,62

170,67 42,67 26,67 10,67

Ix [cm4]

ix [cm]

Iy [cm4]

A

A=8 cm

2

4

2 cm

22.03.11

dr inż. Marek Bartoszek

37

Geometria mas

Wskaźniki zginania przekroju

Mając

momenty bezwładności

I

x

, I

y

i współrzędne środka

ciężkości przekroju można

obliczyć

wskaźniki zginania

W

x

i

W

y

:

Często znaczenie mają

wskaźniki o najmniejszej

wartości bezwzględnej:

W

x



=

I

x

y



oraz

W

x

−

=

I

x

y

−

W

y

−

=

I

y

x

−

oraz

W

y



=

I

y

x



A=8 cm

2

A

4

2 cm

y

x

x

+

x

-

y

–

y

+

512
176

-

+

extr

x [cm]

-4

4

max|x|

4

y [cm]

-8

4

max|y|

8

-64

128

64

-44

44

44

I

x

[cm

4

]

I

y

[cm

4

]

W

x

[cm

3

]

W

x

min

W

y

[cm

3

]

W

y

min

W

x

min

=

I

x

y

extr

=

∣

W

x



∣

W

y

min

=

W

y



=

∣

W

y

−

∣

22.03.11

dr inż. Marek Bartoszek

38

DZIEKUJĘ ZA UWAGĘ

KONIEC wykładu