Technik_geodeta_311[10].Z2.03

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPIS TREŚCI

1. Wprowadzenie

2. Wymagania wstępne

3. Cele kształcenia

4. Materiał nauczania

4.1. Ogólne wiadomości o tyczeniu tras

4.1.1. Materiał nauczania

4.1.2. Pytania sprawdzające

4.1.3. Ćwiczenia

4.1.4. Sprawdzian postępów

4.2. Geodezyjna obsługa budownictwa drogowego, kolejowego i wodnego

4.2.1. Materiał nauczania

4.2.2. Pytania sprawdzające

4.2.3. Ćwiczenia

4.2.4. Sprawdzian postępów

5. Sprawdzian osiągnięć

6. Literatura

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1. WPROWADZENIE

Poradnik będzie Ci pomocny w przyswajaniu wiedzy na temat geodezyjnej obsługi

budownictwa drogowego, kolejowego i wodnego oraz w kształtowaniu umiejętności
związanych z obsługą geodezyjną ich budowy.

W poradniku zamieszczono:

–

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,

–

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

–

materiał nauczania – wiadomości teoretyczne, niezbędne do opanowania treści jednostki
modułowej,

–

zestaw pytań, abyś mógł sprawdzić, czy już opanowałeś określone treści,

–

ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,

–

sprawdzian postępów,

–

sprawdzian osiągnięć, przykładowy zestaw zadań; zaliczenie testu potwierdzi
opanowanie materiału całej jednostki modułowej,

–

literaturę uzupełniającą.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu nauczania jednostki modułowej powinieneś umieć:

–

obsługiwać sprzęt i przyrządy geodezyjne,

–

sprawdzać i rektyfikować instrumenty geodezyjne,

–

wykonywać pomiar kierunku i kąta poziomego i pionowego,

–

wykonywać pomiary sytuacyjne metodą biegunową i ortogonalną,

–

określać zakres instrukcji technicznych i umieć dokonać wyboru instrukcji odpowiedniej
dla planowanych prac geodezyjnych,

–

projektować i stabilizować osnowę pomiarową,

–

sporządzać i aktualizować mapę sytuacyjną na podstawie bezpośredniego pomiaru
w terenie,

–

przetworzyć

wyniki

pomiaru

terenowego

dane

numeryczne

i graficzne

z wykorzystaniem techniki komputerowej,

–

organizować wykonanie prac terenowych w zespołach pomiarowych, zgodnie
z obowiązującymi zasadami bhp i przepisami technicznymi,

–

dobierać sprzęt i instrumenty do wykonania otrzymanego zadania,

–

posługiwać się sprzętem zgodnie z zasadami jego użytkowania oraz odpowiednio
zabezpieczyć w czasie i po zakończeniu pomiaru,

–

stosować obowiązujące instrukcje i wytyczne techniczne związane z wykonaniem
geodezyjnych prac pomiarowych, obliczeniowych i graficznych,

–

sporządzać dokumentację techniczną wykonanych prac pomiarowych i obliczeniowych,

–

wykonywać niwelację geometryczną i obliczyć wysokości punktów,

–

sporządzać profil podłużny i poprzeczny terenu,

–

wykonywać podstawowe obliczenia geodezyjne,

–

dokonywać analizy otrzymanych materiałów geodezyjno-kartograficznych,

–

wykonywać wywiad terenowy i opracować mapę wywiadu,

–

stosować przepisy prawa budowlanego oraz prawa geodezyjnego i kartograficznego
w geodezji inżynieryjnej,

–

klasyfikować geodezyjne osnowy realizacyjne,

–

projektować, pomierzyć, wyrównać i wytyczyć osnowę realizacyjną,

–

opracowywać szkic dokumentacyjny,

–

opracowywać szkic tyczenia,

–

wytyczać punkty projektowanego obiektu różnymi metodami,

–

wytyczać punkty linii równoległej do danej,

–

wytyczać punkty linii o stałym spadku,

–

wyznaczać punkt o projektowanej wysokości,

–

ustalać dokładność tyczenia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

–

wyjaśnić zasady tyczenia tras drogowych, kolejowych i wodnych,

–

opracować geodezyjnie odcinek projektowanej trasy,

–

posłużyć się instrukcjami oraz wytycznymi technicznymi dotyczącymi obsługi inwestycji,

–

obliczyć elementy: łuków kołowych, koszowych, odwrotnych, krzywych przejściowych
(klotoidy), łuków kołowych z krzywymi przejściowymi, łuków pionowych,

–

obliczyć współrzędne punktów leżących na odcinkach krzywoliniowych trasy,

–

obliczyć i wykreślić elementy geometryczne tras przy pomocy geodezyjnych programów
komputerowych obliczeniowych i graficznych,

–

obliczyć elementy niwelety i wykreślić oś trasy w płaszczyźnie pionowej przy pomocy
geodezyjnych programów komputerowych obliczeniowych i graficznych,

–

dobrać metodę tyczenia projektowanych punktów trasy,

–

dobrać sprzęt do pomiarów geodezyjnych,

–

wytyczyć odcinki prostoliniowe tras,

–

wytyczyć odcinki krzywoliniowe trasy,

–

wytyczyć linie przekrojów poprzecznych trasy,

–

obliczyć objętość mas ziemnych przy pomocy geodezyjnych programów komputerowych
obliczeniowych,

–

opracować geodezyjnie projekt stacji i linii kolejowej,

–

wytyczyć rozjazdy i skrzyżowania torów,

–

określić zasady regulacji osi torów,

–

scharakteryzować metody przenoszenia wysokości przez duże powierzchnie wodne,

–

scharakteryzować metody opracowywania poprzecznych przekrojów cieków wodnych,

–

opracować geodezyjnie projekty: rowów melioracyjnych, kanałów, budowli regulacyjnych,

–

dobrać metodę do tyczenia: rowu melioracyjnego, kanału, budowli regulacyjnej,

–

wytyczyć linię zalewową zbiornika wodnego,

–

scharakteryzować podstawowe elementy mostu i wiaduktu,

–

opracować geodezyjnie projekt mostu i wiaduktu,

–

określić zasady geodezyjnej obsługi budowy mostu i wiaduktu,

–

wykonać geodezyjną inwentaryzację powykonawczą,

−

zastosować przepisy bezpieczeństwa i higieny pracy oraz ochrony środowiska podczas
wykonywania pomiarów terenowych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. MATERIAŁ NAUCZANIA

4.1. Ogólne wiadomości o tyczeniu tras

4.1.1. Materiał nauczania

Trasą nazywamy pas terenu przeznaczony pod budowlę inżynierską o znacznej długości

i niewielkiej szerokości. Przebieg danej trasy wyznacza się wytyczając jej oś. Pierwszy etap
tyczenia osi trasy to tyczenie linii prostych, a następnie wpisanie w ich załamania łuków
i krzywych przejściowych.

Metody tyczenia prostych odcinków trasy dobiera się w zależności od długości odcinka

i występujących ewentualnych przeszkód terenowych.

W najprostszym przypadku, tyczenie odcinka prowadzi się od punktu końcowego

w kierunku „na siebie”, wyznaczając punkty pośrednie w odległościach nie większych niż
300 m.

Dla długości odcinków do 2 km postępuje się tak jak przy tyczeniu metodą „w przód”.

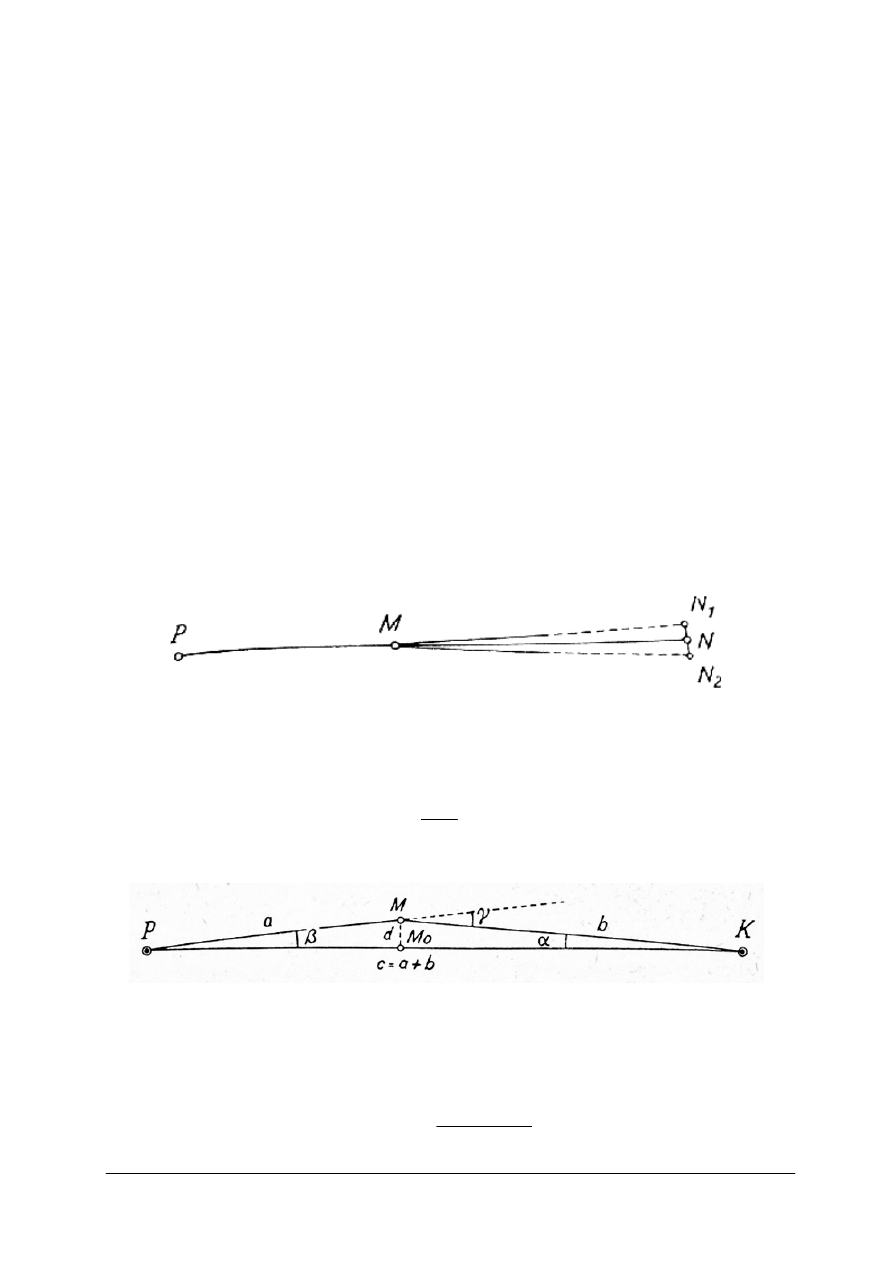
Przy  długościach  odcinków  od  2  do  5  km  stosujemy  sposób  mniej  dokładny.  Celując
teodolitem  z  punktu  początkowego  P  na  punkt  końcowy  K,  wytycza  się  odległy  punkt
kierunkowy  M,  a  następnie  przenosi  się  teodolit  na  punkt  M  i  wytycza  kolejny  punkt  N
(N

w pierwszym położeniu lunety i N

w drugim położeniu lunety) na odcinku M K,

aż dochodzi się do punktu K, wykonując tyczenie w dwóch położeniach lunety( rys. 1).

Rys. 1. Tyczenie prostej PK gdy z P widać K

Sposób dokładniejszy, to założenie między punktami P i K, w okolicy środka odcinka PK,

punktu M i zmierzenie na nim kąta (180˚- γ), a następnie obliczenie przesunięcia d. (rys. 2)

sin

⋅

gdzie a i b to odległości punktu M od P i K wyznaczone z dokładnością 20 m.

Rys. 2. Wtyczanie punktu M w prostą PK

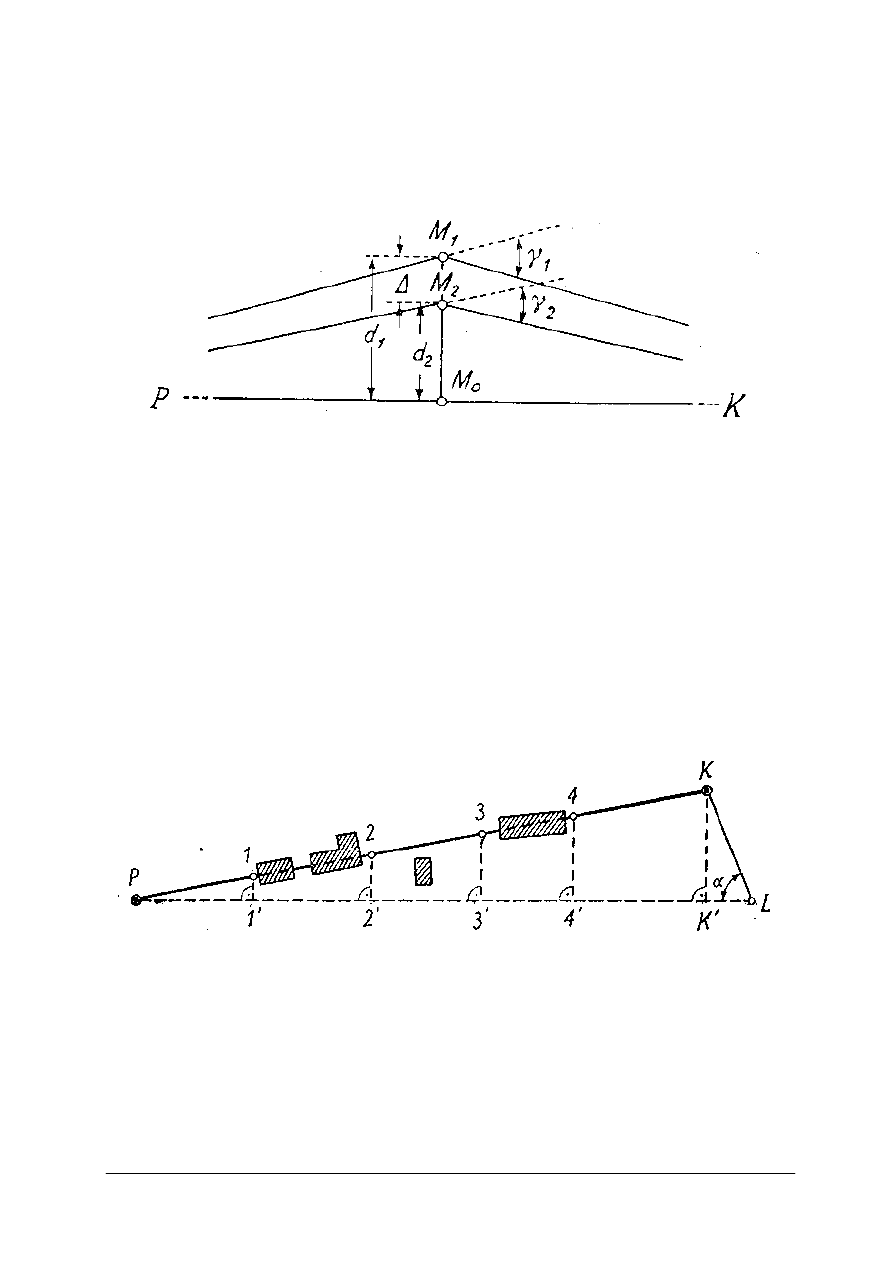
Jeżeli jednak nie mamy możliwości ustalenia długości odcinków a i b, to w pobliżu

prostej PK zakładamy 2 dodatkowe(rys. 3), bliskie sobie punkty M

i M

i obliczamy

przesunięcie d z uproszczonego wzoru

sin

∆ ⋅

−

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

gdzie

−

Δ to odległość między punktami M

i M

−

γ to kąt zmierzony odpowiednio na M

i M

−

to odległość punktu M

od wyznaczanej prostej PK.

Rys. 3. Wtyczanie punktu M

gdy brak odległości PK

Przy długości odcinka większej niż 5 km, do wyznaczenia kierunku na punkt końcowy

stosujemy, dla ułatwienia tyczenia - w dzień heliotrop, a w nocy światło sztuczne.

Jeżeli z punktu początkowego widać punkt końcowy, ale punkty bliskie są niewidoczne,

to  wytycza  się  możliwie  najdalszy  punkt  kierunkowy  prostej  (M).  Następnie  przenosi  się
instrument na punkt M i jeżeli z punktu tego nie widać punktu końcowego K, to celuje się na
punkt  P  i  po  obróceniu  lunety  przez  zenit,  wyznacza  w  dwóch  położeniach  lunety  odległy
punkt  N  na  kierunku  do  K.  Instrument  ustawia  się  na  N  i  postępuje  się  podobnie,  jak  na
punkcie  M,  dochodząc  do  punktu  K’  bliskiego  K.  Jeżeli  z  ważnych  przyczyn  nie  można
punktu  K’  uznać  za  właściwy  punkt  K,  to  przesuwa  się  wszystkie  wyznaczone  punkty
proporcjonalnie do odcinka K K’ i odległości od punktu początkowego.

Jeżeli z powodu wzniesień terenu z punktu początkowego P nie widać punktu końcowego

to należy założyć punkt M, z którego widać punkty P i K, zmierzyć kąt (180˚- γ) i obliczyć
wartość przesunięcia jak w przykładzie przedstawionym na rys.unku 2 lub 3.

Rys. 4. Tyczenie prostej przez drobne przeszkody

Jeżeli na tyczonym kierunku PK znajdują się przeszkody, to zakłada się dodatkowe

konstrukcje i tyczenie wykonuje się w sposób pośredni. Jedna z tych konstrukcji, to założenie
obok  przeszkody  dodatkowej  linii  PL(  rys.  4),  a  następnie  zrzutowanie  na  nią  punktu
końcowego  K  (  K’).  Na  prostej  PL  wybiera  się  punkty  1’,  2’,  3’...w  takich,  miejscach  aby
prostopadłe  do  prostej  pomocniczej  PL,  wystawione  w  tych  miejscach,  przebiegały  obok
przeszkód  terenowych.  Mierzy  się  długości  P1’,  P2’,...oraz  KK’  i  na  podstawie  twierdzenia
Talesa oblicza się długości 1’1,2’2 itd.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

11'

⋅

22 '

2 '

⋅

Obliczone długości 1’1, 2’2 itd. odkłada się na kierunkach prostopadłych wyznaczonych
w punktach 1’, 2’ ..itd.

Rys. 5. Tyczenie prostej przez przeszkodę zajmującą dużą przestrzeń

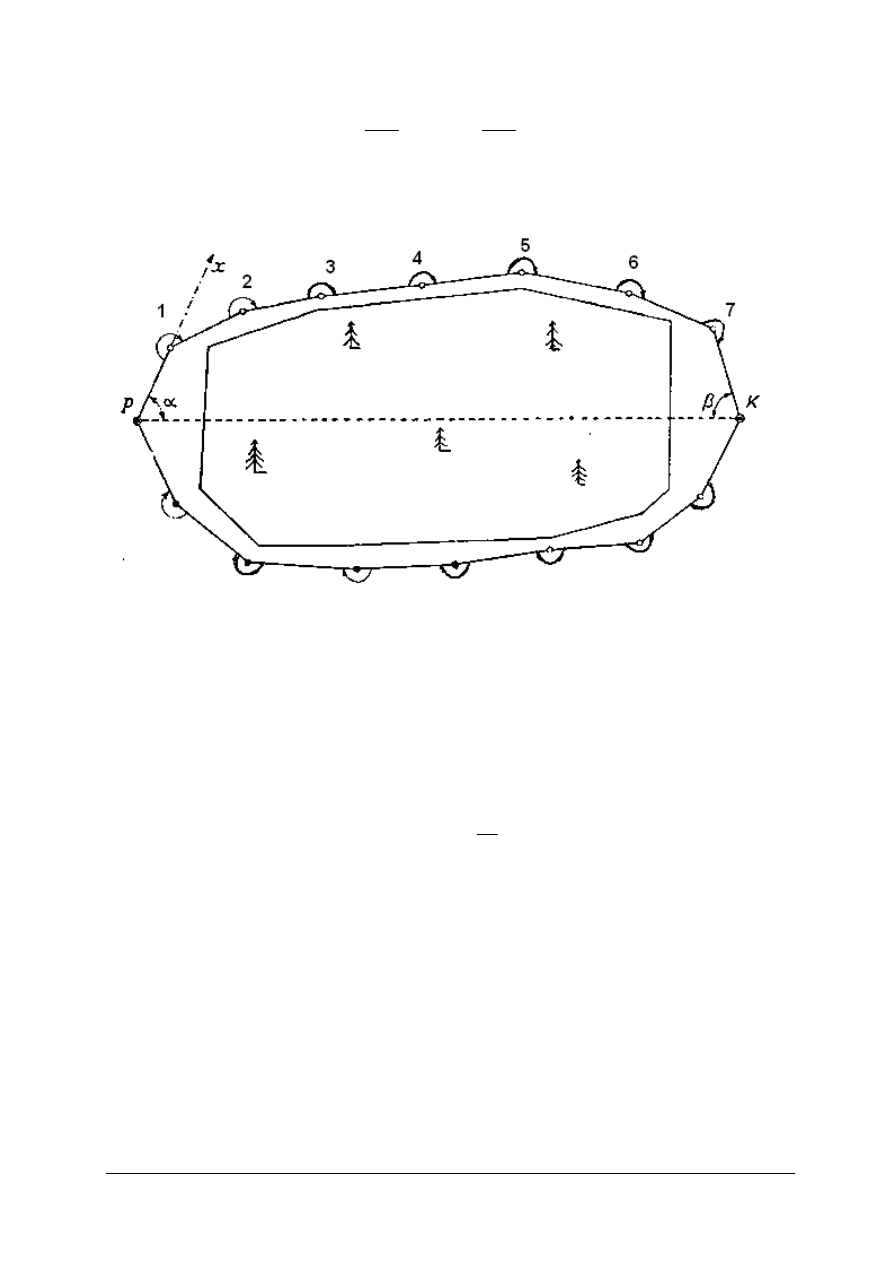
Jeżeli przeszkoda rozciąga się na dużej przestrzeni i celowanie z punktu P na K jest

niemożliwe, a dzieje się tak w przypadku zalesienia terenu (rys. 5), to dookoła przeszkody
zakłada się specjalną osnowę poligonową w kształcie wieloboku zamkniętego, zawierającego
punkt początkowy P i końcowy K.

Punkt początkowy P jest początkiem lokalnego układu współrzędnych prostokątnych,

a bok P1 - osią X-ów. W układzie tym oblicza się współrzędne wszystkich punktów ciągu
poligonowego, a następnie ze współrzędnych punktu końcowego K oblicza się kąt α ze
wzoru;

Obliczony kąt α odkłada się od kierunku P1 i w ten sposób wyznacza się kierunek PK.

Po wytyczeniu odcinków prostych dla danej trasy, w miejsca załamania trasy wpisuje się

łuki kołowe lub inne zestawy krzywych.

Na punkcie wierzchołkowym (rys. 6) W mierzy się kąt β między stycznymi do łuku

w punktach P i K. Następnie oblicza się jego dopełnienie do 180˚, czyli kąt α, zwany kątem
zwrotu stycznych lub kątem środkowym łuku. Aby ustalać położenie punktów łuku konieczna
jest znajomość jego promienia R.

Łuki tyczy się w dwóch etapach; najpierw punkty główne P (początkowy), S (środkowy),

K (końcowy), a następnie punkty pośrednie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

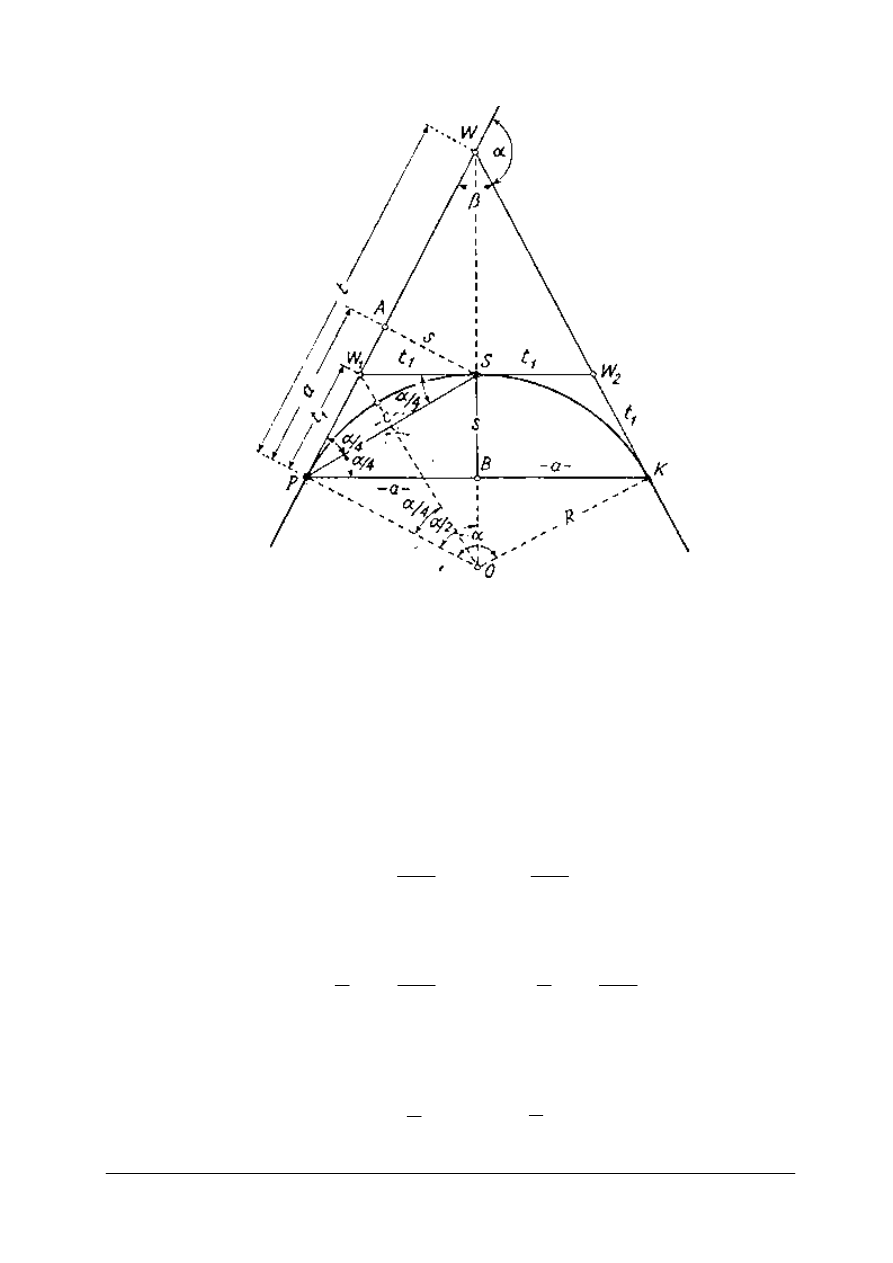
Rys. 6. Łuk kołowy

Punkty P i K, to punkty styczności łuku z ramionami kąta wierzchołkowego β.

180˚ - β = α

Położenie punktów P i K wyznacza się odkładając od wierzchołka W długości stycznej
głównej t, obliczonej ze wzoru

WP=WK= t =R tg(½ α)

Jeżeli nie mamy dostępu do wierzchołka W, to zakładamy dwa punkty pomocnicze A i B, na
ramionach kąta wierzchołkowego β i mierzymy między nimi odległość (d

) oraz kąty δ i γ

na tych punktach. Suma zmierzonych kątów δ i γ daje kąt α, który w trójkącie AWB jest
dopełnieniem kąta β do 180˚. Następnie oblicza się długości odcinków WA i WB
z twierdzenia sinusów.

sin

⋅

;

sin

⋅

Teraz oblicza się różnicę między długością stycznej głównej i długością odpowiednich boków
trójkąta AWB, otrzymując odległości od punktów pomocniczych A i B do szukanych
punktów głównych łuku P i K

sin

R tg

= ⋅

−

⋅

;

sin

R tg

= ⋅

−

⋅

Aby wyznaczyć kolejny punkt główny łuku, punkt środkowy (S) można zastosować, zależnie
od warunków terenowych, jeden z poniższych sposobów.
1. Odłożenie od punktu P, na kierunku do K, długości odcinka „a” i odległości „s”

określonych wzorami

sin

= ⋅

1 cos





−









„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. Odłożenie od punktu P na kierunku do W długości odcinka „a” i odległości „s” od

wyznaczonego w ten sposób punktu A. Odłożenie odcinka a i prostopadłego s można
w obu metodach wykonać symetrycznie również od punktu K, zależnie od warunków
terenowych.

3. Odłożenie od punktu W, wzdłuż dwusiecznej kąta β długości odcinka WS

cos









−













;

4. Odłożenie z punktu P, na dwusiecznej kąta WPK, czyli pod kątem

od stycznej lub od

cięciwy PK, długości odcinka PS

2 sin

Podobnie można odłożyć analogiczną odległość KS od punktu K.
5. Zbudowanie wieloboku stycznych otaczających, czyli obliczenie długości odcinka

R tg

= ⋅

i odłożenie jej od punktu P i od punktu K wzdłuż stycznych. Otrzymane dwa nowe punkty na
stycznych łączy się odcinkiem prostym a w połowie tego odcinka znajduje się szukany punkt
S, czyli środek łuku.

Jeżeli brak w terenie instrumentu to przy wierzchołku W można zbudować konstrukcję

liniową i ze stosunku długości boków w trójkącie WAB ustalić wartości funkcji
występujących we wzorach służących do ustalenia położenia punktów głównych łuku (rys. 7).

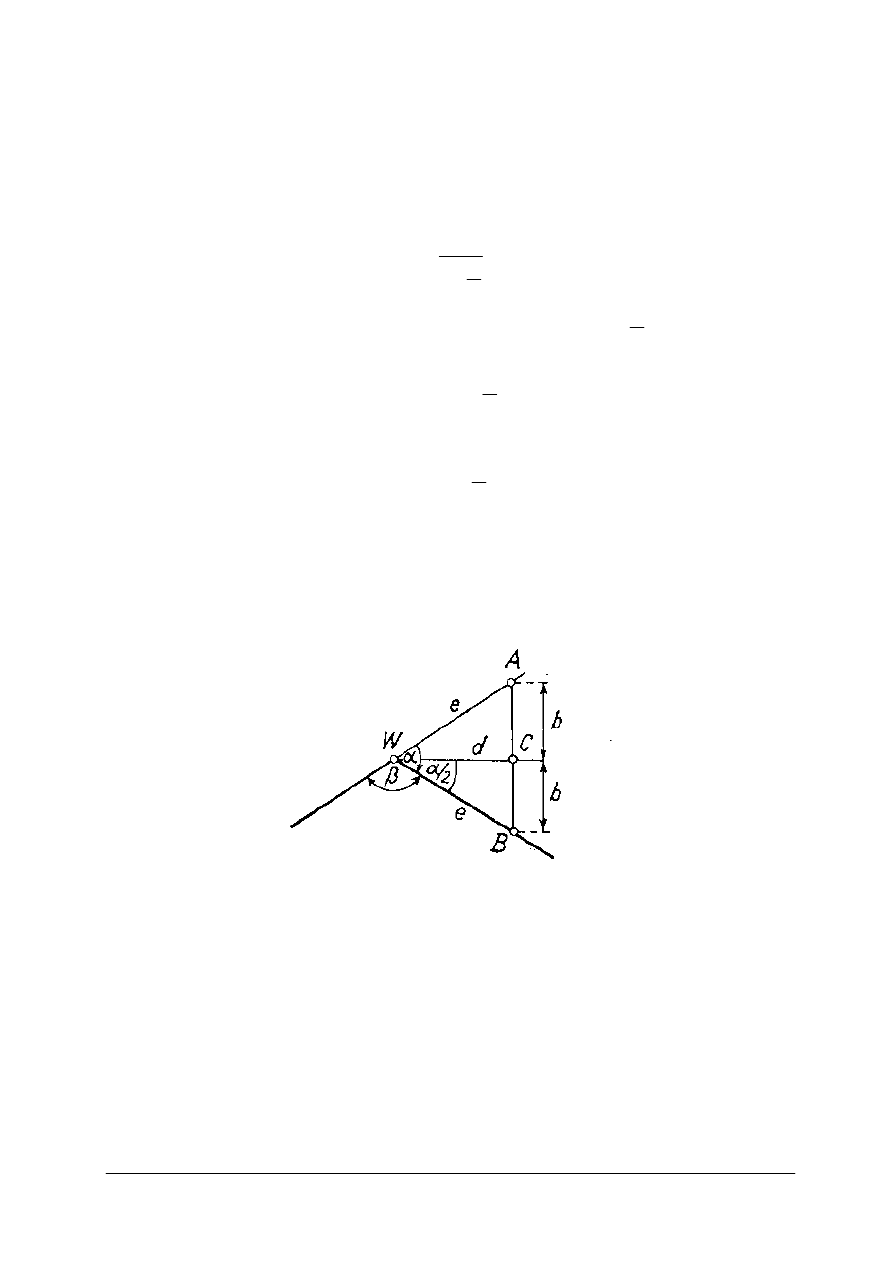
Rys. 7. Konstrukcja liniowa do wyznaczania punktów głównych łuku.

Wyznaczenie punktów głównych łuku nie określa dokładnie przebiegu łuku w terenie.

Trzeba wytyczyć dostatecznie gęsto pewną liczbę punktów pośrednich do których zalicza się
również punkty hektometrowe, wyznaczające odcinki 100 metrowe. Gęstość wyznaczenia
punktów pośrednich zależy od wielkości promienia łuku. Przyjmuje się, że różnica między
długością cięciwy łączącej kolejne dwa punkty, a odległością tych punktów po łuku, nie może
przekraczać 5 mm. Dla promienia łuku ponad 275 m, tyczy się co 20 m, dla R> 100 m - co
10 m, a dla R< 100 m co 5 lub nawet 2 m, zależnie od potrzeby.

Punkty pośrednie łuku można tyczyć różnymi metodami.

Metoda biegunowa polega na odkładaniu od stycznej do łuku w punkcie P lub K kąta φ,
obliczonego dla przyjętej gęstości wyznaczania punktów pośrednich ΔL, ze wzoru

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

∆

⋅

Długość cięciwy oblicza się ze wzoru

c = 2Rsinφ

Tyczenie wykonuje się odkładając od stycznej w punkcie P lub K kąt φ (rys. 8), a następnie
na tym kierunku odkłada się długość cięciwy c, otrzymując punkt 1 łuku. Kolejne punkty 2, 3,
4.otrzymuje się odkładając od stycznej kąty 2 φ, 3 φ, 4 φ, a na wyznaczonym w ten sposób
kierunku znajduje się kolejne punkty pośrednie 2, 3 itd. Zataczając łuk długością cięciwy c od
poprzednio wyznaczonego punktu pośredniego.

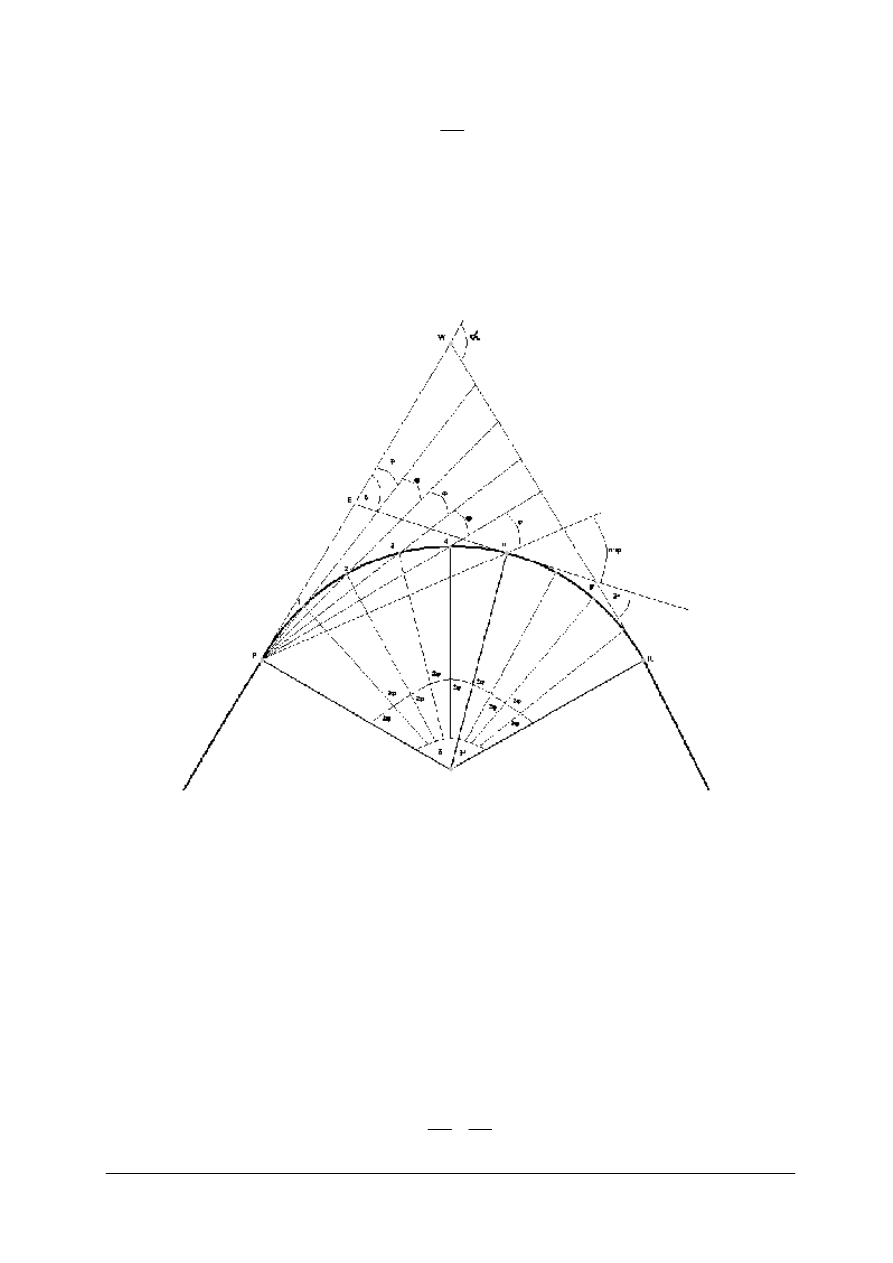
Rys. 8. Wyznaczanie punktów pośrednich metodą biegunową

Metoda biegunowa przy użyciu dwóch teodolitów, to metoda wyznaczania punktów

pośrednich  trasy  za  pomocą  przecięć  dwóch  kierunków,  wyznaczonych  metodą  wcięć
kątowych. Zasada tej metody opiera się na twierdzeniu, że kąty środkowe wspierające się na
jednakowych  łukach  są  sobie  równe,  styczna  zaś  i  cięciwa  przechodząca  przez  punkt
styczności, a odpowiadająca łukowi o kącie środkowym φ, tworzą również kąt φ. Odkładając
od stycznej na stanowisku P kąty: φ, 2φ, 3φ.. i takie same kąty: φ, 2φ, 3φ ... od cięciwy KP na
punkcie K, w przecięciu tych kierunków otrzymamy punkty 1, 2, 3, ... rozmieszczone na łuku.
W  praktyce,  punkty  pośrednie  wyznacza  się  odkładając  kierunki  od  cięciwy  PK  na
stanowisku P i kierunki, będące dopełnieniem poprzednich, do kąta ½α, na punkcie K.

Tyczenie punktów pośrednich łuku można również prowadzić za pomocą rzędnych od

stycznej (rys. 9), przyjętej za oś X. Można odkładać równe, okrągłe wartości na stycznej
i obliczać wartość rzędnej y według wzoru:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

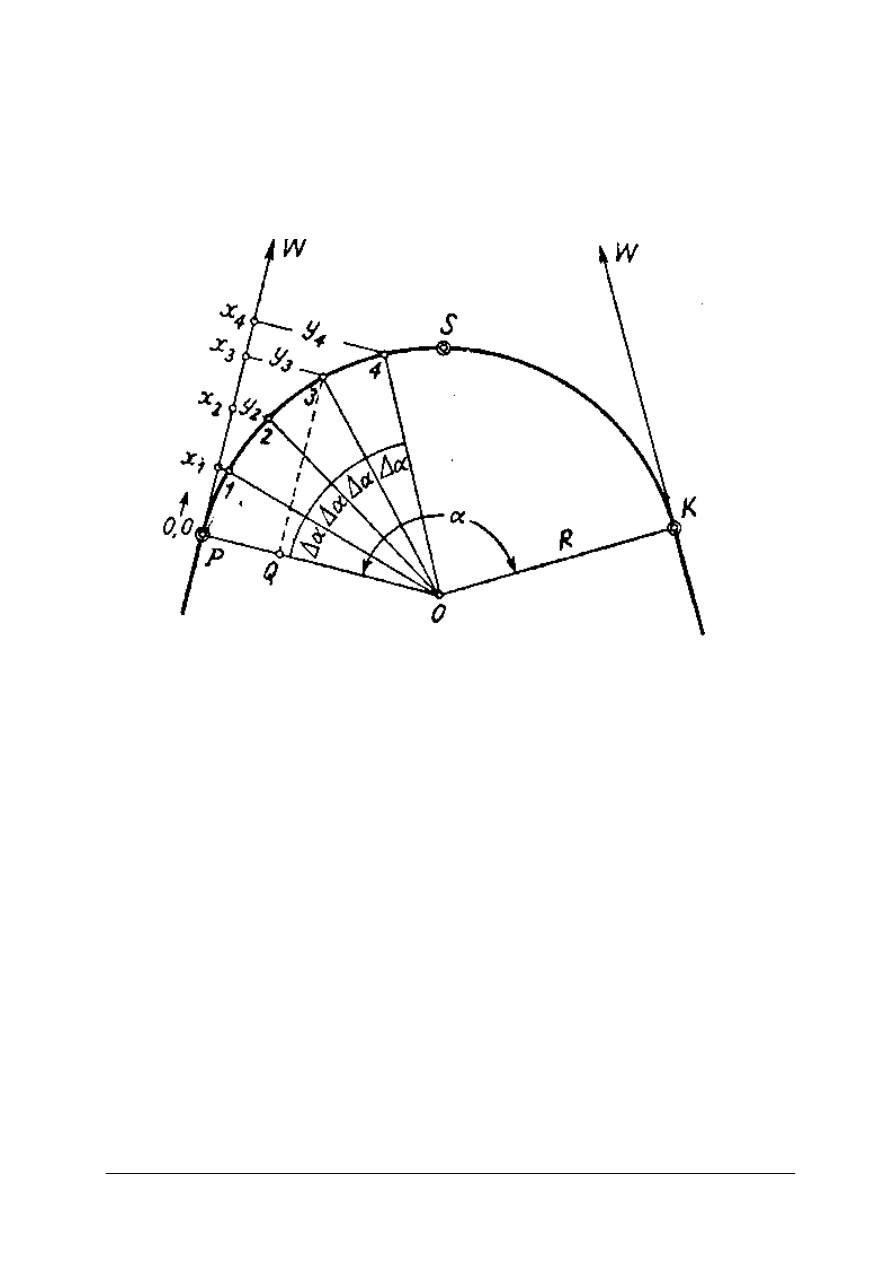
otrzymując punkty na łuku w różnych odległościach. Można też ustalić kąt środkowy φ, dla
którego obliczy się wartości rzędnej i odciętej, a wówczas punkty pośrednie będą wyznaczone
:na łuku w równych odstępach:

sin(

)

∆

;

[

]

1 cos(

)

−

∆

Rys. 9. Tyczenie punktów pośrednich metodą ortogonalną

Do tyczenia w trudnych warunkach terenowych można zastosować metodę zwaną

angielską. Jest to tyczenie od przedłużonej cięciwy. Zależnie od posiadanego sprzętu,
odkładamy początkowo od stycznej, wartości odciętych

cos

, a następnie rzędnych

sin

. Następnie od każdej kolejnej cięciwy odkładamy wartości:

cos 2

oraz

sin 2

, gdzie c - to cięciwa, liczona dla danego φ wg wzoru

2 sin

Przy regulacji rzek, podczas tyczenia łuków nie wyznacza się osi projektowanego koryta

rzeki ale trasę obu brzegów.

Nie zawsze można jednym łukiem połączyć dwa odcinki proste. Można wówczas

zastosować zespół łuków, które w miejscu swego styku mają wspólną styczną. Taki zespół
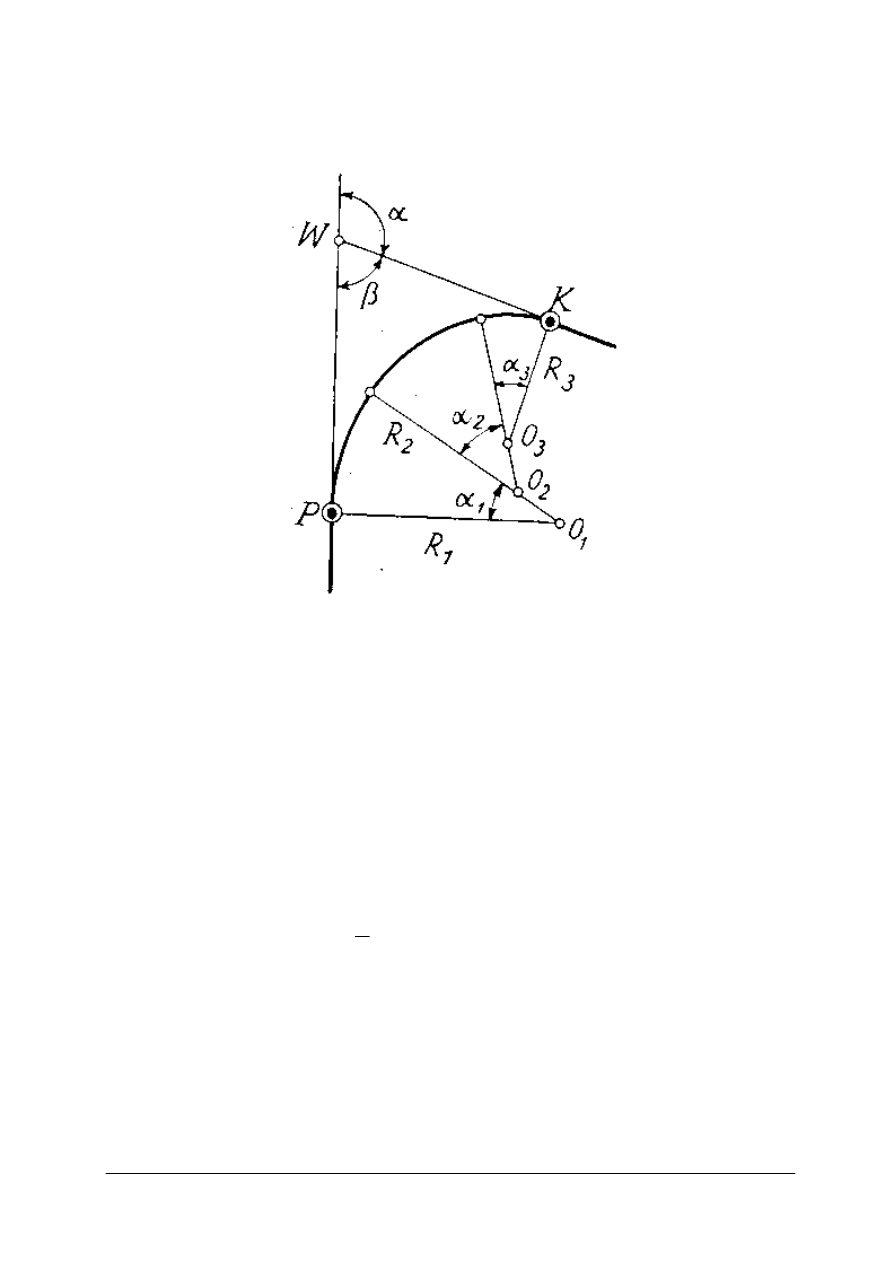
łuków nazywa się łukiem koszowym (rys. 10). Dla takiego zespołu łuków muszą być
spełnione trzy warunki geometryczne: Pierwszy warunek to

180

° −

∑

czyli suma kątów środkowych α odpowiadających poszczególnym łukom kołowym musi być
równa kątowi α zwrotu stycznych głównych, przy wierzchołku W. Długości stycznych
głównych dla łuku koszowego są różne.

Kolejne dwa warunki wynikają z warunku wieloboku zamkniętego. Równania otrzymuje

się rzutując jego boki na dwa dowolne kierunki. Może to być styczna PW (t

) i prostopadły do

niej promień R

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

= (R

-R

) sinα

+ (R

-R

) sin(α

+α

) + R

sin(α

+α

) + t

cos β

=(R-R

) cosα

+ (R

-R

) cos(α

+α

) + R

cos(α

+α

) + t

sin β

Rys. 10. Łuk koszowy

Można też stosować inny rodzaj krzywej, zwanej zwany łukiem odwrotnym. Są to dwa

łuki, posiadające w miejscu styczności wspólną styczną, ale krzywiznami skierowane
w przeciwnych kierunkach i nieoddzielone od siebie wstawką prostą.

Aby ustrzec się od nagle pojawiającej się przy wjeździe na łuk siły odśrodkowej,

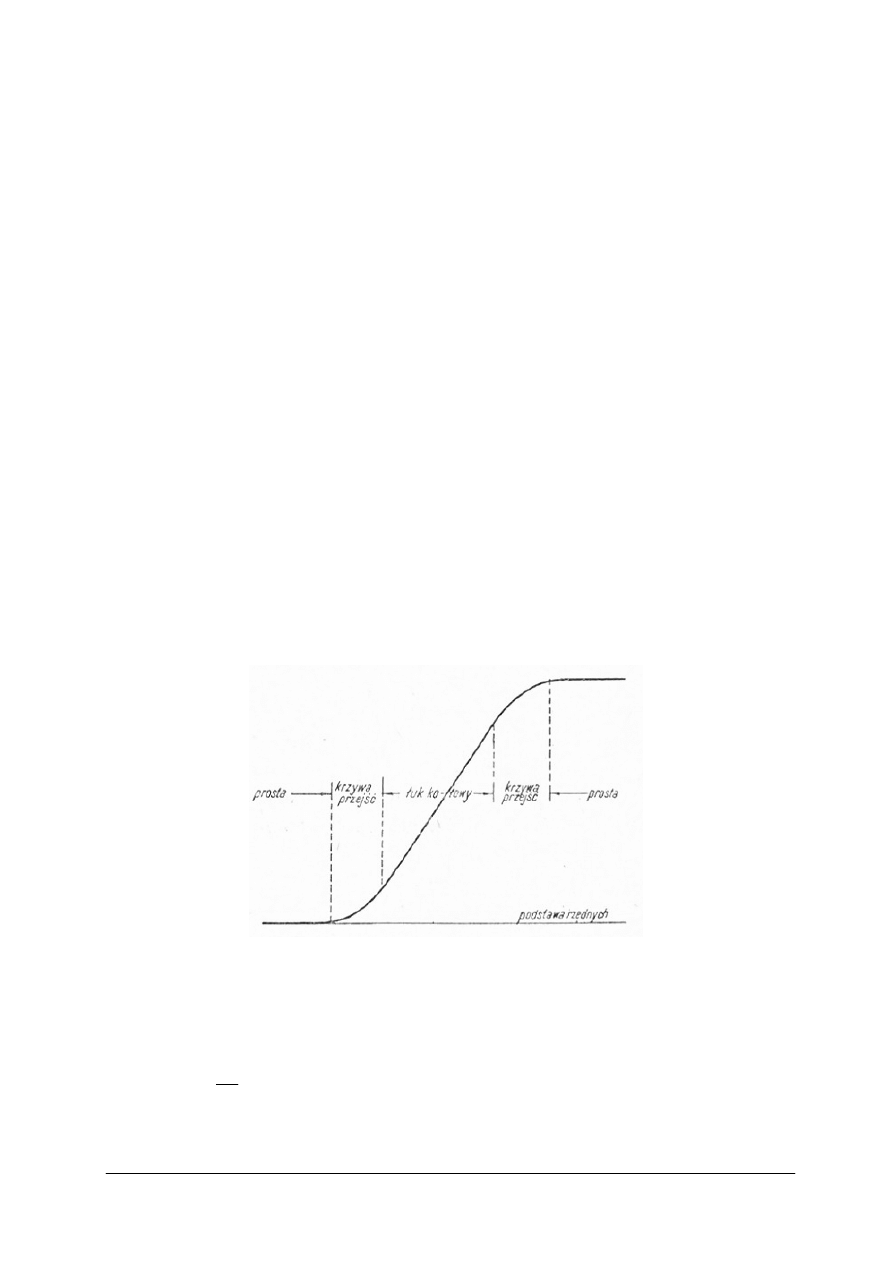
wprowadza  się  między  prostą,  a  łuk  kołowy  odcinek  krzywej,  zwany  krzywą  przejściową.
Krzywa  przejściowa,  to  odcinek  na  którym  zmienia  się  przekrój  poprzeczny  drogi:
z dwuspadowego,  dachowego  na  jednospadowy  (jednostronny).Odcinek  ten  nazywa  się
rampą drogową. Dla trasy kolejowej na łuku tok zewnętrzny jest podwyższony o wielkość h,
która  nazywa  się  przechyłką.  Przechyłka  nie  może  pojawiać  się  nagle,  tylko  musi  być
wystopniowana od zera (przy styku z prostą) do wielkości h (na styku z łukiem).

Promień krzywej przejściowej powinien się zmieniać od ∞ na styku z prostą, do wartości

promienia łuku R, na styku z łukiem. Krzywizna K krzywej przejściowej rośnie od wartości 0

na styku z prostą, do wartości K =

Na odcinku krzywej przejściowej siła odśrodkowa powinna wzrastać od zera do wartości

S na łuku. Warunek ciągłości wzrostu siły odśrodkowej spełniają takie krzywe, jak lemniskata
czy parabola trzeciego stopnia. Najbardziej korzystna jest taka krzywa, której krzywizna
rośnie proporcjonalnie do długości łuku. Warunek ten spełnia krzywa zwana klotoidą.
Warunek proporcjonalności krzywizny K do długości łuku L można zapisać

a K

Po podstawieniu do powyższego wzoru wartości krzywizny K otrzymuje się równanie

naturalne klotoidy

const

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Z równania klotoidy wynika, że dla klotoidy iloczyn promienia krzywizny R i długości

łuku L, mierzonego od punktu stałego, jest w każdym punkcie klotoidy stały. Wartość

a , to

współczynnik proporcjonalności, a liczba „a” to parametr klotoidy. Dla a = 1 otrzymuje się
klotoidę jednostkową.

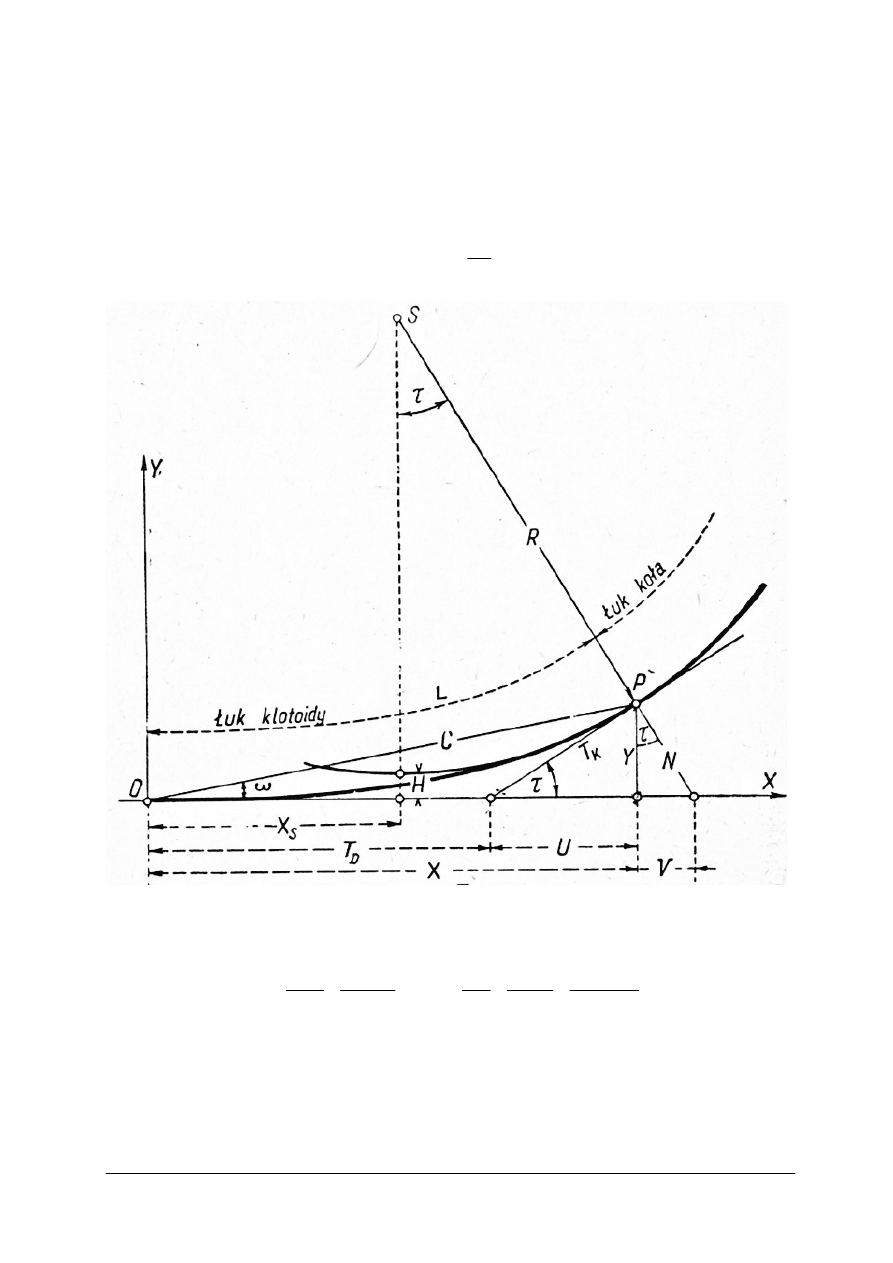
Kąt zwrotu τ stycznej w dowolnym punkcie klotoidy, jest równy połowie długości łuku

podzielonej przez promień krzywizny R

Rys. 11. Klotoida i jej elementy

Współrzędne prostokątne punktów klotoidy określają wzory

...

3456

= −

−

...

336

42240

−

Aby zastosować klotoidę (rys. 11), jako krzywą przejściową między prostą i łukiem
kołowym, posługujemy się jej łukiem, rozpoczynającym się w punkcie przegięcia 0, gdzie
promień R= ∞.

Poza współrzędnymi prostokątnymi X, Y punktów klotoidy oraz wartościami a, R, L i τ,

obliczamy X

, H, Y

T, T

, T

, N, C i ω.

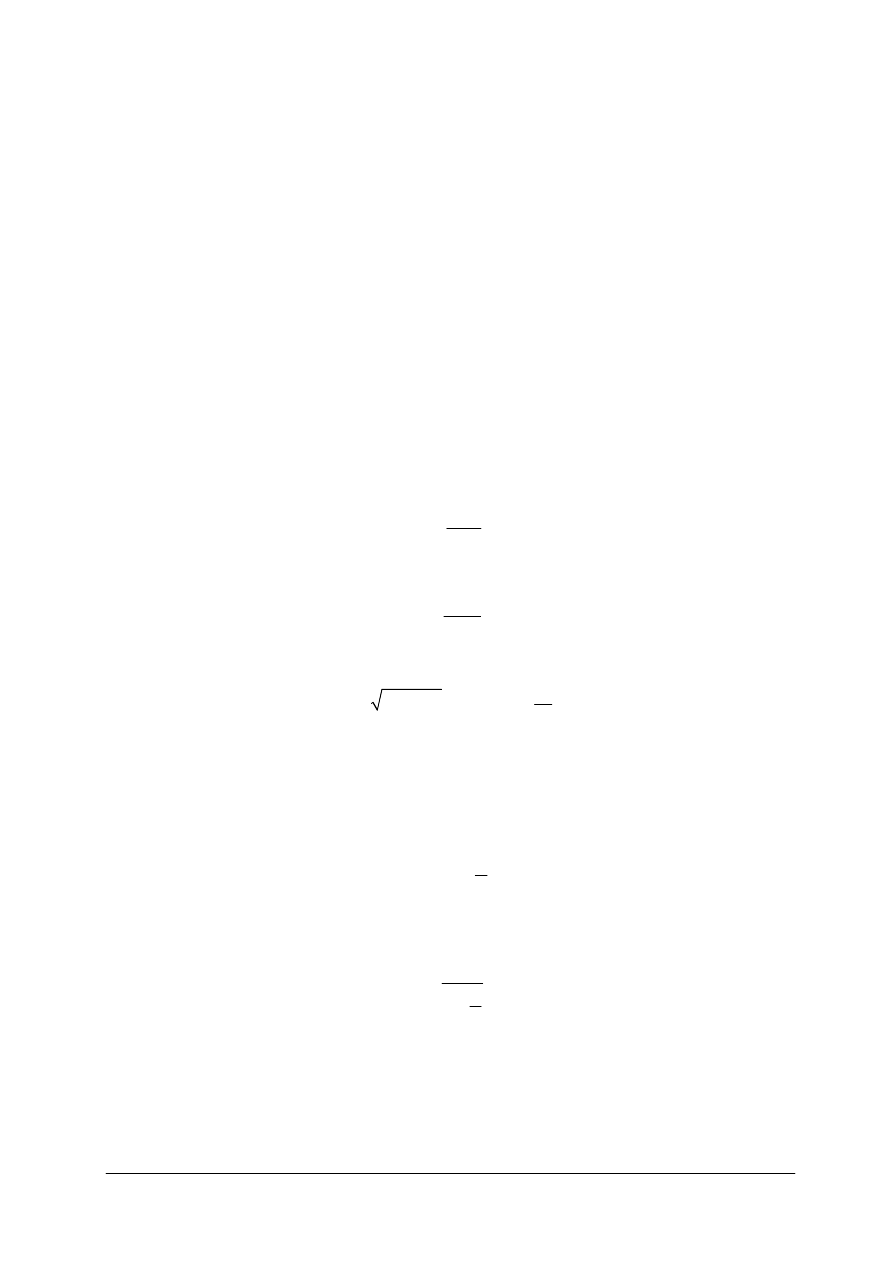
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

- to środek koła krzywizny w punkcie P czyli środek okręgu tworzącego dalszy ciąg trasy.

określa wzór

sin

= −

H - to odsunięcie koła krzywizny od stycznej głównej

(1 cos )

= −

−

- to rzędna środka koła krzywizny

cos

= + = +

T - to długość stycznej głównej, czyli odległość od początku układu do punktu przecięcia się
normalnej ze styczną główną

Ytg

= +

to styczna długa, czyli odległość od początku układu do punktu przecięcia się stycznej

głównej ze styczną w punkcie P klotoidy

Yctg

= −

czyli styczna krótka, to odcinek od punktu P do punktu przecięcia się jej ze styczna

główną

sin

N – to normalna, określona wzorem

cos

Współrzędne biegunowe C i ω dowolnego punktu klotoidy określają wzory

;

arctg

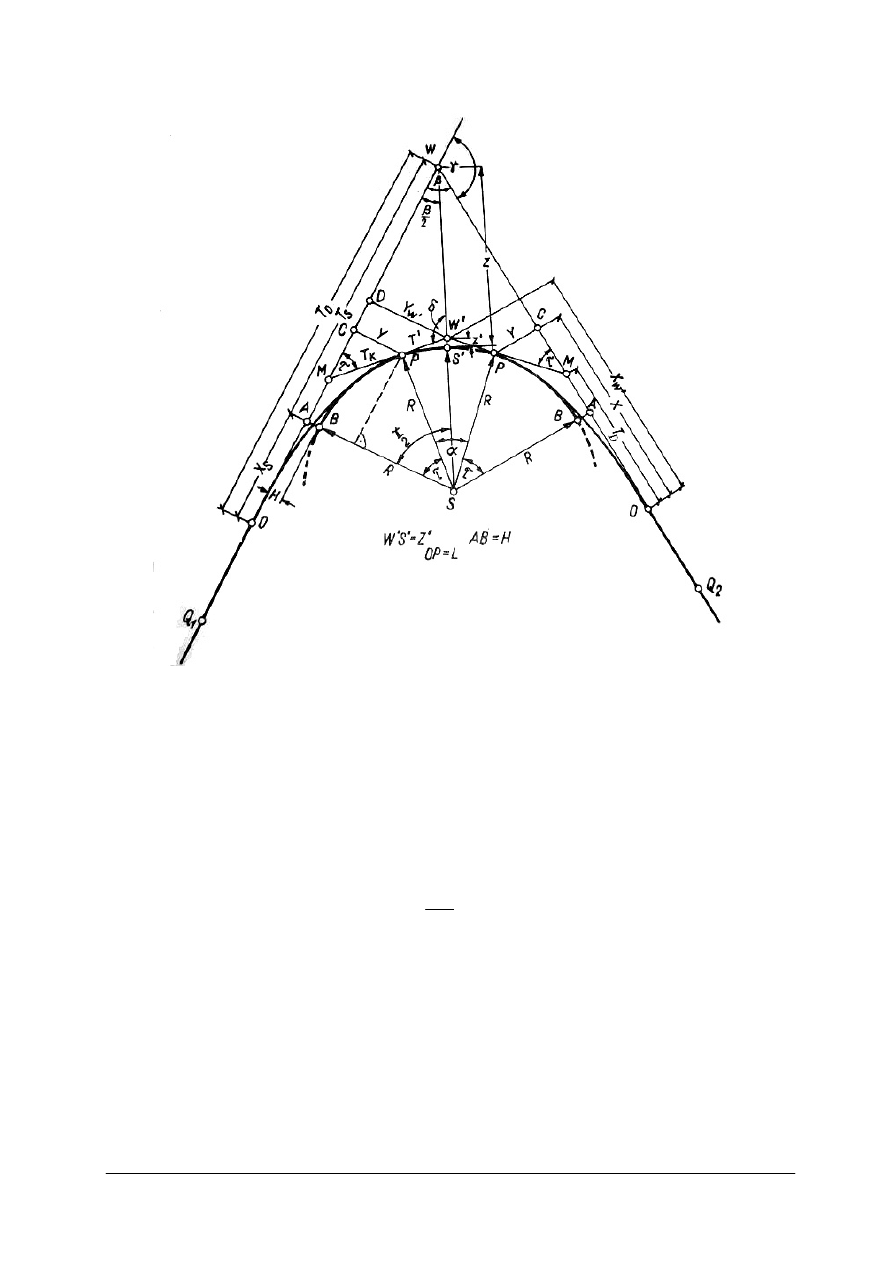
Jeżeli chcemy między dwie proste wpisać łuk kołowy z symetrycznymi łukami klotoid,

to będzie to możliwe tylko wtedy, gdy kąt zwrotu stycznych γ będzie równy 2τ + α, gdzie α
jest częścią kąta, przypadającą na łuk kołowy (rys. 12). Aby wyznaczyć początek i koniec
takiej trasy należy obliczyć odcinek stycznej całkowitej T

(

)

H tg

Na dwusiecznej kąta zwrotu stycznych, od punktu W odkłada się odcinek Z, wyznaczając
w ten sposób środek łuku B

(

)(

cos

− +

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 12. Łuk z symetrycznymi klotoidami

Po wyznaczeniu podstawowych elementów całego układu trasy, należy wyznaczyć

punkty pośrednie dla każdej z jej części składowych. Zarówno dla łuku kołowego, jak i dla
klotoidy. Można to zrobić wykorzystując metodę ortogonalną lub biegunową.

Posługując się metodą ortogonalną, odkłada się kolejne rzędne i odcięte obliczone dla

coraz większych wartości długości L i ustalonej wartości „a” oraz R.

Metoda biegunowa tyczenia klotoidy wymaga obrania stanowiska S, które może się

znajdować w punkcie początkowym O. Na stanowisku S odkłada się od stycznej pierwszy kąt
Δα

jaki tworzy pierwsza cięciwa ze styczną

)

L L

∆ =

∆

+ ∆

gdzie:

ΔL- to odcinki na jakie podzielono tyczony łuk,
L

- to długość łuku od punktu początkowego O do stanowiska S.

Na wyznaczonym w ten sposób kierunku odkłada się obliczoną odległość pierwszego punktu
pośredniego klotoidy od stanowiska itd

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.  Jak można wyjaśnić pojęcie: trasa?
2.  Jakie są metody tyczenia prostych odcinków trasy?
3.  Jakie są sposoby tyczenia prostych przez przeszkody?
4.  Jakimi sposobami można tyczyć punkty główne łuku?
5.  Jak  tyczy  się  punkty  główne  łuku,  gdy  nie  ma  możliwości  pomiaru  kąta  zwrotu

stycznych?

6.  Na czym polega tyczenie punktów pośrednich łuku metodą biegunową?
7.  Na czym polega tyczenie punktów pośrednich łuku metodą ortogonalną?
8.  Na czym polega tyczenie punktów pośrednich łuku metodą angielską?
9.  Jakie warunki geometryczne muszą być spełnione dla łuku koszowego ?
10.  Jak można wyjaśnić pojęcie klotoida?
11.  Jakimi metodami można tyczyć klotoidę?
12.  Jakie są zależności między poszczególnymi elementami klotoidy?

4.1.3. Ćwiczenia

Ćwiczenie 1

Dokonaj wytyczenia punktów głównych łuku kołowego przy dostępnym punkcie

wierzchołkowym.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  dokonać sprawdzenia sprzętu niezbędnego do wykonania pomiarów,
2)  odszukać punkt wierzchołkowy łuku i kierunki stycznych do łuku w tym punkcie,
3)  zmierzyć kąt wierzchołkowy β,
4)  obliczyć kąt α, czyli kąt zwrotu stycznych,
5)  obliczyć długość stycznej głównej t,
6)  ustalić w terenie położenie punktów głównych P i K,
7)  zastabilizować punkty P i K,
8)  obliczyć elementy potrzebne do wyznaczenia punktu S dwoma sposobami,
9)  ustalić położenie punktu S i zastabilizować go,
10)  przeprowadzić kontrolę wyznaczenia położenia punktów głównych łuku w terenie.

Wyposażenie stanowiska pracy:

−

szkice polowe i opis topograficzny punktu wierzchołkowego,

−

poradnik dla ucznia,

−

teodolit ze statywem,

−

taśma, węgielnica, domiarówka, szpilki, szkicownik,

−

paliki, gwoździe, młotek, farba,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 2

Dokonaj wytyczenia punktów głównych łuku kołowego, jeżeli punkt wierzchołkowy jest

niedostępny.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać sprawdzenia sprzętu niezbędnego do wykonania pomiarów,
2) ustalić w terenie kierunki stycznych i założyć na nich dwa wzajemnie widoczne punkty

A i B

3)  zmierzyć długość odcinka AB,
4)  zmierzyć kąty δ i γ na punktach A i B,
5)  obliczyć kąt wierzchołkowy β,
6)  obliczyć kąt α, czyli kąt zwrotu stycznych,
7)  obliczyć długości pozostałych boków w trójkącie AWB,
8)  obliczyć długość stycznej głównej t,
9)  obliczyć  odległości  od  punktów  A  i  B  do  punktów  głównych  łuku  P  i  K;  tj.  długości

odcinków AP i BK ustalić różnice; AP i BK,

10) odłożyć na stycznych długości odcinków AP i BK, znajdując położenie punktów

głównych P i K,

11) zastabilizować punkty P i K,
12) obliczyć długości odcinków a i s, czyli elementy potrzebne do wyznaczenia punktu S

dwoma sposobami,

13) ustalić położenie punktu S i zastabilizować go,
14) przeprowadzić kontrolę wyznaczenia położenia punktów głównych łuku w terenie.

Wyposażenie stanowiska pracy:

−

szkice polowe,

−

poradnik dla ucznia,

−

teodolit ze statywem,

−

taśma, węgielnica, domiarówka, szpilki, szkicownik,

−

paliki, gwoździe, młotek, farba,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

Ćwiczenie 3

Dokonaj wytyczenia punktów pośrednich łuku kołowego metodą biegunową.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  dokonać sprawdzenia sprzętu niezbędnego do pomiaru,
2)  odszukać w terenie wytyczone wcześniej punkty główne łuku kołowego,
3)  ustalić wartość kąta zwrotu stycznych,
4)  wykonać obliczenia, ustalając wartość kąta φ i długość cięciwy c,
5)  wykonać odkładanie kąta φ i jego wielokrotności oraz długości cięciwy c,
6)  zaznaczyć otrzymane punkty pośrednie łuku,
7)  przeprowadzić kontrolę wyznaczenia położenia punktów pośrednich łuku w terenie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wyposażenie stanowiska pracy:

−

szkice polowe i opisy topograficzne punktu wierzchołkowego W oraz punktów P, K i S,

−

poradnik dla ucznia,

−

teodolit ze statywem,

−

taśma, węgielnica, domiarówka, szpilki, szkicownik,

−

paliki, gwoździe, młotek, farba,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

Ćwiczenie 4

Dokonaj wytyczenia w terenie punktów pośrednich łuku kołowego metodą ortogonalną.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  odszukać w terenie wytyczone wcześniej punkty główne łuku kołowego,
2)  ustalić wartość kąta zwrotu stycznych,
3)  wykonać obliczenia wartości rzędnych i odciętych,
4)  wykonać odkładanie obliczonych długości x wzdłuż stycznej oraz prostopadłych y,
5)  zaznaczyć otrzymane punkty pośrednie łuku,
6)  przeprowadzić kontrolę wyznaczenia położenia punktów pośrednich łuku w terenie.

Wyposażenie stanowiska pracy:

−

szkice polowe i opisy topograficzne punktu wierzchołkowego W oraz P, K i S,

−

poradnik dla ucznia,

−

taśma, węgielnica, domiarówka, szpilki, szkicownik,

−

paliki, gwoździe, młotek, farba, materiały piśmiennicze,

−

kalkulator funkcyjny.

Ćwiczenie 5

Oblicz

elementy

wytyczenia

metodą

biegunową,

punktów

głównych,

charakterys.tycznych i hektometrowych dla krzywej składającej się z układu łuku kołowego
z dwoma symetrycznymi klotoidami w oparciu o istniejącą osnowę realizacyjną, obliczając
wcześniej współrzędne punktów łuku i klotoidy.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) odszukać i zapisać potrzebne wzory,
2) obliczyć współrzędne punktów głównych, charakterystycznych i hektometrowych

krzywej,

3) obliczyć miary biegunowe ustalonych punktów względem osnowy realizacyjnej.

Wyposażenie stanowiska pracy:

−

dane dotyczące zaprojektowanego symetrycznego układu krzywych,

−

poradnik dla ucznia,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) wyjaśnić pojęcie: łuk koszowy?



2) wyjaśnić sposób tyczenia linii prostych przez przeszkody?



3) określić sposoby tyczenia punktów głównych łuku?



4) określić podstawowe elementy klotoidy?



5) zastosować sposób tyczenia punktów głównych łuku bez pomiaru

kąta zwrotu stycznych?



6) wykonać tyczenie punktów pośrednich łuku metodą biegunową?



7) wykonać tyczenie punktów pośrednich łuku metodą ortogonalną?



8) wykonać tyczenie punktów pośrednich łuku metodą angielską?



„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2. Geodezyjna obsługa budownictwa drogowego, kolejowego

i wodnego

4.2.1. Materiał nauczania

Prace związane z opracowaniem geodezyjnym dowolnego odcinka trasy
Przedmiotem wytyczania przy różnego rodzaju obiektach są:

−

w odniesieniu do kolei - granice zewnętrzne obszarów kolejowych, osie torów, rozjazdy
i skrzyżowania torów oraz inne urządzenia techniczno - kolejowe, a także towarzyszące
obiekty inżynierskie;

−

w odniesieniu do dróg - granice zewnętrzne pasa  drogowego, charakterys.tyczne punkty
osi  i  korony  drogi,  skrzyżowania  dróg,  drogowe  obiekty  inżynierskie,  urządzenia
techniczno - drogowe;

−

w odniesieniu do cieków wodnych - granice pasa cieku, oś i linie brzegowe kanału, linie
zalewowe zbiorników wodnych, linie brzegowe (w przypadku regulacji rzeki), wodne
budowle inżynierskie.
Dla każdego tyczonego obiektu musi być opracowana dokumentacja projektowa.

Podstawowe (wyjściowe) dane do wytyczania obiektów są zawarte w dokumentacji
projektowej zakładu (obiektu), a w szczególności w planie realizacyjnym i w projektach
technicznych.

Plan realizacyjny i projekty techniczne należy opracować geodezyjnie, to jest

w odniesieniu  do  osnowy  geodezyjnej  określić  dane  liczbowe,  potrzebne  do  wyznaczenia
w terenie  położenia  poszczególnych  elementów  projektowanych  obiektów  budowlanych.
W szczególności, dane te powinny dotyczyć: punktów głównych budowli, przebiegu osi, linii
rozgraniczających,  linii  zabudowy,  usytuowania  obiektów  budowlanych,  jak  również
projektowanego ukształtowania terenu.

Konieczne jest dokonanie wywiadu terenowego, który dla obiektów wydłużonych

(liniowych) jakimi są trasy drogowe, kolejowe czy wodne, polega na ustaleniu sytuacyjnym
i wysokościowym kolejnych punktów głównych obiektu. Sytuacyjne wyznaczenie, to
wyniesienie punktów metodą ortogonalną lub biegunową.

Dokumentem technicznym, według którego wykonuje się tyczenie sytuacyjne, jest szkic

dokumentacyjny,  zawierający  dane  dotyczące  osnowy  realizacyjnej  i  wszystkie  elementy
niezbędne  do  wytyczenia  projektu  w  terenie  oraz  lokalizację  istniejących  przewodów
i urządzeń podziemnych. Szkic dokumentacyjny powinien zawierać także elementy kontrolne,
umożliwiające  na  niezależne  wytyczenie  najważniejszych  punktów  głównych  obiektu  oraz
określające  odległości  do  sąsiednich  istniejących  lub  wznoszonych  obiektów.  Elementy
tyczenia  (miary)  mogą  być  naniesione  na  szkicu  sytuacyjnym,  wykonanym  bez  zachowanie
skali lub też mogą one być zestawione w formie tabelarycznej. Szkice dokumentacyjne można
sporządzić wykorzystując odpowiednie komputerowe programy graficzne.

Do realizacji terenowej projektu trasy, jej budowy oraz eksploatacji, konieczne jest

określenie bieżących odległości poszczególnych punktów trasy od jej początku, czyli
wykonanie kilometrażu trasy.

Oprócz wyznaczenia sytuacyjnego, konieczne jest również prowadzenie prac

wysokościowych:

założenie

reperów

roboczych,

pomiar

przekrojów

podłużnych

i poprzecznych, wyznaczenie niwelety, łuków pionowych i profilowania oraz obliczenie robót
ziemnych.

Niweleta, czyli linia spadków prostych odcinków osi trasy i łuków, wyokrąglających

załamania, musi spełniać kilka zasadniczych warunków. Musi przechodzić przez podaną
wysokość punktu początkowego i końcowego trasy oraz przez podane wysokości punktów

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

pośrednich. Pochylenie niwelety nie mogą przekraczać wartości maksymalnych,
przewidzianych instrukcjami dla danej trasy.

Pochylenie niwelety podaje się w procentach lub w postaci ułamka dziesiętnego.
Rzędne niwelety w poszczególnych punktach załamania terenu oblicza się wiedząc, że

przyrost wysokości h dowolnego punktu niwelety, jest proporcjonalny do odległości x, czyli
do odległości od punktu początkowego. Mając wysokość H

punktu początkowego odcinka

niwelety o danym spadku „i”, można obliczyć wysokości punktów położonych na tym
odcinku w odległościach x od punktu P

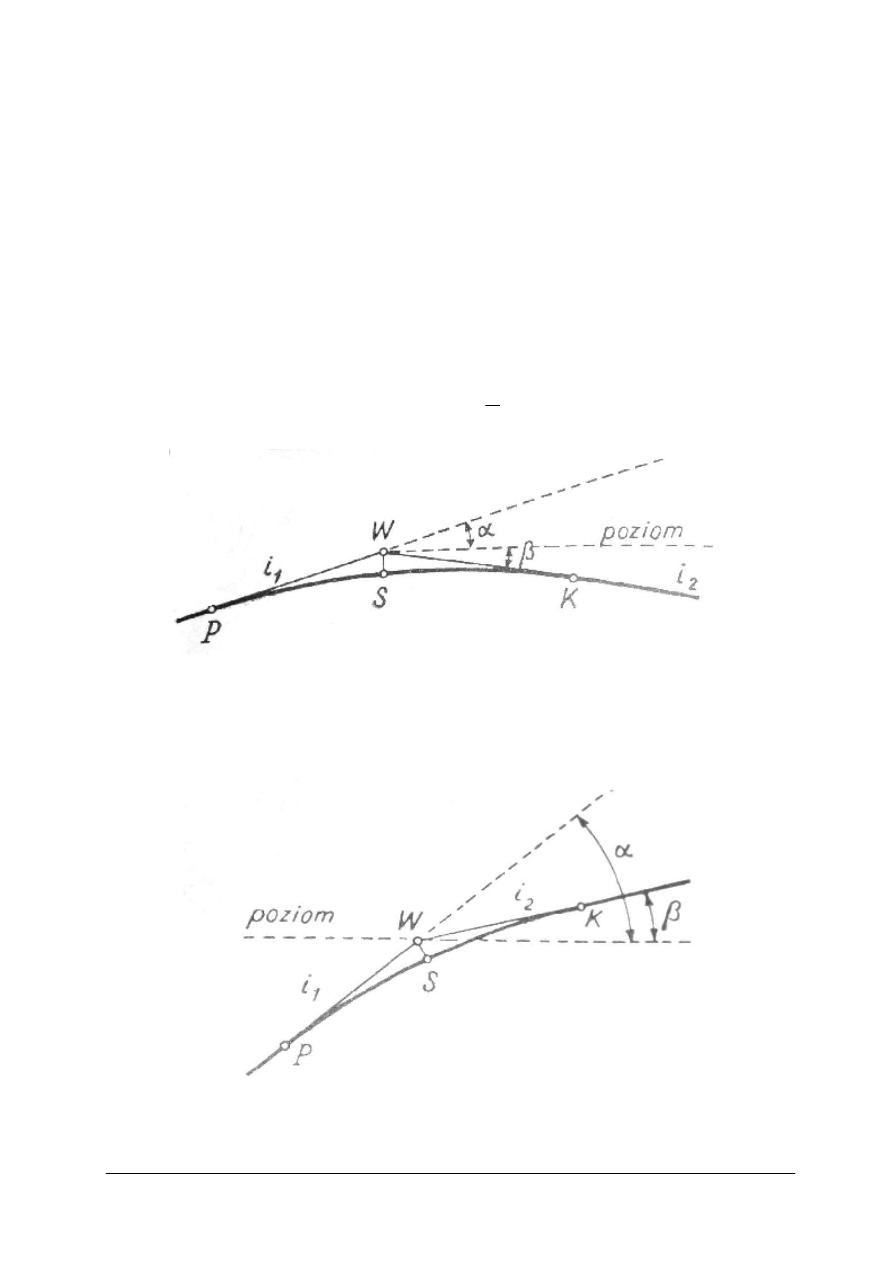
Załamania niwelety po jej zaprojektowaniu należy wyokrąglić, wpisując w nie łuki

pionowe. Wierzchołkiem łuku pionowego jest punkt załamania niwelety. Aby określić
początek i koniec łuku, należy określić długość stycznej t, którą należy odłożyć w obie strony
od wierzchołka. Długość stycznej obliczamy ze wzoru

Rtg

Rys. 13. Łuk pionowy: pochylenia o różnych znakach

Za kąt α podstawiamy (α - β) - jeżeli następujące po sobie pochylenia niwelety mają

jednakowe znaki( rys.14), lub (α + β) - jeżeli następujące po sobie pochylenia niwelety mają
różne znak (rys. 13).

Rys. 14. Łuk pionowy: pochylenia o jednakowych znakach

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Mamy więc

Rtg

α β

Po przekształceniach, przyjmując że:

, otrzymamy

(

)

Jeżeli pochylenie wznoszącej się niwelety oznacza się jako dodatnie (+i), a opadającej

jako ujemne (-i), to wyrażenie w nawiasie można za każdym razem uznać za algebraiczną
różnicę pochyleń, której wartość bezwzględna wynosi „n”, więc

Odległość WS punktu załamania niwelety od środka łuku, można obliczyć ze wzoru:

Po wyznaczeniu punktów P, K i S wyznacza się rzędne punktów pośrednich; najpierw na

stycznej a potem, przez odjęcie lub dodanie wartości y (

), na niwelecie.

Tyczenie wysokościowe należy opierać na reperach roboczych, wyznaczanych z reperów

wysokościowej osnowy realizacyjnej, umiejscowionych w możliwie najmniejszym oddaleniu
od tyczonego obiektu, lecz poza zasięgiem przemieszczeń podłoża, spowodowanych przez
obiekt i w takiej liczbie, aby była zapewniona możliwość kontroli tyczenia.

Do zestawienia kosztorysu robót ziemnych i oceny różnych wariantów projektu trasy

niezbędne  jest  obliczenie  objętości  wykopów  i  nasypów.  Roboty  ziemne  powinny  być
zminimalizowane,  a  objętości  wykopów  i  nasypów  powinny  się  mniej  więcej  równoważyć.
Wzorem  najczęściej  stosowanym  do  obliczenia objętości  mas ziemnych  jest  wzór  Winklera.
Wzór ten określa objętość brył nieregularnych:

(

)

−

gdzie: l - to odległość między przekrojami poprzecznymi,

i p

to całkowite pola przekrojów,

i q

to podstawy odciętych ostrosłupów.

Roboty ziemne takie jak profilowanie nasypów czy wykopów, wykonuje się

bezpośrednio na gruncie. Punkty wyznaczające wysokość, czy głębokość nasypu w osi,
szerokość korony drogi i rowów, ślad przecięcia skarp z terenem, oznacza się palikami,
a właściwe profilowanie prowadzi się przy użyciu trójkątów skarpierskich.

Dokumentem technicznym wykonanego wytyczenia wysokościowego jest szkic tyczenia,

na  którym  uwidacznia  się  wszystkie  dane  liczbowe,  uzyskiwane  w  toku  prac  tyczeniowych
wraz  z  miarami  kontrolnymi  oraz  dane  uzyskane  z  pomiaru  istniejących  urządzeń
podziemnych. Szkic tyczenie  sporządza się  jako dokument wycinkowy jednego, określonego
etapu  wytyczenia.  Szkic  tyczenia  wysokościowego  może  być  sporządzony  na  kopii  szkicu
dokumentacyjnego.

Punkty, będące przedmiotem wytyczenia, a w szczególności punkty główne budowli,

powinny być tak rozmieszczone, aby w każdym momencie budowy było możliwe tyczenie
szczegółów budowli z wymaganą dokładnością. W szczególności, w tym celu główne osie
budowli

należy dodatkowo stabilizować znakami (punktami

zabezpieczającymi),

usytuowanymi poza zasięgiem robót ziemnych; w miarę możliwości, na bokach szczegółowej
osnowy realizacyjnej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wykonanie

wytyczenia

stwierdza

wykonawca

pomiarów,

przez

dokonanie

odpowiedniego  wpisu  w  dzienniku  budowy.  Wykonawca  pomiarów  przekazuje  po  dwa
egzemplarze  szkicu  tyczenia  inwestorowi  lub wykonawcy robót budowlano  -  montażowych.
Wykonawca  przechowuje  szkice  dokumentacyjne  i  szkice  tyczenia  do  chwili  zakończenia
budowy, po czym przekazuje je zamawiającemu.

Ogólne wiadomości o trasach wodnych
Budowle inżynierskie, służące do przeprowadzania drogi nad różnego rodzaju

przeszkodami, to obiekty mostowe. Zależnie od pokonywanej przeszkody mogą to być:

−

przepusty, czyli budowle mostowe nie przerywające ciągłości drogi, służące do
umożliwienia przepływu wody pod nasypami,

−

wiadukty, do przeprowadzania drogi nad suchymi przeszkodami,

−

mosty do przeprowadzania drogi nad przeszkodami wodnymi,

−

estakady to długie budowle prowadzące drogę na inny poziom,

−

akwedukty, wodociągi nadziemne doprowadzające wodę,

−

mosty inundacyjne - budowle służące do odprowadzania wód powodziowych z terenów
zalewowych.

Most, jako budowla inżynierska, składa się z przęseł, czyli ustroju nośnego i podpór.

Most  może  zawierać  jedno  przęsło  lub  wiele.  Podpory  skrajne  -  to  przyczółki,  a  podpory
pośrednie  -  to  filary.  Elementy  konstrukcyjne  mostu,  to  głównie  pomost,  dźwigary  główne
oraz  stężenie  pomostu  i  dźwigarów,  a  także  łożyska.  Elementy  wyposażenia  mostu,  to
głównie:  nawierzchnia,  odwodnienie,  izolacje,  dylatacje,  płyty  przejściowe,  poręcze,  izbice,
oraz instalacje elektryczne. Długość przęsła, to całkowita długość jego konstrukcji. Natomiast
rozpiętość  przęsła,  to  odległość  między  punktami  jego  podparcia.  Światło  mostu  to  suma
świateł poszczególnych przęseł.

Najkorzystniej jest budować most tam, gdzie koryto rzeki jest zwarte i bez bocznych

zalewów,  tam  gdzie  woda  ma  znaczną  głębokość,  a  nurt  utrzymuje  się  wzdłuż  jednego
kierunku.  Najbardziej  niekorzystne  są  miejsca  o  korycie  szerokim  i  płytkim,  ze  zmiennym
nurtem.  Rozpiętość  mostu  powinna  być  możliwie  najkrótsza,  więc  oś  powinna  być
prostopadła do nurtu lub odchylać się od kierunku nurtu nie więcej niż o 10˚.

Aby most spełniał właściwie swoje zadanie, należy uwzględnić przy projektowaniu

warunki ekonomiczne, architektoniczne, hydrotechniczne, geologiczne oraz warunki ruchu
i eksploatacji.

Przed przystąpieniem do projektowania przygotowuje się i aktualizuje podkłady mapowe

w  skalach  od  1:100  000  do  1:10  000.  Zbiera  się  także  materiały,  dotyczące  osnowy
sytuacyjno-  wysokościowej  w  przewidywanym  rejonie  budowy,  na  szerokości  rozlewiska
powiększonej  o  około  300m.  Na  tym  terenie  przeprowadza  się  studia  hydrologiczne
i geologiczne, dotyczące właściwości gruntu, wielkości zlewni i wymiarów mostu. Wykonuje
się  również  pomiary  geodezyjne,  które  obejmują:  pomiar  przekrojów  poprzecznych  doliny
i koryta  rzeki,  pomiary  rzeźby  dna  i  niwelację  spadku  zwierciadła  wody,  wykonanie  mapy
dna i brzegu rzeki oraz przekrojów podłużnych i poprzecznych koryta rzeki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

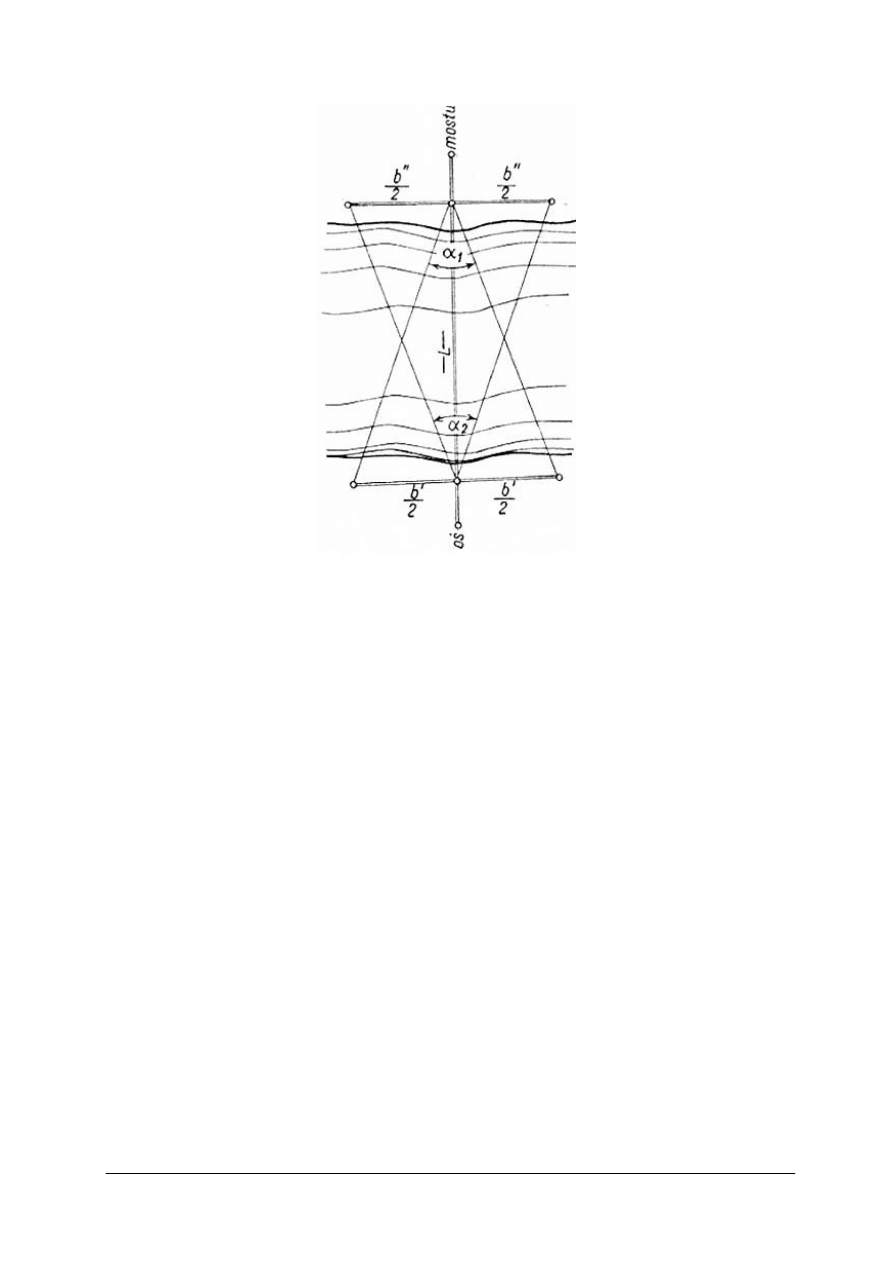
Rys. 15. Osnowa geodezyjna do tyczenia osi mostu

Po zlokalizowaniu trasy mostowej wykonuje się pomiary sytuacyjno- wysokościowe

i opracowuje mapę terenów przyległych do obiektu, w skali 1:5 000 lub 1: 10 000, z cięciem
warstwicowym co 2,5 m. Mapa ta powinna objąć odcinek rzeki o długości równej
pięciokrotnej szerokości koryta rzeki, z czego

powinny biec w górę rzeki, licząc od

projektowanej osi. Teren rozlewiska objęty pomiarem powinien być poszerzony o 300 m
w kierunku poprzecznym do nurtu rzeki.

Dla mierzonego obszaru zakłada się osnowę, w postaci sieci ciągów poligonowych,

łańcucha trójkątów lub czworoboków geodezyjnych. Osnowa wysokościowa musi być
nawiązana do reperów niwelacji państwowej.

Po naniesieniu na mapę wszystkich mierzonych obiektów, otrzymuje się plan generalny

trasy,  według  którego  przystępuje  się  do  szczegółowych  badań  geologicznych
i hydrologicznych  oraz  do  zaprojektowania  i  wyznaczenia  w  terenie  specjalnej  osnowy
budowlano-geodezyjnej  (rys.  15),  na  podstawie  której  tyczy  się  poszczególne  elementy
budowlane  mostu.  Szczegółowe  studia  geologiczne  wykonuje  się  pod  podporami
wyznaczając otwory wiertnicze z dokładnością 1,0÷0,5m , a wysokościowo - od 0,1÷0,01 m.

W osi mostu, co 50 do 100 m, także w górę i w dół rzeki wykonuje się przekroje

poprzeczne na całym mierzonym terenie obejmujące koryto, obszar zalewowy i obszar
o wysokościach większych o dwa m ponad maksymalny stan zalewowy.

Pomiar głębokości wykonuje się zależnie od głębokości; łatą tachimetryczną (do 2 m),

rurką od młynka hydrometrycznego (do 3 m), sondą drążkową (do 4 m), sondą linkową
(do 10 m) i echo sondą (>10 m głębokości). Zależnie od szerokości rzeki gęstość punktów
sondowania wynosi:

−

przy szerokości do 5 m, co 0,5 m,

−

przy szerokości do 10 m, co 1 m,

−

przy szerokości do 200 m, co 5 m,

−

przy szerokości ponad 200 m, co 10 m.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

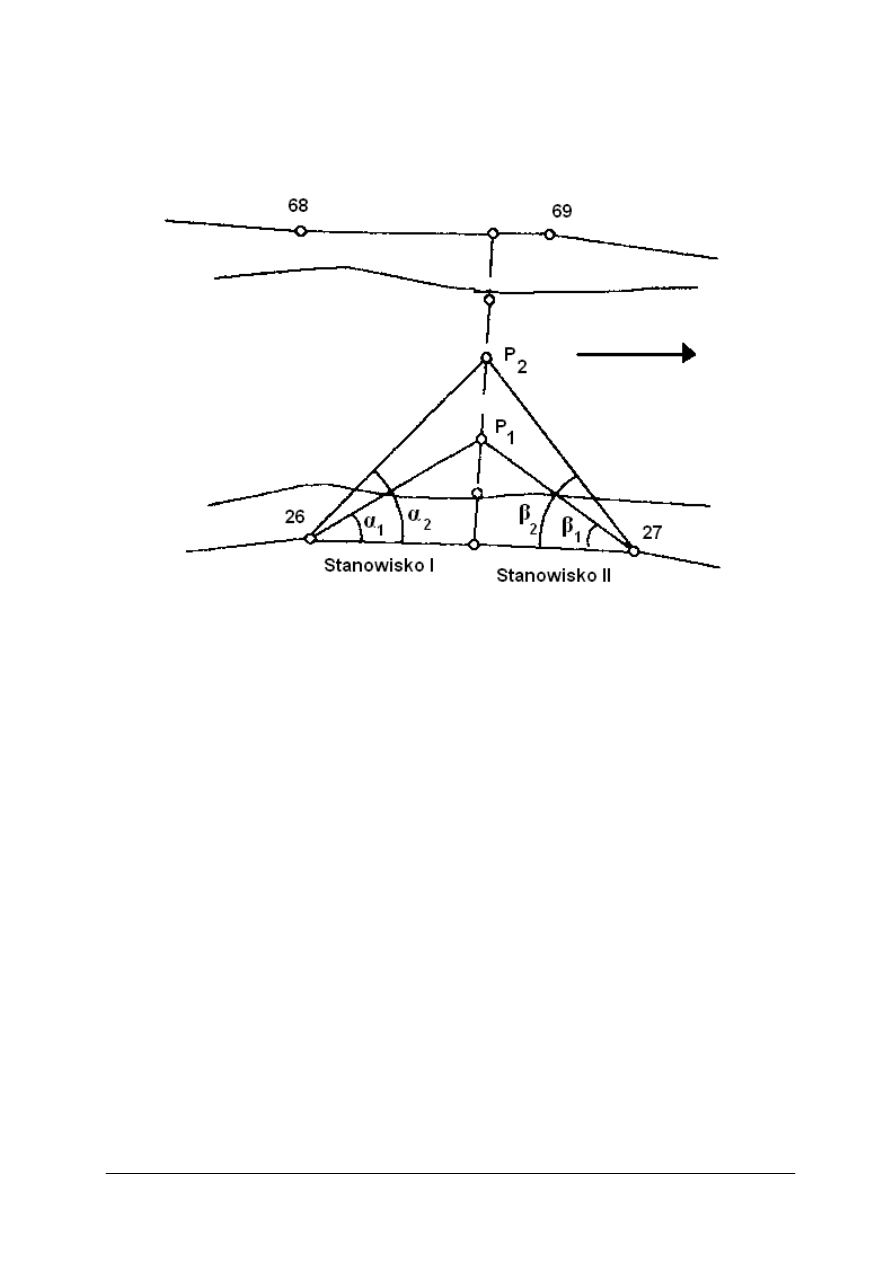
Pomiar położenia punktów sondowań dla przekroju poprzecznego, wykonuje się

najczęściej za pomocą nacechowanej linki stalowej, rozciągniętej wzdłuż przekroju, lub metodą
kątowych wcięć w przód albo metodą biegunową ze stanowisk na brzegu rzeki (rys. 16).

Rys. 16. Wcięcie kątowe do wyznaczania punktów przekroju

Na przekroju podłużnym podaje się rzędne dna rzeki, wysokości obu brzegów, poziomy

korony wałów ochronnych, rzędne jezdni mostów, rzędne dolnych krawędzi przęseł,
wodowskazy, poziome zwierciadła wody z datą, kilometry, hektometry, dopływy i przecięcia
z drogami.

W czasie całego cyklu budowy mostu, oprócz tyczenia elementów głównych mostu, czyli

punktów osi, (które powinny być utrwalone w terenie co najmniej czterema punktami na
jednej linii prostej), przyczółków i filarów, służba geodezyjna wykonuje również inne prace,
takie jak:

−

okresowe sprawdzanie położenia punktów wyznaczających podłużną oś mostu oraz osie
przyczółków i filarów,

−

wyznaczanie obrysu ław fundamentowych, osi pojedynczych pali lub rzędów pali
w nawiązaniu do osi przyczółków i filarów,

−

wyznaczanie miejsc zatopienia kesonów podczas rozpoczynania budowy filarów
nawodnych,

−

przenoszenie osi na kesony w czasie ich zatapiania,

−

przenoszenie osi na rusztowania, deskowanie, ścianki szczelne,

−

przenoszenie wysokości na poszczególne elementy budowy oraz ich sprawdzanie,

−

sprawdzanie pionowości wznoszonych elementów mostu,

−

sprawdzanie osiadania przyczółków i filarów w trakcie ich wznoszenia,

−

wykonywanie próbnych obciążeń pali,

−

kontrola poszczególnych segmentów konstrukcji mostu na stanowisku montażowym,

−

sprawdzanie prawidłowości ułożenia łożysk,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

pomiar kontrolny gotowych przęseł przed przesunięciem na podpory oraz po ustawieniu
na łożyskach,

−

pomiar długości przęseł mostowych,

−

pomiary kontrolne strzałek ugięcia poszczególnych dźwigarów.

Po zakończeniu budowy inwestor zobowiązany jest zlecić wykonanie inwentaryzacji

wybudowanego obiektu. Inwentaryzację powykonawczą obiektu mostowego dzieli się na
dwie części:
1) Inwentaryzacja w celu aktualizacji mapy zasadniczej, która polega na wykonaniu

pomiaru  inwentaryzacyjnego  sytuacyjno-wysokościowego,  w  nawiązaniu  do  istniejącej
osnowy  geodezyjnej,  całego  mostu  wraz  z terenami przyległymi  i  naniesieniu  wyników
pomiaru  na  obowiązującą  mapę  zasadniczą.  Tę  inwentaryzację  wykonuje  służba
geodezyjna inwestora.

2) Inwentaryzacja szczegółowa, to wypełnienie karty inwentaryzacyjnej (numer, klasa

mostu, nazwa rzeki, miejscowość, opis konstrukcji, szkic ogólny terenu w skali 1:25000,
widok ogólny w przekroju podłużnym 1:100, przekrój poprzeczny) oraz opis
szczegółowy konstrukcji. Inwentaryzację szczegółową wykonuje specjalistyczna służba
geodezyjna resortu komunikacji lub służba drogowa.

Przy wznoszeniu budowli nadwodnych duże znaczenie ma znajomość stanu wody. Stan

wody jest zmienny. Do jego pomiaru może służyć łata pionowa przytwierdzona do słupa,
muru oporowego. Początek podziału (zero) tej łaty jest umieszczony jest zawsze poniżej stanu
absolutnie najniższej wody (NNW). Łata taka to łata wodowskazowa. W pobliżu łaty zakłada
się 3-4 repery i co parę lat niweluje się zero łaty. Stan wody odczytuje się z dokładnością

1 cm, czyli z dokładnością połowy działki. Na ważniejszych stacjach wodowskazowych

umieszcza się urządzenia samopiszące, zwane limnigrafami.

Spad rzeki, to różnica wysokości zwierciadła wody między dwoma punktami. Spadek

rzeki to spad względny, czyli spad podzielony przez odległość między punktami. Spadek
wyraża się w promilach. Naturalny spadek rzeki jest większy u źródła a mniejszy u ujścia.

Mierzony poziom wody nie jest trwały i pomiar spadku musi być sprowadzony do

jednego  wyjściowego  momentu  czasu.  Pomiar  podłużnego  spadku  zwierciadła  wody
prowadzi  się  w  jak  najkrótszym  czasie,  mierząc  stan  wody  przy  regularnie  osadzonych
palikach  oraz  w  miejscach  wyraźnej  zmiany  spadku,  a  także  w  miejscach  projektowanych
przekrojów  poprzecznych.  Oddzielnie  niweluje  się  paliki  posuwając  się  w  dół  rzeki,
a oddzielnie  odczytuje  się  stan  wody  w  stosunku  do  główki  pala  lub  wbitego  gwoździa,
posługując się podziałką milimetrową.

Przejście z niwelacją przez szeroką powierzchnię wodną obarczone jest wpływem

refrakcji. Dlatego celowa powinna przechodzić około 2 m (nie niżej niż 1,5 m) nad
zwierciadłem wody. Obserwacje prowadzi się w dni pochmurne, unikając godzin od 10:30 do
12:30 czyli pory największego nasłonecznienia.

Przy szerokości cieku lub zbiornika do 100 m przeprowadza się normalną niwelacje

geometryczną przy czym niwelator musi być dobrze zrektyfikowany, gdyż długości celowych
na stanowiskach nie są jednakowe. Projektując przejście przez rzekę wyszukuje się płycizny
i brody. Jeżeli celowa ma od 100 do 300 m, to zakłada się konstrukcję, w której odczytuje się
dwa punkty wysokościowe, położone na różnych brzegach rzeki, z dwóch różnych stanowisk,
umieszczonych po przeciwnych stronach rzeki.

Przy szerokościach rzek ponad 300 m, stosuje się niwelację trygonometryczną,

uwzględniając poprawkę ze względu na krzywiznę Ziemi.

Regulacja koryt cieków naturalnych, służy poprawie warunków korzystania z wód

i ochronie przeciwpowodziowej. Regulacja wód polega na różnych przedsięwzięciach,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

a w szczególności  na  kształtowaniu  przekroju  podłużnego  i  poprzecznego  oraz  układu
poziomego koryta  cieku  naturalnego.  Regulacja  cieku to  prace  hydrotechniczne  powodujące
zmianę  profilu  poprzecznego  i  podłużnego  wybranego  odcinka  rzeki  w  celu  polepszenia
i ujednolicenia spływu wody, lodu i rumowiska rzecznego. Ostroga to forma kamiennego lub
faszynowego  wału,  poprzecznego  do  biegu  potoku.  Służy  ona  do  ochrony  brzegu  przed
podmywaniem poprzez odepchnięcie nurtu w kierunku osi doliny. Najczęściej regulacja rzeki
polega  na  budowie  obwałowań,  tam,  ostróg  regulacyjnych.  Regulacja  służy  zabezpieczeniu
terenów  wzdłuż  rzeki  przed  powodzią,  melioracji  użytków  rolnych,  ułatwia  budowę  ujęć
wody.

Melioracje wodne polegają na regulacji stosunków wodnych w celu polepszenia

zdolności produkcyjnej gleby, ułatwienia jej uprawy oraz na ochronie użytków rolnych przed
powodziami.  Urządzenia  melioracji  wodnych  dzielą  się  na  podstawowe  i  szczegółowe,
w zależności  od  ich  funkcji  i  parametrów.  Ewidencję  urządzeń  melioracji  wodnych  oraz
zmeliorowanych  gruntów,  prowadzi  marszałek  województwa.  Ewidencja  jest  udostępniana
nieodpłatnie organom administracji publicznej na każde ich żądanie.

Do urządzeń melioracji wodnych podstawowych zalicza się:

1)  budowle piętrzące, budowle upustowe oraz obiekty służące do ujmowania
2)  wód,
3)  stopnie wodne, zbiorniki wodne,
4)  kanały, wraz z budowlami związanymi z nimi funkcjonalnie,
5)  rurociągi o średnicy co najmniej 0,6 m,
6)  budowle regulacyjne oraz przeciwpowodziowe,
7)  stacje pomp, z wyjątkiem wykorzystywanych do nawodnień ciśnieniowych.

Do urządzeń melioracji wodnych szczegółowych zalicza się:

1)  rowy, wraz z budowlami związanymi z nimi funkcjonalnie,
2)  rurociągi o średnicy poniżej 0,6 m,
3)  stacje pomp do nawodnień ciśnieniowych,
4)  ziemne stawy rybne oraz groble na obszarach nawadnianych,
5)  systemy nawodnień podsiąkowych.

Projekt budownictwa wodnego wykonuje się na podkładzie mapowym a ostateczny

wynik  projektowania,  uwidoczniony  na  mapach,  wynosi  się  na  grunt  jako  podstawę  do
rozpoczęcia  robót.  Niektóre  projekty  wymagają  dodatkowych  rysunków,  w  formie
przekrojów  poprzecznych  (kształt  rowu)  lub  szczegółowych  rysunków  w  rzucie  poziomym
i pionowym  (wylot  zbieracza  do  rowu,  przepust  nad  drogą).  Sposób  przenoszenia  projektu
z mapy  w  teren  zależy  od  rodzaju  budownictwa  wodnego.  Kierunek  projektowanego  rowu
wyznacza  się  zwykle  w  oparciu  o  sytuację  uwidocznioną  na  mapie,  natomiast  wielkie
budowle  wymagają  opracowania  szkiców  geodezyjnego  wyznaczenia  projektów,  czyli
szkiców  dokumentacyjnych.  Następny  etap  prac  geodezyjnych  to  kontrola  prawidłowości
budowy,  polegająca  na  dokonaniu  pomiarów  sprawdzających,  czy  dana  budowla  została
ulokowana  w  terenie  zgodnie  z  jej  projektowanym  położeniem  na  planie  generalnym.
Sporządza  się  również  plan  inwentaryzacyjny  wykonanej  budowli,  który  służy  po  oddaniu
budowli  do  eksploatacji,  jako  podstawowy  materiał  ewidencyjny  usytuowania  budowli  oraz
urządzeń inwentaryzacyjnych podziemnych i naziemnych.

Projekt rowów melioracyjnych przedstawia się na mapie sytuacyjno-wysokościowej oraz

sporządza się przekrój podłużny i typowy przekrój poprzeczny. Tyczenie rowów rozpoczyna
się od wytyczenia osi, potem spadków a następnie szerokości wykopu. Położenie osi rowu
ustala się w stosunku do stałych punktów uwidocznionych na mapie. Na projekcie, obok rowu
podane są rzędne górnej krawędzi rowu i rzędne dna rowu (d) i w nawiasie głębokość rowu.
Wzdłuż rowu wpisany jest jego numer, długość i spadek.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Po wytyczeniu osi rowu tyczy się rzędne na początku rowu (przy ujściu) i na jego końcu, na
każdym  hektometrze  i  w  miejscu  załamania  spadków  lub  trasy.  Rzędne  te  wyznacza  się
w terenie  za  pomocą  niwelatora,  osadzając  palik  obok  punktu  osiowego.  Różnice  między
rzędną  palika  a  projektowaną  rzędną  dna  rowu,  wyznacza  się  za  pomocą  łaty  i  poziomicy.
Spadek  dna  rowu  można  wyznaczać  niwelatorem  lub krzyżami  niwelacyjnymi,  po  ustaleniu
punktów załamań.

Drenowanie gruntów wykonuje się za pomocą sączków drenarskich, których przebieg

zaprojektowany  jest  na  mapie  sytuacyjno-wysokościowej.  Tyczenie  projektu  rozpoczyna  się
od  tyczenia  rowu,  a  następnie  wyznaczenia  na  rowie  miejsc  wylotów  zbieraczy  i  kierunku
zbieraczy. Rzędne drenażu tyczy się zaczynając od wylotu do rowu, a następnie, przy znanym
spadku  podłużnym,  tyczy  się  rzędne  wylotów  i  kolejno  spadki  sączków.  Rzędne  wylotów,
rzędne  załamania  spadków  i  rzędne  końców  sączków  oraz  zbieraczy  wyznacza  się
niwelatorem.

Projektowanie tras kanałów rozpoczyna się od wyboru przybliżonego przebiegu trasy na

mapie,  a  następnie  w  terenie.  Po  wstępnym  wytrasowaniu  osi,  wykonuje  się  opisy
topograficzne  punktów  wierzchołkowych  osi  kanału  oraz  pomiar  sytuacyjno-wysokościowy
trasy.  Najodpowiedniejszą  metodą  jest  tutaj  sposób  przekrojów  poprzecznych,  uzupełniony
w miejscach bardziej urozmaiconej sytuacji lub rzeźby, pomiarem tachimetrycznym.

Przed wytyczeniem projektu koryta kanału lub rzeki, opracowuje się sposób przeniesienia

projektu  w  teren.  Trasując  oś,  utrwala  się  punkty  wierzchołkowe,  czyli  punkty  przecięcia
prostoliniowych osi kanału, oraz punkty początkowe i końcowe łuków. Cały łuk wyznacza się
bezpośrednio  przed  rozpoczęciem  robót  ziemnych,  a  dokładność  wyznaczenia  zależy  od
rodzaju  koryta.  Koryto  nieumocnione  wyznacza  się  z  dokładnością

5 cm, a koryto

betonowe - z dokładnością

2 cm.

Ustalenie linii zalewu zbiornika zaczyna się od naniesienia na przekrój podłużny

obliczonych  rzędnych  krzywej  spiętrzenia.  Następnie  nanosi  się  na  mapę  odcinki  warstwic
odpowiadających wysokości tej krzywej. Linii zalewu nie wyznacza się na skarpach nasypów
ani  na  zboczach  o  nachyleniu  ponad  30  ˚.  Projekt  wstępny  wyznaczenia  punktów  na  linii
zalewu opracowuje się na mapie. Jest on podstawą do późniejszego wstępnego wytyczenia tej
linii  w  terenie.  Właściwym  sposobem  wyznaczenia  linii  zalewu  jest  gęste  wyznaczenie
punktów  o  danej  wysokości  za  pomocą  niwelatora,  przy  czym  projekt  rozmieszczenia
punktów  opracowany  na  mapie  ma  jedynie  charakter  orientacyjny.  Odległość  między
wyznaczanymi punktami jest zależna od kształtu warstwicy, ale nie może przekraczać 150 m.
Wytyczone  w  terenie  punkty  utrwala  się  słupkami  betonowymi.  Wytyczona  w  terenie  linia
zalewu jest podstawą do szczegółowego ustalenia przyszłej granicy zbiornika.

Ogólne wiadomości o trasach kolejowych
Linię kolejową stanowi torowisko wraz z budowlami i urządzeniami technicznymi

przystosowanymi do ruchu pociągów. Linie normalnotorowe, to linie o prześwicie
(tj. normalnej szerokości toru, mierzonej między wewnętrznymi krawędziami szyn na
wysokości 14 mm poniżej ich powierzchni tocznych) 1435 mm.

Linie kolejowe składają się ze szlaków i stacji kolejowych. Szlakiem nazywa się odcinek

linii  zawarty  między  semaforami  wjazdowymi  kolejnych  stacji.  Na  szlakach  i  stacjach
kolejowych  stosuje  się  szereg  urządzeń  technicznych,  umożliwiających  zapewnienie
odpowiednich  warunków  ruchu  taboru  kolejowego.  Są  to,  między  innymi,  rozjazdy
i skrzyżowania, czyli urządzenia umożliwiające przejazd pociągu z jednego toru na drugi.

Rozjazdy dzielą się na zwyczajne i krzyżowe.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rozjazd zwyczajny (rys. 17) składa się z trzech zasadniczych części:

−

zwrotnicy, złożonej z dwóch połączonych iglic, których przesunięcie nadaje pociągowi
odpowiedni kierunek jazdy,

−

torów łączących, wygiętych według promienia łuku kołowego, odpowiadającego temu
rozjazdowi,

−

krzyżownicy.
Początek rozjazdu, to styk szyn przed iglicą, a koniec - to styk szyn bezpośrednio za

krzyżownicą,  zarówno  w torze  głównym  jak  i odgałęźnym.  Nachylenie  dwóch krzyżujących
się osi tworzy kąt rozjazdu.  Wyraża się on ułamkiem, którego mianownik oznacza odległość
środka  rozjazdu  względem  dowolnie  obranego  punktu  na  osi  toru  zasadniczego,  licznik
natomiast,  to  długość  prostopadłej,  wystawionej  w  tym  punkcie  do  przecięcia  się
z przedłużeniem

prostej

toru odgałęźnego.

Ułamek

ten

jako

stosunek

dwóch

przyprostokątnych, jest tangensem kąta zawartego między wyżej wymienionymi prostymi
i zwie się skosem rozjazdu: 1:n.

Rys. 17. Budowa rozjazdu zwyczajnego

Typ rozjazdu podaje się najczęściej w formie skróconej np. S42-190-1:9, gdzie S42 - to

typ szyn zastosowany do budowy rozjazdu, 190 - to promień toru odgałęźnego podany
w metrach, a 1:9 - to skos rozjazdu.

Geodezyjne opracowanie projektu linii kolejowej obejmuje określenie niezbędnych miar

kątowych  i  liniowych  oraz  sporządzenie  szkiców,  umożliwiających  terenową  realizację
projektu  technicznego,  wykonanego  przez  specjalistów  z  zakresu  budownictwa  kolejowego.
W projekcie technicznym, projektant określa wszystkie parametry techniczne linii kolejowej:
położenie  sytuacyjne  budowy  (według  kilometrażu  trasy),  rozstaw  torów,  rodzaj  połączeń
torów  i typy  rozjazdów,  promienie  łuków kołowych, długości  krzywych  przejściowych  oraz
inne elementy charakteryzujące budowany obiekt.

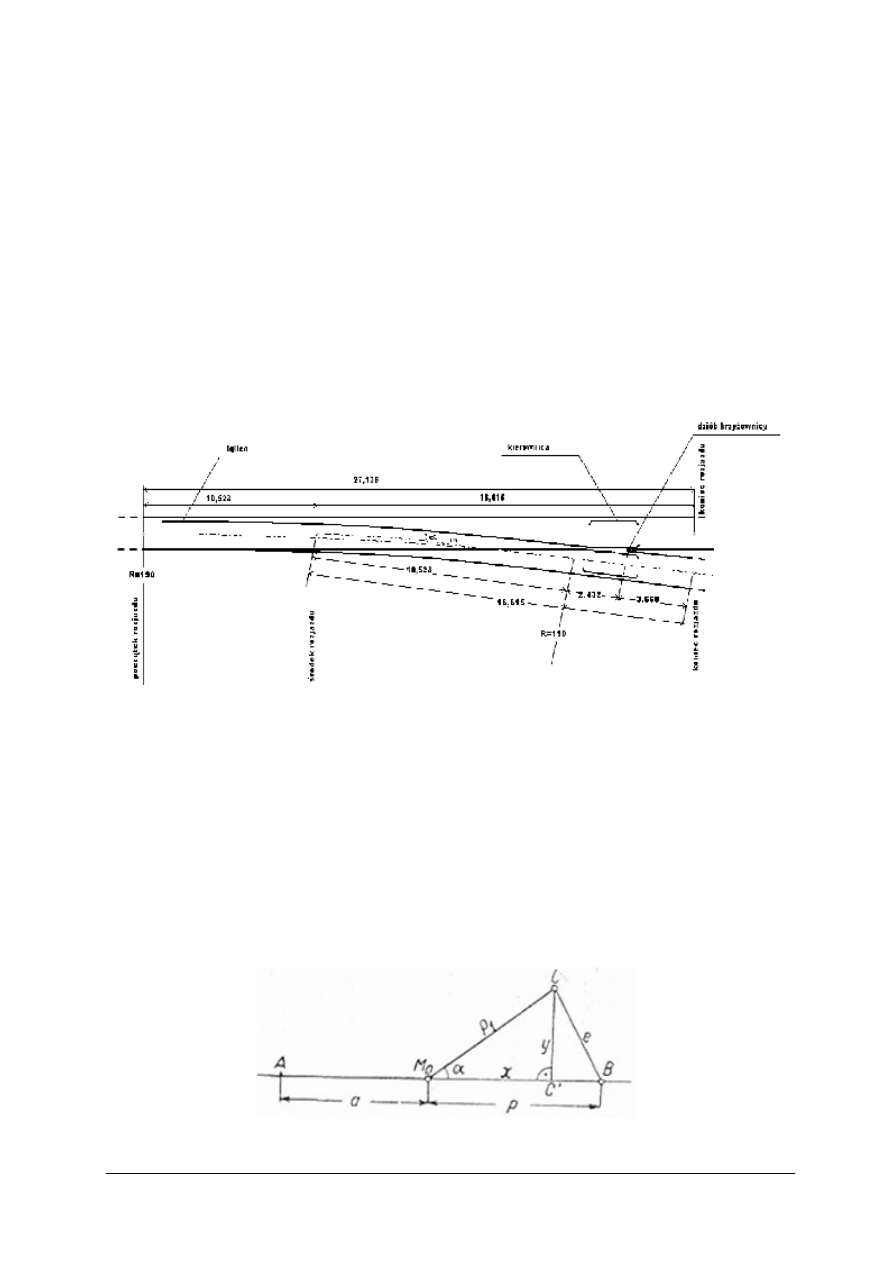
Rys. 18. Tyczenie rozjazdu zwyczajnego

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wytyczenie połączeń torów (rys. 18) polega na określeniu w terenie położenia punktów

środkowych (M

), poszczególnych rozjazdów oraz (w następnej kolejności) punktów

początkowych  (A)  i  końcowych  (B  i  C).  Położenie  punktów  środkowych  wyznacza  się
w odniesieniu  do  istniejącej  linii  kolejowej  bądź  osnowy  geodezyjnej  i  w  odniesieniu  do
założonego w projekcie kilometrażu danego punktu środkowego. Pozostałe punkty wyznacza
się  przez  odłożenie  odpowiednich  miar,  określających  wzajemne  położenie  punktów
głównych poszczególnych rozjazdów.

Położenie końcowego punktu C rozjazdu w torze odgałęźnym wyznacza się w oparciu

o współrzędne prostokątne, odniesione do początku układu obranego w punkcie środkowym
M

rozjazdu. Współrzędne te obliczamy ze wzorów

x = p

cosα y = p

sinα

Wartości p

, α., a, p, e – to wielkości o wartościach odpowiadających odpowiednim

typom rozjazdów.

Wprowadzane

kolejnictwie

coraz

większe

prędkości

wymusiły

zmianę

obowiązujących wcześniej warunków technicznych, a co za tym idzie, konieczność
wykonania przeprojektowania czyli regulację geometrycznego układu torów. Wynik regulacji
utrwalany jest specjalnymi znakami, zwanymi wskaźnikami regulacji.

Istnieją cztery podstawowe metody regulacji osi torów kolejowych. Metoda graficzna,

analityczno  -  graficzna  (czyli  wykres  kątów),  metoda  analityczna  i  metoda  mechaniczna.
Wszystkie wyżej wymienione metody opierają się na pomierzonych w terenie strzałkach i ich
odwzorowaniu.
W  metodzie  graficznej,  na  wykresie  nanosi  się  (przy  podziale  trasy  w  odpowiedniej  skali
długości)  wartości  strzałek  w  naturalnej  wielkości.  Odcinek  prosty  toru  powinien  pokrywać
się z osią długości układu. Łuk kołowy - to prosta równoległa do tej osi, a krzywa przejściowa
-  to  prosta  nachylona,  gdyż  mierzona  strzałka  rośnie  tu  od  zera  przy  styku  z  prostą,  aż  do
wartości strzałki jaką posiada łuk.

Rys. 19. Metoda analityczno graficzna, czyli wykres kątów

Metoda wykresu kątów polega na odkładaniu na poziomej osi odciętych (x) wartości

odległości (Δ)l podziału krzywej w odpowiednio dobranej skali (C

), a na osi y wartości

podziału kąta, pomnożonego przez odpowiednią skalę C

. Wprowadza się tutaj jeszcze skalę

krzywizny C

, przesunięć i sum strzałek. Na wykres nanosi się sumy kolejnych strzałek,

a więc wykresem łuku będzie prosta nachylona do osi x. Wykresem krzywej przejściowej jest
parabola trzeciego stopnia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Metoda analityczna (rys.19) jest analogiczna do metody wykresu kątów, ale bardziej

pracochłonna. Metoda mechaniczna jest analogiczna do metody graficznej przy czym używa
się tu multikalkulatora, na którym dokonuje się mechanicznego odczytu przesunięć strzałek.

Stabilizację projektu regulacji w torze wykonuje się za pomocą wskaźników regulacji osi

toru nacinając odległość i wysokość, czyli usytuowanie w płaszczyźnie poziomej
i wysokościowej.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.  Jakie elementy podlegają tyczeniu przy wyznaczaniu drogi kołowej?
2.  Jakie elementy podlegają tyczeniu przy wyznaczaniu trasy kolejowej?
3.  Jakie elementy podlegają tyczeniu przy wyznaczaniu trasy wodnej?
4.  Co powinien zawierać szkic dokumentacyjny?
5.  Co oznacza pojęcie niweleta?
6.  Jakie są rodzaje obiektów mostowych?
7.  Jakie są metody sondowania dna rzeki?
8.  W jaki sposób wykonuje się przekrój podłużny rzeki?
9.  Jakie są metody regulacji osi torów kolejowych?

4.2.3. Ćwiczenia

Ćwiczenie 1

Wykonaj obliczenie objętości mas ziemnych na podstawie otrzymanych przekrojów

poprzecznych terenu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  odszukać potrzebne wzory,
2)  odczytać z przekrojów poprzecznych, dane potrzebne do obliczeń,
3)  obliczyć objętość mas ziemnych.

Wyposażenie stanowiska pracy:

−

przekroje poprzeczne danego odcinka trasy,

−

poradnik dla ucznia,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

Ćwiczenie 2

Wykonaj wytyczenie punktów głównych rozjazdu kolejowego zwyczajnego o symbolu

S42-500-1:12.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  odszukać wzory potrzebne do obliczenia współrzędnych punktów głównych rozjazdu,
2)  określić parametry danego rozjazdu na podstawie jego symbolu,
3)  obliczyć współrzędne punktu końcowego toru odgałęźnego,
4)  wykonać szkic dokumentacyjny,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5) wyznaczyć w terenie trzy punkty leżące w torze zasadniczym (w linii prostej) i jeden

punkt leżący w torze odgałęźnym,

6) wykonać kontrolę wytyczenia.

Wyposażenie stanowiska pracy:

−

poradnik dla ucznia,

−

teodolit ze statywem,

−

taśma, węgielnica, domiarówka, szpilki, szkicownik,

−

paliki, gwoździe, młotek, farba,

−

materiały piśmiennicze,

−

kalkulator funkcyjny.

Ćwiczenie 3

Opracuj geodezyjnie projekt regulacji cieku wodnego na podstawie otrzymanego

przekroju podłużnego i przekrojów poprzecznych cieku.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)  zapoznać się z otrzymanymi materiałami kartograficznymi,
2)  ustalić długości projektowanych odcinków trasy wodnej,
3)  obliczyć  elementy  niezbędne  do  wytyczenia  sytuacyjnego  i  wysokościowego

poszczególnych punktów charakterystycznych trasy wodnej,

4) wykonać szkic dokumentacyjny projektu regulacji cieku wodnego.

Wyposażenie stanowiska pracy:

−

przekroje poprzeczne i przekrój podłużny danego odcinka trasy wodnej,

−

mapa sytuacyjno - wysokościowa z projektem cieku,

−

plan realizacyjny i projekt techniczny regulacji cieku wodnego,

−

wykaz współrzędnych punktów istniejącej osnowy,

−

poradnik dla ucznia,

−

materiały piśmiennicze, formularze szkiców,

−

kalkulator funkcyjny.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) wyjaśnić pojęcie: obiekt mostowy?



2) wyjaśnić pojęcie: linia kolejowa?



3) określić różnice między szkicem dokumentacyjnym, a szkicem

tyczenia?



4) rozróżnić metody regulacji osi torów kolejowych?



5) wyjaśnić pojęcie: niweleta?



6) określić

sposoby

przenoszenia

wysokości

przez

szerokie

powierzchnie wodne?



7) wyjaśnić sposoby tyczenia rozjazdów?



„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

1.  Przeczytaj uważnie instrukcję.
2.  Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3.  Zapoznaj się z zestawem zadań testowych.
4.  Test zawiera 30 zadań. Do każdego zadania dołączone są 4 odpowiedzi. Tylko jedna jest

prawidłowa.

5. Udzielaj odpowiedzi na załączonej karcie odpowiedzi, stawiając w odpowiedniej rubryce

znak X. W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie
ponownie zakreślić odpowiedź prawidłową.

6. Niektóre zadania wymagają stosunkowo prostych obliczeń, które powinieneś wykonać

przed wskazaniem poprawnego wyniku.

7. Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
8. Jeśli udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego rozwiązanie

na później i wróć do niego, gdy zostanie Ci wolny czas.

9. Na rozwiązanie testu masz 60 minut.

Powodzenia!

ZESTAW ZADAŃ TESTOWYCH

1. Punkty główne łuku to

a)  punkt wierzchołkowy, początkowy i końcowy.
b)  punkt początkowy, środkowy i końcowy.
c)  punkt będący środkiem okręgu oraz punkt początkowy i końcowy łuku.
d)  punkty styczności z ramionami kąta wierzchołkowego.

2. Równanie naturalne klotoidy, w którym a to współczynnik, L - długość, K - krzywizna,

R – promień, ma postać
a)  L = a K.
b)  K= ⅛La.
c)  KR= a = const.
d)  LR = a

= const.

3. Tyczenie prostych odcinków trasy można wykonać metodą

a)  geometryczną w przód.
b)  tachimetryczną.
c)  ortogonalną.
d)  bezpośrednią w przód lub na siebie.

4. Przy tyczeniu prostej przez las, należy

a) założyć wokół przeszkody osnowę w kształcie wieloboku zamkniętego,

zawierającego punkt początkowy i końcowy wytyczanej prostej.

b)  założyć odległy punkt M i obliczyć przesunięcie.
c)  uzyskać zgodę na wycinkę i tyczyć prostą metodą geometryczną.
d)  założyć ciąg tachimetryczny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. Kąt zwrotu stycznych to kąt

a)  między kierunkiem stycznej, a kierunkiem cięciwy do punktu K.
b)  między kierunkiem stycznej, a kierunkiem cięciwy do punktu S.
c)  będący dopełnieniem kąta wierzchołkowego do 180°.
d)  mierzony w rozjeździe kolejowym przy zwrotnicy.

6. Dla łuku o promieniu 200,00 m i kącie wierzchołkowym β = 120°, długość stycznej

głównej wynosi
a)  50,00 m.
b)  115,47 m.
c)  101,90 m.
d)  100,20 m.

7. Wyznaczając punkt środkowy łuku S przy pomocy wieloboku otaczających stycznych,

długości stycznych należy obliczyć ze wzoru
a) t

= R tg (¼α).

b) t

= L sin α.

c) t

= R tg α

d) t

= R sin α.

8. Dla łuku, o promieniu 100.00 m i kąta wierzchołkowego β = 120° ustalono długości

odcinków a (połowa cięciwy) i s (strzałka), aby wyznaczyć położenie punktu S. Długości
tych odcinków wynoszą
a)  a = 50,00 m s = 13,40 m.
b)  a = 35,20 m s = 13,40 m.
c)  a = 69.20 m s = 25,00 m.
d)  a = 40,15 m s = 12.34 m.

9. Łuk koszowy, to łuk składający się

a)  z krzywej koszowej i serpentyny.
b)  z trzech łuków kołowych.
c)  z dwóch odwrotnych parabol trzeciego stopnia.
d)  z łuków kołowych które w miejscu swego styku posiadają wspólną styczną.

10. Kąt zwrotu stycznych łuku koszowego składającego się z trzech łuków kołowych

o kątach środkowych wynoszących odpowiednio 36°, 43° i 52°, wynosi
a)  131°.
b)  83°.
c)  49°.
d)  27°.

11. Przekrój poprzeczny drogi na odcinku łuku kołowego jest

a)  daszkowy.
b)  jednostronny.
c)  dwuspadowy.
d)  prawidłowo wystopniowany.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12. Dla klotoidy o długości L = 260,00 m i promienia R = 500,00 m kąt zwrotu stycznych

wynosi:
a) τ = 25

b) τ = 16

c) τ = 107

d) τ = 205

13. Wzór Winklera służy do obliczania

a)  objętości brył nieregularnych.
b)  wielkości przepływów.
c)  spadków niwelety.
d)  miejsc zerowych robót ziemnych.

14. Obiekty mostowe to

a)  wiadukty, mosty, estakady, akwedukty, mosty inundacyjne.
b)  przepusty, wiadukty, estakady, akwedukty, mosty inundacyjne.
c)  przepusty, mosty, estakady, mosty inundacyjne.
d)  przepusty, wiadukty, mosty, estakady, akwedukty, mosty inundacyjne.

15. Rozpiętość przęsła mostowego to

a)  całkowita długość konstrukcji.
b)  odległość od filara do filara.
c)  długość przekątnej przęsła.
d)  odległość między punktami jego podparcia.

16. Aby można było między dwie proste wpisać łuk kołowy z dwoma symetrycznymi

klotoidami, spełniać warunek
a)  γ>180°.
b)  γ= 2 τ + α.
c)  γ< 2 τ + α.
d)  γ= 180°- (2 τ + α).

17. Szkic dokumentacyjny to szkic

a)  według którego wykonuje się tyczenie, projektowanych obiektów w terenie.
b)  zawierający tylko elementy kontrolne.
c)  który jest dokumentem wytyczenia obiektu w terenie.
d)  wykonywany po zakończeniu tyczenia, projektowanego obiektu w terenie.

18. Niweleta to linia

a)  maksymalnego spadku, proporcjonalnego do odległości.
b)  maksymalnego spadku na danej trasie.
c)  spadków osi trasy i łuków wyokrąglających załamania osi trasy.
d)  tworząca załomy trasy.

19. W kolejnictwie, prześwit to

a) normalna szerokość toru, mierzona na wysokości 14 mm poniżej powierzchni

tocznych szyn.

b)  odległość między osiami sąsiednich torów.
c)  Odległość, jaka musi być zachowana, aby skrajnia nie została przekroczona.
d)  normalna odległość powierzchni tocznych szyn.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

20. Dla rzeki o szerokości do 10 m sondowanie dna wykonuje się co

a)  2 m.
b)  1 m.
c)  0,5 m.
d)  2,5 m.

21. Limnigraf, to urządzenie służące do badania

a)  stanu wody w rzece.
b)  spadku rzeki.
c)  wielkości przepływu.
d)  wytrzymałości mostu.

22. Obliczona rzędna niwelety o spadku + 2%, w punkcie o rzędnej wynoszącej 86.00m, od

jej załamania wynosi
a)  84,5 m.
b)  87,0 m.
c)  87,5 m.
d)  85,0 m

23. Współrzędne biegunowe C, ω punktu klotoidy, który ma współrzędne prostokątne

o wartościach: X = 60,00 Y = 2,00, wynoszą
a) C = 60,03m ; ω = 2

b) C = 58,25m ; ω = 5

c) C = 25,48m; ω = 15

d) C = 10,78m; ω = 8

24. Jedną z metod regulacji osi torów jest

a)  metoda dzielenia strzałki.
b)  metoda wskaźnika regulacji.
c)  wykres kątów.
d)  tyczenie od ukresu do ukresu.

25. Regulację osi torów kolejowych przeprowadza się w oparciu o pomierzone w terenie

a)  miejsca ukresów.
b)  skosy rozjazdów.
c)  wielkości wskaźników.
d)  wartości strzałek.

26. W metodzie graficznej regulacji osi torów kolejowych łuk kołowy odwzorowuje się jako

a)  prosta prostopadła do osi.
b)  prosta równoległa do osi.
c)  parabola trzeciego stopnia.
d)  parabola drugiego stopnia.

27. Podstawowe części rozjazdu zwyczajnego to

a)  zwrotnica złożona z dwóch połączonych iglic, tory łączące i krzyżownica.
b)  krzyżownica złożona z dwóch połączonych iglic, tory łączące i zwrotnica.
c)  zwrotnica złożona z dwóch połączonych iglic, krzyżownica.
d)  zwrotnica złożona z dwóch połączonych iglic oraz tory łączące.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

KARTA ODPOWIEDZI

Imię i nazwisko ..............................................................

Prowadzenie geodezyjnej obsługi budownictwa drogowego, kolejowego
i wodnego

Zakreśl poprawną odpowiedź.

zadania

Odpowiedź

Punkty

Razem: