Narzędzia modelowania niezawodności

1

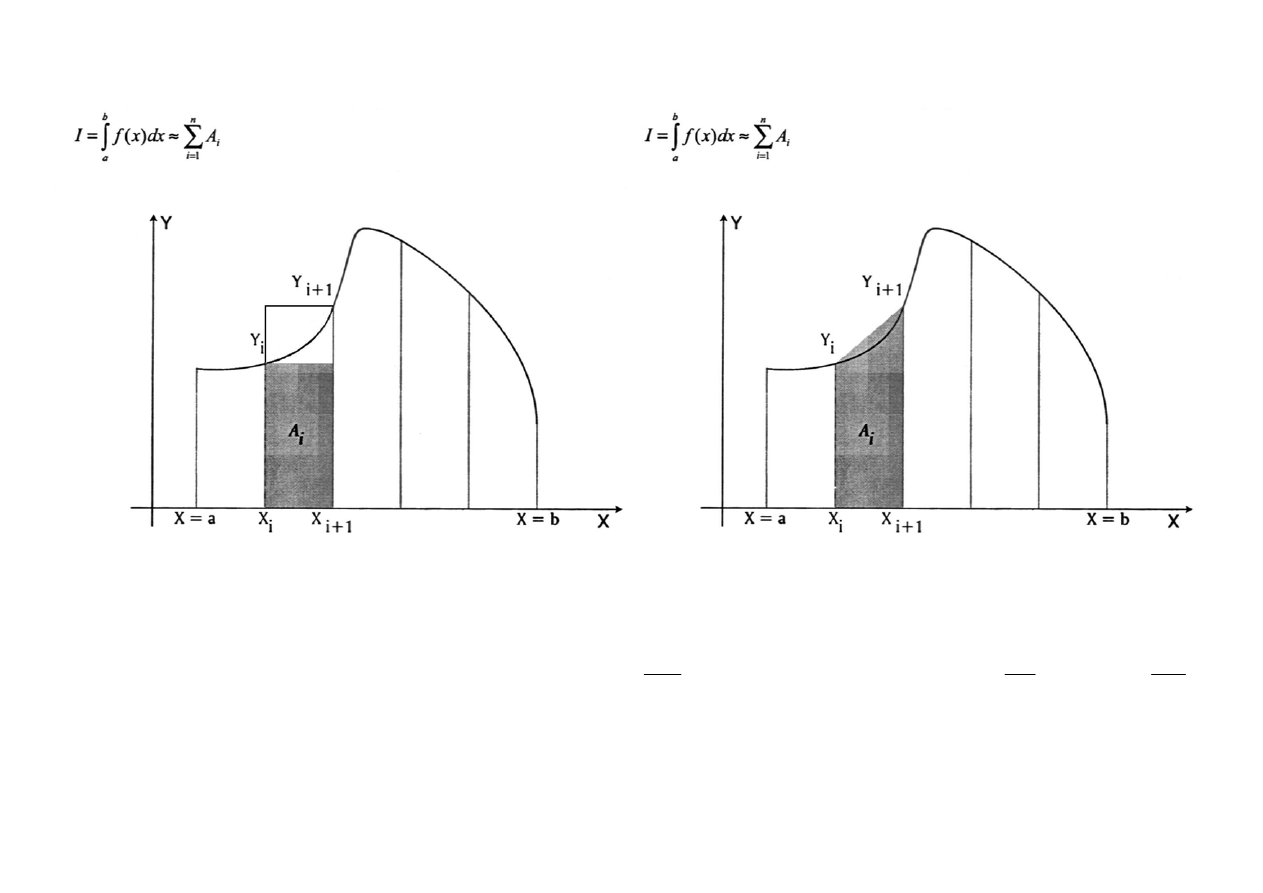
Numeryczne obliczanie całki funkcji

W pierwszym przypadku całkę obliczamy wg wzoru

∑

=

⋅

≈

n

1

i

i

y

∆x

I

albo

∑

=

+

⋅

≈

1

-

n

0

i

1

i

y

∆x

I

a w drugim













+

+

⋅

=













+

+

⋅

≈

∑

∑

−

=

=

2

y

y

2

y

∆x

y

y

2

y

2

∆x

I

n

1

n

2

i

i

1

1

-

n

2

i

n

i

1

Narzędzia modelowania niezawodności

2

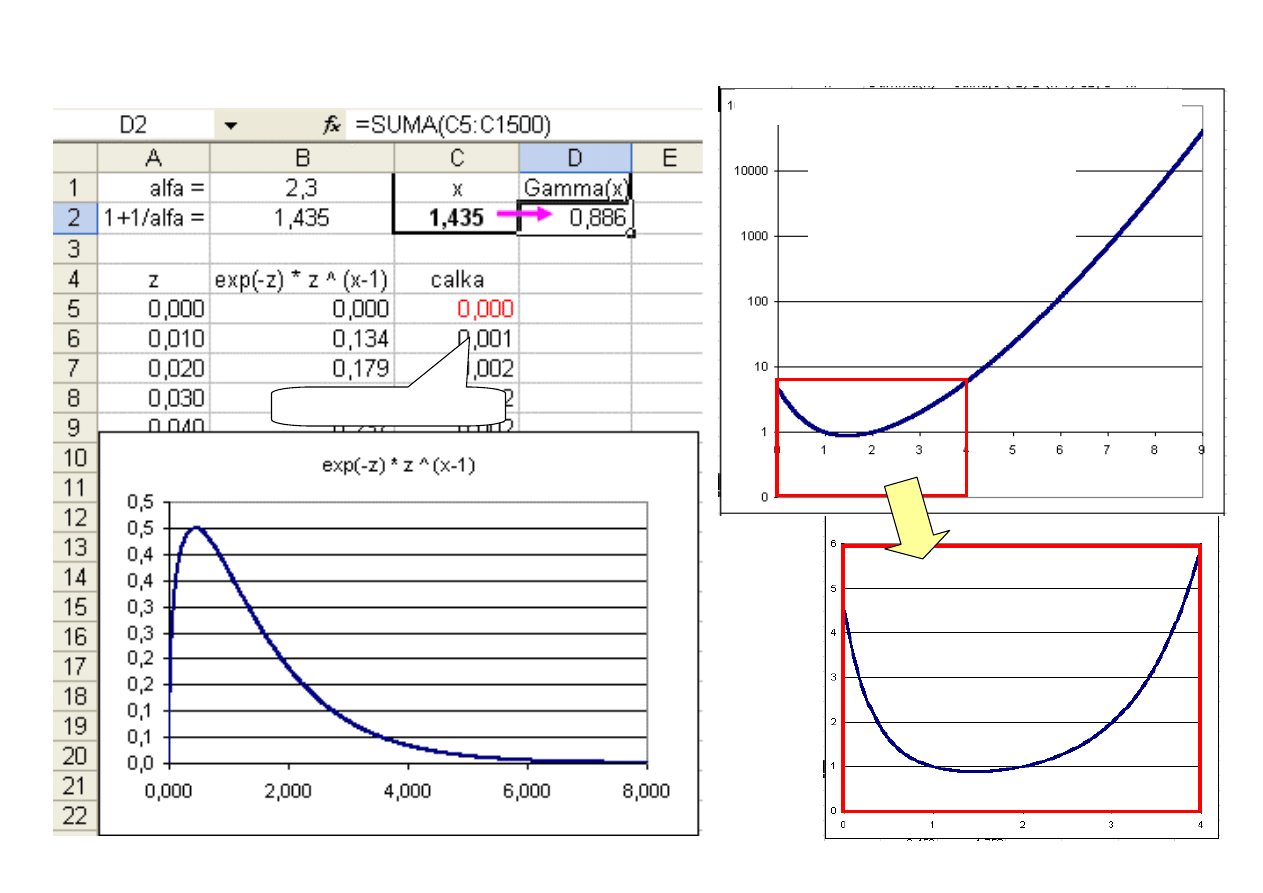
Przykład 15 a. Obliczenie wartości funkcji gamma

∫

∞

−

−

=

0

1

x

z

dz

z

e

Γ(x)

=(B6+B5)*$A$6/2

Narzędzia modelowania niezawodności

3

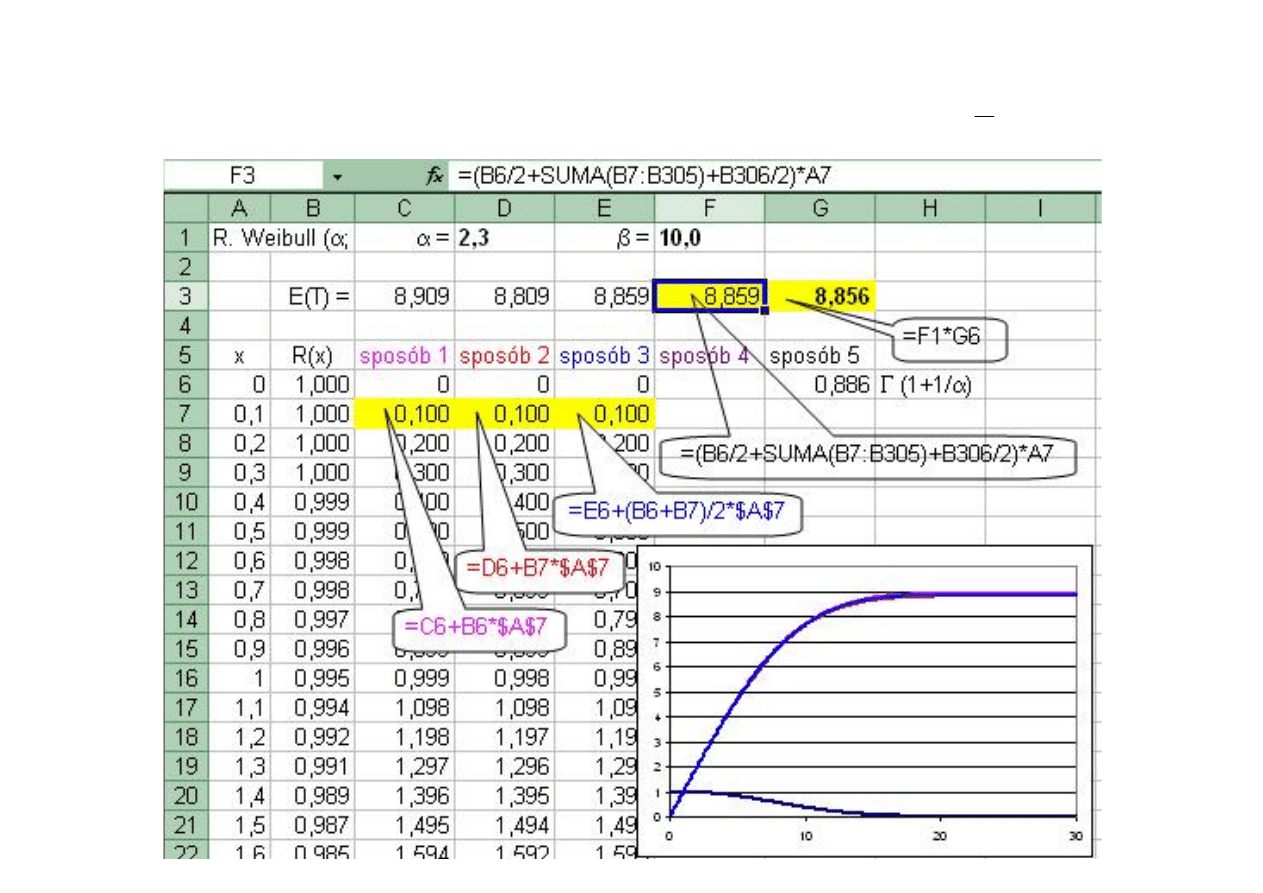
Przykład 15 b. Obliczenie wartości oczekiwanej rozkładu prawdopodobieństwa.

Dla rozkładu Weibulla (

α, β) Î

∫

∞

=

0

R(x)dx

E(T)

)

α

1

Γ(1

β

E(T)

+

=

Narzędzia modelowania niezawodności

4

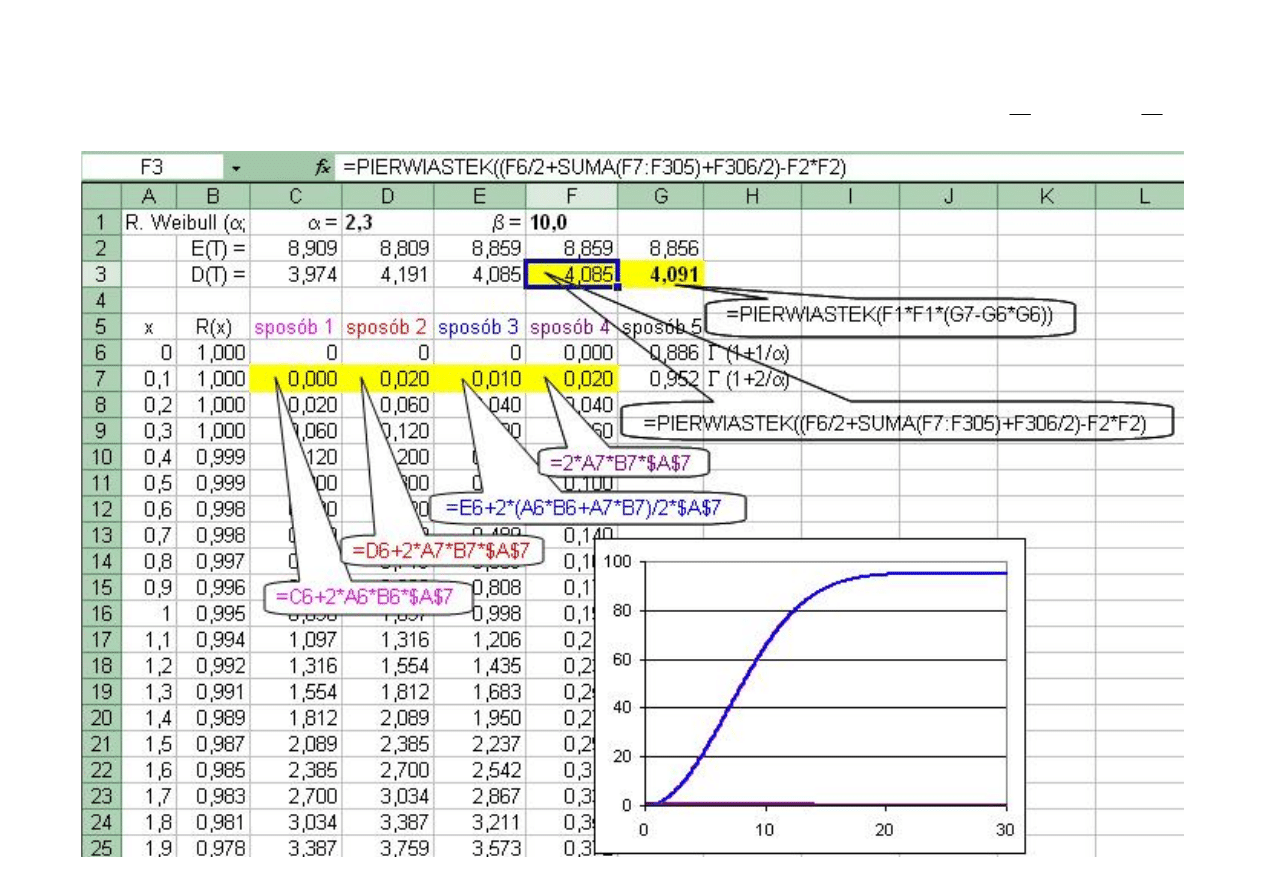
Przykład 15 c. Obliczenie wartości wariancji rozkładu prawdopodobieństwa.

Dla rozkładu Weibulla (

α, β) Î

2

0

2

E(T)

dx

R(x)

x

2

(T)

D

−

=

∫

∞

]

)

α

1

Γ(1

)

α

2

(1

[

β

(T)

D

2

2

2

+

−

+

Γ

=

Narzędzia modelowania niezawodności

5

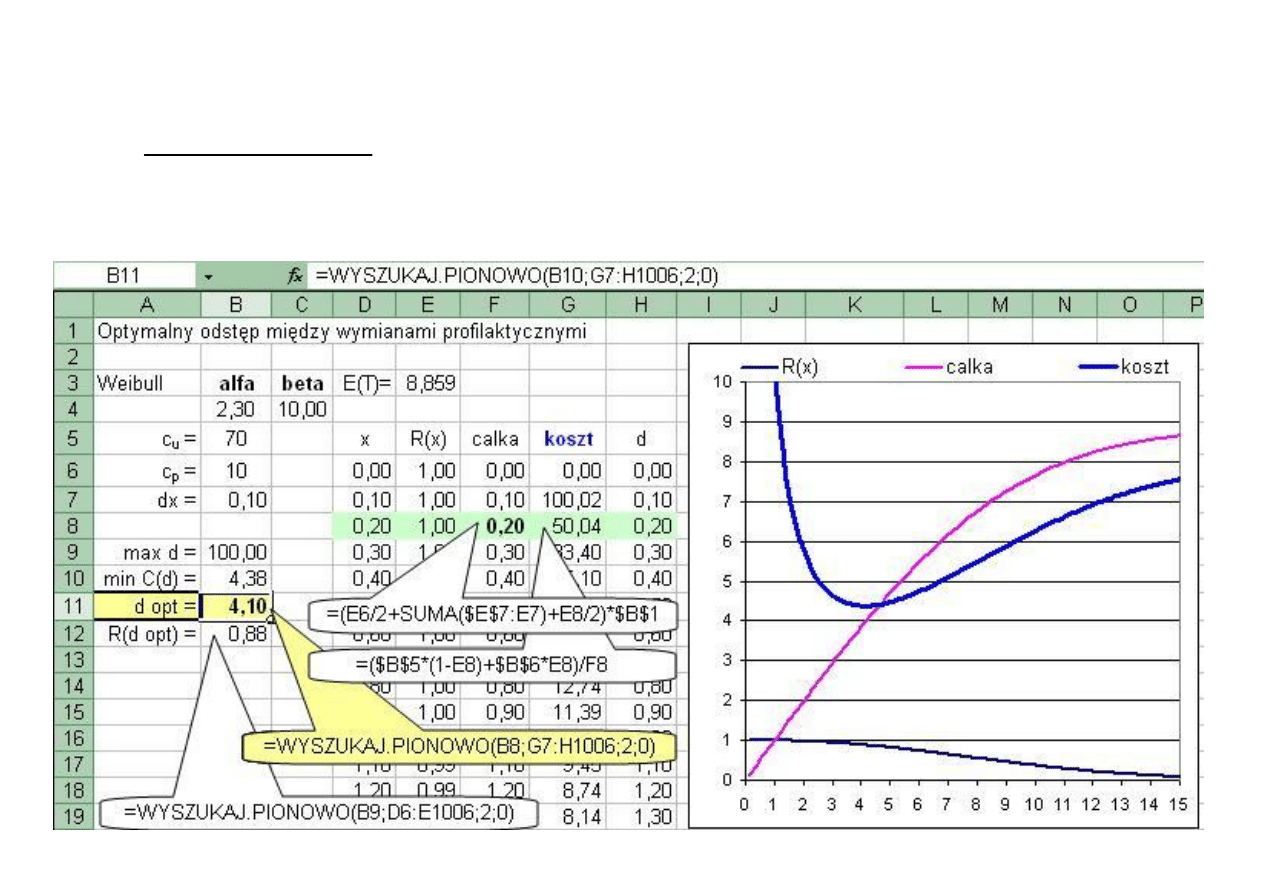
Przykład 15 d. Obliczenie optymalnego ekonomicznie okresu wymian profilaktycznych.

∫

⋅

+

⋅

=

x

0

p

u

dt

R(t)

R(x)

c

F(x)

c

C(x)

gdzie: c

u

– koszt uszkodzenia

c

p

– koszt wymiany profilaktycznej

Narzędzia modelowania niezawodności

6

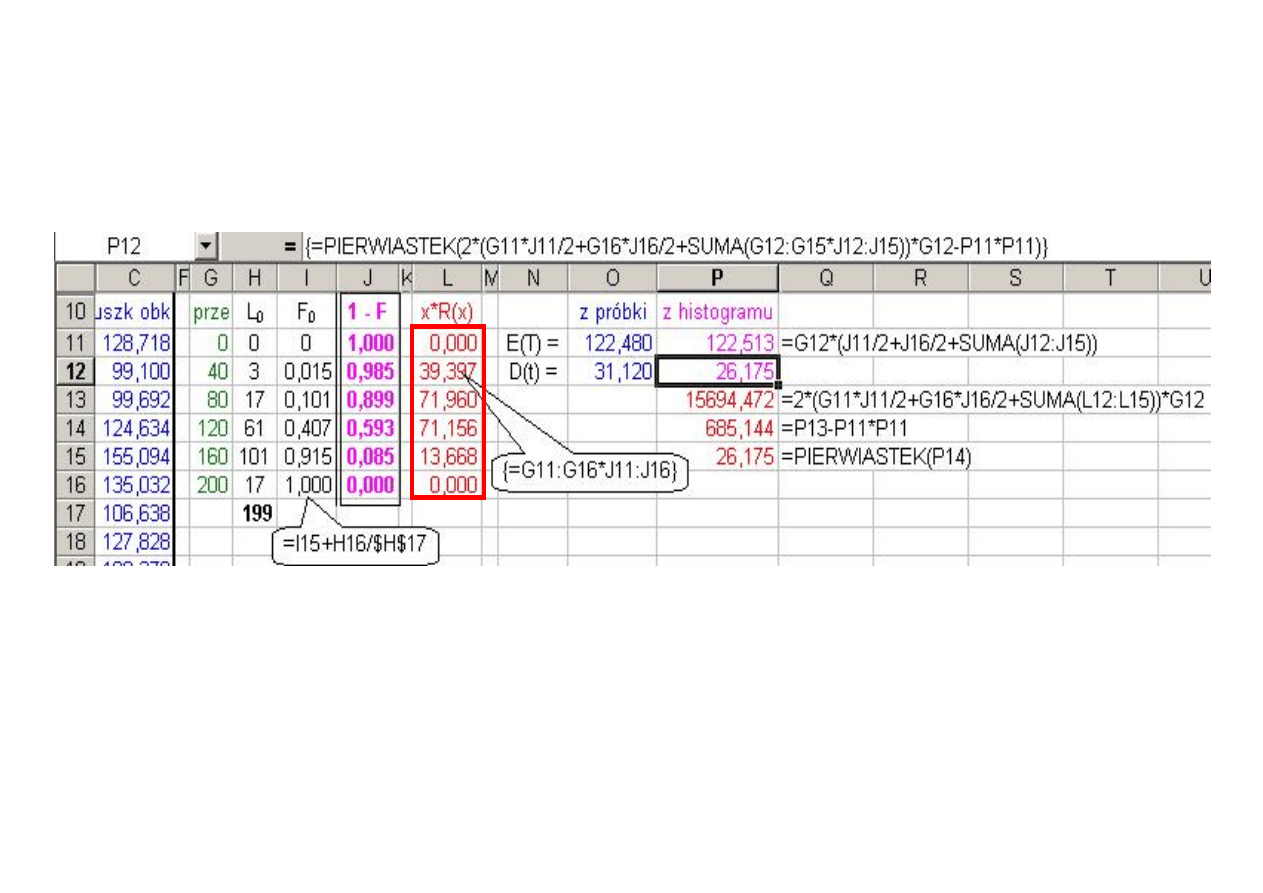
Przykład 15 e. Obliczenie parametrów rozkładu na podstawie histogramu.

∫

∞

=

0

R(x)dx

E(T)

2

0

2

E(T)

dx

R(x)

x

2

(T)

D

−

=

∫

∞