1
1
dr Ewa Więckowska-Bryłka
Katedra Chemii WNoŻ
p. 2036
Wykład 1.
Wielkości podstawowe i
pochodne stosowane w chemii
fizycznej
Szkoła Główna Gospodarstwa Wiejskiego
Wydział Nauk o Żywności
CHEMIA FIZYCZNA
Konsultacje:
• Poniedziałek godz. 11-12
• Środa godz. 10-11
2
Kryteria zaliczenia przedmiotu:
chemia fizyczna
dla studentów I roku kierunku Technologia żywności i żywienie
człowieka WNoŻ – studia stacjonarne
Program studiów dla studentów kierunku: technologia żywności i
żywienie człowieka Wydziału Nauk o Żywności przewiduje w II
semestrze studiów dla przedmiotu Chemia Fizyczna
15 godzin wykładów
(7 tyg. x 2 godz. + 1 tydz. x 1 godz.) i
15 godzin ćwiczeń
laboratoryjnych
(5 tyg. x 3 godz.).
Ćwiczenia z chemii fizycznej
są prowadzone na przemiennie grupami co
drugi tydzień (czyli przez 10 tygodni w semestrze) i rozpoczynają się:
12 marca
– gr. 9, 1, 5 – sala 2010 , gr. 10, 2, 6 – sala 2065
19 marca
– gr. 7, 3, 11 – sala 2010, gr. 8, 4 – sala 2065
zgodnie z godzinami podanymi w tygodniowym planie zajęć.
Studenci wykonują ćwiczenia w zespołach 2– lub 3– osobowych (w
każdej grupie 6 zespołów) według ustalonego harmonogramu (dla każdego
zespołu zaplanowano 5 ćwiczeń)
3
Założenia i cele przedmiotu:
opanowanie przez studenta podstawowych pojęć i praw z zakresu
chemii fizycznej,
poznanie wybranych zjawisk fizykochemicznych,
zaznajomienie się z prostymi metodami badawczymi,
nabycie umiejętności samodzielnego wykonywania pomiarów i
interpretacji ich wyników.
Zgodnie z REGULAMINEM
STUDIÓW, od 1 października 2012 r. w
SGGW
obowiązuje system punktowy odpowiadający standardowi
ECTS (Europejski System Transferu i Akumulacji
Punktów).
Przedmiotowi Chemia Fizyczna przypisano 3 pkt ECTS. Uzyskanie 3
pkt ECTS odzwierciedla
osiągnięcie przez studenta założonych dla
tego przedmiotu
efektów kształcenia, potwierdzone jego zaliczeniem.
4
Efekty kształcenia uwzględnione w sylabusie przedmiotu
Chemia fizyczna to:
student zna podstawowe prawa rządzące procesami fizycznymi i reakcjami
chemicznymi
zna metody opisu przemian fizykochemicznych i chemicznych
zna podstawowe metody i techniki instrumentalnej analizy fizykochemicznej i
chemicznej
zna
podstawowe
metody
opracowywania
i
interpretacji
danych
eksperymentalnych
wykorzystuje poznane zjawiska i równania do opisu oraz oceny właściwości
substancji
posiada umiejętność wykonania pomiarów, ich interpretacji i oceny
wiarygodności
opanował umiejętność samodzielnego uczenia się
posiada umiejętność pracy samodzielnej i zespołowej i jest odpowiedzialny za
odpowiednie warunki i bezpieczeństwo własne i innych.
2
5
Do weryfikacji efektów kształcenia służy:
1.
ocena z 5 sprawozdań pisemnych z wykonanych ćwiczeń laboratoryjnych,
ocenianych w skali 0-3 pkt;
2.
ocena z 5 kolokwiów pisemnych składających się z 2 pytań związanych z
wykonywanym w danym dniu ćwiczeniem przeprowadzanych podczas
ćwiczeń laboratoryjnych, ocenianych w skali 0-5 pkt;
3.
ocena z pisemnego kolokwium składającego się z 7 pytań z materiału
wykładowego, ocenianych w skali 0-5 pkt. Kolokwium to odbędzie się po
zakończeniu wykładów - 22 maja godz. 13-15 (aula III).
Dla każdego z tych trzech elementów określona jest maksymalna liczba punktów
do uzyskania, tj.
1. 15 pkt., 2. 50 pkt., 3. 35 pkt. Razem 100 pkt.
6
Przedmiot zalicza student, który z każdego elementu uzyskał co
najmniej 50% punktów, tzn. odpowiednio: 1. 7,5 pkt., 2. 25 pkt.,
3. 17,5 pkt.
Warunkiem zaliczenia przedmiotu i uzyskania 3 pkt. ECTS jest zaliczenie
wszystkich w/w elementów weryfikacji efektów kształcenia
.
Ocena końcowa z przedmiotu zależy od sumy wszystkich punktów:
50,5-60 pkt. – ocena 3,0; 60,5-70 pkt. – ocena 3,5;
70,5-80 pkt. – ocena 4,0; 80,5-90 pkt. – ocena 4,5;
90,5-100 pkt. – ocena 5,0.
Zgodnie z § 20 pkt. 3. REGULAMINU STUDIÓW:
W przypadku uzyskania w trakcie trwania semestru, w wyniku
przeprowadzenia określonych form weryfikacji efektów kształcenia
określonych w opisie modułu, ocen negatywnych studentowi
przysługuje jeden termin poprawkowy. Termin ten wyznaczany jest
przez osobę odpowiedzialną za moduł i może zostać ustalony w
terminie sesji zaliczeniowej.
7
Studenci, którzy nie uzyskają
50%
możliwej liczby punktów z
kolokwiów ćwiczeniowych, piszą kolokwium z całości materiału
związanego z wykonanymi ćwiczeniami po zakończeniu pracowni
w ustalonym terminie.
Studenci, którzy nie uzyskają
50%
możliwej liczby punktów z
kolokwium wykładowego, piszą kolokwium poprawkowe z
całości materiału wykładowego w dniu 12 czerwca godz. 13-15
(aula III).
Ćwiczenia laboratoryjne są obowiązkowe i wszystkie
przewidziane w programie dla danego zespołu ćwiczeniowego
muszą być wykonane praktycznie.
8
Zgodnie z § 10 pkt. 2, 4 i 5 REGULAMINU STUDIÓW:
2. Obecność studenta na zajęciach innych niż wykłady jest obowiązkowa.
Student nie może mieć więcej niż 20% nieobecności na tych zajęciach -
bez względu na przyczyny.
4. Prowadzący zajęcia decyduje o sposobie i terminie wyrównania
zaległości powstałych wskutek nieobecności studenta na zajęciach.
5. Student, który nie uczestniczył w zajęciach i nie wyrównał zaległości w
sposób opisany w ust. 4, nie może uzyskać zaliczenia modułu.
Studenci przystępują do ćwiczeń przygotowani teoretycznie –
kolokwium piszą przed rozpoczęciem ćwiczeń laboratoryjnych.
Wyniki pomiarów i ich opracowanie studenci przedstawiają w formie
(jednego na zespół) pisemnego sprawozdania formatu A4 (cel
ćwiczenia, krótki wstęp teoretyczny, wykonanie ćwiczenia, wyniki
pomiarów i ich opracowanie).
Wszystkie sprawozdania muszą być
poprawnie opracowane i oddane !
Podręcznik:Eksperymentalna chemia fizyczna
, praca zbiorowa,
Wyd. SGGW, Warszawa 2007, wyd. III zmienione
3
9
Wykaz ćwiczeń laboratoryjnych z chemii fizycznej
(numery ćwiczeń podano wg podręcznika "Eksperymentalna chemia fizyczna", praca
zbiorowa, Wyd. SGGW, Warszawa 2007, wyd. III zmienione).
1 – 1. Wyznaczanie ciepła rozpuszczania, sala 2010
2 – 1. Wyznaczanie gęstości pary i masy molowej metodą Meyera, sala 2065
2 – 2a. Pomiar współczynnika lepkości cieczy za pomocą wiskozymetru Ostwalda, sala 2065
2 – 3. Wyznaczanie zawartości alkoholu etylowego w badanym roztworze, sala 2010
3 – 1. Wyznaczanie współczynnika podziału kwasu octowego w układzie dwóch nie mieszających się
cieczy, sala 2010
4 – 1. Adsorpcja kwasu octowego na węglu aktywowanym, sala 2010
6 – 1. Wyznaczanie stałej szybkości reakcji inwersji sacharozy metodą polarymetryczną, sala 2010
7 – 1. Miareczkowanie konduktometryczne, sala 2065
7 – 2. Wyznaczanie klasycznej stałej dysocjacji z pomiarów przewodnictwa, sala 2065
8 – 1. Miareczkowanie potencjometryczne kwasu zasadą, sala 2065
9 – 1. Oznaczanie grubości osadzonej powłoki miedzianej i wydajności prądowej elektrolizy, sala 2065
10 – 1. Kolorymetryczne oznaczanie stężenia jonów żelaza (III), sala 2010
Sala 2010
Sala 2065
10
Harmonogram ćwiczeń laboratoryjnych z chemii fizycznej
Zespół
Nr tygodnia
A B
C
D
E
F
G
H
I
J
K
L
I
10–1 1–1 2–3
3–1
4–1
6–1
2–1 2–2a 7–1
7–2
8–1
9–1
II
4–1
3–1
6–1
1–1 10–1 2–3
9–1
8–1 2–2a 2–1
7–2
7–1
III
2–1 2–2a 7–1
7–2
8–1
9–1 10–1 1–1
2–3
3–1
4–1
6–1
IV
9–1
8–1 2–2a 2–1
7–2
7–1
4–1
3–1
6–1
1–1 10–1 2–3
V
7–2
7–1
8–1
9–1
2–1 2–2a 6–1 10–1 1–1
2–3
3–1
4–1
Zespoły 2-lub 3-osobowe (6 zespołów w każdej z sal; w momencie rozpoczęcia
pracowni - w sali 2010 zespoły oznaczone literami A-F, w sali 2065 – G-L)
kolor zielony – w sali
2065
Kolor żółty – ćwiczenia wykonywane w
sali 2010
11
Nr grupy: 9 SALA 2010
Zespół Imiona i nazwiska osób w
zespole
Nr ćwiczenia
wykonywanego w dniu
12 03 13 godz. 8 - 11
A
10 –1
B
1–1
C
2–3
D
3–1
E
4–1
F
6–1
12
Rozkład zajęć z chemii fizycznej (we wtorki) dla studentów I roku kierunku
Technologia żywności i żywienie człowieka WNoŻ (studia dzienne) od 12
marca (19 marca) 2013 r. do 26 marca (9 kwietnia) 2013 r.
- pierwsze dwa
tygodnie wg harmonogramu
Sala 2010
Sala 2065
Godz.
Nr grupy Prowadzący
Nr
grupy
Prowadzący
8 – 11
9 (7)
dr B. Parczewska–Plesnar
(dr B. Parczewska–Plesnar)
10 (8)
dr E. Więckowska–Bryłka
(dr E. Więckowska–Bryłka)
11 – 14
1 (3)
dr B. Parczewska–Plesnar
(dr B. Parczewska–Plesnar)
2 (4)
dr E. Więckowska–Bryłka
(dr E. Więckowska–Bryłka)
14 – 17
5 (11)
dr B. Parczewska–Plesnar
6 (-)
dr E. Więckowska–Bryłka
4
13
1. Do każdego ćwiczenia obowiązuje materiał teoretyczny całego
rozdziału o takim numerze jak pierwsza liczba w symbolu
wykonywanego ćwiczenia i Pytania i zadania zamieszczone w
podręczniku po danym ćwiczeniu. Wyjątki dotyczą ćwiczeń z
rozdziału 2, gdzie obowiązuje materiał teoretyczny z poszczególnych
części rozdziału, zgodnie z wymienionymi w ćwiczeniu wymaganiami
kolokwialnymi.
2. W przypadku
ćwiczenia 1–1
obowiązują również
zadania z prawa
Hessa
zamieszczone po teorii rozdziału 1 (np. zad. 48-54 ze str. 48-
50), a przed ćw. 1–1.
Wymagania kolokwialne związane z pytaniami z ćwiczeń:
Wzór nagłówka do sprawozdania:
Nr i tytuł ćwiczenia:
Imię i nazwisko osoby prowadzącej ćwiczenia:
Data wykonania ćwiczenia Godz. Nr grupy
studenckiej
Zespół
Nazwiska osób
wykonujących ćw.
Pkt za spr
Uwagi
prowadzącego:
14
TEMATYKA WYKŁADÓW:
I.
Wielkości podstawowe i pochodne stosowane w chemii
fizycznej
Omówienie sposobu realizacji przedmiotu i kryteriów zaliczenia. Sposób
opracowania wyników pomiarów, sporządzanie wykresów i ich interpretacja
na przykładzie wielkości mierzonych i wyznaczanych podczas ćwiczeń
laboratoryjnych. Definicje, jednostki wg układu SI. Przeliczanie jednostek z
zastosowaniem jednostek pod- i wielokrotnych dla wielkości podstawowych i
ich pochodnych.
II. Termodynamika. Termochemia.
Układ, otoczenie, faza, stan, parametry stanu, funkcje stanu, zasady
termodynamiki. Procesy odwracalne i nieodwracalne. Kryteria samorzutności
procesów. Równania Kirchhoffa. Prawo Hessa. Statyka chemiczna (prawo
działania mas, reguła przekory, izoterma i izobara van't Hoffa). Wyznaczanie
ciepła rozpuszczania.
III.
Płyny.
Gazy: gaz doskonały, równania gazu doskonałego, ciepło molowe, gaz
rzeczywisty, równanie van der Waalsa. Prawa: Daltona i Grahama.
Wyznaczanie masy molowej metodą Meyera.
Ciecze: właściwości cieczy, gęstość, lepkość, metody pomiaru lepkości cieczy,
napięcie powierzchniowe i metody jego wyznaczania. Współczynnik
załamania światła i refraktometria.
15
IV.
Układy jedno i wieloskładnikowe – wielofazowe.
Przemiany i równowagi fazowe. Reguła faz Gibbsa. Roztwory. Prawo Henry'ego.
Napoje gazowane. Choroba kesonowa. Dyfuzja, osmoza. Rola ciśnienia
osmotycznego w procesach biologicznych i w życiu człowieka. Konserwacja
żywności. Prawo Raoulta. Ebulio i kriometria. Destylacja i rektyfikacja. Prawo
podziału Nernsta i ekstrakcja.
V.
Zjawiska powierzchniowe. Adsorpcja i kataliza
Klasyfikacja procesów adsorpcji. Izotermy adsorpcji. Wykorzystanie procesów
adsorpcji: metody chromatograficzne, jonity. Kataliza i reakcje enzymatyczne.
Adsorpcja z roztworu i środki powierzchniowo czynne.
VI.
Koloidy
Układy dyspersyjne. Koloidy, ich klasyfikacja i właściwości. Metody
otrzymywania i oczyszczania koloidów. Dializa. Właściwości optyczne koloidów
– nefelometria i turbidymetria. Punkt izoelektryczny. Elektroforeza. Koagulacja,
denaturacja, peptyzacja. Żele, piany, emulsje (homogenizacja).
16
VII. Metody analizy instrumentalnej
Klasyfikacja metod analizy instrumentalnej. Elektrochemiczne metody
analizy instrumentalnej. Potencjometria – pomiar pH i miareczkowanie
potencjometryczne. Konduktometria i miareczkowanie konduktometryczne.
Elektroliza i kulometria (metoda miareczkowania kulometrycznego).
Wykorzystanie
metod
elektrochemicznych
w
analizie
produktów
pochodzenia naturalnego.
VIII. Metody analizy instrumentalnej
– cd.
Metody spektroskopowe – klasyfikacja ze względu na sposób oddziaływania
promieniowania elektromagnetycznego z materią i wykorzystywany w
badaniach zakres promieniowania. Zasada działania spektrofotometru.
Spektroskopia elektronowa i barwa związków kompleksowych. Prawo
Lamberta - Beera i jego zastosowanie w kolorymetrycznej metodzie
oznaczenia stężenia kompleksu jonów żelaza (III) z kwasem salicylowym.
Spektroskopia UV i IR w analizie produktów pochodzenia naturalnego.
5
17
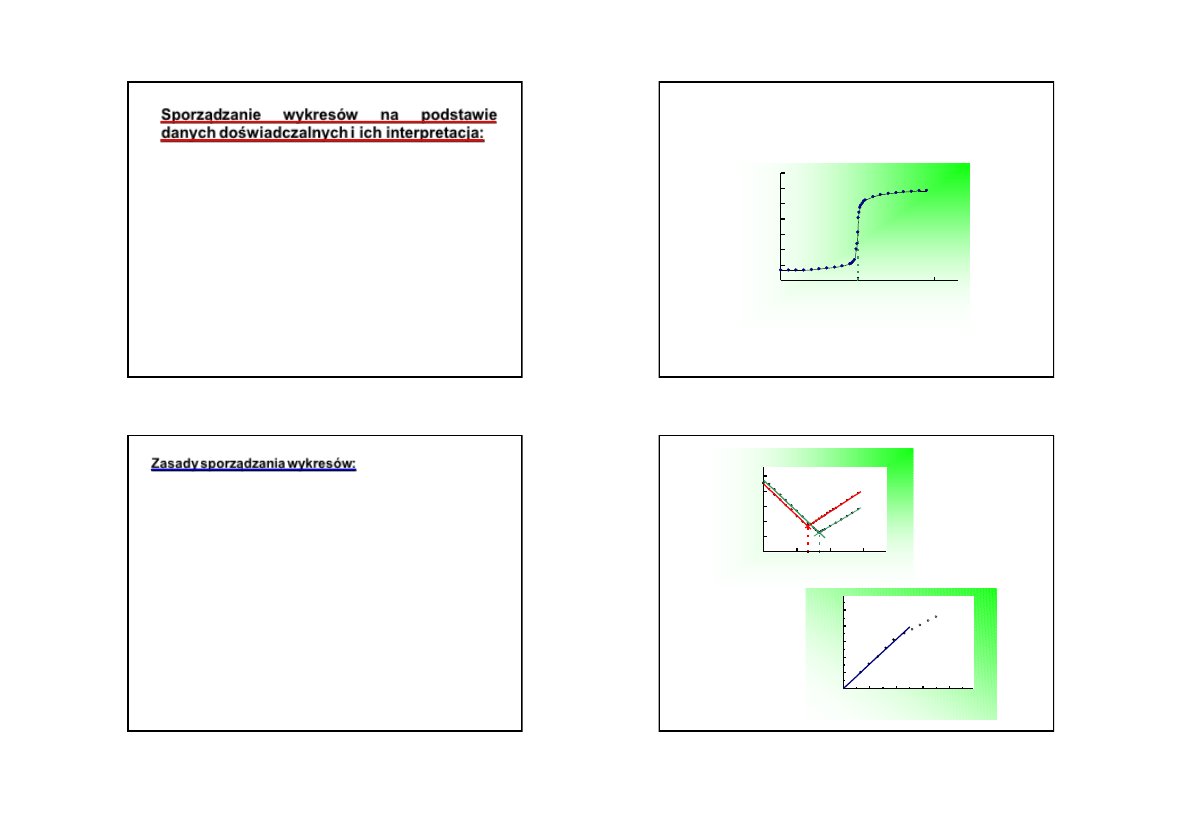
Sporządzanie
wykresów
na
podstawie
danych
doświadczalnych i ich interpretacja:
wykresy na papierze milimetrowym formatu A4 lub
wydruk z komputera (np. z wykorzystaniem
programu Excel)
wyniki
pomiarów zwykle zestawia się w tabelach -
podstawa do poprawnego wykonania wykresu
na kartce papieru milimetrowego nanosimy
układ
współrzędnych (osie współrzędnych x i y) wraz ze
skalą liczbową na osiach i opisem osi.
18
Zasady
sporządzania wykresów:
•
wykres powinien
posiadać tytuł (na górze lub na dole),
•
stosunek
długości osi nie powinien przekraczać 1 : 1,5,
•
w opisie osi
należy podać symbole użytych wielkości i ich
jednostek,
•
jednostki na osiach
współrzędnych x i y powinny być tak dobrane,
aby wykres funkcji y = f(x)
zajmował całą powierzchnię
ograniczoną osiami układu współrzędnych (całą powierzchnię
kartki papieru);
•
skala liczbowa na osiach wykresu (tzw.
podziałka) powinna być
tak naniesiona, aby z wykresu
można było dokonać odczytu z
dokładnością zbliżoną do dokładności pomiarów,
•
najczęściej stosuje się skalę liniową lub logarytmiczną;
•
w skali liczbowej
należy uwzględnić podziałkę główną i
pomocniczą;
•
skale powinny
być określane w sposób ułatwiający odczyt;
najczęściej stosujemy skale typu: 1·10
n
, 2
·10
n
, 4
·10
n
, 5
·10
n
;
powinniśmy unikać wielokrotności nieparzystych: 3, 6, 7, itd.,
•
skale nie
muszą się zaczynać od zera, lecz ich granice powinny
być zbliżone do ekstremalnych wartości zmiennych,
19
•
zmienna
niezależna na osi odciętych
X
, zmienna
zależna
– na osi rzędnych
Y
,
gdyż
y =
f(
x
)
,
np.
pH
= f(
V
),
λ
= f(
V
),
A
= f (
c
)
0
2
4
6
8
10
12
14
0
10
20
v NaOH [cm
3
]
pH
20
0
0,5
1
1,5
2
2,5
0
6
12
18
v
NaOH
[cm
3
]
[mS]
1
2
v
1
v
2
A = 1578,1 c
0
0,1
0,2
0,3
0,4
0,5
0
0,0001 0,0002 0,0003 0,0004
c
Fe(III
) [mol
.
dm
-3
]
A
6
21
•
wartości dwóch zmiennych x i y są współrzędnymi
punktu pomiarowego i
wyznaczają jego położenie na
płaszczyźnie wykresu
•
punkty zaznacza
się kółeczkami, krzyżykami, lub innymi
znakami
•
jeżeli przedstawiamy więcej niż jedną serię danych
pomiarowych (oznaczanych
różnymi znakami lub
kolorami), wykres musi
zawierać legendę
•
punkty obarczone
błędem grubym (znacznie odbiegające
położeniem od pozostałych na siatce pomiarowej)
pomijamy podczas
kreślenia właściwego wykresu
•
po naniesieniu
punktów doświadczalnych przystępujemy
do
odręcznego wykreślenia, tzw.
linii trendu
za
pomocą
przyrządów geometrycznych (linijki, krzywiki)
22
•
wartości
doświadczalne,
otrzymane
na
podstawie
bezpośredniego pomiaru lub obliczone na podstawie wzoru
zawsze obarczone
są pewnym błędem, stąd punkty na
wykresie zwykle nie
leżą idealnie na prostej (wykres 1) lub
krzywej o
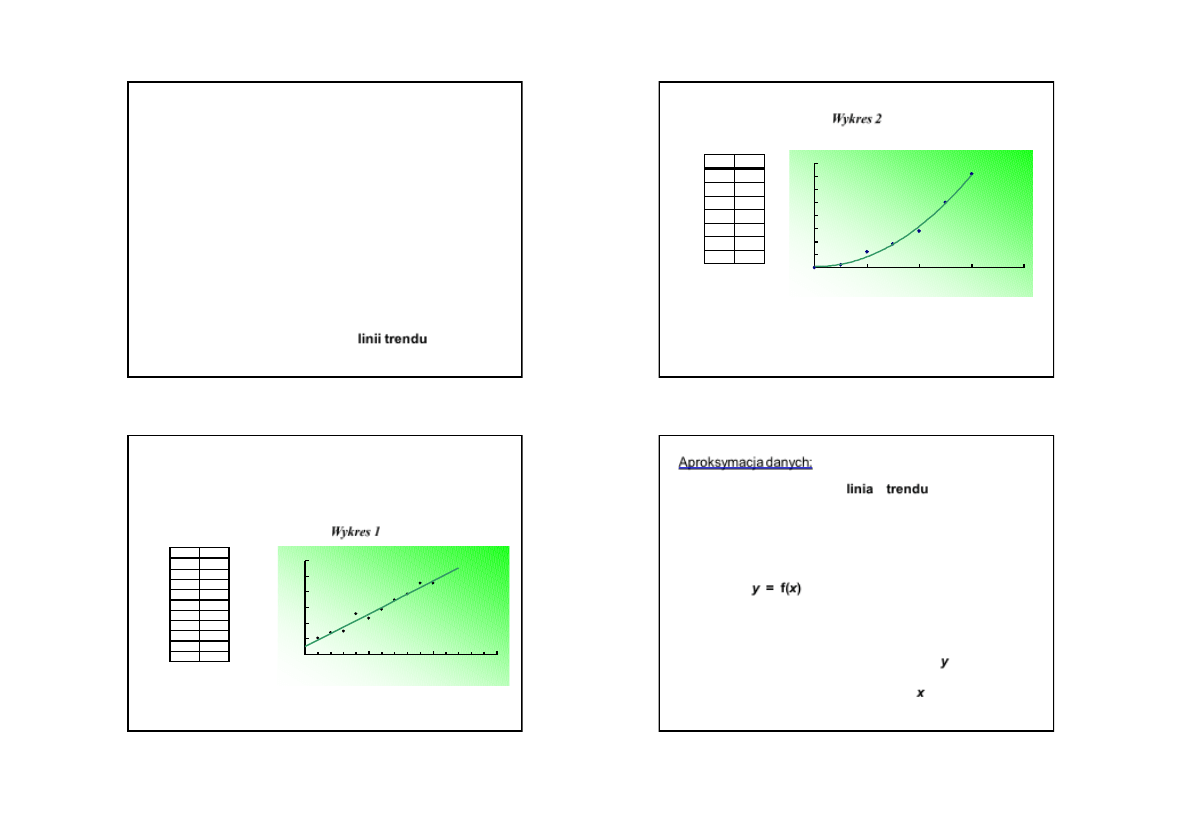
określonym regularnym przebiegu (wykres 2)
Wykres 1
x
y
1
5,2
2
6,9
3
7,4
4
13
5
11,5
6
14,3
7
17,4
8
19,2
9
22,7
10
22,8
y = 2,0848x + 2,5733
R
2
= 0,968
0
5
10
15
20
25
30
0
5
10
15
y
x
23
x
y
0
0
1
2,2
2
12
3
18
4
28
5
50
6
72
Wykres 2
y = 2x
2
- 0,3x + 0,9286
R
2
= 0,993
0
10
20
30
40
50
60
70
80
0
2
4
6
8
y
x
24
Aproksymacja danych:
•
wykresem jest pewna
linia trendu
,
aproksymująca
uzyskany
zbiór danych
•
stosuje
się analityczne metody statystyki matematycznej,
zwane
metodami regresji
liniowej
lub
nieliniowej
•
metody te
umożliwiają wyznaczenie ścisłej zależności
funkcyjnej
y = f(x)
,
równania matematycznego najlepiej
dopasowanego do
wyników pomiarów
•
podczas wykonywania
obliczeń metodami regresji za
pomocą wzorów, są wyznaczane tzw.
reszty regresji
, czyli
różnice
pomiędzy wartością współrzędnej
y
obserwowaną
doświadczalnie i wartością teoretyczną leżącą na linii
regresji,
odpowiadającą danej wartości
x
7
25
•
jedną z metod regresji jest
metoda najmniejszych
kwadratów
, w
której parametry funkcji y = f(x) są
dobierane tak, aby suma
kwadratów reszt regresji
(odchyleń punktów pomiarowych od linii regresji)
była jak najmniejsza
•
miarą stopnia dopasowania wybranego modelu
regresji do danych
doświadczalnych jest
wartość
kwadratu
współczynnika regresji R
2
(im bardziej
zbliżona do 1, tym lepiej dobrano model regresji)
•
w wyniku
obliczeń rysowana jest linia prosta (lub
krzywa) najlepiej
opisująca punkty pomiarowe
•
o znalezionej prostej (lub krzywej)
mówi się, że jest
dopasowana
metodą najmniejszych kwadratów lub,
że jest prostą (lub krzywą) regresji zmiennych y i x.
26
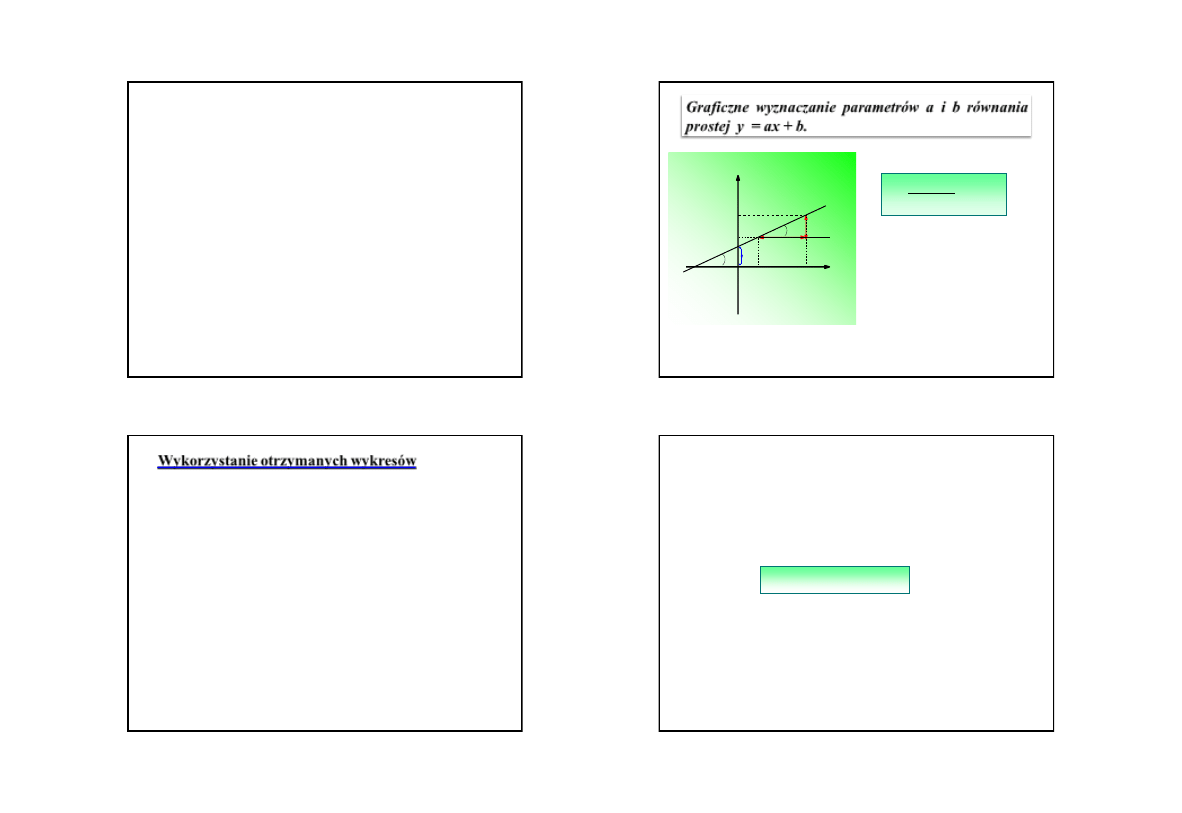
Wykorzystanie otrzymanych wykresów
•
celem
graficznego
zobrazowania
danych
pomiarowych w chemii fizycznej jest znalezienie
wartości stałych fizykochemicznych, będących
często parametrami, lub wynikających z wartości
parametrów
a
lub
b
w
równaniu prostej
y = ax + b
•
parametry
a
i
b
można wyznaczyć
metodą
analityczną
(np.
stosując układy dwóch równań z
dwiema niewiadomymi dla kolejnych
punktów
doświadczalnych o współrzędnych (x
i
, y
i
)) lub
metodą graficzną
•
wartość
a
,
będąca
współczynnikiem kierunkowym
prostej
, jest interpretowana jako tangens
kąta
nachylenia prostej do osi
odciętych
•
wartość parametru
b
równa jest wartości
y
, gdy
x = 0
.
27
Graficzne wyznaczanie parametrów a i b równania
prostej y = ax + b.
tg
x
x
y
y
a
1
2
1
2
y1
y2
x1
x2
y
x
b
Do wzoru na współczynnik a
należy
wstawić
wartości
współrzędnych odczytane z osi
liczbowych wykresu
28
•
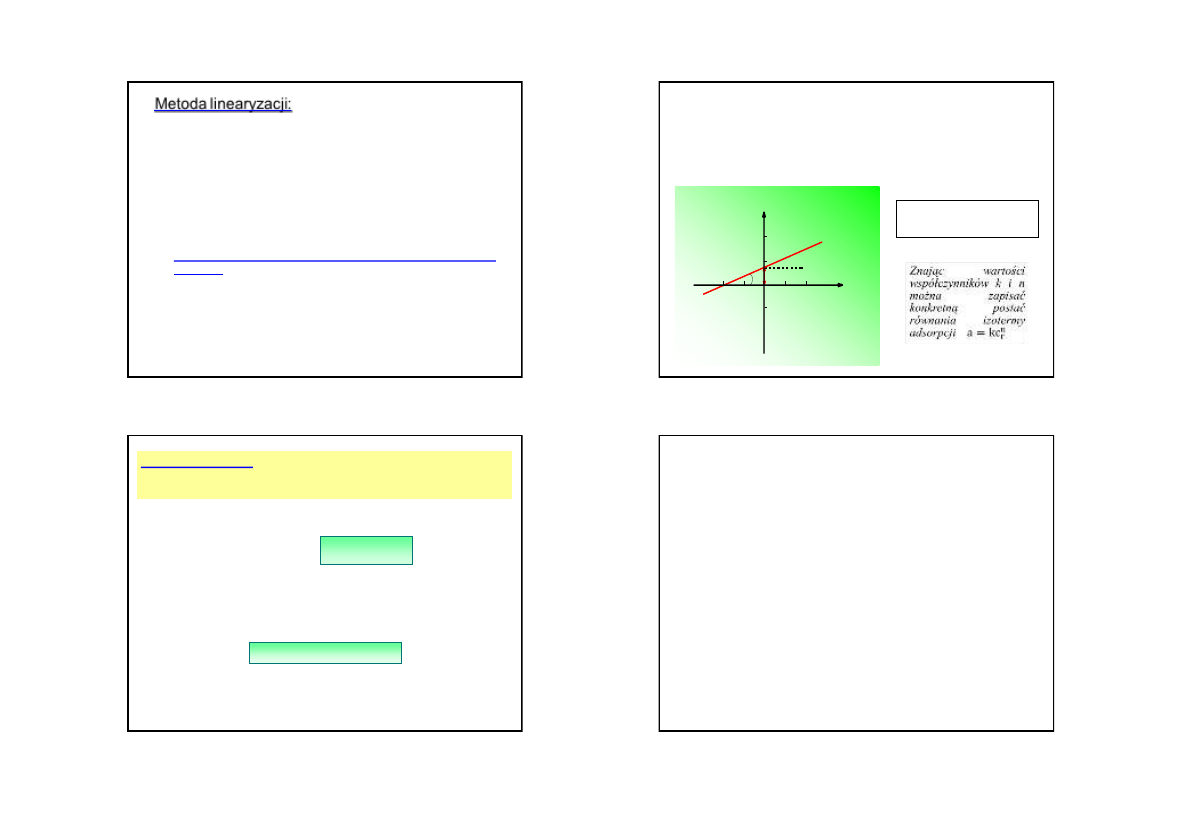
wykres
funkcji
liniowej
jest
wykorzystywany
do
wyznaczenia
stałych fizykochemicznych m. in. w
ćwiczeniu 3–1
•
celem tego
ćwiczenia jest
wyznaczenie izotermy
podziału kwasu octowego w układzie dwóch
niemieszających się cieczy
,
opisanej
ogólnym
równaniem liniowym
w
2
1
2
1
c
k
K
2
k
k
•
sporządzając wykres zależności
y = f(x)
– w tym
przypadku
k = f(c
w
),
znajdujemy
wartość granicznego
stężeniowego współczynnika podziału
k
1
= k
dla
c
w
= 0
,
a
następnie znając wartość
k
1
i
współczynnika
kierunkowego a, obliczamy
stałą dimeryzacji
K
2
.
w którym:
y = k x = c
w
b = k
1
a = 2K
2
·
k
1
2
8
29
Metoda linearyzacji:
•
Stosuje
się wówczas
metodę linearyzacji, czyli
przekształcenia równania nieliniowego do postaci
liniowej
poprzez
odpowiednią
transformację
zmiennych lub
parametrów i dalsza interpretacja
uzyskanej
zależności jako liniowej – wiąże się to ze
sporządzeniem
wykresu
w
nowym
układzie
współrzędnych, takim, w którym punkty pomiarowe
zostaną opisane równaniem prostej.
•
Zależności pomiędzy wielkościami fizykochemicznymi
często nie mają charakteru liniowego i są wówczas
opisywane
za
pomocą
równań
nieliniowych
(potęgowych,
wykładniczych,
wielomianowych,
logarytmicznych). Stosowanie regresji nieliniowych i
interpretacja uzyskanych krzywych
są trudne i
skomplikowane.
30
Metoda linearyzacji
jest wykorzystywana m. in.
do znalezienia
równania matematycznego opisującego zjawisko
adsorpcji (
ćwiczenie 4–1
):
równanie izotermy adsorpcji Freundlicha
,
opisującej
zjawisko adsorpcji kwasu octowego na
węglu aktywowanym
ma
postać wykładniczą:
c
k
=
a
n
r
gdzie: a
– adsorpcja rzeczywista, c
r
– stężenie końcowe adsorbatu w
roztworze w stanie
równowagi, k, n – współczynniki zależne od
rodzaju adsorbenta i adsorbatu.
r
c
log
n
+
k
log
=
a
log
daje
równanie prostej
y = b + ax
gdzie:
y = log a x = logc
r
b = logk a = n
transformacja logarytmiczna do postaci liniowej
31
sporządza się wykres zależności
loga = f (log c
r
)
,
dla co
najmniej 5
pomiarów wartości adsorpcji dla różnych stężeń
adsorbatu
punkt
przecięcia prostej z osią rzędnych odpowiada wartości
logk, natomiast tanges
kąta nachylenia prostej do osi odciętych
– wartości współczynnika n.
log a = log k + n log c
r
y = b + a x
lg k
4
2
-4
-2
2
4
-2
y = loga
x = logc
r
tg = n
32
metoda
lineryzacji
znalazła
analogiczne
zastosowanie w
ćwiczeniu 6–1
do wyznaczenia
stałej szybkości reakcji I rzędu i
ćwiczeniu 1-1
do
wyznaczenia
ciepła
rozpuszczania
kwasu
benzoesowego w wodzie
równania matematyczne, uzyskane na podstawie
wykresów służą do ilościowej interpretacji zjawisk
fizykochemicznych lub
procesów.
9
33
Ćw. 6 - 1 Wyznaczanie stałej szybkości reakcji I rzędu –
reakcja hydrolizy sacharozy w środowisku kwaśnym
Po przekształceniu do postaci liniowej:
Stąd:
k = - a
y = -0,0267x + 3,2044
R² = 0,9933
0
0,5
1
1,5
2
2,5
3
3,5
0
10
20
30
40
50
60
70
t [min]
ln (
t
-
)
k - stała szybkości reakcji,
t – czas ,
– kąt skręcenia
płaszczyzny światła
spolaryzowanego
34
Ćw. 1 – 1 Wyznaczanie ciepła rozpuszczania kwasu
benzoesowego w wodzie
y = -2314,6x + 6,899
R² = 0,9969
-1,2
-1
-0,8
-0,6
-0,4
-0,2
0
0,00313
0,00318
0,00323
0,00328
0,00333
0,00338
0,00343
ln K
1/T
D
H
0
– standardowe molowe ciepło
rozpuszczania,
K – rozpuszczalność,
T – temperatura,
R – stała gazowa
35
Inne zastosowanie
wykresów:
do
celów analitycznych jako
wykresy wzorcowe
y = f(x)
(proste lub krzywe wzorcowe)
wykres wzorcowy jest wykresem
przedstawiającym zależność
wielkości mierzonej
y
w danej metodzie od
stężenia
oznaczanego
składnika
c = x
(lub od prostej funkcji
stężenia,
np. jego
odwrotności lub logarytmu)
jest
sporządzany na podstawie analizy próbek (lub roztworów)
wzorcowych (o znanej
zawartości substancji oznaczanej)
umożliwia oznaczenie nieznanego stężenia danego składnika
w
próbkach o podobnym składzie, co próbki wzorcowe
po oznaczeniu
wielkości mierzonej w tych samych warunkach
pomiarowych i z
użyciem tego samego aparatu, co dla próbek
wzorcowych, z wykresu odczytuje
się nieznane wcześniej
stężenie
nieznane
stężenie badanego roztworu można również obliczyć
wstawiając wartość wielkości mierzonej do równania funkcji
znalezionego
metodą regresji.
36
Przykład:
•
wykonuje
się pomiary absorbancji A dla serii roztworów
wzorcowych monosalicylanu
żelaza (III) o znanych stężeniach c
•
następnie sporządza się wykres wzorcowy zależności A = f(c)
•
po zmierzeniu absorbancji roztworu o nieznanym
stężeniu,
korzystając z wykresu wzorcowego, odczytuje się jego stężenie.
Stężenie substancji w roztworze
można
również
znaleźć
korzystając
z
równania
matematycznego
opisującego
daną zależność
10
37
Analogiczne zastosowanie analityczne
znalazły wykresy w
ćwiczeniach:
•
2
–2a
– zależność współczynnika lepkości roztworów
gliceryny od
stężenia,
•
2
–3
– zależność współczynnika załamania światła od
zawartości alkoholu etylowego.
38
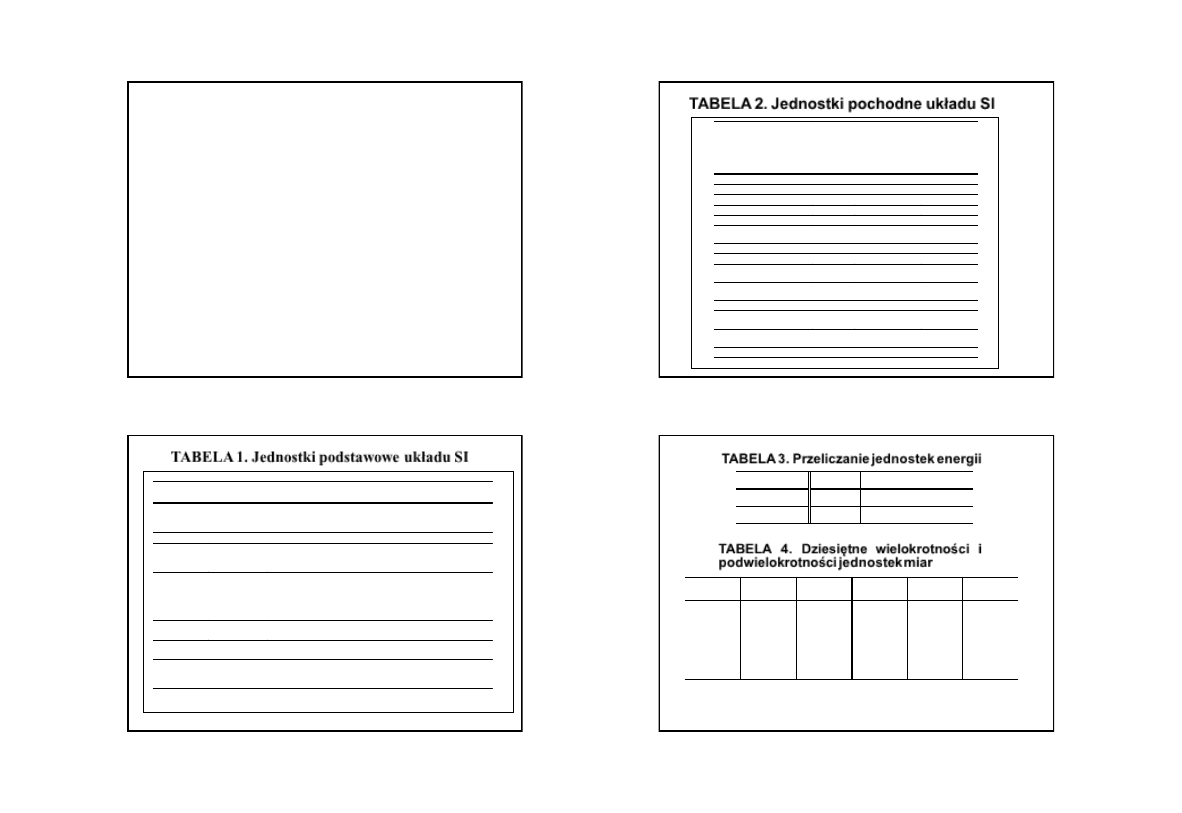
TABELA 1. Jednostki podstawowe układu SI
Wielkość
Nazwa i symbol
jednostki
Definicja
Długość
metr [m]
Metr jest to długość równa 1 650 763,73 długości fali w
promieniowania odpowiadającego przejściu między poziomami 2p
10
a
5d
5
atomu
86
Kr (kryptonu 86)
Masa
kilogram [kg]
Wzorzec
Czas
sekunda [s]
Sekunda jest to czas równy 992 631 770 okresów promieniowania
odpowiadającego przejściu między dwoma nadsubtelnymi poziomami
stanu podstawowego atomu
133
Cs (cezu 133)
Prąd
elektryczny
(natężenie
prądu
elektrycznego)
amper [A]
Amper jest to taki prąd stały, który płynąc przez dwa równolegle
przewody prostoliniowe o nieskończonej długości i znikomo małym
kołowym przekroju poprzecznym, umieszczone w próżni w odległości
jednego metra jeden od drugiego, wywoła między tymi przewodami siłę
2 · 10
–7
niutona na każdy metr długości.
Temperatura
kelwin [K]
Kelwin jest to 1/273,16 temperatury termodynamicznej punktu
potrójnego wody.
Liczność
materii
mol [mol]
Mol jest to ilość substancji składająca się z tylu elementów materii, ile
jest atomów w 0,012 kg węgla
12
C.
Światłość
kandela [cd]
Kandela jest to światłość jaką ma w kierunku prostopadłym pole
substancji doskonale czarnej o powierzchni 1/600 000 m
2
w
temperaturze krzepnięcia platyny pod ciśnieniem 101 325 Pa.
39
TABELA 2. Jednostki pochodne
układu SI
Wielkość
Nazwa i
symbol
jednostki
Relacja między
podstawowymi
jednostkami
układu SI
Relacje
między
innymi
jednostkami
pochodnymi
układu SI
Masa molowa
[M]
kg/mol
Stężenie molowe
[c]
mol/m
3
Objętość molowa
[V]
m
3
/mol
Molalność
[m]
mol/kg
Siła
niuton [N] kg ·m/s
2
Ciśnienie
paskal
[Pa]
kg/(m
·
s
2
)
N/m
2
Energia, praca, ciepło
dżul [J]
kg
· m
2
/s
2
N
·
m
Moc, strumień energii
wat [W]
kg
·
m
2
/s
3
J/s
Ładunek elektryczny
kulomb
[C]
A
· s
Potencjał i napięcie
elektryczne
wolt [V]
kg
·m
2
/(A
· s
3
)
W/A
Opór elektryczny
om [
Ω]
kg
·
m
2
/(A
2
·s
3
)
V/A
Przewodność
elektryczna
simens
[S]
A
2
·
s
3
/(kg
· m
2
)
A/V
Napięcie
powierzchniowe
kg/s
2
N/m
Lepkość dynamiczna
kg/(m
·
s)
Pa
·
s
40
TABELA 3. Przeliczanie jednostek energii
Jednostka
J
kaloria
Dżul [J]
1
2,39 ·10
–1
Kaloria [cal] 4,19
1
TABELA 4.
Dziesiętne wielokrotności i
podwielokrotności jednostek miar
Przedrostek Oznaczenie
Mnożnik
Przedrostek Oznaczenie
Mnożnik
mega
kilo
hekto
deka
M
k
h
da
10
6
10
3
10
2
10
1
decy
centy
mili
mikro
nano
piko
d
c
m
μ
n
p
10
–1
10
–2
10
–3
10
–6
10
–9
10
–12
11
41
TABELA 5.
Stałe fizykochemiczne
Liczba Avogadra
N
A
= 6,0220943 ·10
23
mol
–1
Stała Boltzmanna
k = 1,35805 [J/K ]
Uniwersalna stała gazowa
R = 8,31433 ± 0,00044
[J/(K·mol)]
Prędkość światła w próżni
c = 2,99792 ·10
8
[m/s] ≈ 3 ·10
8
[m/s]
Stała Plancka
h = 6,6256 ·10
–34
[J·s]
Stała Faradaya
F = 96486 ± 0,31 [C/mol] ≈ 96
500 [C/mol]
Ładunek elektronu
e = 1,6021733 · 10
–19
[C]
Stała dielektryczna próżni
= 8,85418782 ·10
–12
[C
2
/(J·
m)]
Przyspieszenie ziemskie
g = 9,806 [m/s
2
]
Objętość molowa gazu
doskonałego w war. normalnych
(101 325 Pa, 273,15 K)
22,41383 ·10
–3
[m
3
/mol] (22,4
dm
3
/mol)
Objętość molowa gazu
doskonałego w war.
standardowych (101 325 Pa, 298
24,4· 10
–3
[m
3
/mol] (24,4
dm
3
/mol)
42
Przykład 1. Wyraź 15 dm w: a) metrach, b)
centymetrach i c) milimetrach.
Wykorzystujemy współczynniki przeliczeniowe (w). W związku z
tym, że
b)
1 dm = 10
–1
m, 1 cm = 10
–2
m , 1 dm = 10 cm
w = 10
1
cm/dm ,
15 dm = 15 dm · 10
1
cm/ dm = 150 cm
Rozwiązanie:
a)
1 dm = 10
–1
m, współczynnik przeliczeniowy
w
= 10
–1
m/dm
,
stąd: 15 dm·10
–1
m/dm = 1,5 m
c)
1 dm = 10
–1
m, 1 mm = 10
–3
m,
w = 10
2
mm/dm
15 dm = 15 dm · 10
2
mm/dm = 1500 mm
43
Przykład
2.
Długość
promieniowania
absorbowanego przez
roztwór wynosi 300 nm.
Wyraź ją w: a) m, b) pm.
Przedrostek nano (n) wiąże się z mnożnikiem jednostki miary
wynoszącym 10
–9
m.
W związku z tym:
b)
3·10
–7
m · 10
12
pm/m = 3 ·10
5
pm.
a)
300 nm ·10
–9
m/nm = 3·10
–7
m,
Rozwiązanie:
44
Przykład 3. Wyraź objętość: a) 30 dm
3
w m
3
, b)
1500 cm
3
w m
3
i dm
3
, c) 2000 mm
3
w cm
3
i dm
3
.
Rozwiązanie:
c)
1 mm
3
= 10
–3
cm
3
,
2000 mm
3
·10
–3
cm
3
/mm
3
= 2 cm
3
1 mm
3
= (10
–2
dm)
3
= 10
–6
dm
3
,
2000 mm
3
·10
–6
dm
3
/mm
3
= 2·10
–3
dm
3
a)
1 dm
3
= 10
–3
m
3
30 dm
3
·10
–3
m
3
/dm
3
= 3,0·10
–2
m
3
b)
1 cm
3
= 10
–6
m
3
1500 cm
3
·10
–6
m
3
/cm
3
= 1,5·10
–3
m
3
1 cm
3
= (10
–1
dm)
3
= 10
–3
dm
3
1500 cm
3
·10
–3
dm
3
/cm
3
= 1,5·10
–1
dm
3
12
45
Przykład 4. Średnica pewnej cząstki elementarnej o
kształcie w przybliżeniu kulistym wynosi 2,20 nm. Oblicz:
a) jej
powierzchnię w nm
2
i m
2
oraz b)
objętość w nm
3
i m
3
.
Rozwiązanie:
gdzie r – promień kuli
2r = 2,20, r = 1,10 nm = 1,10·10
–9
m
S = 4 · 3,14 (1,10 nm)
2
= 13,82 nm
2
1 nm
2
= (10
–9
m)
2
= 10
–18
m
2
S = 13,82 nm
2
·10
–18
m
2
/nm
2
= 1,382·10
–17
m
2
2
r
4
S
Wstawiając dane otrzymujemy:
V = 4/3 · 3,14 (1,10 nm)
3
= 5,57 nm
3
1 nm
3
= (10
–9
m)
3
= 10
–27
m
3
V = 5,57 nm
3
·10
–27
m
3
/nm
3
= 5,57·10
–27
m
3
3
r
3
4
V
b)
Objętość kuli V wyraża wzór:
a)
Powierzchnię kuli S wyraża wzór:
46
Przykład 5. Objętość molowa gazu doskonałego w
warunkach normalnych (pod
ciśnieniem 101 325 Pa i
w temperaturze 273,15 K) wynosi 0,02241 m
3
/mol. Ile
wynosi w dm
3
/mol?
1 m
3
= (10 dm)
3
= 10
3
dm
3
0,02241 m
3
/mol·10
3
dm
3
/m
3
= 22,41 dm
3
/mol
Rozwiązanie:
47
Przykład 6. Wyraź: a) 780 g w kilogramach i tonach, b)
500 mg w gramach i kilogramach, c) 25 kg w gramach
i miligramach.
Rozwiązanie:
c)
1 g = 10
–3
kg, 1 kg = 10
3
g
25 kg · 10
3
g/kg = 25·10
3
g = 2,5·10
4
g
1 mg = 10
–6
kg, 1 kg = 10
6
mg
a)
1 g = 10
–3
kg, 780 g·10
–3
kg/g = 0,780 kg
1 tona = 10
3
kg = 10
3
kg·10
3
g/kg =10
6
g
1 g = 10
–6
t
780 g·10
–6
t/g = 7,80·10
–4
t
b)
1 mg = 10
–6
kg
500 mg·10
–6
kg/mg = 5·10
–4
kg
48
Przykład 7. Oblicz gęstość benzenu w kg/m
3
,
jeżeli 200
cm
3
tego rozpuszczalnika
waży 174,74 g.
Rozwiązanie:
d
benzenu
= 174,74 g / 200 cm
3
= 0,8737 g/cm
3
1g = 10
–3
kg, 1 cm
3
= 10
–6
m
3
0,8737 g/cm
3
= (0,8737 g·10
–3
kg /g): (1 cm
3
·10
–6
m
3
/cm
3
) =
0,8737·10
–3
·10
6
kg/m
3
= 873,7 kg/m
3
V
m
d
Korzystamy ze wzoru na gęstość:
13
49
Przykład 8. 0,1 mola HCl waży 3,65 g. Oblicz masę
molową HCl w kg/mol.
Wstawiamy dane do przekształconego wzoru:
M = m / n = 3,65 g : 0,1 mola = 36,5 g/mol
1 g = 10
–3
kg
M = 36,5 g/mol·10
–3
kg/g = 36,5·10
–3
kg/mol
Rozwiązanie:
Liczba moli
n
określona jest wzorem:
n = m/M
50
Przykład 9. W 100 cm
3
alkoholu etylowego o
gęstości d = 0,7851 g/cm
3
rozpuszczono 1,54 g
jodu. Oblicz c
p
roztworu.
Rozwiązanie:
Obliczamy masę alkoholu etylowego m
r
:
m
r
= d · V = 100 cm
3
· 0,7851 g/cm
3
= 78,51 g
Masa roztworu m
R
= 78,41 + 1,54 = 80,05 g
c
p
= (1,54 g : 80,05 g)·100 % = 1,9 %
100%
R
m
s
m
p
c
r
s
R
m
m
m
m
s
– masa substancji, m
r
- masa rozpuszczalnika, m
R
- masa roztworu
51
Przykład 10. Wyraź w molach/m
3
następujące stężenia
roztworów: a) 0,05 mol/dm
3
, b) 5 mmoli/cm
3
.
Rozwiązanie:
b)
1 mmol = 10
–3
mola
1 cm
3
= 10
–6
m
3
(5 mmoli·10
–3
mola/mmol): (1 cm
3
·10
–6
m
3
/cm
3
)
= 5·10
–3
·10
6
mol/m
3
= 5·10
3
mol/m
3
R
s
m
V
n
c
a)
1 dm
3
= 10
–3
m
3
0,05 mol/dm
3
= 0,05 mol : (1dm
3
·10
–3
m
3
/dm
3
) =
0,05·10
3
mol/dm
3
= 50 moli/dm
3
52
Przykład 11. Na zmiareczkowanie 20 cm
3
roztworu NaOH
zużyto 25 cm
3
0,2 molowego roztworu H
2
SO
4
. Oblicz miano
roztworu NaOH. Masa molowa NaOH wynosi 40 g/mol.
otrzymujemy:
T = (0,5 mol/dm
3
·40 g/mol ) : 1000 cm
3
/ dm
3
= 0,02 g/cm
3
1
2
4
2
SO
H
NaOH
n
n
1
2
4
2
SO
H
m
NaOH
m
)
v
c
(
)
v
c
(
1000
s
m
M
c
T
Rozwiązanie:
2 NaOH + H
2
SO
4
Na
2
SO
4
+ H
2
O
W związku z tym, że n = C
m
· v
Obliczamy c
m
NaOH wstawiając dane do przekształconego wzoru:
c
m
NaOH = (2·0,2·0,025) : 0,020 = 0,5 mol/dm
3
Stosując wzór na miano roztworu
Z równania reakcji:
wynika, że stosunek liczby moli
14
53
Siłę
definiuje
się jako iloczyn masy i przyspieszenia.
Jednostką siły jest
niuton N
.
1 niuton jest to
siła, która masie 1 kg nadaje
przyspieszenie 1 m/s
2
:
1 N = 1
kg·1 m/s
2
= 1
kg·m/s
2
Ciśnienie
definiuje
się jako iloraz siły działającej
prostopadle i
równomiernie na daną powierzchnię przez
pole tej powierzchni. Jednostka
ciśnienia –
paskal
należy
do jednostek pochodnych
układu SI. Liczbowo 1 paskal
równy jest sile jednego niutona działającej prostopadle na
płaską powierzchnię 1 m
2
.
1 Pa = 1 N/m
2
= 1 kg/(m·s
2
)
54
1 kilopaskal = 1kPa = 1000 Pa = 10
3
Pa,
1 megapaskal = 1 MPa = 10
6
Pa.
•
atmosfera fizyczna, atm
– 1 atm równa jest ciśnieniu słupa
rtęci o wysokości 76 cm, gęstości 13,5951 g/cm
3
(w
temperaturze
273
K)
pod
działaniem normalnego
przyspieszenia ziemskiego,
•
milimetr
słupa rtęci, mm
Hg
, tor Tr
– 1 mm
Hg
= 1Tr = 1/760
atm, 1 atm = 760 mm
Hg
.
Ciśnieniu 101 325 Pa odpowiada 760 mm
Hg
czyli 1 atm.
Jednostkami
ciśnienia nie należącymi do układu SI, a dość
często stosowanymi są:
Jednostką wielokrotną jest
1 hektopaskal = 1 hPa = 10
2
Pa
.
Jednostkami wielokrotnymi
paskala
najczęściej stosowanymi są:
55
Przykład 12. Ciśnienie atmosferyczne w warunkach
standardowych wynosi 101 325 Pa.
Wyraź tę wartość
w hPa.
Rozwiązanie:
1 hPa = 10
2
Pa 1 Pa = 10
–2
hPa
101325 Pa · 10
–2
hPa/Pa = 1013,25 hPa
Przykład 13. Wyraź ciśnienie 10 atmosfer w MPa.
1 MPa = 10
6
Pa, 1 Pa = 10
–6
MPa
10 atm = 10 atm·101 325 Pa/atm = 1 013 250 Pa
1 013 250 Pa·10
–6
MPa/Pa = 1,013250 MPa
Rozwiązanie:
56
1 watogodzina = 1
W·h = 3600 W·s = 3600 J.
Jednostką
pracy
,
energii
oraz
ilości ciepła
jest
dżul
(
J
). 1
dżul jest pracą wykonaną przez siłę
równą 1 niutonowi na drodze 1 metra w kierunku
działania siły:
1 dżul = 1 J = 1 N·1 m = 1 N·m = 1 Pa·m
3
=
1 watosekunda = 1 W·s = 1 kg·m
2
/s
2
Jednostkami wielokrotnymi są:
1 kilodżul = 1kJ = 10
3
J
oraz nie należąca do układu SI jednostka:
15
57
• Kaloria piętnastostopniowa
jest
ilością energii
dostarczanej na
sposób ciepła potrzebną do
ogrzania 1 g wody od 14,5 do 15,5
o
C pod
ciśnieniem 101 325 Pa.
1 cal15 = 4,1855 J.
• Kaloria międzynarodowa
: 1 cal
int
= 4,1868 J
• Kaloria termochemiczna
– cal stosowana w
termochemii i termodynamice chemicznej:
1 cal = 4,1840 J.
Jednostką wielokrotną jest kilokaloria kcal:
1 kcal = 1000 cal = 4184,0 J = 4,1840 kJ.
Jednostką ilości energii nie należącą do układu SI, ale
znajdującą szerokie zastosowanie jest
kaloria
– cal,
stosowana w kilku odmianach.
58
Ciepło parowania wody w cal/mol wynosi:
0,5383 cal/g·18 g/mol = 9,6894 cal/mol
1 cal = 4,1868 J
9,6894 cal/mol·4,1868 J/cal = 40,5675 J/mol
1 J = 10
–3
kJ
40,5675 J/mol·10
–3
kJ/J = 0,0405675 kJ/mol
Przykład 14. Ciepło parowania wody w
temperaturze 373,15 K wynosi 0,5383 cal/g.
Wyraź tę wartość w dżulach i kilodżulach na
mol. Masa molowa wody 18 g/mol.
Rozwiązanie:
59
Temperatura
jest
wielkością skalarną określoną w
każdym punkcie ciała lub układu, której średnia wartość
jest
miarą energii wewnętrznej całego ciała lub układu.
•
W przypadku
skali Celsjusza
– skali stustopniowej jako
ciecz
termometryczną zastosowano rtęć, której
rozszerzalność zmienia się wraz z temperaturą.
Obecnie w powszechnym
użyciu są trzy
skale
temperatury
: Celsjusza, Fahrenheita
(głównie poza
Europą – USA, Kanada) i Kelvina.
Jednostka temperatury
wiąże się ściśle ze sposobem
ustalenia
skali
temperatury
w
odniesieniu
do
temperatury odpowiednich
wzorców.
Jako punkty skrajne w tej skali
przyjęto temperaturę
krzepnięcia i wrzenia czystej wody (0
o
C i 100
o
C
odpowiednio).
Stopień Celsjusza 1
o
C stanowi
jedną
setną wymienionego przedziału temperatury.
60
W wyniku ekstrapolacji
objętości lub ciśnienia gazu
doskonałego do wartości zerowej, otrzymano punkt
zerowy skali
bezwzględnej, tzw.
zero
bezwzględne
(absolutne),
powiązane z temperaturą w skali Celsjusza
zależnością:
• Skala bezwzględna temperatury
, zwana
skalą
Kelvina
, oparta
została na rozważaniach nad
rozszerzalnością gazu doskonałego.
T (K) = t (
o
C) + 273,15
16
61
•
Ze
skalą
Kelvina
związana
jest
bezpośrednio
termodynamiczna skala temperatur
oparta na temperaturze
tzw. punktu
potrójnego czystej wody (punktu współistnienia
obok siebie w stanie
równowagi: wody ciekłej, jej pary
nasyconej i lodu; parametry tego punktu: temperatura T =
273,16 K, czemu odpowiada 0,01
o
C i
ciśnienie p = 610,5 Pa).
Jednostką podstawową temperatury w układzie SI jest
kelwin
K
, definiowany jako jednostka temperatury termodynamicznej:
Wartość stopnia w skali Celsjusza i w skali Kelvina jest jednakowa:
1
o
C = 1 K, a temperatura zera
bezwzględnego (absolutnego) jest
przesunięta w stosunku do zera w skali Celsjusza o 273,15
o
C,
czyli 0 K odpowiada
– 273,15
o
C lub 0
o
C odpowiada 273,15 K.
1 K = 1/273,16
części temperatury termodynamicznej
punktu
potrójnego wody
.
62
Przykład 15. Wyraź temperaturę: a) 20 K, b) 25 K, c)
200 K w skali Celsjusza.
T (K) = t (
o
C) + 273,15
W naszym zadaniu: T = –183 + 273,15 = 90,15 K
Przykład 16. Temperatura wrzenia tlenu pod
ciśnieniem standardowym wynosi –183
o
C. Ile
wynosi w skali
bezwzględnej?
Rozwiązanie:
Korzystamy ze wzoru:
T (K) = t (
o
C) + 273,15
a)
20 K odpowiada t = 20 – 273,15 = –253,15
o
C
b)
25 K odpowiada t = 25 – 273,15 = –248,15
o
C
c)
200 K odpowiada t = 200 – 273,15 = –73,15
o
C
Rozwiązanie:
63
Do jednostek podstawowych
układu SI należy jednostka
natężenia prądu elektrycznego
–
amper
(
A
).
Jednostkami podwielokrotnymi
są:
1 mA = 10
–3
A,
1
µA = 10
–6
A.
t
Q
I
s
C
A
Q = I
.
t
Jednostką pochodną jest
kulomb C
– jednostka
ładunku elektrycznego.
Jednostką wielokrotną jest amperogodzina A · h :
1 A · h = 3600 A·s = 3600 C.
1 kulomb
jest to
ładunek elektryczny przepływający
przez
powierzchnię w czasie 1 sekundy, gdy natężenie
prądu płynącego przez tę powierzchnię wynosi 1 A:
1 kulomb = 1 C = 1
A·s (amperosekunda)
.
64
Z definicji stałej Faradaya wynika, że 1 molowi elektronów odpowiada
ładunek 96 486 C. Z kolei liczba Avogadra, czyli liczba cząstek w
jednym molu wynosi 6,022·10
23
. Oznaczając ładunek pojedynczego
elektronu jako q
e
obliczamy dalej:
Przykład 18. Elektrolizę prowadzono prądem o natężeniu
0,1 A w
ciągu 0,5 godziny. Oblicz jaki ładunek płynął w
ciągu 1 sekundy.
Przykład 17. Oblicz ile wynosi ładunek elektryczny
1 elektronu.
Rozwiązanie:
Q = I
.
t =0,1 A·0,5 h·3600 s/h = 180 C
Rozwiązanie:
q
e
= 96 486 C/mol : (6,022·10
23
) elektronów /mol =
1,6022·10
–19
C/ elektron.
17
65
Jednostką
potencjału
elektrycznego
,
napięcia
elektrycznego U
i
siły elektromotorycznej
E
SEM
jest
wolt V
.
Jednostką
oporu elektrycznego
jest
om
:
1 om = 1 = 1V/1A = 1 kg
· m
2
/(s
3
· A
2
)
Jednostkami podwielokrotnymi są:
1 milisimens = 1 mS = 10
–3
S,
1 mikrosimens = 1 µS = 10
–6
S.
Odwrotnością
oporu
elektrycznego
R
jest
przewodnictwo
elektryczne
(
przewodność
elektryczna
).
Jednostką tej wielkości jest
simens S
:
Wymiarem wolta jest:
1 wolt = 1 V = 1 W/1A = 1 kg·m
2
/(s
3
·A).
Jednostką podwielokrotną jest miliwolt: 1 mV = 10
–3
V.
1 simens = 1 S = 1/
= 1 s
3
· A
2
/( kg·m
2
).
66
b)
1 µS = 10
–6
S
150 µS · 10
–6
S/µS = 1,5·10
–4
S
R = 1 / (1,5 · 10
–4
S) = 0,66·10
4
= 6,6·10
3
R = 6,6 · 10
3
·10
–3
k
= 6,6 k
.
Przykład 19. Zmierzone przewodnictwo roztworu
wynosiło: a) 10 mS, b) 150 µS. Wyraź te wartości w
jednostce SI i oblicz
opór tego roztworu w omach i
kiloomach.
Rozwiązanie:
a)
1 mS = 10
–3
S
10 mS·10
–3
S/mS = 10
–2
S
W związku z tym, że R = 1/
, obliczamy
R = 1/10
–2
S = 10
2
i dalej R = 10
2
·10
–3
k
= 10
–1
k
67
• Lepkość dynamiczna
– definiuje się ją jako siły tarcia
występujące w cieczach podczas przesuwania się
jednych warstw cieczy
względem drugich.
Jednostką
lepkości
dynamicznej
jest
Pa
.
s
(
paskalosekunda
).
Jest liczbowo
równa sile przypadającej na jednostkę
powierzchni, potrzebnej do utrzymania jednostkowej
różnicy prędkości między warstwami cieczy odległymi od
siebie o
jednostkę długości.