2010-04-19

1

Hala stalowa bez transportu

Słup mimośrodowo ściskany

1

P R O J E K T O W A N I E

KONSTRUKCJE METALOWE

Konstrukcje metalowe – projektowanie

2

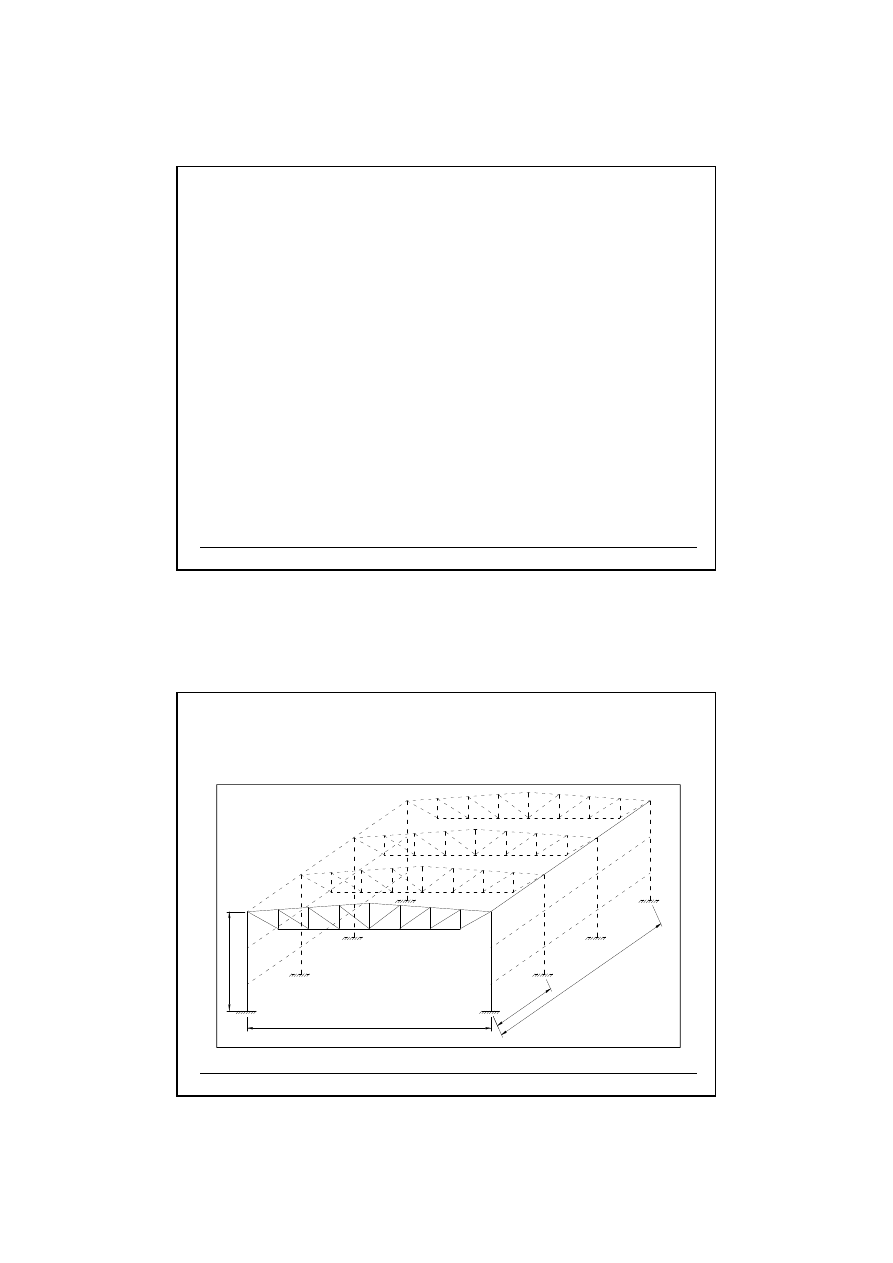
10.0. Wymiarowanie słupa.

L

H

n*a

a

10.1. Schemat statyczny głównego układu no

ś

nego hali.

2010-04-19

2

Konstrukcje metalowe – projektowanie

3

10.2. Wst

ę

pny dobór przekroju słupa

1. Najcz

ęś

ciej przyjmowane profile słupów mimo

ś

rodowo

ś

ciskanych:

Profile:

I

IPE

HEB
HEA

Konstrukcje metalowe – projektowanie

4

2. Parametry przekroju wst

ę

pnie dobranego

h =

b

f

=

t

f

=

t

w

=

R =

Przyjęto IPE …… ze stali ……… (S235JR lub S355J0)

I

X

=

I

y

=

W

pl,x

=

W

pl,y

=

W

el,x

=

W

el,y

=

i

X

=

i

y

=

f

d

=

2010-04-19

3

Konstrukcje metalowe – projektowanie

5

m

k

= ……….. [kN/mb]

γ

f

= 1,35 lub 0,85x1,35

≈

1,15

m

o

= ………...[kN/mb]

3. Zebranie obci

ąż

e

ń

. Ci

ęż

ar własny słupa.

Konstrukcje metalowe – projektowanie

6

10.3. Zestawienie ekstremalnych sił wewn

ę

trznych w słupie

1. Zestawienie sił w tabeli na podstawie oblicze

ń

statycznych:

nr pr

ę

ta

siła

normalna

siła tn

ą

ca

moment

zginaj

ą

cy

kombinacja

obci

ąż

e

ń

uwagi

N

Ed

[kN]

V

Ed

[kN]

M

Ed

[kNm]

1

N

Ed,max

V

Ed,odp

M

Ed,odp

np. komb 3

1

N

Ed,odp

V

Ed,odp

M

Ed,max

np. komb 6

2

N

Ed,odp

V

Ed,max

M

Ed,odp

np. komb 2

W tabeli zestawi

ć

warto

ś

ci obliczeniowe sił wewn

ę

trznych dla przekroju

słupa zlokalizowanego przy utwierdzeniu.

2010-04-19

4

Konstrukcje metalowe – projektowanie

7

10.4. Sprawdzenie klasy przekroju.

1. Klasa

ś

rodnika

dwuteownika.

Konstrukcje metalowe – projektowanie

8

10.4. Sprawdzenie klasy przekroju

2. Klasa półki dwuteownika.

3. Wniosek: Przekrój jest klasy ……

2010-04-19

5

Konstrukcje metalowe – projektowanie

9

10.5. No

ś

no

ś

ci przekroju słupa na

ś

cinanie

1. Warunek smukło

ś

ci

ś

cianki przy

ś

cinaniu

2. Wyznaczenie pola czynnego przy

ś

cinaniu – A

v

ε

⋅

<

72

t

h

w

w

(6.22)

Konstrukcje metalowe – projektowanie

10

2. No

ś

no

ś

ci przekroju na

ś

cinanie

3. Sprawdzenie warunków no

ś

no

ś

ci przekroju na

ś

cinanie.

(6.18)

(6.17)

Rd

,

c

Ed

V

V

≤

0

M

y

V

Rd

,

pl

Rd

,

c

3

f

A

V

V

γ

=

=

2010-04-19

6

Konstrukcje metalowe – projektowanie

11

4. Sprawdzenie warunków pomini

ę

cia wpływu

ś

cinania przy zginaniu

Wpływ

ś

cinania na no

ś

no

ść

przy zginaniu mo

ż

na pomija

ć

, je

ż

eli:

• przekrój jest stateczny przy

ś

cinaniu

• siła poprzeczna nie przekracza 50% no

ś

no

ś

ci plastycznej przekroju przy

ś

cinaniu.

W przeciwnym razie przyjmuje si

ę

zredukowan

ą

no

ś

no

ść

obliczeniow

ą

przekroju,

ustalon

ą

przy zało

ż

eniu,

ż

e w polu czynnym przy

ś

cinaniu wyst

ę

puje zredukowana

granica plastyczno

ś

ci:

2

,

2

1

Ed

pl Rd

V

V

ρ





⋅

=

−













y

'

y

f

)

1

(

f

⋅

ρ

−

=

gdzie:

(6.29)

Konstrukcje metalowe – projektowanie

12

10.6. No

ś

no

ś

ci przekroju słupa na

ś

ciskanie.

1. No

ś

no

ść

przekroju na

ś

ciskanie osiowe

0

M

y

Rd

,

pl

Rd

,

c

f

A

N

N

γ

⋅

=

=

- dla przekrojów klas 1, 2 i 3

(6.10)

2. Sprawdzenie warunków no

ś

no

ś

ci przekroju na

ś

ciskanie

Rd

,

c

Ed

N

N

≤

2010-04-19

7

Konstrukcje metalowe – projektowanie

13

3. Wpływ siły podłu

ż

nej na zginanie przekroju

Rd

,

pl

Ed

N

25

,

0

N

⋅

<

0

M

y

w

w

Ed

f

t

h

5

,

0

N

γ

⋅

⋅

⋅

<

Mo

ż

na pomin

ąć

wpływ siły podłu

ż

nej na no

ś

no

ś

ci plastyczn

ą

przekroju

przy zginaniu je

ż

eli:

(6.33)

(6.34)

Konstrukcje metalowe – projektowanie

14

10.7. Wyznaczenie no

ś

no

ś

ci przekroju słupa na zginanie.

1. No

ś

no

ść

na zginanie

0

M

y

pl

Rd

,

pl

Rd

,

c

f

W

M

M

γ

⋅

=

=

0

M

y

min

,

el

Rd

,

el

Rd

,

c

f

W

M

M

γ

⋅

=

=

- dla przekrojów klas 1 i 2

- dla przekrojów klas 3

(6.13)

(6.14)

2010-04-19

8

Konstrukcje metalowe – projektowanie

15

2. No

ś

no

ść

na zginanie z siła podłu

ż

n

ą

Rd

,

pl

f

Rd

,

pl

Ed

Rd

,

pl

Rd

,

y

,

N

Rd

,

c

M

A

t

b

2

A

5

,

0

1

N

N

1

M

M

M

≤













⋅

⋅

−

−















−

=

=

(6.36)

Je

ż

eli warunki 6.33 i 6.34 nie s

ą

spełnione jednocze

ś

nie no

ś

no

ść

przekroju

na zginanie wyznaczamy wg wzoru (dla dwuteowników walcowanych):

5

,

0

A

t

b

2

A

f

≤

⋅

⋅

−

Gdzie:

3. Sprawdzenie warunku no

ś

no

ś

ci przekroju na zginanie.

Rd

,

c

Ed

M

M

≤

Przekrój słupa sprawdzi

ć

dla N

ed i

M

Ed

z dwóch kombinacji – N

Ed,max

oraz M

Ed,max

Konstrukcje metalowe – projektowanie

16

No

ś

no

ść

(stateczno

ść

) elementów

ś

ciskanych i zginanych.

0

Rd

,

z

Ed

,

z

mz

Rd

,

y

LT

Ed

,

y

my

Rd

y

Ed

1

M

M

C

M

M

C

N

N

∆

−

≤

⋅

+

⋅

χ

⋅

+

⋅

χ

0

Rd

,

z

Ed

,

z

mz

Rd

,

y

LT

Ed

,

y

my

Rd

z

Ed

1

M

M

C

M

M

C

N

N

∆

−

≤

⋅

+

⋅

χ

⋅

+

⋅

χ

(NA. 20)

2010-04-19

9

Konstrukcje metalowe – projektowanie

17

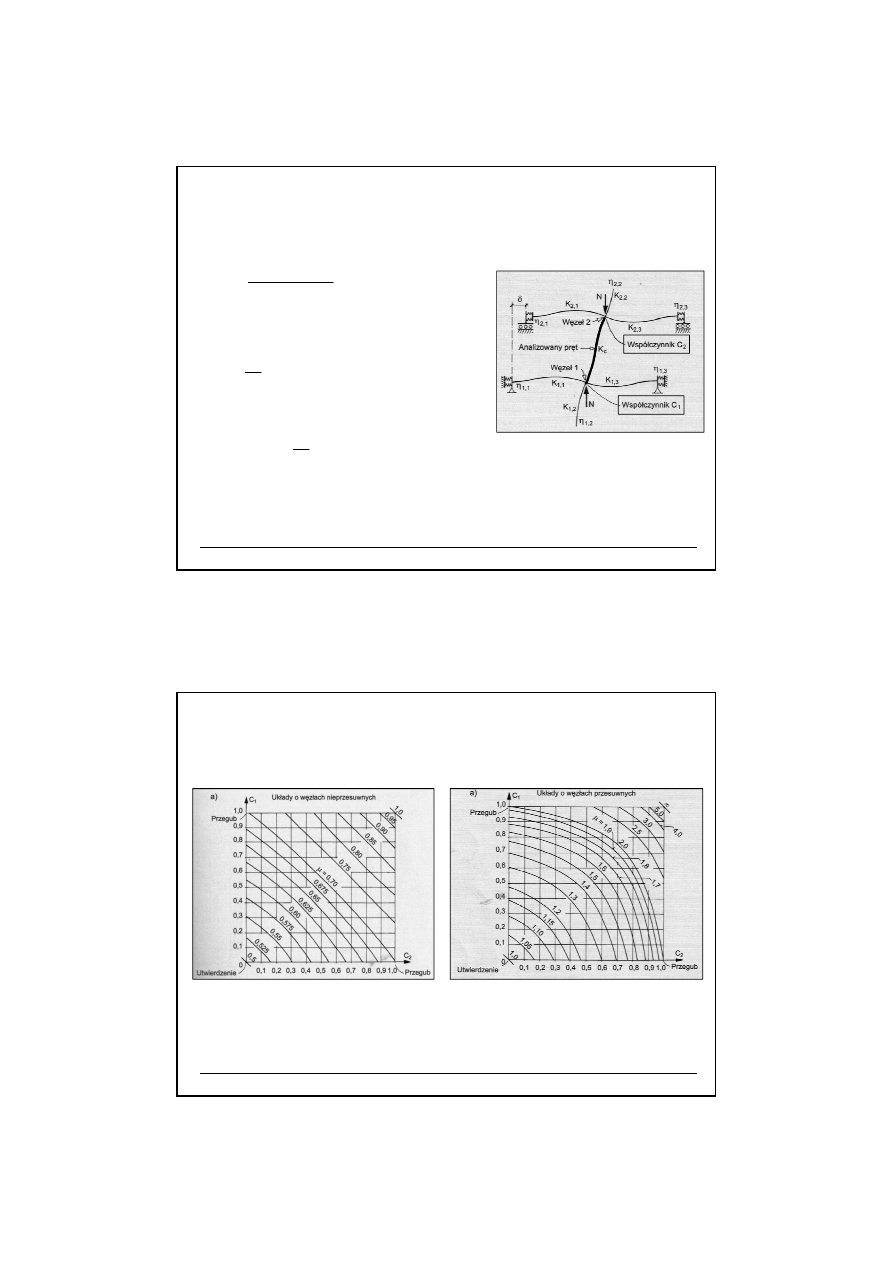
1. Współczynniki wyboczenia – stopie

ń

podatno

ś

ci w

ę

złów ramy

)

K

K

(

K

C

o

c

c

i

+

=

3

,

0

C

i

≥

lecz

h

I

K

c

c

=

∑













⋅

η

=

b

b

o

l

I

K

Ź

ródło:

A.Biegus „Stalowe budynki halowe”, Arkady 2003

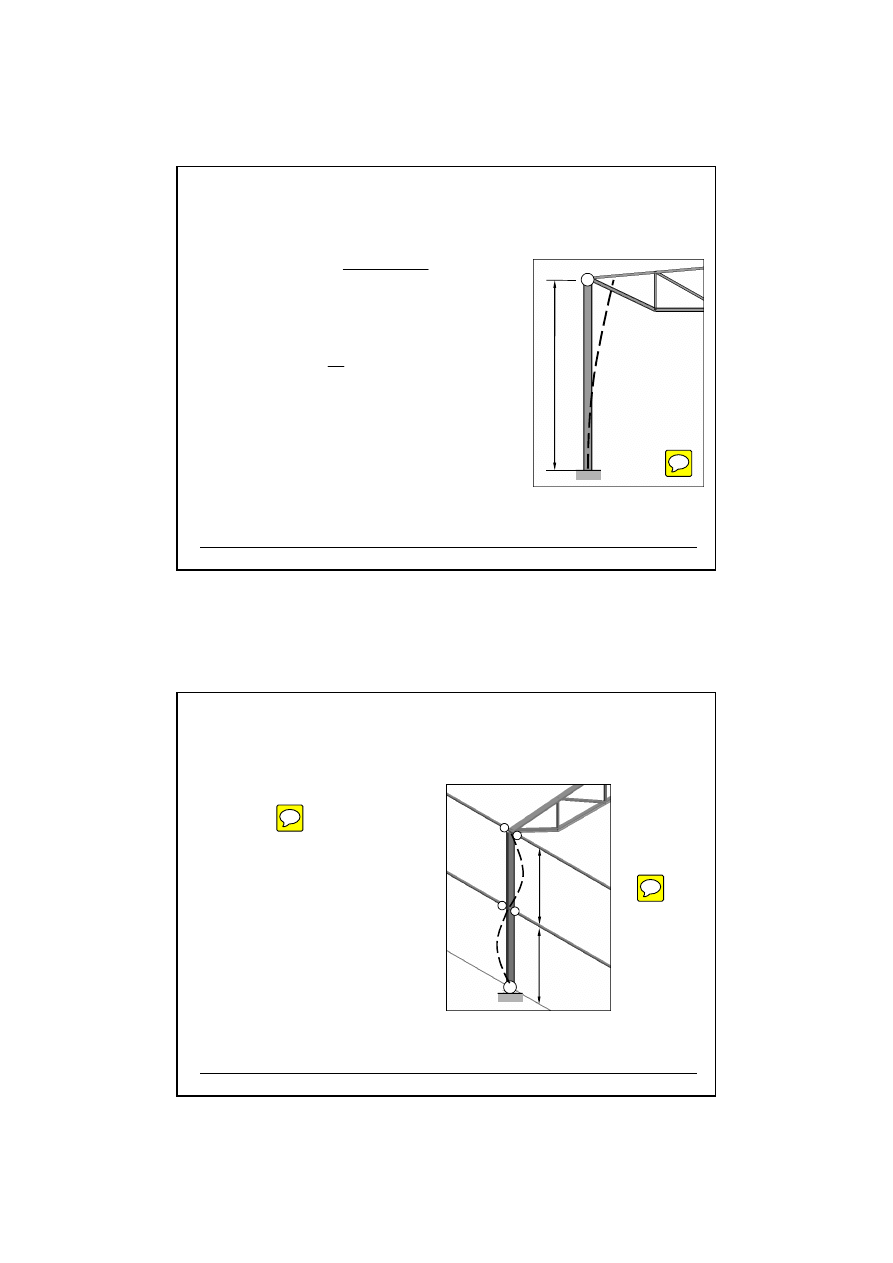
10.8. Wyznaczenie no

ś

no

ś

ci słupa na

ś

ciskanie i zginanie.

Konstrukcje metalowe – projektowanie

18

Nomogramy do okre

ś

lania współczynnika długo

ś

ci wyboczeniowej.

Ź

ródło:

A.Biegus „Stalowe budynki halowe”, Arkady 2003

2010-04-19

10

Konstrukcje metalowe – projektowanie

1. Współczynniki długo

ś

ci wyboczeniowej – płaszczyzna YZ

l

y

0

l

I

K

b

b

o

=













⋅

η

=

∑

- dla w

ę

zła górnego słupa

c

o

K

K

=

- dla sztywnej stopy słupa

1

C

1

=

⇒

5

,

0

C

2

=

⇒

)

K

K

(

K

C

o

c

c

i

+

=

19

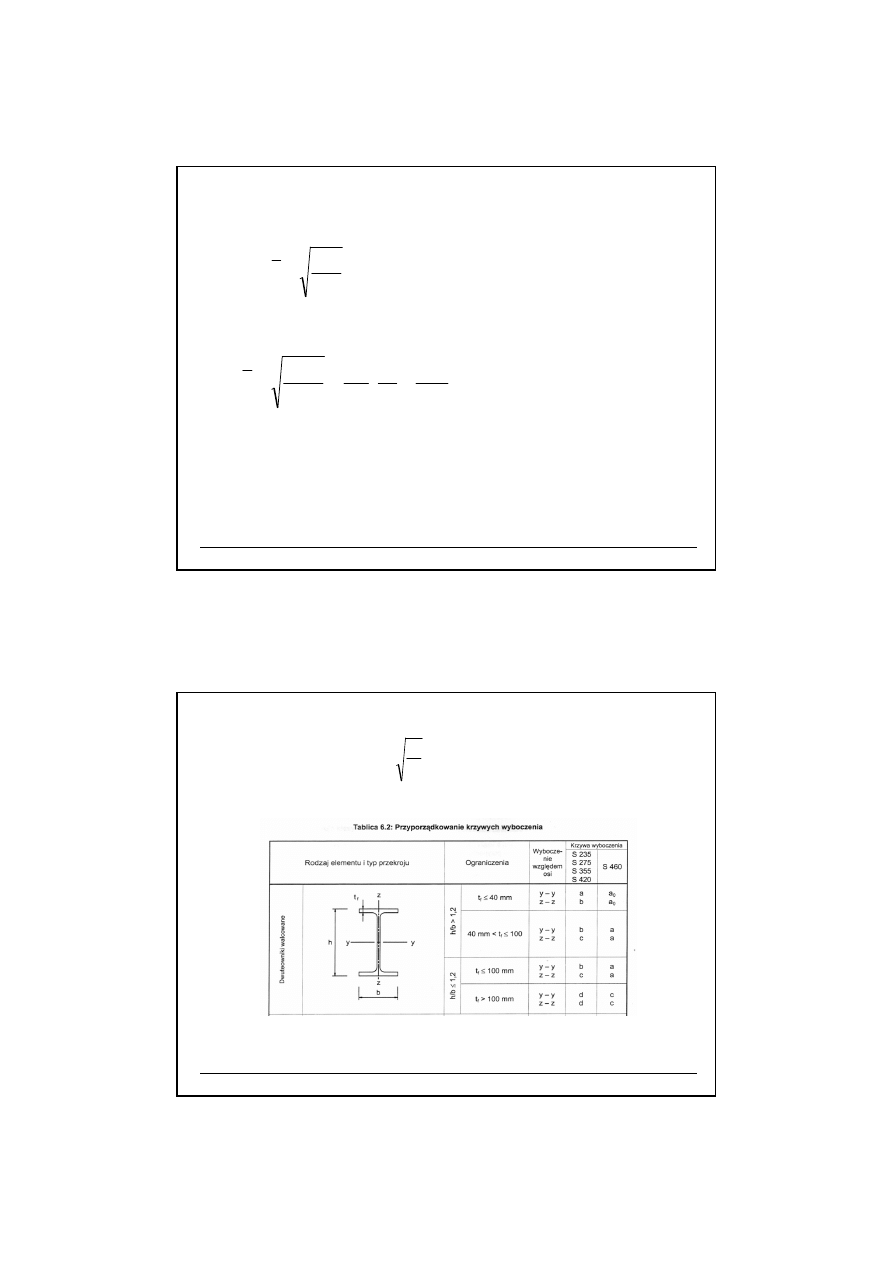
10.8.1. Współczynniki wyboczenia

- χ

z

i χ

y

Konstrukcje metalowe – projektowanie

2. Współczynniki długo

ś

ci wyboczeniowej – płaszczyzna XY

l

z1

l

z2

20

2010-04-19

11

Konstrukcje metalowe – projektowanie

21

3. Smukło

ść

wzgl

ę

dna przy wyboczeniu wg:

cr

y

N

Af

=

λ

(6.49)

4. Smukło

ś

ci wzgl

ę

dna przy wyboczeniu pr

ę

ta prostego :

(6.50)

dla przekrojów klas 1, 2, 3

1

1

cr

cr

y

i

l

1

i

L

N

f

A

λ

⋅

⋅

µ

=

λ

⋅

=

⋅

=

λ

dla przekrojów

klas 1, 2, 3

gdzie:

i

– promie

ń

bezwładno

ś

ci przekroju brutto wzgl

ę

dem odpowiedniej osi

L

cr

– długo

ść

wyboczeniowa w rozpatrywanej płaszczy

ź

nie wyboczenia

Konstrukcje metalowe – projektowanie

22

5. Smukło

ś

ci porównawcza :

ε

⋅

=

⋅

π

=

λ

9

,

93

f

E

y

1

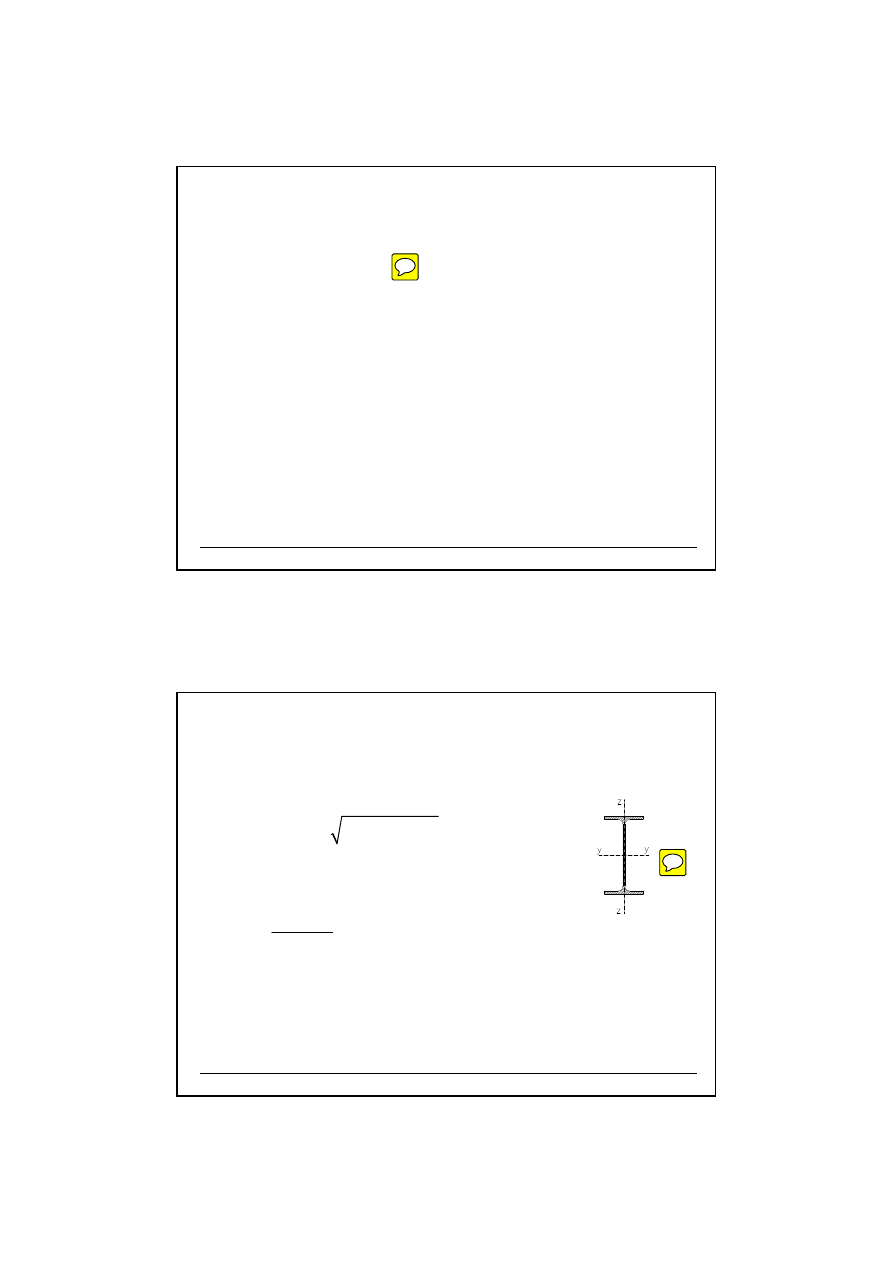
6. Krzywa wyboczenia:

2010-04-19

12

Warto

ść

współczynników wyboczenia

χ

z

i χ

y

mo

ż

na wyznaczy

ć

wg

Rysunku 6.4. EC 3-1-1

23

7. Współczynniki wyboczenia

χ

z

i χ

y

Konstrukcje metalowe – projektowanie

24

1. Moment krytyczny przy zwichrzeniu

(

)

2

2

cr

z

g

g

M

k N

c

0, 25 z

0, 5 z

= ⋅

⋅

+

⋅

−

⋅

gdzie:

- siła krytyczna przy wyboczeniu gi

ę

tnym

( )

2

z

2

z

l

J

E

N

⋅

µ

⋅

⋅

π

=

10.8.2. Współczynnik zwichrzenia

- χ

LT

2010-04-19

13

2

z

1

J

J h

4

ω

≈ ⋅ ⋅

(

)

3

3

T

f

f

w

w

1

J

2 b t

h

t

3

= ⋅ ⋅ ⋅ + ⋅

l – wysoko

ść

słupa,

z

g

– miejsce działania obci

ąż

enia (w przypadku obci

ąż

enia belki

momentem zginaj

ą

cym nale

ż

y przyj

ąć

z

g

=0)

k – współczynnik zale

ż

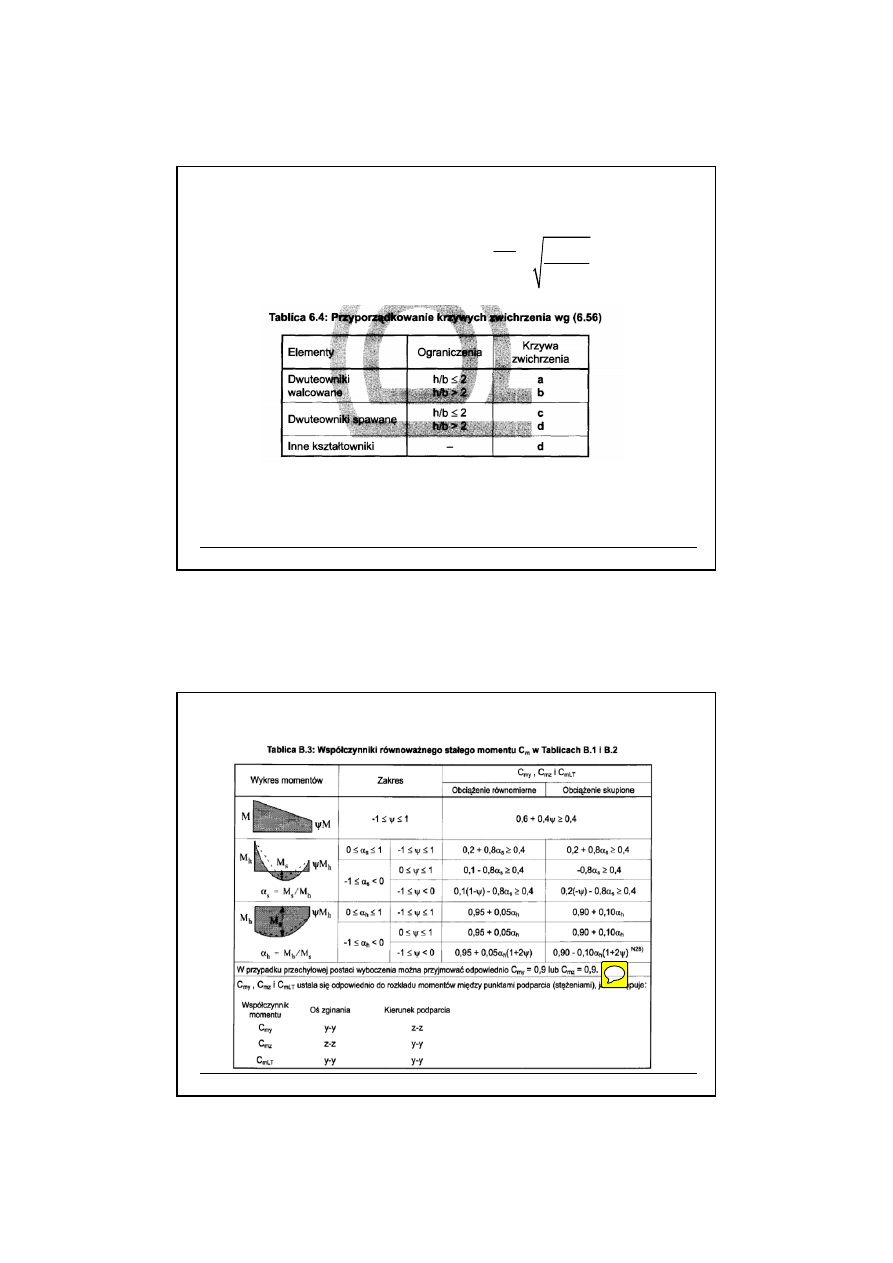
ny od rozkładu momentów (wg Tablicy 1)

2

2

T

z

J

0, 039 l

J

c

J

ω

+

⋅ ⋅

=

„+”

Konstrukcje metalowe – projektowanie

25

Ź

ródło:

Sz. Pałkowski, K. Popiołek „Zwichrzenie
belek stalowych w uj

ę

ciu PN-EN 1993-1-1”,

In

ż

ynieria i Budownictwo 6/2008.

Konstrukcje metalowe – projektowanie

26

Tablica 1

2010-04-19

14

Konstrukcje metalowe – projektowanie

27

2. Warto

ść

współczynnika zwichrzenia

y

y

LT

cr

W

f

M

λ

⋅

=

- smukło

ść

wzgl

ę

dna przy zwichrzeniu

(6.56)

Warto

ść

współczynnika zwichrzenia

χ

LT

mo

ż

na wyznaczy

ć

wg Rysunku 6.4.

EC 3-1-1

2010-04-19

28

Hala bez transportu - Cz. 1

10.8.3. Współczynnik momentu

-

C

my

2010-04-19

15

Składnik poprawkowy (oszacowanie maksymalnej redukcji)

2010-04-19

29

Hala bez transportu - Cz. 1

1

,

0

0

=

∆

- Przekroje klasy 1 i 2

- Przekroje klasy 3















−

+

=

∆

1

W

W

2

,

0

1

,

0

i

,

el

i

,

pl

i

,

0

10.8.4. Składnik poprawkowy

- ∆

0

(NA. 20)

Konstrukcje metalowe – projektowanie

30

10.8.5. No

ś

no

ść

(stateczno

ść

) słupa.

•

Stateczno

ść

słupa sprawdzi

ć

dla dwóch kombinacji – z N

Ed,max

oraz M

Ed,max

0

Rd

,

y

LT

Ed

,

y

my

Rd

y

Ed

1

M

M

C

N

N

∆

−

≤

⋅

χ

⋅

+

⋅

χ

0

Rd

,

y

LT

Ed

,

y

my

Rd

z

Ed

1

M

M

C

N

N

∆

−

≤

⋅

χ

⋅

+

⋅

χ

(NA. 20)

2010-04-19

16

Konstrukcje metalowe – projektowanie

31

10.9. Sprawdzenie przemieszczenia poziomego słupów (SGU).

Zgodnie z punktem 7.2.2 (1)B) nale

ż

y sprawdzi

ć

przemieszczenia poziome,

które wg zalece

ń

zał

ą

cznika krajowego (NA. 23) nie powinny przekroczy

ć

:

- w układach jednokondygnacyjnych :

150

H

w

max

≤

w

max

- okre

ś

li

ć

na podstawie oblicze

ń

statycznych wymiarowanego

przekroju słupa dla kombinacji od obci

ąż

e

ń

charakterystycznych.

Konstrukcje metalowe – projektowanie

32

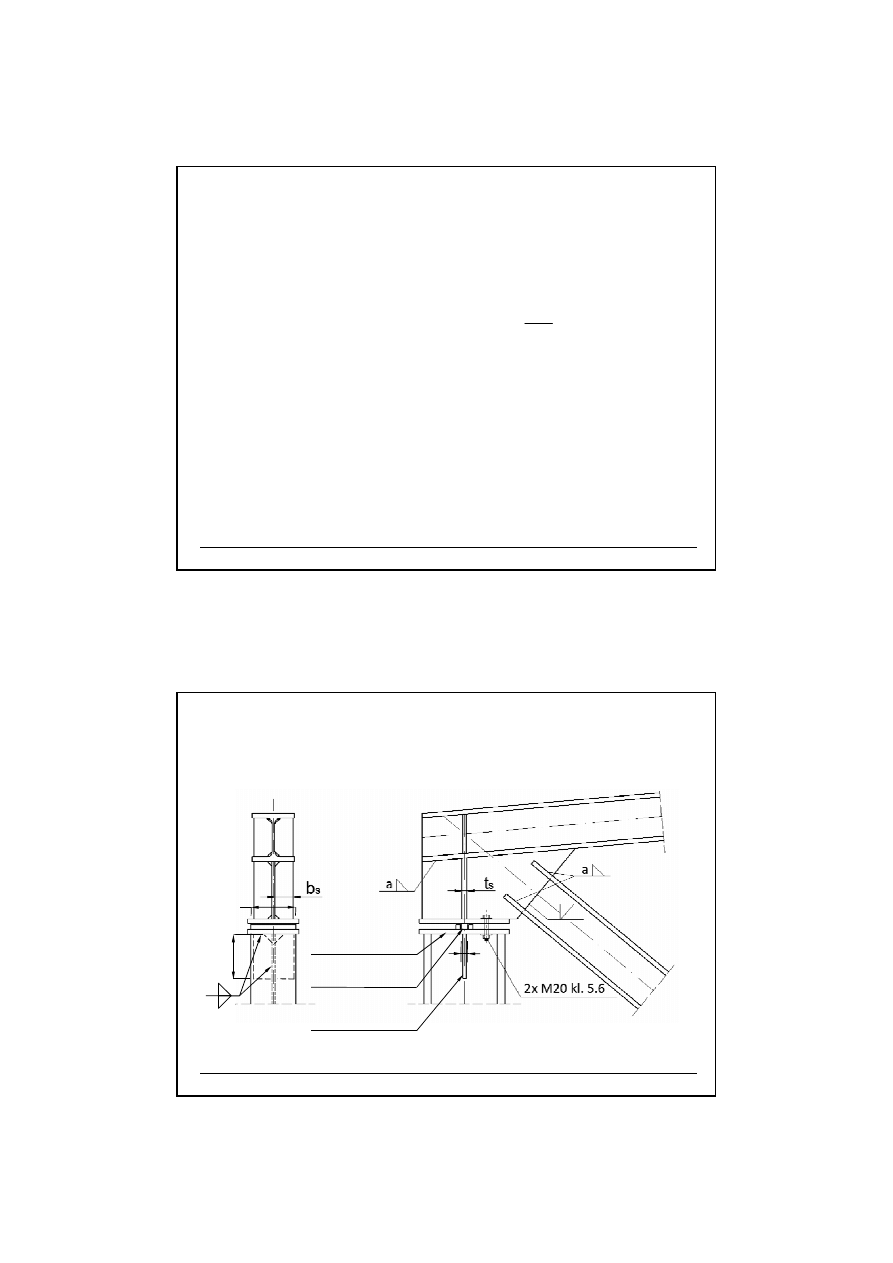
10.10. Głowica słupa.

1. Konstrukcja głowicy – typowe rozwi

ą

zania

Żebro głowicy

Blacha pozioma

Płytka centrująca

b

c

h

a

2010-04-19

17

Konstrukcje metalowe – projektowanie

33

2. Grubo

ść

blachy poziomej.

t

bl poziomej

> 12 mm

przyj

ę

to : t

bl poziomej

= 16 mm

3. Wymiary płytki centruj

ą

cej.

Grubo

ść

płytki centruj

ą

cej :

t

pc

> 20 mm

przyj

ę

to : t

pc poziomej

= 25 mm

s

b

2

b

≥

)

mm

20

;

t

min(

c

s

≥

Konstrukcje metalowe – projektowanie

34

4.

Ż

eberka głowicy słupa.

•

Szeroko

ść

ż

eberek sztywni

ą

cych przyj

ąć

tak

ą

sam

ą

jak szeroko

ść

ż

eber w

ę

zła podporowego wi

ą

zara.

•

Wysoko

ść

ż

eberek z uwagi na no

ś

no

ść

spoin pionowych:

•

Poziome spoiny pachwinowe przyj

ąć

takie same jak poziome spoiny

w w

ęź

le podporowym wi

ą

zara.

l

a

4

R

II

⋅

⋅

=

τ

2

M

w

u

II

f

3

γ

β

≤

τ

mm

20

l

h

+

=

Wymiary spoin „a” i „l” powinny spełnia

ć

warunki:

...

a

t

7

,

0

a

t

2

,

0

min

max

=

→

⋅

≤

≤

⋅

2010-04-19

18

Konstrukcje metalowe – projektowanie

35

5.

Ś

ruby do poł

ą

czenia z wi

ą

zarem

Przyj

ąć

konstrukcyjnie : > M20, M24 – klasy 5.6

Konstrukcje metalowe – projektowanie

36

Koniec oblicze

ń