PODSTAWY

METODY SYMBOLICZNEJ

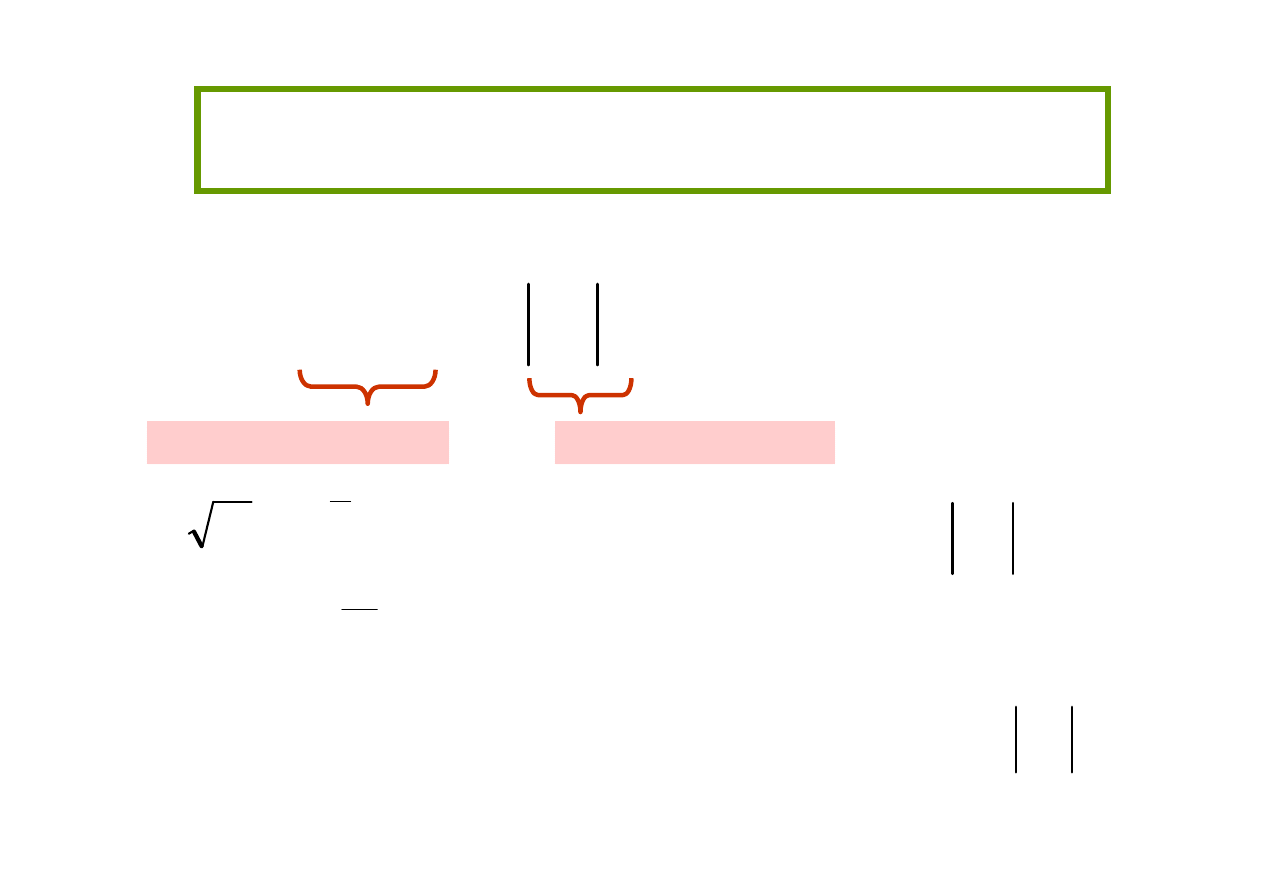
Podstawowe własno

ś

ci i działania na

liczbach zespolonych

ϕ

j

e

X

jb

a

x

=

+

=

Posta

ć

algebraiczna

Posta

ć

wykładnicza

2

j

e

1

-

j

π

=

=

ϕ

-j

e

j

X

b

a

x

=

−

=

∗

2

2

2

X

b

a

x

x

=

+

=

⋅

∗

2

j

-

e

j

-

π

=

liczba zespolona sprz

ęż

ona

z x

1

)

(

1

2

=

−

−

=

j

j

j

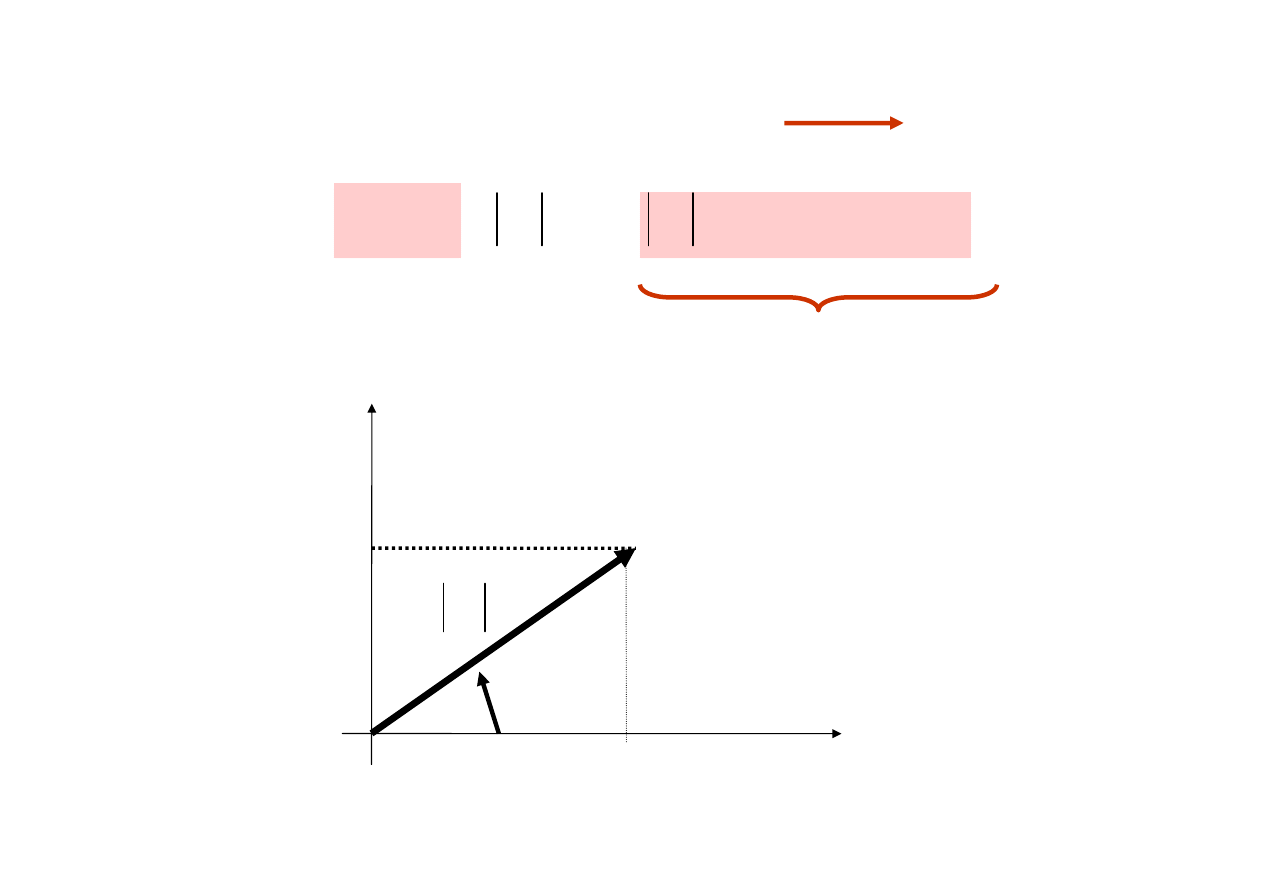
Wzór Eulera

ϕ

+

ϕ

=

ϕ

jsin

cos

e

j

to

Poniewa

ż

posta

ć

trygonometryczna

Re(X)

X

X

ϕ

[

]

ϕ

ϕ

ϕ

sin

cos

e

j

j

j

X

X

b

a

X

+

=

=

+

=

)

Im( X

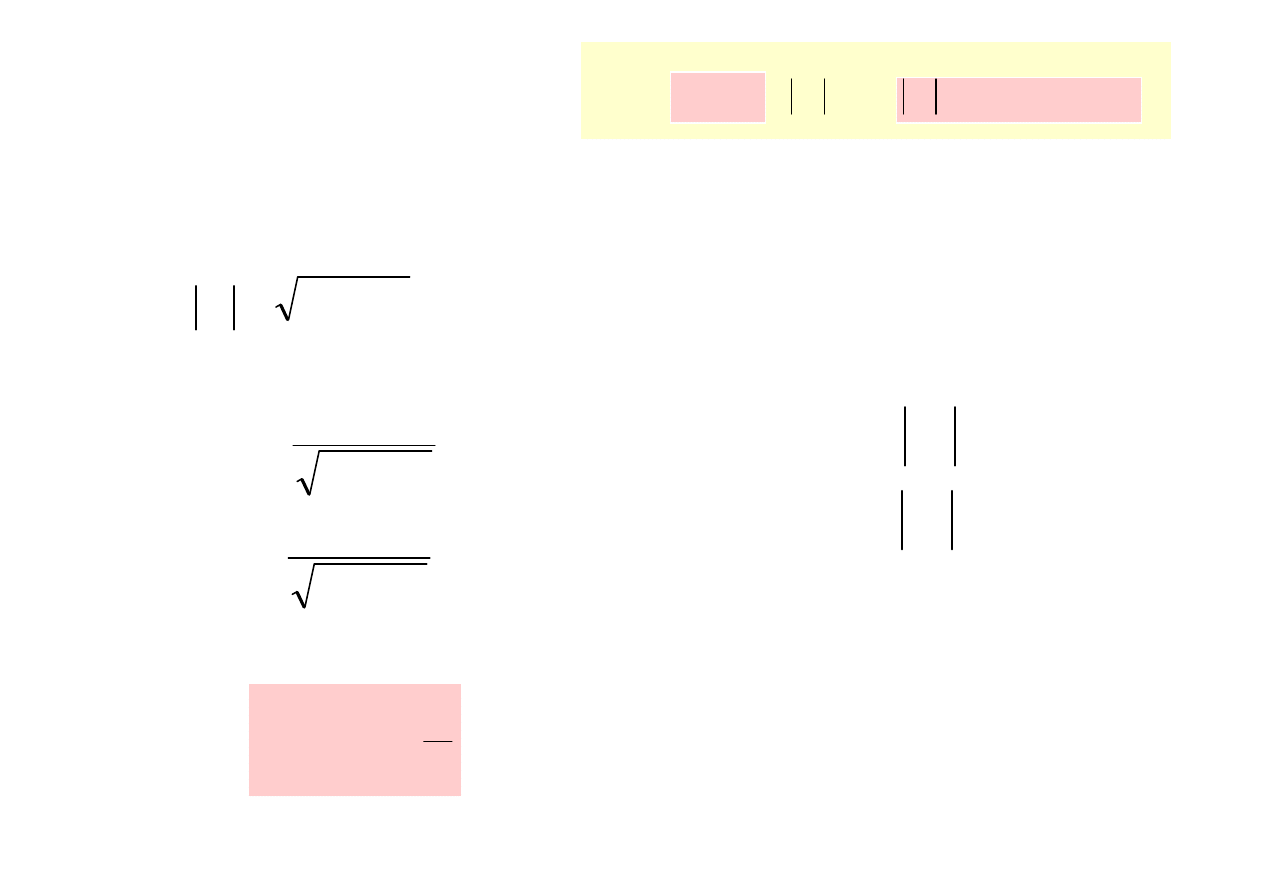
Jak przej

ść

z jednej postaci do drugiej ?

2

2

b

a

X

+

=

2

2

2

2

sin

cos

b

a

b

b

a

a

+

=

+

=

ϕ

ϕ

natomiast

ϕ

ϕ

sin

cos

X

b

X

a

=

=

[

]

ϕ

ϕ

ϕ

sin

cos

e

j

j

j

X

X

b

a

X

+

=

=

+

=

a

b

arctg

=

ϕ

lub

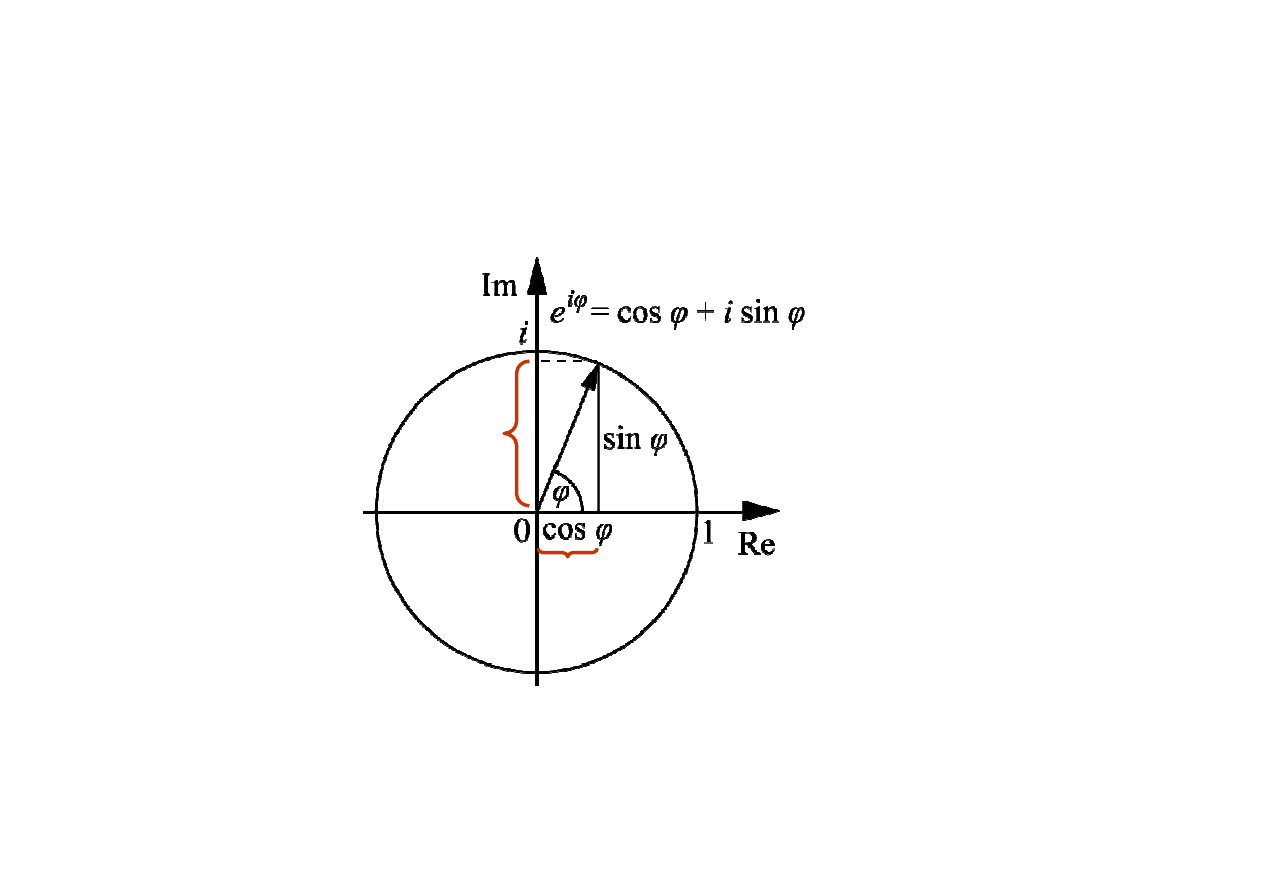
Eulerowska formuła graficznego przedstawienia liczby zespolonej

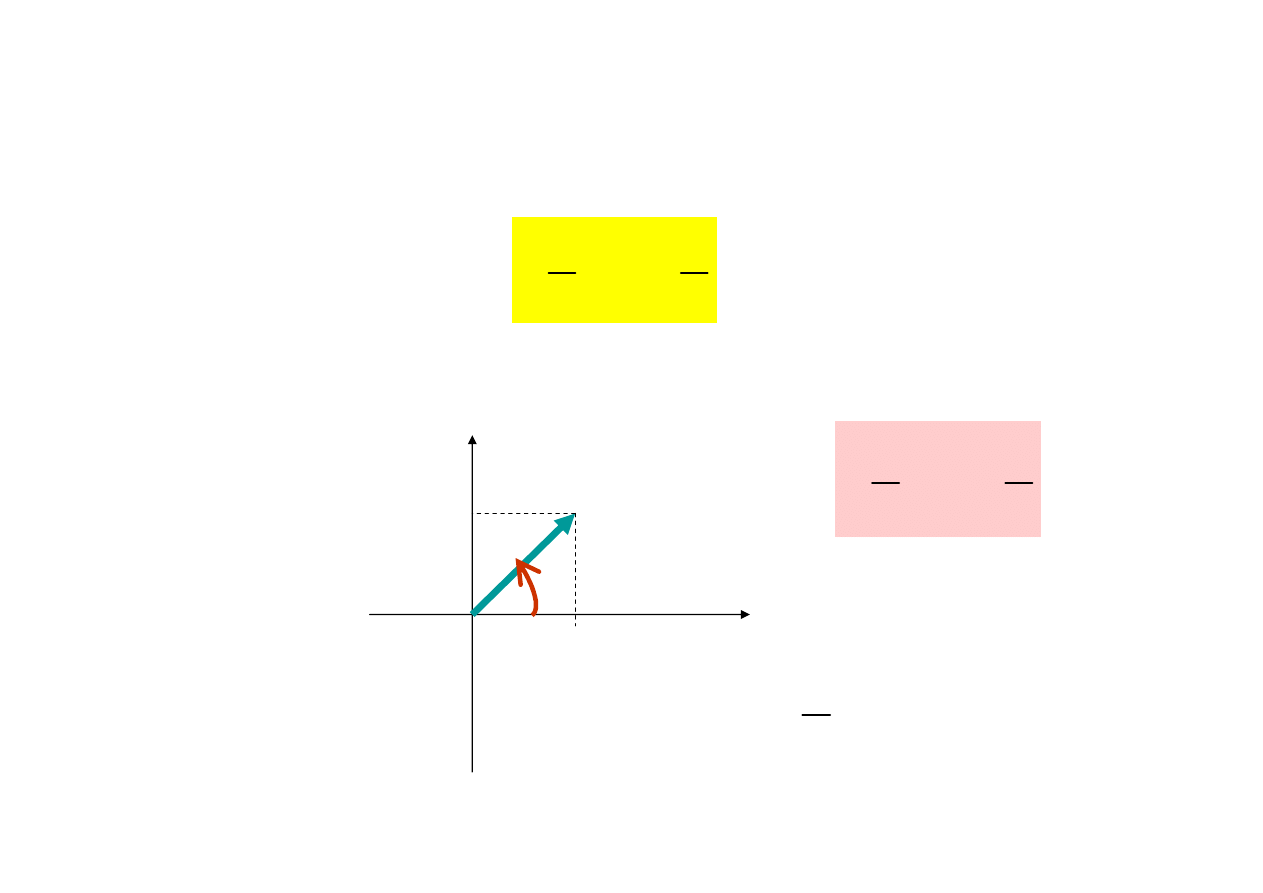
UWAGA !!!

I je

ż

eli

a > 0 to

2

2

π

<

ϕ

<

π

−

a

b

tg

arc

=

ϕ

i

a

b

Re

Im

2

2

π

<

ϕ

<

π

−

K

ą

t

φ

le

ż

y w I lub IV

ć

wiartce

Przyjmujemy X = a + j b

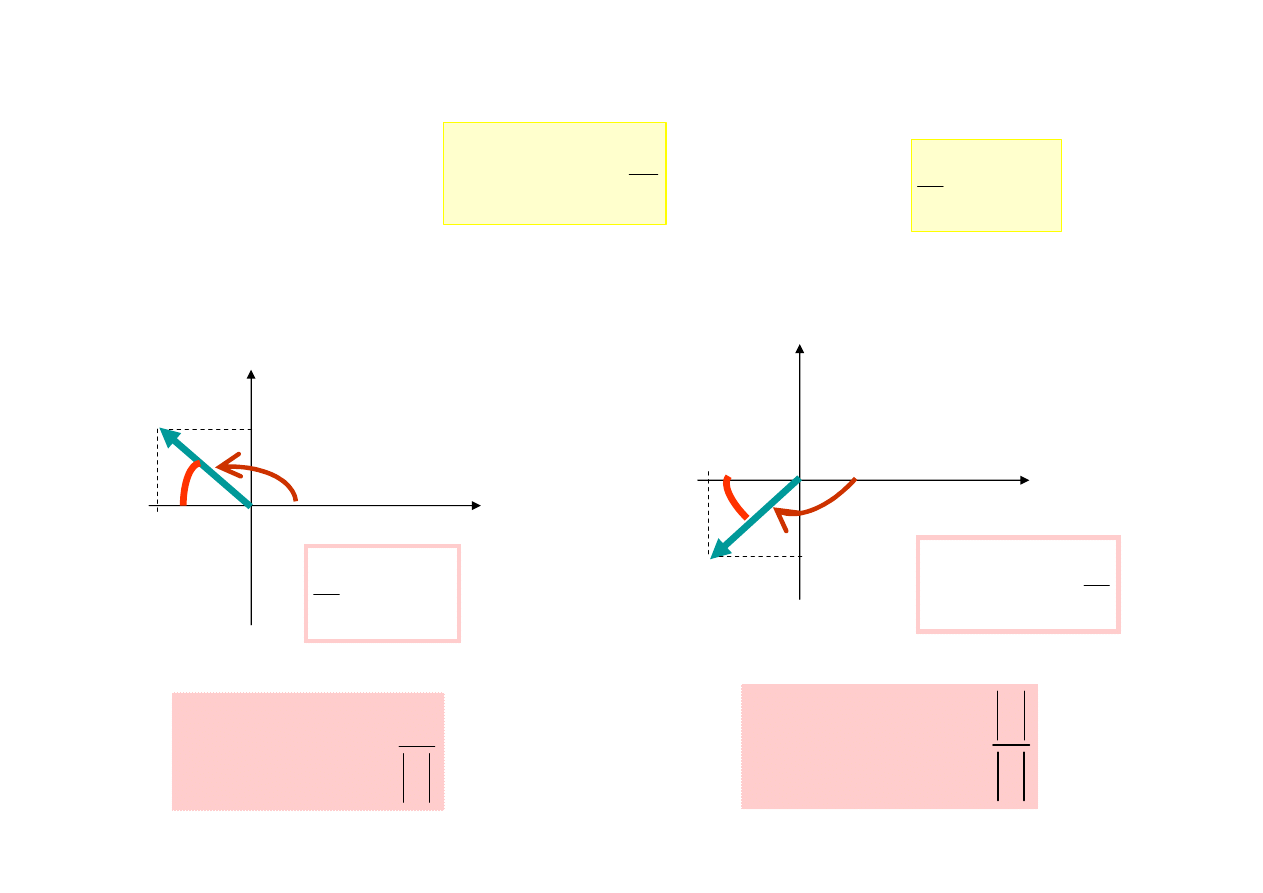
a < 0 to

2

π

ϕ

π

−

<

<

−

π

ϕ

π

<

<

2

lub

Je

ż

eli

a

b

Re

Im

2

π

ϕ

π

−

<

<

−

a

tg

arc

b

−

=

π

ϕ

a

b

tg

arc

+

−

=

π

ϕ

a

b

Re

Im

π

ϕ

π

<

<

2

K

ą

t

φ

le

ż

y III

ć

wiartce

K

ą

t

φ

le

ż

y II

ć

wiartce

Przedstawienie przebiegów sinusoidalnych

za pomoc

ą

liczb zespolonych

(

)

(

)

(

)

[

]

x

x

m

t

j

m

mt

t

sin

j

t

cos

X

e

X

X

x

ϕ

+

ω

+

ϕ

+

ω

=

=

=

ϕ

+

ω

rozpatrzmy zespoloną funkcję czasu postaci…

( )

(

)

)

t

(

x

t

sin

X

X

Im

x

m

mt

=

ϕ

+

ω

=

Część urojona tej funkcji

ma postać wartości chwilowej wielkości sinusoidalnie
zmiennej

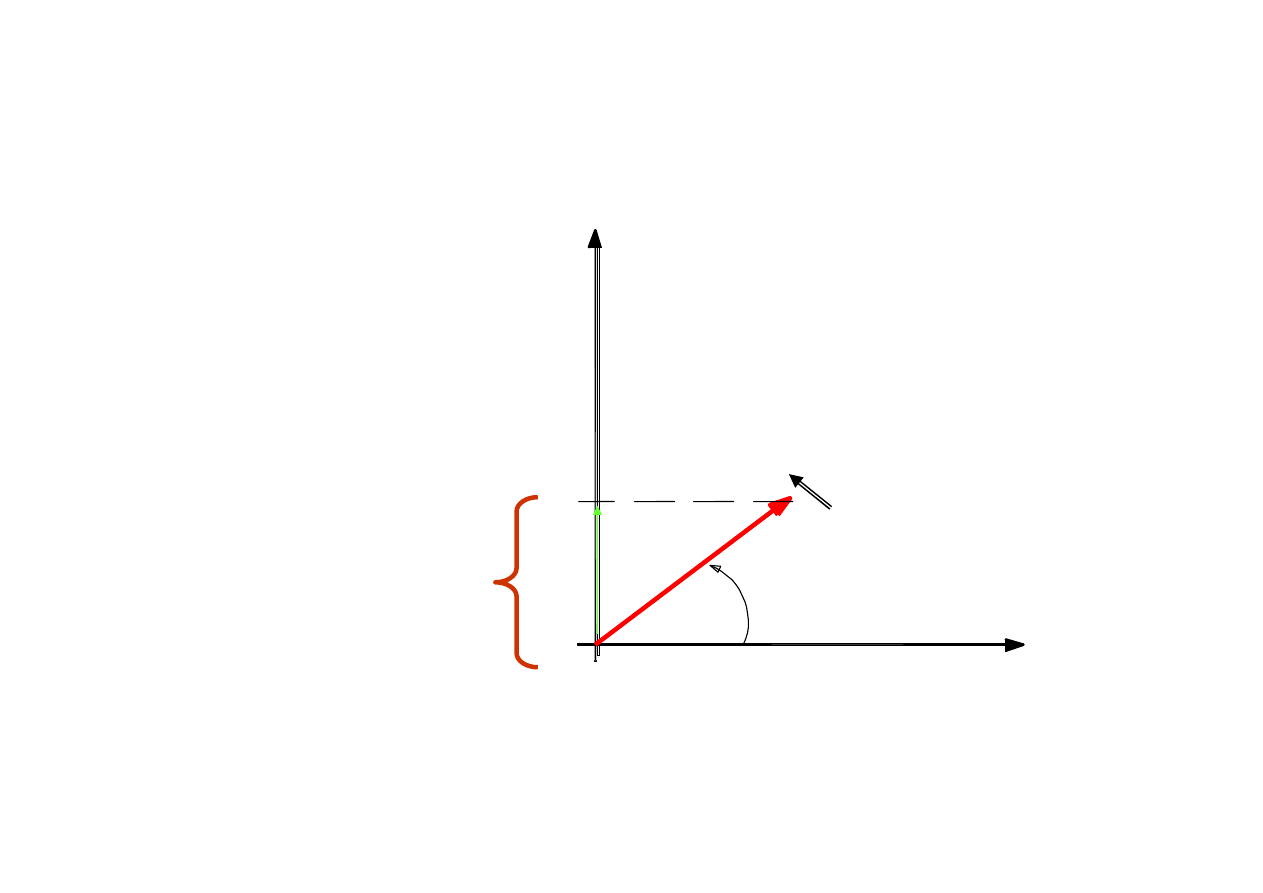
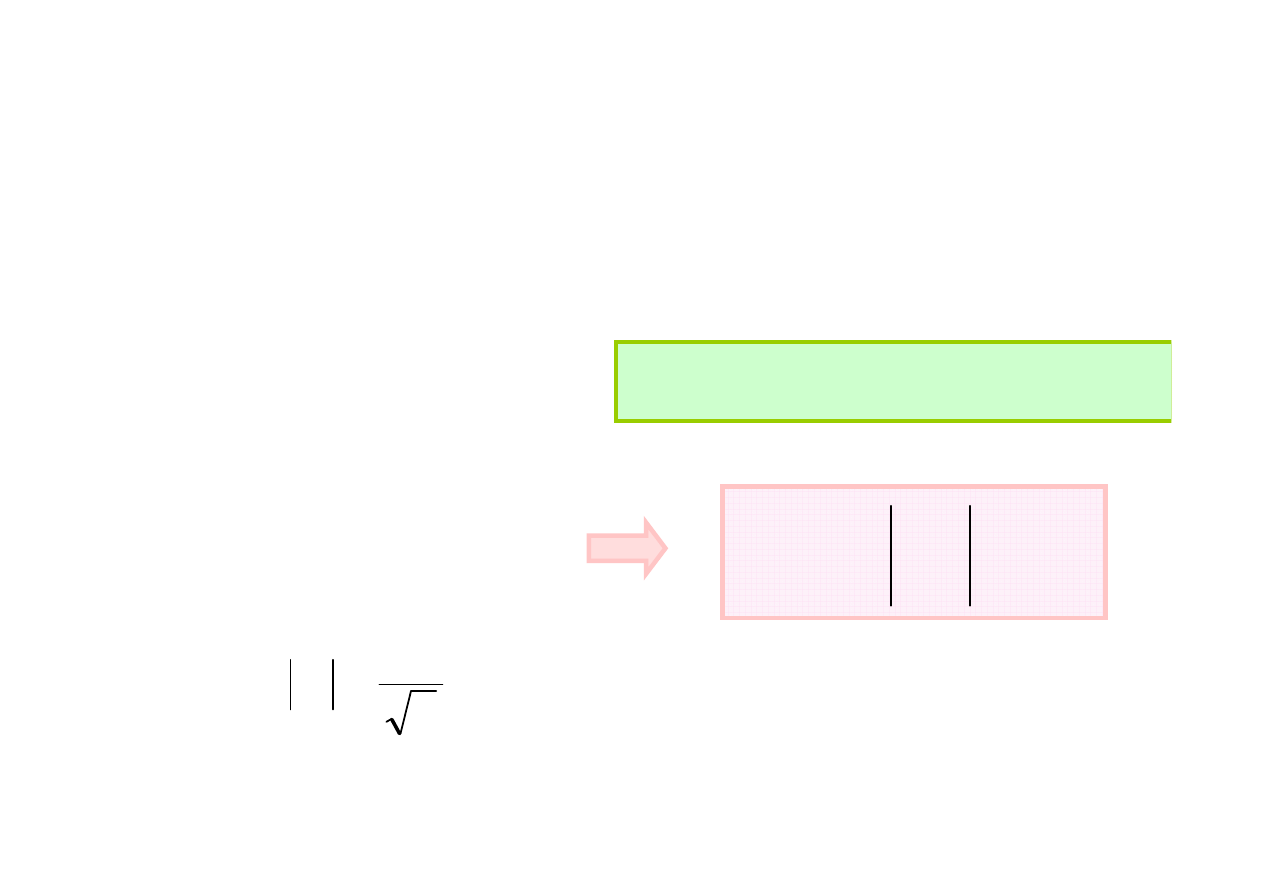
Obrazem geometrycznym X

mt

na płaszczyźnie

zmiennej zespolonej jest wektor o długości X

m

wirujący ze stałą prędkością kątową ω w dodatnim
kierunku trygonometrycznym.

Rzut tego wektora na oś urojonych jest równy
X

m

sin(ωt + φ

Z

)

I określa sinusoidalną funkcję czasu

Inaczej….

x

ϕ

t

ω

+

ω

Im(X

mt

)

X

m

Odwzorowanie funkcji X

mt

na płaszczy

ź

nie

)

Re(

mt

X

)

sin(

)

(

X

m

t

X

t

x

ϕ

ω

+

=

Definicja

warto

ś

ci symbolicznej (zespolonej) wielko

ś

ci

sinusoidalnej

Wartością symboliczną

(zespoloną)

wielkości

sinusoidalnie zmiennej:

(

)

x

m

t

sin

X

)

t

(

x

ϕ

+

ω

=

x

j

e

X

X

ϕ

=

Nazywamy wyra

ż

enie postaci:

gdzie

2

m

X

X

=

warto

ść

skuteczna

X

ϕ

to faza pocz

ą

tkowa

to

{ }

mt

X

Im

{ }

mt

X

Re

m

X

x

t

ϕ

ω

+

(

)

x

m

t

X

ϕ

ω

+

sin

wektor ruchomy

m

X

(

)

x

m

t

X

ϕ

ω

+

sin

x

ϕ

oś czasu

wektor nieruchomy

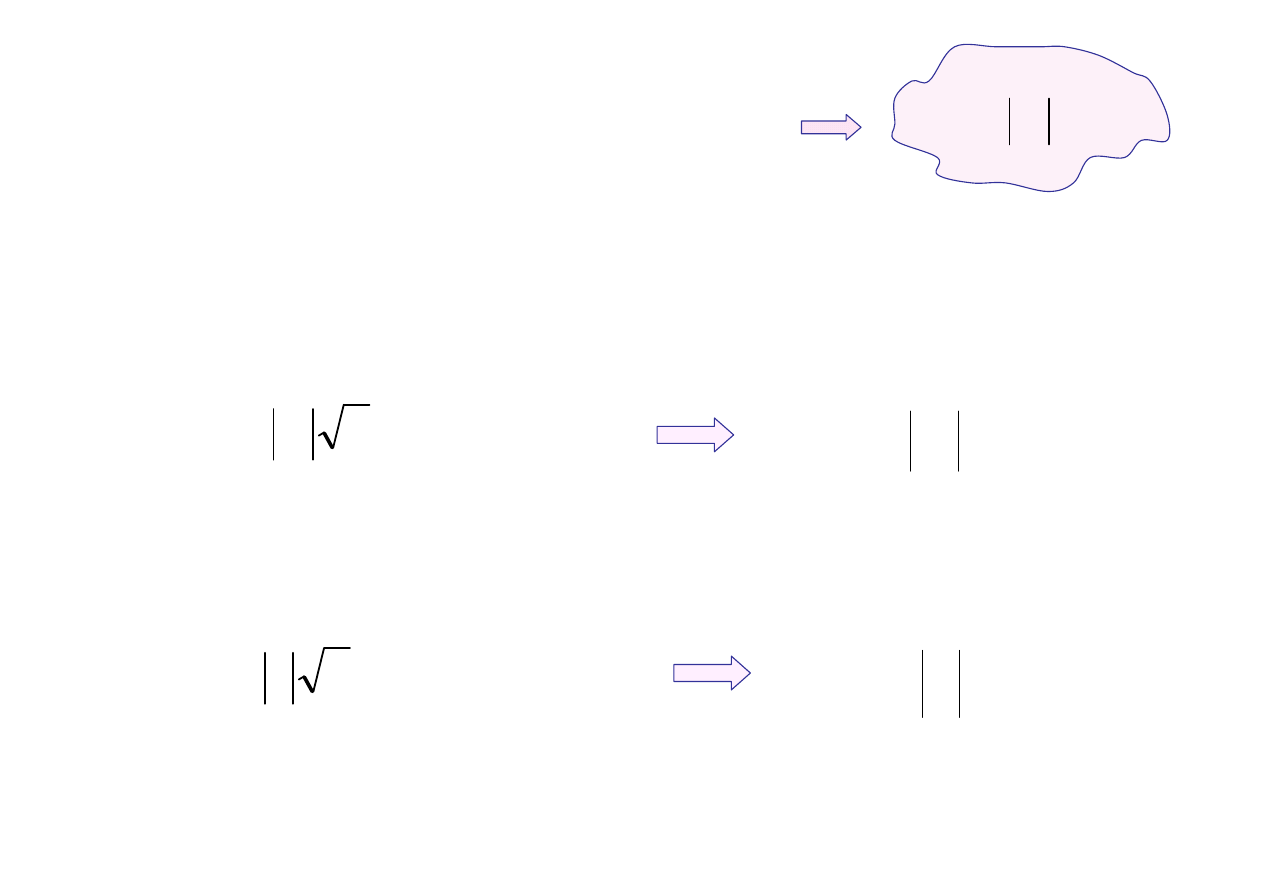
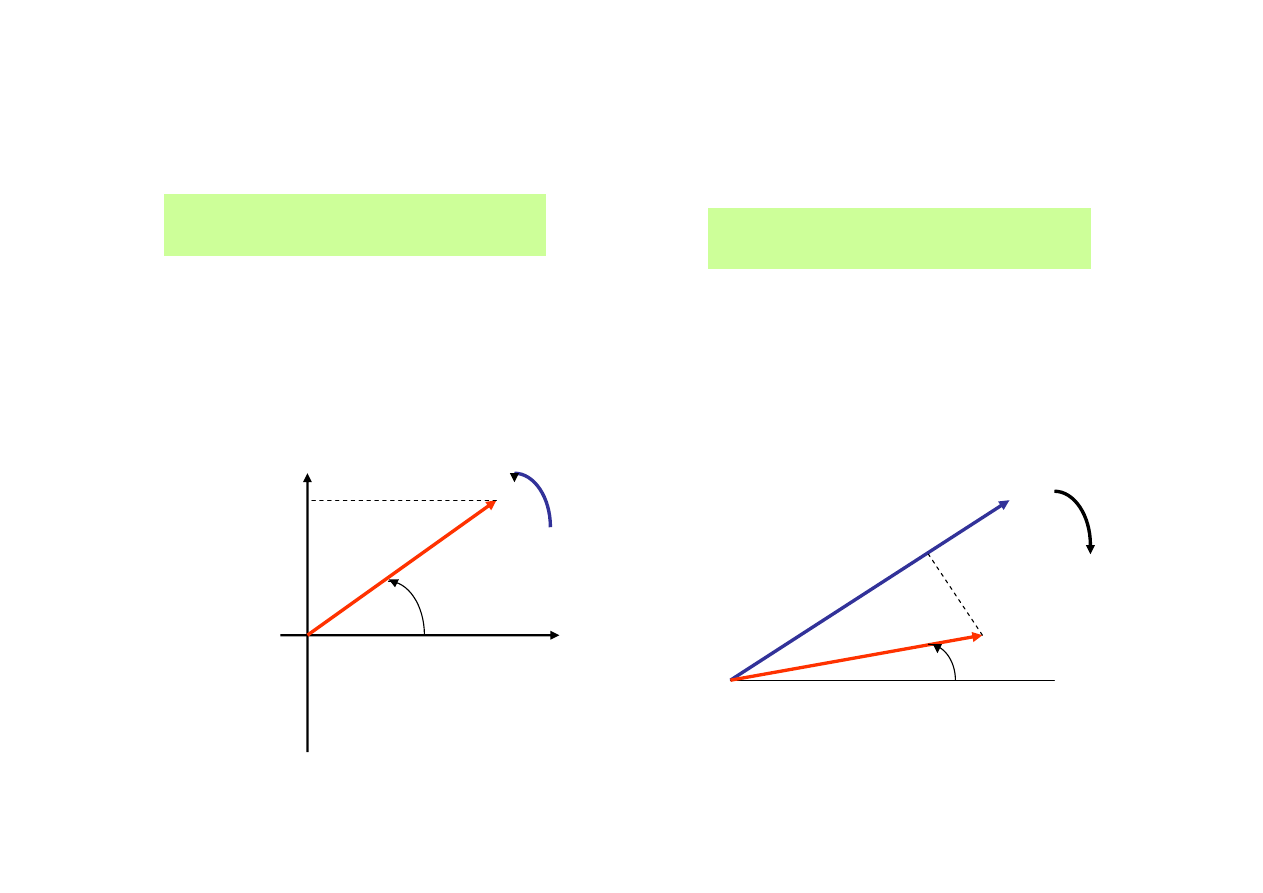
W oparciu o ten zapis funkcji zespolonej

Pr

ą

d i napi

ę

cie sinusoidalnie zmienne

mo

ż

na

przedstawi

ć

nast

ę

puj

ą

co :

u

j

e

U

U

ϕ

=

)

sin(

2

)

(

i

t

I

t

i

ϕ

ω

+

=

i

j

e

I

I

ϕ

=

)

sin(

2

)

(

u

t

U

t

u

ϕ

ω

+

=

X

j

e

X

X

ϕ

=

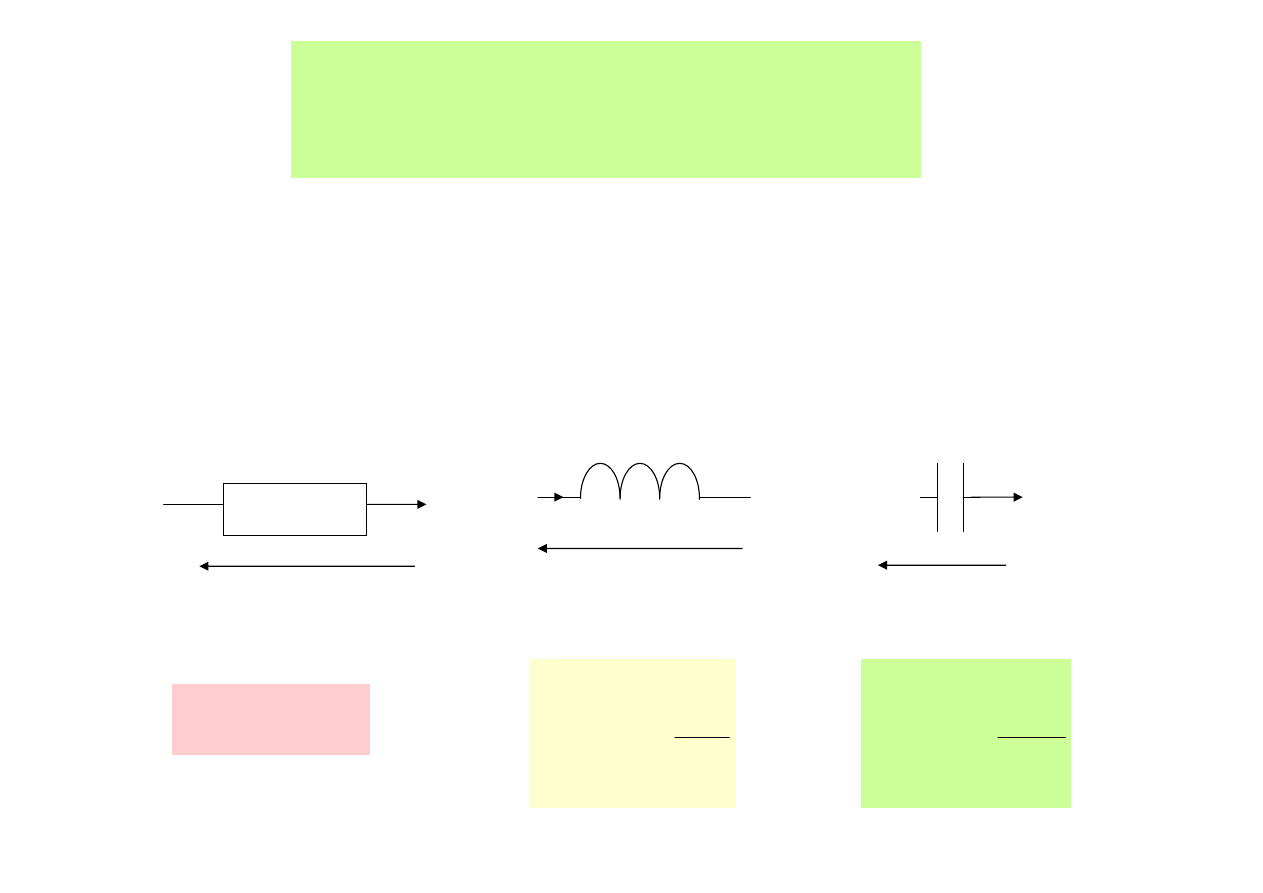
Podstawowe prawa obwodowe

w metodzie symbolicznej

Ri

u

=

i

u

R

rezystor

dt

di

L

u

=

L

u

i

u

i

C

dt

du

C

i

=

cewka

kondensator

Przypomnienie zale

ż

no

ś

ci dla warto

ś

ci chwilowych

Lemat

– w

matematyce -

twierdzenie pomocnicze, którego

głównym zastosowaniem jest uproszczenie dowodów
innych, bardziej istotnych twierdze

ń

. Formalnie jednak

ka

ż

dy lemat jest pełnoprawnym twierdzeniem, a

zaklasyfikowanie pewnego twierdzenia jako lematu
wynika jedynie ze sposobu jego u

ż

ycia w innym,

obszerniejszym kontek

ś

cie

PRAWA KIRCHHOFFA

1. Pr

ą

dowe prawo Kirchhoffa

(PPK )

∑

=

=

m

k

k

i

1

0

0

1

=

∑

=

m

k

k

I

Na podstawie odpowiednich lematów matematycznych

czyli:

W dowolnym węźle lub przekroju suma algebraiczna prądów w
postaci symbolicznej równa się zeru

PRAWO OHMA

u

j

e

U

U

ϕ

=

)

sin(

2

)

(

i

t

I

t

i

ϕ

ω

+

=

i

j

e

I

I

ϕ

=

)

sin(

2

)

(

u

t

U

t

u

ϕ

ω

+

=

Zakładamy

,

ż

e posta

ć

napi

ęć

i pr

ą

dów w obwodzie jest

nast

ę

puj

ą

ca

Prawo Ohma dla opornika

i

u

R

rezystor

Ri

u

=

Na podstawie lematów

RI

U

=

0

=

−

=

=

=

i

u

i

u

I

R

U

ϕ

ϕ

ϕ

ϕ

ϕ

i

u

j

j

e

I

R

e

U

ϕ

ϕ

=

Nie ma przesuni

ę

cia mi

ę

dzy pr

ą

dem i

napi

ę

ciem dla rezystora

I

U

u

i

ϕ

ϕ

=

Wykres wskazowy dla rezystora

dla rezystora

nie ma przesuni

ę

cia mi

ę

dzy pr

ą

dem i napi

ę

ciem

0

=

−

=

i

u

ϕ

ϕ

ϕ

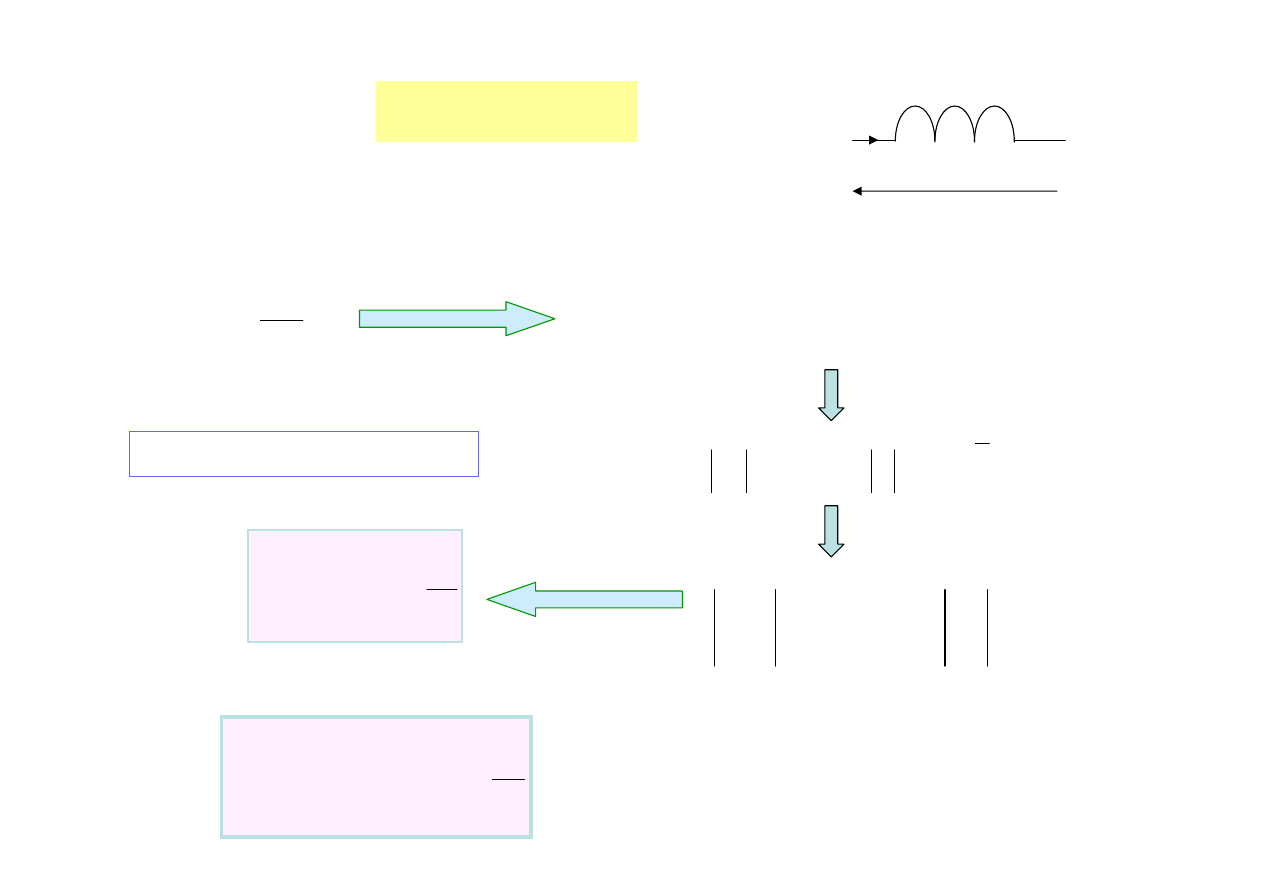
Cewka

u

i

dt

di

L

u

=

LI

j

U

ω

=













+

=

2

π

ϕ

ϕ

i

u

j

j

e

I

L

e

U

I

L

U

ω

=

2

π

ϕ

ϕ

+

=

i

u

2

π

ϕ

ϕ

ϕ

=

−

=

i

u

Na podstawie lematów

Napi

ę

cie wyprzedza pr

ą

d o k

ą

t 90

0

ω

L=X - reaktancja cewki

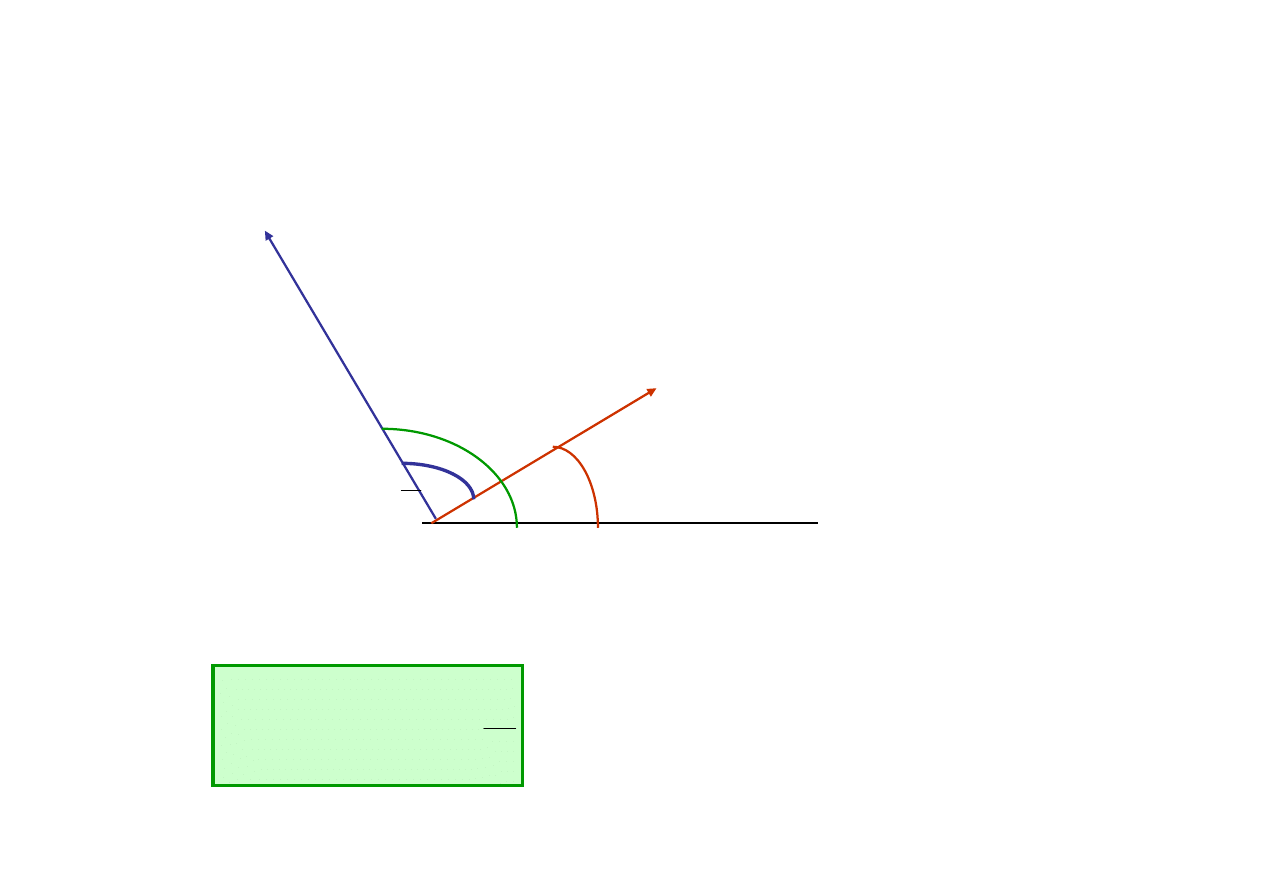
u

ϕ

i

ϕ

2

π

ϕ

=

U

I

2

π

ϕ

ϕ

ϕ

=

−

=

i

u

Napi

ę

cie wyprzedza pr

ą

d o k

ą

t 90

0

Wykres wskazowy

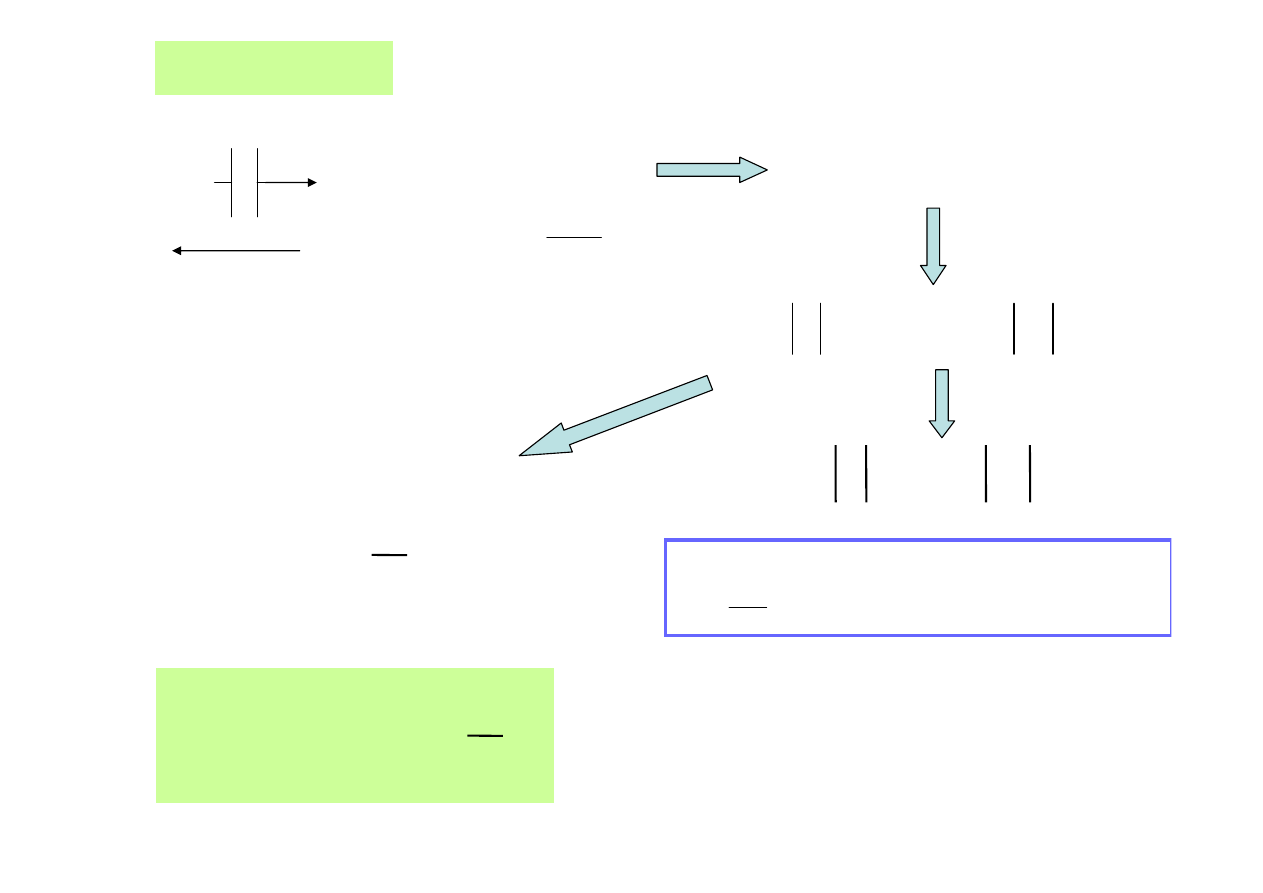
kondensator

Pr

ą

d wyprzedza napi

ę

cie na

kondensatorze o k

ą

t 90

0

2

π

ϕ

ϕ

ϕ

−

=

−

=

i

u

2

π

ϕ

ϕ

+

=

u

i

dt

du

C

i

=

u

i

C

ω

=

U

C

I

ω

=

CU

j

I

u

i

j

j

e

U

C

j

e

I

ϕ

ϕ

ω

=

ω

C – susceptancja kondensatora

a reaktancja kondensatora

X

C

=

ω

1

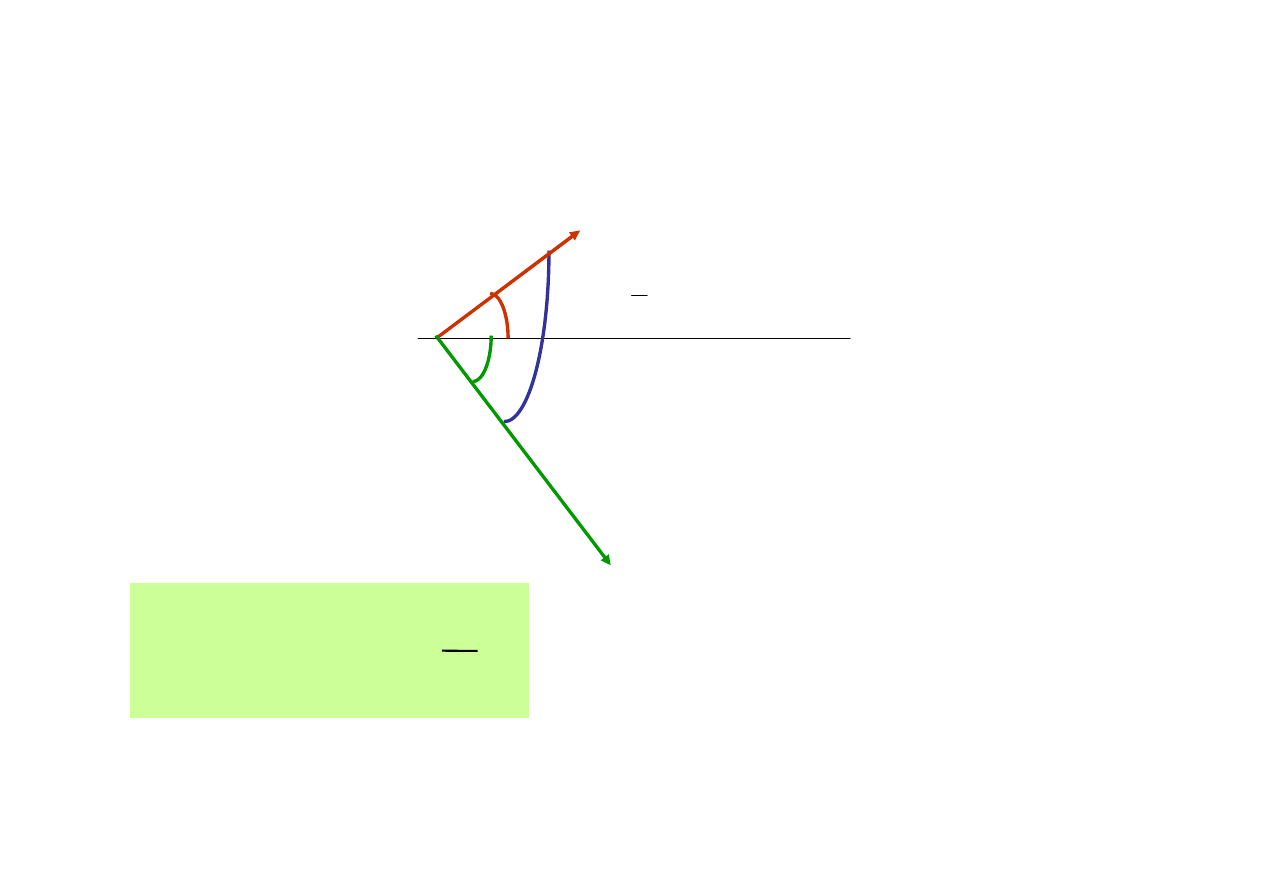
2

π

ϕ

−

=

i

ϕ

I

u

ϕ

U

Pr

ą

d wyprzedza napi

ę

cie na

kondensatorze o k

ą

t 90

0

Wykres wskazowy

2

π

ϕ

ϕ

ϕ

−

=

−

=

i

u

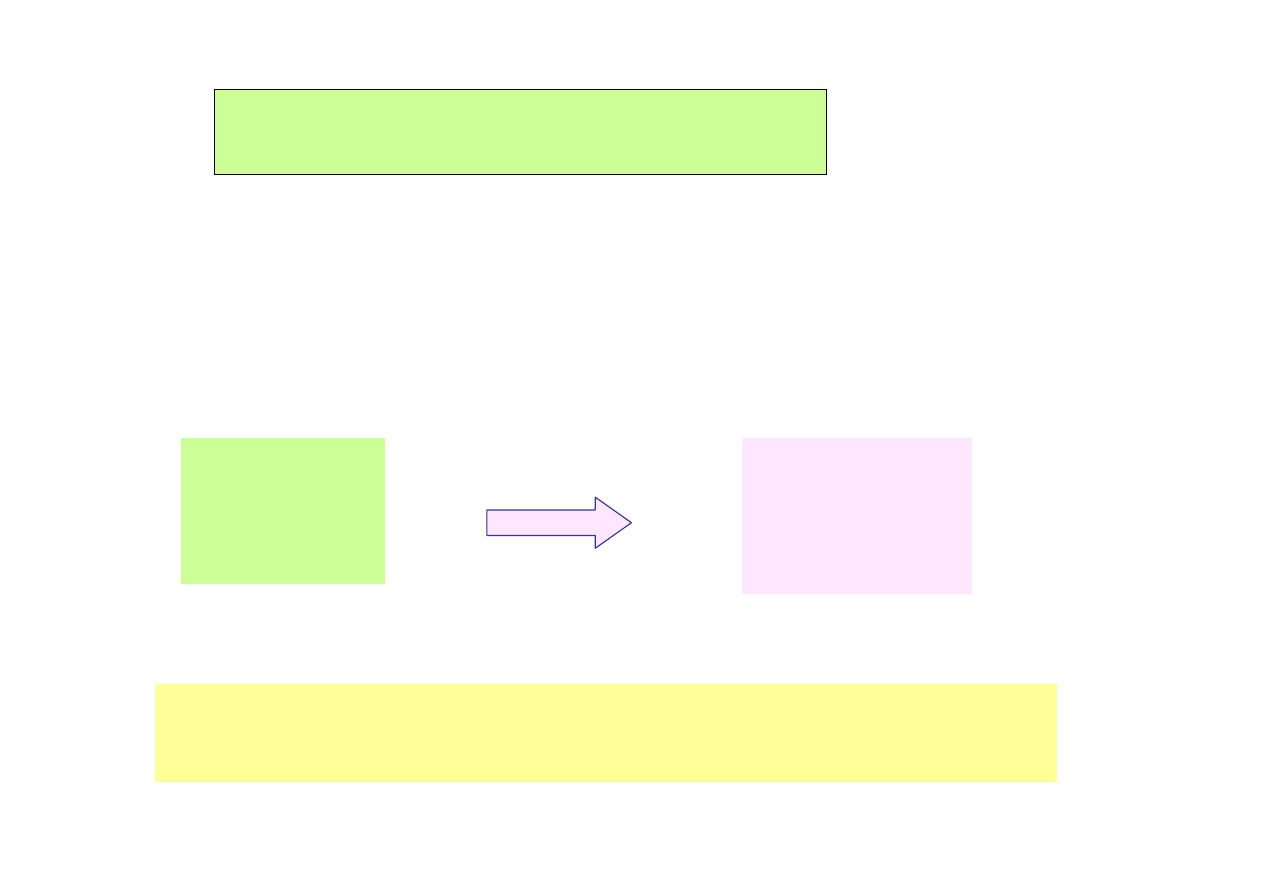
2. Napi

ę

ciowe prawo Kirchhoffa

(NPK)

∑

=

=

n

k

k

u

1

0

0

1

=

∑

=

n

k

k

U

Na podstawie odpowiednich
lematów matematycznych

Algebraiczna suma napięć w postaci symbolicznej w
obwodzie zamkniętym równa się zero

Impedancja i admitancja

Rozpatrujemy dwójnik liniowy nie zawierający źródeł
niezależnych

Impedancją dwójnika

nazywamy iloraz wartości

symbolicznych napięcia i prądu

I

U

Z

=

[ ]

Ω

=

1

Z

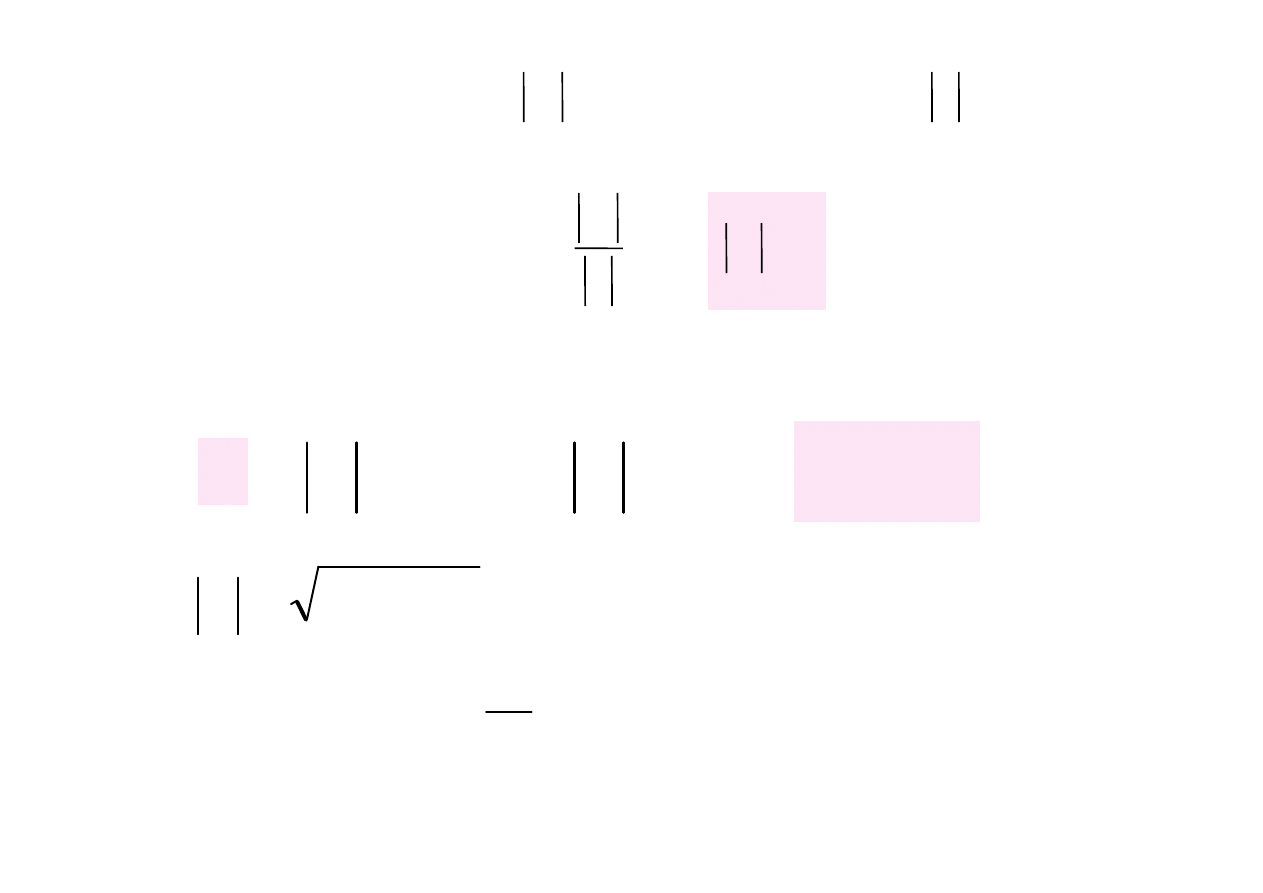
jX

R

Z

j

Z

Z

+

=

+

=

ϕ

ϕ

sin

cos

R

X

Z

X

R

Z

arg

arg

2

2

=

=

+

=

ϕ

poniewa

ż

:

to

ϕ

ϕ

j

j

e

Z

e

I

U

Z

=

=

ϕ

j

e

I

I

i

=

ϕ

j

e

U

U

u

=

oraz

wi

ę

c impedancj

ę

mo

ż

na przedstawi

ć

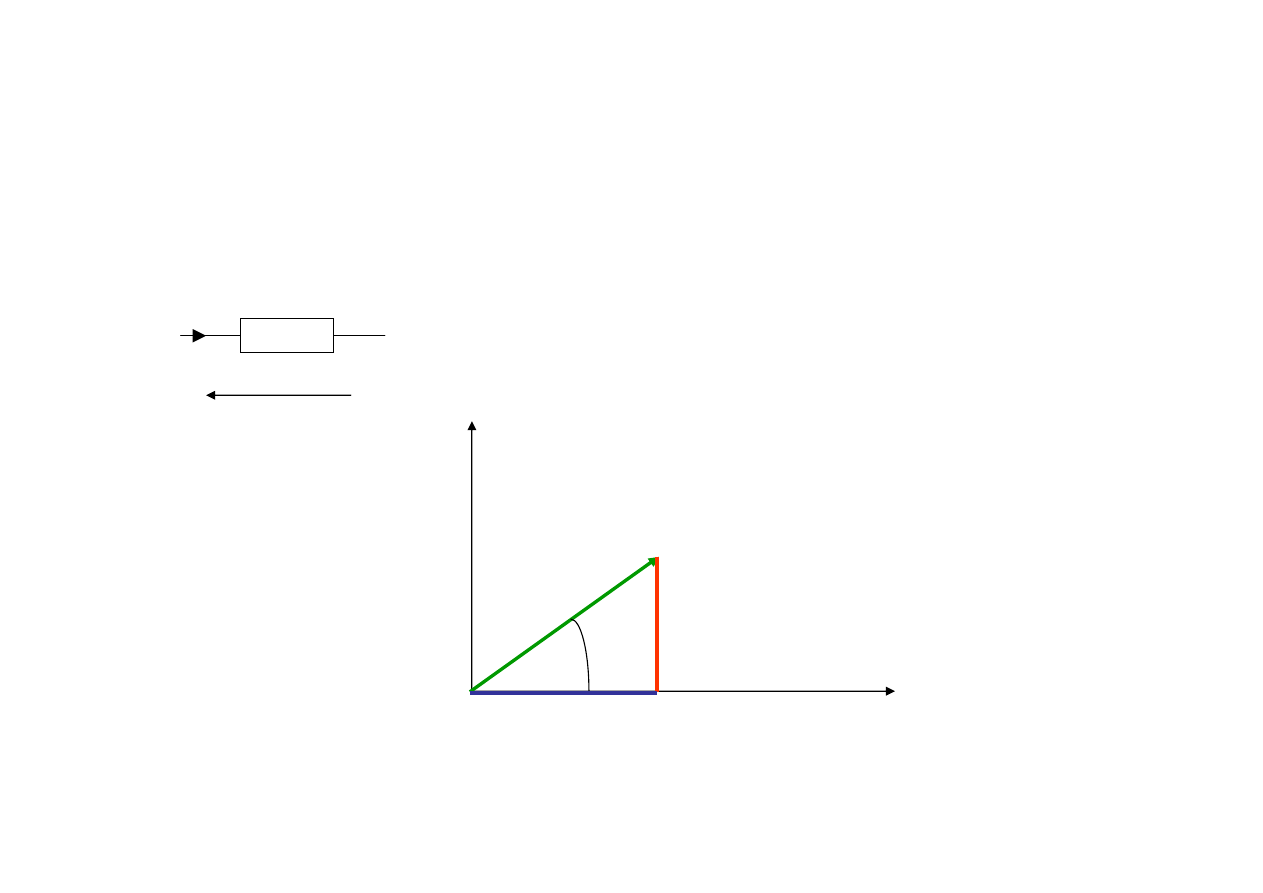
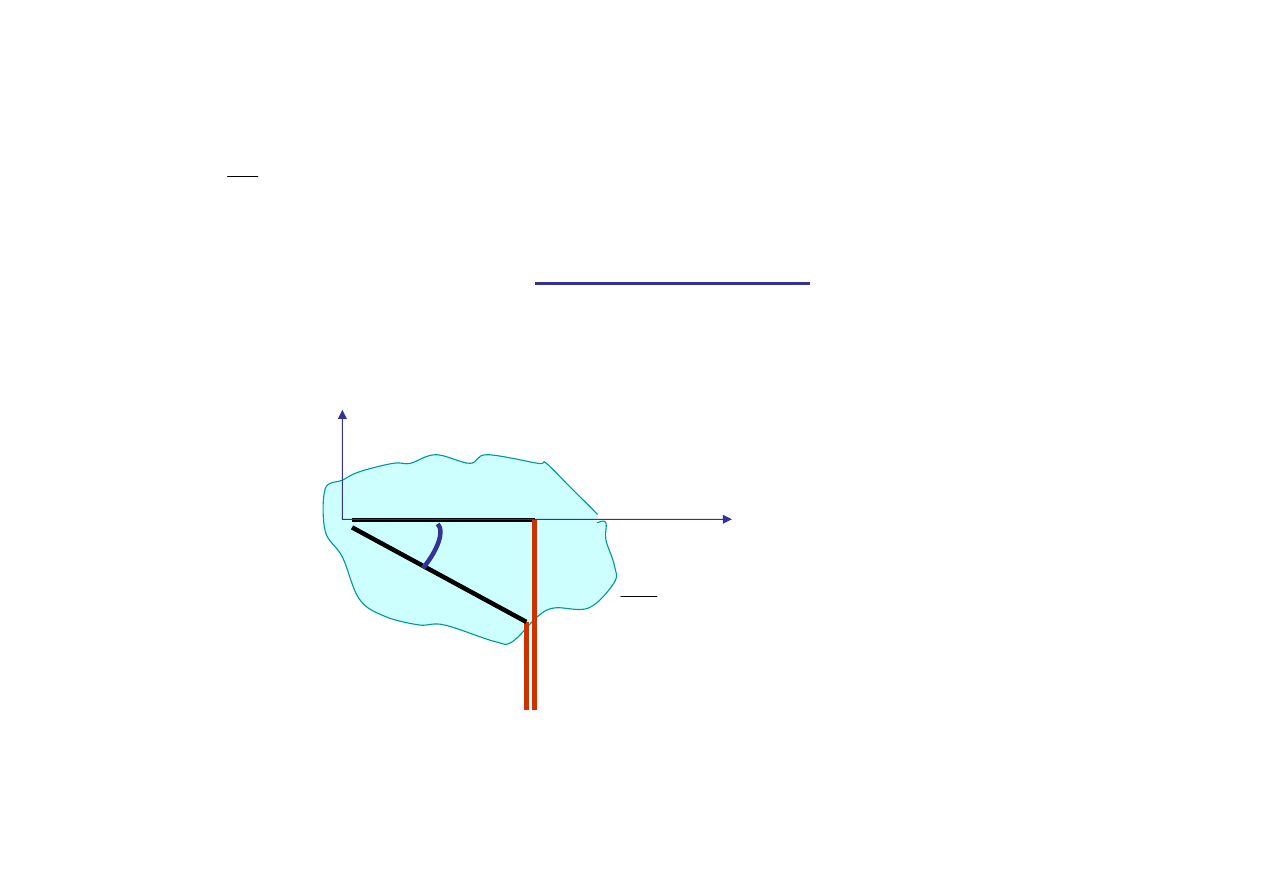
Impedancja na płaszczy

ź

nie zmiennej zespolonej

ϕ

Im(Z)

Z=R+jX

jX

R

Re(Z

)

Z

I

U

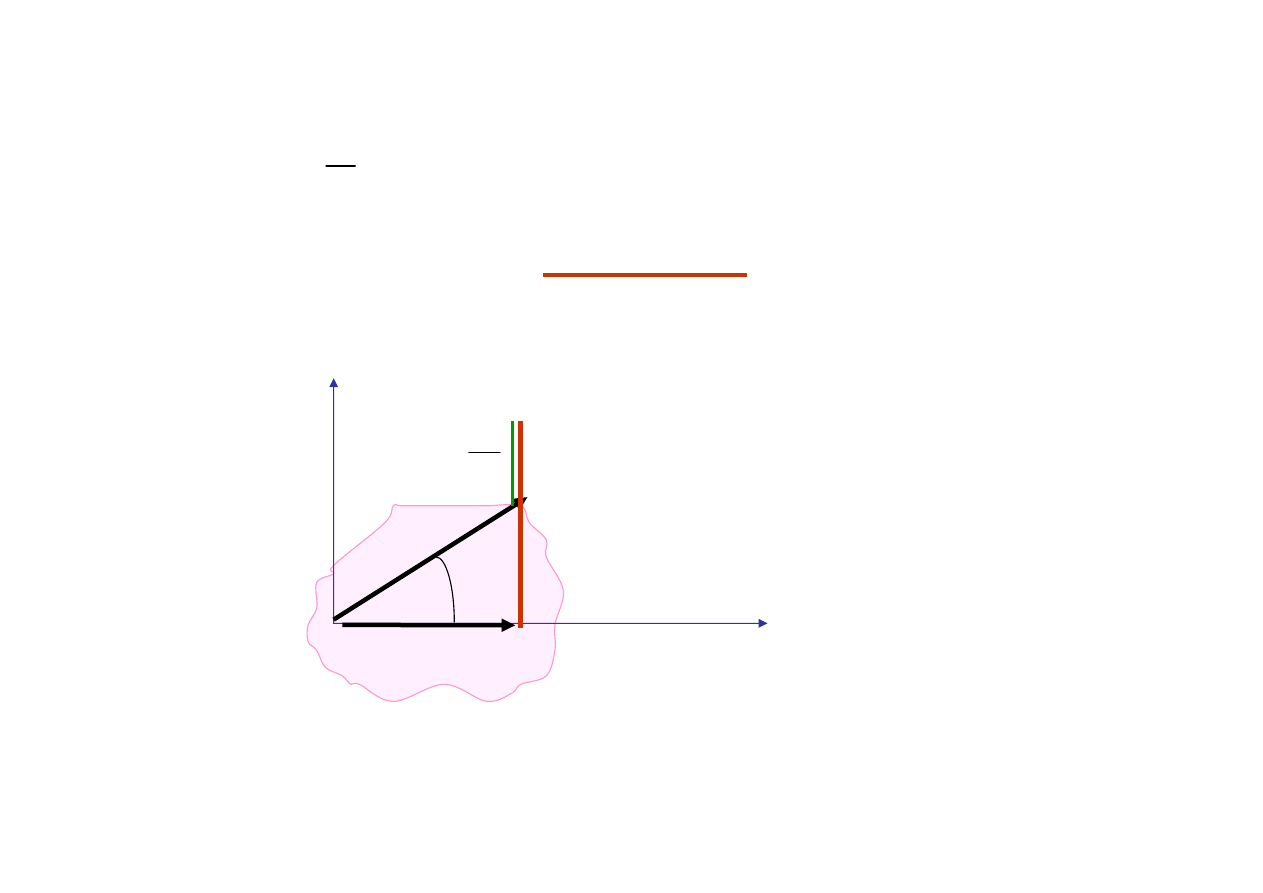
R>0, X>0

Dwójnik ma charakter

indukcyjny

2

0

π

ϕ

<

<

ϕ

R

)

Im(Z

jX

R

Z

+

=

)

Re(Z

L

X

L

ω

=

C

X

c

ω

1

−

=

0

2

<

<

−

ϕ

π

R>0, X<0

Dwójnik ma charakter

pojemnościowy

R

C

X

C

ω

1

−

=

L

X

L

ω

=

)

Im( Z

)

Re( Z

Z

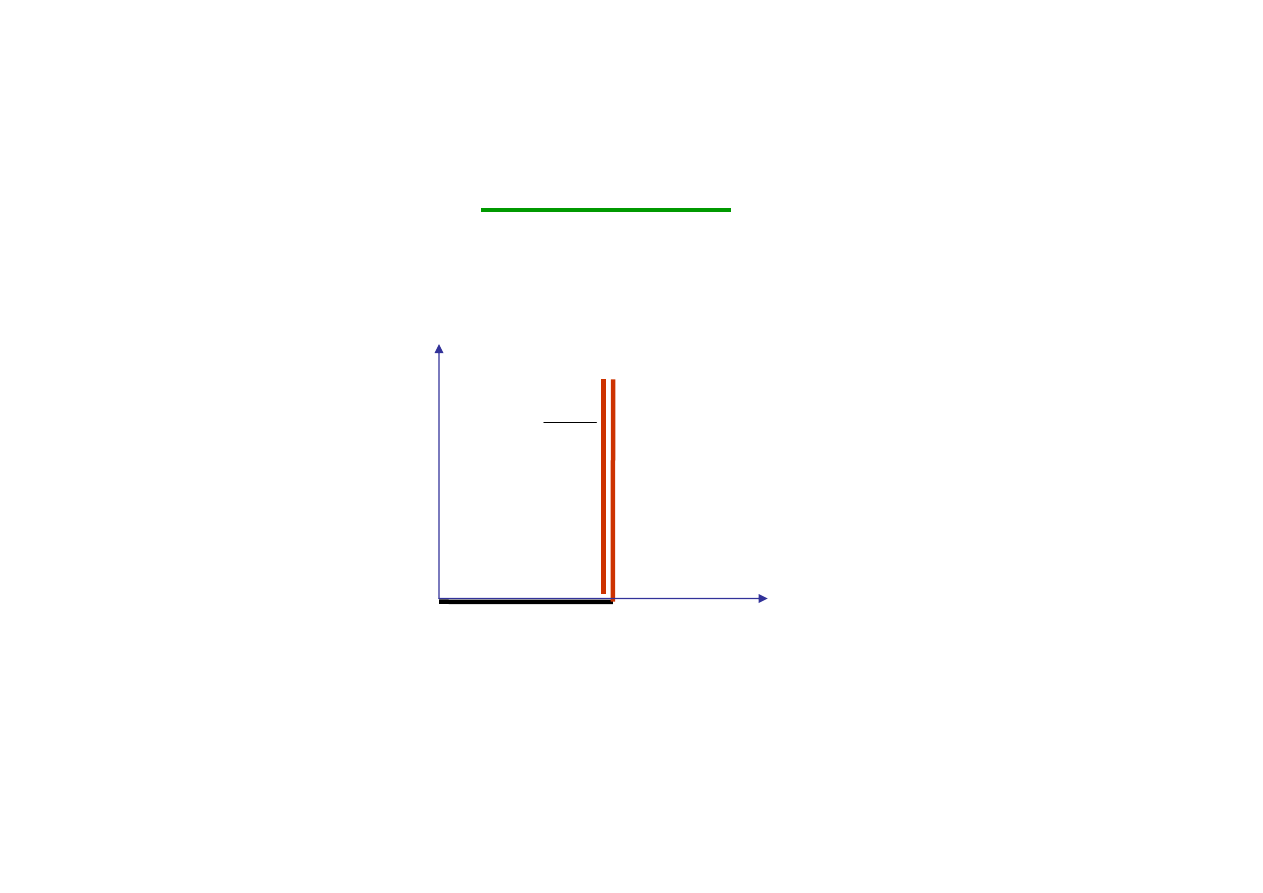
Z=R

C

X

C

ω

1

−

=

L

X

L

ω

=

)

Re( Z

)

Im( Z

Dwójnik jest

rezystancyjny

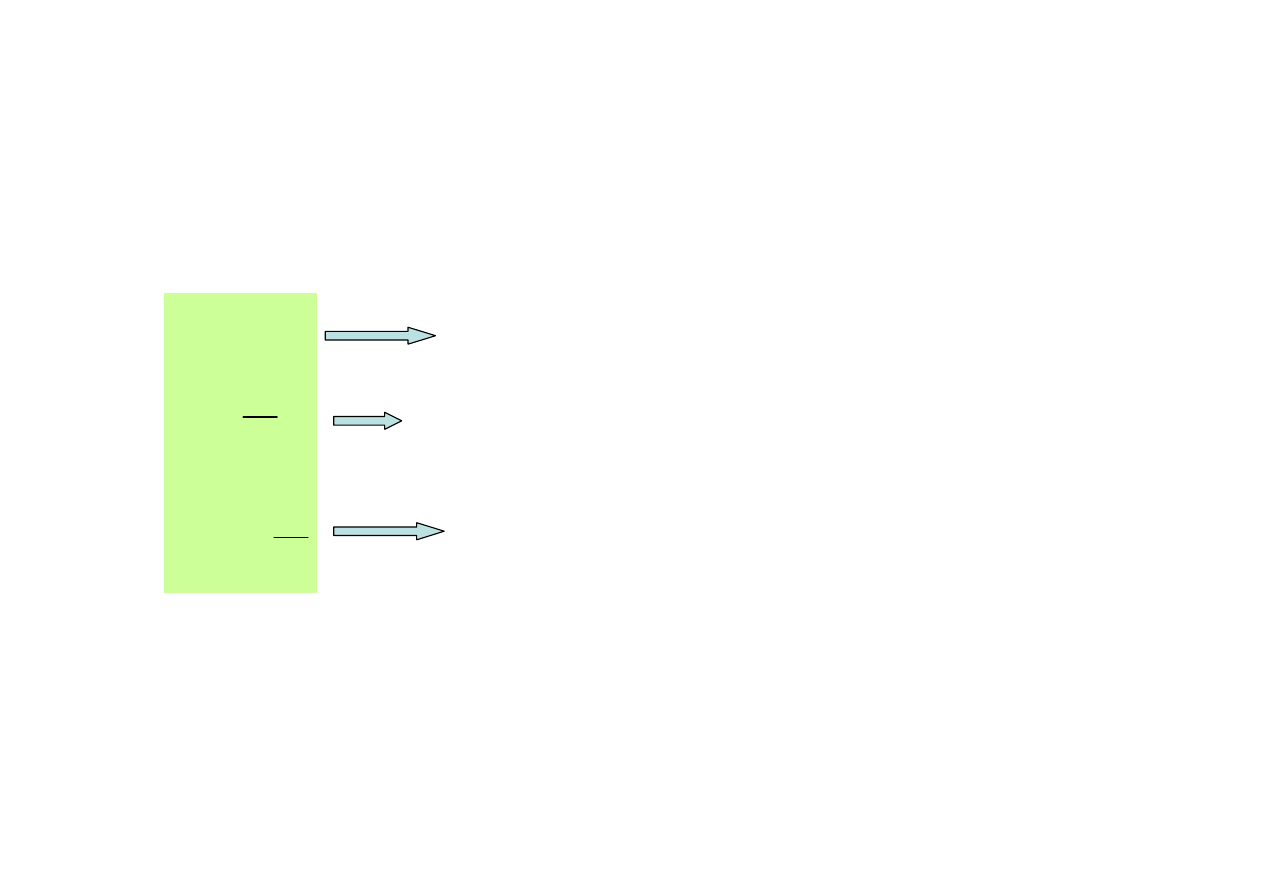
2

2

0

π

ϕ

π

ϕ

ϕ

−

=

=

=

Dwójnik jest rezystancyjny

Dwójnik jest czysto indukcyjny

Dwójnik jest czysto pojemnościowy

Szczególne przypadki