L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

11

Wyznaczanie równoważnika elektrochemicznego wodoru i

testowanie pierwszego prawa Faradaya

J.Kurzyk

Ćwiczenie 11

2

ĆWICZENIE

11

Wyznaczanie równoważnika elektrochemicznego wodoru i
testowanie pierwszego prawa Faradaya

J.Kurzyk

1.

Wprowadzenie

Głównym celem ćwiczenia jest wyznaczenie równoważnika elektrochemicznego
wodoru. Zastosowana metoda pomiarowa pozwali jednocześnie na sprawdze-
nie, czy zależność masy wodoru, jaka wydziela się podczas elektrolizy, od ła-
dunku, jaki przepływa między elektrodami ma charakter liniowy. Tego typu
zależność wynika z pierwszego prawa Faradaya, a zatem wyniki naszych po-
miarów będą jednocześnie testem tego prawa. Wyznaczenie wartości równo-
ważnika elektrochemicznego wodoru pozwala nam dodatkowo wyliczyć war-
tość stałej Faradaya oraz wartość ładunku elementarnego.

1.1

Dysocjacja elektrolityczna

Woda jest najbardziej znanym i jednocześnie bardzo dobrym rozpuszczalnikiem wielu

substancji. Już na początku badań nad elektrycznością zauważono, że wodne roztwory nie-
których związków chemicznych (należą do nich wszystkie kwasy, zasady i sole) przewodzą
prąd elektryczny, a inne nie. Pod koniec XIX wieku problemem tym zajmował się szwedzki
chemik i fizyk Svante Arrhenius. Wysunął on przypuszczenie, że cząsteczki kwasów, zasad i
soli pod wpływem wody ulegają rozpadowi na jony dodatnie i ujemne. Proces ten nazywany
jest

dysocjacją elektrolityczną

, a powstały w wyniku dysocjacji elektrolitycznej roztwór

związku chemicznego –

elektrolitem

. Za opracowanie teorii dysocjacji elektrolitycznej Arrhe-

nius otrzymał w 1903 roku nagrodę Nobla w dziedzinie chemii.

Podczas dysocjacji elektrolitycznej jonami dodatnimi stają się atomy metali oraz wodór, a

jonami ujemnymi reszty kwasowe i zasadowe, np.

H SO → 2H + SO ,

KOH → K + OH ,

CuSO → Cu + SO .

Dysocjacja elektrolityczna jest procesem odwracalnym. W elektrolitach ciągle zachodzi

proces dysocjacji i odwrotny do niego proces

rekombinacji

. Oznacza to, że nieustannie jedne

cząstki rozpadają się na jony, a z kolei niektóre jony na powrót łączą się w obojętne elek-
trycznie cząsteczki. Jednak w danych warunkach (w danej temperaturze i przy danym stęże-
niu roztworu) w roztworze znajduje się mniej więcej stała liczba jonów obu rodzajów. Stosu-
nek liczby moli cząstek związku chemicznego, które uległy dysocjacji do liczby moli wszyst-

Wyznaczanie równoważnika elektrochemicznego wodoru …

3

kich cząstek związku nazywamy

stopniem dysocjacji

. Elektrolity dzielimy na tzw.

elektrolity

słabe

i

elektrolity mocne

. W przypadku elektrolitów słabych stopień dysocjacji jest bardzo

mały. Przykładem elektrolitu słabego jest wodny roztwór kwasu węglowego H

2

CO

3

. W przy-

padku elektrolitów mocnych stopień dysocjacji jest bliski jedności. Przykładem takiego elek-
trolitu jest wodny roztwór kwasu siarkowego H

2

SO

4

, z jakim mamy do czynienia w tym ćwi-

czeniu. Elektrolit jako całość jest elektrycznie obojętny – ilość ładunku elektrycznego na jo-
nach dodatnich jest taka sama jak na jonach ujemnych.

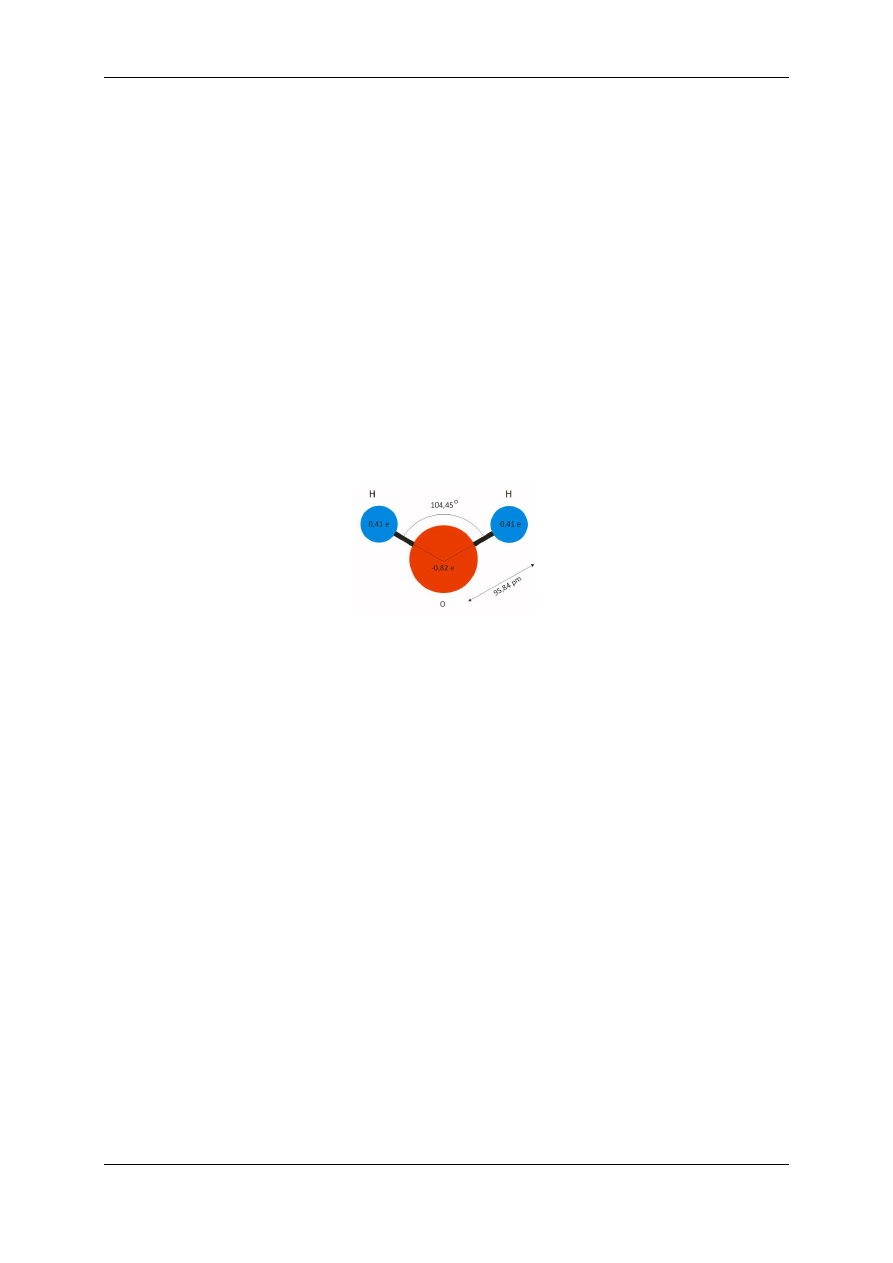
Bardzo dobre właściwości dysocjacyjne wody wynikają z budowy jej cząsteczki. Ułożenie

atomów wodoru w stosunku do atomu tlenu i wiążące się z tym przesunięcie efektywnego
ładunku ujemnego względem efektywnego ładunku dodatniego (patrz rysunek 1.1), sprawia,
że cząsteczka wody jest tzw.

cząsteczką polarną

, czyli ma trwały moment dipolowy. Oznacza

to, że wytwarza wokół siebie pole elektryczne, chociaż jest elektrycznie obojętna. Moment
dipolowy cząsteczki wody jest dość wysoki co przejawia się w bardzo dużej względnej przeni-
kalności dielektrycznej wody wynoszącej w temperaturze pokojowej ok. 80.

Rys. 1.1 Model cząsteczki wody.

Dysocjacja cząsteczek związku rozpuszczonego w wodzie wywołana jest polem elektrycznym
cząsteczek wody, które otaczają cząsteczki rozpuszczonej w wodzie substancji chemicznej i
zderzają się z nimi wskutek ruchów termicznych. Zdolność do dysocjacji wykazują cząsteczki,
w których występują

wiązania jonowe

lub

kowalencyjne

silnie spolaryzowane.

Do samorzutnej dysocjacji dochodzi również w czystej wodzie:

H O + H O → H O + OH .

Jednak w warunkach normalnych stopień dysocjacji wody jest bardzo mały. Zaledwie jedna
cząstka wody na 10

7

cząstek ulega dysocjacji, dlatego czysta chemicznie woda nie przewodzi

prądu elektrycznego.

1.2

Przepływ prądu w elektrolitach, elektroliza

Elektrolity są dość dobrymi przewodnikami prądu elektrycznego. Mechanizm przewo-

dzenia prądu elektrycznego przez elektrolity jest inny niż w metalach. Główna różnica polega
na tym, że nośnikami prądu w metalach są elektrony, zaś w elektrolitach nośnikami są jony
dodatnie i ujemne. W przeciwieństwie do metali przewodnictwo elektryczne elektrolitów
wzrasta z temperaturą, gdyż wraz z temperaturą wzrasta tzw. ruchliwość jonów, a także
(zwłaszcza w przypadku słabych elektrolitów) stopień dysocjacji. Uporządkowany ruch jonów

Ćwiczenie 11

4

w elektrolitach, czyli prąd elektryczny, uzyskujemy za pomocą zewnętrznego pola elektrycz-
nego wytworzonego przez zanurzone w elektrolicie elektrody, pomiędzy którymi panuje róż-
nica potencjałów. Elektrodę o dodatnim potencjale nazywamy

anodą

, a elektrodę o poten-

cjale ujemnym

katodą

. Pod wpływem pola elektrycznego jony dodatnie poruszają się w kie-

runku katody i dlatego nazywamy je

kationami

. Jony ujemne poruszają się w kierunku anody

i nazywamy je

anionami

.

Rys. 1.2 Ruch jonów elektrolitu w polu elektrycznym.

Po dojściu kationu (jonu dodatniego) do katody następuje

redukcja

, czyli pobranie

elektronu (lub elektronów) przez jon. W przypadku jonu wodoru w wyniku redukcji powstaje
wodór, który uwalnia się z roztworu.

2H + 2 → H ↑.

W przypadku, gdy kationem był jon metalu, w wyniku redukcji powstaje atom tego metalu,
który następnie osadza się na elektrodzie.

Cu + 2 → Cu.

Z kolei na anodzie dochodzi do procesu

utleniania

(oddawania elektronów). W procesach

chemicznych zachodzących na anodzie bardzo często aktywny udział biorą cząsteczki wody.
W przypadku elektrolitów kwasowych na anodzie dochodzi do procesu

H O → ½O ↑ +2H + 2e,

np.

SO − 2e → SO ,

SO + H O → ½O ↑ +2H + SO .

Ostatecznie, podczas elektrolizy wodnego roztworu kwasu siarkowego będziemy obserwo-
wać wydzielanie się wodoru na katodzie i tlenu na anodzie.

Całość procesów fizyko-chemicznych zachodzących w elektrolicie pod wpływem przyłożone-
go zewnętrznego pola elektrycznego nazywamy

elektrolizą

. Elektroliza ma duże znaczenie

praktyczne i jest szeroko stosowana w wielu gałęziach przemysłu, m.in. do

•

Produkcji gazów takich jak wodór, tlen, chlor.

•

Produkcji metali takich jak glin, lit, potas, sód.

Wyznaczanie równoważnika elektrochemicznego wodoru …

5

•

Galwanizacji, czyli pokrywania przedmiotów metalowych cienką warstwą innego me-
talu (np. cynkowanie blach, posrebrzanie biżuterii, chromowanie, niklowanie).

•

Otrzymywania bardzo czystej chemicznie miedzi (rafinacja miedzi).

•

Produkcji wielu związków chemicznych.

1.3

Prawa Faradaya

Zjawisko elektrolizy badał w XIX wieku Michael Faraday – angielski fizyk i chemik. Sformu-

łował on dwa prawa nazywane na jego cześć prawami Faradaya.

Pierwsze prawo Faradaya

stwierdza, że masa

substancji, jaka wydziela się podczas

elektrolizy na każdej z elektrod jest proporcjonalna do ilości ładunku , jaki przepływa przez
elektrolit

=

,

przy czym współczynnik proporcjonalności występujący w tym prawie, nazywany

równo-

ważnikiem elektrochemicznym

wydzielonej na elektrodzie substancji, zależy wyłącznie od

rodzaju substancji, a nie zależy od rodzaju elektrolitu, jego stężenia, rozmiaru i kształtu elek-
trod, temperatury i innych czynników zewnętrznych. W układzie SI jednostką równoważnika
elektrochemicznego jest kg/C, jednak ze względu na małą wartość równoważników elektro-
chemicznych wygodniej jest używać jednostki mg/C. Równoważnik elektrochemiczny jest
liczbowo równy masie substancji, jaka wydzieli się na elektrodzie, jeśli przez elektrolit prze-
płynie jednostkowy ładunek.

Drugie prawo Faradaya

bywa podawane w różnych postaciach. Jedna z tych postaci jest

następująca: stosunek równoważników elektrochemicznych różnych substancji jest równy
stosunkowi ich gramorównoważników

= .

Gramorównoważnikiem

(inaczej równoważnikiem chemicznym)

jonu nazywamy stosunek

jego

masy molowej

(masy jednego mola substancji) do wartościowości

= .

Drugie prawo Faradaya można również sformułować tak: stosunek gramorównoważników
substancji do ich równoważników elektrochemicznych jest dla wszystkich substancji jedna-
kowy

= ,

czyli

= ∙ = = !"#$%.

Ćwiczenie 11

6

Stosunek ten oznaczamy literą

i nazywamy

stałą Faradaya.

Stała Faradaya jest liczbowo

równa ładunkowi elektrycznemu, jaki powoduje wydzielenie się na elektrodzie

1/ części mo-

la substancji o wartościowości . Stała Faradaya wynosi

= 96 485,3365.21/

C

mol.

Z interpretacji fizycznej stałej Faradaya, wynika, że jest ona równa iloczynowi ładunku ele-
mentarnego i liczby Avogadra

3

4

:

= 3

4

.

2.

Metoda pomiaru

Jak pokazano w punkcie 1.2, podczas elektrolizy wodnego roztworu kwasu siarkowego na

katodzie wydziela się wodór, a na anodzie tlen. Wykorzystamy to do wykonania pomiaru
równoważnika elektrochemicznego wodoru

1

. W eksperymencie przeprowadzimy elektrolizę

10% roztworu kwasu siarkowego przy stałej wartości prądu elektrycznego. Jeśli przez elek-
trolit przepływa prąd elektryczny o stałej wartości

5, to ładunek przeniesiony przez elektrolit

w czasie

6 (czytaj tau) wynosi = 5 ∙ 6. Wobec tego, zgodnie z pierwszym prawem Faradaya,

masa substancji wydzielonej na każdej elektrod po czasie

6 będzie równa:

.6/ = 56.

Podczas eksperymentu będziemy mierzyć masę wodoru, jaki wydzieli się po czasie
6 , 6 , … 6

8

.6 < 6 < ⋯ < 6

8

/. Pomiar masy będzie pomiarem pośrednim polegającym na

odczytaniu objętości

; wydzielonego wodoru i wyznaczeniu jego gęstości < w danych warun-

kach

. = <;/. Następnie do zebranych punktów pomiarowych {

>

, 6

>

}, @ = 1. . # dopasuje-

my metodą najmniejszych kwadratów prostą typu

= A6. Takie podejście ma dwie zalety. Po

pierwsze, sprawdzimy zgodność naszych wyników z pierwszym prawem Faradaya. Po drugie,
znajomość współczynnika kierunkowego

A prostej = A6. oraz natężenie prądu 5 jaki płynął

przez elektrolit podczas naszego eksperymentu pozwoli nam na wyznaczenie równoważnika
elektrochemicznego wodoru ze wzoru

=

A

5.

Oczywiście musimy zdawać sobie sprawę, że przeprowadzony przez nas test słuszności
pierwszego prawa Faradaya nie jest kompletny. Sprawdzimy jedynie proporcjonalność wy-
dzielonej na elektrodzie masy wodoru do ładunku jaki przepłynął między elektrodami. Nie
możemy na tej podstawie stwierdzić, czy współczynnik proporcjonalności (równoważnik
elektrochemiczny) będzie taki sam w przypadku innego elektrolitu, w którym wydziela się
wodór, w przypadku innego stężenia elektrolitu, innej geometrii elektrod itp., a także, czy dla
innych substancji zależność wydzielonej masy od ładunku ma też charakter liniowy.

1

Wydzielający się podczas elektrolizy tlen w dużym stopniu rozpuszcza się w wodzie i dlatego wyznaczenie,

opisaną tu metodą, równoważnika elektrochemicznego tlenu obarczone byłoby zbyt dużym błędem.

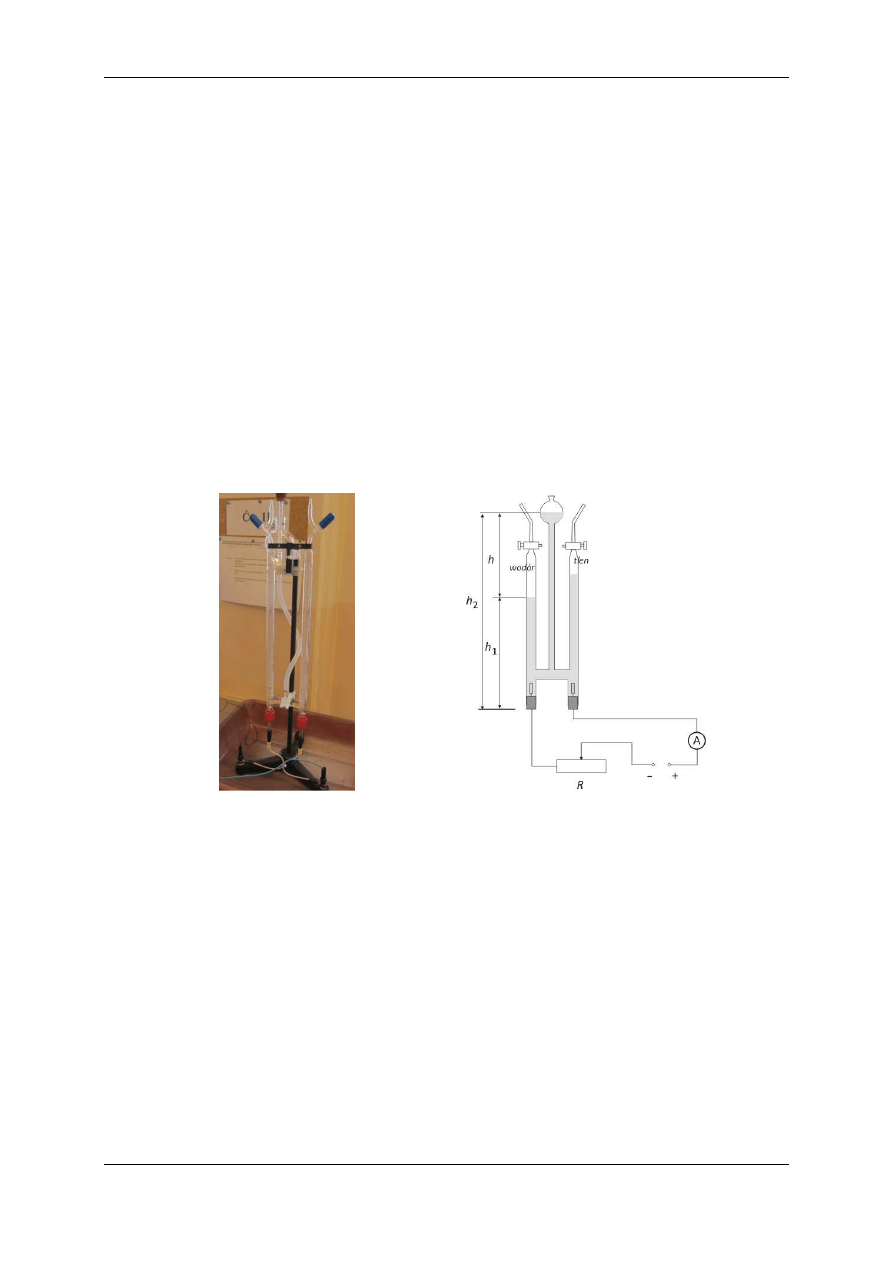
Wyznaczanie równoważnika elektrochemicznego wodoru …

7

3.

Wykonanie ćwiczenia

3.1

Opis układu pomiarowego

Elektrolizę 10% wodnego roztworu kwasu siarkowego przeprowadzimy w tzw. aparacie

Hofmanna (patrz. rysunek 2.1). Są to trzy połączone ze sobą rurki (naczynia połączone), z
których dwie boczne, nazywane

biuretami

, mają wprowadzone od dołu elektrody (na ogół

platynowe) a od góry wyposażone są w zaworki pozwalające na szczelne zamknięcie rurek.
Środkowa rurka, w górnej części zakończona jest szklaną bańką, w której zbiera się elektrolit
wypierany przez gazy gromadzące się w bocznych biuretach (patrz. rysunek 2.2). Na po-
wierzchni obu biuret naniesiona jest skala pozwalająca na mierzenie objętości gazów, jakie
zbierają się w rurkach podczas elektrolizy. Do elektrod umieszczonych w biuretach przykła-
damy napięcie z zasilacza prądu stałego poprzez opornicę suwakową, dzięki której możemy
ustawić żądane natężenie prądu płynącego przez elektrolit. Schemat układu pomiarowego
przedstawia rysunek 2.2.

Rys. 2.1. Aparat Hoffmana.

Rys. 2.2. Schemat układu pomiarowego.

3.2

Przebieg pomiarów

W ćwiczeniu mamy do czynienia z roztworem kwasu siarkowego. Należy zatem za-

chować szczególną ostrożność. Podczas wypuszczania gazów z biuret, wyloty rurek dobrze
jest osłonić kawałkiem ręcznika papierowego, a zaworki na biuretach odkręcać powoli.

1.

Po zmontowaniu układu pomiarowego (patrz rys. 2.2) i zgodzie osoby prowadzącej włą-
czamy zasilanie i ustawiamy natężenie prądu na ok. 0,2 A. Zaworki na biuretach powinny
być zakręcone. Po czasie ok. 2 minut wyłączamy zasilanie i ostrożnie wypuszczamy gazy z
obu biuret, po czym ponownie zakręcamy zaworki. Opisane czynności mają na celu nasy-
cenie roztworu wodorem, tak aby wodór, jaki będzie się wydzielał w dalszej części ekspe-
rymentu w całości opuszczał roztwór.

Ćwiczenie 11

8

2.

Ustawiamy katetometr (przyrząd służący do zdalnego pomiaru długości pionowych od-
cinków) tak, aby przez lunetkę katetometru można było obserwować poziom roztworu w
biurecie, w której będzie się zbierał wodór oraz poziom roztworu w zbiorniczku wyrów-
nawczym (patrz. rys. 2.2). Katetometr powinien być ustawiony dokładnie w pionie. Służą
do tego: pion zawieszony na katetometrze oraz dwie śruby regulacyjne umieszczone w
podstawie katetometru.

3.

Odczytujemy i zapisujemy aktualne ciśnienie atmosferyczne oraz temperaturę otocze-
nia

2

.

4.

Włączamy jednocześnie zasilacz i stoper. Kontrolujmy czy natężenie prądu płynącego
przez elektrolit nie zmieniło się i w razie potrzeby korygujemy natężenie prądu suwakiem
opornicy.

5.

Po dwóch minutach (120 s) wyłączamy zasilacz i odczekujemy ok. 0,5-1 minuty, aż wszyst-
kie pęcherzyki wodoru wypłyną na powierzchnię. Następnie odczytujemy objętość wodo-
ru

; (należy zwrócić uwagę na kierunek skali na powierzchni biurety i wartość najmniej-

szej działki skali). Za pomocą katetometru mierzymy poziomy roztworu

3

ℎ i ℎ jak na ry-

sunku 2.2 (Uwaga: gazu nie wypuszczamy!)

6.

Czynności opisane w punktach 4 i 5 powtarzamy ok. 7-10 razy.

7.

Zebrane dane pomiarowe zapisujemy na bieżąco w tabeli (patrz tabela 3.1).

8.

Po zakończeniu pomiarów ostrożnie wypuszczamy gazy z obu biuret i porządkujemy sta-
nowisko.

Tabela 3.1. Fragment tabeli do zapisywania wyników pomiarów w ćw. 11.

Lp.

6 [s]

; [cm ]

ℎ [cm]

ℎ [cm]

1

0

0

–

–

2

120

…

3.3

Obliczenia

Po wykonaniu pomiarów opisanych w poprzednim punkcie znamy objętość

; wydzielo-

nego na katodzie wodoru w funkcji czasu. Masę wydzielonego wodoru wyliczymy z zależ-
ności

= <;,

gdzie

< jest gęstością wodoru w danych warunkach, czyli w danej temperaturze G i danym

ciśnieniu

H. Z tablic odczytujemy gęstość <

I

wodoru w tzw.

warunkach normalnych

, tzn. w

temperaturze

G

I

= 273,15 K i pod ciśnieniem H

I

= 1023,25 hPa. Korzystając z równania

stanu gazu

2

Do obliczeń potrzebne są nam temperatury: elektrolitu, wydzielonego wodoru i pary wodnej nad elektrolitem.

W warunkach naszego eksperymentu możemy z dużą dokładnością przyjąć, że te temperatury są równe tempe-
raturze otoczenia.

3

Nie ma znaczenia poziom odniesienia, tzn. poziom, względem którego mierzymy oba poziomy, gdyż nas inte-

resuje jedynie różnica poziomów

ℎ i ℎ , czyli wysokość ℎ słupa roztworu.

Wyznaczanie równoważnika elektrochemicznego wodoru …

9

H ∙ ;

G =

H

I

∙ ;

I

G

I

i definicji gęstości dostajemy

< = ; = ;

I

∙

HG

I

H

I

G.

Stąd otrzymujemy wzór na gęstość

< wodoru o temperaturze G znajdującego się pod ciśnie-

niem

H przyjmuje postać

< = <

I

∙

HG

I

H

I

G.

Ciśnienie

H wodoru możemy wyliczyć z warunku równowagi ciśnień. W biurecie z katodą,

nad powierzchnią elektrolitu znajduje się wodór i para wodna. Suma ciśnień cząstkowych
obu gazów (

H wodoru i H

O

pary wodnej) musi równoważyć ciśnienie atmosferyczne

H

P

i ci-

śnienie wywierane przez słup o wysokości

ℎ cieczy o gęstości <

Q

, czyli tzw. ciśnienie hydro-

statyczne

H

R

równe

H

R

= <

Q

Sℎ.

Z warunku równowagi ciśnień mamy

H + H

O

= H

P

+ H

R

.

Stąd ciśnienie wodoru wynosi

H = H

P

− H

O

+ <

Q

Sℎ.

Ciśnienie (tzw. prężność) nasyconej pary wodnej dla danej temperatury odczytujemy z tablic
lub wyliczamy z empirycznego wzoru (wg PN-EN ISO 13788: 2003)

H

O

= 6,105 ∙

e

17,269∙t

237,3+t

hPa,

gdzie

% jest temperaturą pary wodnej w stopniach Celsjusza.

Gęstość

<

Q

10% wodnego roztworu kwasu siarkowego w temperaturze

% °C odczytujemy z

tablic lub wyliczamy z empirycznego wzoru

<

Q

.%/ = 1,0745 − 0,000420 ∙ %

g

cm .

Podczas obliczeń zwróćmy uwagę na jednostki. Jeśli ciśnienie atmosferyczne, ciśnienie nor-
malne i prężność pary podajemy w hPa, to ciśnienie hydrostatyczne też musimy podać w
hPa. Warto zauważyć, że jeśli do obliczeń ciśnienia hydrostatycznego wodoru

.H

R

= <

Q

Sℎ/

weźmiemy wartość gęstości

<

Q

roztworu w

V

WX

Y

, wysokość słupa roztworu

ℎ w cm, wartość

przyśpieszenia ziemskiego

g w

X

Z

[

, a wynik podzielimy przez 10, to otrzymamy wynik w

hPa

.1 g/cm =

10

kg/m , 1 cm =

10

m, 1 hPa =

10

Pa,

10 ∙ 10 /10

=

1/10

/.

Ćwiczenie 11

10

Pomocnicze dane, które będą nam potrzebne podczas liczenia masy wodoru zapisujemy w
tabeli (patrz tabela 3.2).

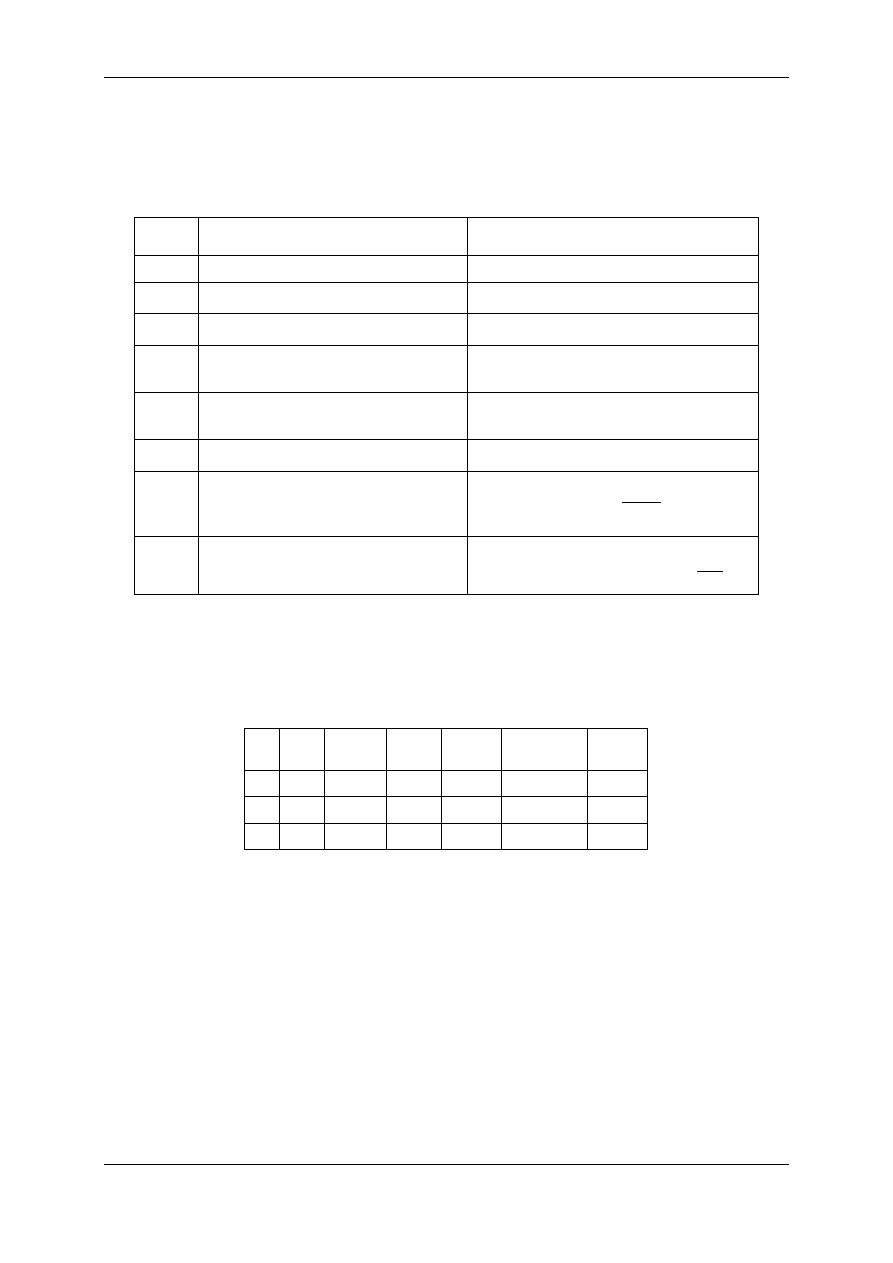
Tabela 3.2. Tabela pomocniczych wielkości potrzebnych podczas wyliczania masy wodoru, jaki wydzielił się
podczas elektrolizy.

Symbol

wielkości

Opis

Wartość

H

I

ciśnienie normalne

1013,25 hPa

G

I

temperatura normalna

273,15 K

<

I

gęstość wodoru w warunkach normalnych

0,08989 mg/cm

3

%

temperatura elektrolitu, pary wodnej

i wodoru w skali Celsjusza

odczytujemy z termometru w °C

G

temperatura elektrolitu, pary wodnej

i wodoru w skali Kelwina

G = % + 273,15

H

P

ciśnienie atmosferyczne

odczytujemy z barometru w hPa

H

O

prężność nasyconej pary wodnej dla tem-

peratury

%

z tablic lub ze wzoru

H

O

= 6,105 ∙ e

], ^_∙`

], `

hPa

ρ

r

gęstość 10% roztworu wodnego kwasu

siarkowego dla temperatury

%

z tablic lub ze wzoru

<

Q

.%/ = 1,0745 − 0,00042 ∙ %

g

cm .

Po zgromadzeniu wszystkich potrzebnych danych przystępujemy do wyliczenia masy wodoru
zależnej od czasu przepływu prądu przez elektrolit. Wyniki obliczeń zapisujemy w tabeli
(patrz tabela 3.3).

Tabela 3.3 Fragment tabeli do zapisywania wyników obliczeń

H, <, w ćw. 11.

Lp.

6 [s] ; [cm

3

]

ℎ [cm] H [hPa] < [mg/cm

3

]

[mg]

1

0

–

–

–

–

0

2

120

...

3.4

Opracowanie wyników pomiarów

3.4.1

Równoważnik elektrochemiczny wodoru

Po wyliczeniu mas wydzielonego wodoru w poszczególnych czasach sporządzamy wy-

kres zależności masy wydzielonego wodoru

od czasu przepływu prądu

6 i do punktów

pomiarowych dopasowujemy metodą najmniejszych kwadratów prostą

= A

τ

(możemy

skorzystać z programu WykresLab). Sprawdzimy tym samym, czy przebieg naszego ekspery-
mentu jest w zgodzie z pierwszym prawem Faradaya, tzn. czy masa wodoru wydzielającego
się na katodzie była proporcjonalna do ładunku, jaki przepływał między elektrodami.

Wyznaczanie równoważnika elektrochemicznego wodoru …

11

Wartość równoważnika elektrochemicznego wodoru znajdujemy ze związku:

=

A

5.

Niepewność wyznaczenia wartości równoważnika elektrochemicznego wodoru wyliczamy ze
wzoru:

a. / = ∙ bc

a.A/

A d + c

a.5/

5 d .

Następnie zapisujemy wynik pomiaru zgodnie z regułami zapisu omówionymi w [3] rozdz. 8.
Wynik porównujemy (patrz [3] rozdz. 10) z tablicową wartością równoważnika elektroche-
micznego wodoru, czyli sprawdzamy, czy

ePfg

mieści się wyznaczonym przez nas przedziale

h − a. /, + a. /i. Wartość tablicowa równoważnika elektrochemicznego wodoru jest
równa

ePfg

= 0,01044 mg/C.

3.4.2

Stała Faradaya

Korzystając z otrzymanego w poprzednim punkcie wyniku oraz drugiego prawa Fara-

daya, możemy wyliczyć stałą Faradaya. Korzystamy ze wzoru

= ∙ .

Dla wodoru H

2

w tablicach znajdujemy

= 2,0016 g/mol = 2001,6 mg/mol oraz = 2.

Niepewność masy molowej wodoru możemy zaniedbać, a zatem

a. / = ∙

a. /

.

Otrzymany wynik porównujemy z wartością tablicową:

ePfg

= 96485,3365.21/ C/mol.

3.4.3

Ładunek elementarny

Korzystając z wyniku otrzymanego w poprzednim punkcie i interpretacji fizycznej stałej Fara-
daya (patrz punkt 1.3) wyliczamy wartość ładunku elementarnego

=

3

4

.

Z tablic znajdujemy wartość liczby Avogadro

3

4

= 6,02214129 ∙ 10 mol . Niepewność

wyznaczenia ładunku elementarnego liczymy ze wzoru

a. / = ∙

a. /

.

Otrzymany wynik porównujemy z wartością tablicową:

= 1,602176487.40/ · 10

_

C.

Ćwiczenie 11

12

4.

Literatura

[1] T. Dryński, Ćwiczenia laboratoryjne z fizyki, PWN, Warszawa 1978.

[2] Praca pod red. B.Oleś i M. Duraj: Ćwiczenia laboratoryjne z fizyki, cz.I. wyd.4, Wyd. PK,

Kraków 2008.

[3] J. Kurzyk, Niepewności pomiaru – wersja podstawowa, Dok. wewnętrzny IFPK, 2014.

[4] D. Halliday, R. Resnick, Fizyka, t. 2, PWN, Warszawa 2006.

[5]

http://physics.nist.gov/cuu/Constants/index.html

- tablice stałych fizycznych.