D
D
Y
Y
N
N
A
A
M
M
I
I
K
K
A
A
P
P
Ł
Ł
Y
Y
N
N
Ó
Ó
W
W
D
D
O
O
S
S
K
K
O
O
N
N
A
A
Ł
Ł
Y
Y
C
C
H
H
P
P
ł
ł
y
y
n
n
y
y
:
:
c
c
i
i
e
e
c
c
z
z
e
e
,
,
g
g
a
a
z
z
y
y
C
C
i
i
e
e
c
c
z
z
e
e
d
d
o
o
s
s
k
k
o
o
n
n
a
a
ł
ł
e
e
:
:
¾ gęstość cieczy na całej długości przewodu się nie zmienia,
¾ brak tarcia wewnętrznego, cząstki idealnie ruchliwe, cząstki nieściśliwe,
¾ spełnia prawa Eulera, Pascala i Archimedesa,
G
G
a
a
z
z
y
y
d
d
o
o
s
s
k
k
o
o
n
n
a
a
ł
ł
e
e
:
:
9 zbiór punktów o idealnej sprężystości i braku wzajemnych oddziaływań,
9 spełnia prawa Boyle’a-Mariotta, Gay-Lussaca-Charlesa, Clapeyrona
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
A
A
C
C
I
I
Ą
Ą
G
G
Ł
Ł
O
O
Ś
Ś
C
C
I
I
S
S
T
T
R
R
U
U
M
M
I
I
E
E
N
N
I
I
A
A
C
C
I
I
E
E
C
C
Z
Z
Y
Y
(
(
S
S
T
T
R
R
U
U
G
G
I
I
)
)
W
W
R
R
U
U
C
C
H
H
U
U
U
U
S
S
T
T
A
A
L
L
O
O
N
N
Y
Y
M
M
:
:
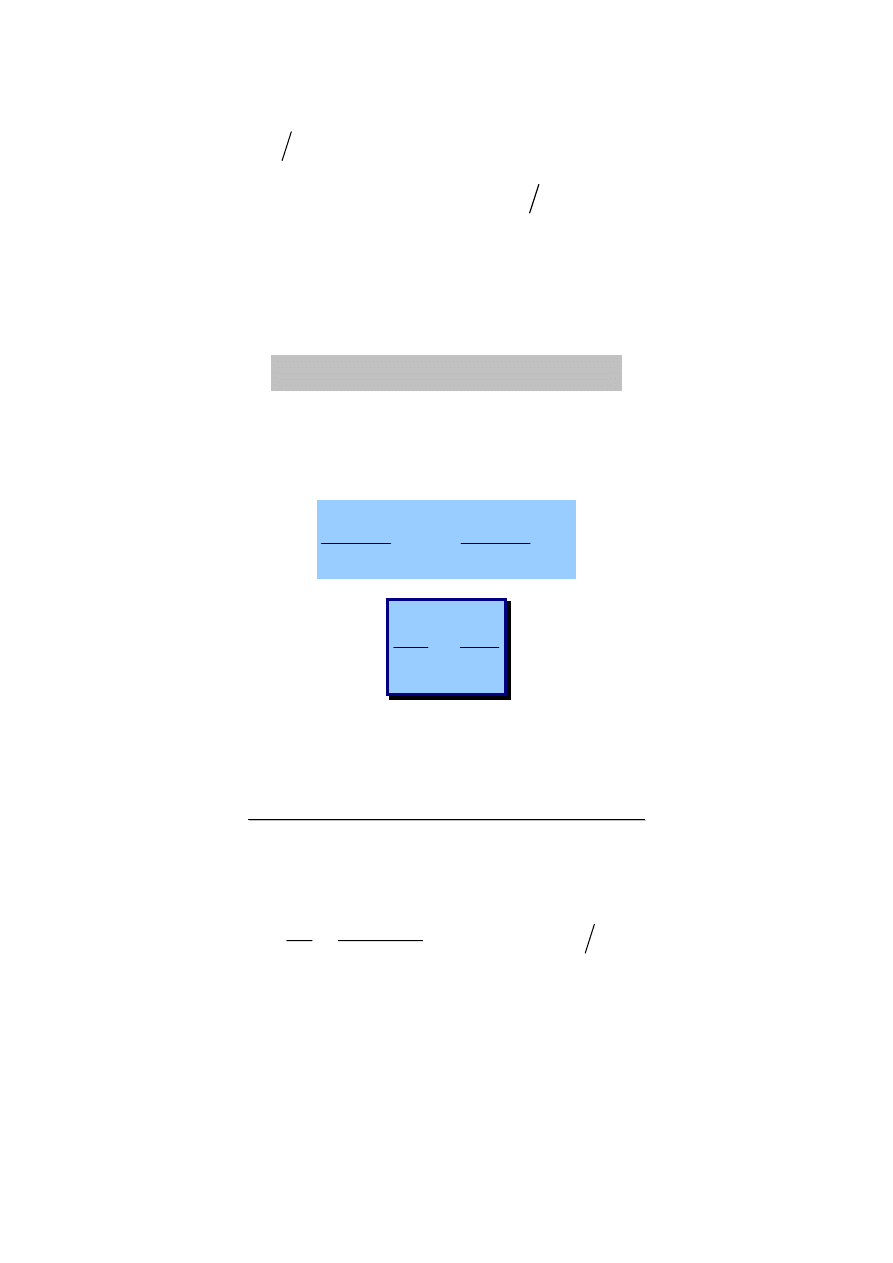
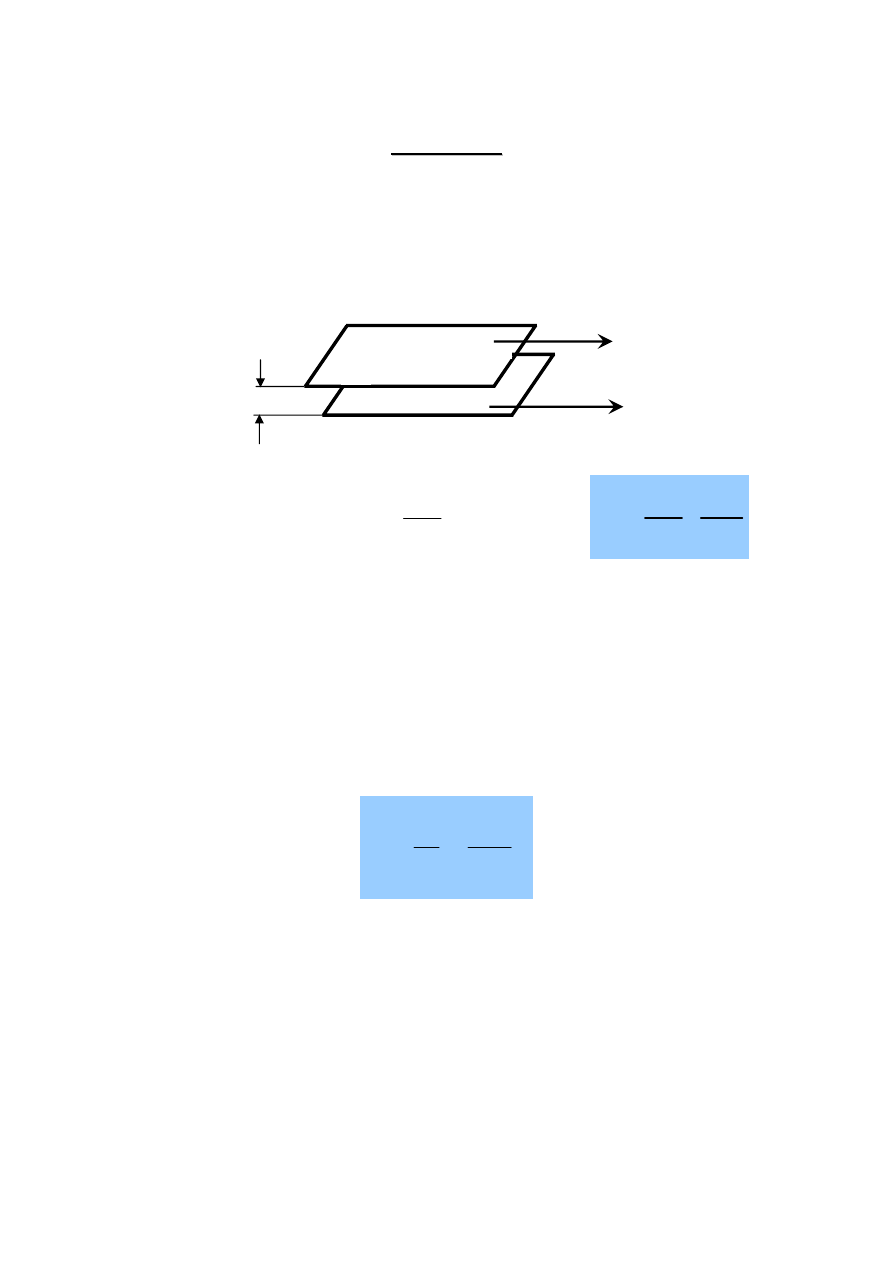
Założenie: ciecz wypełnia przewód całkowicie!
S
1
S =3S’
3
3
S
2
Natężenie przepływu masy cieczy płynącej ruchem ustalonym przez dowolny
przewód, jest stałe we wszystkich przekrojach przewodu, prostopadłych do
kierunku przepływu. Zatem MASOWE NATĘŻENE PRZEŁYWU:
W
1
=W
2
=.......=W
n
]
s
kg
[
L
u
S
W
ρ
⋅
⋅
=
u - średnia prędkość przepływu,
ρ
- gęstość płynu,
S - pole powierzchni przekroju przewodu,
s]
m
[
3
u
S
U
⋅
=
OBJĘTOŚCIOWE NATĘŻENIE PRZEPŁYWU
s]
kg
[
L
U
W
ρ
⋅
=
zakładając brak zmian gęstości płynu na całej długości przewodu (przepływ
izotermiczny, płyny są wówczas nieściśliwe) można stwierdzić, że:
U
1
=U
2
=.....=U
n
n
n
u
S
u
S
u
S
⋅
=
⋅⋅
⋅⋅
=
⋅
=
⋅
2
2
1
1
2
2
1
1
u
S
u
S
⋅
=
⋅
zakładając przekrój kołowy pole przekroju
S
wyniesie odpowiednio:
2
2
2
1
2
1
4
4
u
d
u
d
⋅
⋅
=
⋅
⋅
π
π
2
1
2
2
2
1
d
d
u
u
=
P
P
R
R
Ę
Ę
D
D
K
K
O
O
Ś
Ś
Ć
Ć
M
M
A
A
S
S
O
O
W
W
A
A
S
S
T
T
R
R
U
U
M
M
I
I
E
E
N
N
I
I
A
A
C
C
I
I
E
E
C
C
Z
Z
Y
Y
Jest to stosunek masowego natężenia przepływu do pola powierzchni
przekroju przewodu.
]
m
kg
[
2
s
u
S
u
S
S
W
w
L
L
L
⋅
⋅
=
⋅
⋅
=
=
ρ
ρ
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
E
E
B
B
E
E
R
R
N
N
O
O
U
U
L
L
I
I
E
E
G
G
O
O
D
D
L
L
A
A
P
P
Ł
Ł
Y
Y
N
N
U
U
D
D
O
O
S
S
K
K
O
O
N
N
A
A
Ł
Ł
E
E
G
G
O
O
gęstość płynu jest wielkością stałą
ρ
L
=const
Energia kinetyczna:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
=
=
2
2
2
2
2
1
2
2
2
2
u
u
dm
dmu
mv
dE
K
L
d
u
S
dm
ρ
τ
⋅
⋅
⋅
=
Praca sił ciśnienia (energia potencjalna ciśnienia):
τ
τ
d
u
S
p
d
u
S
p
dA
2
2
2
1
1
1
−
=
Energia potencjalna położenia:
2
2
2
1
1
1
gz
d
u
S
gz
d
u
S
dE
L
L
p
τρ
τρ
−
=
Z
Z
A
A
S
S
A
A
D
D
A
A
Z
Z
A
A
C
C
H
H
O
O
W
W
A
A
N
N
I
I
A
A
E
E
N
N
E
E
R
R
G
G
I
I
I
I
(wzrost energii kinetycznej powoduje jednoczesny spadek
energii potencjalnej położenia i ciśnienia):
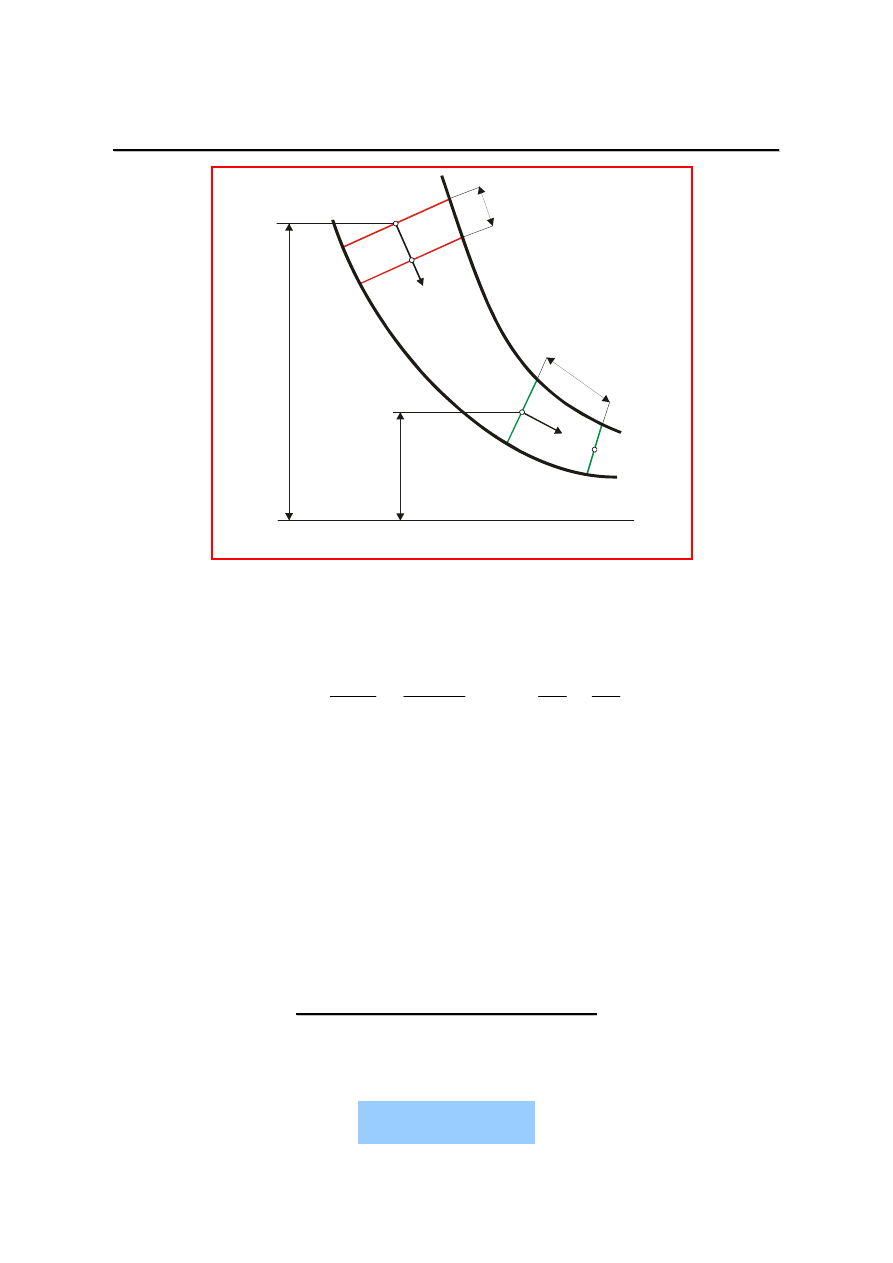
dA
dE
dE
p
k
+
=
dl
1
dl
2
u
1
p
1
p
2
1
2
1’
2’
S
1
S
2
u
2
poziom zerowy
z
1
z
2
po podstawieniu i skróceniu przez
τ
d
u
S
⋅
⋅
, ponieważ zachowana jest zasada
ciągłości strugi otrzymuje się:
const
z
g
p
u
z
g
p
u
L
L
=
⋅
+
+
=
⋅
+
+
2
2
2
2
1
1
2
1
2
2
ρ
ρ
/:g
w powyższym równaniu każdy z członów ma wymiar [m
2
/s
2
]
H
z
g
p
g
u
L
=
+
⋅
+
ρ
2
2
natomiast w powyższym równaniu każdy z członów ma wymiar [m]
Z równania tego wynika, że suma trzech wysokości a mianowicie
wysokości odpowiadającej ciśnieniu dynamicznemu
g
u
2
2
, wysokości
odpowiadającej ciśnieniu statycznemu
g
p
L
⋅
ρ
i wysokości niwelacyjnej
(odniesienia)
z
jest wielkością stałą dla jednostki masy strugi w każdym
przekroju przewodu.
lub inaczej
W czasie ustalonego ruchu cieczy doskonałej suma energii kinetycznej,
energii ciśnienia i energii potencjalnej położenia dla jednostki masy
płynącej strugi cieczy jest wielkością stałą.
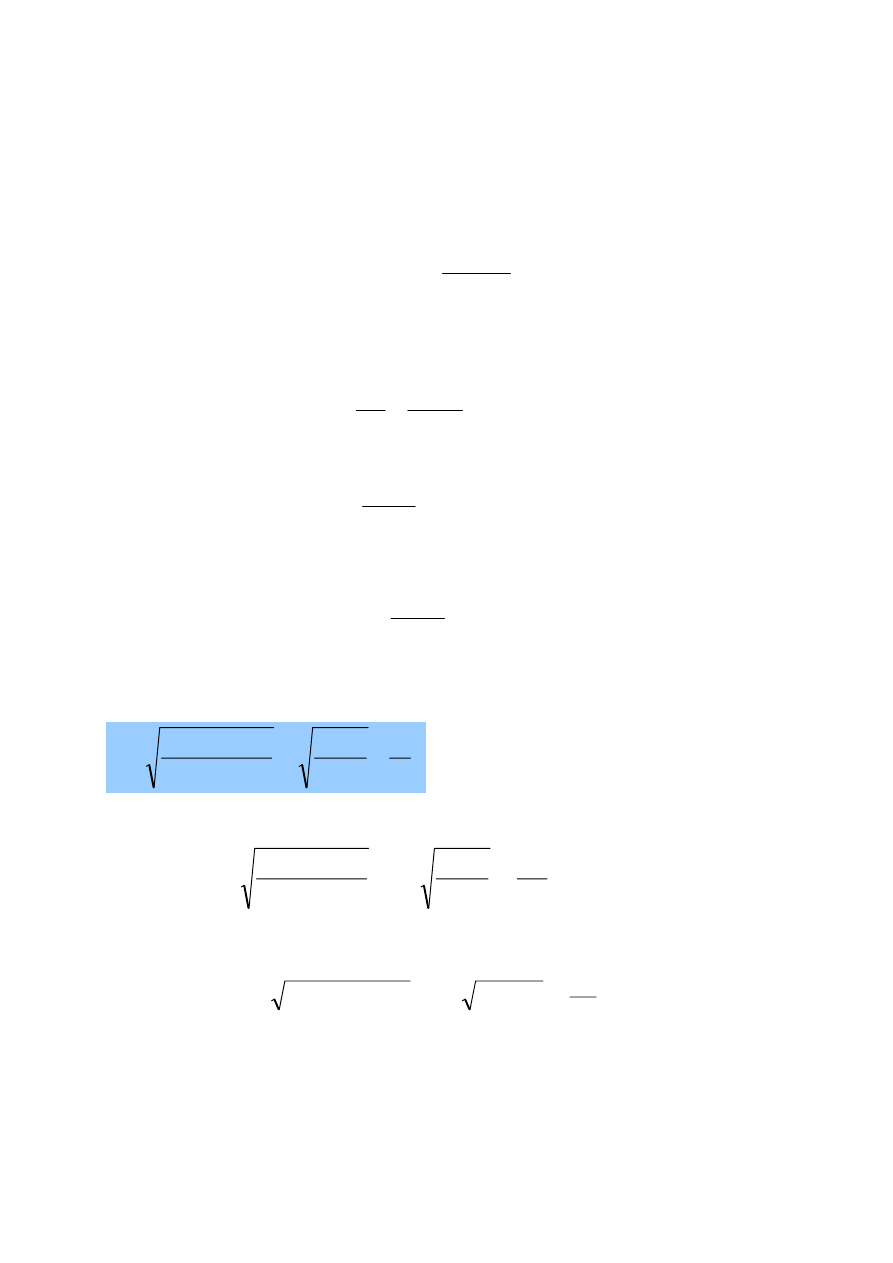
W większości w praktyce przewody są poziome lub bardzo zbliżone do
poziomu, czyli z
1
=z
2
(człony te opuszcza się w równaniu). Przekształcając dalej
równanie Bernouliego, mnożąc przez
g
⋅
ρ
otrzymuje się:
ρ
⋅
−
=
−
2
2
1
2
2
2
1
u
u
p
p
czyli zwiększenie prędkości spowoduje spadek ciśnienia i odwrotnie.
Gdy natomiast w równaniu
const
z
g
p
g
u
L
=
+
⋅
+
ρ
2
2
opuści się z i pomnoży
obie strony przez
g
⋅
ρ
otrzyma się następujące równanie
const
p
u
=
+
⋅
2
2
ρ
.
Każdy z członów ma wymiar ciśnienia [Pa], zatem otrzymuje się wyrażenie
na ciśnienie całkowite
p
c
, gdzie
2
2
ρ
⋅
u
jest
ciśnieniem dynamicznym
p
d
a
p
jest ciśnieniem statycznym
p
s
.
Stąd prędkość można obliczyć w oparciu o
następujący wzór:
⎥⎦
⎤
⎢⎣
⎡
⋅
=
−
⋅
=
s
m
)
(
ρ
ρ
d
s
c
p
p
p
u
2
2
Objętościowe natężenie przepływu wynosi zatem:
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
=
−
⋅
⋅
=
⋅
=
s
m
)
(
3
ρ
ρ
d
s
c
p
S
p
p
S
u
S
U
2
2
Natomiast masowe natężenie przepływu jest następujące:
⎥⎦
⎤
⎢⎣
⎡
⋅
⋅
=
−
⋅
⋅
=
⋅
⋅
=
s
kg
)
(
d
s
c
p
S
p
p
S
u
S
W
ρ
ρ
ρ
2
2
I
I
N
N
T
T
E
E
R
R
P
P
R
R
E
E
T
T
A
A
C
C
J
J
A
A
G
G
R
R
A
A
F
F
I
I
C
C
Z
Z
N
N
A
A
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
A
A
B
B
E
E
R
R
N
N
O
O
U
U
L
L
I
I
E
E
G
G
O
O
D
D
L
L
A
A
C
C
I
I
E
E
C
C
Z
Z
Y
Y
D
D
O
O
S
S
K
K
O
O
N
N
A
A
Ł
Ł
E
E
J
J
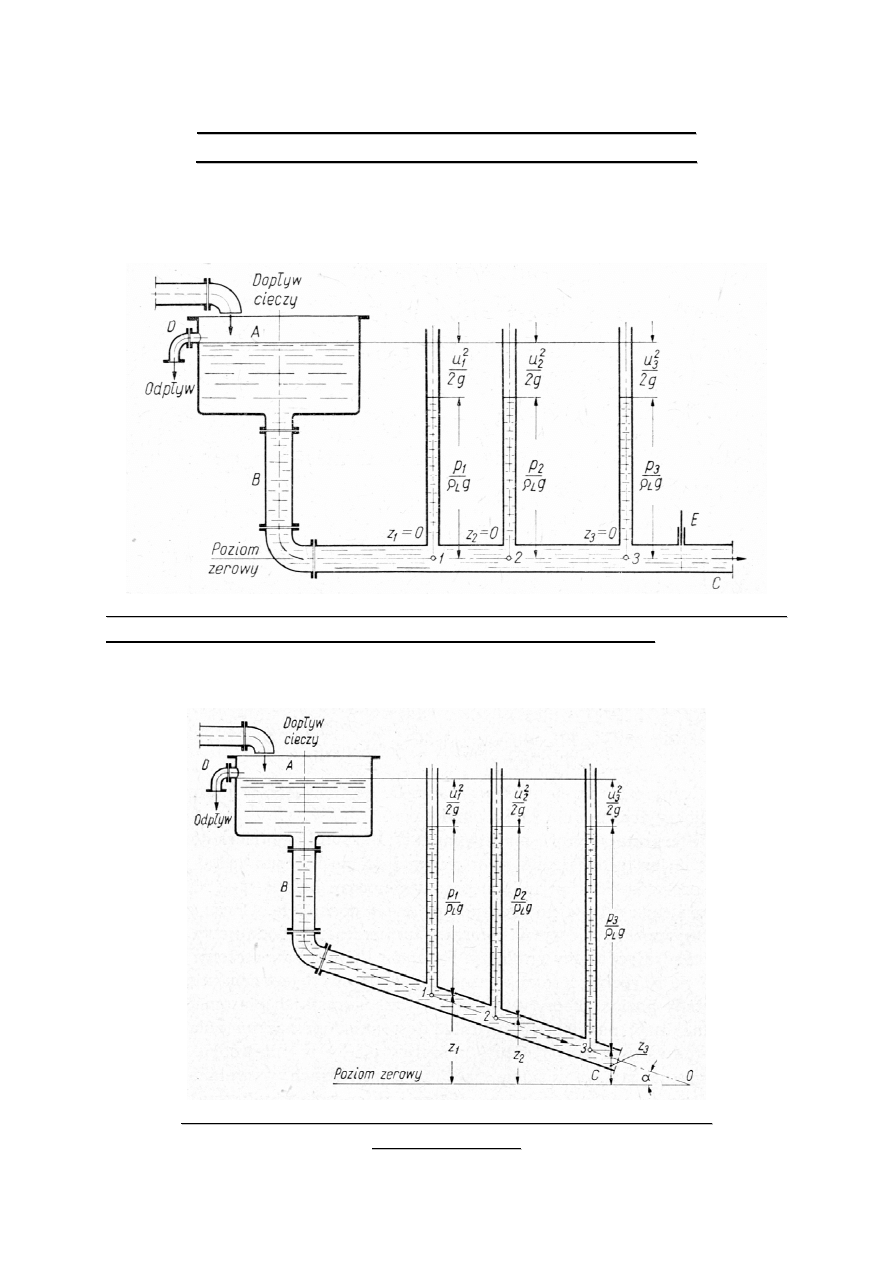
1. Równoległy, poziomy przebieg przewodu w stosunku do poziomu
odniesienia. Przekrój przewodu wzdłuż całej długości jest stały tzn., że
prędkość przepływu też jest stała.
I
I
s
s
t
t
n
n
i
i
e
e
j
j
e
e
z
z
a
a
t
t
e
e
m
m
n
n
i
i
e
e
z
z
m
m
i
i
e
e
n
n
n
n
o
o
ś
ś
ć
ć
w
w
y
y
s
s
o
o
k
k
o
o
ś
ś
c
c
i
i
:
:
o
o
d
d
n
n
i
i
e
e
s
s
i
i
e
e
n
n
i
i
a
a
,
,
c
c
i
i
ś
ś
n
n
i
i
e
e
n
n
i
i
a
a
s
s
t
t
a
a
t
t
y
y
c
c
z
z
n
n
e
e
g
g
o
o
i
i
d
d
y
y
n
n
a
a
m
m
i
i
c
c
z
z
n
n
e
e
g
g
o
o
p
p
r
r
z
z
y
y
w
w
/
/
w
w
p
p
o
o
ł
ł
o
o
ż
ż
e
e
n
n
i
i
u
u
p
p
r
r
z
z
e
e
w
w
o
o
d
d
u
u
.
.
2. Przewód przebiega pod kątem
α w stosunku do poziomu odniesienia.
Przekrój przewodu jest stały.
M
M
i
i
m
m
o
o
z
z
m
m
i
i
e
e
n
n
n
n
o
o
ś
ś
c
c
i
i
w
w
a
a
r
r
t
t
o
o
ś
ś
c
c
i
i
t
t
r
r
z
z
e
e
c
c
h
h
w
w
y
y
s
s
o
o
k
k
o
o
ś
ś
c
c
i
i
i
i
c
c
h
h
s
s
u
u
m
m
a
a
j
j
e
e
s
s
t
t
w
w
i
i
e
e
l
l
k
k
o
o
ś
ś
c
c
i
i
ą
ą
s
s
t
t
a
a
ł
ł
ą
ą
.
.
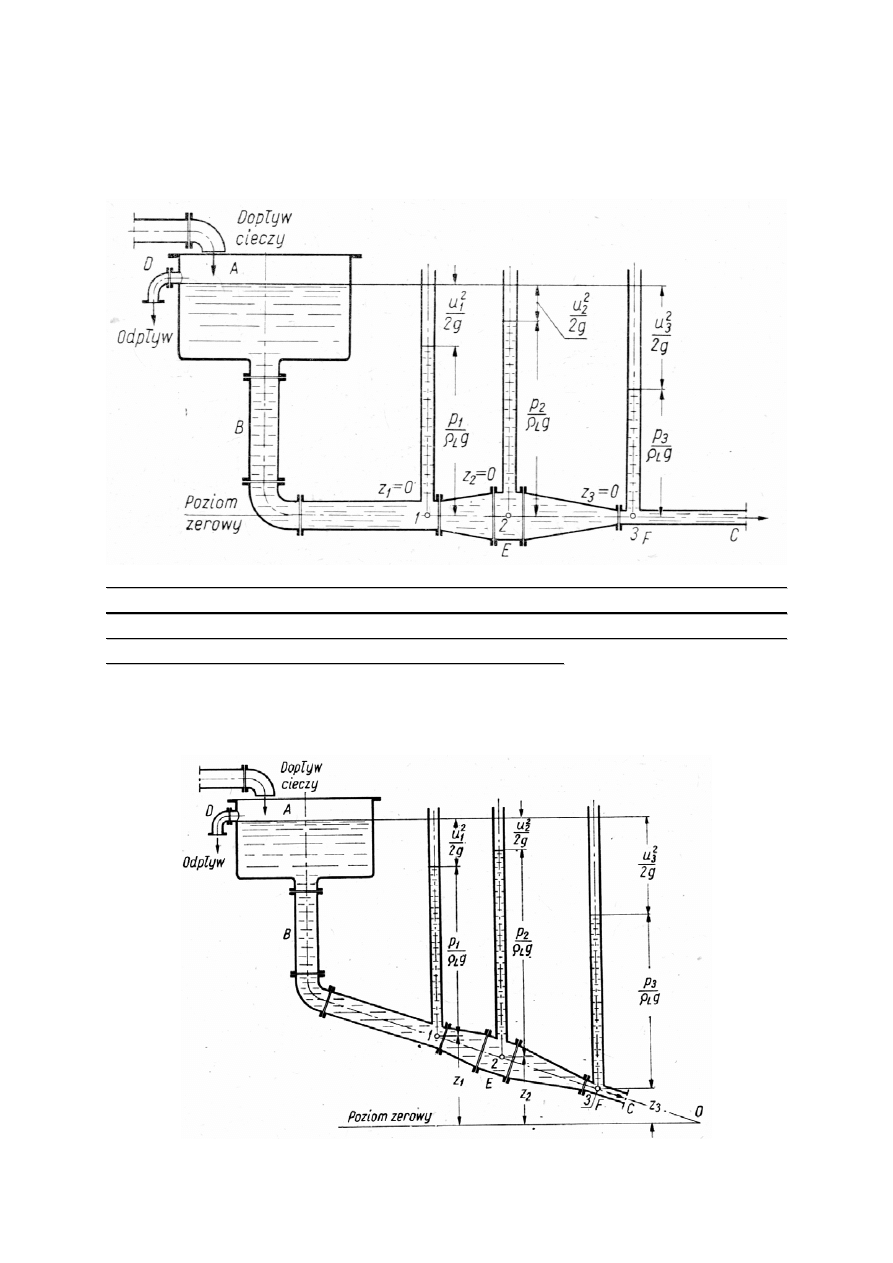
3. Równoległy, poziomy przebieg przewodu w stosunku do poziomu
odniesienia. Przekrój przewodu zmienny tzn., że prędkości są różne
w różnych przekrojach przewodu.
Z
Z
w
w
i
i
ę
ę
k
k
s
s
z
z
e
e
n
n
i
i
e
e
p
p
r
r
z
z
e
e
k
k
r
r
o
o
j
j
u
u
o
o
z
z
n
n
a
a
c
c
z
z
a
a
z
z
m
m
n
n
i
i
e
e
j
j
s
s
z
z
e
e
n
n
i
i
e
e
p
p
r
r
ę
ę
d
d
k
k
o
o
ś
ś
c
c
i
i
p
p
r
r
z
z
e
e
p
p
ł
ł
y
y
w
w
u
u
t
t
z
z
n
n
.
.
z
z
m
m
n
n
i
i
e
e
j
j
s
s
z
z
e
e
n
n
i
i
e
e
e
e
n
n
e
e
r
r
g
g
i
i
i
i
k
k
i
i
n
n
e
e
t
t
y
y
c
c
z
z
n
n
e
e
j
j
w
w
z
z
r
r
a
a
s
s
t
t
a
a
n
n
a
a
t
t
o
o
m
m
i
i
a
a
s
s
t
t
c
c
i
i
ś
ś
n
n
i
i
e
e
n
n
i
i
e
e
s
s
t
t
a
a
t
t
y
y
c
c
z
z
n
n
e
e
.
.
O
O
d
d
w
w
r
r
o
o
t
t
n
n
i
i
e
e
g
g
d
d
y
y
p
p
r
r
z
z
e
e
k
k
r
r
ó
ó
j
j
z
z
m
m
n
n
i
i
e
e
j
j
s
s
z
z
a
a
s
s
i
i
ę
ę
,
,
w
w
z
z
r
r
a
a
s
s
t
t
a
a
e
e
n
n
e
e
r
r
g
g
i
i
a
a
k
k
i
i
n
n
e
e
t
t
y
y
c
c
z
z
n
n
a
a
c
c
z
z
y
y
l
l
i
i
c
c
i
i
ś
ś
n
n
i
i
e
e
n
n
i
i
e
e
d
d
y
y
n
n
a
a
m
m
i
i
c
c
z
z
n
n
e
e
a
a
s
s
p
p
a
a
d
d
a
a
c
c
i
i
ś
ś
n
n
i
i
e
e
n
n
i
i
e
e
s
s
t
t
a
a
t
t
y
y
c
c
z
z
n
n
e
e
.
.
4.
Przebieg przewodu pod kątem
α w stosunku do poziomu odniesienia.
Przekrój przewodu zmienny tzn., że prędkości są różne w różnych
przekrojach przewodu.
(Interpretacja identyczna jak w przypadku 2 i 3).
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
E
E
B
B
E
E
R
R
N
N
O
O
U
U
L
L
I
I
E
E
G
G
O
O
D
D
L
L
A
A
P
P
Ł
Ł
Y
Y
N
N
Ó
Ó
W
W
R
R
Z
Z
E
E
C
C
Z
Z
Y
Y
W
W
I
I
S
S
T
T
Y
Y
C
C
H
H
C
C
Z
Z
Ę
Ę
Ś
Ś
Ć
Ć
E
E
N
N
E
E
R
R
G
G
I
I
I
I
J
J
E
E
S
S
T
T
T
T
R
R
A
A
C
C
O
O
N
N
A
A
I
I
Z
Z
A
A
M
M
I
I
E
E
N
N
I
I
A
A
N
N
A
A
N
N
A
A
C
C
I
I
E
E
P
P
Ł
Ł
O
O
W
W
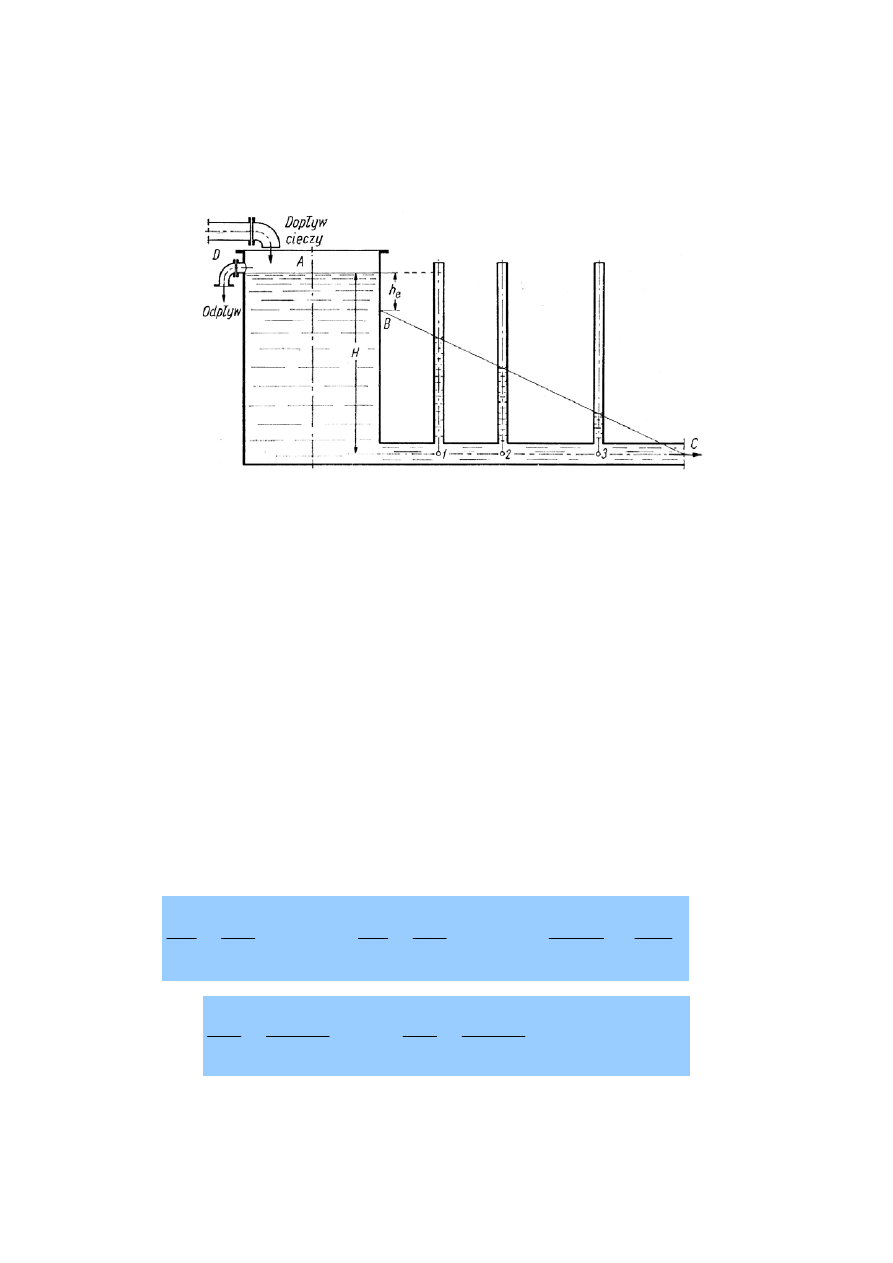
y
y
s
s
o
o
k
k
o
o
ś
ś
ć
ć
h
h
e
e
o
o
d
d
p
p
o
o
w
w
i
i
a
a
d
d
a
a
e
e
n
n
e
e
r
r
g
g
i
i
i
i
k
k
i
i
n
n
e
e
t
t
y
y
c
c
z
z
n
n
e
e
j
j
,
,
k
k
t
t
ó
ó
r
r
a
a
j
j
e
e
s
s
t
t
s
s
t
t
a
a
ł
ł
a
a
d
d
l
l
a
a
k
k
a
a
ż
ż
d
d
e
e
g
g
o
o
z
z
p
p
r
r
z
z
e
e
k
k
r
r
o
o
j
j
ó
ó
w
w
(
(
ś
ś
r
r
e
e
d
d
n
n
i
i
c
c
a
a
p
p
r
r
z
z
e
e
w
w
o
o
d
d
u
u
j
j
e
e
s
s
t
t
n
n
i
i
e
e
z
z
m
m
i
i
e
e
n
n
n
n
a
a
)
)
.
.
O
O
b
b
s
s
e
e
r
r
w
w
o
o
w
w
a
a
n
n
e
e
s
s
t
t
r
r
a
a
t
t
y
y
c
c
i
i
ś
ś
n
n
i
i
e
e
n
n
i
i
a
a
t
t
ł
ł
u
u
m
m
a
a
c
c
z
z
y
y
s
s
i
i
ę
ę
o
o
p
p
o
o
r
r
a
a
m
m
i
i
j
j
a
a
k
k
i
i
e
e
m
m
u
u
s
s
i
i
p
p
o
o
k
k
o
o
n
n
a
a
ć
ć
c
c
i
i
e
e
c
c
z
z
w
w
c
c
z
z
a
a
s
s
i
i
e
e
p
p
r
r
z
z
e
e
p
p
ł
ł
y
y
w
w
u
u
.
.
O
O
p
p
o
o
r
r
y
y
t
t
e
e
w
w
y
y
n
n
i
i
k
k
a
a
j
j
ą
ą
z
z
w
w
y
y
s
s
t
t
ę
ę
p
p
o
o
w
w
a
a
n
n
i
i
a
a
t
t
a
a
r
r
c
c
i
i
a
a
w
w
e
e
w
w
n
n
ę
ę
t
t
r
r
z
z
n
n
e
e
g
g
o
o
c
c
i
i
e
e
c
c
z
z
y
y
r
r
z
z
e
e
c
c
z
z
y
y
w
w
i
i
s
s
t
t
y
y
c
c
h
h
j
j
a
a
k
k
r
r
ó
ó
w
w
n
n
i
i
e
e
ż
ż
m
m
o
o
g
g
ą
ą
b
b
y
y
ć
ć
z
z
w
w
i
i
ą
ą
z
z
a
a
n
n
e
e
z
z
n
n
a
a
g
g
ł
ł
ą
ą
z
z
m
m
i
i
a
a
n
n
ą
ą
p
p
r
r
z
z
e
e
k
k
r
r
o
o
j
j
u
u
p
p
r
r
z
z
e
e
w
w
o
o
d
d
u
u
i
i
k
k
i
i
e
e
r
r
u
u
n
n
k
k
u
u
p
p
r
r
z
z
e
e
p
p
ł
ł
y
y
w
w
u
u
,
,
i
i
s
s
t
t
n
n
i
i
e
e
n
n
i
i
e
e
m
m
n
n
a
a
p
p
r
r
z
z
e
e
w
w
o
o
d
d
z
z
i
i
e
e
k
k
u
u
r
r
k
k
ó
ó
w
w
,
,
z
z
a
a
w
w
o
o
r
r
ó
ó
w
w
,
,
z
z
a
a
s
s
u
u
w
w
i
i
t
t
p
p
.
.
.
.
)
,
,
,
,
(
F
F
u
L
d
f
P
η
ρ
=
Δ
⎥
⎦
⎤
⎢
⎣
⎡
Δ
+
⋅
+
+
=
⋅
+
+
2
2
s
m
L
str
L
L
p
z
g
p
u
z
g
p
u
ρ
ρ
ρ
2
2
2
2
1
1
2
1
2
2
lub
[m]
str
L
L
h
z
g
p
g
u
z
g
p
g
u
+
+
⋅
+
=
+
⋅
+
2
2
2
2
1
1
2
1
2
2
ρ
ρ
gdzie:
Δp
str
i h
str
– straty ciśnienia spowodowane oporami przepływu,
K
K
R
R
Y
Y
T
T
E
E
R
R
I
I
U
U
M
M
R
R
E
E
Y
Y
N
N
O
O
L
L
D
D
S
S
A
A
η
ν
η
ρ
d
w
d
u
d
u
L
⋅
=
⋅
=
⋅
⋅
=
Re
Ruch laminarny
Ruch przejściowy
Ruch burzliwy
Re<2100
2100<Re<3000
3000<Re<500000
R
R
O
O
Z
Z
K
K
Ł
Ł
A
A
D
D
P
P
R
R
Ę
Ę
D
D
K
K
O
O
Ś
Ś
C
C
I
I
PROMIEŃ HYDRAULICZNY -
B
S
obwód
ia
powierzchn
r
h
=
=
ŚREDNICA ZASTĘPCZA -
B
S
r
d
h
e
4
4
=
=
Strugi czynnika układają się równolegle do
osi przewodu, rozkład prędkości ma kształt
paraboli. Prędkość maksymalna przypada w
osi przewodu.
u
śr
=0,5 u
max
u
śr
≅
0,8 u
max
Strugi czynnika wirują
w różnych kierunkach,
rozkład prędkości ma
kształt spłaszczonej
krzywej. W środkowej
części przewodu prędkość
pozostaje ta sama, maleje
do zera przy ściankach.
u
śr
≅
0,85 u
max
r. laminarny
r. przejściowy
r. burzliwy
L
L
E
E
P
P
K
K
O
O
Ś
Ś
Ć
Ć
Lepkość płynów rzeczywistych wywołuje opór podczas przesuwania
się cząstek lub warstewek płynu względem siebie. Siły lepkości (siły
tarcia wewnętrznego) występują tylko w czasie ruchu.
S
S
I
I
Ł
Ł
A
A
T
T
A
A
R
R
C
C
I
I
A
A
dA
dx
du
dT
⋅
=
η
stąd
dA
dT
du
dx ⋅
=
η
gdzie:
η - współczynnik lepkości dynamicznej [kg/m·s]=[Pa·s]
1 Poise=1P=0,1 kg/m·s
1cP=0,001 kg/m·s
ν - współczynnik lepkości kinematycznej [m
2
/s]
⎥
⎦
⎤
⎢
⎣
⎡
=
s
m
2
ρ
η
ν
1 Stokes=0,0001 m
2
/s
1cSt=0,01 St
Lepkość dynamiczna cieczy zmniejsza się ze wzrostem temperatury,
praktycznie nie zależy od ciśnienia. Dla gazów lepkość dynamiczna zwiększa
się z temperaturą, gdy są to gazy doskonałe nie zależy od ciśnienia. Lepkość
kinematyczna dla gazów silnie zależy od ciśnienia, dlatego posługujemy się tzw.
zredukowaną lepkością kinematyczną
ν
dx
u
u+du
dA
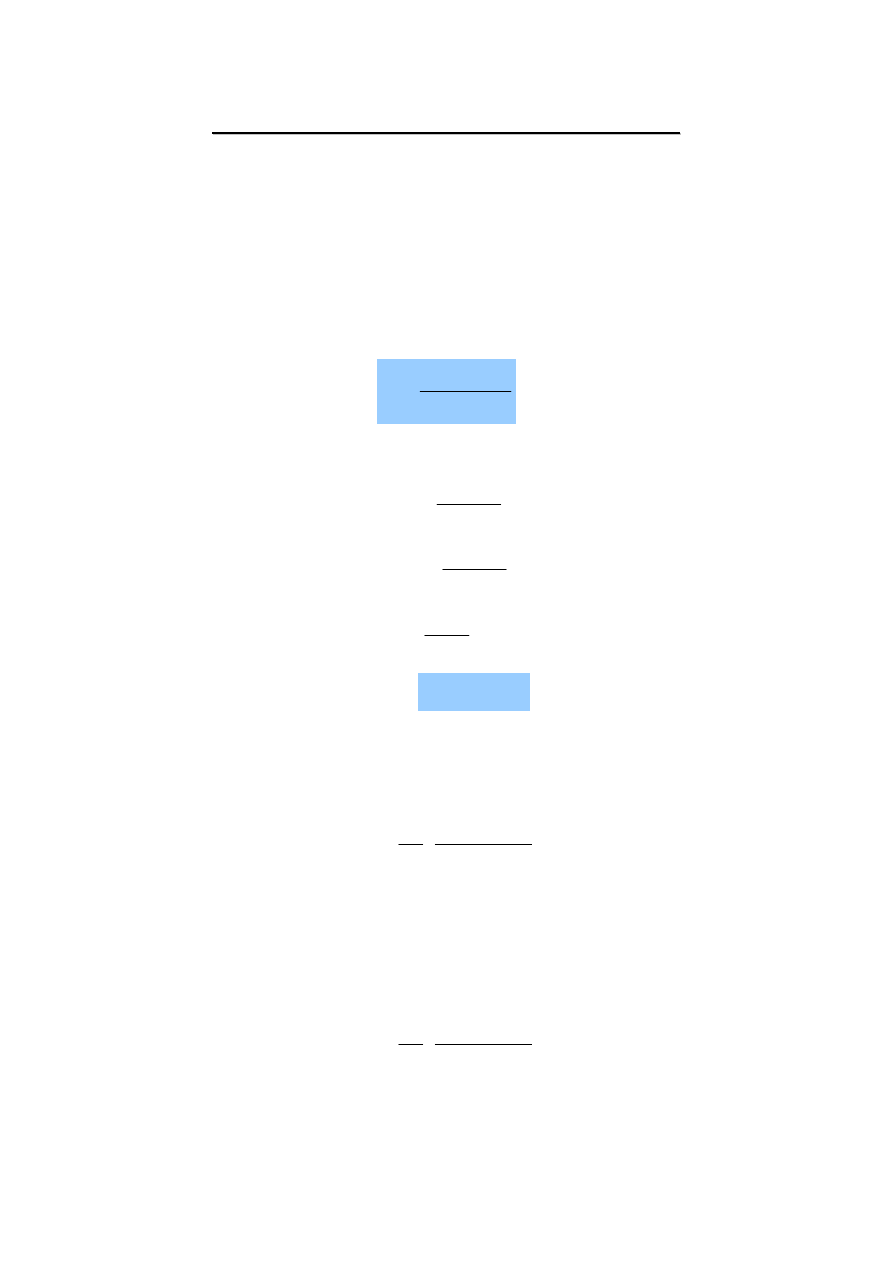
D
D
Y
Y
N
N
A
A
M
M
I
I
K
K
A
A
P
P
Ł
Ł
Y
Y
N
N
Ó
Ó
W
W
R
R
Z
Z
E
E
C
C
Z
Z
Y
Y
W
W
I
I
S
S
T
T
Y
Y
C
C
H
H
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
E
E
P
P
O
O
I
I
S
S
E
E
U
U
I
I
L
L
L
L
E
E
’
’
A
A
Wyprowadza się w oparciu o równowagę sił działających na element
poruszającego się płynu. Na taki element działają: siła ciężkości, siła parcia
(wywołująca ruch), siła przeciwparcia, siły ściskające element płynu i siła tarcia.
Postać równania jest następująca: W założeniu płyn porusza się
RUCHEM UWARSTWIONYM, CZYLI LAMINARNYM.
L
d
P
U
L
⋅
⋅
Δ
⋅
=
η
π
128
4
zaś prędkość maksymalną, która przy w/w założeniu przypada w osi przewodu
i prędkość średnią można wyliczyć w oparciu o wzory:
L
d
P
u
L
śr
⋅
⋅
Δ
=
η
32
2
L
d
P
u
L
⋅
⋅
Δ
=
η
16
2
max
stąd
2
max
=
śr
u
u
zatem
u
u
⋅
= 2
max
RUCH BURZLIWY
Dla ruchu burzliwego objętościowe natężenie przepływu i prędkość
maksymalną można wyznaczyć w oparciu o wzory:
4
60
49
2
max
d
u
U
⋅
⋅
⋅
=
π
u
u
⋅
≅ 18
,
1
max
RUCH PRZEJŚCIOWY
Natomiast dla przejściowego przepływu płynu w/w wyznacza się w oparu
o podane niżej wzory:
4
60
49
2
max
d
u
U
⋅
⋅
⋅
=
π
u
u
⋅
≅ 25
,
1
max
D
D
Y
Y
N
N
A
A
M
M
I
I
K
K
A
A
P
P
Ł
Ł
Y
Y
N
N
Ó
Ó
W
W
R
R
Z
Z
E
E
C
C
Z
Z
Y
Y
W
W
I
I
S
S
T
T
Y
Y
C
C
H
H
STRATY CIŚNIENIA WYWOŁANE TARCIEM WEWNĘTRZNYM
)
,
,
,
,
(
F
F
u
L
d
f
P
η
ρ
=
Δ
zgodnie z analizą wymiarową
2
Re
- kryterium podobieństwa geometrycznego
Re
- kryterium Reynoldsa
Eu=
- kryterium Eulera
b
e
g
L
Eu
A
d
L
K
d
u d
p
u
ρ
η
ρ
−
⎛ ⎞
= ⎜ ⎟
⎝ ⎠
=
⋅ ⋅
=
Δ
⋅
Na podstawie doświadczeń ustalono, że wykładnik potęgowy b=1, natomiast
wykładnik potęgowy e i współczynnik proporcjonalności A przybierają różne
wartości.
Stąd spadek ciśnienia można wyrazić następująco:
2
2
2
Re
2
2
przy czym
(Re)
e
L u
L u
p
A
d
d
f
ρ
ρ
λ
λ
−
⋅
⋅
Δ =
⋅
⋅ ⋅
= ⋅ ⋅
=
CIŚNIENIE HYDROSTATYCZNE
Różnica ciśnień na dwóch poziomach płynu o gęstości
ρ
L
i odległych
w kierunku pionowym h wynosi:
[Pa]
g
h
p
L
⋅
⋅
=
Δ
ρ
Jeżeli na zwierciadłem panuje ciśnienie p
0
to w dowolnym punkcie cieczy
oddalonym o h od zwierciadła ciśnienie wynosi:
g
h
p
p
L
⋅
⋅
+
=
ρ
0
OPORY TARCIA WEWNĘTRZNEGO:
Spadek ciśnienia płynu w czasie przepływu przez rurę o długości L
i niezmiennej średnicy d, spowodowany oporami tarcia wewnętrznego:
2
2
ρ
λ
⋅
⋅
⋅
=
Δ
u
d
L
p
-
r. Darcy-Weisbacha
gdzie:
λ − współczynnik oporu tarcia wewnętrznego, funkcja liczby Reynoldsa,
a) RUCH LAMINARNY:
Re
64
=
λ
zatem
2
32
d
L
u
p
⋅
⋅
=
Δ
η
-
r. Poiseuille’a
b) RUCH BURZLIWY (rura gładka):
gdy 3·10
3
<Re<10
5
4
Re
3164
,
0
=
λ
-
r. Blasiusa
gdy 3·10
3
<Re<3·10
6
32
,
0
Re
5
,
0
0052
,
0
+
=
λ
-
r. Koo
gdy 10
5
<Re<10
8
237
,
0
Re
221
,
0
0032
,
0
+
=
λ
-
r. Nikuradsego
gdy 10
4
<Re<10
7
2
,
0
Re
184
,
0
=
λ
-
r. Blasiusa
c) RUCH BURZLIWY (rura szorstka):
2
)
72
,
3
lg
2
(
1
k
d
⋅
=
λ
gdzie: k – szorstkość bezwzględna [m],
Oprócz oporów tarcia wewnętrznego wyróżniamy
o
o
p
p
o
o
r
r
y
y
l
l
o
o
k
k
a
a
l
l
n
n
e
e
(
(
z
z
m
m
i
i
a
a
n
n
a
a
k
k
i
i
e
e
r
r
u
u
n
n
k
k
u
u
l
l
u
u
b
b
k
k
s
s
z
z
t
t
a
a
ł
ł
t
t
u
u
g
g
e
e
o
o
m
m
e
e
t
t
r
r
y
y
c
c
z
z
n
n
e
e
g
g
o
o
r
r
u
u
r
r
o
o
c
c
i
i
ą
ą
g
g
u
u
)
), zatem opory sumaryczne
są sumą oporów tarcia wewnętrznego i oporów lokalnych.
2
2
n
n
u
p
ρ
ζ
⋅
Δ =
⋅
ζ - współczynnik oporu lokalnego zależny od rodzaju oporu np. nagłe
przewężenie lub rozszerzenie przewodu, istnienie zaworu na przewodzie,
zmiana kierunku przepływu itp.
Zatem:
2
2
2
2
n
n
L u
u
p
p
d
ρ
ρ
λ
ζ
⋅
⋅
Δ + Δ = ⋅ ⋅
+ Σ ⋅
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
ZADANIE 1
Przewodem o średnicy wewnętrznej 42mm płynie wodny roztwór
gliceryny o gęstości 1190 kg/m
3
(15
°C). Obliczyć prędkość liniową oraz
objętościowe natężenie przepływu jeśli w ciągu godziny przepływa
6000kg roztworu.
ZADANIE 2
Do rurek wymiennika ciepła przewodem o średnicy wewnętrznej 200
mm dopływa ciecz z prędkością 0,7m/s. W rurkach, które mają średnice
wewnętrzną 14mm prędkość przepływu wynosi 2,8m/s. Obliczyć liczbę
rurek w wymienniku. Gęstość cieczy jest stała.
ZADANIE 3
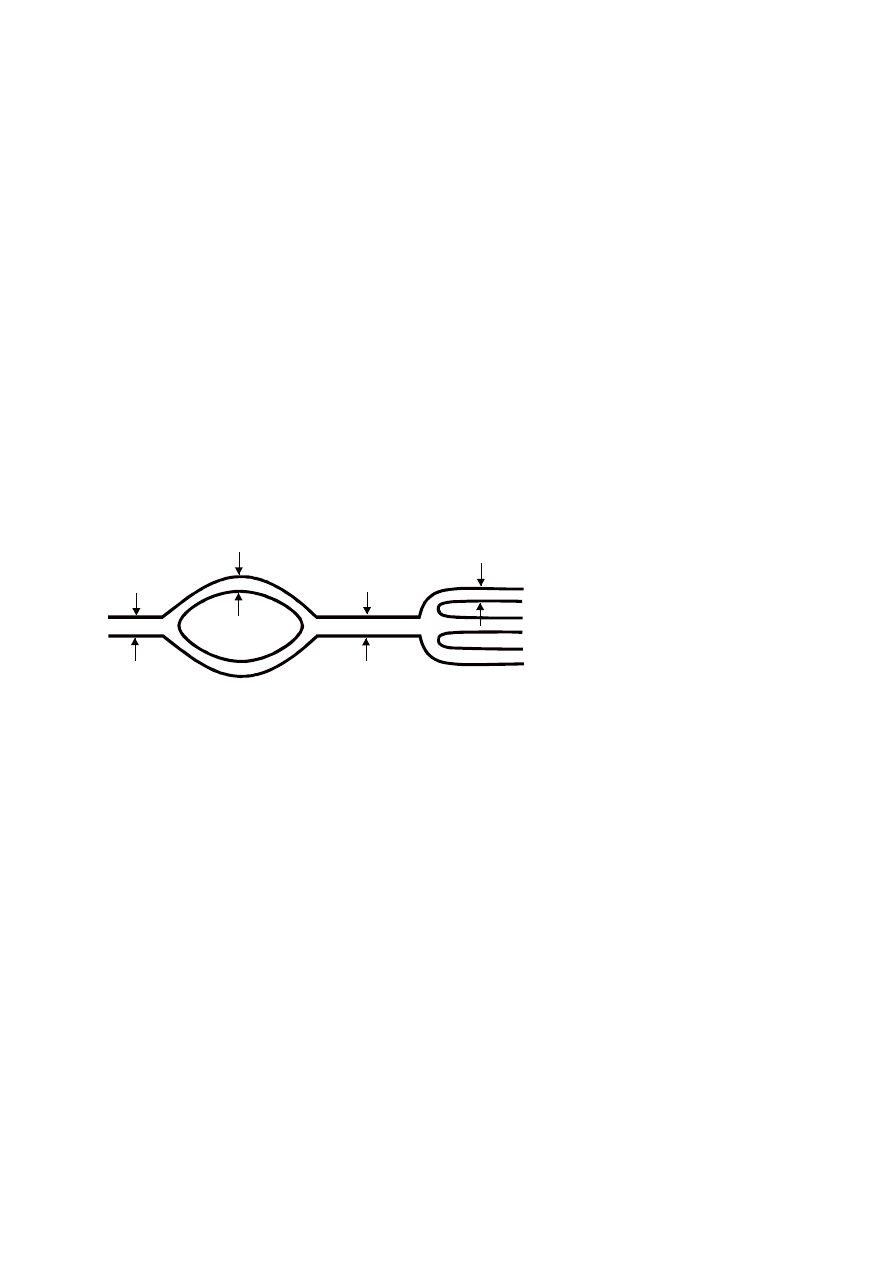
Rurociąg wygląda następująco:
Średnica D
1
wynosi 0,13m
zaś prędkość przepływu
cieczy u
1
=0,07m/s.
Następnie rurociąg
rozdziela się na dwie nitki
a średnica D
2
wzrasta
dwukrotnie w porównaniu z D
1
. Kolejno rurociąg łączy się w jedną nitkę i
średnica D
3
wynosi 0,64m. Na koniec rurociąg rozdziela się na trzy nitki.
Obliczyć u
2
, u
3
, u
4
i D
4
. Ponadto wiadomo, że gęstość jest stała a
D
4
=18%D
3
’
. UWAGA: S
4
=3S
4
.
ZADANIE 4
W poziomej rurze o średnicy 30mm, w której płynie woda (
ρ
L
=1000
kg/m
3
) panuje ciśnienie statyczne równe 87 mmHg. Całkowite ciśnienie
wynosi 154 mmHg. Wyznaczyć prędkość przepływu wody i objętościowe
natężenie przepływu.
ZADANIE 5
Ciśnienie całkowite w przewodzie o przekroju 250x270mm, którym
płynie gliceryna (
ρ
L
=1261,3 kg/m
3
) wynosi 115 mmHg. Wiedząc, że
objętościowe natężenie przepływu wynosi 0,25 m
3
/s wyznaczyć ciśnienie
statyczne panujące w płynącej glicerynie. Przewód jest poziomy.
D
1
D
2
D
3
D
4
ZADANIE 6
Dany jest poziomy przewód o zmiennym przekroju. Natężenie
objętościowe przepływu wody przez ten przewód wynosi 0,07m
3
/s. W
pierwszej części przewodu gdzie d
1
=250mm ciśnienie statyczne wynosi
1,2 mH
2
O. Wyznaczyć ciśnienie statyczne panujące w drugiej części
przewodu, gdzie d
2
=470mm. Przyjąć gęstość wody równą 1000kg/m
3
.
ZADANIE 7
Oblicz objętościowe natężenie przepływu płynu poruszającego się
ruchem laminarnym w przewodzie o powierzchni przekroju 10cm
2
,
którego prędkość w osi przewodu wynosi u
max
=2cm/s.
ZADANIE 8
Rurociągiem o średnicy 120mm, w temperaturze 30
o
C, ruchem
laminarnym płynie roztwór gliceryny z prędkością średnią 5m/s. Obliczyć
straty ciśnienia spowodowane występowaniem sił tarcia wewnętrznego i
objętościowe natężenie przepływu wiedząc, że lepkość kinematyczna
gliceryny w w/w temperaturze wynosi 5,3·10
-4
m
2
/s, gęstość roztworu
gliceryny jest równa 1190kg/m
3
a długość rurociągu wynosi natomiast
4000mm.