Pa

ństwowa Wyższa Szkoła Zawodowa im. Witelona w Legnicy

Wydział Nauk Technicznych i Ekonomicznych

Kierunek: ZIP

Specjalno

ść: -

Studia: stacjonarne

Ewa Jabło

ńska

Rok studiów: drugi

Grupa: pierwsza

Nr zespołu: 16

Rok akademicki : 2014/2015

Referat z przedmiotu: „Podstawy projektowaniainżynierskiego”

Podstawowe modele matematyczne stosowane w projektowaniu

Referat napisany pod kierunkiem:

dr. in

ż. Jerzy Kwaśnik

Legnica 2015

2

Spis tre

ści

1.

Definicja pojęcia modelowania matematycznego

3

2.

Podstawowe cechy modeli

3

3.

Cele tworzenia modeli

3

4.

Podział modeli

4

4.1. Podział modeli ze wzgledu na ich konstrukcje

4

4.2. Podział modeli ze względu na ich relacje do modelowego systemu

4

4.2.1. White – box

5

4.2.2. Black – box

5

4.2.3. Gray – box

6

4.2.4. Glass – box

6

5.

Tworzenie modeli matematycznych

7

6.

Metody matematyczne przedstawione na konkretnym przykładzie

7

6.1. Optymalny system dynamiczny

7

7.

Podsumowanie

9

Bibliografia

10

Spis rysunków

11

3

1.

Definicja poj

ęcia modelowania matematycznego

Modelowanie matematyczne to użycie języka matematyki do opisania zachowania

jakiegoś układu (na przykład układu automatyki, biologicznego, ekonomicznego,

elektrycznego, mechanicznego, termodynamicznego).

Praktyka inżynierska często wymaga sterowania układem lub wykonania analizy jego

zachowania, do czego używa się modelowania matematycznego. W analizie inżynier buduje

opisowy model układu będący hipotezą co do sposobu działania układu i na podstawie tego

modelu może wnioskować co do wpływu potencjalnych zakłóceń na stan układu.

W sterowaniu model może posłużyć do teoretycznego wypróbowania różnych strategii

sterowania bez wpływania na rzeczywisty układ.

Model matematyczny opisuje dany układ za pomocą zmiennych. Wartości zmiennych

mogą należeć do różnych zbiorów: liczb rzeczywistych, całkowitych, wartości logicznych,

ciągów znakowych i tym podobnych.

Zmienne reprezentują pewne właściwości układu, na przykład zmierzone wartości wyjść

układu, wartości liczników, wystąpienia zdarzeń (tak/nie) i tym podobne.

Właściwy model to grupa funkcji wiążących ze sobą różne zmienne i w ten sposób

opisujących powiązania między wielkościami w układzie.

2.

Podstawowe cechy modeli

•

Model systemu jest z reguły uproszczeniem rzeczywistości.

•

Model systemu powinien zewnętrznie, w zakresie nas interesującym, zachowywać się

podobnie jak system, aczkolwiek może mieć inną strukturę wewnętrzną.

•

Modele systemów mają z reguły znacznie mniejszą ilość wejść i wyjść niż systemy

rzeczywiste.

•

Model systemu powinien cechować się łatwością wykorzystania zgodnie

z przeznaczeniem.

3.

Cele tworzenia modeli

•

BADANIE – czyli model służy do wyjaśnienia zachowania się sytemu w określonych

warunkach.

•

PROGNOZOWANIE – czyli model służy do przewidywania zachowania się systemu

w przyszłości.

•

PROJEKTOWANIE – czyli model służy do optymalizacji struktury i parametrów

projektowanego systemu.

•

KIEROWANIE – czyli model służy do podejmowania decyzji w działającym

systemie.

4

4.

Podział modeli

4.1. Podział modeli ze wzgl

ędu na ich konstrukcję

•

Koncepcyjne albo jakościowe – np. model Ptolemeusza systemu słonecznego lub

model systemu motywacji pracownika do wydajnej pracy.

•

Fizyczne – np. model koryta rzeki w skali laboratoryjnej, lub model samolotu

testowany w tunelu aerodynamicznym.

•

Analogowe – np. symulacja systemu sieci wodociągowej za pomocą złożonego układu

elektrycznego, lub symulacja systemu sterowania za pomocą analizatora

analogowego.

•

Matematyczne – w postaci układu zależności matematycznych.

•

Komputerowe – za pomocą odpowiedniego programu komputerowego. Modele takie

budowane są z równań matematycznych, zależności statystycznych i reguł

probabalistycznych. Ich specyfiką jest możliwość symulowania ewolucji systemu

poprzez krokowe zmiany parametrów wyjściowych.

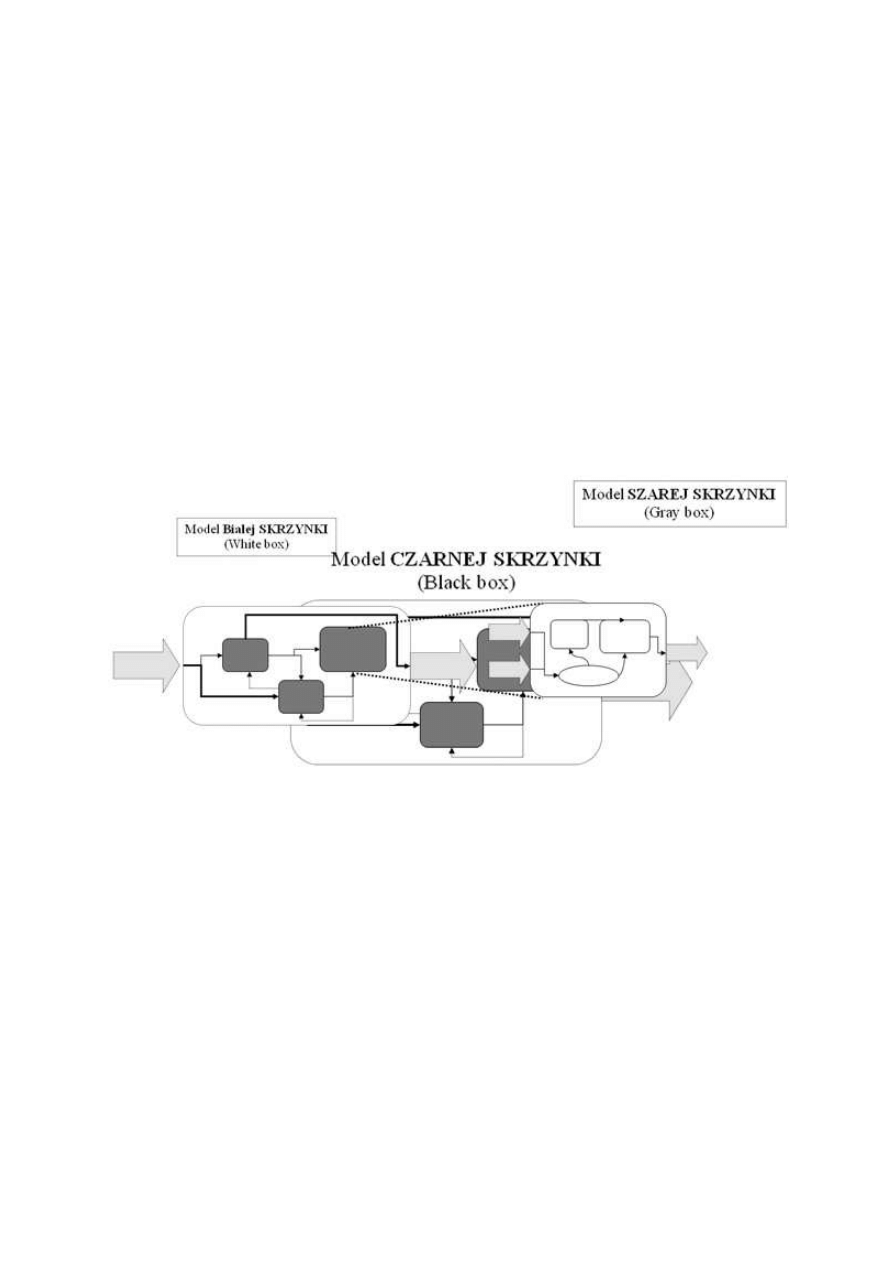
4.2. Podział modeli ze wzgl

ędu na ich relacje do modelowego systemu

Problemy modelowania matematycznego często klasyfikuje się jako "czarne skrzynki"

(ang. black-box) lub "białe skrzynki" (ang. white-box), w zależności od ilości informacji

o układzie posiadanych przed modelowaniem. Model "czarnej skrzynki" przedstawia układ,

o którym nie posiadamy absolutnie żadnej informacji, podczas gdy model "białej skrzynki"

przedstawia układ, o którego działaniu mamy pełną wiedzę. W rzeczywistości wszystkie

układy plasują się pomiędzy tymi dwoma idealnymi modelami. Zazwyczaj preferowane jest

wykorzystanie możliwie dużej ilości wiedzy a priori, jak to tylko możliwe, aby uzyskany

model był dokładniejszy.

5

4.2.1.

White - box

Modele "białej skrzynki" są uważane za prostsze, gdyż jeśli tylko wiedzy a priori

użyto poprawnie, to model będzie zachowywał się zgodnie z rzeczywistym układem. Często

informacja posiadana wcześniej o układzie ukazuje nam rodzaj zależności (charakter funkcji)

wiążącej zmienne układu. Użytkownik widzi strukturę aktywu i w zasadzie może go dowolnie

modyfikować. Przykładem mogą tu być wszelkiego rodzaju wzorce projektowe, wzorce

dokumentacji, fragmenty tekstu programów, itp.

Model białej skrzynki jest najłatwiejszy do wdrożenia, gdyż zasadniczo polega na

opisaniu pewnego wykonanego fragmentu dokumentacji lub oprogramowania.

Taki opis może być jednak trudno generalizowalny, zaś zmiany aktywu przez osoby

inne niż konstruktor aktywu są ryzykowne i mogą doprowadzić do naruszenia założonych na

początku własności. Z drugiej strony, dokładny opis fragmentów, które mogą podlegać

zmianom oraz określenie dopuszczalnego zakresu zmian może okazać się bardzo trudnym

zadaniem.

PRZYKŁAD: Użycie białej skrzynki następuje poprzez skopiowanie i zmodyfikowanie.

4.2.2.

Black – box

W modelach "czarnej skrzynki" należy wyznaczyć zarówno postać funkcji wiążącej

wielkości w układzie, jak i wartości liczbowych parametrów tych funkcji. Nie posiadając

wiedzy a priori próbujemy użyć funkcji możliwie ogólnych, by objąć nimi wszystkie różne

modele. Często używanym sposobem na uzyskanie modelu "czarnej skrzynki" jest użycie

sieci neuronowych, które nie zakładają niczego o nadchodzących do nich danych.

Podstawowym problemem występującym przy używaniu zestawów wielu funkcji opisujących

układ jest szybko wzrastający poziom trudności przy estymacji parametrów funkcji, gdy ilość

tych parametrów wzrasta. Model czarnej skrzynki uważa się za najbardziej pożądany

stereotyp aktywu ponownego użycia. Z drugiej strony, jest to model najtrudniejszy do

opracowania, szczególnie w małych organizacjach.

„Czarna skrzynka” może być użyta poprzez odsyłacz lub poprzez skopiowanie.

Częściej stosowane jest kopiowanie aktywu, które z kolei może być nie wskazane, gdy aktyw

jest na bieżąco utrzymywany (pielęgnowany) przez odpowiednią komórkę.

W takim przypadku kopiowanie powoduje, że akcje usunięcia błędów

i modyfikacje wprowadzane na bieżąco przez opiekunów aktywu nie będą automatycznie

propagowane do kopii funkcjonujących w nowszych i pozornie doskonalszych systemach.

PRZYKŁAD: Przykładem czarnej skrzynki może być np. biblioteka procedur w postaci

skompilowanej czy też zamknięty pod względem formy formularz.

6

4.2.3.

Gray – box

Element pośredni między modelem czarnej, a białej skrzynki. W modelu szarej

skrzynki konstruktor aktywu będzie mógł określić, które części aktywu i dla jakich

użytkowników będą widoczne.

4.2.4.

Glass – box

Model szklanej skrzynki. Przy tym modelu zarówno budowa aktywu, jak i jego cechy

zewnętrzne są widoczne, chociaż nie można ich zmienić. Znajomość budowy aktywu i

zrozumienie zasad jego działania sprzyjają właściwemu stosowaniu, ale niemożność

dokonania jakichkolwiek zmian może być źródłem frustracji.

Rys.1. Przedstawienie graficzne niektórych elementów podziału modeli ze względu na ich

relacje do modelowania systemu.

Ż

ródło: opracowanie własne.

7

5.

Tworzenie modeli matematycznych

Tworzenie modelu matematycznego obejmuje trzy główne etapy:

•

specyfikację modelu

•

identyfikację modelu

•

weryfikację modelu

•

6.

Metody matematyczne przedstawione na konkretnym przykładzie

6.1. Optymalny system dynamiczny

Zastosowana w nim optymalizacja wraz z symulacją dynamiki, pozwala na ocenę

oraz wybór, takich rozwiązań, które były najlepiej oceniane przez pryzmat przyjetych

(zamodelowanych) kryteriów jakości. Mierzyły one długookresowe skutki polityk

decyzyjnych, funkcjonujacych w systemie, a dotyczących m.in. produkcji, zapasów,

sprzedaży, zaopatrzenia w surowce.

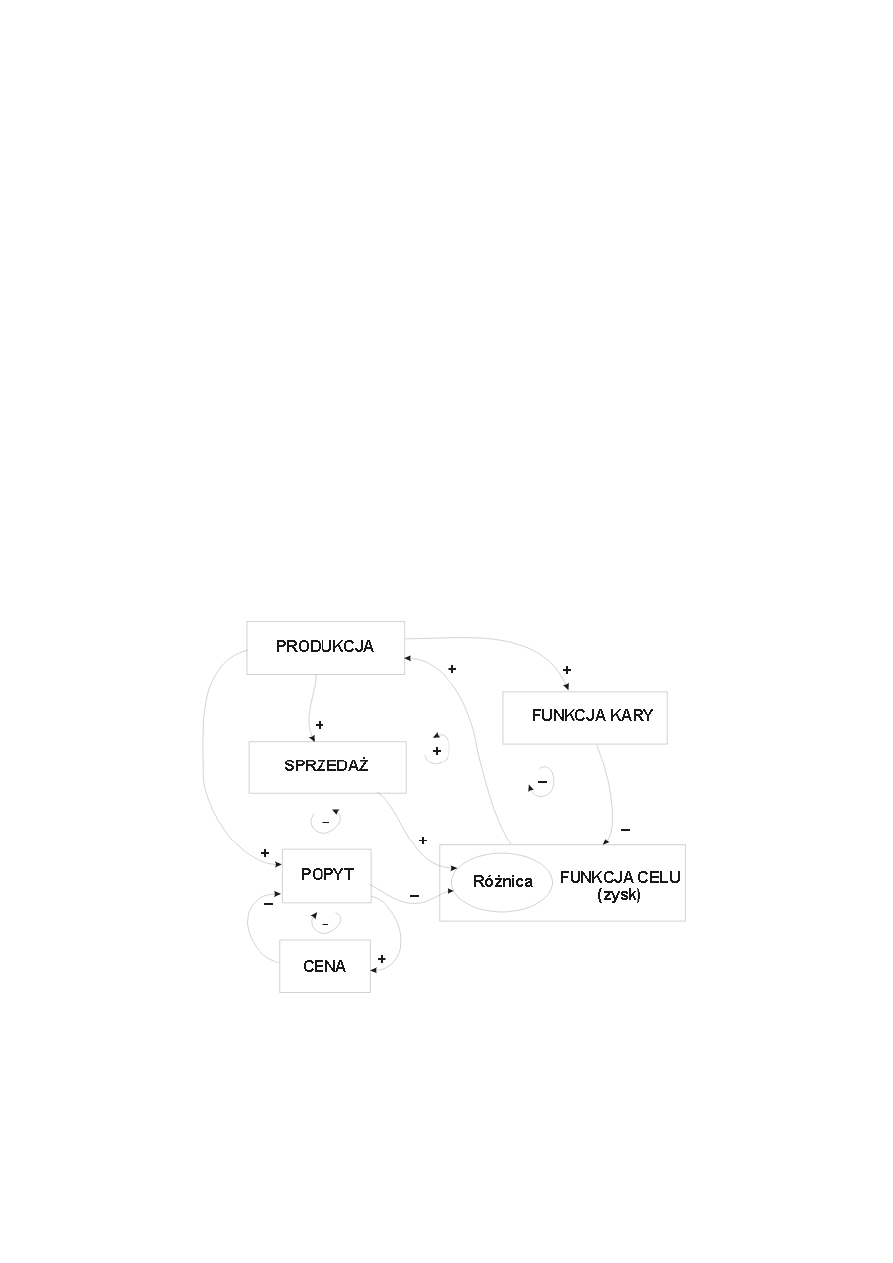
Rys.2. Elementarne sprzężenia w optymalnym modelu dynamicznym przy maksymalizacji

zysku.

Ź

ródło: opracowanie własne.

8

Rysunek

2

przedstawia

główne

sprzężenie

związane

z

optymalizacją

(maksymalizacją zysku zastosowaną n amodelu budowanym według filozofii Dynamiki

Systemowej.

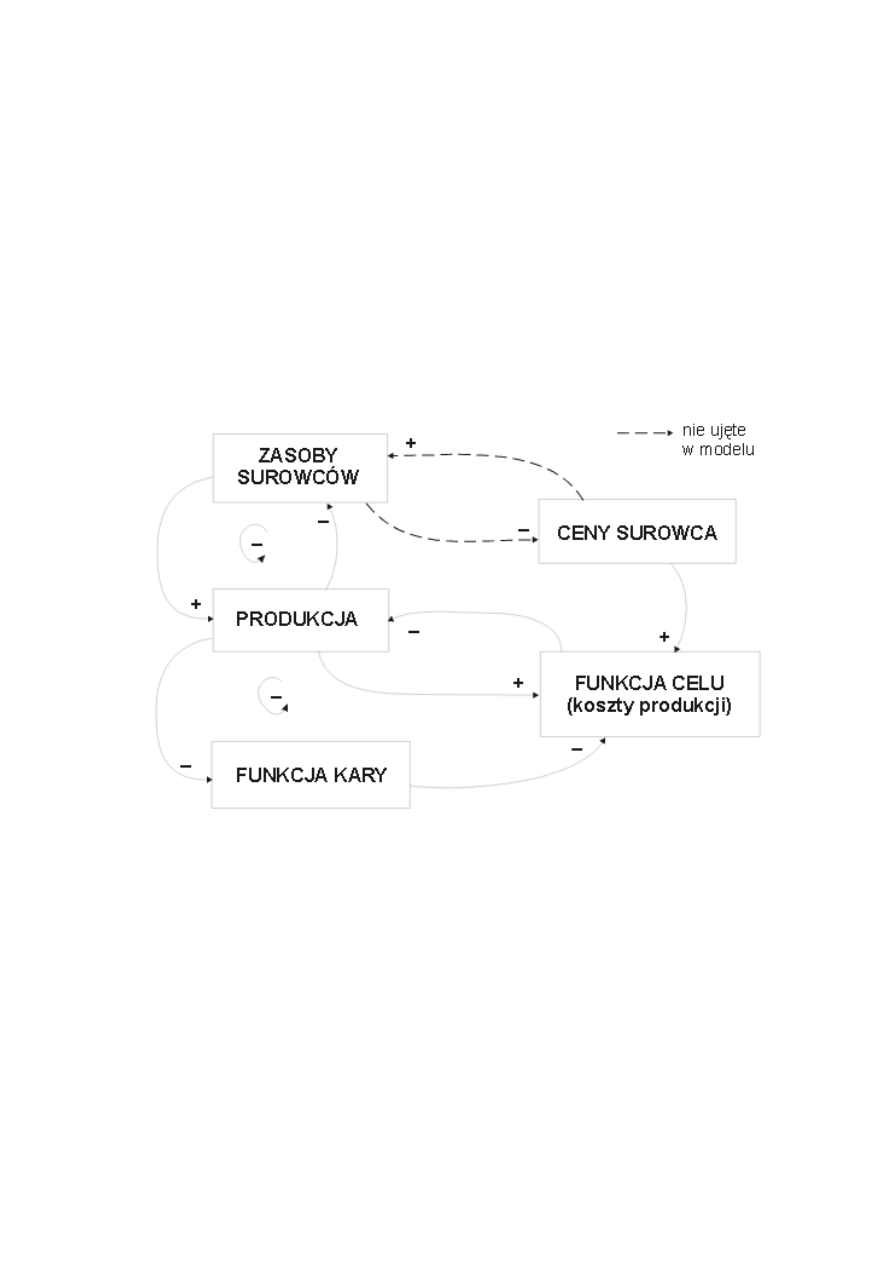
Rys.3. Elementarne sprzężenia w optymalnym modelu dynamicznym przy minimalizacji

kosztów.

Ź

ródło: opracowanie własne.

9

7.

Podsumowanie

Modele matematyczne pozwalaja zobaczyć strukturę projektowanych systemów

oraz efekt wzmocnienia występujący w tych strukturach. Współdziałanie istniejących modeli

matematycznych wyznacza dynamikę zachowań się systemu.

Trudności w wybieraniu modelu matematycznego oraz jego wpływu na zachowanie

systemu jako całości, moga byc przezwyciężone przez dalsze badania deoretyczne oraz przez

szerszy niz ma to miejsce obecnie opis struktur w modelach złożonych systemów

w literaturze przedmiotu.

10

Bibliografia

[1]

Kasperska E.,Mateja-Losa E., Słota D., Some dynamics balance of production via

optimization and simulation with System Dynamics method, in: Proc. 19

th

International

Conference of the System Dynamics Society, J. H. hines, V. G. Diker, R. S. Langer, J. I.

Rowe, ed., SDS, 2001, 1-18.

[2]

Kasperska E., Mateja-Losa E., Słota D., Optimal dynamic balance of raw materials – some

concept of embedding optimization in simulation on system dynamics models and vice versa,

in: Proc. 20 International Conference of the SystemDynamics Society, p. I. Davidsen, E.

Mollona, V. G. Diker, R. S. langer, J. I. Rowe, ed., SDS, 2002, 1-23.

[3]

opracowanie własne.

{4}

Kasperska E., Mateja-Losa E., Modele matematyczne wybranych archetypów

systemowych i ich symulacja, Zeszyty Naukowe. Matematyka – Fizyka/Politechnika Śląska,

2004, 91.

[5]

http://www.maths.com.pl/?q=analiza

[6]

http://www.sms.am.put.poznan.pl/eskrypty_pliki/inzynieriasystemow/modeleimodelo

wanie.pdf

11

Spis rysunków

Rys.1. Przedstawienie graficzne niektórych elementów podziału modeli ze względu na ich

relacje do modelowania systemu.

Ż

ródło: opracowanie własne.........................................................................................................6

Rys.2. Elementarne sprzężenia w optymalnym modelu dynamicznym przy maksymalizacji

zysku.

Ź

ródło: opracowanie własne.........................................................................................................7

Rys.3. Elementarne sprzężenia w optymalnym modelu dynamicznym przy minimalizacji

kosztów.

Ź

ródło: opracowanie własne......................................................................................................8