Microsoft Word - instrukcja4a.doc

KINETYKA SUSZENIA W ZŁOŻU FLUIDALNYM

„Fluidyzacja jest to proces dwufazowy, polegający na tym, że warstwa materiału

sypkiego ułożona na ruszcie jest doprowadzona do stanu pseudopłynnego za pomocą strugi
płynu tłoczonego z dołu.”

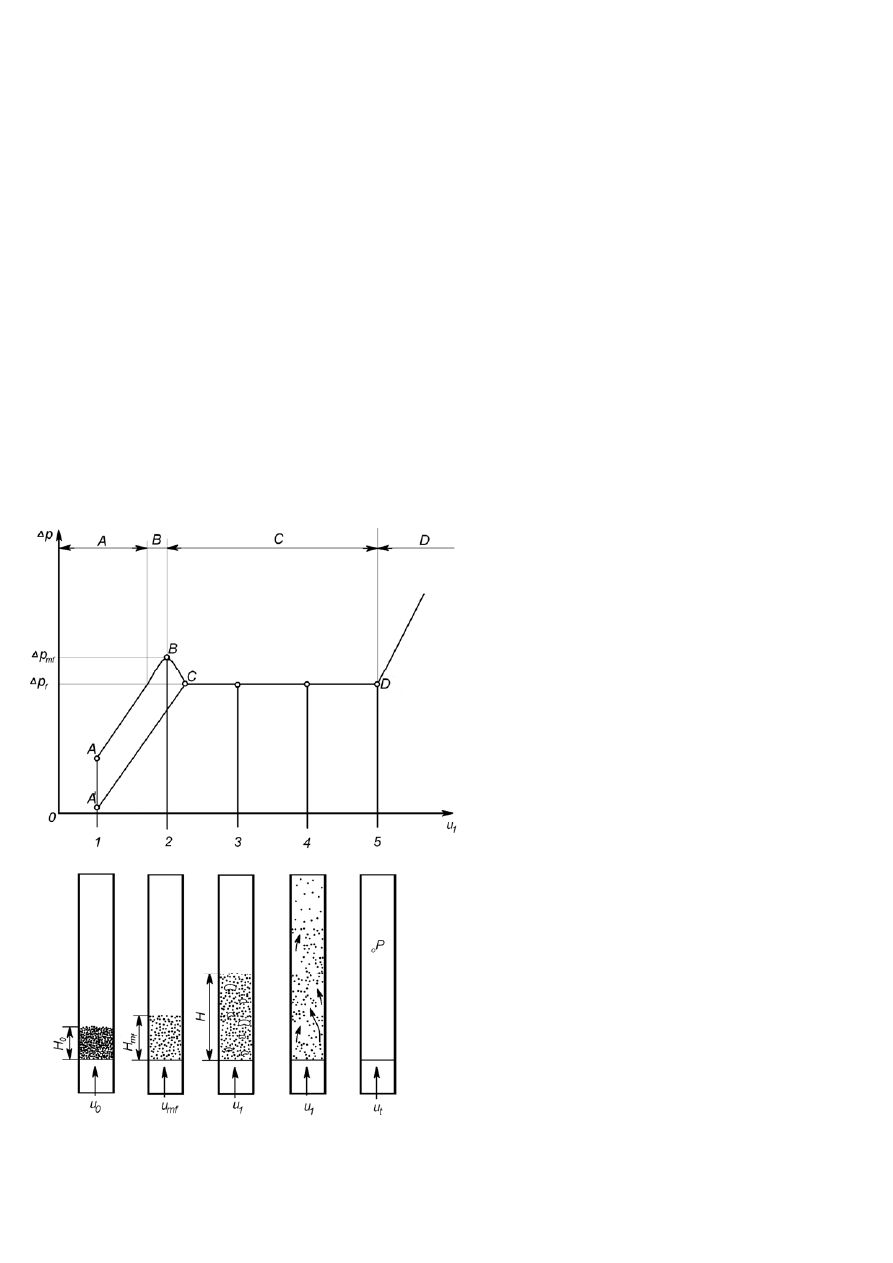
Jeżeli przez nieruchomą warstwę materiału ziarnistego znajdującego się w aparacie o

stałym przekroju przepływa gaz , to wzrostowi jego prędkości liniowej będzie odpowiadać
wzrost oporów przepływu jak to jest pokazane na wykresie poniżej. W momencie kiedy
nadciśnienie gazu pod warstwą materiału ziarnistego przekroczy jego ciśnienie statyczne,
następuje pewna ekspansja i nieruchoma warstwa osiąga ziarnista osiąga największą
porowatość. Prędkość płynu która odpowiada takiemu stanowi warstwy nosi nazwę prędkości
krytycznej u

. Dalszy wzrost prędkości przepływu powoduje przejście warstwy nieruchomej

w stan fluidalny, cechujący się intensywnym wzajemnym wymieszaniem ziarna i ustaleniem
oporów przepływu.

Stan fluidalnym trwa w aparacie aż do momentu osiągnięcia prędkości zawieszenia

(wywiewania) u

zaw

, powyżej której ziarna ciała stałego są wywiewane z aparatu.

Fluidyzacja

różne stany , które zależą od prędkości fluidyzacji u- jest to prędkość

płynu przed rusztem.

Na rysunku obok widać różne

stany jednofrakcyjnej warstwy fluidalnej,
oraz, poniżej, ich ujęcie jakościowe.
Stan 1. To stan nieruchomy. Cząstki
podtrzymywane są przez kontakt z innymi
cząstkami. Warstwa ma minimalną
porowatość ε

. Spadek ciśnienia rośnie

wraz ze wzrostem u=u

Stan 2. Warstwa ruchoma. Cząstki nadal
pozostają we wzajemnym kontakcie,
przesuwają się względem ściany
wykonując przy tym ruchy oscylacyjne.
Nadciśnienie płynu zrównuje się z
ciśnieniem wywieranym przez warstwę.
Stan ten to inaczej początek fluidyzacji,
u

, porowatość złoża to ε

=ε

spadek ciśnienia Δp

jest wtedy

największy.
Stan 3 i 4. Warstwa fluidalna, u

. Gdy

prędkość gazu rośnie, warstwa ekspanduje
i staje się fluidalną warstwą turbulentną, w
której zachodzi intensywne mieszanie w
całej objętości. Cechą charakterystyczną
jest tu praktycznie stały spadek ciśnienia
Δp

, pomimo wzrostu prędkości. Wraz ze

wzrostem prędkości rośnie wysokość
złoża oraz jego porowatość.
Stan 5. Prędkość przepływu zrównuje się z
prędkością opadania cząstek, tu kończy się
fluidyzacja (ε=1). Gdy prędkość gazu jest
większa od prędkości swobodnego

opadania cząstek, cząstki są wywiewane i unoszone w strudze gazu, zaczyna się wtedy
transport pneumatyczny.

Charakterystyczny „garb” (łuk BC) odpowiada spadkowi ciśnienia, który towarzyszy

opisanej poprzednio ekspansji złoża. Prosta CD charakteryzuje ustalony opór przepływu gazu
odpowiada właściwej fluidyzacji. Przy stopniowym zmniejszaniu prędkości przepływu gazu
od u

zaw

przez u

do prędkości wyjściowej opory przepływu zmieniają się wzdłuż drogi DCA.

Krzywa AB odpowiada złożu nieuporządkowanemu o porowatości ε

, które wymaga

większego spadku ciśnienia przy danej prędkości gazu niż złoże uporządkowane (odcinek
CA’) o porowatości ε’

Z praktycznego punktu widzenia istotną rzeczą jest określenie prędkości krytycznej u

dla danego złoża. Istnieje duża różnorodność ujęć tego problemu w literaturze.

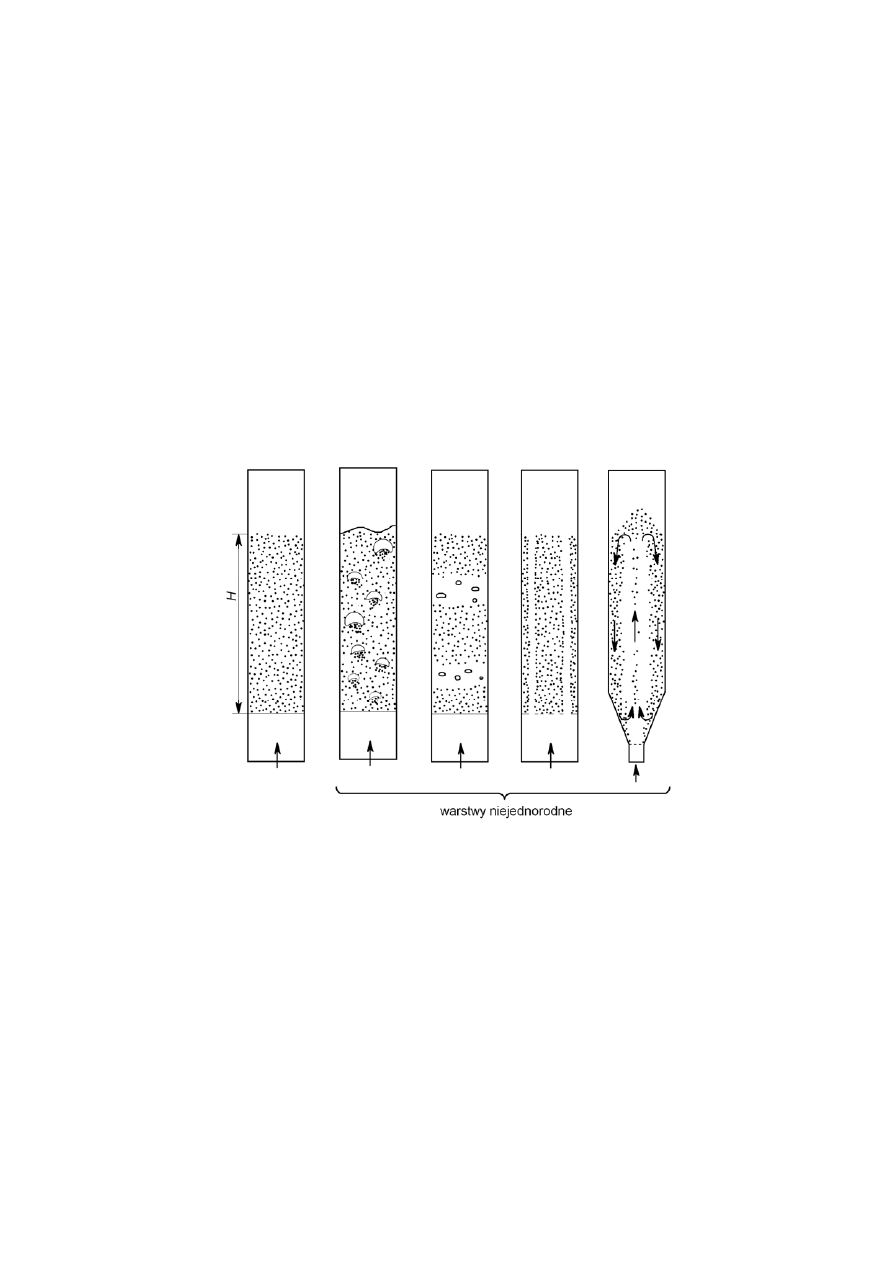
Należy jeszcze krótko omówić rodzaje warstw fluidalnych, które przedstawione

zostały na rysunku poniżej. Jak widać warstwy fluidalne dzielimy na jednorodne i
niejednorodne. Warstwa jednorodna ma taką samą porowatość w całej objętości, warstwa
niejednorodna zaś charakteryzuje się zmianom porowatość w poszczególnych miejscach
warstwy. Warstwy niejednorodne to: warstwa pęcherzykowa, tłokowa, kanalikowa i
fontannowa.

Warstwa pęcherzykowa – część gazu płynie w postaci pęcherzy.
Warstwa tłokowa (pulsująca) – pęcherze urastają to rozmiarów średnicy kolumny, tworząc
poprzeczne warstwy gazu, zaś warstwa zawiesiny znajduje się pomiędzy nimi.
Warstwa kanalikowa – występują pionowe kanały, przez które przepływa część gazu.
Warstwa fontannowa – cząstki wnoszą się do góry w rdzeniu kolumny a opadają na dół w
pobliżu ścian.

KRYTYCZNA PRĘDKOŚĆ FLUIDYZACJI

Większość badaczy wychodzi z założenia, że początek fluidyzacji następuje w

momencie zrównoważenia ciśnienia statycznego warstwy ze spadkiem ciśnienia w warstwie
nieruchomej . Jeżeli warstwa ziarnista o gęstości ρ

posiada w punkcie krytycznym

porowatość ε

, to jej pozorna gęstość wyniesie (1- ε

) ρ

Tak więc, przy wysokości H

odpowiadającej stanowi krytycznemu otrzymuje się zależność.















)

(

(1)

Która w połączeniu z jednym ze stosowanych równań na obliczenie spadku ciśnienia

w nieruchomej warstwie ziarnistej daje poszukiwaną zależność na u

W literaturze spotyka się często określenie prędkości krytycznej w postaci równań

kryterialnych typu Re

=f(Ar).

Jedna z najczęściej cytowanych zależności ma postać







(2)

Gdzie

)

(





















Z równań tych można określić krytyczną liczbę Reynoldsa, a następnie prędkość

krytyczną









(3)

Todes natomiast do równania (1) wprowadził spadek ciśnienia wynikający z równania

Erguna

)

(

)

(

150



























(4)

I otrzymał następującą zależność

)

(

)

(

150

)

(































(5)

Mnożąc obustronnie równanie (5) przez wyrażenie

)

(











Otrzymamy uogólniony zapis liczby Archimedesa w funkcji Re

)

(

150















(6)

Lub liczby Re

w funkcji liczby Ar

)

(

150









(7)

Dla większości materiałów stałych drobnoziarnistych porowatość krytyczna przyjmuje

wartość ok. 0,4; przy takim założeniu równanie (7) upraszcza się do postaci:

1400





(8)

Todes ustalił ponadto w drodze doświadczalno-teoretycznej ogólne równanie

interpolacyjne, z którego można obliczyć liczbę Re dla dowolnej wartości porowatości:











(9)

W przypadku szczególnym gdy ε=1, z równania (9) otrzymuje się znaną zależność na

prędkość swobodnego opadania cząstek w środowisku płynnym. W ten sposób dochodzi się
do pewnego ujednolicenia opisu matematycznego hydrodynamiki ciała stałego w ośrodku
płynnym. Ponieważ prędkość opadania cząstki ciała stałego w nieruchomym płynie jest

równa tzw. prędkości zawieszenia w procesie fluidyzacji (ε=1), więc wykres 1 ….. może być
uogólniony na bazie równań.

Zdolność danego układu monodyspersyjnego (Ar=const) do fluidyzacji charakteryzuje

stosunek

)

(

zaw



(10)

Istnieje wiele postaci zależności (8) podawanych przez różnych autorów. Na

podstawie równań (8) i (9) przy ε=1 można wprost napisać, że

zaw











1400

(11)

Stosunek rzeczywistej prędkości płynu u, odniesionej do całkowitego przekroju

aparatu, do prędkości krytycznej u

nosi nazwę liczby fluidyzacji



(12)

Jak wiadomo, opory przepływu w warstwie fluidalnej są niezależne od prędkości

płynu, tak więc musi obowiązywać równanie (1) w całym zakresie istnienia fluidyzacji od u

do u

zaw

, czyli



























)

(

)

(

(13)

Gdzie:
H – wysokość dynamiczna złoża fluidalnego [m]
ε – rzeczywista porowatość złoża

Równanie (13) pozwala na obliczenie oporów przepływu lub wysokości dynamicznej
warstwy fluidalnej dla dowolnej porowatości wynikającej z równania (9).

METODYKA POMIARÓW

Celem ćwiczenia jest określenie przebiegu spadku ciśnienia powietrza przepływającego przez
monodysperdyjną nieruchomą fluidalną warstwę ziarnistą, w zależności od prędkości
przepływającego gazu, określenie prędkości krytycznej i prędkości zawieszenia.
Ćwiczenia należy rozpocząć od doboru materiału monodyspersyjnego zgodnie z zaleceniami
prowadzącego ćwiczenie. Kolumnę należy napełnić materiałem ziarnistym do określonej –
przez prowadzącego ćwiczenie – wysokości statycznej H

. Po upewnieniu się, że zawór jest

zamknięty należy przełącznik z napisem „sieć”, a następnie uruchomić dmuchawę,
odpowiednim przyciskiem na tablicy rozdzielczej. Otwierając stopniowo zawór odczytywać
wskazania manometrów różnicowych w celu określenia spadku ciśnienia na kryzie
pomiarowej oraz spadku ciśnienia w kolumnie aż do momentu gdy powietrze przepływające
osiągnie prędkość zawieszenia. Następnie należy zawór stopniowo przymykać, jednocześnie
odczytując i notując wskazania manometrów różnicowych, ąz do jego całkowitego
zamknięcia i wyłączyć dmuchawę. Po zakończeniu pomiarów należy usunąć z wnętrza
kolumny wypełnienie ziarniste; można w tym celu użyć odkurzacza stanowiącego
wyposażenie stanowiska.

OPRACOWANIE WYNIKÓW

Na podstawie danych zestawionych w tabeli należy:

1. Sporządzić wykres Δh=f(u).

Na podstawie wskazań manometrów zwężki pomiarowej obliczyć natężenie
przepływu Q

, a stąp prędkość przepływu gazu w kolumnie fluidalnej. Otrzymane w

ten sposób prędkości przyporządkować wskazaniom manometru różnicowego
odpowiadającym oporom przepływu przez warstwę ziarnistą stacjonarną i fluidalną w

kolumnie i sporządzić wykres Δh=f(u) Wykres należy sporządzić w tradycyjnym
układzie współrzędnych oraz w układzie współrzędnych logarytmicznych.

2. Obliczyć prędkość krytyczną i zawieszenia.

Policzyć średnicę zastępczą ziarna d

a następnie liczbę Ar. Tak obliczonej liczbie Ar z

wykresy przyporządkować liczby Ly

i Ly

zaw

, a następnie obliczyć u

i u

zaw

Poszukać w literaturze innych wzorów na prędkość krytyczną i prędkość zawieszenia.
Otrzymane wyniki porównać z wartościami pomiarowymi.

3. Obliczyć stosunek prędkości

zaw

Dla uprzednio wyliczonej liczby Ar z wykresu 2 odczytać

zaw

i porównać go z takim

samym stosunkiem wynikającym z wartości pomiarowych i wartości obliczonych.

4. Obliczyć wartość kryterium stopnia jednorodności fluidyzacji





Lp Opory

złoża

ziarnistego

Opory na

zwężce

pomiarowej

Wydatek

powietrza

Prędkość

liczona

na pusty

aparat

zaw

Wartości obliczone

Wartości pomiarowe

=225 mm

=0,4

Literatura:

„Ćwiczenia laboratoryjne z inżynierii chemicznej”, skrypt PK, Kraków 1994

„Przepływy dwufazowe”, Z. Orzechowski , PWN, Warszawa 1990

„Fluidyzacja”, J. Ciborowski, PWT, Warszawa 1957