Metody Numeryczne w Mechanice -

Ćwiczenia laboratoryjne (M.Pyrz)

1

Obliczanie wartości i wektorów własnych

1.

Programowanie

Napisać skrypt w Scilabie umożliwiający wyznaczenie wartości własnej danej macierzy rzędu

n za pomocą metody potęgowej. Poszukiwana będzie wartość własna o największym module

(oraz odpowiadający jej wektor własny).

Algorytm :
wybrać wektor początkowy x

(0)

i znormalizować go stosując normę euklidesową

(0)

1

=

q

.

Dla iteracji

1, 2, 3, ...

k

=

, obliczyć następujące wielkości

(k)

(k-1)

x

= Aq

,

(k)

( )

(k-1)

j

k

j

λ

=

x

q

(k)

(k)

(k)

=

x

q

x

.

Zatrzymać iteracje po spełnieniu kryterium stopu

( )

(

1)

k

k

λ

λ

ε

−

−

<

.

Po kolejnych iteracjach

( )

1

lim

k

k

λ

λ

→∞

=

oraz

( )

1

lim

k

k

→+∞

=

x

x , gdzie

1

λ

jest wartością

własną o największym module, natomiast

1

x jest wektorem własnym odpowiadającym

wartości

1

λ

.

2.

Test i sprawdzenie poprawności

Wyznaczyć wartość własną o największym module (i odpowiadający jej wektor własny) dla

macierzy A.

Przeprowadzić obliczenia dla dokładności

ε

=10

-1

, 10

-2

, …, 10

-6

startując z wektorów x

1

(0)

=

[1 0.5 1 0.5]

T

oraz z x

2

(0)

= [0.5 -1 0 0]

T

i podać liczbę iteracji niezbędnych do uzyskania

rozwiązania.

Porównać wynik z rozwiązaniem otrzymanym za pomocą funkcji

spec i sformułować

wnioski.

2 10

8

0

4

1

1

5

0

2

8 12

2

1

4

8

A













=













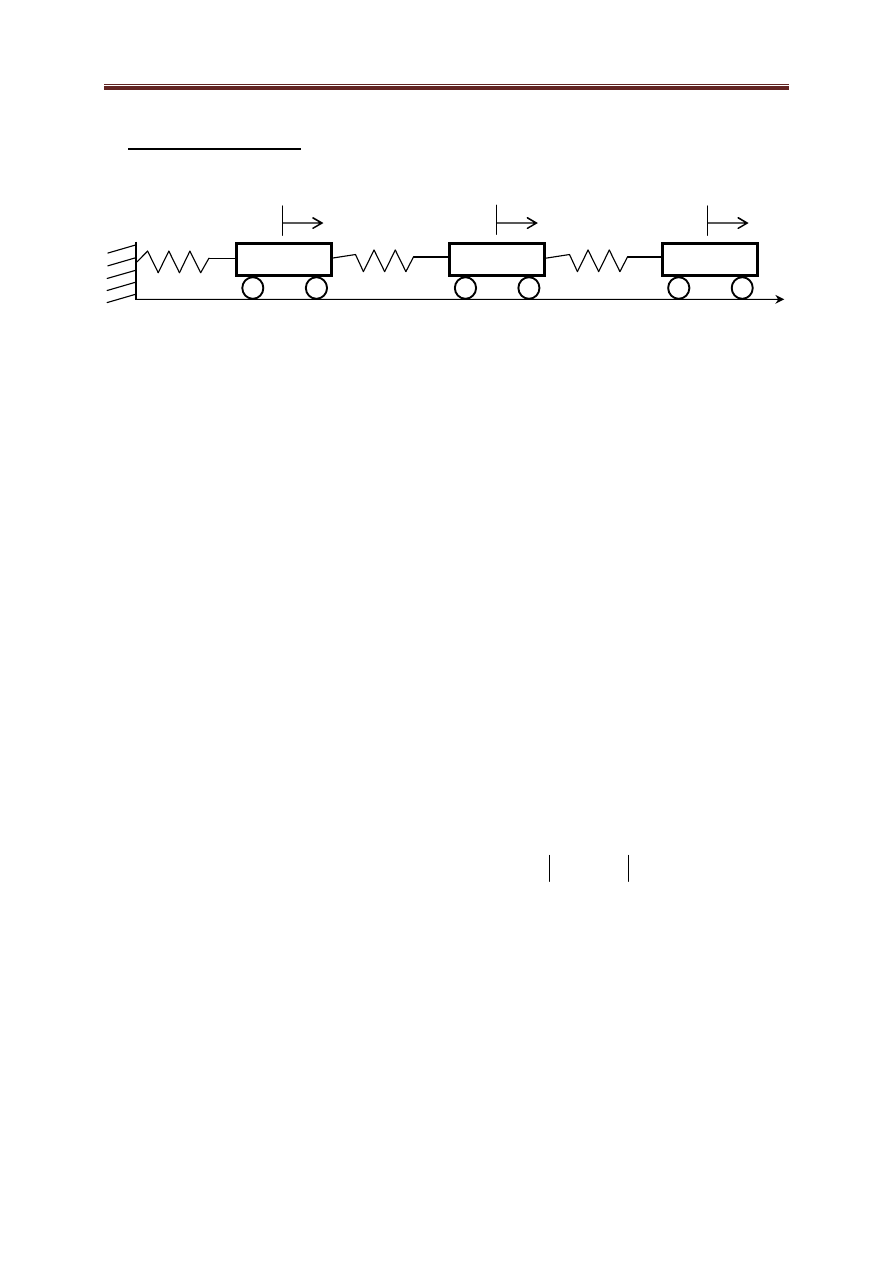
Metody Numeryczne w Mechanice -

Ćwiczenia laboratoryjne (M.Pyrz)

2

3.

Przykład obliczeniowy

Rozważamy przedstawiony na rysunku układ mas połączonych sprężynami:

gdzie x1(t), x2(t) i x3(t) przedstawiają oscylacje poziome(w funkcji czasu t) mas m1, m2 i m3

wokół położenia równowagi, k1, k2 i k3 są sztywnościami sprężyn.

Zakładamy, że x1(t), x2(t) i x3(t) spełniają następujący układ różniczkowych równań ruchu:

''

0

3

''

0

3

3

''

0

k1+ k2

-k2

0

x1(t)

m1

0

0

x1 (t)

-k2

k2+ k3

k

x2(t)

0

m2

0

x2 (t)

0

k

k

x3(t)

0

0

m3

x3 (t)



 

 

 

  







  









−

+

=







  















  









−



 

 

 

  

x1″(t), x2″(t) i x3″(t) oznaczają drugie pochodne x1(t) , x2(t) i x3(t) po czasie.

Poszukujemy rozwiązania układu równań różniczkowych czyli funkcji x1(t), x2(t) i x3(t) w

postaci:

sin(

),

sin(

),

(

sin(

)

x1(t)

a1

t

x2(t)

a2

t

x3 t)

a3

t

ω θ

ω θ

ω θ

=

+

=

+

=

+

, gdzie a1, a2, a3,

ω

i

θ

są stałymi niezależnymi od czasu.

a)

Wykazać, ze

ω

2

jest wartością własną macierzy

b)

Przyjmując wartości: k1 = k2 = k3 = m1 = m2 = m3 = 1.

wyznaczyć (stosując metodę potęgową) największą wartość własną podanej macierzy oraz

odpowiadający jej wektor własny (kryterium stopu:

001

.

0

)

1

(

)

(

=

≤

−

−

ε

λ

λ

k

k

, wektor

początkowy:

[

]

(0)

0.8

1.0

0.4

=

−

T

x

).

c)

Wyznaczyć wszystkie częstotliwości i postaci drgań korzystając z funkcji

spec

d) Korzystając z funkcji

spec przeprowadzić obliczenia

ω

(i postaci drgań) dla układu mas i

sprężyn charakteryzowanego przez (wystarczy wybrać jeden dowolny przpadek) i
przedstawić schematycznie uzyskane postaci drgań.

i)

k1 =3, k2 = 2, k3 =1 et m1 = 1, m2 = 1, m3 = 1,

ii)

k1 =1, k2 = 1, k3 =1 et m1 = 1, m2 = 2, m3 = 3,

iii)

k1 =1, k2 = 1, k3 =1 et m1 = 1, m2 = 4, m3 = 1.

x1(t)

x2(t)

x3(t)

m1

m2

m3

k1

k2

k3

x

(k1+ k2)/m1

-k2/m1

0

-k2/m2

(k2 + k3)/m2

-k3/m2

0

-k3/m3

k3/m3



















