3

BADANIE PRZENIKALNOŚCI DIELEKTRYCZNEJ

I WSPÓŁCZYNNIKA STRAT DIELEKTRYCZNYCH

MATERIAŁÓW IZOLACYJNYCH STAŁYCH

I. WIADOMOŚCI TEORETYCZNE

1. Polaryzacja dielektryków

Atomy z punktu widzenia elektryczności składają się z dodatnich jąder atomo-

wych otoczonych przez ujemne chmury elektronowe. Ładunek ujemny chmur
elektronowych równoważy dodatni ładunek jądra, każdy więc atom (element mate-
rii) jest elektrycznie obojętny. Działanie pola elektrycznego na materię objawiać
się może przesunięciem względem siebie różnoimiennych ładunków bądź zmianą
orientacji w przestrzeni pary tych ładunków. Wszelkie przesunięcia i zmiany poło-
ż

enia ładunków noszą nazwę polaryzacji materiału a pary rozsuniętych ładunków

przeciwnego znaku tworzą tzw. dipole elektryczne. Ogólnie rzecz biorąc mechani-
zmy polaryzacji można podzielić na stratne i bezstratne. Polaryzacje odbywające się
bez strat to polaryzacje deformacyjne związane z częstotliwościami drgań wła-
snych cząsteczek leżącymi w paśmie odpowiadającym promieniowaniu świetlnemu.

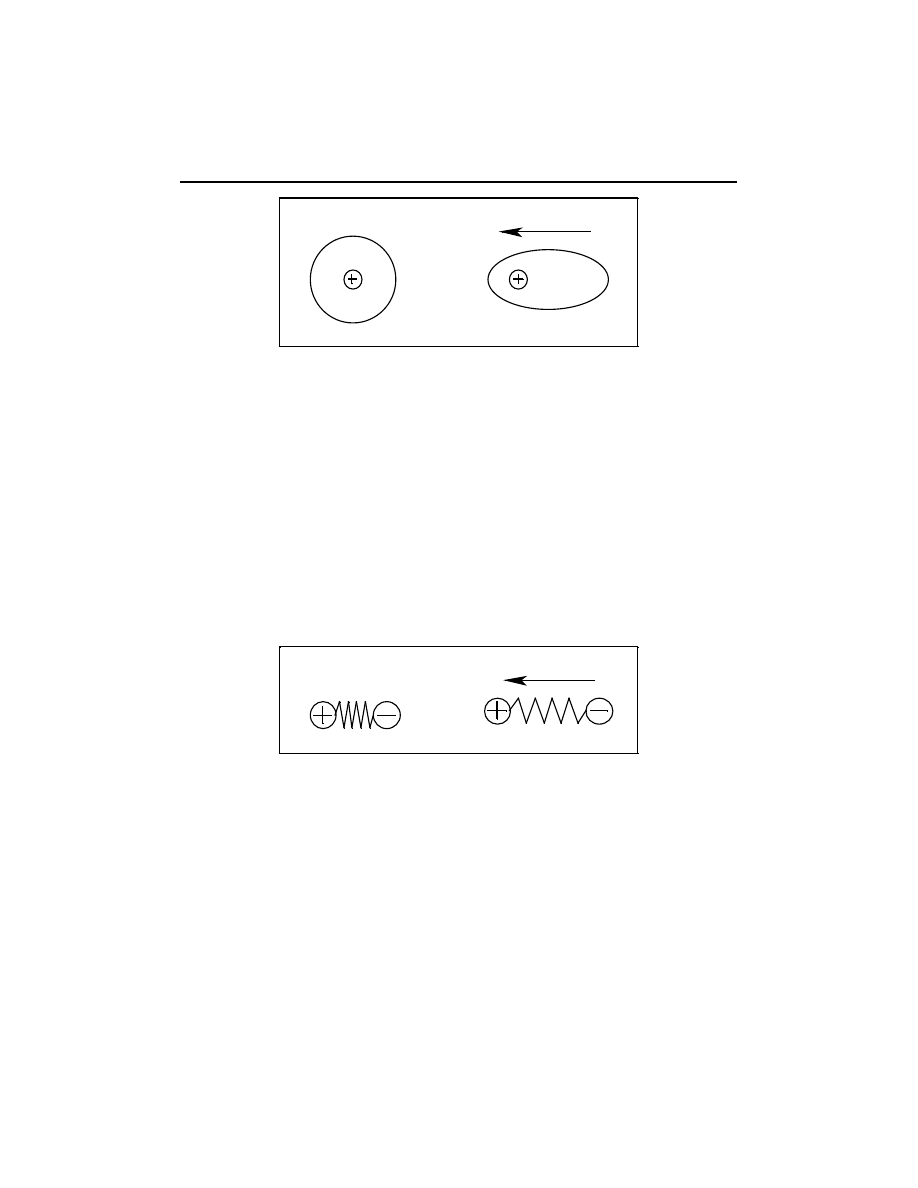
1.1. Polaryzacja elektronowa

Przyłożone pole elektryczne powoduje przesunięcie powłok elektronowych wzglę-

dem dodatnich jąder. „Środki ciężkości” ładunków nie pokrywają się i powstaje
indukowany moment dipolowy. Polaryzacja ta zachodzi w czasie 10

–15

÷

10

–13

s

zależnie od rodzaju dielektryka. Nie pociąga za sobą strat energii i nazywana jest
polaryzacją deformacyjną. Wywołany przez nią prąd elektryczny jest czysto pojem-
nościowy. Polaryzacja ta występuje w materiałach o cząsteczkach symetrycznych.

34

Ć

wiczenie 3

E

Rys. 3.1. Polaryzacja elektronowa

Przenikalność dielektryczna względna dielektryków charakteryzujących się wy-

stępowaniem tego mechanizmu polaryzacji

ε

’ = 2

÷

4. Przedstawiciele: polistyren,

polietylen, olej mineralny, policzterofluoroetylen, parafina.

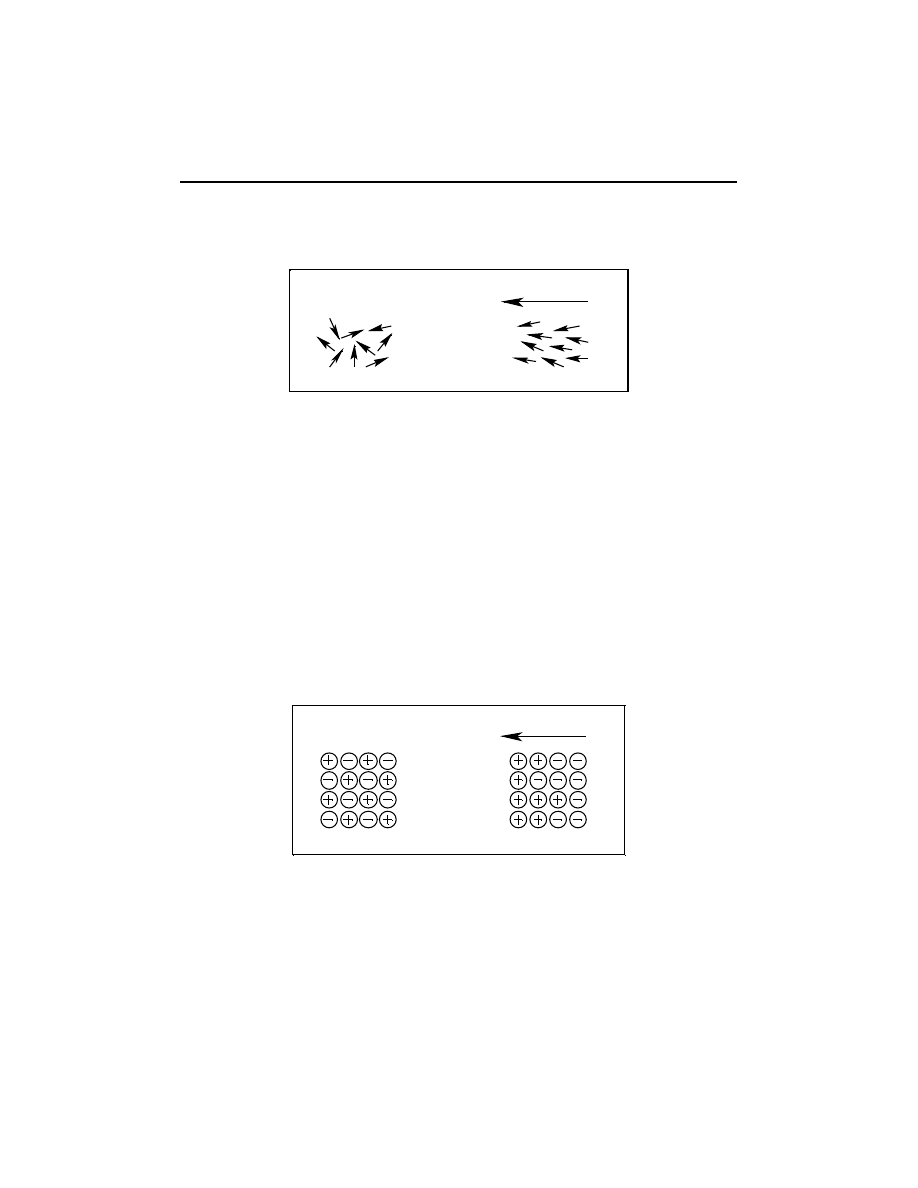
1.2. Polaryzacja atomowa (jonowa)

Ten rodzaj polaryzacji występuje w materiałach których cząstki zbudowane są

z niejednakowych atomów i chmury elektronowe jednych atomów są przesunięte
w kierunku drugich silniej je wiążących. Atomy w takiej cząsteczce posiadają
przewagę ładunków – jedne dodatnich, drugie – ujemnych. Przesunięcie tych wy-
padkowych ładunków względem siebie stanowi istotę tej polaryzacji. Niezależnie
od tej polaryzacji skręcanie powstałych w ten sposób dipoli w kierunku pola jest
ź

ródłem polaryzacji dipolowej.

E

Rys. 3.2. Polaryzacja atomowa

Polaryzacja atomowa, zwana też jonową, jest również polaryzacją deformacyj-

ną odbywającą się bez strat. Polaryzacja ta zachodzi w czasie 10

–14

÷

10

–12

s.

Przenikalności elektryczne względne dielektryków charakteryzujących się wystę-
powaniem tej polaryzacji wynoszą

ε

’ = 4

÷

12. Przedstawiciele: szkło, mika, mate-

riały ceramiczne, kwarc.

1.3. Polaryzacja dipolowa

Asymetryczny rozkład ładunków pomiędzy niejednakowymi atomami jest źró-

dłem trwałych momentów dipoli istniejących także w nieobecności zewnętrznego

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

35

pola elektrycznego. Ponieważ są one zorientowane w różnych kierunkach ich mo-
ment wypadkowy jest na ogół bliski zeru. Pod wpływem przyłożonego pola ze-
wnętrznego na dipole działają momenty sił dążące do zgodnego z polem ich usta-
wienia.

E

Rys. 3.3. Polaryzacja dipolowa

Polaryzacja dipolowa, zwana też polaryzacją orientacji, jest polaryzacją stratną

– zachodzi w czasie 10

–10

÷

10

–2

s. Obroty dipoli związane są z pokonywaniem

oporów ośrodka – występuje więc rozpraszanie energii. Przenikalność elektryczna
wynosi:

ε

’ = 3

÷

6. Przedstawiciele materiałów charakteryzujących się występo-

waniem tego mechanizmu polaryzacji to: guma wulkanizowana, bakelit, polichlo-
rek winylu, polioctan winylu.

1.4. Polaryzacja ładunku przestrzennego

Polaryzacja ta wynika z ruchu nośników elektryczności. które mogą się prze-

suwać w dielektryku na pewnych odległościach. Ruch nośników jest hamowany
powodując, że ładunki nie mogą być swobodnie zobojętniane na elektrodach. Po-
wstaje ładunek przestrzenny powodujący zniekształcenie pola przejawiające się we
wzroście pojemności materiału.

E

Rys. 3.4. Polaryzacja ładunku przestrzennego

Polaryzacja ładunku przestrzennego należy do grupy mechanizmów polaryzacji

określanych jedną nazwą – polaryzacja makroskopowa. Istotą tych polaryzacji jest
przesuwanie się ładunków na pewnych odcinkach wewnątrz materiału izolacyjne-
go. Odmianami tej polaryzacji są np: polaryzacja wysokonapięciowa (jest funkcją
napięcia), polaryzacja strukturalna, polaryzacja warstwowa.

36

Ć

wiczenie 3

Czas zachodzenia polaryzacji zależy od struktury materiału i mechanizmu zwią-

zanego z ruchem ładunku – od ułamków sekund (10

–3

s) do minut a nawet godzin.

Przedstawicielami materiałów charakteryzujących się występowaniem polary-

zacji makroskopowej są: dielektryki niejednorodne (np. izolacja papierowo-olejo-
wa) oraz dielektryki z dużą ilością jonów swobodnych (np. polimetakrylan metylu).

1.5. Zjawisko polaryzacji – podsumowanie

Zazwyczaj w materiałach izolacyjnych występuje wypadkowe działanie kilku

rodzajów polaryzacji. Mechanizmy polaryzacji charakteryzuje częstotliwość drgań
własnych powyżej której polaryzacja nie nadąża za zmianami pola przyłożonego.
Te charakterystyczne częstotliwości to: częstotliwości rezonansowe (polaryzacje
bezstratne) oraz częstotliwości relaksacyjne (polaryzacje stratne).

Po przyłożeniu pola o częstotliwości przekraczającej częstotliwość charaktery-

styczną dla danego mechanizmu polaryzacji polaryzacja ta zostaje wygaszona –
przestaje występować Objawia się to zmniejszeniem pojemności układu.

Jeżeli częstotliwość przyłożonego pola będzie równa częstotliwości rezonan-

sowej bądź relaksacyjnej wystąpi silne pochłanianie energii objawiające się wy-
stępowaniem w pobliżu tej częstotliwości ekstremum współczynnika strat dielek-
trycznych tg

δ

.

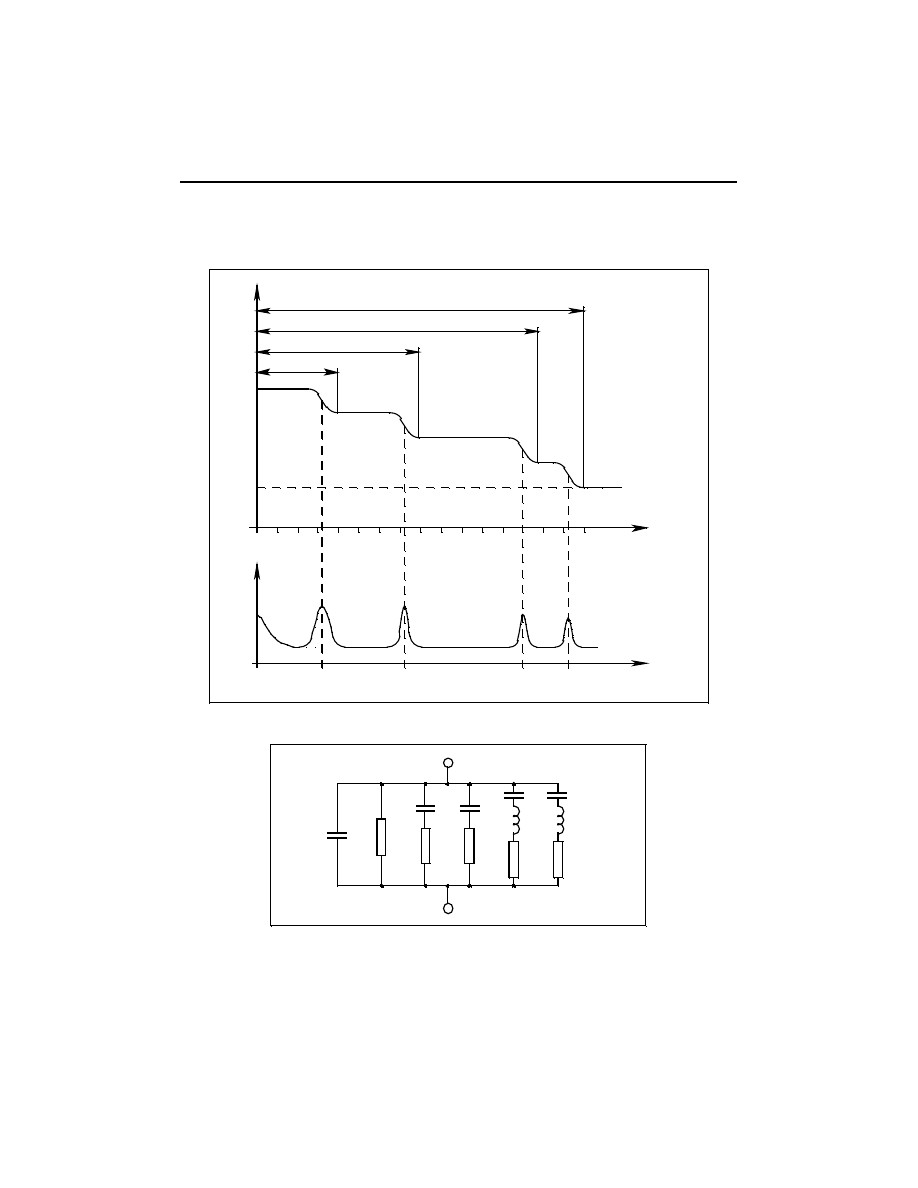
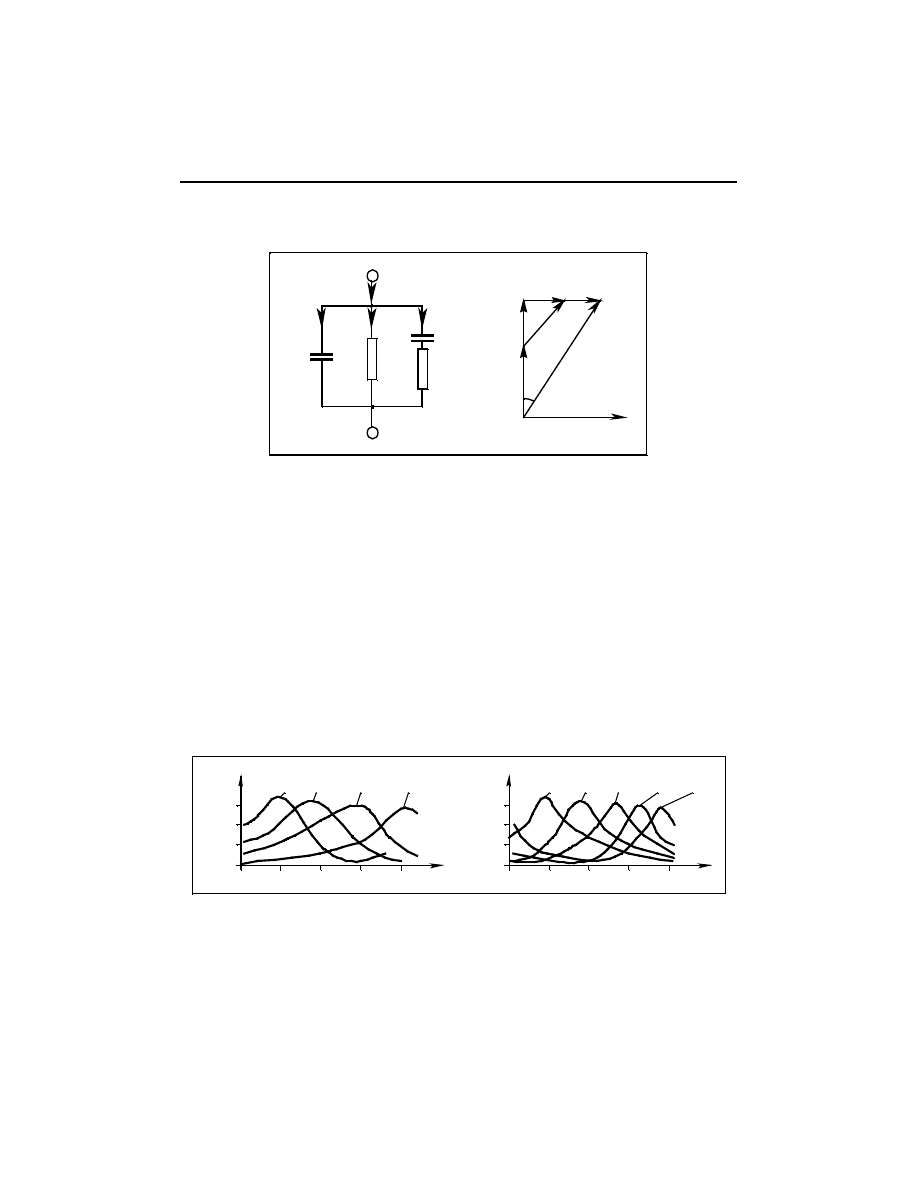
Na rysunku 3.5 przedstawiono zależność

ε

’ = f

(f) i tg

δ

= f

(f) dla hipotetyczne-

go dielektryka charakteryzującego się występowaniem czterech omówionych me-
chanizmów polaryzacji. Zależności te przedstawiono w sposób uproszczony poka-
zujący charakter występujących zmian. W rzeczywistości zmiany te są bardziej
rozmyte, zwłaszcza w zakresie niskich częstotliwości.

Rysunek 3.6 przedstawia schemat zastępczy hipotetycznego dielektryka z wystę-

pującymi w nim czterema omówionymi mechanizmami polaryzacji. Stałe czasowe
R

1

C

1

i R

2

C

2

to stałe czasowe relaksacji. Ich odwrotności odpowiadają częstotliwo-

ś

ciom relaksacyjnym polaryzacji dipolowej i ładunku przestrzennego. Gałęzie

z indukcyjnościami reprezentują polaryzacje szybkie związane z absorpcją rezo-
nansową.

2. Przenikalność i podatność dielektryczna

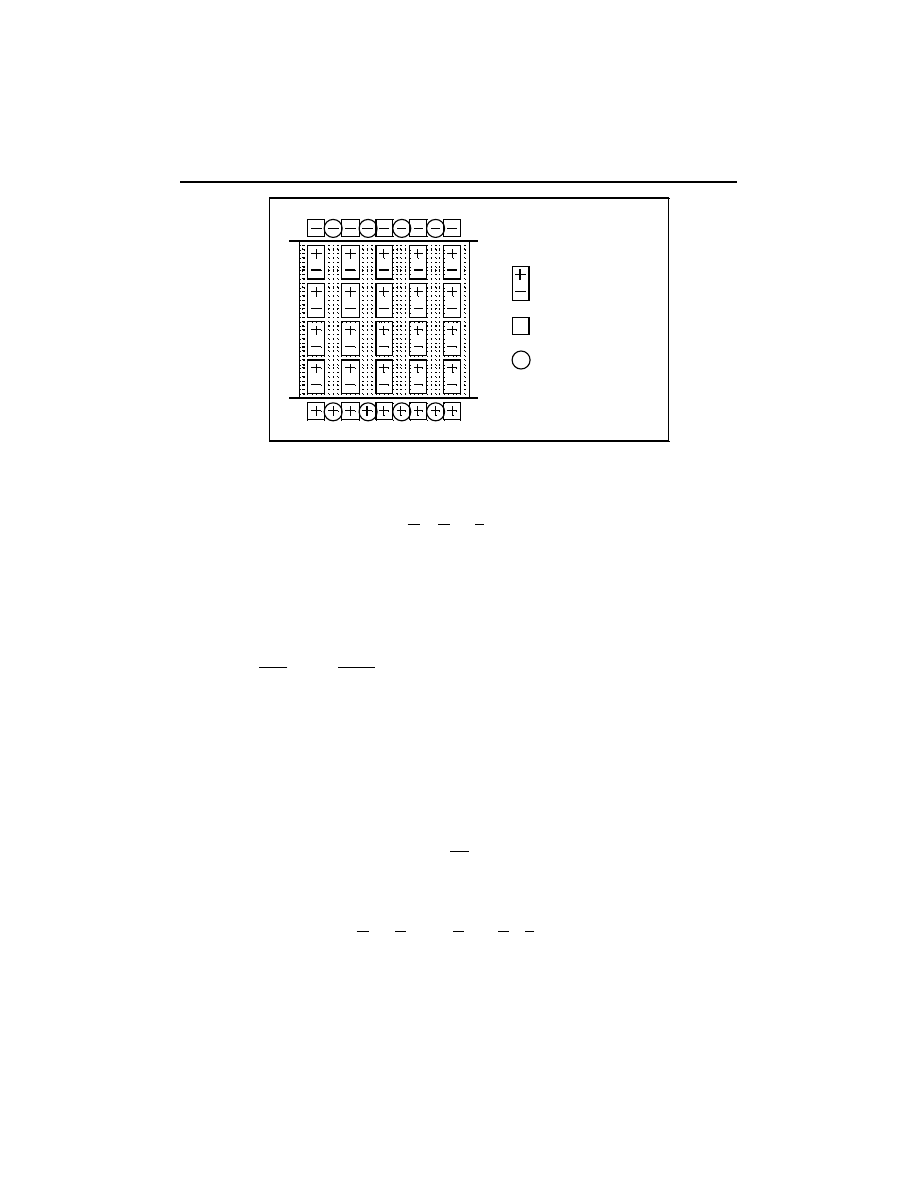
Ogólnie zjawisko polaryzacji można sobie wyobrazić jako działanie łańcuchów

dipolowych formowanych pod wpływem przyłożonego pola, których końce wiążą
ładunki przeciwnego znaku znajdujące się na elektrodach (rys. 3.7).

Gęstość powierzchniową ładunku zgromadzonego na każdej z elektrod przed-

stawia liczbowo wektor indukcji dielektrycznej D prostopadły do powierzchni.
Ładunek ten to suma ładunku swobodnego i związanego. Gęstość ładunku związa-
nego reprezentuje wektor polaryzacji P. Pole elektryczne wewnątrz dielektryka jest

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

37

związane z ładunkiem swobodnym. Natężenie pola elektrycznego jest proporcjo-
nalne do gęstości powierzchniowej tego ładunku swobodnego zgromadzonego na
elektrodzie. Ilość ładunku swobodnego nie zależy od rodzaju materiału i dla danej
geometrii elektrod ma wartość stałą.

log(f )

log(f

3

)

log(f

4

)

16

14

tg

δ

log(f

1

)

log(f

2

)

8

6

4

2

1

dipolowa

ε

'

makroskopowa

atomowa

12

log(f )

10

elektronowa

Rys. 3.5. Występowanie mechanizmów polaryzacji w zależności od częstotliwości ze-

wnętrznego pola elektrycznego

L

3

R

u

C

g

R

2

R

3

R

1

R

4

L

4

C

2

C

1

C

3

C

4

Rys. 3.6. Schemat zastępczy dielektryka: C

g

- pojemność geometryczna,

R

u

- rezystancja upływu, C

1

R

1

, C

2

R

2

- gałęzie związane

z polaryzacjami stratnymi, C

3

L

3

R

3

, C

4

R

4

L

4

- gałęzie związane

z polaryzacjami bezstratnymi

38

Ć

wiczenie 3

- dipol elektryczny

- ładunek swobodny

- ładunek związany

Rys. 3.7. Zjawisko polaryzacji dielektrycznej

Dla wektorów reprezentujących gęstości powierzchniowe ładunku można napi-

sać zależność

D

D

P

=

+

0

,

(3.1)

gdzie D

0

- indukcja dielektryczna w próżni – reprezentuje gęstość powierzchniową

ładunku swobodnego, przy czym

D

0

=

ε

0

E

,

(

3.2)

gdzie

ε

π

0

9

1

36

10

=

⋅

⋅

⋅

−

A s

V m

- współczynnik proporcjonalności.

Wektor gęstości strumienia elektrycznego w próżni i wektor linii sił pola zwią-

zane są ze sobą współczynnikiem proporcjonalności

ε

0

zwanym przenikalnością

dielektryczną próżni lub stałą dielektryczną. Istnienie tego współczynnika wynika
z rozważań wymiarowych.

Dla ośrodka innego niż próżnia współczynnikiem proporcjonalności będzie

przenikalność dielektryczna (lub elektryczna) ośrodka

ε

. Wprowadzając przenikal-

ność dielektryczną względną

ε

ε

ε

'

=

0

,

(3.3)

możemy zgodnie z wzorem (3.1) napisać

D

E

E

E

P

=

=

=

+

ε

ε ε

ε

'

0

0

,

(3.4)

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

39

stąd wektor polaryzacji

( )

P

E

E

E

=

−

=

− ⋅

ε ε

ε

ε ε

'

'

0

0

0

1

.

(3.5)

Wyrażenie

ε

ε

κ

'

− =

=

1

0

P

E

(3.6)

będące stosunkiem gęstości ładunków związanych do gęstości ładunków swobod-
nych przedstawia sobą wielkość zwaną podatnością dielektryczną materiału ozna-
czaną przez

κ

(kappa). Biorąc pod uwagę występowanie różnych rodzajów polary-

zacji można mówić o podatności na polaryzację: elektronową, atomową, dipolową,
makroskopową. Możemy napisać

κ

κ

κ

κ

κ

=

+

+

+

=

+

+

+

P

P

P

P

D

e

a

d

m

e

a

d

m

0

.

(3.7)

W związku z powyższym przenikalność dielektryczna względna ośrodka die-

lektrycznego będzie sumą podatności dielektrycznych na różne rodzaje polaryzacji
zwiększoną o 1

ε

κ

κ

κ

κ

'

= +

+

+

+

1

e

a

d

m

.

(3.8)

Jedną z wielkości charakteryzujących układ izolacyjny jest jego pojemność

elektryczna opisana zależnością

C

Q

U

D S

U

E S

U

C

=

= ⋅ =

⋅

=

ε ε

ε

'

'

0

0

,

(3.9)

gdzie: Q - ładunek zgromadzony na każdej z elektrod, S - powierzchnia elektrody,

U - napięcie przyłożone do elektrod, C

0

- pojemność układu próżniowego.

Zgodnie z ostatnią zależnością przenikalność dielektryczna względna pokazuje

ile razy pojemność układu z dielektrykiem jest większa od pojemności układu
próżniowego. Pojemność natomiast przedstawia sobą swoistą chłonność ładunku
elektrycznego przez układ przy danym napięciu między jego elektrodami.

3. Zależność przenikalności elektrycznej od temperatury i częstotliwości

Wartość przenikalności elektrycznej materiału izolacyjnego zależy od rodzajów

występujących w nim polaryzacji oraz od gęstości materiału (stanu skupienia)
czyli od liczby ładunków związanych mieszczących się w jednostce objętości.

W przypadku

polaryzacji elektronowej, którą charakteryzują się dielektryki

stałe o cząsteczkach symetrycznych, wpływ temperatury jest nieznaczny. Zmniej-

40

Ć

wiczenie 3

szenie się

ε

’ wraz ze wzrostem temperatury związane jest z maleniem gęstości

materiału. Wpływ częstotliwości praktycznie nie występuje.

Dielektryki charakteryzujące się występowaniem

polaryzacji atomowej wyka-

zują wzrost

ε

’ ze wzrostem temperatury. Polaryzacja zostaje ułatwiona wskutek

osłabienia więzi między jonami. Od częstotliwości przenikalność dielektryczna
praktycznie nie zależy.

Przy występowaniu

polaryzacji dipolowej i makroskopowej występuje silna

zależność

ε

’ od częstotliwości i temperatury. Jeżeli ruch nośników lub obroty di-

poli nadążają za zmianami pola przenikalność elektryczna ma stałą wartość. Po
przekroczeniu przez częstotliwość pola przyłożonego pewnej granicy polaryzacja
zaczyna zanikać. Granica ta, zwana częstotliwością relaksacji, zależy od temperatury.
Wpływ temperatury może objawiać się ułatwieniem bądź utrudnieniem obrotu dipoli.

4. Pojęcie współczynnika strat dielektrycznych tg

δδδδ

Straty energii w dielektryku charakteryzuje współczynnik strat dielektrycznych.

Ź

ródła tych strat to:

−

upływność materiału,

−

polaryzacje stratne,

−

wyładowania niezupełne (przy wysokim napięciu).

Po względem zachowania elektrycznego dielektryk odpowiada kondensatorowi

połączonemu z rezystorem. Obok składowej prądu ładowania występuje prąd strat:
Dla połączenia równoległego R i C i napięcia sinusoidalnego możemy napisać

I

I

I

j C

G

U

C

R

=

+

=

+

⋅

(

)

ω

,

(3.10)

gdzie G = 1/R.

tg

I

I

RC

R

C

δ

ω

=

=

1

.

(3.11)

Przy napięciu sinusoidalnie zmiennym proces ładowania i rozładowania powta-

rza się okresowo. Prąd ładowania I

C

wyprzedza wektor napięcia o 90

°

. Prąd upły-

wu jest zgodny w fazie z napięciem, ale prąd związany z polaryzacją stratną ma
zarówno składową czynną jak i bierną. Schemat zastępczy układu i wykres wekto-
rowy uwzględniający występowanie polaryzacji stratnej przedstawia rysunek 3.8.

Współczynnik strat dielektrycznych w takim przypadku będzie przedstawiał wzór

tg

I

I

I

I

R

acz

C

ab

δ =

+

+

(3.12)

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

41

Wartość współczynnika strat tg

δ

zależy od rodzaju materiału (polaryzacja

i upływność), wartości napięcia (wyładowania niezupełne) oraz pośrednio od tem-
peratury i częstotliwości.

I

I

c

I

u

a)

b)

I

acz

I

a

I

c

I

ab

R

a

C

a

I

a

C

g

R

u

I

U

δ

I

u

Rys. 3.8. Schemat zastępczy (a) i wykres wektorowy prądów w dielek-

tryku (b): C

g

- pojemność geometryczna, R

u

- rezystancja upływu,

R

a

, C

a

- rezystancja i pojemność absorpcyjna, I

C

- prąd pojem-

nościowy, I

u

- prąd upływu, I

a

- prąd absorpcji (I

acz

- czynny,

I

ab

- bierny)

5. Zależność tg

δδδδ

od temperatury i częstotliwości

Dielektryki charakteryzujące się tylko

polaryzacją elektronową wykazują du-

żą

stałość tg

δ

w szerokim zakresie częstotliwości. Ze wzrostem temperatury tg

δ

przeważnie rośnie. Związane jest to ze wzrostem upływności na skutek wzmożonej
jonizacji. Dielektryki o polaryzacji elektronowej mają tg

δ

pomijalnie mały.

Dielektryki o

polaryzacji atomowej mają również mały współczynnik strat

dielektrycznych tg

δ

(polaryzacja bez strat). Zależność od temperatury wynika

również ze zmian prądu upływu. Zależność od częstotliwości jest znikoma.

50Hz

60°C

5

4

3

Hz

10

10

10

f

100°C

90°C

80°C

70°C

2

10

0,005

80

10kHz

70

1kHz

ϑ

°C

90

100kHz

0

tg

δ

60

0,015

0,010

0,005

0

50

10

tg

δ

1

0,015

0,010

Rys. 3.9. Zależność tg

δ

od temperatury i częstotliwości dla polioctanu winylu

Dielektryki

dipolowe charakteryzują się silną zależnością tg

δ

zarówno od czę-

stotliwości jak i temperatury. Największe straty występują przy częstotliwości relak-
sacji. Powyżej tej częstotliwości ruch dipoli nie nadąża za zmianami pola, poniżej

42

Ć

wiczenie 3

– energia tracona w jednostce czasu maleje gdyż straty związane z obrotem dipoli
rozkładają się na dłuższy odcinek czasu. Wpływ temperatury objawia się utrudnie-
niem bądź ułatwieniem obrotów dipoli – częstotliwość relaksacyjna jest funkcją
temperatury. Przy stałej częstotliwości największe straty odpowiadają ściśle okre-
ś

lonej temperaturze, a przy stałej temperaturze ściśle określonej częstotliwości

(rys. 3.9). Powyższe uwagi dotyczą również polaryzacji ładunku przestrzennego.

W przypadku dielektryków uwarstwionych można wyodrębnić kilka częstotli-

wości relaksacyjnych. Każda warstwa wnosi swoją częstotliwość i swoje maksi-
mum tg

δ

. Z drugiej strony w dielektrykach uwarstwionych podstawowe znaczenie

mają inne rodzaje polaryzacji makroskopowej (strukturalna, warstwowa), którym
odpowiadają inne częstotliwości relaksacyjne.

6. Zespolona przenikalność dielektryczna

Przy rozpatrywaniu zachowania się dielektryków w niewielkim zakresie czę-

stotliwości wprowadzone pojęcia przenikalności elektrycznej i współczynnika strat
dielektrycznych dobrze służą praktyce. Można wtedy założyć stałość pojemności
a występujące straty przedstawić w schemacie zastępczym w postaci rezystora.

W szerszym zakresie częstotliwości przenikalność elektryczna, a więc i pojem-

ność, nie może być uznana za stałą – będzie funkcją częstotliwości przyłożonego
pola. Funkcją częstotliwości będą również straty. Momenty dipolowe potrzebują
czasu dla powstawania i znikania, podobnie nośniki prądu muszą być uruchamiane
i przyspieszane zanim ustali się ich stała prędkość unoszenia. Opóźnienie pomię-
dzy chwilą wytworzenia pola i indukowaniem momentów dipolowych powoduje
przesunięcie fazowe pomiędzy napięciem i prądem zmniejszając kąt fazowy prą-
dów polaryzacji poniżej 90

°

. Powstają prądy czynne, które nie są wywołane wę-

drówką nośników ładunków. Sinusoidalnie zmienne pole przyłożone powoduje
powstanie sinusoidalnie zmiennej indukcji i sinusoidalnie zmiennego pola elek-
trycznego. Opóźnienie, o którym mowa powyżej, powoduje powstanie przesunię-
cia fazowego pomiędzy D i E. Aby zespolona zależność między tymi wielkościami
(wzór (3.3)) miała matematyczny sens, przenikalność elektryczna musi być rów-
nież wielkością zespoloną. Możliwe staje się wtedy przedstawienie procesów ma-
gazynowania i rozpraszania energii bez określania pochodzenia strat.

Opisując dotychczas, przy użyciu rachunku zespolonego, prąd płynący przez

pojemność przyłączoną do źródła napięcia sinusoidalnego, przedstawiamy nastę-
pujące zależności na prąd pojemnościowy i czynny

I

j

C

U

j C U

C

=

⋅ =

⋅

ωε

ω

'

0

, I

G U

R

= ⋅

,

(3.13)

stąd prąd całkowity i współczynnik strat wynoszą

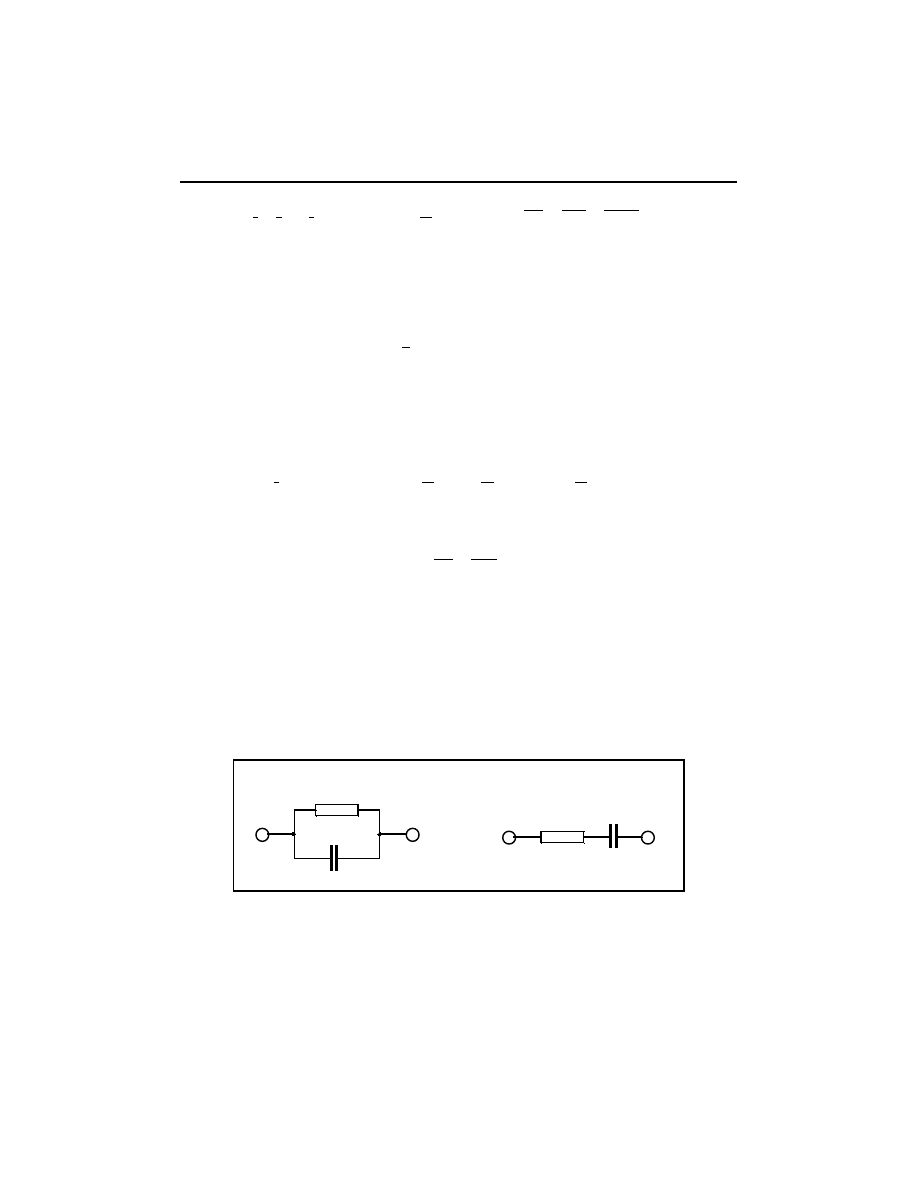
Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

43

I

I

I

j C

G

U

R

C

=

+

=

+

⋅

(

)

ω

, tg

I

I

G

C

RC

R

C

δ

ω

ω

=

=

=

1

.

(3.14)

Reakcja częstotliwościowa obwodu określona przy pomocy powyższych wzo-

rów nie zgadza się z obserwacją. Człon przewodnościowy prądu może nie przed-
stawiać sobą procesu ruchu ładunków, ale inny proces pochłaniania energii.

Wprowadzając zespoloną względną przenikalność elektryczną w postaci

ε ε

ε

'

'

'

=

−

rz

ur

j

,

(3.15)

gdzie:

ε

’

rz

- rzeczywista względna przenikalność elektryczna wyrażająca zdolność

magazynowania energii w dielektryku,

ε

’

ur

- urojona względna przenikalność

elektryczna wyrażająca zdolność rozpraszania energii,

można zależność na prąd płynący przez pojemność wyrazić następująco

I

j

j

C U

C U

j C U

rz

ur

ur

rz

=

−

⋅

=

⋅

+

⋅

ω ε

ε

ω

ε

ω

ε

( '

'

)

'

'

0

0

0

.

(3.16)

Współczynnik strat dielektrycznych przedstawia następująca zależność

tg

I

I

R

C

ur

rz

δ

ε

ε

=

=

'

'

.

(3.17)

7. Obwody równoważne

Obwód równoważny to taki obwód, którego odpowiedź na przyłożone napięcie

w szerokim zakresie częstotliwości jest taka sama jak dielektryka. Dla jednej wy-
branej częstotliwości istnieje dowolna liczba interpretacji układowych zwanych
schematami zastępczymi, z których najprostsze to obwody: równoległy i szerego-
wy (rys. 3.10).

C

s

R

s

b)

C

r

R

r

a)

Rys. 3.10. Schemat zastępczy równoległy (a) i szeregowy (b) dielektryka

Dla każdej częstotliwości możemy zbudować schemat zastępczy dielektryka

równoległy lub szeregowy, ale wartości pojemności i rezystancji w tych schema-

44

Ć

wiczenie 3

tach mogą być dla każdej częstotliwości inne. Obliczone z tych schematów warto-
ś

ci

ε

’

rz

i

ε

’

ur

mogą zgadzać się z pomierzonymi tylko dla jednej częstotliwości.

Rozpatrzmy schemat równoległy. Admitancja układu wynosi

Y

R

j C

r

r

=

+

1

ω

,

(3.18)

z drugiej strony admitancja to stosunek prądu do napięcia

Y

I

U

C

j

ur

rz

=

=

+

ω

ε

ε

0

( '

' ) .

(3.19)

Porównując części rzeczywiste i urojone wyrażeń (3.18) i (3.19) otrzymujemy

ε

ω

'

ur

r

R C

=

1

0

,

ε

'

rz

r

C

C

=

0

, tg

C R

ur

rz

r

r

δ ε

ε

ω

=

=

'

'

1

.

(3.20)

Analogicznie postępując możemy otrzymać następujące zależności dla sche-

matu szeregowego

ε

ω

ω

'

ur

s

s

s

s

s

C

C

R C

R C

=

⋅

+

0

2

2

2

1

,

ε

ω

'

rz

s

s

s

C

C

R C

=

⋅

+

0

2

2

2

1

1

, tg

R C

s

s

δ ω

=

.

(3.21)

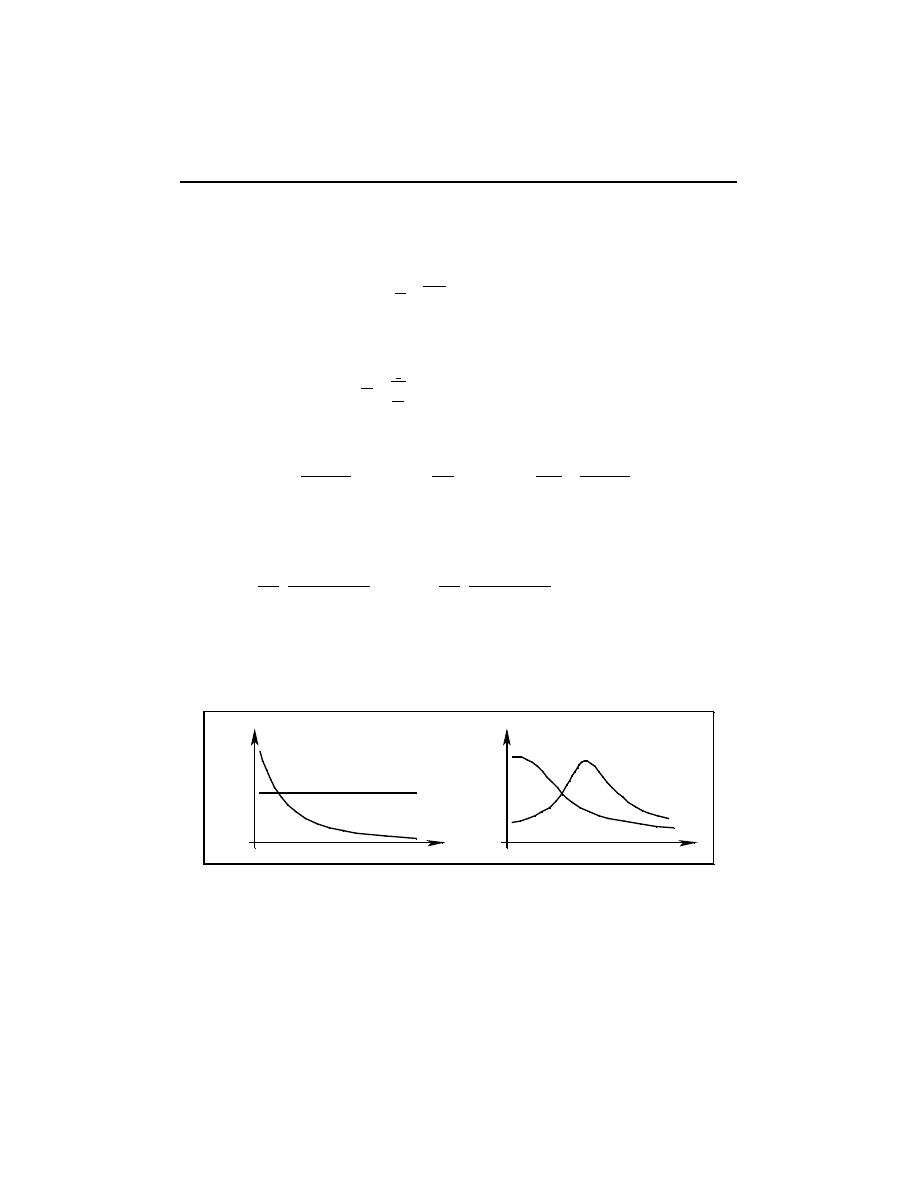
Na rysunku 3.11 przedstawiono zależność przenikalności od częstotliwości dla

hipotetycznych dielektryków dla których schematy równoległy i szeregowy stano-
wią obwody równoważne. Zależności te są słuszne w przypadku braku polaryzacji
stratnych (straty tylko upływnościowe) i stałej pojemności.

ε

'

rz

ε

'

ur

a)

ε

'

ω

ω

b)

ε

'

ur

ε

'

rz

ε

'

Rys. 3.11. Charakterystyki częstotliwościowe przenikalności elektrycznej dla obwodu równoważ-

nego równoległego (a) i szeregowego (b)

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

45

8. Metody pomiaru pojemności i współczynnika strat dielektrycznych

Wybór metody pomiarowej zależy od wymaganej częstotliwości pomiarowej.

Norma PN-86/E-04403 wymienia następujące układy pomiarowe:

−

mostek Scheringa

zakres 15 Hz

÷

1 kHz,

−

mostek Giebego-Zicknera

zakres 15 Hz

÷

500 kHz,

−

mostek transformatorowy

zakres 15 Hz

÷

50 MHz,

−

metoda rezonansowa określenia

równoległej rezystancji

zakres 100 kHz

÷

50 MHz,

−

metoda rezonansowa określania

szerokości krzywej rezonansowej

zakres 10 kHz

÷

100 MHz,

−

miernik dobroci

zakres 10 kHz

÷

300 MHz,

−

mostek czteropojemnościowy

zakres 100 kHz

÷

300 MHz.

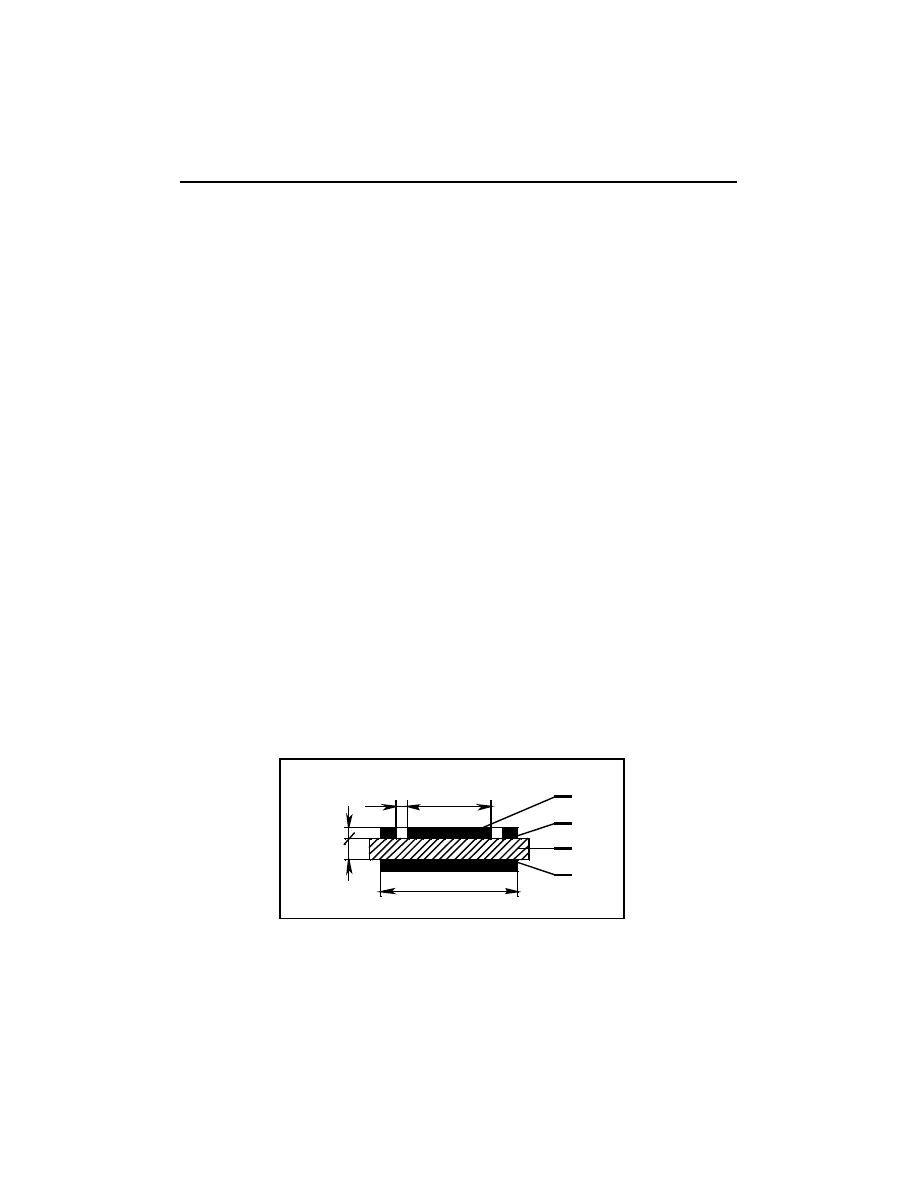
Przy pomiarach przenikalności dielektrycznej i współczynnika strat dielek-

trycznych zaleca się stosowanie układu trójelektrodowego (rys. 3.12). Dokładność
pomiaru zależy również od dokładności przylegania elektrod do próbki. Wykorzy-
stać można następujące elektrody:

−

wykonane z powłok półprzewodzących,

−

wykonane metodą metalizacji natryskowej,

−

elektrody napylane,

−

elektrody wypalane (np. w przypadku próbek ceramicznych),

−

elektrody z ciekłych metali,

−

elektrody grafitowe,

−

elektrody z folii metalowej (naklejane).

Zastosowanie masywnych ciężkich elektrod nie jest zalecane ale przy dobrym

dopasowaniu powierzchni próbki i elektrod umożliwia wykonanie pomiarów z
wystarczającą dokładnością.

d

1

h

g

D

3

4

a

2

Rys. 3.12. Płaski układ elektrod okrągłych do pomiaru C i tg

δ

:

1 - elektroda pomiarowa, 2 - elektroda ochronna,
3 - próbka, 4 - elektroda napięciowa

46

Ć

wiczenie 3

Wyznaczenie przenikalności elektrycznej względnej wymaga obliczenia po-

jemności kondensatora próżniowego C

0

. W przypadku zastosowania płaskiego

układu trójelektrodowego, takiego jak na rysunku 3.12, pojemność C

0

oblicza się

przy pomocy następującego wzoru

C

d

B g

h

0

0

2

4

=

⋅

+ ⋅

ε π

(

)

,

(3.22)

gdzie: B

h

g

g

h

= −

⋅ ⋅

⋅











1 2 932

0 7854

,

log cosh

,

dla a << h, B

=

1 dla a > h,

ε

π

0

11

1

36

10

=

⋅

−

F

cm

9. Kierunki rozwojowe materiałów elektroizolacyjnych stałych

Rozwój materiałów organicznych związany jest z powstawaniem dielektryków

o coraz wyższej odporności temperaturowej. W dziedzinie temperaturowo odpor-
nych syciw i kauczuków coraz powszechniej stosuje się materiały silikonowe. Inny
materiał, opracowany w latach 50-tych XX wieku policzterofluoroetylen (350

°

C),

znalazł szerokie zastosowanie poza elektrotechniką (np. jako teflon). Wysoką od-
pornością temperaturową charakteryzują się poliimidy (folia kapton H – 240

°

C)

oraz polisiarczek fenylu (260

°

C).

W zakresie wytrzymałości mechanicznej materiałów organicznych stworzone

zostały kompozyty szklano-epoksydowe realizujące wytrzymałość porównywalną
z metalami. Podobne funkcje spełniają termoplastyczne poliwęglany.

Przedstawiony rozwój materiałów o zwiększonej odporności temperaturowej

pozwala na zmniejszenie ciężaru i rozmiarów maszyn elektrycznych. Na szczegól-
ną uwagę zasługuje możliwość realizacji izolacji klasy H przez następujące ro-
dzaje materiałów:

−

papiery typu nomex impregnowane żywicą silikonową,

−

folie z poliimidów bez lub z lakierami klejącymi,

−

przetwory mikowe z włóknem szklanym impregnowane żywicą silikonową.

W okresie burzliwego rozwoju związków chemii organicznej wyodrębniono

grupę tworzyw termoplastycznych (np. polistyren, polietylen, polipropylen i inne)
odznaczających się:

−

doskonałymi własnościami dielektrycznymi (tg

δ

rzędu 10

–4

, wytrzyma-

łość elektryczna E

p

= 16

÷

55 kV/mm),

−

odpornością na czynniki chemiczne,

−

dużą wydajnością procesu wytwarzania.

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

47

Szczególne znaczenie uzyskał polietylen, który dzięki nowym technologiom

wytwarzania, stał się podstawowym materiałem przy produkcji kabli średnio i wyso-
konapięciowych a także wysokonapięciowych linii napowietrznych izolowanych.

Szereg materiałów uzyskało duże znaczenie w elektronice, gdzie jednym

z najważniejszych parametrów decydującym o przydatności jest niski tg

δ

. Przy-

kładowo, niskim współczynnikiem stratności (10

–5

÷

10

–4

) przy wielkich częstotli-

wościach charakteryzuje się policzterometylopenten.

Stały rozwój tworzyw organicznych umożliwia wprowadzenie nowych dielek-

tryków do praktyki w elektrotechnice. Obecne wysiłki idą w kierunku zwiększenia
odporności temperaturowej, odporności chemicznej przy działaniu olejów i syciw,
jak również obniżenia tg

δ

.

Jednocześnie należy podkreślić, że specjalne wymagania w zakresie pracy izo-

lacji w wyższych temperaturach, próżnioszczelności oraz znacznej przenikalności
elektrycznej zapewniają tylko dielektryki nieorganiczne.

10. Pytania kontrolne

1.

Omówić mechanizmy polaryzacji

2.

Pojęcie przenikalności elektrycznej materiałów

3.

Podać definicję tg

δ

i omówić jego zależność od temperatury i częstotliwości

4.

Zespolona przenikalność dielektryczna

5.

Obwody równoważne

6.

Pomiary pojemności i współczynnika strat dielektrycznych

Literatura

1.

Antoniewicz J.:

Własności dielektryków. WNT, Warszawa 1971

2.

PN-72/E-04400

Materiały elektroizolacyjne stałe. Przygotowanie i badanie

próbek. Znormalizowane warunki otoczenia

3.

PN-86/E-04403

Materiały elektroizolacyjne stałe. Metody pomiaru przeni-

kalności elektrycznej i współczynnika strat dielektrycznych

4.

Siciński Z.:

Badanie materiałów elektroizolacyjnych. WNT, Warszawa 1968

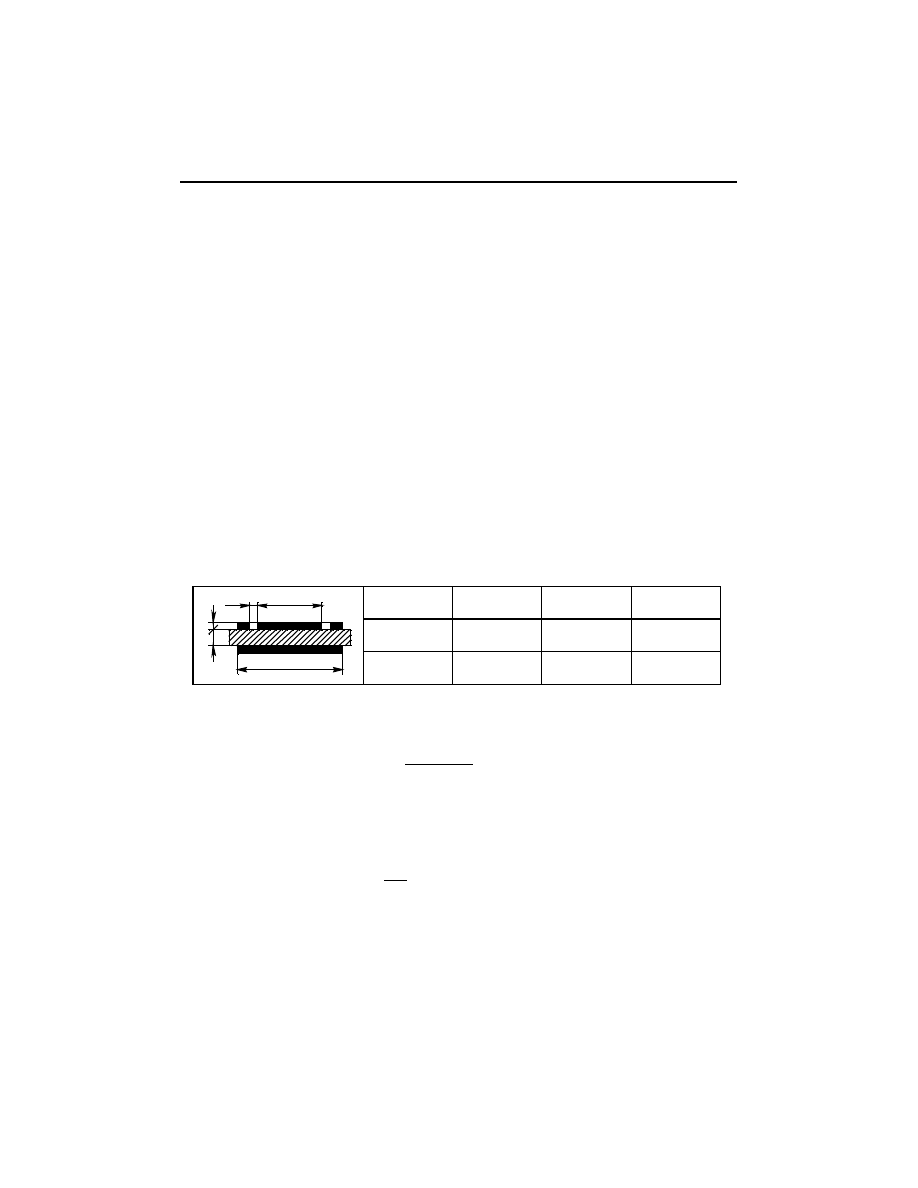
48

Ć

wiczenie 3

II. BADANIA

1. Pomiar przenikalności dielektrycznej i współczynnika

strat dielektrycznych dielektryków stałych

W ćwiczeniu należy dokonać pomiarów

ε

i tg

δ

badanych próbek dielektryków

stałych w układzie trójelektrodowym. Pomiary wykonujemy mostkiem Scheringa
(w układzie Giebego-Zicknera) dla kilku częstotliwości pomiarowych. Sposób
wykonywania pomiarów według załączonej instrukcji mostka i norm PN.

Otrzymane wyniki pomiarów należy wykorzystać do obliczenia względnej

przenikalności dielektrycznej zespolonej zakładając schemat zastępczy dielektryka
w postaci równoległego połączenia elementów RC. Potrzebną do obliczeń pojem-
ność C

0

określamy z wymiarów geometrycznych układu elektrod. Pomiaru grubo-

ś

ci próbek (h) dokonujemy śrubą mikrometryczną w trzech miejscach. Do obliczeń

bierzemy wartość średnią. Należy również obliczyć wartości elementów schematu
zastępczego równoległego R

r

i C

r

.

Wymiary elektrod przedstawia tabela 3.1.

Tabela 3.1

Wymiary elektrod

d

D

g

a

mm

mm

mm

mm

D

g

h

d

a

76

110

2

10

Pojemność C

0

obliczamy z wzoru

C

d

g

h

0

0

2

4

=

⋅

+

ε π

(

)

, gdyż a > h.

(3.23)

Przy pomiarze zakładającym równoległe połączenie elementów RC rzeczywistą

i urojoną przenikalność elektryczną względną możemy obliczyć z wzorów

ε

'

rz

x

C

C

=

0

,

ε

ε

δ

'

'

ur

rz

x

tg

=

⋅

,

(3.24)

gdzie C

x

i tg

δ

x

- pomierzone wartości pojemności i współczynnika strat dielek-

trycznych

Badanie przenikalności elektrycznej i współczynnika strat dielektrycznych...

49

Wartości elementów schematu zastępczego równoległego C

r

i R

r

przedstawiają

wzory

C

C

r

x

=

,

R

C tg

r

r

x

=

1

ω

δ

.

(3.25)

Obliczone wartości

ε

’

rz

,

ε

’

ur

, C

r

i R

r

są na ogół słuszne tylko dla jednej często-

tliwości, tej przy której wykonywany był pomiar. Pomimo, że dla schematu rów-
noległego

ε

’

rz

= const (nie zależy od częstotliwości) to wartości tej przenikalności

obliczone z pomiarów wykonywanych przy różnych częstotliwościach będą two-
rzyły funkcję

ε

’

rz

= f(

ω

) odpowiadającą rzeczywistej zależności tej przenikalności

od częstotliwości wynikającej z rzeczywistego obwodu równoważnego.

Również policzone wartości elementów C

r

i R

r

będą w ogólnym przypadku inne

dla każdej częstotliwości pomiarowej. Obliczone elementy C

r

i R

r

składają się na

schemat zastępczy równoległy słuszny tylko dla danej częstotliwości.

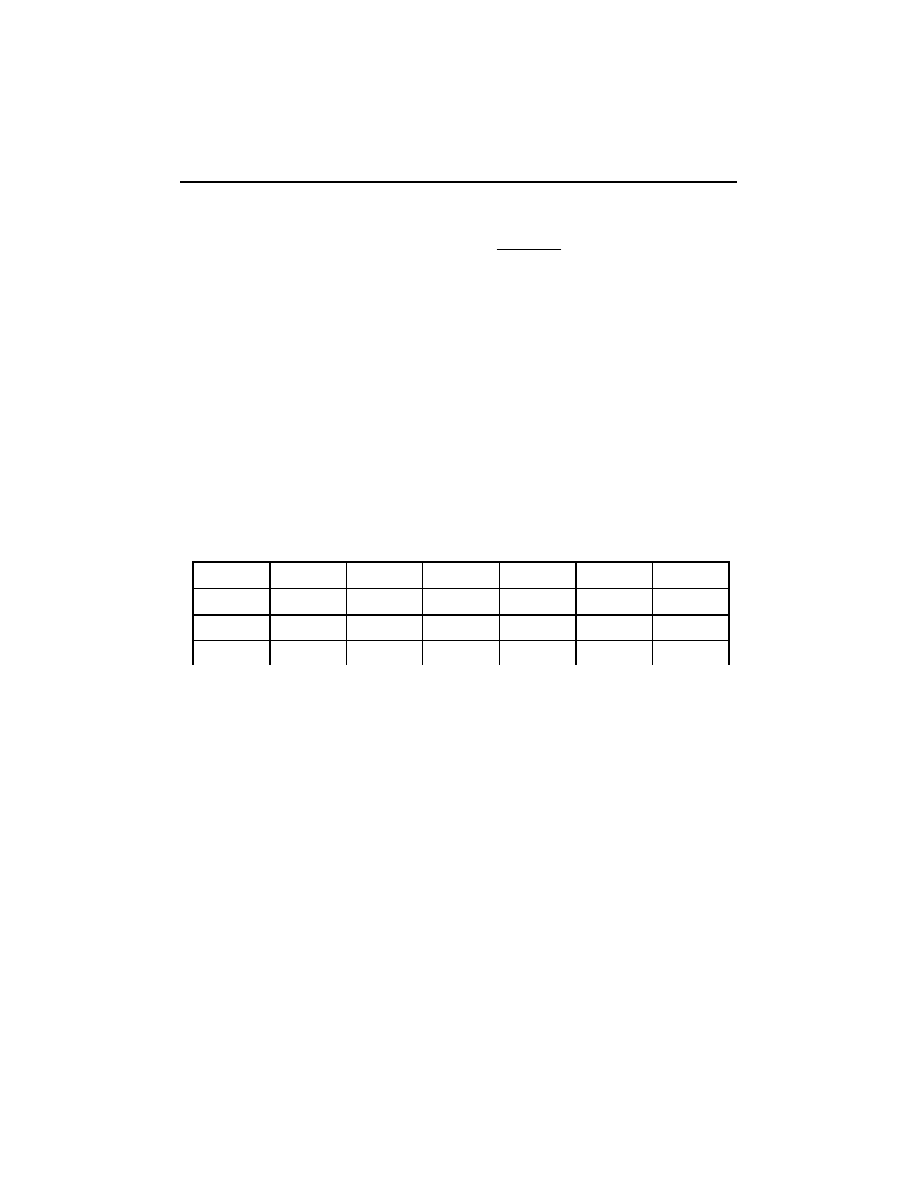
Wyniki pomiarów i obliczeń należy przedstawić w tabeli 3.2.

Tabela 3.2

Wyniki pomiarów i obliczeń

próbka (nazwa) ............................, hśr = ......... mm, C

0

= ........... pF

ϑ

= .........

°

C,

f

C

x

tg

δ

x

ε

’

rz

ε

’

ur

R

r

C

r

kHz

pF

–

–

–

k

Ω

pF

2. Opracowanie wyników pomiarów i wnioski

−

wykreślić charakterystyki

ε

’

rz

= f

(f) oraz

ε

’

ur

= f

(f),

−

przedstawić własne spostrzeżenia i wnioski dotyczące pomiarów, ich do-
kładności oraz otrzymanych wyników,

−

omówić zależność wartości elementów R

r

i C

r

od częstotliwości.