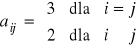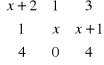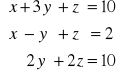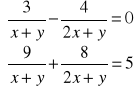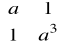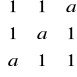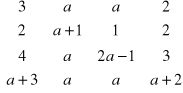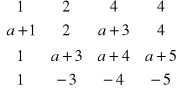Zadania z matematyki dla studentów I- go roku studiów stacjonarnych
Zestaw 7
Wyznaczniki (c.d.)
1. |
Oblicz det(A
A = |
2. |
Wiedząc, że det A = 3 i det B = 2 oraz det (4A A i B. |
3. |
Oblicz wyznaczniki macierzy:
A
C |
4*. |
Wykaż, że jeśli A jest macierzą skośno-symetryczną stopnia nieparzystego, to detA = 0. |
5. |
Rozwiąż równania:
a) det2A =3200, gdzie A =
b) det(B - 3I) = 0, gdzie B |
6. |
Stosując wzory Cramera rozwiąż układy równań:
a) |
7. |
Ustal, dla jakiej wartości parametru a macierz jest nieosobliwa.
A =
Wyznacz macierze odwrotne do danych stosując metodę wyznacznikową. |
8*. |
Ustal, dla jakiej wartości parametru a macierz jest nieosobliwa.
a) |
Wyszukiwarka
Podobne podstrony:
matma zad, Z3, Zadania z matematyki dla studentów I-go roku studiów stacjonarnych
matma zad, Z17, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z12, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z10, Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
matma zad, Z11, Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
matma zad, Z4, Zadania z matematyki dla studentów 1-go roku studiów stacjonarnych
matma zad, Z5, Zadania dla studentów 1-go roku
matma zad, Z7J, ZADANIA Z MATEMATYKI
matma zad, Z7J, ZADANIA Z MATEMATYKI
Zad MECH-IZR ESO II, Przykładowe zadania przygotowawcze dla studentów Wydziału Mechanicznego
Zadania i odpowiedzi, Zad.MST-09, Matematyka dla MSB
Zadania i odpowiedzi, Zad.MST-05, Zadania z MATEMATYKI dla pierwszego roku
Zadania z matematyki dla 3 roku dziennych, Uczelnia
Zadanie-podatki-dla studentów 2010, Ogrodnictwo, Semestr V, Ekonomika, Ekonomika z chomika ;)
jajo matematyczne, karty pracy dla klas I-III, zadania matematyczne dla kl.1
więcej podobnych podstron