Statystyka-nauka o metodach wykrywania i badania prawidłowości występujących w zjawiskach masowych.

-opisowa-opis statystyczny badanej zbiorowości

-matematyczna- wnioskowanie statystyczne

OPIS STATYSTYCZNY- dotyczy tylko zbiorowości statystycznej, jego przedmiotem są obserwacje badania pełnego, dokonuje się go za pomocą narzędzi tj, średnia arytm, odchylenie stand itp.

WNIOSKOWANIE SATYSTYCZNE - ma miejsce gdy badanie jest reprezentacyjne (próba losowa), a jego wyniki są uogólniane na cała populację generalną z której pochodzi próba

ZBIOROWOŚĆ STATYSTYCZNA -(populacja) zbiór dowolnych elementów podobnych , ale nie identycznych pod względem właściwości objętych badaniem. Wyróżniamy zbiorowość jednowymiarową (jednocechową) i wielowymiarową (wielocechową )

JEDNOSTKA STATYSTYCZNA - elementy składowe zbiorowości poddane obserwacji, w tej samej zbiorowości mogą wystąpić różne jednostki statystyczne

CECHY STATYSTYCZNE - właściwości jednostek statystycznych

Wyróżniamy cechy

1)stałe ( rzeczowe, czasowe, przestrzenne)

2)zmienne - właściwości różnicujące poszczególne elementy zbiorowości

a)niemierzalne (jakościowe)- określane słownie , np. płeć

b)mierzalne(ilościowe) - wyrażane za pomoca licz o różnych mianach (cm,lata,zł)

• quasi-ilosciowe (porządkowe) określają natężenie badanej właściwości w sposób opisowy, np. oceny z egzaminu

• skokowe (dyskretne)- może być wyrażona wyłącznie liczbami zmieniającymi się skokowo, bez wartości pośrednich(lp osób w grupie)

• ciagłe - może przyjmować każda wartość z okresonego przedziału liczbowego , np. wzrost, waga, powierzchnia mieszkania, czas dojazdu do pracy,dochody przedś.

POMIAR - proces okreslający wielkość (nasilenie) badanej cechy

Skale pomiarowe

1. nominalna - pomiar polega na przypisaniu jednostki do określonej kategorii; stwierdzić tylko można że 2 jednostki sa takie same lub inne, dotyczy cech jakościowych, dot takich cech, jak płeć, stan cywilny, status zawodowy, religia), skala slaba

2. porządkowa(rangowa)- pozwala na uporządkowanie elementów w zależności o ich znaczenia lub rozmiarów (rosnąco, malejąco), dot. cech jakościowych, np. miejsca zajęte przez zawodników, klasy społeczne, wykształcenie, status zawodowy,, sila reakcji na bodźce), s. slaba

3. przedziałowa(interwałowa)- określa nie tylko kolejność jednostek , ale również różnice między nimi., np. lata kalendarzowetemperatura, rok urodzenia, wartość zero jest umowna - zero nie oznacza że nie ma takiej wartość (0s C), dot cech ilościowych, s. mocna

4. ilorazowa (stosunkowa) pozwala określić zarówno różnice jak i ilorazy (stosunki) danych, występuje zero absolutne tj zero znaczy że cecha nie występuje,

Np. wieku(wlatach), wagi,

płac, dochodów, cen towarów,

czas dostawy, dot. Cech

ilościowych, s. silna

SZEREGI STATYSTYCZNE

Po sklasyfikowaniu danych statystycznych według jakiegoś kryterium otrzymujemy szereg statystyczny.

Szeregi statystyczne dzielimy na:

1. szczegółowe

2. rozdzielcze

3. czasowe

4. przestrzenne

Szczegółowe - najczęściej stosowany jest wtedy, gdy liczba jednostek objętych badaniem jest mała (10, 20 osób)

Rozdzielcze - stanowi zbiorowość statystyczną podzieloną na klasy wg określonej cechy jakościowej lub ilościowej z podaniem liczebności każdej z klas. Jeden z szeregów statystycznych przedstawiający budowę (strukturę ) zbiorowości, czyli jej podział na części z

określonego, rzeczowego punku widzenia. Cecha statystyczna na podstawie której dokonuje się podziału zbiorowości

na mniejsze części, może być cechą niemierzalną lub mierzalną. W szeregu rozdzielczym w jednej kolumnie w sposób

uporządkowany przedstawiony jest wykaz klasyfikacyjny, czyli warianty badanej cechy, a w drugiej kolumnie

przedstawione są liczebności odpowiadające poszczególnym klasom z wykazu. Jest to więc uporządkowany i

pogrupowany zbiór informacji dotyczących badanej cechy określonej zbiorowości

Szeregi rozdzielcze dzielimy na: punktowe i przedziałowe.

Punktowy szereg rozdzielczy - buduje się wówczas, gdy liczba wariantów badanej cechy niewielka, a każdy z tych wariantów występuje kilka razy w badanej zbiorowości.

Szereg rozdzielczy przedziałowy - stanowi zbiorowość statystyczną podzieloną na klasy wg określonej cechy jakościowej lub ilościowej z podaniem liczebności każdej z klas.

Konstrukcja szeregu rozdzielczego z przedziałami klasowymi.

1. określenie empirycznego obszaru zmienności (rozstępu) cechy

2. ustalenie liczby przedziałów klasowych (k) i ich długości (h) najczęściej wg wzoru:
   

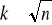
zaś

Uwaga!!! Istotne jest ustalenie granic poszczególnych klas.

Prezentacja pierwszej klasy. Jej granice dolne to z reguły minimalna wartość liczby lub cechy.

Prezentacja graficzna szeregów statystycznych.

WYKRESY STATYSTYCZNE- graficzna forma prezentacji danych oraz prezentacja i analiza uogólnionych informacji statystycznych. Każdy wykres powinien zawierać tytuł, żródło danych i legendę..

Najczęściej stosuje się wykresy:

a)liniowe (diagramy i krzywe liczebności)

b)powierzchniowe(wykresy słupkowe i kołowe)

c)pasmowe, d)bryłowe, e)punktowe,

f)mapowe, g) kombinowane

HISTOGRAM -(liczebności, częstości, l. i cz. skumulowanej) Rodzaj wykresu słupkowego oparty na prostokątnym układzie współrzędnych; Histogram składa się z pionowych

przylegających do siebie prostokątów (słupków). Długości podstaw tych prostokątów są proporcjonalne do rozpiętości

przedziałów klasowych, a wysokość do ich liczebności na jednostkę rozpiętości. Zwykle histogram służy do przedstawiania struktury szeregów rozdzielczych o równych przedziałach klasowych i wówczas wysokość prostokąta jest proporcjonalna do liczebności. Budując histogram na podstawie szeregu o nierównych przedziałach klasowych, należy uprzednio obliczyć liczebności przypadające w danym przedziale na jednostkę jego rozpiętości. Histogram umożliwia poznanie typu rozkładu zbiorowości statystycznych wg badanej cechy

MIARY ŚREDNIE

Miary klasyczne -obliczane są one na podstawie wszystkich danych

Średnia aryt. - to suma wartości zmiennnej wszystkich jednostek badanej zbiorowości podzielonej przez liczbę tych jednostek; średnia wartość cechy

Średnia harmoniczna - jest odwrotnością średniej arytmetycznej z odwrotnością wartości zmiennych stosuje się ją jeśli cecha wyrażona jest w przeliczeniu na jednostke innej cechy, np., gęstość zaludnienia (osoba/km2), dochód na osobę (zł/os), cena (zł/kg), prędkość (km/godź0

Średnia geometryczna - stosuje się ją trzeba zgadać tempo zmian zjawiska, przy analizie szeregów czasowych.

Miary pozycyjne-do ich wyznaczenia stosuje się tylko niektóre wartości cechy, wybrane ze względu na pozycję, jaką zajmują w uporządkowanym zbiorze danych.

Mediana (Q2) -dzieli zbiorowość w stosunku2:2, interp: wartość cechy środkowej jednostki. 50% jednostek ma wartość cechy nie wiekszą, 50% nie mniejszą,

Dominanta -, mówi o tym która wartość cechy występuje najczęściej. największa liczba jednostek posiada określona wartość cechy

Q2 - dzieli zbiorowość w stosunku 1:4, Interp:25 % jednostek ma co najwyżej...,

A 75% co najmniej

Q3 - 75% jednostem ma co najwyżej .., a 25% co najmniej

Procedura wyznaczania kwartyli:

1)uporządkować dane, 2) wyznaczyć pozycje poszukiwanych kwartyli, 3)obliczyć lub odszukać wartość kwartyli

Wzajemne relacje między średnią, medianą i dominant - za ich pomocą najłatwiej określić asymetrie rozkładu:

1) x=Do=Mewszystkie 3 miary średnie są równe to rozkładem symetrycznym.

2)x>Me >D Wartość średniej jest większa niż wartość mediany i wartość mediany jest większa od wartości dominanty tj. - oznacza że wartość cechy większości jednostek statystycznych jest niższa od średniej arytmetycznej. Taki rozkład nosi nazwę rozkładu o asymetrii prawostronnej. (dodatniej)

3) x< Me<D- Wartość średniej jest mniejsza niż wartość mediany i wartość mediany jest mniejsza od wartości dominanty. Oznacza że wartość cechy większości jednostek statystycznych jest wyższa od średniej arytmetycznej. Jest to rozkład o asymetrii lewostronnej.

Równanie Pearsona (zależność między średnią, medianą i dominantą) Do=3Me-2x

Miary zróżnicowania

Rozstęp - jest różnicą między największą i najmniejszą wartością zmiennej w badanej zbiorowości Interp: wartość cechy zawiera się w przedziale

Rozstęp międzykwartylowy (RQ) -jest to różnica między kwarylem 1 a 3. Interp: dla 50 % środkowych jednostek różnica między największa a najmniejszą wartością cechy wynosi..

Odchylenie ćwiartkowe (Q)- jest to połowa zakresu zmienności 50% środkowych jednostek: Interp: przeciętne odchylenie 50 % środkowych jednostek od mediany

Odchylenie przeciętne (d) - jest średnią arytmetyczną bezwzględnych wartości (modułów) odchyleń wartości cechy od jej średniej arytmetycznej, okresla o ile wszystkie jednostki danej zbiorowości różnią się średnio ze zwględu na wartość zmiennej od średniej arytmetycznej.

Interp.:średni rozrzut pomiarów wokół średniej

Wariancja - jest to średnia wartość podniesionych do kwadratu odchyleń od średniej.(podniesiona do kw żeby pozbyć się minusów) Interp: średni kwadrat odchylenia wartości cechy od średniej ..( do kwadratu)

Odchylenie standardowe - określa o ile wszystkie jednostki zbiorowości różnią się od średniej arytmetycznej badanej zmiennej. Jest pierwiastkiem z wariancji Interp: wartość cechy poszczególnych jednostek różni się przeciętnie od średniej

Współczynnik zmienności (Vs)- to iloraz odchylenia standardowego i średniej w danym rozkładzie, wyrażony w procentach. Mówi o tym jaki procent średniej aryt stanowi odchylenie standardowe.

Informuje o sile dyspersji. 0-20% zroż c. -słabe, 20-40%-umiarkowane, 40-60%-silne, 60 % i powyżej-bardzo silne. Gdy silne i bardzo silne to zbiorowość niejednorodna

Interp; Odchylenie standardowe liczby napraw stanowi ..% średniej wartości cechy

Typowy obszar zmienności- typowe jednostki to takie które mieszczą się w przedziale (x-s;x+s), różnią się od średniej mniej niż o odchylenie Interp: liczba napraw typowego urządzenia.....

Pozycyjny współczynnik zmienności (Vq) - odchylenie standardowe podzielone przez medianę razy 100%, info jaki procent mediany stanowi odchylenie ćwiartkowe, przedziały analogicznie jak w Vs

Miary asymetrii (skośności)

Współczynnik Pearsona (Ap) - pozwala określić kierunek i siłę asymetrii; jego wartość jest liczbą z przedziału [-1,1], gdy Ap> 0 a. prawostronna(dodatnia), Ap<0 lewostronna ujemna, Ap=0 symetria.

Przedziały określające siłę asymetrii: 0-02 a. rozkładu bardzo słaba, 0,2-0,4 -słaba, 0,4-0,6 umiarkowana, 0,6-0,8silna, powyżej 0,8 bardzo silna

Pozycyjny współczynnik asymetrii (Aq) określa kierunek i siłę asymetrii jedynie w centralnej części rozkładu, mierzy asymetrię Interp: 50% środkowych jednostek, kierunek i siła określana jak z Ap

Klasyczny współczynnik asymetrii (As)- najbardziej precyzyjna miara asymetrii rozkładu, przyjmuje wartości z przedziału

[-2,2], również określa kierunek (lewo, prawo), i siłę asymetrii: 0-0,4 a. roz bardzo słaba, 0,4-0,8 słaba, 0,8-1,2 umiarkowana, 1,2-1,6 silna, powyżej 1,6 bardzo silna

Zmienna losowa i jej rozkłady

Zmienna losowa- funkcja przyporządkowująca każdemu zdarzeniu elementarnemu wartość liczbową, oznacza się ją jako X,Y.

Zmienna losowa skokowa to zmienna, która przyjmuje niektóre wartości, np.liczba osób w grupie studenckiej.

Zmienna losowa ciągła to zmienna, która przyjmuje wszystkie wartości z pewnego przedziału liczbowego, np. wzrost, waga.

Dystrybuanta zmiennej losowej X- funkcja F określona na zbiorze liczb rzeczywistych, taka, że F(x)=P(X=<x).

Własności: 0=<F(x)=<1 dla x∈R, funkcja niemalejąca (F(x₁)=< F(x₂))

Rozkład zmiennej losowej skokowej

Funkcją rozkładu prawdopodobieństwa zmiennej losowej skokowej nazywa się funkcję określoną wzorem P(X=x_i)=p_i, gdzie x_i są wartościami tej zmiennej, a p_i prawdopodobieństwami im odpowiadającymi. Funkcja rozkładu może być dana za pomocą wzoru, tabeli lub wykresu. Rozkład zmiennej losowej skokowej można opisać podając funkcję rozkładu prawdopodobieństwa albo dystrybuantę.

Rozkład zmiennych losowych charakteryzuje się za pomocą następujących parametrów:

• miary położenia - wartość oczekiwana

• miary zmienności (rozproszenia, dyspersji) - wariancja i odchylenie standardowe

Wartość oczekiwana E(x) to wartość, wokół której skupiają się realizacje zmiennej losowej uzyskiwane w wyniku wielokrotnie powtarzanego doświadczenia. Własności:

-wartość oczekiwana stałej równa się stałej E(C)=C,

-wartość oczekiwana sumy dwóch zmiennych losowych X i Y równa się sumie wartości oczekiwanych tych zmiennych E(X+ Y)=E(X)+E(Y),

- wartość oczekiwana iloczynu dwóch niezależnych zmiennych losowych jest równa iloczynowi wartości oczekiwanych tych zmiennych E(CX)=E(C)*E(X)

Wariancja D²(X) - miara rozproszenia wartości zmiennej wokół wartości oczekiwanej. Im mniejsza jest wariancja, tym bardziej wartości zmiennej skupiają się wokół wartości oczekiwanej.

Odchylenie standardowe D(X) jest pierwiastkiem z wariancji.

Rozkład zmiennej losowej ciągłej

Jeżeli dystrybuanta F(x) zmiennej losowej ciągłej X ma pochodną f(x) w całym przedziale zmienności X, to pochodną tę nazywa się funkcją gęstości prawdopodobieństwa. F'(x)=f(x)

Funkcja gęstości opisuje rozkład zmiennej losowej ciągłej, znając ją można wyznaczyć dystrybuantę. Podstawowymi parametrami zmiennej losowej ciągłej są: wartość oczekiwana, wariancja i odchylenie standardowe.

Rozkłady zmiennych losowych skokowych

Rozkład zero-jedynkowy (dwupunktowy)

Zmienna losowa X ma rozkład zero-jedynkowy, jeśli przyjmuje tylko dwie wartości: 0 i 1. Wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem q=1-p.

P(X=1)=p, P(X=0)=q, p+q=1

Parametry rozkładu zero-jedynkowego:

• wartość oczekiwana E(X)=p

• wariancja D²(X)=p*q

Rozkład dwumianowy (Bernoullego)

Zmienna losowa X ma rozkład dwumianowy, jeżli przyjmuje wartość k(k=0,1,2,....n) z prawdopodobieństwem P_n,p(X=k)=(ⁿ_k)p^k(1-p)^n-k dla k=0,1,...,n

Zmienna losowa X określana jest jako liczba k sukcesów w n doświadczeniach.

Parametry rozkładu dwumianowego:

• wartość oczekiwana E(X)=np

• wariancja D²(X)=np(1-p)= npq

• odchylenie standardowe D(X)=√npq

Rozkład Poissona

Zmienna losowa X ma rozkład Poissona, jeśli przyjmuje wartość k(k=0,1,2,...) z prawdopodobieństwem P(X=k)=λ^ke^-λ/k! gdzie parametr λ=const.

Ten rozkład dobrze opisuje te doświadczenia losowe, w których obserwuje się dużą serię prób przy małym prawdopodobieństwie sukcesu w pojedynczej próbie. Gdy n>=30 oraz p=<0,2, rozkład Poissona można stosować jako przybliżenie rozkładu Bernoullego.

Dla rozkładu Poissona:

• wartość oczekiwana E(X)=λ

• wariancja D²(X)=λ

Rozkłady zmiennych losowych ciągłych

Rozkład równomierny (jednostajny, prostokątny)

Zmienna losowa X, określona w przedziale <a,b>, ma rozkład równomierny, jeżeli jej funkcja gęstości prawdopodobieństwa określona jest wzorem

0 dla x<a

f(x)= 1/b-a dla a=<x=<b

• dla x>b

Rozkład normalny

Parametry rozkładu normalnego:

• wartość oczekiwana E(X)=m

• wariancja D²(X)=σ²

• odchylenie standardowe D(X)=σ

Zmienna losowa X ma rozkład normalny ze średnią m (wartością oczekiwaną) i odchyleniem standardowym (σ), X~N(m;σ). Wykresem funkcji gęstości rozkładu normalnego jest tzw. krzywa Gaussa (w kształcie dzwonu), krzywa ta jest symetryczna względem prostej o równaniu x=m (prostej równoległej do osi OY, przechodzącej przez punkt m na osi OX), w punkcie x=m funkcja osiąga maksimum, pole powierzchni pod krzywą Gaussa jest równe 1 (jest to funkcja gęstości prawdopodobieństwa).

Położenie i kształt krzywej Gaussa zależy od :

• wartości średniej (m)

• odchylenia standard. (σ).

Zmiany m będą powodować przesuwanie się wykresu funkcji gęstości wzdłuż osi OX bez zmiany jego kształtu, natomiast zmiany odchylenia standardowego będą zmieniać kształt wykresu bez zmiany jego położenia. Jednoczesne zmiany obu parametrów spowodują zmianę i położenia i kształtu wykresu funkcji gęstości. Zwiększanie parametru m powoduje przesuwanie wykresu w prawą stronę, zwiększanie parametru σ sprawia, że wykres staje się szerszy i niższy.

Rozkład normalny standaryzowany to rozkład normalny ze średnią m=0 i odchyleniem standardowym σ=1.

Reguła trzech sigm

Dla każdego rozkładu normalnego prawdziwe są równości:

• P(m-σ<X<m+σ)=0,6827

• P(m-2σ<X<m+2σ)=0.9545

• P(m-3σ<X<m+3σ)=0,9973

w tym przedziale znajdują się prawie wszystkie wartości zmiennej losowej X, czyli prawdopodobieństwo przyjęcia przez zmienną losową X wartości spoza tego przedziału jest bardzo mało, równe zeru.

Rozkłady z próby

Populacja generalna - tworzą ją wartości danej cechy u wszystkich jednostek dużej zbiorowości. Próba - pewna skończona część populacji. Powinna być reprezentatywna! (losowy sposób pobierania i duża liczebność).

Rozkład średniej arytmetycznej

Z populacji o rozkładzie normalnym N(m,σ) losuje się n-elementową próbę i przez xi oznacza się kolejne wyniki w próbie. Wniosek: rozkład średniej arytmetycznej w próbach pochodzących z populacji o rozkładzie normalnym jest zależny od odchylenia standardowego zależny od odchylenia standardowego (σ) w populacji. Wraz ze wzrostem liczebności próby odchylenie standardowe statystyki X maleje. Oznacza to, że średnia arytmetyczna podlega mniejszej zmienności niż pojedyncze wyniki.

Rozkład χ²

zał: niech X₁,..., X_v będzie ciągiem niezależnych zmiennych losowych o rozkładzie normalnym standaryzowanym N(0;1). Statystyka ta ma rozkład chi kwadrat z liczbą stopni swobody równą v. Liczba stopni swobody jest parametrem rozkładu zmiennej losowej o rozkładzie χ². Wartość tego parametru jest liczbą składników tej zmiennej.

Parametry zmiennej losowej o tym rozkładzie:

• wartość oczekiwana E(χ²)=v

• wariancjaD2(χ²)=2v

Kształt funkcji gęstości prawdopodobieństwa rozkładu χ² zmienia się wraz ze zmianą liczby stopni swobody (v). Przy małej liczbie stopni swobody rozkład jest skrajnie asymetryczny, natomiast wraz ze wzrostem liczby stopni swobody rozkład χ² zbliża się do rozkładu normalnego. Zmienne losowe mające rozkład χ² przyjmują tylko wartości nieujemne.

Zależność: P(χ²>=χ²_α,ν)=α , a wartość χ²_α,ν nazywa się wartością krytyczną

χ² α

χ²_α,ν

Rozkład t-Studenta

Zał: niech X₀, X₁,..., X_ν będą niezależnymi zmiennymi losowymi o rozkładzie normalnym standaryzowanym N(0;1).

Kształt funkcji gęstości tego rozkładu jest zbliżony do rozkładu normalnego standaryzowanego N(0;1) i zależy od liczby stopni swobody. Im liczba swobody jest większa, tym bardziej rozkład t-Studenta przypomina rozkład N(0;1). Rozkład t-Studenta jest symetryczny względem osi OY, czyli ma wartość oczekiwaną równą zeru.

Parametry zmiennej losowej o rozkładzie t-Studenta:

• wartość oczekiwana E(t)=0

• wariancja D²(t)=^ν/_ν-2= ^n-1/_n-3

Wartości krytyczne: P(| t | >=t_α,ν=α

Rozkład Fishera-Snedecora

Zał: niech X₁,X₂,..., X_u i Y₁, Y₂,..., Y_ν będą niezależnymi zmiennymi losowymi o rozkładzie normalnym standaryzowanym N(0;1).

Zmienna F ma rozkład Fishera-Snedecora z liczbą stopni swobody U (dla licznika) i ν (dla mianownika). Zmienna F powstaje jako iloraz dwóch zmiennych o rozkładzie χ².

Parametry zmiennej losowej o rozkładzie Fishera-Snedecora:

* wartość oczekiwana E(F)=^ν/_ν-2

* wariancja D²(F)=2v²(u+v-2) / u(v-2)²(v-4)

Wartości zmiennej F są zawsze większe od jedności.

Zależność: P(F>=F_α,u,ν)=α (F_α,u,ν -wartość krytyczna)

ESTYMACJA (ocena parametrów) - polega na pobieraniu losowo pewnego n-elementowego fragmentu populacji generalnej (tzw próby) i oszacowaniu nieznanych parametrów całej zbiorowości

Estymator jest narzędziem wnioskowania statystycznego. Estymator jest to funkcja wyników z próby, czyli statystyka służąca do oszacowania nieznanej wartości parametru populacji. Wartość estymatora z konkretnej próby jest liczbą zwaną oceną parametru

Estymator jest nieobciążony jeżeli wartość oczekiwana estymatora jest równa szacowanemu parametrowi

ESTYMACJA PRZEDZIAŁOWA - to szacowanie wartości nieznanych parametrów populacji za pomocą tzw przedziałów ufności

Przy omawianiu przedziału ufności dla dwóch średnich generalnych możliwe są trzy sytuacje (dot. też hipotez):

• m1<m2 dla p=1-α

• m1=m2

• m1>m2

Przedział ufności -przedział, który z prawdopodobieństwem (1-α) zwanym poziomem ufności lub współczynnikiem ufności, pokrywa nieznaną wartość szacowanego parametru. Poziom ufności jest bliski jedności (0,9; 0,95;0,98; 0,99)

Interp: na podstawie przeprowadzonego badania z prawdopodobieństwem 1 - α (=poziomem ufności) można stwierdzić że (...) mieści się w przedziale (przedział ufności)

Długość przedziału ufności dla średniej (m)populacji generalnej zależy od :

1)liczebności próby - im większa , tym przedział krótszy

2) poziomu ufności (1-α) - im wyższy, tym przedział dłuższy

3) rozrzutu wyników w próbie - im rozrzut mniejszy, tym przedzial krótszy

u_{α -} wartość w standardowym rozkładzie normalnym

Rodzaje przedziałów

1. Przedział ufności dla średniej populacji generalnej

2. Przedział ufności dla różnicy dwóch średnich

3. Przedział ufności dla wariancji i odchylenia standardowego

4. Przedział ufności dla wskaźnika struktury (w w próbie, p dla populacji)

HIPOTEZY STATYSTYCZNE - pewne przypuszczenie o parametrach populacji lub o rozkładzie populacji. Hipotezy statystyczne są formalnym zapisem przypuszczeń merytorycznych sformułowanych w trakcie rozwiązywania problemów naukowych i praktycznych. Testowaną hipotezę statystyczną oznacza się symbolem H0 i nazywa się hipotezą zerową. Obserwujemy cechę X w pewnej populacji. Hipoteza - to przypuszczenie dotyczące rozkładu prawdopodobieństwa tej cechy. Prawdziwość tego przypuszczenia jest oceniana na podstawie wyników próby losowej. Jest to każdy sąd (przypuszczenie) dotyczące populacji wydany bez przeprowadzenia badania wyczerpującego.

Weryfikacja hipotez - proces decyzyjny, na podstawie przeprowadzonego eksperymentu trzeba zdecydować czy hipotezę (przypuszczenie) odrzucamy jako mało prawdopodobne czy ją przyjmujemy, tzn wynik eksperymentu nie przeczy hipotezie. Do weryfikacji poszczególnych hipotez musza być użyte odpowiednie narzędzia statystyczne, a ryzyko błędnego wnioskowania stosunkowo małe

Rodzaje hipotez :

Hipotezy parametryczne - dotyczą parametrów populacji

1. Hipoteza o średniej populacji generalnej (średnia m populacji generalnej jest równa znanej wartosci m0)

2. H. o równości średnich dwóch populacji generalnych m1 i m2

3. H. o równości dwóch wariancji

Hipotezy nieparametryczne - dotyczą rozkładów

1. H. o zgodności rozkładu empirycznego z rozkładem teoretycznym określonym przez H (rozkład badanej cechy jest zgodny z rozkładem określonym przez hipotezę)

2. H. o zgodności rozkładów kilku populacji rozkład baanej cechy w kilku populacjach jest taki sam)

Ad H. o średniej populacji

Hipoteza zerowa (h0) średnia m populacji generalnej jest równa znanej liczbie m0 ( H0:m=m0)

Hipoteza alternatywna - odwrotne założenie jak w przypadku H0

( H1:m/=m0)

• Jeżeli m=, n<30 to liczymy t_obl, i t _α,v, ale jeśli m mniejsze/większe to t2α,v

• Jeżeli m=, n>30 to liczymy uobl i uα

• H0 odrzucamy jako mało prawdopodobną jeżeli

tobl<-t α v lub tobl> t α,v

• Nie mamy podstaw do odrzucenia gdy -tα,v<tobl<tα,v

BŁĘDY, które można popełnić w czasie weryfikacji hipotezy

• Błąd 1 rodzaju - polega na odrzuceniu hipotezy, która była prawdziwa,; prawdopodobieństwo jego popełnienia jest równe poziomowi istotności α

• Błąd 2 rodzaju - polega na nie odrzuceniu hipotezy fałszywej; prawdopodobieństwo jego popełnienia jest oznaczane symbolem β.

Poziom istotności - to prawdopodobieństwo popełnienia błędu 1 rodzaju, Najczęściej przyjmuje wartości 0,1; 0,05; 0,01; 0,001

Moc testu ( 1-β) prawdopodobieństwo popełnienia błędu 2 rodzaju. Im β jest mniejsze tym test jest mocniejszy.

Ad H o równości średnich dwóch populacji generalnych

Procedura weryfikacji h0:

a) na podstawie próby wyznaczyć wartość statystyki t-studenta( ze wzoru)

b) dla ustalonego poziomu istotności α i liczby stopni swobody (v=n1+n2-2) odczytać z tablicy wartości tα,v

c) H0 odrzucamy jako mało

prawdopodobną jeżeli

tobl<-t α lub tobl> t α,v

d) Nie mamy podstaw do

odrzucenia gdy -

tα,v<tobl<tα,v

NIR - Najmniejsza istotna różnica tak nazywa się wyrażenie t α,v sr.. Jest to taka wartość różnicy dwóch badanych cech, która może być jeszcze uznania za wartość losowa (przypadkową). Różnice większe od NIR musza być uznane jako nielosowe

Ad H. o równości 2 wariancji

Założenie że wariancje analizowanej cechy w obu populacjach s ą jednakowe.

Procedura weryfikacji hipotezy

a) wyznaczyć wartość empiryczną Fishera-Snedecora (tak aby była większa od jedności) według wzoru

b) dla ustalonego poziomu istotności α odczytać z tablicy wartość krytyczną Fα,v,u, w ten sposób otrzymamy obszar krytyczny dla tej hipotezy Stopnie swobody dla wariacji: u =n1-1 w liczniku,

v-n2-1 w mianowniku

c) wnioskowanie : jeżeli

Fobl> Fα,v,u to hipoteze

H0: σ²₁ = σ²_2, odrzucamy na poziomie istotności (α) - wariancje w badanych populacjach róznią się istotnie , i na odwrót.

Ad. Hipoteza o zgodności rozkładu emipirycznego z rozkładem teoretycznym określonym przez hipotezę

Jeżeli H0 jest prawdziwa to statystyka ma rozkład χ² Pearsona, z liczbą stopni swobody v=k-1-u; Zastosowanie tej hipotezy wymaga znajomości liczebności teoretycznej w poszczególnych przedziałach klasowych. Należy znać teoretyczną liczbę obserwacji należących do danego przedziału przy założeniu, że rozkład empiryczny jest zgodny z teoretycznym rozkładem hipotetycznym.

Test χ² Pearsona , wykorzystywany jako test zgodności ma kilka wad:

-1)może być stosowany tylko dla dużych prób ( żeby można było zestawić szereg rozdzielczy)

- 2)to że dane są zestawione w szereg rozdzielczy z pewną dowolnością , rzutuje na wartość statystyki empirycznej.

AD. Hipoteza o zgodności rozkładu kilku populacji

Można zastosować rozkład chi-kwadrat Pearsona;

Jeżeli χ^{2 obl} >χ²α,v, to H0 odrzucamy, i wnioskujemy że cecha X w badanych populacjach ma różny rozkład;

Jeżeli χ^{2 obl} <χ²α,v,, to nie odrzucamy h0, i w badanych populacjach rozkład cechy X jest taki sam

ANALIZA REGRESJI

Próba wielocechowa - zbiór obserwacji dotyczących więcej niż jednej cechy obiektów pewnej populacji

Teoria korelacji i regresjii - metody statystyczne, które zajmują się badaniem wzajemnych zależności cech

Analiza korelacji - zawiera się w analizie dwuwymiarowej, jej celem jest stwierdzenie czy między badanymi cechami zachodzą określone zależności, jaka jest ich siła i jaki jest kierunek tych zależności

Korelacja dodatnia - wzrostowi wartości jednej cechy odpowiada wzrost średnich wartości drugiej cechy

Korelacja ujemna - wzrostowi wartości jednej cechy odpowiada średnich wartości drugiej cechy.

Układ punktów na diagramie koleracyjnym:

1. siła zależności - niewielki rozrzut punktów na wykresie świadczy o dużej sile związku

2. kierunek z. - określenie czy korelacja jest dodatnia lub ujemna

3. kształt - postać funkcji matematycznej, jeżeli punkty na wykresie układają się wzdłuż lini prostej to jest korelacja liniowa, gdy wzdłuż lini krzywej to korelacja krzywoliniowa

X - zmienna niezależna

Y - zmienna zależna

Szereg korelacyjny - przedstawia dane indywidualne, jest szeregiem szczegółowym, dwuwymiarowym (przedstawia 2 cechy jednocześnie); ma postać tablicy

Diagram korelacyjny(rozrzut punktów, chmura punktów) - przedstawia w sposób graficzny dane z szeregu korelacyjnego.

Współczynnik koleracji liniowej r Pearsona (r w próbie, a p w poplulacji)- jest liczbą niemianowaną (jest niezależny od jednostek w jakich wyrażone są obie porównywane cechy; należy do przedziału < -1; 1 >.

Interpretujemy dwa elementy współczynnika korelacji:

1. znak współczynnika korelacji;

2. wartość współczynnika korelacji;

Jeżeli chodzi o znak to:

a) jeżeli r > 0, to większym wartościom jednej cechy odpowiadają większe wartości drugiej cechy; jest to zależność dodatnia (rosnąca, stymulująca);

b) jeżeli r < 0, to większym wartościom jednej cechy odpowiadają mniejsze wartości drugiej cechy; jest to zależność ujemna (malejąca, limitująca);

c) jeżeli r = 0, to bez względu na wartość przyjmowane przez jedna z cech, średnia wartość drugiej cechy jest taka sama; są to cechy nieskolerowane

Jeżeli r= +1 , to istnieją takie liczby a i b, że Y = aX + b - zależność między cechami jest ściśle liniowa.

Jeżeli r= 1, to a > 0, oraz jeżeli r = -1 to a <0.

W związku z tym współczynnik korelacji traktowany jest jako miernik liniowej zależności między cechami X oraz Y. Wartość współczynnika korelacji interpretowana jest ; że im |r| jest bliższe 1, tym bardziej liniowa jest zależność między cechami. Korelację między X i Y obliczamy ze wzoru r

, gdzie COV(X,Y) to kowariancja- suma iloczynów odchyleń od średniej; miara łącznego zróżnicowania obu cech. √varX-odchylenie stand. cechy X; √varY- odchylenie stand. cechy Y

Ocena siły związku

0,0-0,2-brak; 0,2-0,4-słaba; 0,4-0,7 średnia; 0,7-0,9silna, 0,9-1bardzo silna

im większa jest liczebność próby tym wartość współczynnika jest bliższa rzeczywistości.

ESTYMACJA PARAMETRÓW LINIOWEJ FUNKCJI REGRESJI

Czynności związane z opracowywaniem próby dwucechowej:

1)przedstawienie jej graficznie w układzie współrzędnych prostokątnych na płaszczyźnie (daje to możliwość zorientowania się w rodzaju zależności między badanymi cechami)

Metoda najmniejszych kwadratów - według niej funkcja y=f(x) możliwie najdokładniej przedstawia zależność między cechami y i x, jeśli suma kwadratów różnic f(x)=y, czyli suma kwadratów odchyleń wartości szacowanych z równania y(x)=f(x) od wartości empirycznych y jest najmniejsza ∑[f(x)-y]²

Współczynnik regresji liniowej (b)

określa szybkość zmian cechy y przy zmianie wartości cechy x.

Współczynnik regresji mówi nam o tym, o ile zmieni się zmienna zależna y przy wzroście zmiennej x o jednostkę.

Współczynnik determinacji to kwadrat współczynnika korelacji pomnożony przez 100% (r²*100%)

Informuje jaka część zmienności cechy y spowodowana jest wpływem liniowym cechy niezależnej x.

INDEKSY STATYSTYCZNE

Dynamika badanego zjawiska to zmiany poziomu (wzrost lub spadek) tego zjawiska w danych jednostkach czasu np.godziny, miesiące, lata.

Szereg dynamiczny- służy do prezentacji poziomu zjawisk obserwowanych w kolejnych okresach, jest to ciąg obserwowanych poziomów danego zjawiska (X) uporządkowanych według przyjętej jednostki czasu (t), oznaczając okresy kolejnymi numerami 1,2,... oraz przez Xt zaobserwowane poziomy zjawisk , otrzymuje się tabelaryczną postać szeregu d.

Indeksy statystyczne- służą do badania dynamiki zjawisk, są miarami, które pozwalają ocenić zmiany jakie następują w poziomie badanego zjawiska w badanych okresach w porównaniu z poziomem tego zjawiska w czasie przyjętym za podstawę badania.

*Indeksy indywidualne (proste)- obliczane dla pojedynczej jednostki zbiorowości, służą do porównania w czasie poziomów zjawisk jednorodnych

a) jednopodstawowe - porównanie poziomu jakiegoś zjawiska w kolejnych okresach z jednym i tym samym poziomek w dowolnie wybranym okresie

b)łańcuchowe- porównywanie poziomu zjawiska z okresu na okres

*Indeksy agregatowe (zespołowe)-obliczane dla zespołu jednostek zbiorowości.

Agregat to pewna całość powstała w wyniku połączenia niejednorodnych części; najbardziej jednorodny agregat to PKB.

Omawia się głównie dwa typy indeksów agregatowych

1)cen, 2) ilości

Główne indeksy agregatowe:

1)prosty agregatowy indeks cen- porównanie poziomu cen w badanym okresie do cen z okresu bazowego.

jego główna wada to

-zależność od przyjęcia określonych jednostek (np. kg) w stosunku do których podawane są ceny

-przyjmuje się że wszystkie artykuły mają takie samo znaczenie

2)agregatowy indeks cen Laspeyresa

tu przyjmuje się wagi (wielkości sprzedarzy) z okresu bazowego

3)agregatowy indeks cen Paaschego-

przyjmuje się wagi z okresu badanego

Względny przyrost - wskaźnik służący do określenia przyrostu poziomu danego zjawiska wyróżniamy:

1. względny przyrost o podstawie stałej

2. względny przyrost łańcuchowy( zwany też tempem)

Istnieje ścisły związek między tempem a indeksem łańcuchowym

Ciąg indeksów łańcuchowych informuje o zmieniającej się w czasie dynamice obserwowanego zjawiska.. Średnią wielkość indeksu łańcuchowego liczy się za pomocą średniej geometrycznej

Inter: jeżeli indeks cen przyjmuje wartość z%, to mówi się, że zestaw artykułów (usług) z okresu bazowego (badanego), jest o ....droższy lub tańszy, niż miało to miejsce w okresie bazowym.

---