1

                                                            

Prof. Dr Franciszek Kubiczek

e-mail:fkub@onet.eu       

Rok akademicki 
2010/2012

11

   REGRESJA LINIOWA - 

PREDYKCJA

(LINEAR REGRESSION - 

PREDICTION)

2

STATYSTYCZNA TEORIA KORELACJI I REGRESJI

 „Rak płuc jest powiązany z paleniem papierosów” – im więcej pali się 

papierosów, tym bardziej jest prawdopodobne, że zachoruje się na raka!!

 Narzędzie do dokładnego określania stopnia, w jakim zmienne są ze sobą 

powiązane. Pozwala zweryfikować (także negatywnie) rozpoznane 

powiązanie, jak również wykryć nierozpoznane dotychczas współzależności.

 Podstawowym problemem statystyki korelacji i regresji jest stwierdzenie, 

czy między zmiennym (zjawiskami, procesami, zdarzeniami) występuje jakiś 

związek, jakaś zależność i czy związek ten jest mniej lub bardziej ścisły.

3



Sir Francis Galton (kuzyn Darwina) – 1822-1911, twórca eugeniki, 

daktyloskopii, prekursor badań nad inteligencją, statystyk, meteorolog, 

antropolog, kryminolog. Pisarz, lekarz. Opracował metody statystyczne 

badania rozkładu uzdolnień 

w populacjach, wprowadził pojęcie testu umysłowego (składały się z zadań 

psychofizycznych) . Za odpowiedzialne za inteligencję i zdolności umysłowe 

uważał dwie zmienne: energię działania i wrażliwość zmysłową. 



W 1899 r. w pracy „Naturalna dziedziczność” ogłosił, że rozmiary nasion 

groszku pachnącego mają tendencję w kolejnych generacjach do 

powracania 

(to regress)

 

do swego średniego rozmiaru, podobnego związku dopatrzył się także 

między wzrostem syna i ojca itd.



Dopasowywał do tych par liczb linię prostą opisującą tę zależność

GALTON – TWÓRCA STATYSTYCZNEJ TEORII REGRESJI

4



KORELACJA 

(Correlation)

 daje możliwość stwierdzenia, czy istnieje 

związek (niekoniecznie przyczynowo-skutkowy) miedzy badanymi cechami 

(zmiennymi) oraz jaka jest jego siła i kierunek



REGRESJA 

(Regression)

 daje możliwość oszacowania (estymacji) wartości 

jednej cechy (zmiennej zależnej, objaśnianej) na podstawie wartości 

przyjmowanych przez drugą cechę (zmienną niezależną, objaśniającą)



FUNKCJA REGRESJI  

(Function of regression)

 której parametry 

można oszacować przy pomocy metody najmniejszych kwadratów (MNK). 

Równanie opisujące związek statystyczny między zmiennymi  nazywa się 

równaniem lub modelem regresji. 

ISTOTA REGRESJI

5

METODA NAJMNIEJSZYCH KWADRATÓW 

MNK

 

LEAST SQUARES METHOD



K. F. Gauss

 – twórca metody (1809 r. , w wieku 25 lat)



Metoda powstała w kontekście estymacji sześciu stałych w czasie parametrów 
określających położenie ciała niebieskiego na orbicie eliptycznej



Początek szerszego stosowania 1950-1960



Najmniejszy błąd kwadratowy jako kryterium oceny, stąd nazwa metody 
najmniejszych kwadratów



Metoda najmniejszych kwadratów polega na estymacji parametrów modelu 
regresji zapisanego w postaci addytywnej (sumarycznej), która pozwala na 
znalezieniu takich wartości tych parametrów, że suma kwadratów odchyleń 
pomiędzy rzeczywistymi (empirycznymi) a teoretycznymi (obliczonymi z 
równania regresji) wartościami zmiennej objaśnianej jest najmniejsza. Model 
jest tym lepiej dopasowany do danych rzeczywistych, im różnice miedzy 
zaobserwowanymi wartościami zmiennej objaśnianej (Y) a jej wartościami 
teoretycznymi są mniejsze.

6

MODELE REGRESJI

 Model ekonometryczny 

(Econometric model

):

 równanie (lub układ 

równań) opisujące zależność   pomiędzy zjawiskami ekonomicznymi

   - 

przyczynowo-skutkowe

 

(cause and effect model):

 w których między 

zmiennymi objaśnianymi a zmiennymi objaśniającymi zachodzi związek  

przyczynowo-skutkowy

   - 

symptomatyczne:

 bez związku przyczynowo-skutkowego, ale w których      

                           zachodzi statystyczny silny związek korelacyjny; może to 

oznaczać, że inne zmienne (tzw. symptomatyczne) oddziałują  silnie na 

zmienne objaśniające włączone do modelu

   - 

autoregresyjne 

(autoregression):

 w których w roli zmiennych 

objaśniających występują  opóźnione w czasie zmienne objaśniane

   - 

tendencji rozwoju:

 opisują rozwój zjawisk w czasie (bez analizy przyczyny 

zjawisk bądź związków miedzy zmiennymi)

7

ETAPY BUDOWY MODELU (RÓWNANIA) 

REGRESJI

 Określenie istoty zjawiska, które jest badane; wybór modelu

 Wybór zmiennych objaśniających (x), spośród wielu czynników wpływających 

na zmienną objaśnianą (y); informacje o tym zdobywamy w rezultacie analizy 

korelacji miedzy zmiennymi.

 Jeżeli modelujemy zjawisko, które ma swoją rozwiniętą teorię, wtedy z tej 

teorii możemy uzyskać informację o potencjalnych zmiennych objaśniających, 

a niekiedy nawet o analitycznej postaci funkcji regresji. 

 Zdarza się, że zmienne uważane za przyczynę nie mogę zostać zmierzone lub 

informacja o nich nie jest osiągalna. Wtedy sięgamy do innych zmiennych, 

pośrednio mówiące o pierwotnych przyczynach. Takie zmienne nazywamy 

symptomatycznymi i ich wykorzystanie w modelu jest uzasadnione.

8

ETAPY BUDOWY MODELU (RÓWNANIA) 

REGRESJI

 W wielu zjawiskach, liczba potencjalnych zmiennych objaśniających jest 

bardzo duża 

i nie możemy ich wszystkich zamieścić w równaniu regresji. Ograniczeniem 

jest jednak zwykle liczba posiadanych (lub możliwych do zdobycia) informacji 

liczbowych 

o wartościach tych zmiennych. 

 Wnioskowanie przyczynowo-skutkowe wymaga nie tylko spełnienia formalnych 

wymagań poprawności równania regresji, lecz przede wszystkim logicznej i 

merytorycznej analizy modelowanego zjawiska. 

9

ETAPY BUDOWY MODELU (RÓWNANIA) 

REGRESJI

 Wybór postaci analitycznej modelu: określenie postaci funkcji matematycznych 

opisujących zależność zmiennej objaśnianej od zmiennych objaśniających;

 Najczęściej stosowanym modelem regresji jest model liniowy oraz 

jednorównaniowy 

 Oszacowanie (estymacja) parametrów modelu (równania)

 Weryfikacja modelu: sprawdzenie czy model adekwatnie opisuje badaną 

rzeczywistość ekonomiczną

 Wnioskowanie na podstawie modelu: analiza ekonomiczna i prognozowanie

10

RÓWNANIE REGRESJI LINIOWEJ (LINEAR REGRESSION 

EQUATION)

        Y = a x + b             

         [Y – (a x + b)]

2

 = minimum 

 

Y 

– zmienna objaśniana (dane rzeczywiste)

Y

 – zmienna objaśniana (dane teoretyczne z równania regresji)

x

 – zmienna objaśniająca

a, b

 – parametry strukturalne równania regresji

a

  - współczynnik regresji 

(regression coefficient) 

b

  - wyraz wolny (tzw. parametr skali); podaje wartość zmiennej y, gdy zmienna 

x 
      przybiera wartość zero.     

^

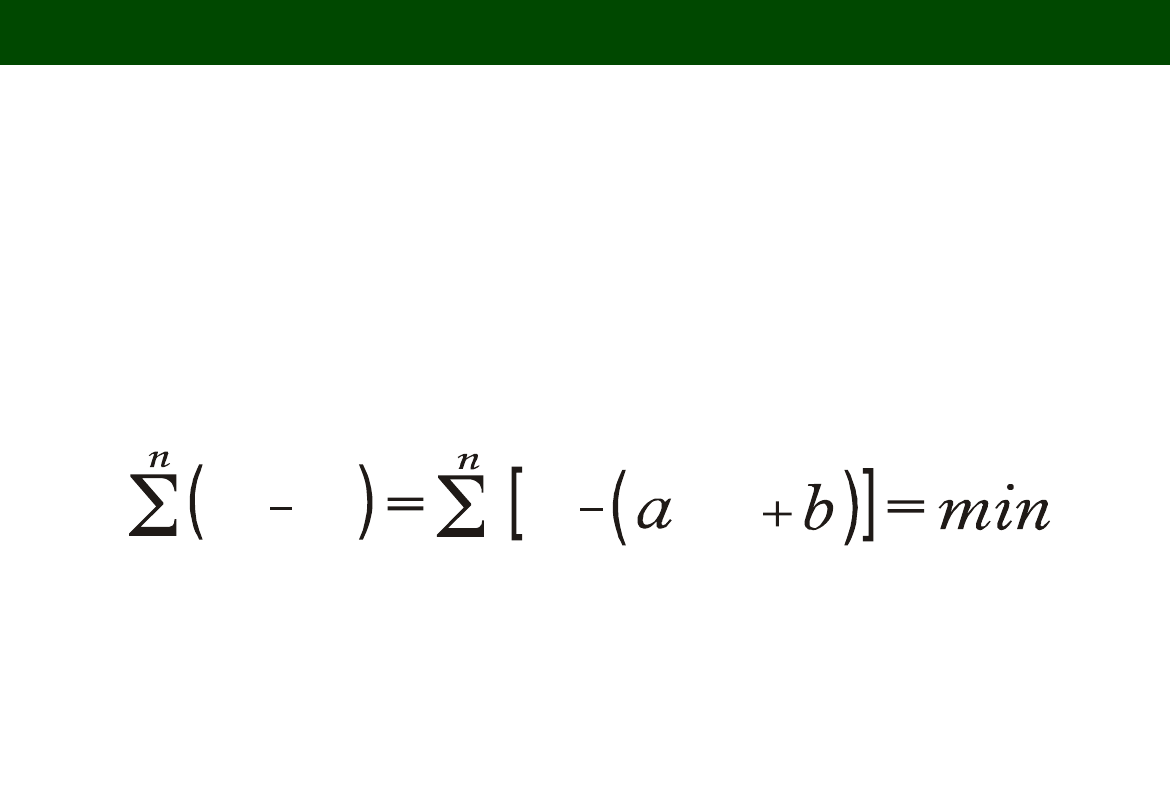
11

RÓWNANIE REGRESJI LINIOWEJ (LINEAR REGRESSION 

EQUATION)



Parametry tej funkcji (a i b) muszą być tak dobierane, aby wartość sumy 

kwadratów odchyleń wartości rzeczywistych cechy (Y) od wartości tej cechy, 

obliczonej na podstawie tego równania (Y) była jak najmniejsza, czyli:

i

i

i

i

. 

y

y

x

y

i = 1

i = 1

^

2

2

12

RÓWNANIE REGRESJI



Gdy obliczymy parametry równania a i b i wstawimy je do równania otrzymamy 

empiryczne równanie regresji wyprowadzone z konkretnego szeregu danych 

statystycznych. Estymacja parametrów liniowej funkcji regresji polega na 

znajdowaniu takich wartości, aby model regresji jak najlepiej pasował do 

danych rzeczywistych. 



Mając to równanie możemy obliczyć zmienną zależną (objaśnianą) podstawiając 

konkretną wartość zmiennej niezależnej (objaśniającej)



Wyniki te możemy wykorzystać do prognozowania kształtowania się 

konkretnego zjawiska w konkretnej przyszłości, badania wariantów 

rozwojowych;



Współczynnik regresji: informuje, o ile, średnio biorąc, zmieni się przeciętny 

poziom zmiennej zależnej (objaśnianej - Y), jeśli wartość zmiennej niezależnej 

(objaśniającej – X), przy której stoi współczynnik, wzrośnie (spadnie) o 

jednostkę, natomiast wartości pozostałych zmiennych objaśniających nie ulegną 

zmianie.

13

 Estymacja: zastosowanie odpowiednich metod statystycznych w celu 

otrzymania jak najlepszych wartości występujących w modelu parametrów 

w oparciu o rzeczywiste dane liczbowe.

 Weryfikacja: sprawdzenie, czy otrzymane oszacowania (estymacje) 

wytrzymują konfrontację z  teorią (równaniem regresji) oraz czy dane 

potwierdzają poprawność przyjętego modelu. Szacujemy istotność 

otrzymanych parametrów równania (równań). Jeżeli model nie spełnia 

stawianym wymaganiom możemy opracować nowy: zmienić postać 

funkcji, zebrać nowe dane, wykorzystać inną teorię.

ESTYMACJA I WERYFIKACJA

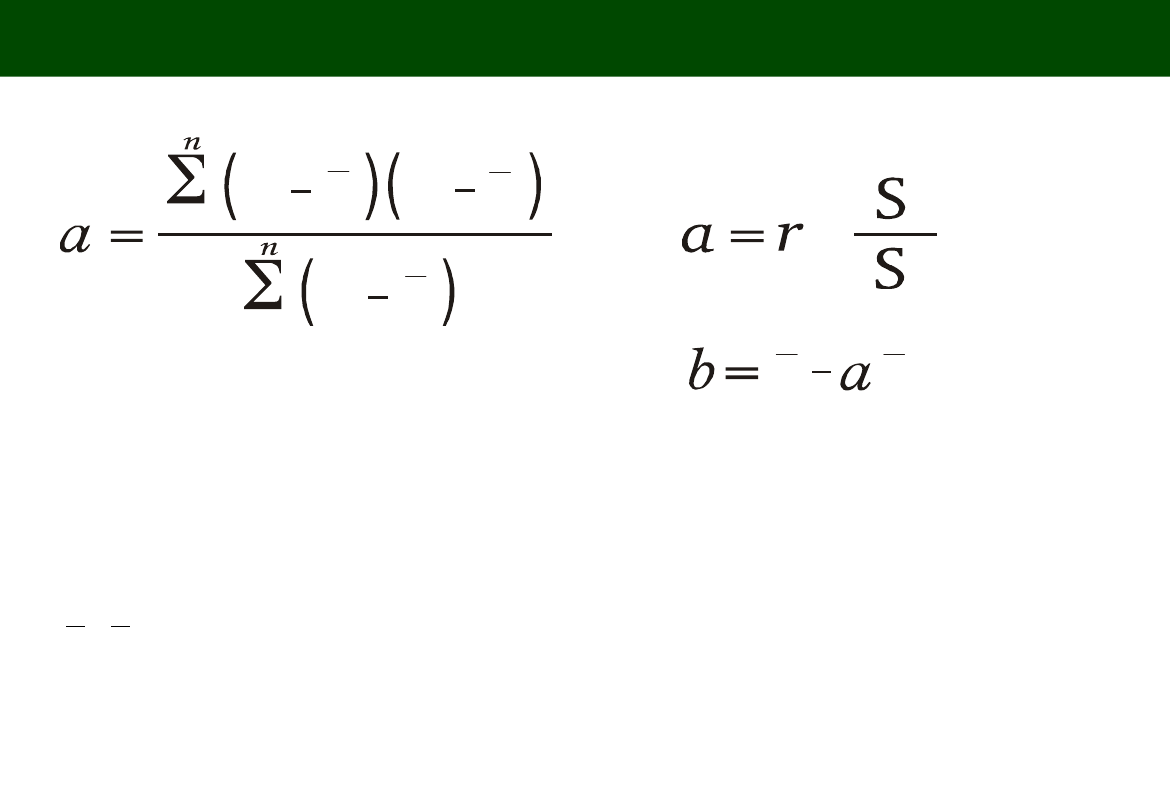
14

OBLICZANIE PARAMETRÓW RÓWNANIA REGRESJI

 

(Estimate of the 

parameters)

i

i

i

y

x

x

x

x

y

i = 1

i = 1

2

x

y

  a, b – 

parametry (współczynniki) równania 

regresji

x

i 

, 

y

i  

–

 

wartości rzeczywiste zmiennych

x

,  

y   

- 

wartości średnie zmiennych

    r

xy

 –  

współczynnik korelacji

S

x

, S

y

 – 

odchylenia standardowe

lub

. 

y

y

x

x

15

WERYFIKACJA OSZACOWANIA PARAMETRÓW

( VERIFICATION OF THE ESTIMATION)

S to odchylenie standardowe wartości rzeczywistych (empirycznych) cechy y od 

jej wartości teoretycznych     uzyskanych z liniowej funkcji regresji dla tych 

samych wartości cechy x; 

im mniejsze S tym większa precyzja dopasowania linii regresji do danych 

rzeczywistych

V to współczynnik zmienności, miara natężenia odchyleń

y

^

i

i

y y

^

2



V 

=         

 x 

100

S

y

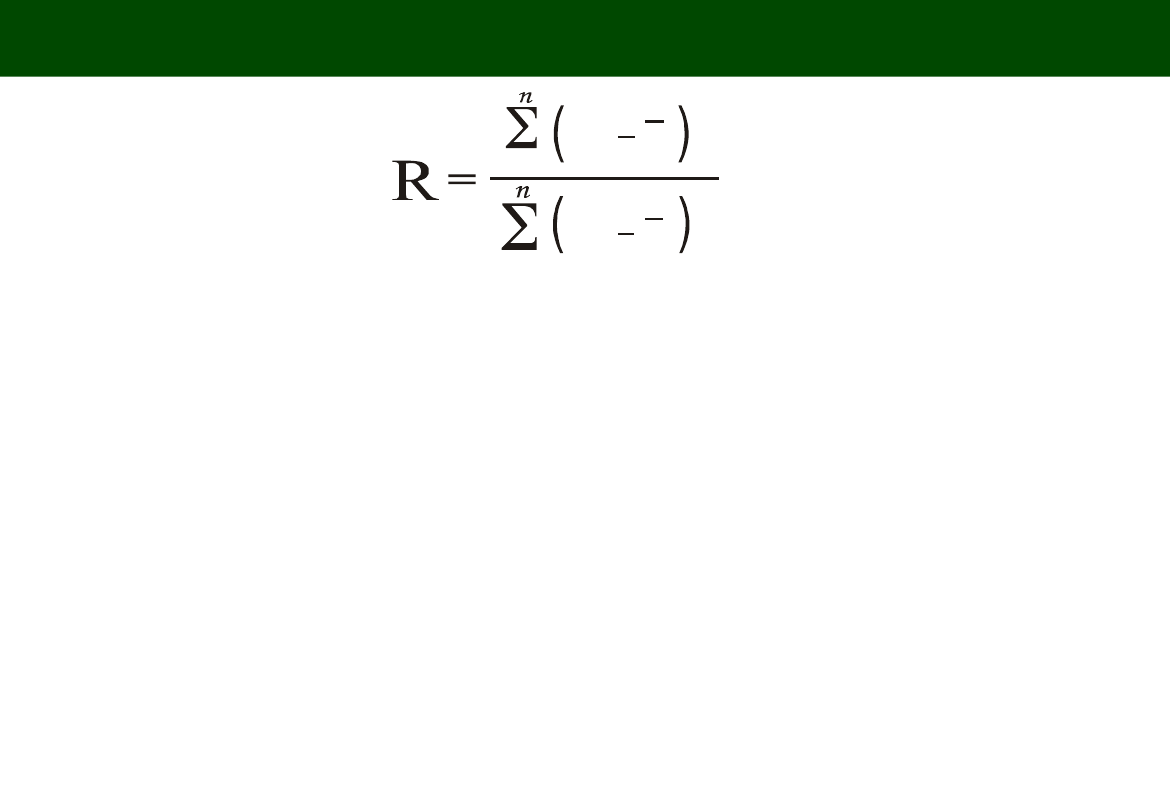
16

WSPÓŁCZYNNIK DETERMINACJI (DETERMINATION 

COEFFICIENT)

Współczynnik determinacji informuje, jaka część zmienności zjawiska (Y) jest 

wyjaśniana przez zaobserwowane zmiany w wartościach zmiennych 

objaśniających.

R

2

 jest miarą siły liniowego związku między zmiennymi, czyli miarą 

dopasowania linii regresji do danych rzeczywistych i przyjmuje wartości od 0 

do 1 i oznacza w skrajnych wypadkach:

– 0 - zupełny brak dopasowania funkcji regresji do danych rzeczywistych

– 1 - idealne dopasowanie funkcji regresji do danych rzeczywistych

Im większe R

2

 tym dopasowanie jest lepsze i tym większe można mieć 

zaufanie do regresji

i

i

y

y

y

y

i = 1

i = 1

^

2

2

2

17

WSPÓŁCZYNNIK ZBIEŻNOŚCI (CONVERGENCE 

COEFFICIENT)

                                   

Z  = 1 – R

2

- Informuje, jaka część całkowitej zmienności cechy y nie jest wyjaśniana 

regresją liniową względem cechy x;

- Jeżeli funkcja regresji jest idealnie dopasowana to

 

R

2

 = 1

, 

czyli 

Z

b

 =

 0 

i 

odwrotnie,

- Jeżeli funkcja regresji zupełnie odbiega od danych rzeczywistych

 

to

 

R

2 

= 0

, 

czyli

 

Z

b

 = 1

18

TABLICA KORELACYJNA



Tablicę budujemy porządkując szeregi danych wg wartości zmiennej niezależnej, 

np. wg czasu, wartości PKB na mieszkańca, wysokości wynagrodzenia,



Z oglądu tablicy wnioskujemy intuicyjnie, czy istnieje jakiś związek (choćby 

liczbowy) pomiędzy zmiennymi, np. wraz ze wzrostem PKB na mieszkańca 

wydłuża się długość życia, wraz ze wzrostem ceny spada popyt



Jako specjaliści w danej dziedzinie może stwierdzić lub przyjąć hipotezę, że 

pomiędzy zmiennymi istnieje związek przyczynowo-skutkowy



Dopiero obliczenie współczynników korelacji i determinacji pozwoli określić 

kierunek 

i siłę ewentualnej korelacji pomiędzy danymi zmiennymi



Po stwierdzeniu korelacji, jej siły i kierunku przystępujemy do wyboru rodzaju 

krzywej regresji. Pomocny jest w tym celu diagram (wykres) korelacji. Układ 

punktów na wykresie powinien wskazać na rodzaj krzywej (lub prostej) regresji

19

KORELACJA  I  REGRESJA

RYNEK

CENY 

zł/szt.

x

i

ILOŚCI 

SPRZEDANE

  w szt.

y

i

1

2

3

1995

1 050

1 200

1996

1 050

1 250

1999

1 100

1 200

1993

1 150

 1 100

2000

1 150

1 150

1998

1 200

1 150

2001

1 200

   950

1992

1 250

1 000

1994

1 300

   900

1997

1 350

   800

RAZE

M

   11 800

       10 700

TABLICA KORELACYJNA (Correlation table)

REGRESJA

0

200

400

600

800

1000

1200

1400

0

200

400

600

800

1 000

1 200

1 400

1 600

Ilości sprzedane

Z oglądu tablicy i wykresu widać 
intuicyjnie, że występuje korelacja, gdyż 
wraz ze wzrostem ceny maleje sprzedaż 
oraz, że dobrym przybliżeniem będzie 
regresja liniowa.

20

OBLICZANIE WSPÓŁCZYNNIKA KORELACJI I 

DETERMINACJI

93

,

0

135252

126000

3

,

448

7

,

301

126000

201000

91000

126000

*















Współczynnik determinacji

  

r 

2

= (-0,93)

2

 = 0,87  

tzn. , że w 87% 

zmiana ceny wpływa na zmianę sprzedaży

r

 

=

Współczynnik korelacji

SILNA KORELACJA UJEMNA

i

x

x

i

y

y

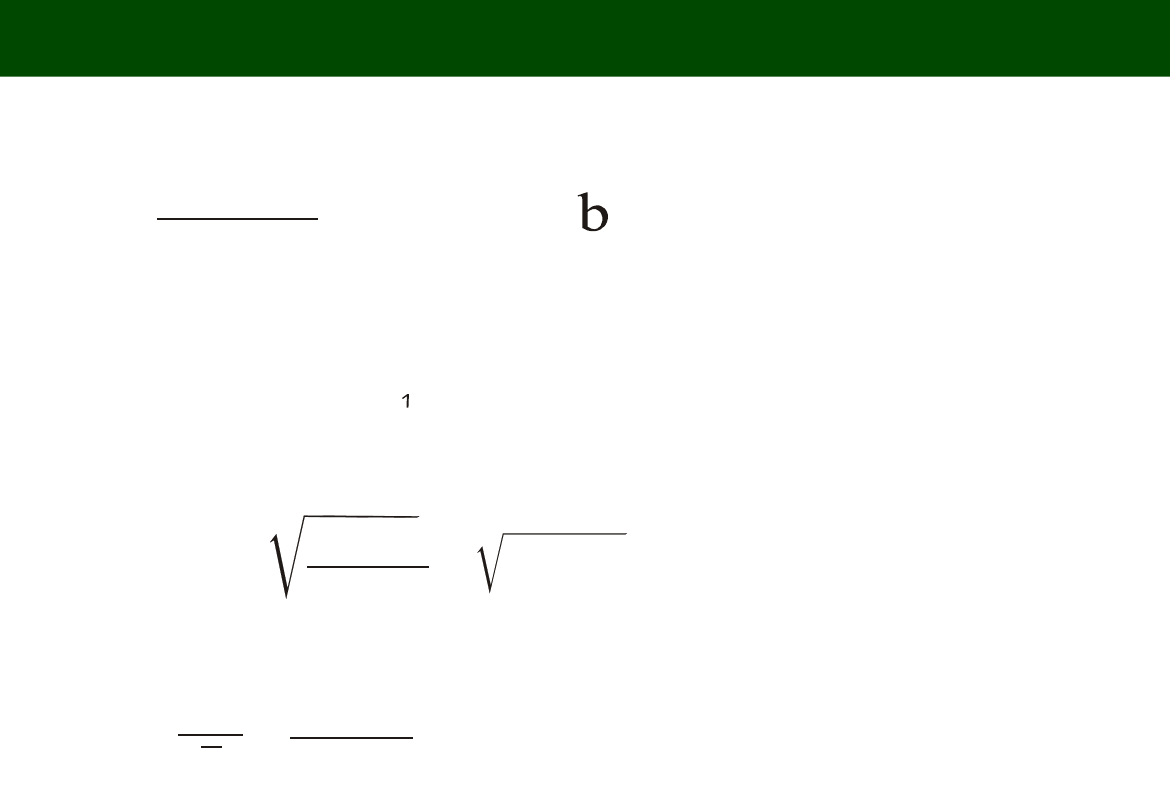
21

OBLICZANIE PARAMETRÓW RÓWNANIA REGRESJI

 

Współczynnik regresji

- 1 2 6 0 0 0

- 1 , 3 8

9 1 0 0 0

=

=

a

. 

1 0 7 0   +   1 , 3 8     1 1 8 0   =   2 6 9 8

=

 Równanie regresji

y

^

-   1 , 3 8         + 2 6 9 8

=

x

 Błąd standardowy

 Współczynnik zmienności

. 

S

y x

y

5 7 , 6

0 , 0 5 4     1 0 0   =   5 , 4 %

1 0 7 0

=

=

S

y x

2 6 5 4 2

3 3 1 7 , 7

5 7 , 6   s z t u k

8

=

=

=

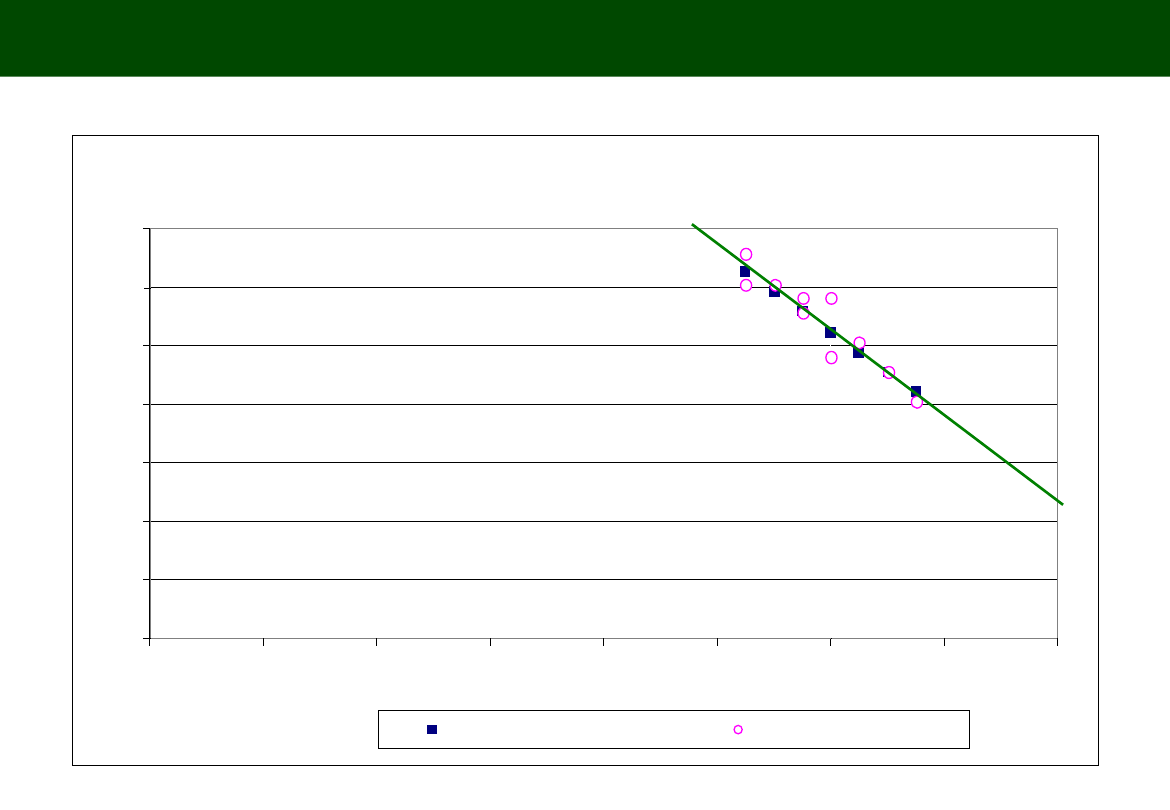
22

REGRESJ
A

0

200

400

600

800

1000

1200

1400

0

200

400

600

800

1 000

1 200

1 400

1 600

Równanie regresji

Ilości sprzedane

WYKRES KORELACYJNY (DIAGRAM OF CORRELATION)

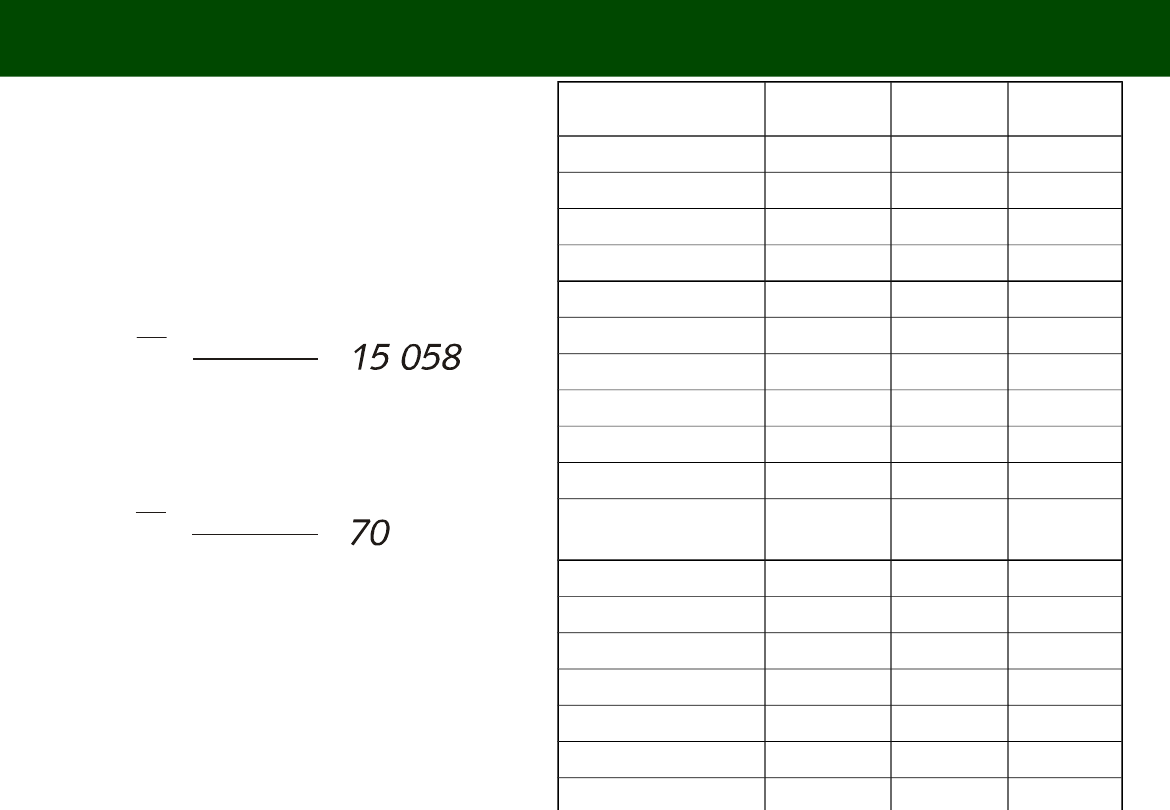
23

NAZWA KRAJU

NR KRAJU 

i

PKB 

X

i

ŻYCIE 

y

i

0

1

2

3

INDIE

35.

   1 700

57,70

EGIPT

34.

   3 130

62,86

BUŁGARIA

4.

   3 860

67,11

BIAŁORUŚ

3.

   4 840

62,87

BRAZYLIA

32.

   6 160

63,81

MEKSYK

40.

   7 858

67,84

ARGENTYNA

30.

10 200

68,42

KOREA

39

13 447

67,66

IZRAEL

36.

17 310

75,49

NOWA 

ZELANDIA

41.

17 777

73,40

CHINY

33.

22 000

66,70

AUSTRALIA

31.

22 704

75,04

BELGIA

2.

23 569

73,88

JAPONIA

37.

23 880

76,36

AUSTRIA

1.

23 884

73,54

KANADA

38.

24 359

74,55

USA

42.

30 588

72,50

RAZEM

632 420  2 925

TABLICA KORELACYJNA

x

x

1

=

=

n



y

y

1

=

=

n



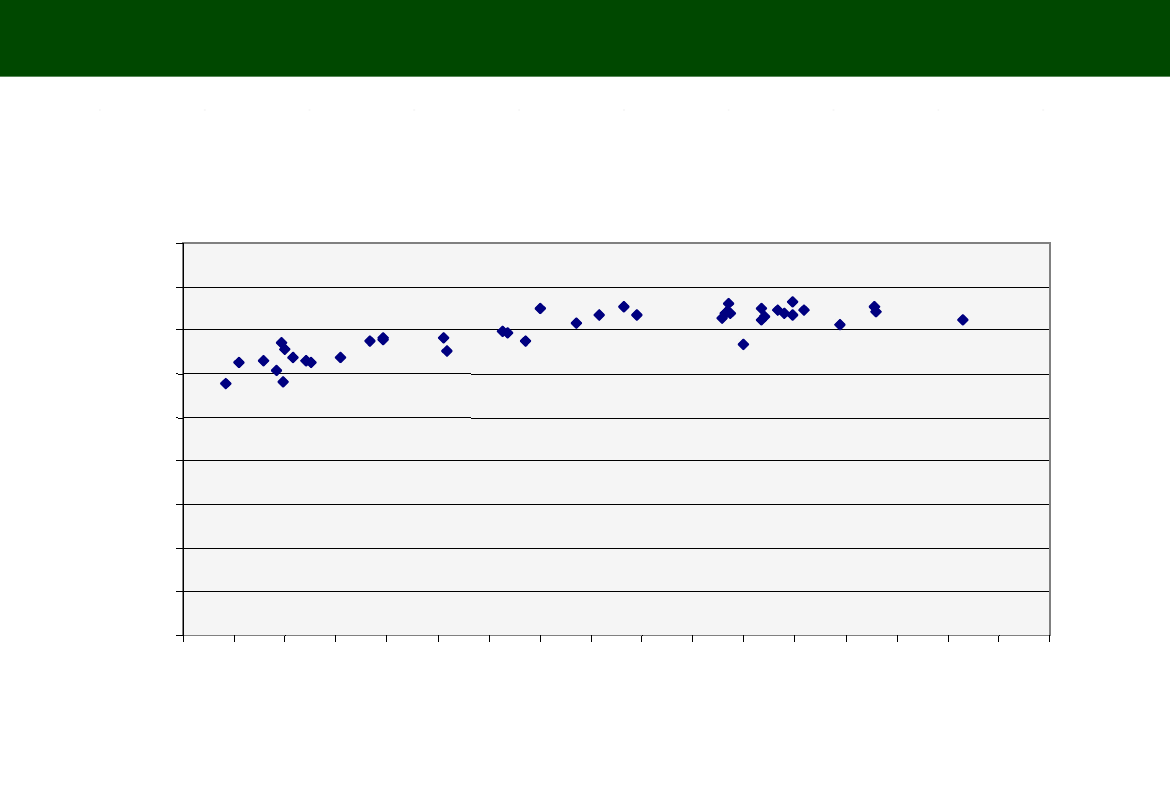
24

PRZECIĘTNE DALSZE TRWANIE ŻYCIA W LATACH W RELACJI DO PKB NA 1  MIESZKAŃCA

0

10

20

30

40

50

60

70

80

90

0

2

 0

0

0

4

 0

0

0

6

 0

0

0

8

 0

0

0

1

0

 0

0

0

1

2

 0

0

0

1

4

 0

0

0

1

6

 0

0

0

1

8

 0

0

0

2

0

 0

0

0

2

2

 0

0

0

2

4

 0

0

0

2

6

 0

0

0

2

8

 0

0

0

3

0

 0

0

0

3

2

 0

0

0

3

4

 0

0

0

WYKRES KORELACYJNY

25

WSPÓŁCZYNNIKI KORELACJI I DETERMINACJI



KORELACJI  

(Correlation coefficient)

 R = 0,85, tzn. że korelacja jest 

silna i jednokierunkowa, tzn. że związek między poziomem PKB na mieszkańca 

a długością życia jest silny oraz że wzrost PKB powoduje wydłużanie życia 

ludności



DETERMINACJI  

(Determination coefficient)

 R

2

 = 0,85

2

 =  0,72, tzn. 

że w 72% poziom PKB na mieszkańca wyjaśnia (określa) poziom długości życia



INTERDETERMINACJI  

(Indetermination coefficient)

 1 – R

2

 = 1 - 

0,72 = 0,28, 

tzn. że w 28% poziom długości życia zależy od innych czynników niż poziom 

PKB na mieszkańca



Po obliczeniu tych współczynników i stwierdzeniu istnienia korelacji 

przystępujemy do dalszych kroków mających na celu wypracowanie równania 

regresji

26



a = 

1 589 587 : 3 081 243 874 = 0,00052 $/rok

         

co oznacza, że każde 1000$ PKB na mieszkańca wydłuża życie o 0,52 

roku



b = 

70 – 0,52  15,1 = 62,2 lata

        

(70 = średnia trwania życia, 15,1 = średni PKB)



Równanie regresji liniowej:

         Y = 0,52 x

i

 + 62,2   

(PKB w tys. USD)

. 

OBLICZENIE WSPÓŁCZYNNIKÓW RÓWNANIA 

REGRESJI

27

WYKRES KORELACYJNY



Trzeba się dobrze przyjrzeć (wzrokowo – dosłownie) wykresowi pod kątem 

wybory formy regresji: liniowej bądź nieliniowej, jeśli nieliniowej to wg 

jakiej krzywej



Wybierając formę regresji (rodzaj funkcji) przystępujemy do obliczeń 

współczynników równania regresji

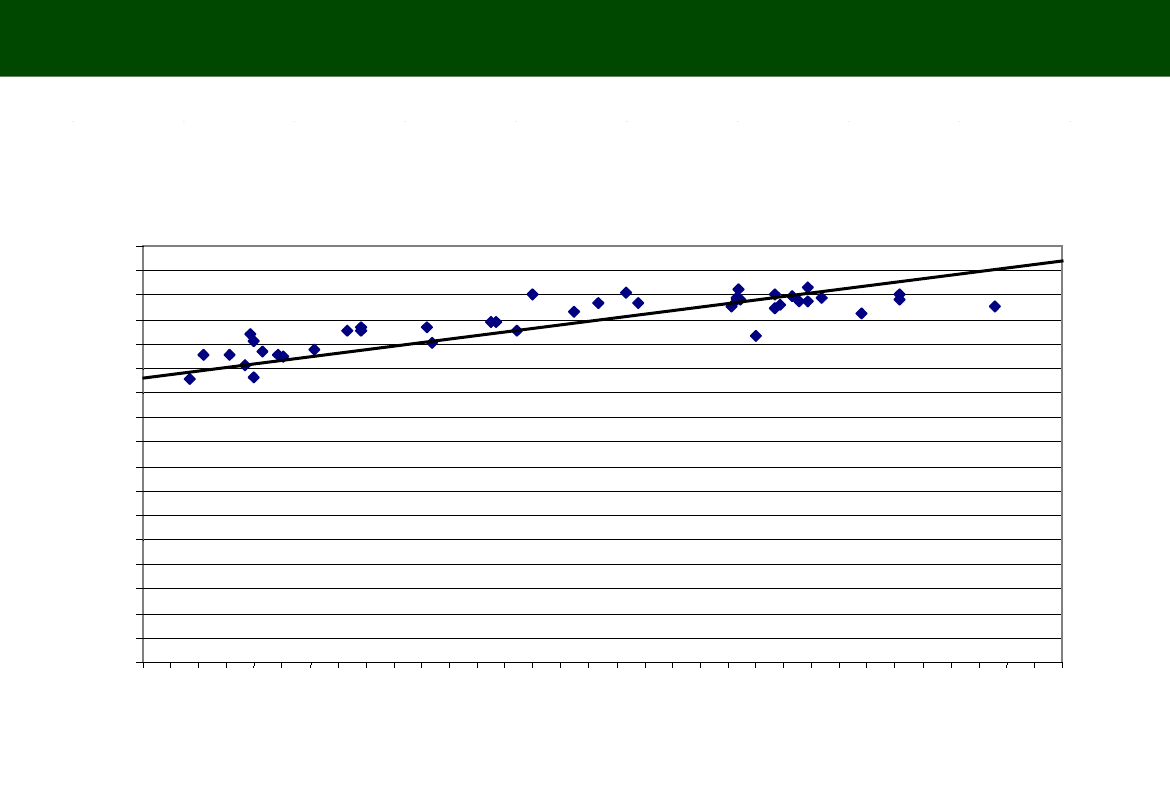
28

WYKRES FUNKCJI REGRESJI I DANYCH 

RZECZYWISTYCH

PRZECIĘTNE DALSZE TRWANIE ŻYCIA W LATACH W RELACJI DO PKB NA 1 MIESZKAŃCA 

0

5

10

15

20

25

30

35

40

45

50

55

60

65

70

75

80

85

0

1

 0

0

0

2

 0

0

0

3

 0

0

0

4

 0

0

0

5

 0

0

0

6

 0

0

0

7

 0

0

0

8

 0

0

0

9

 0

0

0

1

0

 0

0

0

1

1

 0

0

0

1

2

 0

0

0

1

3

 0

0

0

1

4

 0

0

0

1

5

 0

0

0

1

6

 0

0

0

1

7

 0

0

0

1

8

 0

0

0

1

9

 0

0

0

2

0

 0

0

0

2

1

 0

0

0

2

2

 0

0

0

2

3

 0

0

0

2

4

 0

0

0

2

5

 0

0

0

2

6

 0

0

0

2

7

 0

0

0

2

8

 0

0

0

2

9

 0

0

0

3

0

 0

0

0

3

1

 0

0

0

3

2

 0

0

0

3

3

 0

0

0

29

PROGNOZY SZEREGÓW CZASOWYCH  (Time series 

forecating)



Wyrównywanie szeregów czasowych przy pomocy średniej ruchomej 

nazywaliśmy metodą mechaniczną



Wyrównywanie szeregów czasowych przy pomocy równań regresji liniowej (lub 

nieliniowej) i MNK nazywamy metodą analityczną



W tych równaniach zmienną niezależną (x) jest czas (lata, miesiące itp.), 

najczęściej oznaczana jako zmienna t. 



Równania regresji mogą służyć prognozowaniu szeregów czasowych, 

zwłaszcza 

w perspektywie średnio i długookresowej 

(time specific regression).

              Równanie:

    

y = b + a  t

. 

30

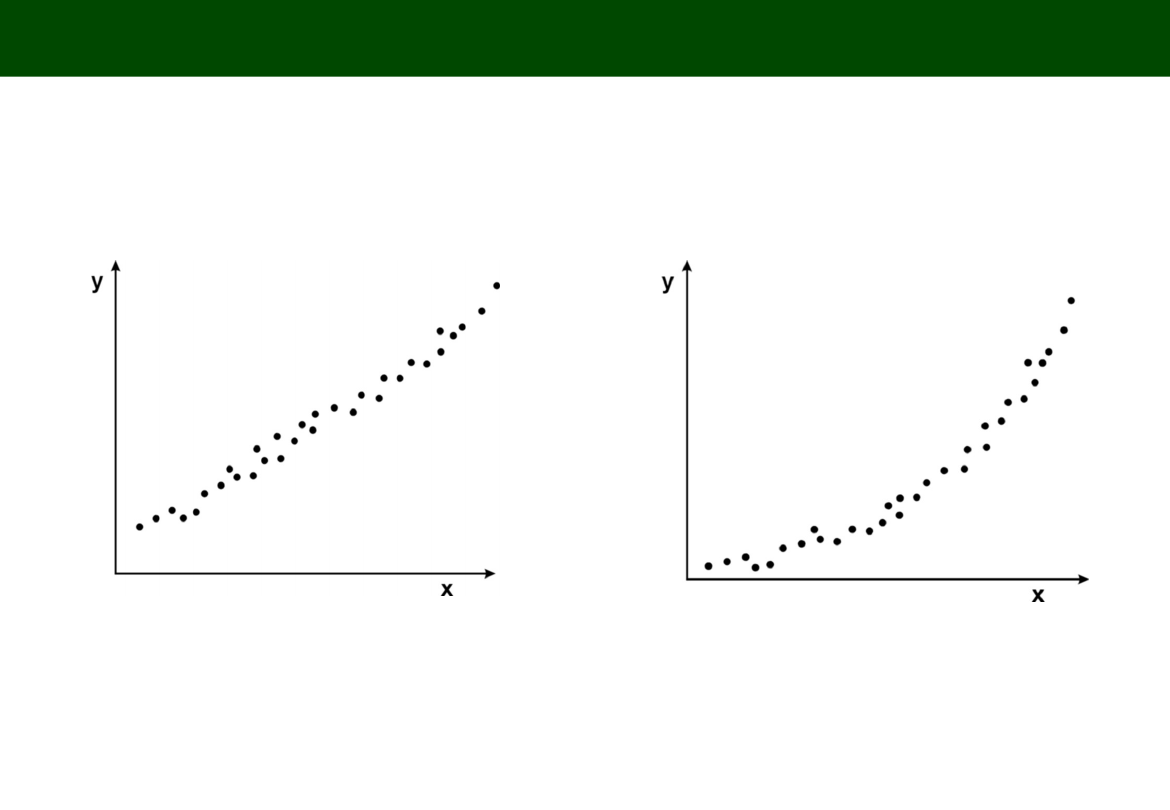
TYPOWE POSTACI ZWIĄZKÓW DWÓCH ZMIENNYCH

FUNKCJA LINIOWA (Linear) FUNKCJA WYKŁADNICZA (potential)

Y = ab

x

Y = aX + b

31

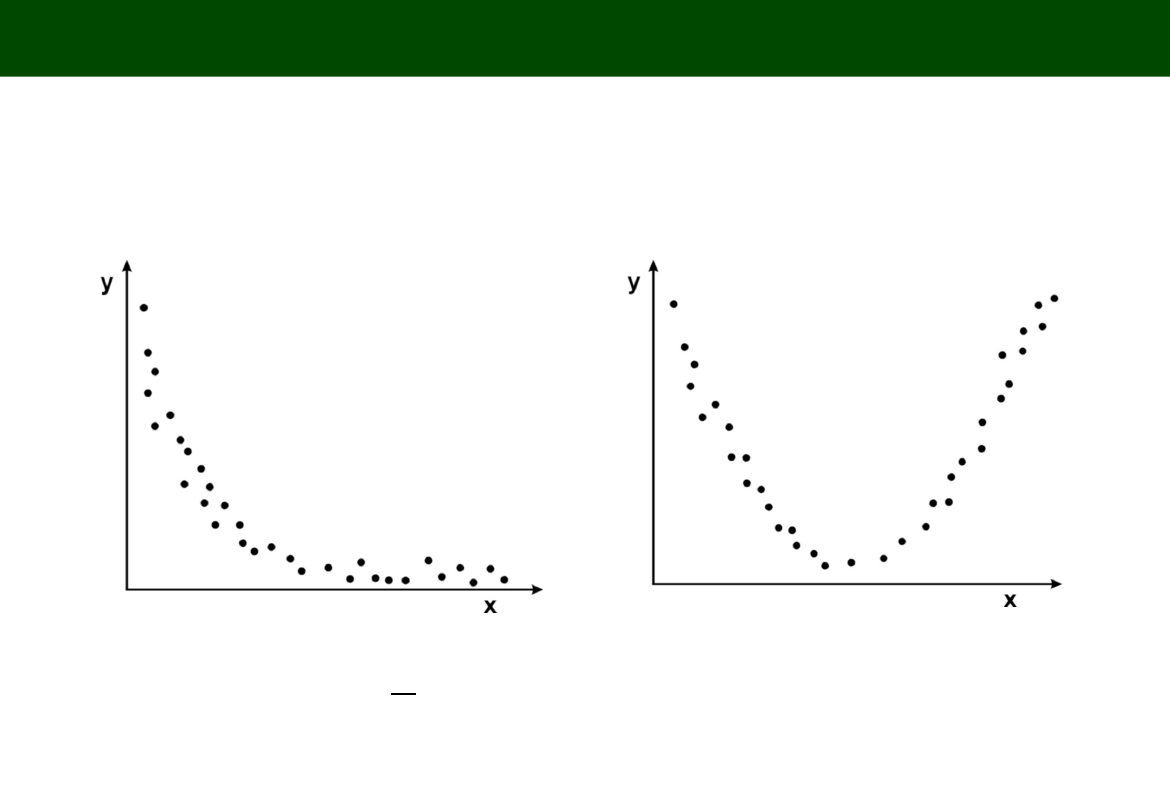
TYPOWE POSTACI ZWIĄZKÓW DWÓCH ZMIENNYCH

FUNKCJA HIPERBOLICZNA FUNKCJA PARABOLOCZNA (parabolic)

KWADRATOWA

Y = a + 
b 

1
X

Y = a + bX + 
cX

2

32

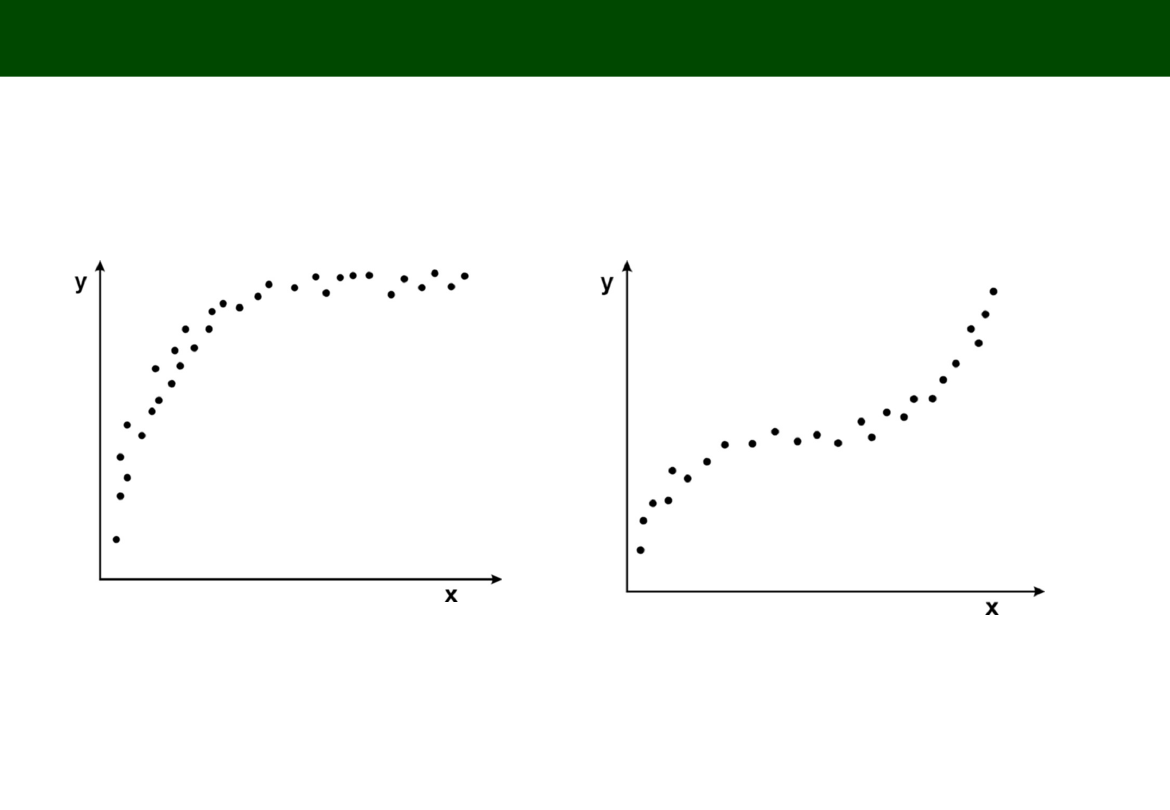
TYPOWE POSTACI ZWIĄZKÓW DWÓCH ZMIENNYCH

FUNKCJA LOGARYTMICZNA

FUNKCJA WIELOMIANOWA (polynominal)

Y = a

0

 + a

1

X + a

2

X

2

+ a

3

X

3

+ 

…+a

n

X

n

Y = a + blnX

33

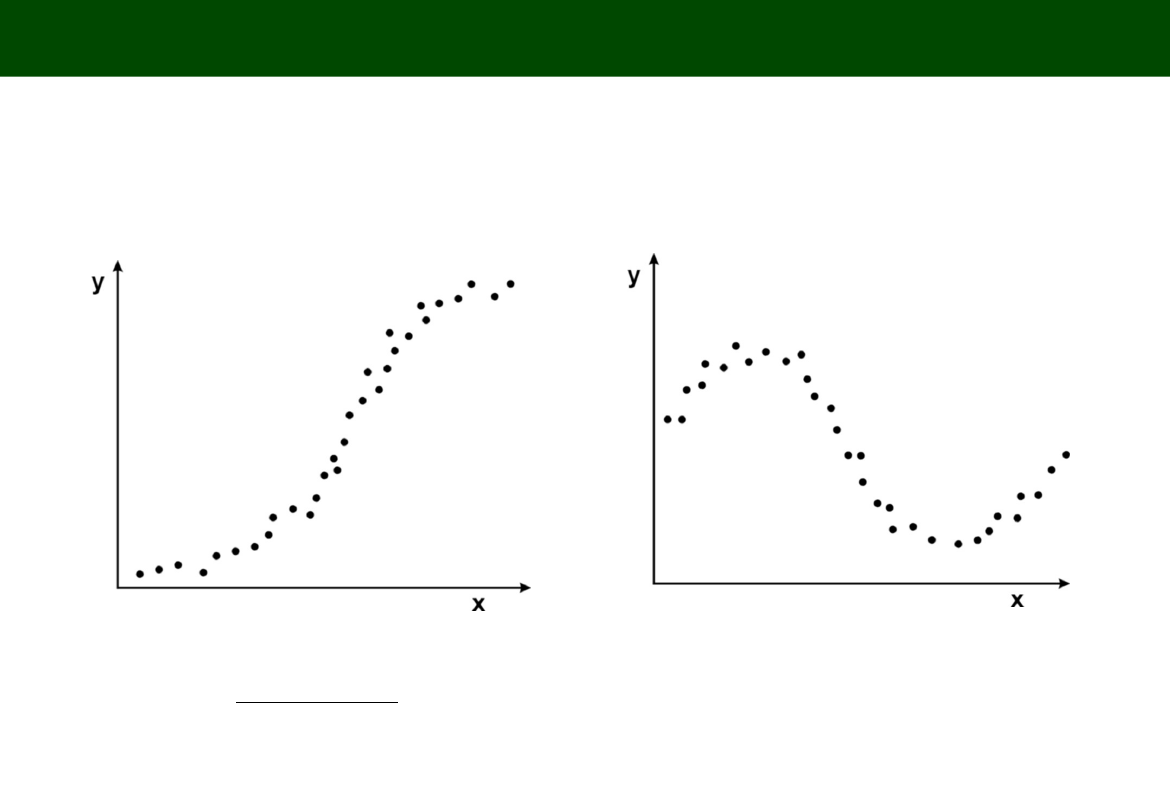
TYPOWE POSTACI ZWIĄZKÓW DWÓCH ZMIENNYCH

FUNKCJA LOGISTYCZNA (logistic)

FUNKCJA

TRYGONOMETRYCZNA (sine)

Y 
= 

a

0

1 + a

1

e

-

x

Y = a sinX + b

34

PROBLEM WYBORU KRZYWEJ DO REGRESJI



Aby wybrać właściwą dla danego zjawiska postać   krzywej musimy sporządzić 

wykres punktowy i dobrze się przyjrzeć kształtowi rozmieszczenia się  punktów 

 x

i 

y

i



Mając do dyspozycji wiele postaci krzywych (parabolicznych, wykładniczych, 

logistycznych, trygonometrycznych itp.) musimy sami wybrać tę, która jest 

najbliższa zjawisku ukazanemu na wykresie



Tę właśnie wybraną krzywą dopasowujemy do zjawiska poszukując parametry 

równania funkcji jej odpowiadającej przy pomocy MNK



Jeśli dla wybranej krzywej błąd standardowy okaże się zbyt duży, poszukujemy 

innej postaci krzywej lub zrezygnować z metody regresji na rzecz metod 

mechanicznych (średnia ruchoma, wyrównanie wykładnicze Browna)

35

 Ocenę dokładności prognozy opartej o równanie regresji prowadzimy przy 

pomocy tzw. błędu predykcji

 Jeśli wielkość błędu (stopnia precyzji) jest akceptowalna pozostajemy przy 

wybranej formie regresji (np. liniowej)

 Jeśli jest zbyt wysoki, poszukujemy innej krzywej bądź innej formy regresji, 

np. wielorakiej, gdyż być może na zmienną zależną ma wpływ więcej niż 

jedna – dotychczas brana pod uwagę - zmienna

BŁĄD PREDYKCJI

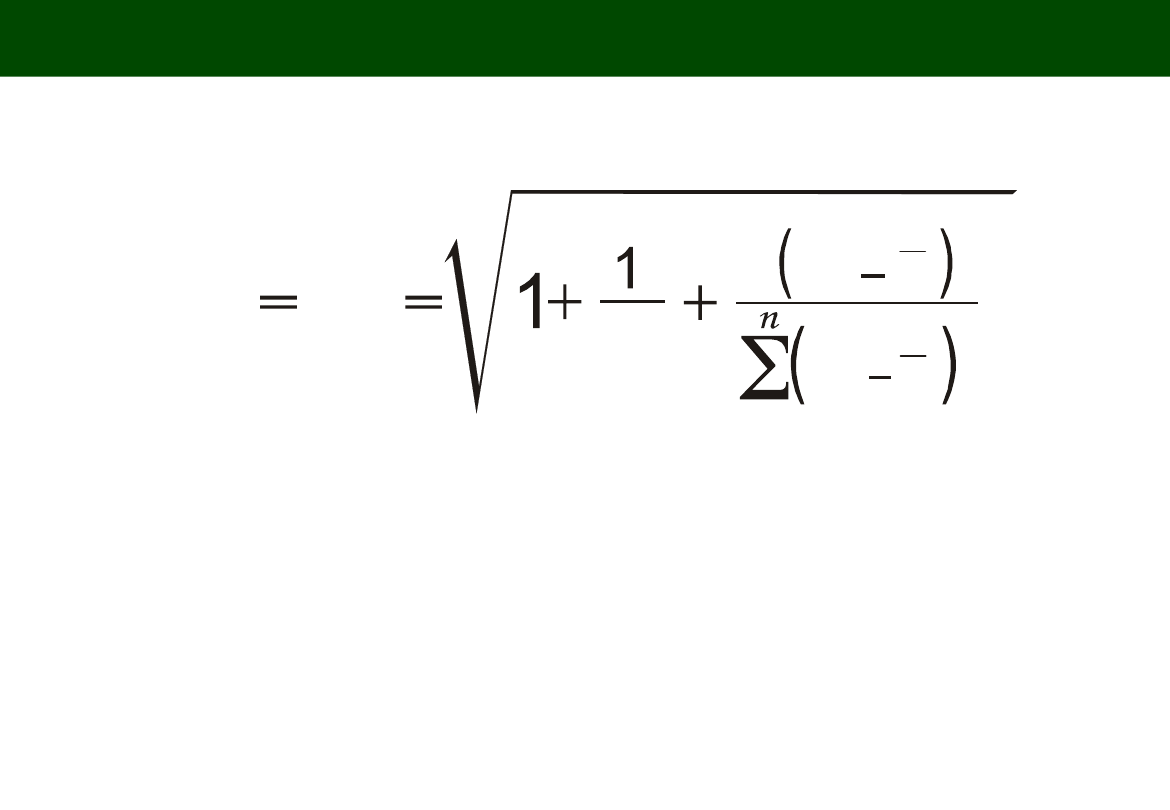
36

BŁĄD PREDYKCJI (PREDICTION ERROR)

Y 

p,n

 =  

wartość cechy y dla ustalonej wartości cechy x równej

  x 

k

i

x

x

x

x

S

y

S

k

p ,n

i = 1

2

2

2

n

37



W analizie regresji często się zdarza, że zmienna (y) zależy od więcej niż jednej 

zmiennej niezależnej (x), które ją objaśniają przyczynowo



Często w modelach posługujemy się układem wielu równań, a nie tylko jednym 

równaniem z wieloma zmiennymi



Jeśli do równania regresji włączymy kilka takich zmiennych powstaje model 

regresji wielorakiej

                 

Y = b + a

1 

x

1

 + a

2 

x

2

 + ... + a

k 

x

k

 + e

gdzie:

 

x

i

 – 

zmienne niezależne wpływające na

 

y

        

a

i

 - 

współczynniki regresji wiążące daną zmienną

 

x

i

 

ze zmienną zależną

 

y

        

b

 -  

wielkość stała 

         e

 – 

współczynnik losowy

REGRESJA WIELORAKA (MULTIPLES 
REGRESION)

38

ANALIZA REGRESJI WIELORAKIEJ (Multiple regression 

analysis)



Zadaniem analizy regresji wielorakiej jest:



Budowa właściwego równania (liniowego lub nieliniowego), jako modelu 

zjawiska



Oszacowanie wartości parametrów (oraz składnika losowego) równania przy 

pomocy MNK



Obliczenie standardowego błędu oszacowania parametrów wg wzoru RMSE 

oraz współczynników  korelacji, determinacji i regresji wielorakiej.

Uwaga:

 współczynnik regresji wielorakiej mierzy część zmienności zmiennej 

           zależnej (objaśnianej), która została wyjaśniona oddziaływaniem 

           zmiennych niezależnych (objaśniających) występujących w danym 

modelu 

           regresji

39

REGRESJA WIELORAKA - 

PRZYKŁAD



Firma Alka-Seltzer nasiliła kampanię promocji swoich produktów 

chemicznych. W ciągu 10 tygodni firma śledziła swoje wydatki na reklamę 

radiowo-telewizyjną (zmienna x

1 

) oraz wydatki na pokazy w sklepach 

(zmienna x

2 

).



Wielkość sprzedaży to zmienna zależna Y.



Analityk przeprowadził badania statystyczne modelu liniowej regresji 

wielorakiej wg równania: 

       Y = b +

 

a

1

x

1

 + a

2

x

2

 + e

wiążącego wielkość sprzedaży z dwiema zmiennymi.

40

REGRESJA WIELORAKA - PRZYKŁAD



Rezultat analiz to równanie regresji (miano w tys. $):

                       

Y = 47,2 + 1,6 x

1

 + 1,15 x

2

        a

1

 = 1,6 

oznacza, że każdy 1 000$ wydatków (w danym okresie) na 

reklamę radiowo-telewizyjną przynosi wzrost sprzedaży o 1 600$ w 

dłuższym okresie czasu

        a

2

 = 1,15 

oznacza, że każdy 1 000$ wydatków (w danym okresie) na 

pokazy w sklepach przynosi wzrost sprzedaży o 1 150$ w dłuższym 

okresie czasu

41

REGRESJA WIELORAKA - PROGNOZOWANIE



 Prognozowanie:

    x

1

 = 

10 000$ (wydatki na reklamę)

    x

2

 = 

5 000$ (wydatki na pokazy w sklepach)

                            

Y = b + a

1 

x

1

 + a

2 

x

2

    

            Y = 47,2 + 1,6 

x

 10 000 + 1,15 

x 

 5 000 = 68 

900$

           

42

REGRESJA NIELINIOWA (NONLINEAR 
REGRESSION)



W praktyce czasami między zmienną zależną (Y) a zmiennymi niezależnymi 

(x

i 

) zachodzą nieliniowe związki korelacyjne; najlepiej informuje o tym 

wykres korelacyjny (rozrzutu).



W wielu przypadkach model nieliniowy można przekształcić w liniowy 

(modele linearyzowane), który jest znacznie prostszy w analizie i 

oszacowaniu parametrów



Gdy to przekształcenie jest zbytnim uproszczeniem zjawiska, poszukujemy 

modeli wykładniczych, logarytmicznych, logistycznych, trygonometrycznych 

itd., które lepiej (bardziej adekwatnie do rzeczywistości) opisują badane 

zjawisko.

43

REGRESJA LINIOWA I NIELINIOWA



Jeżeli chcemy sprawdzić, czy linia prosta nadaje się do wyrównania szeregu 

(przy pomocy MNK), badamy pierwsze przyrosty wyrazów danego szeregu



Jeśli te przyrosty są mniej więcej równe, to dla wyrównania szeregu można 

(w pierwszej przymiarce) przyjąć linię prostą (regresję liniową)  wg równania  

                                    

y = a x + b



Jeśli przyrosty stale wzrastają lub maleją to należy posłużyć się wielomianem 
wyższego stopnia np. 

                                      

y = b + a x + c x

2



Jeśli przyrosty względne są stałe to można się posłużyć wzorem na funkcję 
wykładniczą:

                                      

y = a (1+p)

t

, 

 gdzie a=wartość wyjściowa, p=stopa przyrostu, t= czas

44

MODELE EKONOMETRYCZNE  (Econometric models)



Modele rozwoju gospodarki narodowej Langego,  Kaleckiego, Pajestki itd., 

w których interesują nas  głównie trendy



Modele koniunktury gospodarek lub branż, w których interesują nas cykle

i wahania sezonowe



Modele rynkowo-produktowe, w których interesują nas elastyczności cenowo-

dochodowe w kontekście popytu i podaży



W modelach tych wielkie znaczenie ma właściwe statystyczne oszacowanie 

parametrów równań. Wtedy modele te nabierają wartości analityczno-

prognostycznych

45

MODELE EKONOMETRYCZNE  (Econometric models)



W sferze finansów zaproponowano modelowanie zjawisk wysokiej 

częstotliwości; dotyczy to głównie kursów walut, kursów akcji, które 

zmieniają się niezmiernie często.  Do analizowania takich procesów powstała 

nowa klasa modeli o nazwie ARCH.



Jej twórca Robert Engle otrzymał za to Nagrodę Nobla w 2003 r.



W innych obszarach ekonomii, gdzie posługujemy się danymi o niskiej 

częstotliwości, a więc miesięcznych, kwartalnych czy rocznych 

zaproponowano nowe podejście modelowe, które złożyło się na teorię 

kointegracji.



Za nią Nagrodę Nobla otrzymał Clive Granger.

46

MODEL Langego



Model Oskara Langego:

STOPA PRZYROSTU PRODUKTU KRAJOWEGO

 = iloczyn stopy inwestycji 

i efektywności inwestycji 

                          

D/D = 

I

/D 

x

 D/

I

                                 

R = a 

x

 b

STOPA INWESTYCJI

 

= 

iloraz wydatków na inwestycje i produktu krajowego 

(udział inwestycji w produkcie krajowym)

 – 

a = I/D

EFEKTYWNOŚĆ INWESTYCJI

 

= iloraz przyrostu produktu i wydatków na 

inwestycje (przyrost produktu na 1 zł inwestycji)

 – 

b = D/I

47

PROBLEMY



 Dla polityka gospodarczego: 

    - ustalić stopę inwestycji



 Dla analityka-statystyka:

    - oszacować statystycznie (na podstawie długiego szeregu czasowego i 
prognoz) przy
      pomocy MNK współczynnik makroekonomicznej  efektywności   inwestycji 

Przykład:
   

a = 0,15 (15% produktu krajowego)

    b = 0,3

    R = a  b = 0,15  0,3= 0,045

    Przy założonym a = 0,15 i oszacowanej efektywności 0,3 produkt krajowy 
wzrasta
     o 4,5% rocznie

. 

.  

48

MODEL I. Kudryckiej

         

PKB

t 

= - 102,98 + 1,529 K

t 

+ 0,485 

Z

t

gdzie:  PKB

t 

- indeks dynamiki PKB w cenach stałych (1990=100)

               K

t 

-  indeks dynamiki majątku trwałego w cenach  stałych (1990=100)

               Z

t

 -  indeks dynamiki przeciętnej liczby pracowników (1990=100)

               

R

2 

= 97,69 !

49

 Historia modelu logistycznego sięga końca XIX w.: P.F. Verhulst i R.F.Pearl 

 Pierwsze zastosowania: prognoza wzrostu populacji

 Podstawy modelu: J. Berkson 1944 r. – „Application of the logistic function to 

bio-assay”

 Pełny model regresji logistycznej zastosowany po raz pierwszy w 1972 r. 

przez D.J. Finneya – „Probit analysis” 

REGRESJA LOGISTYCZNA  (LOGISTIC 

REGRESSION)

50

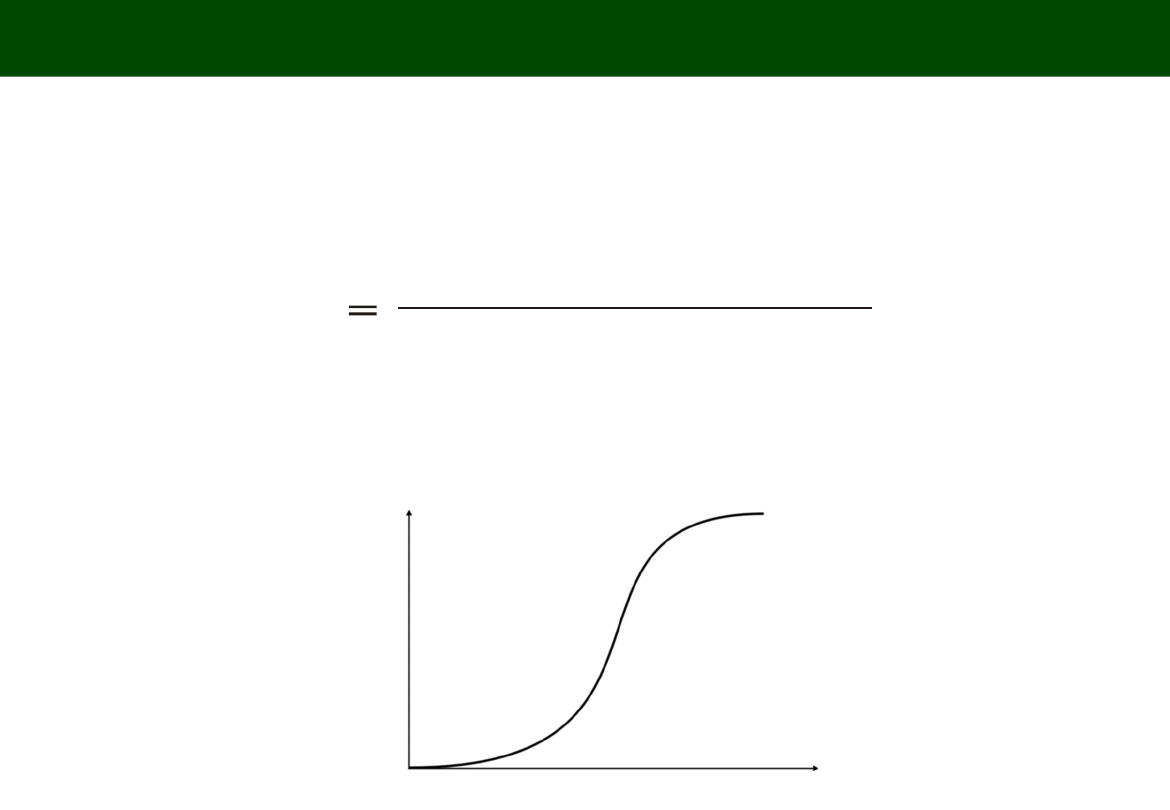
KRZYWA LOGISTYCZNA  (Logistic 
curve)

               Y

t

 = a/(1+b  e

–ct

)

    

gdzie:

 

Y

t 

 - 

wartość funkcji logistycznej w punkcie t

          a, b i c – 

to parametry funkcji logistycznej

         

 wartość

 a – 

odpowiada poziomowi nasycenia

          e – 

podstawa logarytmu naturalnego

          t - 

czas



Funkcja logistyczna wzrasta najpierw powoli, potem w tempie coraz bardziej 

przyspieszonym i osiągnąwszy punkt przegięcia tempo maleje i wreszcie 

niemal całkowicie ustaje zbliżając się do punktu nasycenia

.  

51

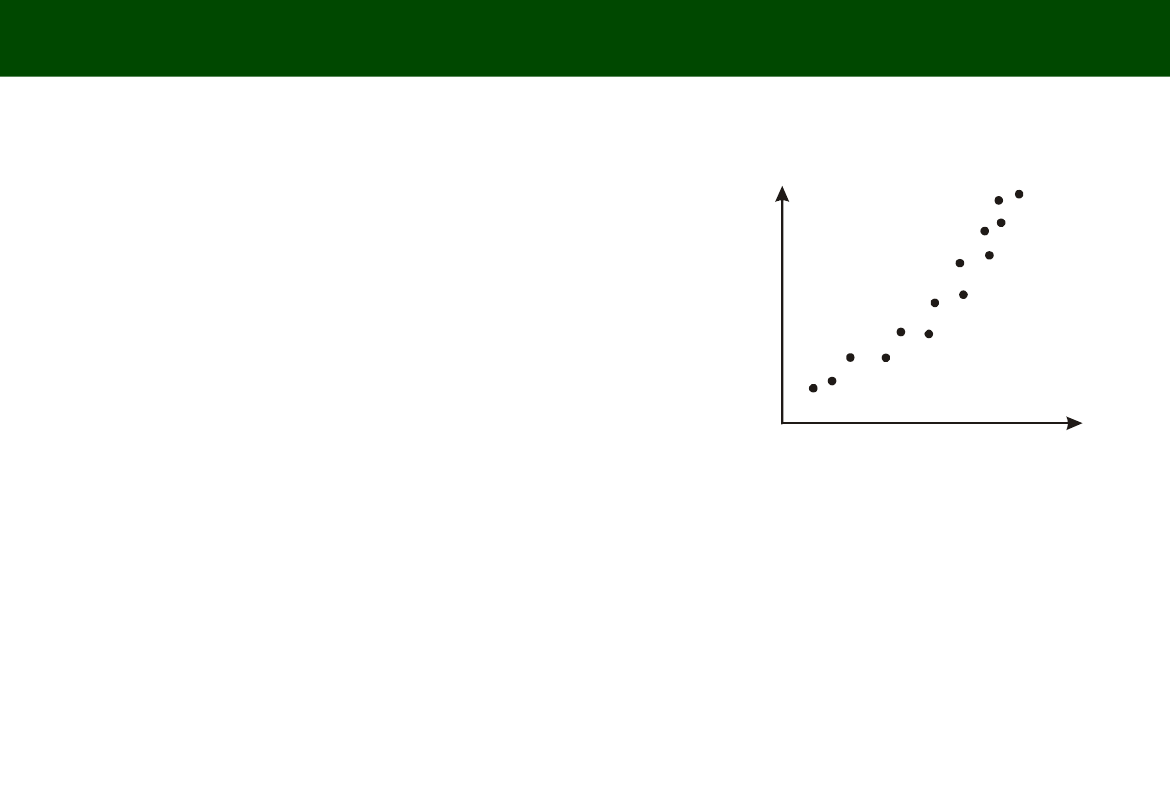
KRZYWA LOGISTYCZNA (Krzywa Gompertza) PRZYKŁAD

Tendencja rozwoju zasobów produkcyjnych linii automatycznie sterowanych

a = 8 000 – 

oszacowany poziom nasycenia, z pewnością zmieni się w miarę  

                        upływu czasu i za kilka lat wzrośnie

. 

8   0 0 0

-   0 , 3 0 6 7 3

t

1   +   6 8 , 1 2 7 8 6     e

t

Y

52

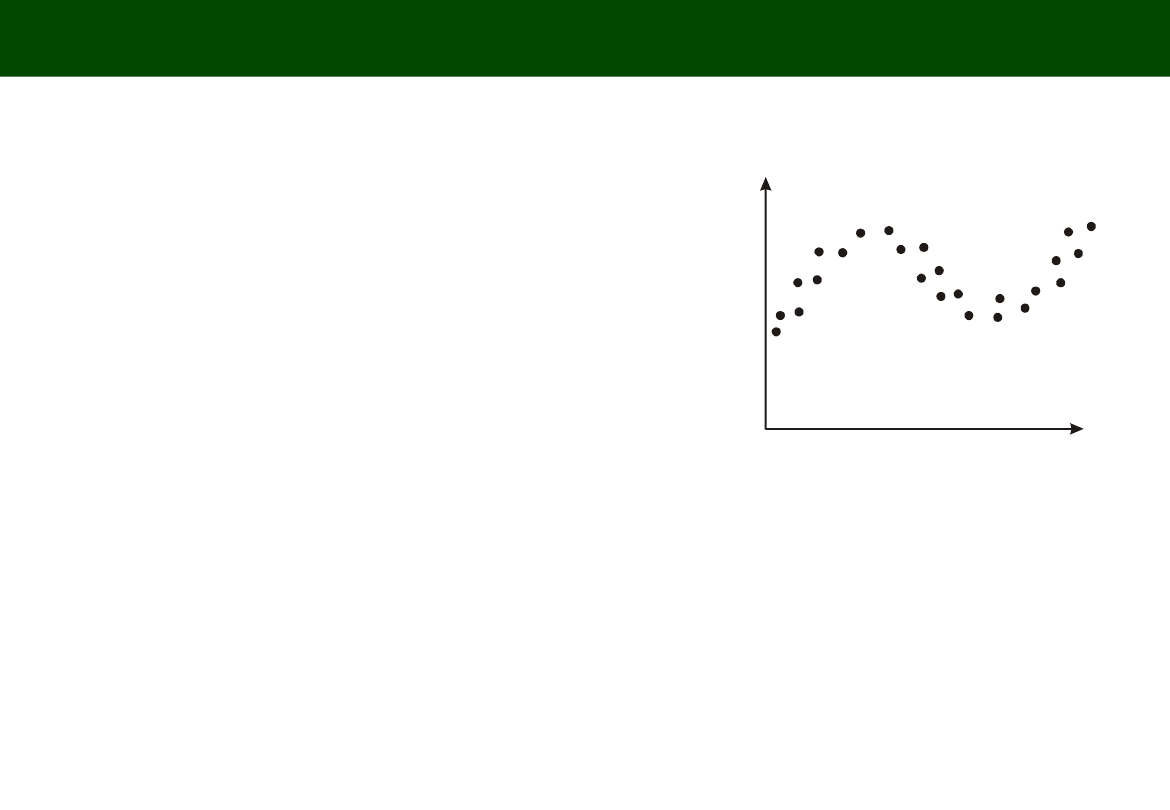
KRZYWA WYKŁADNICZA (Exponential regression)

                        Y

t

 = a  b

t

gdzie: 

Y

t

 

– wartość funkcji wykładniczej w punkcie 

t

a i b

 to parametry funkcji

a 

– to punkt wyjściowy (startu) funkcji wzrostu

b 

– współczynnik przyrostu np. PKB



 

Funkcja wykładnicza wzrasta w tempie stałym wg współczynnika b



  Przydatna w analizach i prognozowaniu procesów rozwojowych

.  

y

x

53

KRZYWA WYKŁADNICZA - PRZYKŁAD



Tendencja rozwoju w kraju x



Parametry (świat): 

a = 6 490 $ 

(PKB na 1 mieszkańca świata) 

b = 1,02 

(dynamika wzrostu)

Równanie: 

Y = 6 490   1,02

t



Parametry (Polska): 

a = 10 309 

$  PKB na 1 mieszkańca w 2002r.

b = 1,035 

(dynamika wzrostu)

Równanie:

  Y = 10 309  1,035

t

 

       dla t=10     Y=10 309  1,035

10

=10 309  

1,41=14 541

  Y = 10 309  1,05

t

 

         dla t=10     Y=10 309  1,05

10 

= 10 309  

1,63=16 792

. 

.  

.  

.  

.  

.  

.  

54

FUNKCJA TRYGONOMETRYCZNA (Sine curve)

   y

t

= a + b  sin(2



t

/p+c)

gdzie:

 

a, b, p i c

 - 

parametry równania

a

 – 

średnia w danym okresie

b

 – 

amplituda wahań liczona od średniej danego okresu

p

 – 

długość okresu

c – 

faza liczona od początku układu współrzędnych



Przydatna w analizach wahań sezonowych i cykli koniunkturalnych

.  

y

x

55

FUNKCJA PRODUKCJI (Production 
function)



Najpopularniejsza: funkcja produkcji typu Cobba-Douglasa, model 

dwuczynnikowy nieliniowy



Podstawowe narzędzie analizy rozwoju procesu produkcyjnego



Funkcja pozwala określić, jakiego poziomu produkcji można oczekiwać w 

określonym 

w przyszłości okresie, przy danych czynnikach produkcji: kapitale i pracy 

bądź przy różnych ich kombinacjach

56

FUNKCJA PRODUKCJI



Ogólna postać funkcji produkcji Cobba-Douglasa:

V

t

 – 

produkcja 

K

t

 – 

kapitał 

L

t

 - 

praca 

    a, b i c

 -

 

parametry równania, 

             d 

–

 

czynnik losowy

             t 

-

 

czas



Szacowanie parametrów i czynnika losowego wg MNK

lub          K

t

 – 

środki trwałe

                 L

t

 - 

środki obrotowe

. 

. 

. 

t

t

t

V   =   a     K       L       e

57

FUNKCJA PRODUKCJI

O postaci logarytmicznej typu Cobba-Douglasa w przemyśle 
przetwórczym:

         ln 

PKB 

P

t 

 = 0,225 + 0,173 ln ZP

t  

+ 0,817 ln MP

t

gdzie:

PKB 

P

t 

- 

wartość PKB wytworzona w przemyśle przetwórczym w cenach 2000 

r.

    ZP

t

 - 

przeciętna liczba zatrudnionych w przemyśle przetwórczym

   MP

t

 - 

wartość majątku trwałego w przemyśle przetwórczym w cenach 2000 

r.

        R

2

=94,59 !

58

PROBLEMY PRAKTYCZNE

 

Zbudować właściwy model:

 a. dobór czynników (zmiennych niezależnych)

 b. wybór postaci funkcji

 Szacowanie parametrów:

a. zebranie danych statystycznych

b. zastosowanie MNK

 Interpretacja modelu:

a. ograniczenia danych statystycznych

b. świadomość krzywej

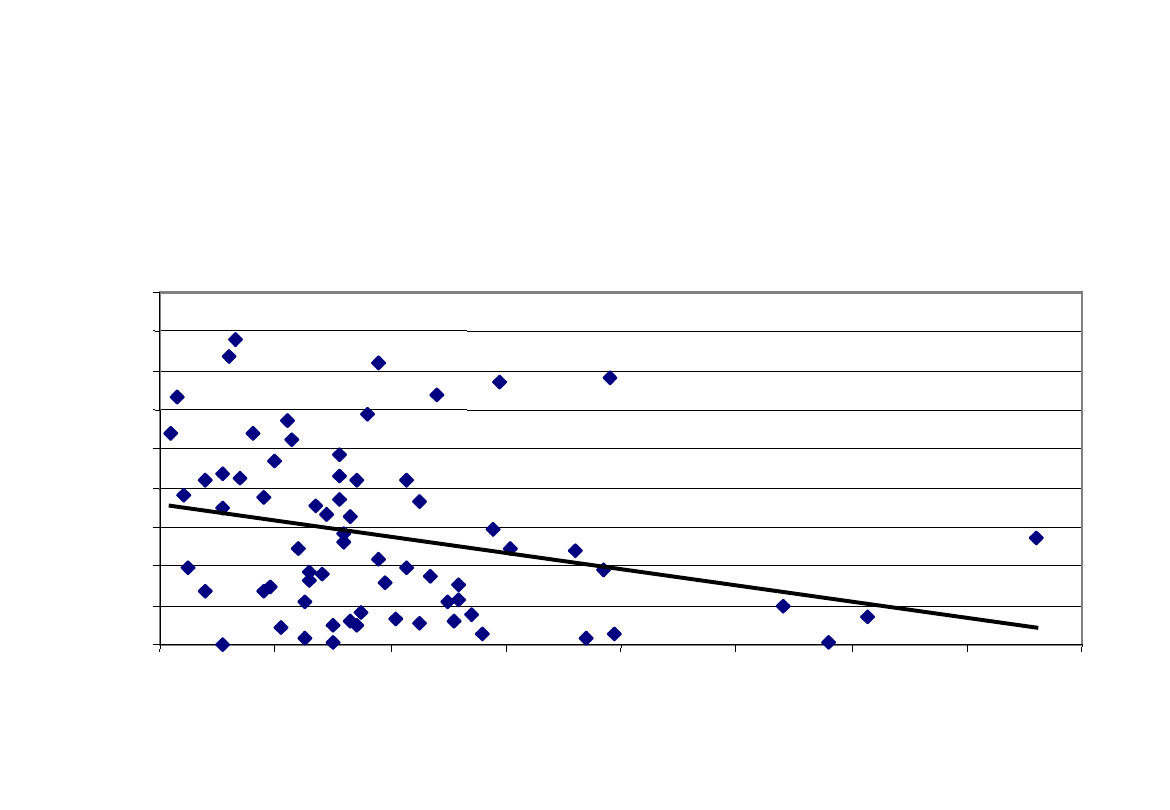
59

ŚWIAT: Korelacja między wskaźnikiem przedsiębiorczości i 

czasem niezbędnym na rozpoczęcie działalności

Time to start a business vs. # of SMEs

0

10

20

30

40

50

60

70

80

90

0

20

40

60

80

100

120

140

160

Time to start a business (days)

#

 o

f 

S

M

E

s 

p

e

r 

1

.0

0

0

 p

e

o

p

le

y = - 0,21x + 36,7

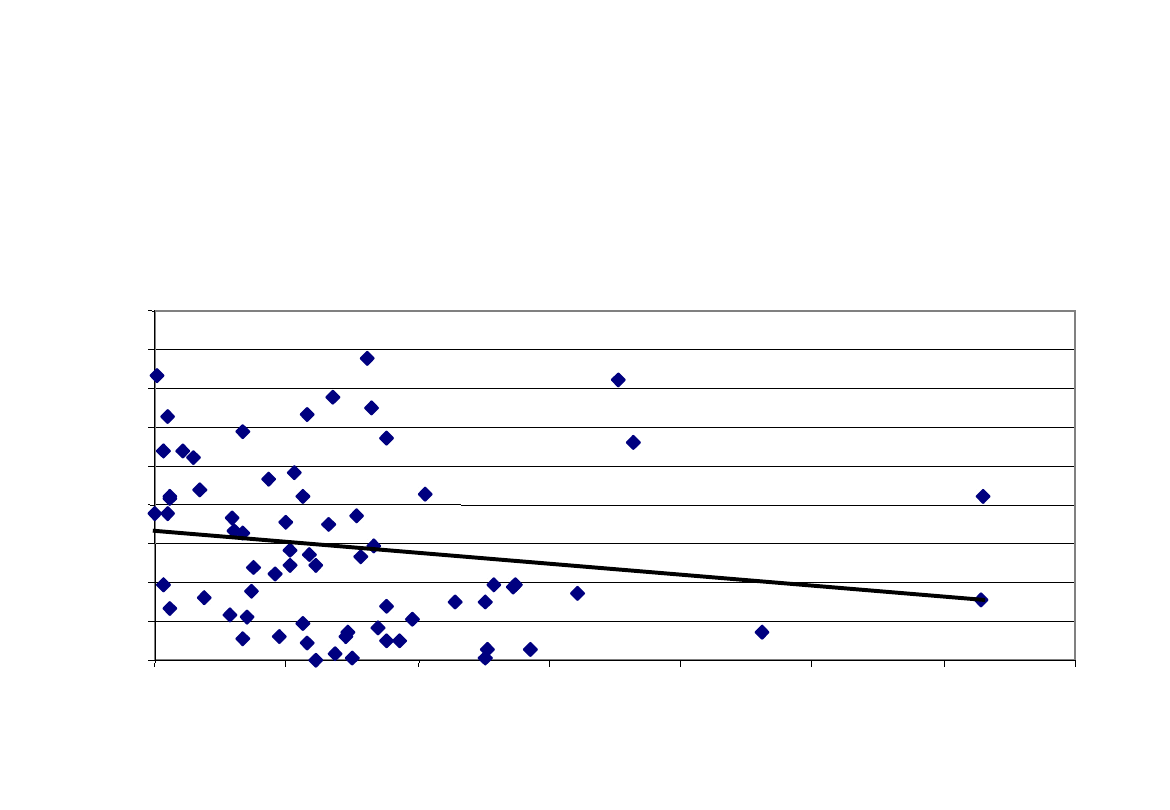
60

Cost to start a business vs. # of SMEs

0

10

20

30

40

50

60

70

80

90

0

10

20

30

40

50

60

70

Cost to start a business (% of income per capita)

#

 o

f 

S

M

E

s 

p

e

r 

1

.0

0

0

 p

e

o

p

le

ŚWIAT: Korelacja między wskaźnikiem przedsiębiorczości 

i nakładami niezbędnymi dla rozpoczęcia działalności

 

y = - 0,28x + 33,3

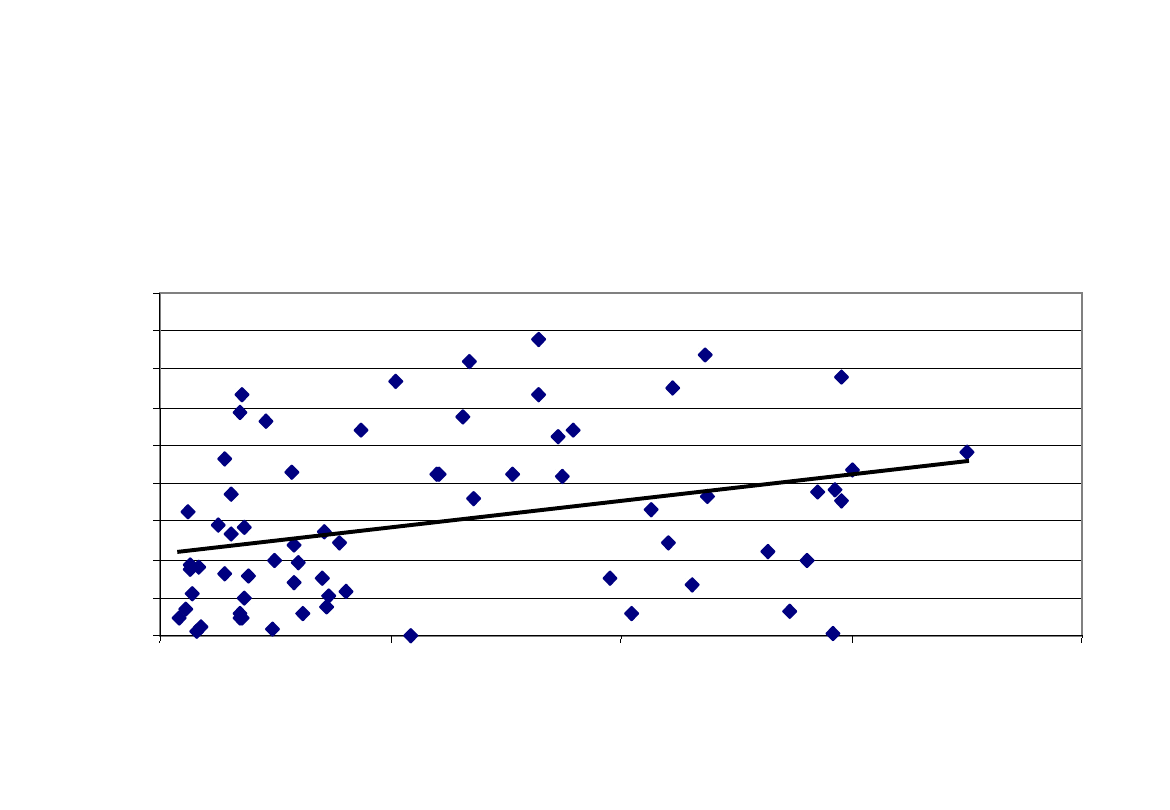
61

Private Credit vs. # of SMEs

0

10

20

30

40

50

60

70

80

90

0

50

100

150

200

Private credit as % of GDP

#

 o

f 

S

M

E

s 

p

e

r 

1

.0

0

0

 p

e

o

p

le

ŚWIAT: Korelacja między wskaźnikiem przedsiębiorczości 

i dostępnością do kredytu

y = 0,14x + 21,7

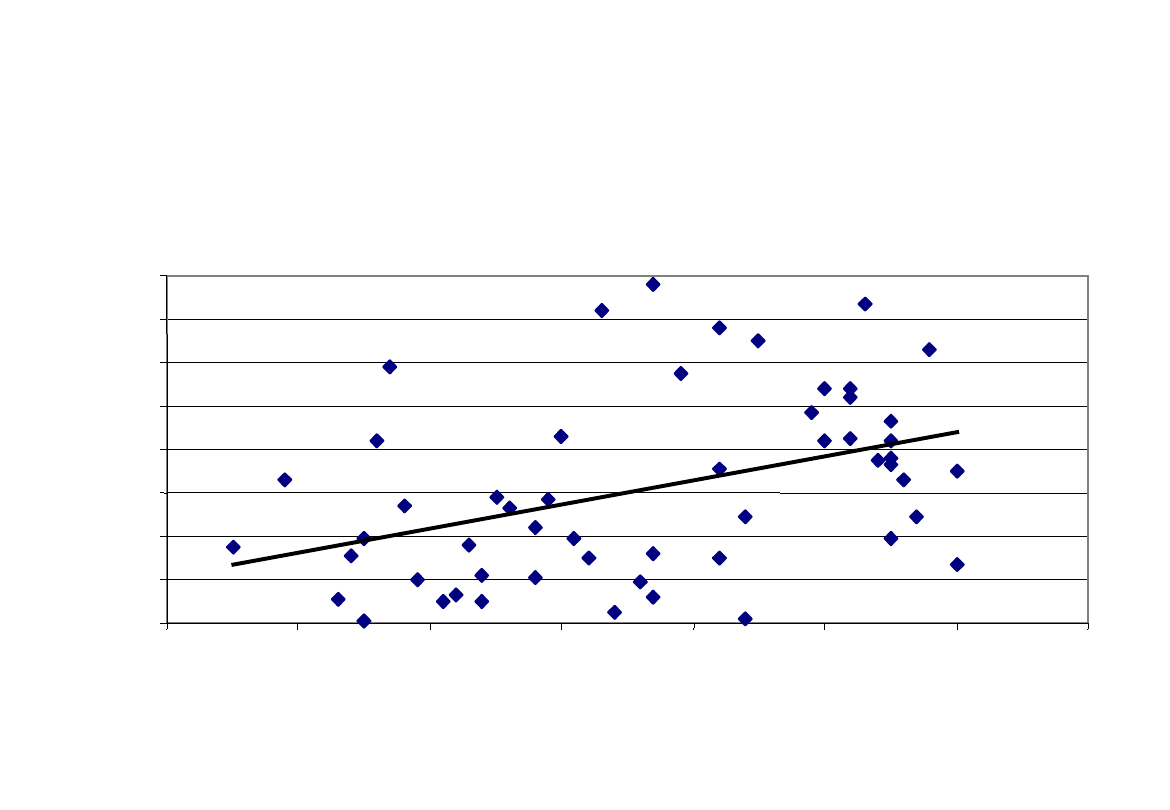
62

ŚWIAT: Korelacja między wskaźnikiem 

przedsiębiorczości 

i klimatem inwestycyjnym

Investment Climate vs. # of SMEs

0

10

20

30

40

50

60

70

80

15

25

35

45

55

65

75

85

Investment Climate Index

#

 o

f 

S

M

E

s 

p

e

r 

1

.0

0

0

 p

e

o

p

le

y = 0,45x + 11

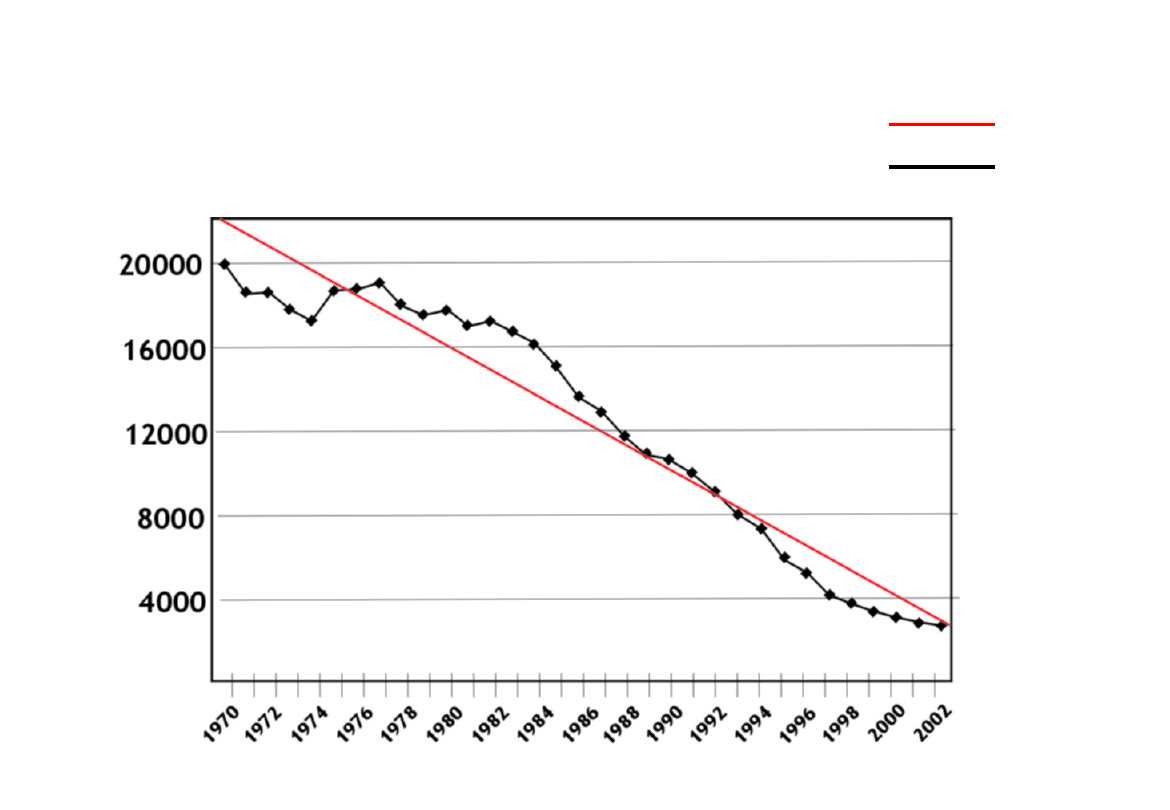
63

POLSKA: Tendencje zmian w umieralności niemowląt w latach 1970 

- 2002

Liczba zgonów

lata

y = -595,4 x + 22496,49

Wartości 
empiryczne

Wartości 
teoretyczne

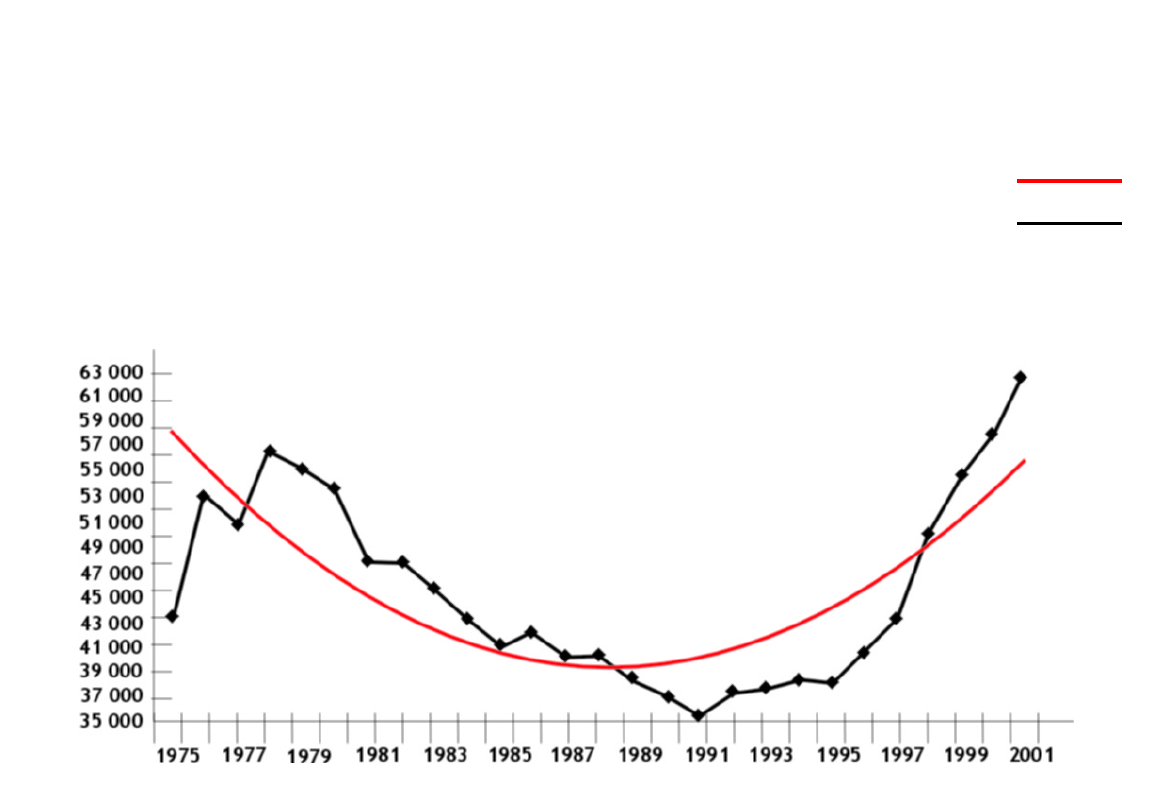
64

POLSKA: Przeobrażenia struktury społeczno-ekonomicznej ludności 

migrującej

w latach 1975-2001

Trend empiryczny i teoretyczny napływu ludności z wyższym 

wykształceniem

Liczba osób

lata

y = 104,94 t

2

 – 3044,7t + 61394

S

y 

=

 

5084,01

R

2

= 0,5894

Wartości 
empiryczne

Wartości 
teoretyczne

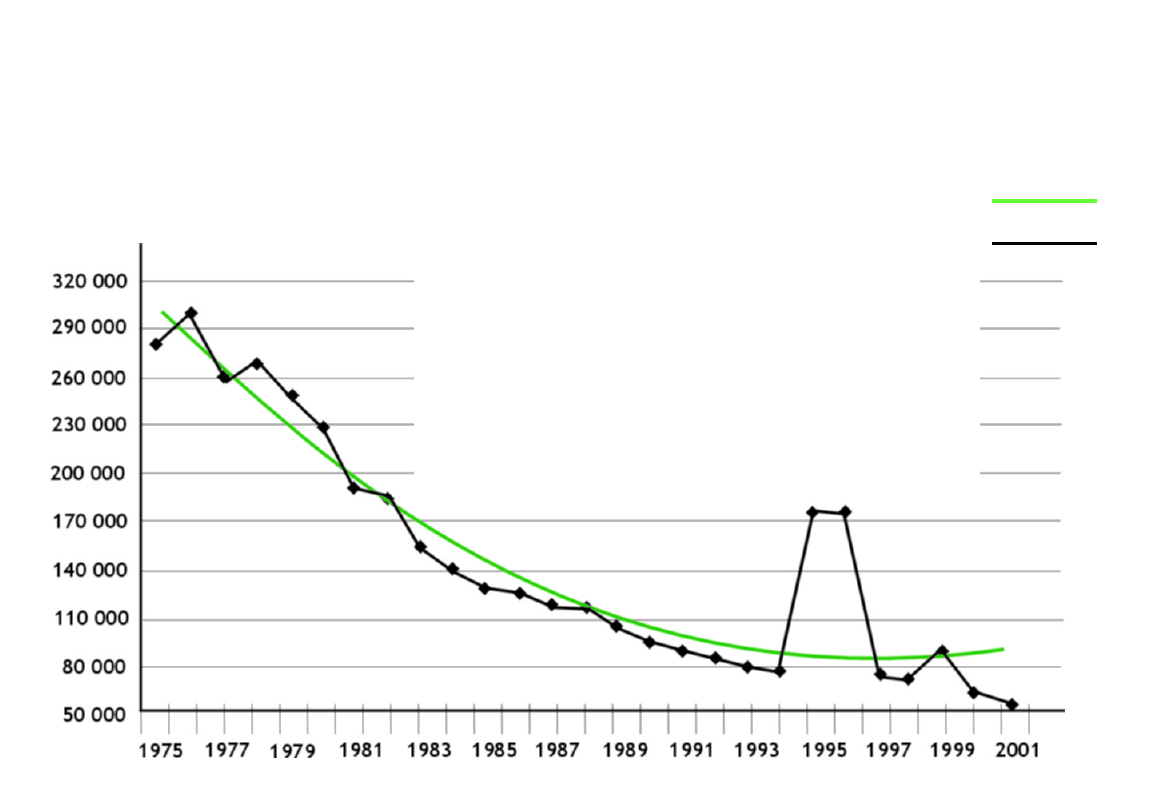
65

Liczba osób

lata

Wartości 
empiryczne

Wartości 
teoretyczne

POLSKA: Przeobrażenia struktury społeczno-ekonomicznej ludności 

migrującej

w latach 1975-2001

Trend empiryczny i teoretyczny napływu ludności z wykształceniem 

podstawowym i niepełnym podstawowym

y = 452,44 t

2

 – 20813t + 321383

S

y 

=

 

30418,55

R

2

= 0,849