Informacje podstawowe

 

Podstawowym źródłem informacji do dokładnego i bezpiecznego prowadzenia statku po morzu obok książek locji, spisów świateł itp. jest mapa morska, która zawiera szereg ważnych informacji potrzebnych nawigatorowi. Są to informacje o ukształtowaniu wybrzeża, dna morskiego, głębokościach, niebezpieczeństwach podwodnych np. wraki statków, portach, pływach i prądach, deklinacji magnetycznej, budowlach i innych obiektach nawigacyjnych na lądzie i wodzie jak latarnie morskie, latarniowce, stawy, pławy, o nakazanych trasach statków (ruty), o niebezpiecznych akwenach, łowiskach i wiele innych. Informacje te są zawsze przedstawiane za pomocą symboli, skrótów i znaków, które publikuje każdy wydawca map.
Na polskich jachtach do nawigacji używa się polskie i angielskie pomoce nawigacyjne. W/w symbole, znaki, skróty można znaleźć w angielskim wydaniu Admiralty Chart of Abbreviations

W zależności od przeznaczenia mapy nawigacyjne dzieli się na mapy generalne, mapy drogowe, mapy brzegowe, mapy podejściowe oraz plany.

W odróżnieniu od globusa żadna mapa nie jest wiernym obrazem Ziemi, ponieważ tak naprawdę nie można przedstawić bez zniekształceń powierzchni kuli na płaszczyźnie. Najlepszym rozwiązaniem było by używanie w nawigacji globusa, ale jest to niemożliwe gdyż uzyskanie odpowiedniej dokładności wymagałoby globusów o monstrualnych rozmiarach.

Zniekształcenie powierzchni Ziemi na mapie (płaszczyźnie) zależy od sposobu odwzorowania, czyli tzw. rzutu. Mapa przeznaczona do prowadzenia nawigacji musi być wykonana w takim rzucie, który zapewnia przede wszystkim wierność kątów. Czyli kierunki wykreślane na mapie powinny odpowiadać kierunkom rzeczywistym, linie dróg statków powinny być na mapie liniami prostymi, również sposób mierzenia odległości powinien być łatwy. Warunek ten może być spełniony, jeżeli południki i równoleżniki będą się przecinać pod kątem prostym (układ zwany siatką mapy), czyli taki jak w rzeczywistości na powierzchni kuli ziemskiej. Jedynie mapa wykonana w rzucie Merkatora spełnia te wymagania.

Twórcą tego rzutu był holenderski kartograf Gerard Kremer (Mercator). Pierwsza taka mapa powstała ok. roku 1569. Rzut Merkatora nie jest dosłownie rzutem geometrycznym, powstaje on, bowiem na drodze skomplikowanych obliczeń matematycznych.

Po wybraniu obszaru z globusa, który chcemy przedstawić na mapie, ograniczamy go równoleżnikami i południkami, tworząc w ten sposób siatkę mapy. Obszar ten rozcinamy wzdłuż południków i rozkładamy na płaszczyźnie (operacja podobna do obierania skórki pomarańczy). "Prostujemy" południki, czyli doprowadzamy do prostokątności siatki powstającej mapy. Jak widać następuje wówczas duże zniekształcenie powierzchni np. umowna wyspa w kształcie koła, leżąca bliżej bieguna północnego miałaby na tej mapie kształt spłaszczonej elipsy. Takie zniekształcenie powierzchni jest na mapie niedopuszczalne. Należy, więc dokonać ostatniej czynności polegającej na takim "rozciągnięciu" równoleżników, aby zlikwidować zniekształcenia powierzchni. Czyli osiągnąć wymaganą wierność kątów. Łatwo zauważyć, że im dalej od równika, to "rozciągnięcie" równoleżników musi być większe. Powoduje to charakterystyczną cechę mapy Merkatora - zmieniającą się wraz z szerokością geograficzną podziałkę mapy. Widać to wyraźnie na rysunku - obszar 45° szerokości geograficznej jest dwukrotnie większy od tego samego obszaru położonego na równiku. Dlatego też odmierzając odległość np. 1 Mm czyli 1' na południku, rozchylenie cyrkla nawigacyjnego będzie wzrastało jeśli będziemy zbliżać się ku biegunom.

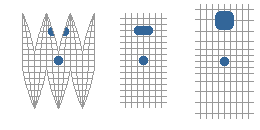
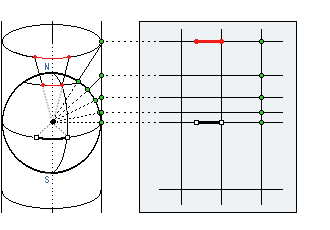
Rysunki przedstawiają schematyczne zasady powstania rzutu Merkatora.

Nanoszenie pozycji

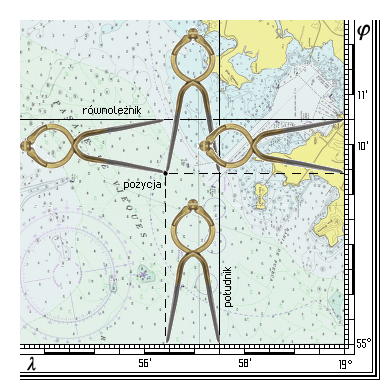
Chcąc nanieść pozycję na mapę lub odczytać współrzędne pozycji korzysta się z siatki geograficznej (południki i równoleżniki oznaczone w stopniach, minutach i sekundach). Określając szerokość geograficzną należy odmierzyć cyrklem nawigacyjnym odległość od pozycji do najbliższego równoleżnika, a następnie przenieść i odłożyć tę odległość od tego samego równoleżnika na bocznej prawej lub lewej ramce mapy. Długość geograficzną mierzy się podobnie z tą tylko różnicą, że odległość od pozycji mierzy się do najbliższego południka i odczytuje się na dolnej lub górnej ramce mapy.

Współrzędne przykładowej pozycji to:
φ = 55° 09,4' N ;   λ = 018° 56,4' E

Zwykle współrzędne odczytuje się z GPS-u i nanosi na mapę. Jest to rutynowa czynność i można się pomylić, co może się później okazać tragiczne w skutkach

Odczytywanie odległości

Chcąc odczytać odległość między dwoma punktami, należy przenieść tą odległość cyrklem nawigacyjnym na boczną, lewą lub prawą ramkę mapy i na tej samej szerokości geograficznej odczytać ilość minut, czyli mil morskich.

Na rysunku są dwie mierzone odległości które wynoszą 1,1 Mm. Należy pamiętać, że odległość, przebytą drogę mierzymy tylko na bocznych ramkach mapy, odmierzając zawsze na tej samej wysokości gdzie akurat jest odmierzana odległość

Wyznaczanie kursów

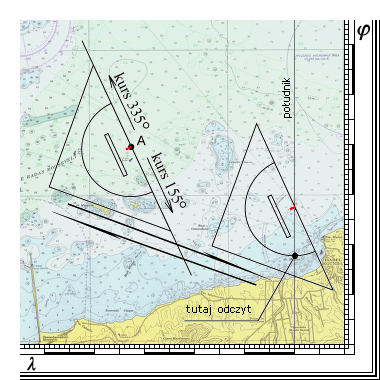
W nawigacji morskiej kierunek (kurs) wykreśla się na mapie, jako linię prostą przechodzącą przez dwa punkty. Ów kierunek określany jest za pomocą kąta zawartego między kierunkiem północnym a kierunkiem danej linii. Kursy i namiary wykreśla się za pomocą trójkąta nawigacyjnego. Dla ułatwienia należy go kłaść na mapę zawsze kątem prostym w dół, do siebie. Odczyt jest zawsze od strony kąta prostego. Na prawo od południka to kursy od 0 do 180° (na trójkącie skala zewnętrzna - zielona), na lewo od południka to kursy od 180° do 360° (na trójkącie skala wewnętrzna - czerwona).

Przykładowo gdy chcemy od punktu "A" wyznaczyć kurs 335° lub 155° , należy przyłożyć trójkąt nawigacyjny do najbliższego południka tak by przeszedł on przez środek przeciwprostokątnej (zaznaczony punkt, czerwona kreska na ekierce) i żądany kierunek na skali, w tym wypadku 155° lub 335° . Przeciwprostokątna tak ułożonego trójkąta wskazuje pożądany kierunek. Następnie należy przy pomocy linijki przesunąć równolegle trójkąt, tak by przeciwprostokątna przeszła przez punkt "A".

Pomiar odległości i szybkości ze statku.

Zarówno na lądzie jak i na morzu mamy do czynienia z pomiarem odległości oraz szybkości. Na lądzie jest to rzecz prosta - mamy tu odległość i szybkość, i nic więcej. Na morzu nie jest to takie proste. Mamy tutaj dwie odległości i dwie szybkości, a mianowicie "po wodzie" i "względem dna". Skąd to się bierze. Statek pływa po wodzie (to oczywiste) i tutaj mamy odległość po wodzie i szybkość po wodzie, natomiast nawigację prowadzimy na mapie (to też oczywiste) ale tutaj mamy, i odległość, i szybkość "po dnie". Zatem, rodzi się pytanie, czy te odległości się różnią między sobą i czy dotyczy to również szybkości. Oczywiście, że tak, czasami te różnice są bardzo duże.

Jak to się dzieje? Droga "po wodzie" jest zawsze dłuższa od drogi "na dnie", na którą głównie wpływa falowanie morza i sterowanie.

Dla nikogo nie jest tajemnicą, że na morzu są fale. Dla bardzo dużego uproszczenie pomińmy rodzaje fal i ich wymiary, cykliczność itd. Faktem jest, że statek prawie nigdy nie płynie dłuższy czas na morzu równym jak stół, wobec tego jego droga przebyta na zafalowanym morzu jest dużo dłuższa niż droga "przebyta" na mapie (równej jak stół).
Proszę spojrzeć na uproszczony rysunek:
Przyjmując długość fali 30 metrów (wysokość 3 metry) to:
1. Na odcinku ABC statek przebędzie 60 metrów, a
2. Na odcinku AXBYC około 62 metry
Jaka będzie różnica po przebyciu 100 Mm czyli 185200 metrów?

Tutaj mamy do czynienia z trzema czynnikami: dryf (wiatr), znos (prąd), umiejętność trzymania kursu przez sternika. Wskutek tych czynników statek nie płynie dokładnie po KDd, wobec tego KK jest często poprawiany co automatycznie wydłuża drogę.
Taka nawigacja trwa do momentu, kiedy nawigator określi swoją pozycję PO, ale i tak pozycję tą opisze tak: czas (licznik), stan logu (mianownik). Gdy nawigator ma dwie PO to odległość (dokładną i prawdziwą) między nimi może zdjąć z mapy i wówczas okazuje się, że odległość z mapy nie równa się wskazaniom logu, mimo to wpisuje stan logu. I tutaj powinien obliczyć Współczynnik Korekcyjny Logu (wkl).

Log nie rejestruje ani prędkości, ani przebytej odległości względem dna.

Nawigatora interesuje faktycznie (prawdziwa) przebyta droga i prawdziwa szybkość statku. Jak już wspomniano w poprzednich rozdziałach, przypomnijmy to:
1. Odległość na morzu mierzy się w milach morskich (Mm). 1 Mm = 1852,0 m
2. Szybkość na morzu mierzy się w węzłach (w). 1 w = 1 Mm / godz. (1 w = 1 Mm / h)

Do pomiaru, i odległości, i szybkości służy urządzenie, które nazywa się log.

Log zaburtowy typu Cherub III 1-śruba; 2-kabel do wskaźnika elektrycznego; 3-koło zamachowe; 4-licznik przebytej drogi. Na zdjęciu brak loglinki.

Tarcza licznika przebytej drogi logu Cherub III 1-wskazówka dziesiętnych części mili; 2-wskazówka mili; 3-wskazówka setek mil.

 

Rozróżniamy kilka rodzajów logów:

• Log ręczny - Bardzo dawno wyszedł z użycia, jednak do dzisiaj przetrwała forma "Logu butelkowego" używana z powodzeniem na jachtach i to z dobrym skutkiem. (tylko szybkość).

• Log burtowy - Używany na statkach o małej prędkości. Na burcie statku maluje się dwa znaczniki o znanej odległości między nimi - jest to "baza pomiarowa", wyskalowana w metrach. Pomiar wykonuje się następująco: rzuca się z tej burty, gdzie namalowana jest baza, jakiś dobrze widoczny, pływający przedmiot. Jak jest na trawersie pierwszego znaku włącza się stoper. Jak jest na trawersie drugiego znaku zatrzymuje się stoper i oblicza (tylko) szybkość statku w/g wzoru:
  Vs = 2L/t
  Vs - szybkość statku po wodzie [w]
  L - długość bazy w [m]
  t - czas jaki upłyną "przepłynięcia" przedmiotu miedzy znakami bazy [sek]
  
  

• Log mechaniczny - Walker'a - Najdłużej używany przez statki, prawie aż do wprowadzenia systemów hiperbolicznych do określania pozycji, które jednocześnie obliczały przebytą drogę jak i szybkość, a co najważniejsze względem dna. Zasada logu mechanicznego polega na zasadzie obrotu śruby w wodzie, której ruch jest przekazywany przez loglinę do licznika zegarowego. Log mechaniczny składa się z licznika zegarowego, logliny, koła zamachowego, śruby oraz podstawki (podkówki) do zamocowania zegara na burcie. Niektóre logi mechaniczne mają repetytory, które przekazują odczyt do kabiny nawigacyjnej. Przekaźnictwo zazwyczaj jest elektryczne. Koło zamachowe spełnia rolę regulatora obrotów i amortyzatora. Licznik zazwyczaj ma trzy wartości: setki mil, mile i kable. Logi te wskazywały li-tylko przebytą drogę bez szybkości.
  Długość logliny w zależności od Vs (szybkości statku) wynosi:
  Vs = 10w - 75 metrów
  Vs = 14w - 90 metrów
  Vs = 16w - 110 metrów
  Vs = 18w - 120 metrów

• Log elektryczny (Czernikijewa) - Działa na zasadzie przeliczania impulsów elektrycznych na szybkość (w) i przebytą odległość (Mm). Z dna statku wypuszcza się rurkę w której jest zminiaturyzowana śruba okrętowa. W zależności od szybkości statku obraca się ona wolniej lub szybciej przekazując te obroty w postaci impulsów do urządzenia przelicznikowego a potem na wskaźnik w kabinie nawigacyjnej.

• Log ciśnieniowy (Saal'a) - Działa na tej samej zasadzie co log elektryczny, z tym że ma tu zastosowanie ciśnienie jakie wytwarza się w rurce (rurka Pitot'a). Czym większe ciśnienie tym większa szybkość. Oczywiście log ten wskazuje również przebytą drogę przez statek.

Śruba okrętowa jako log - Śrubę okrętową, a właściwie jej obroty również wykorzystuje się jako log. Często szybkość w zależności od obrotów śruby określa się na mili pomiarowej, potem podaje się w dokumentacji, dla wiadomości nawigatorów.

Współczynnik korekcyjny logu
Wyrazem dokładnej pracy logu jest współczynnik korekcyjny logu. Jest to stosunek odległości prawdziwej w Mm, do odległości wskazanej przez log w Mm.

D - odległość prawdziwa, zdjęta z mapy między dwoma PO
OL1 - odczyt (stan) logu w PO1
OL2 - odczyt (stan) logu w PO2
WK - współczynnik korekcyjny logu
Log wskazuje za mało WK > 1
Log wskazuje za dużo WK < 1

Przykłady:
WK = 38 / 45 = 0,84 log wskazuje za dużo
WK = 50 / 40 = 1,25 log wskazuje za mało

Jednostki miar w nawigacji morskiej

W nawigacji umownie zakłada się, że Ziemia jest kulą geometryczną, której promień, zwany średnim promieniem Ziemi wynosi R = 6371,1km. Każde koło o promieniu równym promieniowi kuli ziemskiej, które swą płaszczyzną przechodzi przez środek Ziemi nazywa się kołem wielkim. Kołami wielkimi są zatem równik i wszystkie południki.

W nawigacji morskiej stosuje się jednostki miar które nie należą do układu SI. Podstawową jednostką długości używaną w nawigacji jest mila morska (Mm). Jedna mila morska jest równa długości jednej minuty koła wielkiego Ziemi, czyli wycinka łuku równego jednej minuty na którymkolwiek południku. Kabel (kbl) jest równy jednej dziesiątej mili morskiej.

1 Mm =

2 π × 6371100

= 1852 m

360 × 60

Jednostką prędkości używaną w nawigacji morskiej jest węzeł (w). Prędkość jednego węzła jest to prędkość jachtu pokonującego odległość jednej mili morskiej w czasie jednej godziny.

1 w =

1852 m

= 0,514 m/s

= 0,5 m/s

3600 s

Tercja południkowa to odległość 0,514m, którą w ciągu sekundy pokonuje jacht płynący z prędkością 1w.

Głębokość wody, wysokość przedmiotów na lądzie (np. latarnie morskie itp.) jest określana w metrach (m).
UWAGA: Jeszcze są w obiegu wydawnictwa, gdzie operuje się angielskim systemem miar, a mianowicie: sążnie, stopy, itd. Przed użyciem mapy do nawigacji, zaleca się dokładnie zapoznać z uwagami na niej umieszczonymi.

1 Mm = 1852m
1 kbl = 185,2m
1w = 1Mm/godz
1' (na południku, boczne ramki mapy) = 1Mm

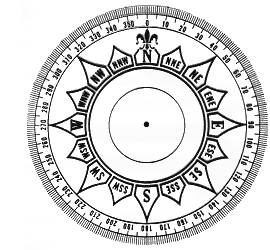
Kierunek na morzu jest to linia prosta zmierzająca w kierunku interesującego nas obiektu (namiar), albo miejsca do którego chcemy dotrzeć (kurs). Kierunek określany jest za pomocą kąta zawartego między kierunkiem północnym (czyli południkiem na mapie) a kierunkiem danej linii. Róża wiatrów czyli wyskalowana tarcza kompasu pozwala nam określać te kierunki. Wyróżnia się cztery systemy liczenia kierunków, pierwszy z nich jest powszechnie stosowany w nawigacji morskiej.

• System okrężny od N zgodnie z ruchem wskazówek zegara od 0 do 360°

• System połówkowy od widocznego bieguna czyli N lub S w kierunku E lub W, od 0 do 180° System stosowany najczęściej w astronawigacji.

• System ćwiartkowy od N lub S w kierunku E lub W, od 0 do 90°

• System rumbowy tarcza jest podzielona na 32 rumby, gdzie każdy rumb jest równy 1/32 kąta pełnego. Każdy rumb ma swoją nazwę.

Przykład: 225° (system okrężny) = N135°W (system połówkowy) = S45°W (system ćwiartkowy) = SW (system rumbowy).

System połówkowy od ćwiartkowego różni się zapisem. W połówkowym podaje się biegun (widoczny) zawsze z trzema cyframi. Tymczasem w systemie ćwiartkowym podajemy tylko dwie cyfry. 

Wszystkie kierunki na morzu określa się w stopniach i zawsze w tym samym kierunku - ze statku na dany obiekt, czy też pozycję. Tak odczytane w stopniach kierunki, potem przenosimy na mapę.

Matematyka w nawigacji i astronawigacji

Jeżeli staniesz twarzą w kierunku bieguna północnego to:
wszystko na lewo, czyli na 'West' [W] ma znak " - "
wszystko na prawo, czyli na 'East' [E] ma znak " + "

Analogicznie, jak staniesz na pokładzie twarzą w kierunku dziobu, to po lewej znak " - ", z prawej " + " . Potem obojętnie jak się obrócisz (chodzi tu o dziób jednostki), wszystko co z lewej będzie " - ", natomiast z prawej " + " .

Rozwiązanie II-go problemu loksodromy, trójkątem drogowym.

Dane:    φA = 57° 46'0 N	Szukane: KDd = ?
λA = 010° 44'0 E	d = ?
φB = 56° 00'0 N
λB = 003° 00'0 E

 

1. Obliczamy różnicę szerokości i długości: rφ = φB - φA = (+56° 00'0) - (+57° 46'0) = (-1° 46'0) = (-106'0) rλ = λB - λA = (+003° 00'0) - (+010° 44'0) = (-7° 44'0) = (-464'0) 2. Obliczamy φśr: 2. Obliczamy KDd: log rλ = 2,66652 log cos φśr = 9,73747 colog rφ = 7,97469 log tg KDd = 0,37868 KDd = S 67°5 W KDd = 247°5 Dlaczego w systemie ćwiartkowym mamy S i W ? Odpowiedź jest przy obliczeniu różnicy szerokości i długości. Tam przy rφ jest znak "-" oraz przy rλ jest znak "-". 4. Obliczamy d, czyli drogę: d = rφ sec KDd log rφ = 2,02531 log sec KDd = 0,41367 log d = 2,43898 d = 274,75 Mm 2. Odpowiedź: KDd = 245°5 d = 274,75 Mm

 

REASUMUJĄC. Trójkąt drogowy wykorzystujemy:

• Gdy droga nie przekracza 600 Mm.

• Przy małych rφ.

• Gdy loksodroma nie przechodzi przez równik.

 

Trójkąt Merkatora (Δ Merkatora)

Trójkąt Merkatora jest odpowiednikiem trójkąta loksodromicznego na mapie Merkatora.

Trójkąt Merkatora jest trójkątem prostokątnym o jednej przyprostokątnej równej różnicy długości geograficznej dwóch punktów leżących na mapie Merkatora i drugiej przyprostokątnej równej różnicy powiększonej szerokości geograficznej na mapie Merkatora.

Trójkąt Merkatora używa się przy obliczeniu φ_B ; λ_B lub KDd ; d przy pomocy powiększonej szerokości.
Δ loksodromicznemu odpowiada na mapie Δ Merkatora. Przy pomocy Δ Merkatora możemy obliczyć dokładnie KDd, natomiast "d" musimy obliczyć z Δ drogowego.

Elementy Δ Merkatora

rV = VB - VA	różnica powiększonej szerokości
rλ = λB - λA	różnica długości
AB	droga, powiększona odległość
KDd	kurs, kąt drogi nad dnem
rλ i rV	wyrażone w minutach długościowych

 

Przeciwprostokątna AB jest odległością powiększoną w takim samym stopniu jak powiększona szerokość.

Trójkąt Merkatora.

Porównanie Δ drogowego z Δ Merkatora.

Δ A B C - drogowy (nawigacyjny)
Δ A B' C' - Merkatora

Δ drogowy	Δ Merkatora	Zależności
rφ	rV	rV = rφ sec φśr
a	rλ	rλ = a sec φśr
d	AB'	AB' = d sec φśr
KDd	KDd

Δ drogowy jest Δ podobnym do Δ Merkatora, który powstał z przemnożenia Δ loksodromicznego o sec φ_śr

Powiększona szerokość [V]

Definicja "Powiększonej szerokości" jest jedna, ale zawarte w tej definicji różne określenia powodują, że mamy do czynienia z wieloma określeniami "powiększonej szerokości", na przykład:

• Powiększona szerokość nazywa się odległość na mapie Merkatora, liczona po linii południka, od równika do danego równoleżnika, jeżeli podziałka na równiku równa się jedności.

• Powiększona szerokość jest to oddalenie na mapie Merkatora równoleżnika danej szerokości od równika wyrażona w minutach długościowych.

Loksodroma i ortodroma

Linia biegnąca po powierzchni kuli ziemskiej, przecinająca południki geograficzne pod jednakowym kątem nazywana jest loksodromą. Jeżeli kąt ten będzie równy zeru to loksodroma pokrywać się będzie z jednym z południków geograficznych. Jeżeli kąt będzie równy 90° to loksodroma pokrywać się będzie z jednym z równoleżników geograficznych.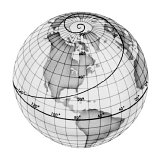
Można więc powiedzieć, że loksodromami są wszystkie południki i równoleżniki geograficzne. W pozostałych przypadkach loksodroma tworzy spiralną linię, która stopniowo zmierza do bieguna.

Wykreślona na mapie Merkatora linia prosta (kurs) zawsze przecina południki pod takim samym kątem, a więc jest loksodromą. Jacht utrzymujący taki kurs względem kompasu porusza się po loksodromie - czyli nie po najkrótszej drodze (za wyłączeniem kiedy loksodromą jest jeden z południków geograficznych lub równik).

Najkrótszą odległością na kuli ziemskiej pomiędzy dwoma punktami jest ortodroma, czyli odcinek koła wielkiego, który zawarty jest między tymi punktami. Ortodromami i loksodromami są jedynie równik i południki geograficzne. Wybierając żeglugę po ortodromie największe korzyści otrzymuje się przy pokonywaniu dużych odległości, powyżej 500Mm, z dala od równika, gdy punkt wyjścia i punkt docelowy leżą na zbliżonej szerokości geograficznej.

 

 

Wykreślona na mapie Merkatora ortodroma jest krzywą wybrzuszoną ku bliższemu biegunowi. Nawigując tradycyjnymi metodami żegluga po ortodromie staje się dość skomplikowana, co nie stanowi większego problemu jeżeli jacht wyposażony jest w odpowiednie urządzenia (np. C-MAP). Żegluga po ortodromie jest niczym innym jak żeglugą loksodromiczną, ponieważ odbywa się odcinkami loksodromy. A odpowiedni program komputerowy w połączeniu z odbiornikiem GPS może na bieżąco korygować kurs jachtu.

 

Żegluga po loksodromie

Żeglugę po loksodromie nazywamy żeglugę przy, której droga statku tworzy kąt prosty z południkami. W praktyce mamy do czynienia tylko z żeglugą po loksodromie, gdyż żegluga odcinkami ortodromy odbywa się po loksodromie.

Zasadnicze problemy żeglugi po loksodromie:

• Dane: φ_A ; λ_A ; KDd ; d (odległość do przebycia)
  Szukane: φ_B ; λ_B

• Dane: φ_A ; λ_A ; φ_B ; λ_B
  Szukane: KDd ; d (nad dnem)

Oba problemy obliczamy zwykle wykresowo na mapie. Zachodzą jednak wypadki, kiedy musimy je rozwiązać rachunkowo (przy dużych odległościach, braku odpowiedniej mapy, gdy skala mapy jest mała).
Przy rachunkowym rozwiązaniu istnieją dwa sposoby:

1. Za pomocą średniej szerokości (Trójkąt drogowy)

2. Za pomocą powiększonej szerokości (Trójkąt Merkatora)

Trójkąt loksodromiczny

Δ ABC jest trójkątem prostokątnym przy wierzchołku C; elementami tego trójkąta są:
Bok AC = rφ - różnica szerokości.
Bok CB = a - zboczenie nawigacyjne.
Bok AB = d - odcinek loksodromy.

CAB = KDd

Trójkąt ten nazywamy trójkątem loksodromicznym.
Trójkąt loksodromiczny jest to trójkąt na kuli ziemskiej utworzony przez: różnicę szerokości, zboczenie nawigacyjne, loksodromę i KDd.
Boki Δ loksodromicznego są wyrażone w milach morskich (Mm).
Δ loksodromiczny nie jest Δ płaskim ani sferycznym, stąd też mamy trudności w wyprowadzeniu zależności tego trójkąta.

Trójkąt loksodromiczny       Trójkąt drogowy (nawigacyjny)

Jeżeli trójkąt loksodromiczny ABC jest mały (droga nie przekracza 600 Mm) wówczas możemy go uważać za trójkąt płaski prostokątny o kącie prostym (90°) przy C, o tych samych elementach, które ma trójkąt loksodromiczny na kuli; taki trójkąt nazywamy drogowym.
Trójkąt drogowy jest to trójkąt płaski o tych samych elementach co trójkąt loksodromiczny na kuli.
Trójkąt drogowy nie istnieje. Służy on nam tylko do obliczeń.

Wyprowadzenie zależności między elementami trójkąta drogowego

---