2.3 Zadania do rozwiązania
2.3.1
Korzystając z twierdzenia o przesunięciu w dziedzinie zmiennej zespolonej wyznaczyć transformaty funkcji α t
a) f t
( ) = e cos t
ω
α t
b) f t
( ) = e sin t
ω
α t
c) f t
( ) = t ⋅ e
2.3.2
Wyznaczyć transformatę funkcji f t ( ) = t sin t
ω
2.3.3
Korzystając z twierdzenia o różniczkowaniu w dziedzinie zmiennej zespolonej wyznaczyć transformaty funkcji: 2
a) f ( t) = t b) f t
( ) = t cos t
ω
2
c) f t
( ) = t sin t
ω
3 −α t
d) f t
( ) = t e
2.3.4
Wyznaczyć transformatę funkcji: f ( t) = (
1 t −τ )
2.3.5
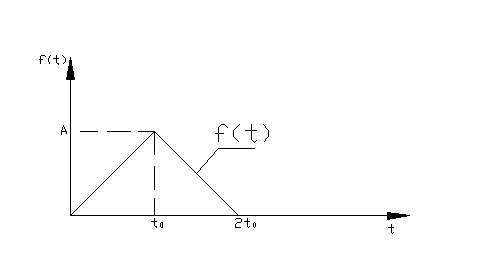
Wyznaczyć transformatę funkcji y(t) o przebiegu podanym na rysunku 2.3.1.
rys2.3.1
_________________________________________________
1 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
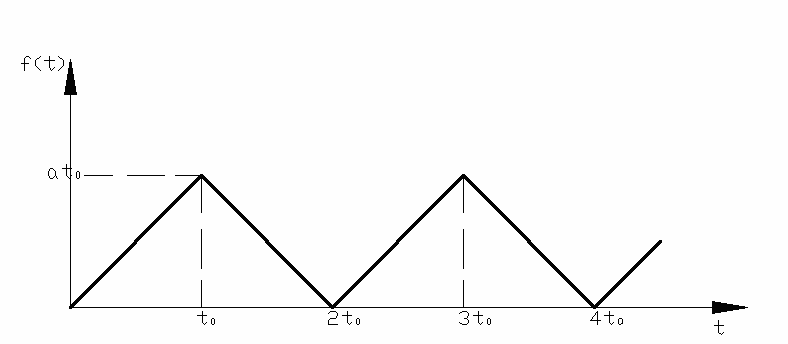
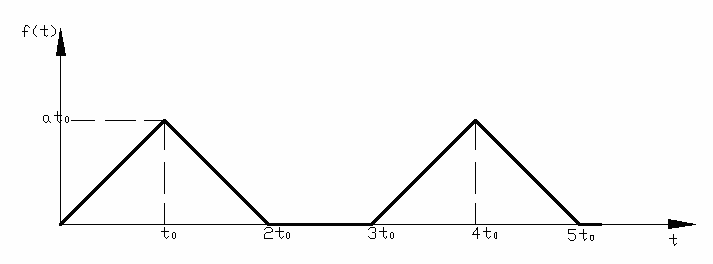
2.3.6
Wyznaczyć transformatę funkcji:
π
sin ω t, dla 0 < t < f t
( ) =
ω
,
0 dla 0 < t < π
ω
2.3.7
Wyznaczyć transformatę funkcji sin ω t 2.3.8
Wyznaczyć transformaty funkcji a)
b)
2.3.9
2
s
Wyznaczyć oryginał funkcji F ( s ) =
( s − 1)( s − 2 )( s − 3) _________________________________________________
2 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
2.3.10
Wyznaczyć oryginał funkcji
3
s + 2 s + 1
a) F ( s ) =
( s + 1)( s − 1)( s − 2 )( s + 3) 2
s
+ 1
b) F ( s ) =
s ( s + 1)( s − 2 ) 2.3.11
1
Wyznaczyć oryginał funkcji F ( s ) =
2
s ( s + 1)
2.3.12
2
s
+ 2 s + 1
Wyznaczyć oryginał funkcji F ( s ) =
2
3
s
( s + 3)
2.3.13
Wyznaczyć oryginał funkcji
s 20
a) F ( s ) =
2
3
( s + 1) ( s + 3) 1
b) F ( s ) =
3
s − 1
2.3.14
Rozwiązać
metodą
operatorową
Laplace’a
równanie:
2
d x + dx
4
+ 13 x = 0 dla warunków początkowych x(0)=0,x’(0)=0
2
dt
dt
2.3.15
Rozwiązać metodą operatorową Laplace’a równanie: 2
T y&
& + 2ζ T y& + y = x ( t )
, dla zerowych warunków początkowych y oraz y’, x(0)=1(t), 0<ζ <1
_________________________________________________
3 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
2.3.16
Rozwiązać równania
2
d x
dx
a)
+ 2
+ 4 x = 0 ,
x(0) = 1, x&( t) = -1
2
dt
dt
d 2 x
dx
b)
+ 10
+ 74 x = 28 sin 4 t , zerowe warunki początkowe dt 2
dt
c) x& ( t ) + x ( t ) = cos( t ) , x(0) = 4,
d)
−3 t
x&
& ( t ) + 4 x ( t ) = e
,
x(0) = 0, x&( t) =1
e) x&
& + 3 x& ( t ) + 2 x ( t ) = 2 , x(0) = 1, x&( t) =0
f) x&
& + x& ( t ) + 5 x ( t ) = 5 , x(0) = 3, x&( t) =0
_________________________________________________
4 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
Wyszukiwarka
Podobne podstrony:
Marecki, Zadanie do samodzielnego rozwiazania, Zadanie do samodzielnego rozwiązania
Zadania do samodzielnego rozwiązania 2
Zadania do samodzielnego rozwiązania ANOVA, nauka, EKONOMETRIA
5.3.1 Zadania do samodzielnego rozwiązania
Podział wyniku finansowego - zadanie do samodzielnego rozwiązania, Ekonomia, 3 semestr inne, rachunk
1.3.1 Zadania do samodzielnego rozwiązania
ZADANIA DO SAMODZIELNEGO ROZWIĄZANIA (1)
Ścinanie zadania do samodzielnego rozwiązania-2013
4.3.1 Zadania do samodzielnego rozwiązania
7.3.1 Zadania do samodzielnego rozwiązania
Klasa przekroju zadania do samodzielnego rozwiazania
Ścinanie zadania do samodzielnego rozwiązania 2013
Zginani
więcej podobnych podstron