Materia wspó finansowany ze !rodków Unii Europejskiej
w ramach Europejskiego Funduszu Spo ecznego
Centralna
Komisja
Egzaminacyjna
Próbny egzamin maturalny z matematyki
listopad 2009
Klucz odpowiedzi do zada zamkni!tych
i przyk"adowe rozwi#zania zada otwartych
2
Klucz odpowiedzi do zada zamkni!tych
Nr zadania
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Odpowied$ A C
B
B
C
A
B
A
D
A
C
B
B
C
C
D
A
D
C
D
A
A
D
D
A
Przyk"adowe rozwi#zania zada otwartych
Zadanie 26. (2 punkty)
Rozwi"# nierówno!$
2
3
2
0
x
x
! " .
Rozwi#zanie:
Obliczam miejsca zerowe funkcji kwadratowej
# $
2
3
2
f x
x
x
%
! :
# $
2
3
4 1 2
9 8 1
& %
' ' % %
1
& %
1
3 1
1
2
x
%
%
2
3 1
2
2
x
!
%
%
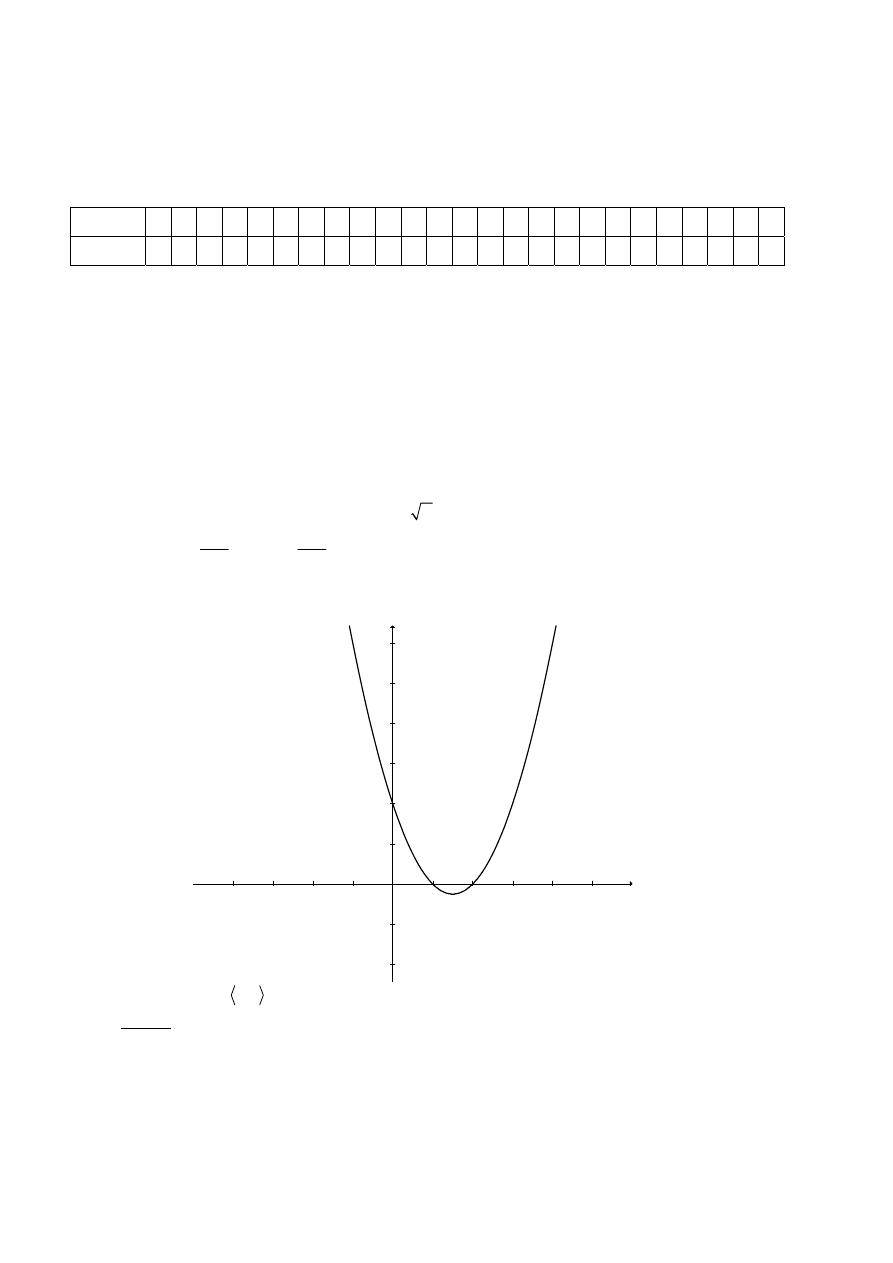
Rysuj% fragment wykresu funkcji kwadratowej f i na jego podstawie odczytuj%
rozwi"zanie nierówno!ci:
-4
-3
-2
-1
1
2
3
4
5
-2
-1
1
2
3
4
5
6
x
y
Odpowied&:
1, 2 .
x (
Uwaga: Mo#na przedstawi$ funkcj% f w postaci
# $ #
$#
$
1
2
f x
x
x
%
i odczyta$
rozwi"zanie nierówno!ci.
3
Zadanie 27. (2 punkty)
Rozwi"# równanie
3
2
7
2
14
0
x
x
x
!
% .
Rozwi#zanie:
Stosuj% metod% grupowania, by przedstawi$ lew" stron% równania w postaci iloczynowej:
#
$ #
$
#
$
#
$
3
2
2
2
7
2
14
7
2
7
2
7
x
x
x
x
x
x
x
x
!
%
!
%
!
.
Z równania
#
$
#
$
2
2
7
0
x
x
!
% otrzymujemy, #e
2
2
0
x ! % lub
7
0
x %
.
Równanie
2
2
0
x ! %
nie ma rozwi"za'. Rozwi"zaniem równania
7
0
x %
jest liczba 7.
Odpowied&: Jedynym rozwi"zaniem jest
7
%
x
.
Zadanie 28. (2 punkty)
W uk adzie wspó rz%dnych na p aszczy&nie punkty
#
$
2, 5
A %
i
#
$
C
6, 7
%
s" przeciwleg ymi
wierzcho kami kwadratu
ABCD. Wyznacz równanie prostej BD.
Rozwi#zanie:
Obliczam wspó czynnik kierunkowy prostej
AC:
7 5
1
6 2
2
AC
a
%
%
, a nast%pnie wyznaczam
wspó czynnik kierunkowy prostej
BD prostopad ej do AC:
2
BD
a
% .
Wyznaczam wspó rz%dne !rodka
S odcinka AC:
# $
2 6 5 7
,
4, 6
2
2
S
!
!
)
*
%
%
+
,
-
.
i wyznaczam
równanie prostej o wspó czynniku kierunkowym 2
, przechodz"cej przez punkt S.
Odpowied&:
2
14
y
x
%
!
.
Zadanie 29. (2 punkty)
K"t jest ostry i
4
tg
3
/
% . Oblicz
/
/
cos
sin
!
.
Rozwi#zanie:
I sposób rozwi"zania:
Z definicji funkcji tangens mamy
sin
4
cos
3
/
/
% , zatem
4
sin
cos
3
/
/
%
. Podstawiam t% równo!$
do to#samo!ci
2
2
sin
cos
1
/
/
!
% i otrzymuj%
2
2
4
cos
cos
1
3
/
/
)
* !
%
+
,
-
.
, a st"d
2
9
cos
25
/
%
.
Zatem
5
3
cos
%
/
lub
5
3
cos
%
/
. Ujemny wynik odrzucam, poniewa# zgodnie z warunkami
zadania k"t
/ jest k"tem ostrym. Obliczam warto!ci funkcji
4
sin
5
/
% , a nast%pnie warto!$
wyra#enia
4
3
7
sin
cos
5
5
5
/
/
!
% ! % .
Odpowied&:
5
7
cos
sin
%
!
/
/
.
4
II sposób rozwi"zania:
Rysuj% trójk"t prostok"tny, w którym oznaczam przyprostok"tne 3x i 4x oraz
zaznaczam k"t ostry
/
tak, aby
4
tg
3
/
% .
4x
3x
Z twierdzenia Pitagorasa obliczam d ugo!$ przeciwprostok"tnej:
# $ # $
2
2
2
4
3
25
x
x
x
!
%
.
Zatem przeciwprostok"tna ma d ugo!$ 5x . Obliczam warto!ci funkcji
4
sin
5
/
%
i
3
cos
5
/
% . St"d
4
3
7
sin
cos
5
5
5
/
/
!
% ! % .
Odpowied&:
5
7
cos
sin
%
!
/
/
.
Zadanie 30. (2 punkty)
Wyka#, #e dla ka#dego m ci"g
,
.
*
+
-
)
!
!
!
12
9
,
6
3
,
4
1
m
m
m
jest arytmetyczny.
Rozwi#zanie:
I sposób rozwi"zania:
Wystarczy sprawdzi$, #e zachodzi nast%puj"cy zwi"zek mi%dzy s"siednimi wyrazami
ci"gu:
1
1
2
n
n
n
a
a
a
!
!
%
.
Mamy
1
1
4
m
a
!
%
,
2
3
6
m
a
!
%
,
3
9
12
m
a
!
%
.
Zatem
1
3
2
1
9
3
3
9
4
12
3
4
12
2
2
24
24
6
m
m
a
a
m
m
m
m
a
!
!
!
!
! ! !
!
!
%
%
%
%
%
.
St"d wynika, #e ci"g
,
.
*
+
-
)
!
!
!
12
9
,
6
3
,
4
1
m
m
m
jest arytmetyczny dla ka#dego
m.
II sposób rozwi"zania:
Mamy
1
1
4
m
a
!
%
,
2
3
6
m
a
!
%
,
3
9
12
m
a
!
%
.
Wystarczy sprawdzi$, #e
2
1
3
2
a
a
a
a
%
.
Obliczamy:
6
3
12
9
4
1
6
3
!
!
%
!
!
m
m
m
m
12
6
2
9
12
3
3
6
2
!
%
!
m
m
m
m
12
3
12
3
!
%
!
m
m
5
Zadanie 31. (2 punkty)
Trójk"ty
ABC i CDE s" równoboczne. Punkty A, C i E le#" na jednej prostej. Punkty K, L i M
s" !rodkami odcinków
AC, CE i BD (zobacz rysunek). Wyka#, #e punkty K, L i M
s" wierzcho kami trójk"ta równobocznego.
Rozwi#zanie:
Z warunków zadania wynika, #e
60
BAC
DCE
%
%
0
, wi%c odcinki
AB i CD s"
równoleg e. Czworok"t
ACDB jest trapezem. Odcinek KM "czy !rodki boków
nierównoleg ych w tym trapezie, wi%c jest równoleg y do jego podstaw. Wobec tego
60
MKL %
0
.
Podobnie
60
ACB
CED
%
%
0
, wi%c odcinki
BC i DE s" równoleg e. Czworok"t BCED
jest trapezem. Odcinek
ML "czy !rodki boków nierównoleg ych w tym trapezie, wi%c jest
równoleg y do jego podstaw. Wobec tego
60
KLM %
0
.
Odpowied&: Dwa k"ty trójk"ta
KLM maj" miar% 600 , zatem jest to trójk"t równoboczny.
Zadanie 32. (5 punktów)
Ucze' przeczyta ksi"#k% licz"c" 480 stron, przy czym ka#dego dnia czyta jednakow" liczb%
stron. Gdyby czyta ka#dego dnia o 8 stron wi%cej, to przeczyta by t% ksi"#k% o 3 dni
wcze!niej. Oblicz, ile dni ucze' czyta t% ksi"#k%.
Rozwi#zanie:
Oznaczam:
x – liczba stron przeczytanych ka#dego dnia, y – liczba dni.
Zapisuj% i rozwi"zuj% uk ad równa':
#
$ #
$
480
8
3
480
x y
x
y
' %
12
3
! '
%
24
Z pierwszego równania mamy
480
x
y
%
, zatem
#
$
480
8
3
480
y
y
y
)
*
!
'
%
'
+
,
-
.
#
$#
$
480 8
3
480
y
y
y
!
%
Po uproszczeniu otrzymuj% równanie
2
3
180
0
y
y
% .
Rozwi"zaniem równania s" liczby: –12 oraz 15. Odrzucam ujemn" liczb% dni.
Odpowied&: Ucze' przeczyta ksi"#k% w ci"gu 15 dni.
A
B
C
D
E
K
L
M
6
Zadanie 33. (4 punkty)
Punkty
# $
2, 0
A %
i
#
$
12, 0
B %
s" wierzcho kami trójk"ta prostok"tnego ABC
o przeciwprostok"tnej AB. Wierzcho ek C le#y na prostej o równaniu
y
x
% . Oblicz
wspó rz%dne punktu
C.
Rozwi#zanie:
I sposób rozwi"zania:
Punkt
C le#y na prostej o równaniu
x
y %
i na okr%gu, którego !rodkiem jest !rodek
przeciwprostok"tnej, a promie' jest równy po owie d ugo!ci tej przeciwprostok"tnej.
Obliczam d ugo!$ przeciwprostok"tnej
AB:
#
$ #
$
10
0
0
2
12
2
2
%
!
%
AB
.
Wyznaczam wspó rz%dne !rodka przeciwprostok"tnej:
# $
7, 0
S %
.
Zapisuj% równanie okr%gu:
#
$
25
7
2
2
%
!
y
x
Rozwi"zuj% uk ad równa'
#
$
4
3
1
%
!
%
25
7
2
2
y
x
x
y
Otrzymuj% równanie z jedn" niewiadom":
0
12
7
2
%
!
x
x
Rozwi"zaniem tego równania s" liczby:
1
4
x % ,
2
3
x % .
Odpowied&: Warunki zadania spe niaj" dwa punkty:
# $
4
,
4
%
C
oraz
# $
3, 3
C %
.
II sposób rozwi"zania:
Oznaczmy wspó rz%dne punktu C przez
#
$
,
x y
. Wtedy
#
$ #
$
10
0
0
2
12
2
2
%
!
%
AB
,
#
$ #
$
2
2
2
0
AC
x
y
%
!
,
#
$ #
$
2
2
12
0
BC
x
y
%
!
.
Trójk"t ABC jest prostok"tny, wi%c spe niona jest równo!$
2
2
2
AB
BC
AC
%
!
, czyli
#
$
#
$
2
2
2
2
2
2
12
10
x
y
x
y
!
!
!
%
.
Punkt C le#y te# na prostej o równaniu
x
y %
, zatem aby obliczy$ jego wspó rz%dne, nale#y
rozwi"za$ uk ad równa':
#
$
#
$
4
3
1
%
%
!
!
!
x
y
y
x
y
x
2
2
2
2
2
10
12
2
2
2
2
2
2
4
4
24
144
100
4
28
48
0
x
x
x
x
x
x
x
x
! !
!
!
!
%
!
%
0
12
7
2
%
!
x
x
1
2
4,
3
x
x
%
%
Odpowied&: Warunki zadania spe niaj" dwa punkty:
# $
4
,
4
%
C
oraz
# $
3, 3
C %
.
7
Zadanie 34. (4 punkty)
Pole trójk"ta prostok"tnego jest równe
2
60 cm . Jedna przyprostok"tna jest o 7 cm d u#sza
od drugiej. Oblicz d ugo!$ przeciwprostok"tnej tego trójk"ta.
Oznaczam: a, b – d ugo!ci przyprostok"tnych danego trójk"ta.
Zapisuj% uk ad równa'
7
1
60
2
a
b
a b
% !
1
2
3
' %
24
Otrzymuj% równanie z jedn" niewiadom"
#
$
1
7
60
2
b
b
!
%
, którego pierwiastkami s" liczby
8
b % oraz
15
b %
.
Odrzucam ujemny pierwiastek, gdy# b jest d ugo!ci" odcinka. Zatem
8
b %
,
8 7 15
a % ! %
.
Teraz obliczam d ugo!$ przeciwprostok"tnej
2
2
2
2
8
15
289
17
c
a
b
%
!
%
!
%
%
.
Odpowied&: Przeciwprostok"tna ma d ugo!$ 17 cm.