1
Rozwiązywanie równań nieliniowych i ich układów.
Wyznaczanie zer wielomianów.
Plan wykładu:
1. Wyznaczanie pojedynczych pierwiastków rzeczywistych
równań nieliniowych metodami
a) połowienia (bisekcji)
b) Regula Falsi
c) siecznych
d) Newtona
2. Wyznaczanie zer wielokrotnych
a) modyfikacja metod przy znajomości krotności pierwiastka
b) modyfikacja metod siecznych i Newtona dla przypadku ogólnego
c) Proces
2
Aitkena
3. Rozwiązywanie układów równań nieliniowych
4. Wyznaczanie zer rzeczywistych i zespolonych wielomianów
a) metoda Lehmera-Schura
b) metoda Łobaczewskiego
c) dzielenie wielomianów
d) metoda iterowanego dzielenia
2
Równanie nieliniowe z jedną niewiadomą
Poszukujemy zera rzeczywistego ciągłej
funkcji f(x), czyli szukamy rozwiązania równania:
f (x) = 0
, x 2 fx
1
; x
2
; : : : ; x
k
g; x 2 R
3
Uwagi:
1) Nie istnieją wzory pozwalające obliczyć
dokładnie pierwiastki równania – trzeba
używać
schematów iteracyjnych
. Często
w obliczeniach inżynierskich nie jest znana
postać równania nieliniowego.
2) Rozwiązanie problemu uzyskane metodą
iteracyjną będzie przybliżone
(z zadaną dokładnością)
3) Jak w każdej metodzie iteracyjnej, o tym
jak szybko znajdziemy zadowalające
przybliżenie pierwiastka zależeć będzie od
samej metody, od przybliżenia założonego
na starcie oraz od postaci funkcyjnej
równania.
Metoda połowienia (bisekcji)
Rozwiązania szukamy w przedziale, w którym
znajduje się miejsce zerowe funkcji, w tzw.
przedziale izolacji pierwiastka
(wewnątrz
tego przedziału pierwsza pochodna funkcji nie
zmienia znaku). Przedział wyznacza się na
podstawie wykresu funkcji lub w przypadku
wielomianów algebraicznych – analitycznie.
Założenia:
1) w przedziale [a,b] znajduje się dokładnie
jeden pierwiastek
2) Na końcach przedziału wartosci funkcji
mają różne znaki tj.
Algorytm
1. Dzielimy przdział izolacji na pół
2. Sprawdzamy czy spełniony jest warunek
jeśli tak to mamy rozwiązanie, jeśli nie to
przechodzimy do kolejnego puntu
3. z dwóch przedziałów [a,x
1
] oraz [x
1
,b]
wybieramy ten, w którym wartości funkcji
na krańcach przedziałów mają różne znaki
4. Powtarzamy kroki 1-3, co powduje że
długości kolejnych przedziałów maleją
f (a)
¢ f(b) < 0
x
1
=
b + a
2
f (x
1
) = 0
f (x
i
)
¢ f(x
i+1
) < 0
jx
i
¡ x
i+1
j =
1
2
i
(b
¡ a)
4
Lewe krańce przedziałów tworzą ciąg niemalejący
ograniczony z góry. Natomiast prawe tworzą ciąg nie
rosnący ograniczony z dołu. Istnieje ich wspólna
granica w punkcie
. Punkt ten jest poszukiwanym
rozwiązaniem równania nieliniowego.
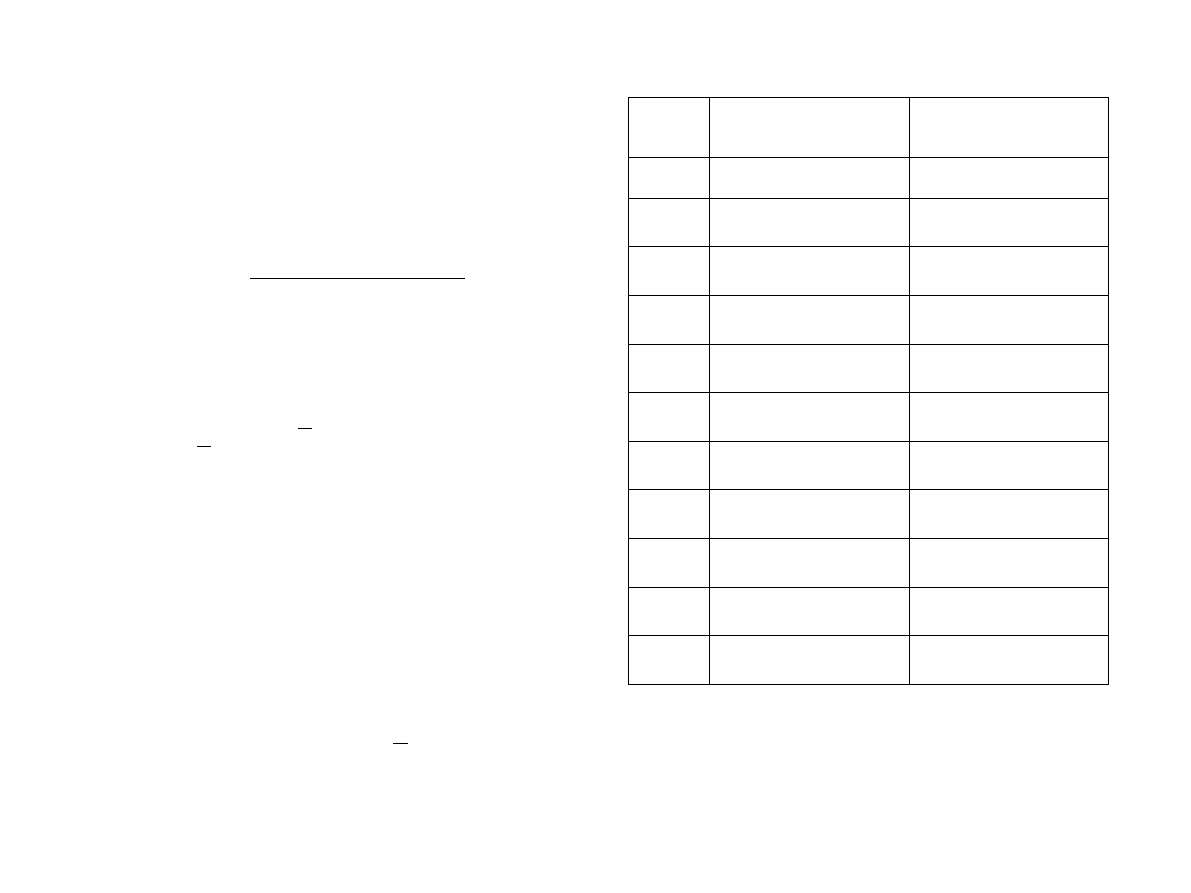
Przykład. Znaleźć w przedziale [1,2] metodą
połowienia pierwiastek równania
Wewnątrz przedziału wartość pierwszej pochodnej
funkcji jest dodatnia (nie zmienia znaku) – więc jest to
przedział izolacji pierwiastka.
x
3
+ x
2
¡ 3x ¡ 3 = 0
f (x) = x
3
+ x
2
¡ 3x ¡ 3
f (1) =
¡4
f (2) = 3
f (a)
¢ f(b) = f (1)f(2) = ¡12 < 0
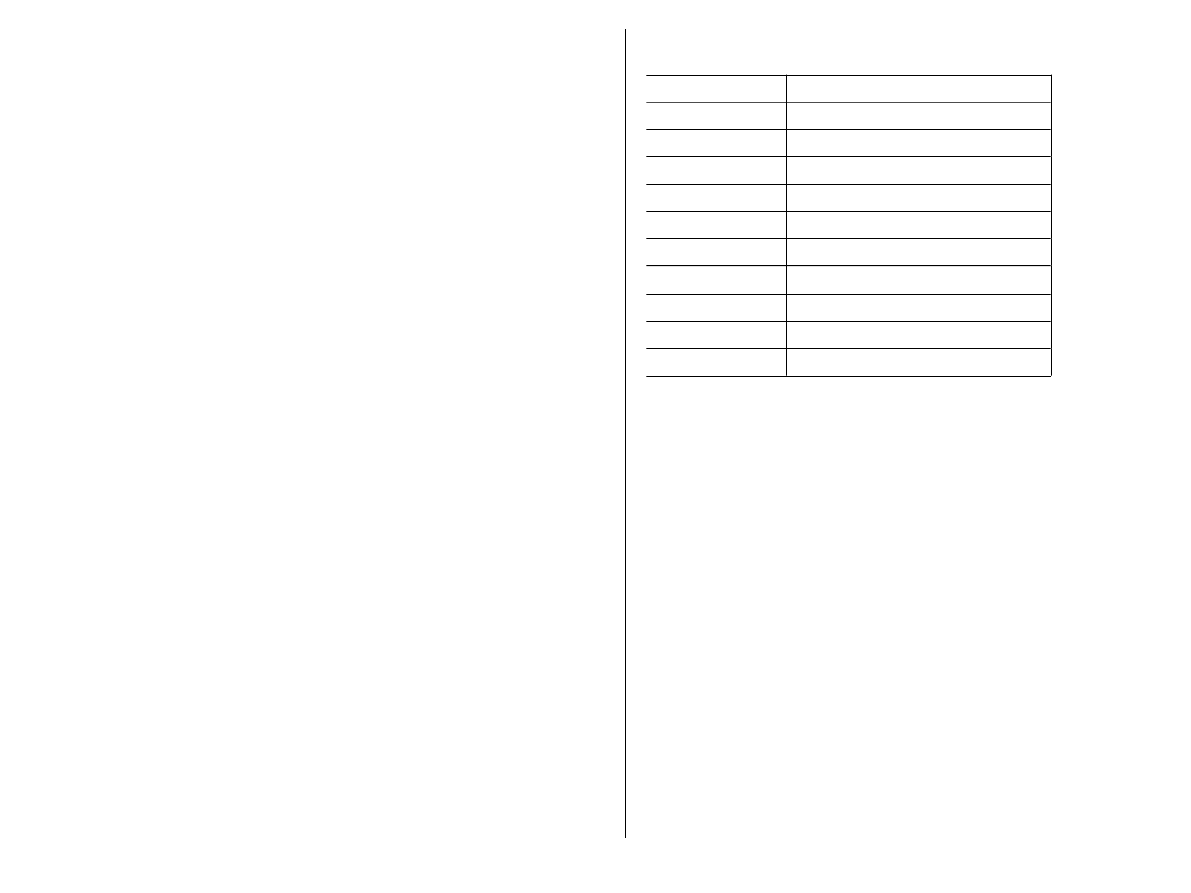
x
f(x)
1.0
-4
2.0
3
1.5
-1.874
1.75
0.17187
1.625
-0.94335
1.6875
-0.40942
1.71875
-0.12487
1.73437
0.02198
..............
.............
1.73205
0.0000000
Wyniki kolejnych przybliżeń rozwiązania
Wadą metody wolna zbieżność w otoczeniu
punktu stanowiącego rozwiązanie. Zaletą jest
natomiast niezawodność metody.
5
Wzór iteracyjny.
Jeżeli g(y) stanowi funkcję odwrotną do f(x)
to dla zbioru punktów
funkcję g(y) można przybliżyć (aproksymować)
wielomianem Lagrange'a
Oznaczmy
Jeśli x=a jest rozwiązaniem (pierwiastkiem)
to wówczas y=0
(x
i+1-j
– to wcześniej wyznaczone przybliżenia)
gdzie wielomian l
j
ma postać
Wzór na x
i+1
określa metodę iteracyjną rozwiązywania
równania nieliniowego.
fy
1
; y
2
; : : : ; y
n
g
g(y)
¼
n
X
j=1
l
j
(y)g(y
j
)
x
i+1
¡j
= g(y
j
)
x
i+1
=
n
X
j=1
l
j
(0)x
i+1
¡j
Wzór ten można zapisać w bardziej ogólnej
postaci
który jest
n-punktowym wzorem
iteracyjnym
.
Szczególnym przypadkiem są metody
jednopunktowe wykorzystujące do
znalezienia przybliżenia w i+1 iteracji przy
znajomości przybliżenia wyznaczonego w i-
tym kroku
Zbieżność metody iteracyjnej
Ciąg przybliżeń jest zbieżny gdy
Błąd rozwiązania w i-tej iteracji
W punkcie x=a metoda jest rzędu p, jeśli
istnieje liczba rzeczywista
x
i+1
= F (x
i
; x
i
¡1
; : : : ; x
i
¡n+1
)
x
i+1
= F (x
i
)
"
i+1
= a
¡ x
i+1
lim
i
!1
x
i
= a
p
¸ 1
l
j
=
(y
¡ y
1
) : : : (y
¡ y
j
¡1
)(y
¡ y
j+1
) : : : (y
¡ y
n
)
(y
j
¡ y
1
) : : : (y
j
¡ y
j
¡1
)(y
j
¡ y
j+1
) : : : (y
j
¡ y
n
)
6
lim
i
!1
jx
i+1
¡ aj
jx
i
¡ aj
p
= lim
i
!1
j"
i+1
j
j"
i
j
p
= C
6= 0
dla której zachodzi
Liczbę C nazywamy
stałą asymptotyczną
błędu
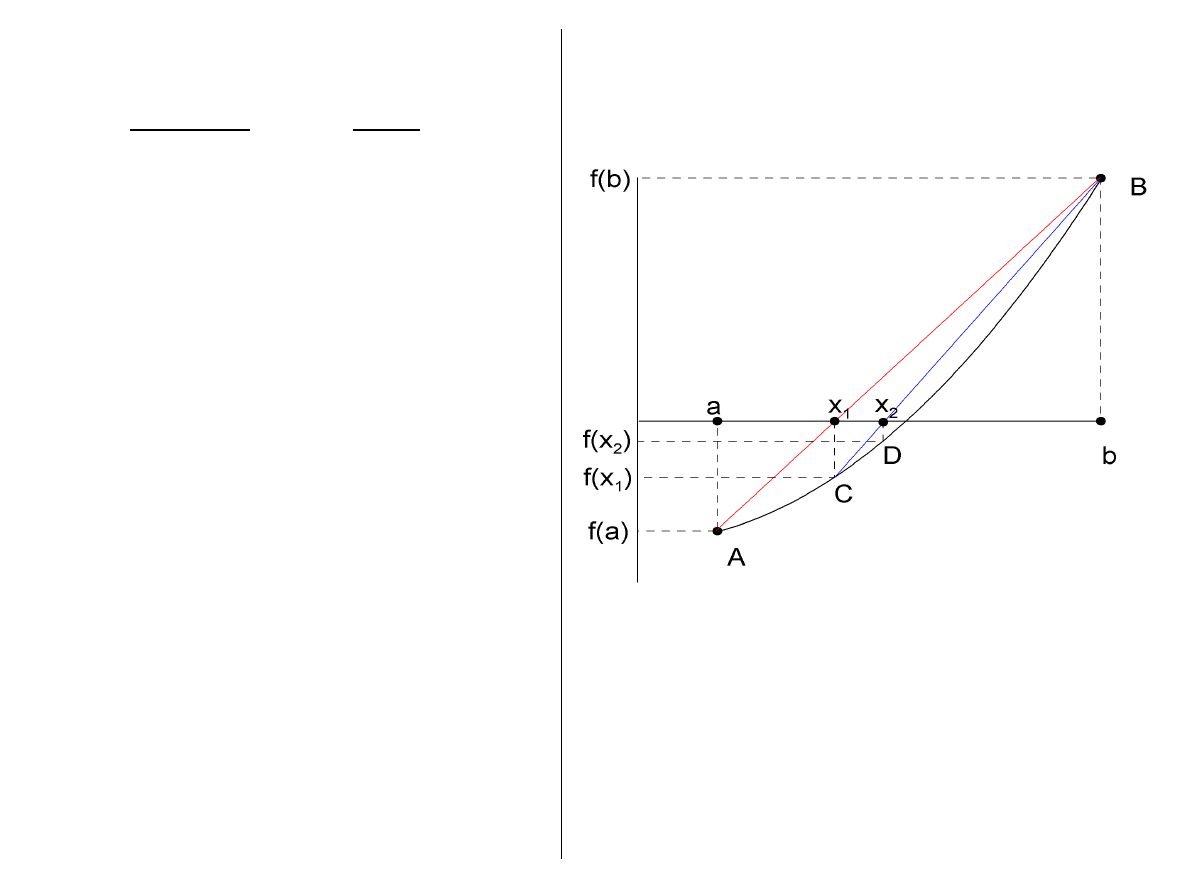
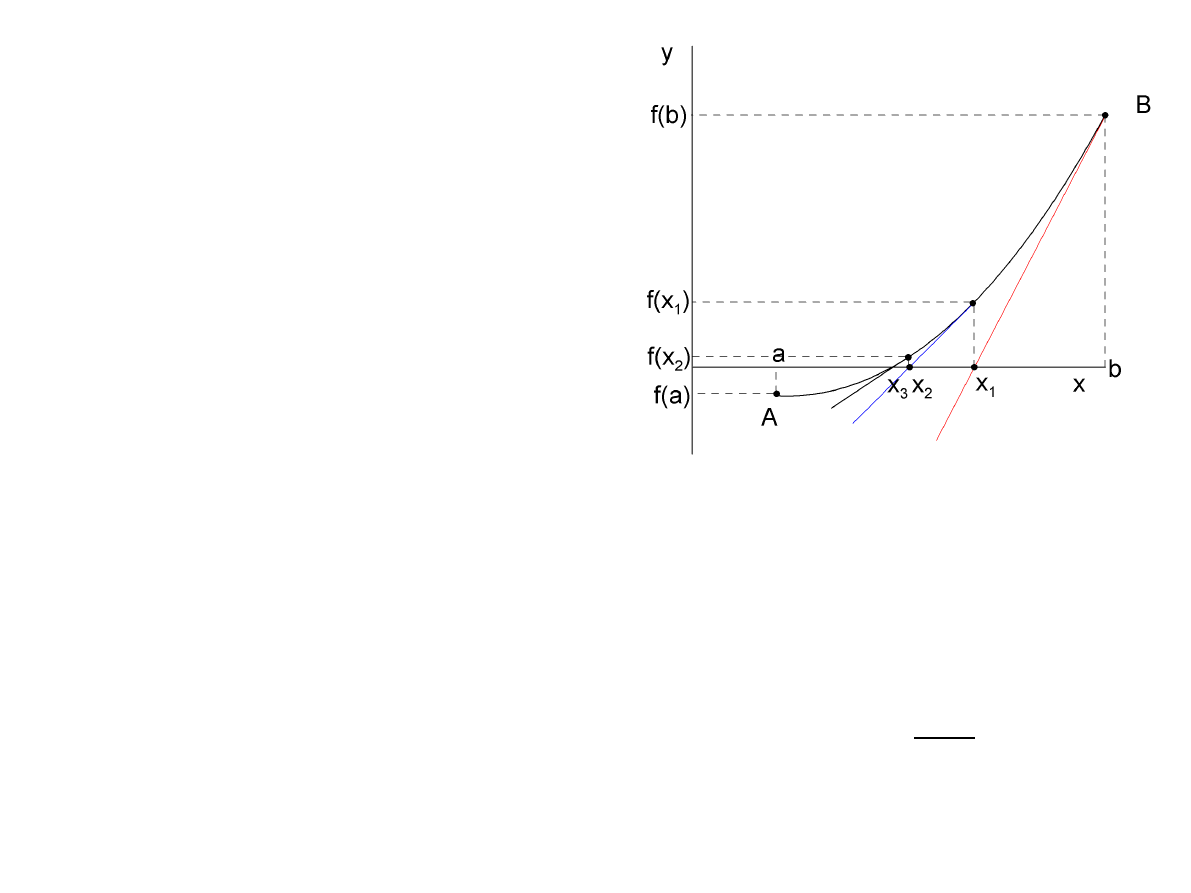
Metoda Regula Falsi
W metodzie tej wykorzystuje się założenie
istnienia lokalnej liniowości funkcji (fałszywe,
stąd nazwa). Zakładamy ponadto:
1) w przedziale [a,b] funkcja ma tylko jeden
pierwiastek pojedynczy
2) f(a)f(b)<0
3) funkcja jest klasy C
2
4) pierwsza i druga pochodna nie zmieniają
znaku w przedziale [a,b]
Rys. Idea metody Regula Falsi dla funkcji wypukłej
j"
i+1
j = Cj"
i
j
p
j"j < 1 ) j"
i+1
j << j"
i
j
p
7
Sposób postępowania:
1. przez punkty A i B prowadzimy prostą o
równaniu:
2. punkt x
1
w którym prosta przecina oś 0x
przyjmuje się za pierwsze przybliżenie
szukanego pierwiastka równania:
3. sprawdzamy warunek, czy: f(x
1
)=0, jeśli tak
to przerywamy oblicznia
4. jeśli to sprawdzamy na końcach
którego przedziału ([A,x
1
], [x
1
,B]) wartości
funkcji mają różne znaki – przez te punkty
prowadzimy kolejną prostą powtarzając kroki
1-4
Jeśli w przedziale [A,B]
a) f
(1)
(x)>0 oraz f
(2)
(x)>0 to B jest punktem
stacjonarnym (prawy brzeg ustalony)
b) f
(1)
(x)>0 oraz f
(2)
(x)<0 to A jest punktem
stacjonarnym
Metoda generuje ciąg przybliżeń. Elementy ciągu
można wyznaczyć rekurencyjnie
y
¡ f(a) =
f (b)
¡ f(a)
b
¡ a
(x
¡ a)
x
1
= a
¡
f (a)
f (b)
¡ f(a)
(b
¡ a)
f (x
1
)
6= 0
x
k+1
= x
k
¡
f (x
k
)
f (b)
¡ f(x
k
)
(b
¡ x
k
)
k = 1; 2; 3; : : :
x
0
= a
Błąd przybliżenia szacujemy korzystając z tw.
Lagrange'a o przyrostach:
gdzie:
Ponieważ
więc dostajemy oszacowanie
gdzie
m -oznacza kres dolny pierwszej pochodnej
Błąd bezwzględny można oszacować znając
wartości dwóch kolejnych przybliżeń x
k
i x
k+1
.
Przekształcając wzór rekurencyjny otrzymujemy:
I dodajemy z lewej strony wyraz
f (®) = 0
m = inf
x
2[a;b]
jf
0
(x)
j
¡f(x
k
) =
f (x
k
)
¡ f(b)
x
k
¡ b
(x
k+1
¡ x
k
)
f (®) = 0
f (®)
¡ f(x
k
) =
f (x
k
)
¡ f (b)
x
k
¡ b
(x
k+1
¡ x
k
)
f (x
k
)
¡ f(®) = f
0
(c)(x
k
¡ ®)
c
2 [x
k
; ®]
jx
k
¡ ®j ·
jf(x
k
)
j
m
8
Po zastosowaniu tw. Lagrange'a otrzymujemy:
Następnie przekształcamy do postaci
Dla
gdzie:
kres dolny
kres górny
oszacowanie błędu bezwględnego ma postać
»
k
2 (x
k
; ®)
¹
x
k
2 (x
k
; b)
(®
¡ x
k
)f
0
(»
k
) = (x
k+1
¡ x
k
)f
0
(¹
x
k
)
j® ¡ x
k+1
j =
jf
0
(¹
x
k
)
¡ f
0
(»
k
)
j
jf
0
(»
k
)
j
jx
k+1
¡ x
k
j
jf
0
(x
k
)
¡ f
0
(»
k
)
j · M ¡ m
m = inf
x
2[a;b]
jf
0
(x)
j
M = sup
x
2[a;b]
jf
0
(x)
j
j® ¡ x
k+1
j ·
M
¡ m
m
jx
k+1
¡ x
k
j
Nie znamy wartości m i M. W niewielkim otoczeniu
pierwiastka można pochodną można zastąpić
ilorazem różnicowym:
Metoda Regula Falsi jest zbieżna do dowolnej funkcji
ciągłej w przedziale [a,b] jeśli wartość pierwszej
pochodnej jest ograniczona i różna od zera w
otoczeniu pierwiastka. Obliczenia przerywa się jeśli
dwa kolejne przybliżenia różnią się o mniej niż
założone
. Wadą jest wolna zbieżność ciągu
przybliżeń –
rząd metody p=1
.
j® ¡ x
k+1
j »
¯
¯
¯
¯
f (x
k+1
)
f
0
(x
k+1
)
¯
¯
¯
¯
»
¯
¯
¯
¯
x
k+1
¡ x
k
f (x
k+1
)
¡ f (x
k
)
¯
¯
¯
¯jf(x
k+1
)
j
9
Metoda siecznych
Jest modyfikacją metody Regula Falsi. Prostą
przeprowadza się przez dwa ostatnie
przybliżenia x
k
i x
k-1
(
metoda dwupunktowa
).
Kolejne przybliżenia w metodzie siecznych
wyznacza się według relacji rekurencyjnej:
Zbieżność metody jest znacznie szybsza niż w
metodzie RF. Rząd metody
Należy dodatkowo przyjąć, że |f(x
k
)| mają
tworzyć ciąg wartości malejących. Jeśli w
kolejnej iteracji |f(x
k
)|zaczyna rosnąć, należy
przerwać obliczenia i ponownie wyznaczyć
punkty startowe zawężając przedział izolacji.
Przykład. szukamy dodatniego pierwiastka
równania
p =
1
2
(1 +
p
5)
¼ 1:618
x
k+1
= x
k
¡
f (x
k
)(x
k
¡ x
k
¡1
)
f (x
k
)
¡ f(x
k
¡1
)
f (x) = sin(x)
¡
1
2
x
Regula Falsi
Metoda
siecznych
x
3
1.75960
1.75960
x
4
1.84420
1.93200
x
5
1.87701
1.89242
x
6
1.88895
1.89543
x
7
1.89320
1.89549
x
8
1.89469
x
9
1.89521
x
10
1.89540
x
11
1.89546
x
12
1.89548
x
13
1.89549
x
1
= ¼=2
x
2
= ¼
10
Metoda Newtona (metoda stycznych)
Algorytm:
1) z końca przedziału [a,b] w którym funkcja ma
ten sam znak co druga pochodna należy
poprowadzić styczną do wykresu funkcji y=f(x)
2) styczna przecina oś 0X w punkcie x
1
który
stanowi pierwsze przybliżenie rozwiązania
3) sprawdzamy czy f(x
1
)=0, jeśli nie to z tego
punktu prowadzimy kolejną styczną
4) druga styczna przecina oś 0X w punkcie x
2
ktróry stanowi drugie przybliżenie
5) kroki 3-4 powtarzamy iteracyjne aż spełniony
będzie warunek
Równanie stycznej poprowadzonej z punktu B:
i dla y=0, otrzymujemy pierwsze przybliżenie:
y
¡ f(b) = f
0
(b)(x
¡ b)
x
1
= b
¡
f (b)
f
0
(b)
jx
k+1
¡ x
k
j · "
11
Korzystamy z rozwinięcia Taylora:
Gdzie
Wiemy że f(
)=0 , więc po przekształceniu wzoru
Taylora otrzymujemy
Korzystając ze wzoru na pierwsze przybliżenie,
możemy oszacować odległość nowego przybliżenia
od dokładnego rozwiązania:
czyli punkt x
1
leży na prawo od pierwiastka
Natomiast z tw. Lagrange'a wynika że
czyli punkt x
1
leży po lewej stronie punktu B.
Powyższe warunki pokazują, że kolejne iteracje
przybliżają nas do rozwiązania dokładnego
f (®) = f (b) + f
0
(b)(®
¡ b) +
1
2
f
00
(c)(®
¡ b)
2
c
2 [®; b]
® = b
¡
f (b)
f
0
(b)
¡
1
2
f
00
(c)
f
0
(b)
(®
¡ b)
2
®
¡ x
1
=
¡
1
2
f
00
(c)
f
0
(b)
(®
¡ b)
2
< 0
x
1
¡ b = ¡
f (b)
f
0
(b)
< 0
x
1
2 [®; b]
Równanie stycznej w k-tym przybliżeniu
Równanie rekurencyjne na położenie k-tego
przybliżenia pierwiastka równania nieliniowego w
metodzie Newtona jest następujące
Metoda Newtona jest więc
metodą
jednopunktową
.
Oszacowanie błędu przybliżenia w metodzie
Newtona
Rząd zbieżności metody wynosi
p=2
.
y
¡ f(x
k
) = f
0
(x
k
)(x
¡ x
k
)
x
k+1
= x
k
¡
f (x
k
)
f
0
(x
k
)
(k = 1; 2; : : :)
"
i+1
=
¡
f
00
(»)
2f
0
(x
i
)
"
2
i
12
Przykład. Zastosować metodę Newtona do
znalezienia pierwiastka kwadratowego
dodatniej liczby c
Szukamy miejsca zerowego funkcji
Wykorzystujemy relację rekurencyjną
co poprzekształceniu daje
Rozwiązania szukamy w takim przedziale [a,b],
w którym spełnione są warunki
x
2
¡ c = 0
f (x) = x
2
¡ c
f
0
(x) = 2x
x
k+1
= x
k
¡
x
2
k
¡ c
2x
k
0 < a < c
1=2
b >
1
2
(a + c=a)
x
k+1
=
1
2
µ
x
k
+
c
x
k
¶
Poszukiwanie pierwiastków wielokrotnych
równania nieliniowego
def. Liczbę
nazywamy r-krotnym (r
≥ 2 )
pierwiastkiem równania f(x)=0 wtedy i tylko
wtedy, gdy jest (r-1) -krotnym pierwiastkiem
równania:
Metody: połowienia, RF, siecznych nadają się do
poszukiwania pierwiastków tylko o
nieparzystej
krotności
. Rząd metody siecznych obniża się
(wolniejsza zbieżność). Metoda Newtona pozwala
znaleźć pierwiastki o parzystej i nieparzystej
krotności.
Aby utrzymać rząd metody (przyśpieszyć zbieżność)
stosuje się modyfikacje wzorów rekurencyjnych.
a) Znamy krotność r pierwiastka równania.
Wówczas możemy wykorzystać tę informację w
metodzie Newtona
(w praktyce bardzo rzadko znamy wartość r przez co
zastosowanie powyższego wzoru jest mocno
ograniczone)
f
0
(x) = 0
x
k+1
= x
k
¡ r
f (x
k
)
f
0
(x
k
)
13
a
¡ x
k+1
= a
¡ x
k
+ r
f (x
k
)
f
0
(x
k
)
(a
¡ x
k+1
)f
0
(x
k
) = G(x
k
)
Obliczmy różnicę pomiędzy rozwiązaniem
dokładnym a k+1 przybliżeniem
Gdzie
Różniczkujemy G(x) j-krotnie
Wykorzystujemy fakt że a jest pierwiastkiem r-
krotnym
Z rozwinięcia Taylora w punkcie x=a dostajemy
oraz
G(x) = (a
¡ x)f
0
(x) + rf (x)
G
(j)
(x)
=
(a
¡ x)f
(j+1)
(x)
¡ jf
(j)
(x)
+
rf
(j)
(x)
G
(j)
(a)
=
0
(j = 0; 1; : : : ; r)
G
(r+1)
(a)
6= 0
G(x) =
(x
¡ a)
r+1
(r + 1)!
G
(r+1)
(»
1
)
f
0
(x) =
(x
¡ a)
r
¡1
(r
¡ 1)!
f
(r)
(»
2
)
Kombinacja dwóch ostatnich zależności prowadzi do
związku pomiędzy błędami w k i w k+1 iteracji
Ponieważ
Więc metoda Newtona dla pierwiastka krotności r ma
rząd zbieżności
p=2
.
f
(r)
(»
2
)
6= 0
G
(r+1)
(a)
6= 0
"
k+1
=
1
r(r + 1)
G
(r+1)
(»
1
)
f
(r)
(»
2
)
"
2
k
j"
k+1
j
j"
k
j
2
· C
"
k+1
= (a
¡ x
k+1
) =
G(x
k
)
f
0
(x
k
)
14
x
k+1
= x
k
¡ u(x
k
)
x
k
¡ x
k
¡1
u(x
k
)
¡ u(x
k
¡1
)
x
k+1
= x
k
¡
u(x
k
)
u
0
(x
k
)
u
0
(x
k
) = 1
¡
f
00
(x
k
)
f
0
(x
k
)
u(x
k
)
u(x) =
f (x)
f
0
(x)
b) Jeśli wiemy że pierwiastek jest wielokrotny
ale nie znamy jego krotności r wówczas
możemy badać zera funkcji
Funkcja u(x) ma zero krotności 1 w punkcie
x=a. We wzorach iteracyjnych dokonujmey
podstawienia u(x) za f(x)
a) w metodzie siecznych
b) w metodzie Newtona
gdzie:
Przykład. Wyznaczyć dodatni pierwiastek
równania
µ
sin(x)
¡
1
2
x
¶
2
= 0
m. Newtona
m. Newtona - r
m. Newtona - u(x)
x
2
1.78540
2.00000
1.80175
x
3
1.84456
1.90100
1.88963
x
4
1.87083
1.89551
1.89547
x
5
1.88335
1.89549
1.89549
x
6
1.88946
x
7
1.89249
x
8
1.89399
x
9
1.89475
x
10
1.89512
x
11
1.89531
x
12
1.89540
x
13
1.89545
x
14
1.89547
x
15
1.89548
x
16
1.89549
x
1
=
1
2
15
Proces
2
Aitkena
Jeśli metoda jest zbieżna liniowo to można ją w
prosty sposób przyśpieszyć
gdzie |C
i
| dąży do stałej asymptotycznej błędu. Po
wielu iteracjach powinniśmy otrzymać przybliżenie
Zwiększamy indeks i o 1 i eliminujemy stałą
Następnie obliczamy a
Procedurę tę można stosować jedynie dla metod
zbieżnych liniowo, gdy kolejne 3 przybliżenia są
bliskie poszukiwanemu rozwiązaniu.
a
¡ x
i+1
= C
i
(a
¡ x
i
)
(
jC
i
j < 1)
a
¡ x
i+1
¼ ¹
C(a
¡ x
i
);
j ¹
C
j = C
a
¡ x
i+2
a
¡ x
i+1
¼
a
¡ x
i+1
a
¡ x
i
a
¼
x
i
x
i+2
¡ x
2
i+1
x
i+2
¡ 2x
i+1
+ x
i
16
Układy równań nieliniowych
Układ równań nieliniowych
zapisujemy w postaci wektorowej
Dla takiej postaci układu wyprowadza się wzory
iteracyjne. Ogólny wzór iteracyjny
(
wielokrokowy
)
Zakladamy że funkcja wektorowa f ma w
otoczeniu rozwiązania
funkcję odwrotną
Jeśli punkt
jest odwrotny do punktu x (wektora
przybliżonych rozwiązań)
f
j
(x
(1)
; x
(2)
; : : : ; x
(n)
) = 0; (j = 1; 2; : : : ; n)
To można funkcję g(y) rozwinąć w szereg Taylora w
otoczeniu punktu y
i
Gdzie: jest pochodną
cząstkową funkcji h względem zmiennych
w punkcie x
wektor s:
x
(i
1
)
; x
(i
2
)
; : : : ; x
(i
n
)
fff (x
x
x)
=
0
fff
=
(f
1
; f
2
; : : : ; f
n
)
x
x
x
=
(x
(1)
; x
(2)
; ; : : : ; x
(n)
; )
F
F
F = (F
1
; F
2
; : : : ; F
n
)
®
®
® = (®
1
; ®
2
; : : : ; ®
n
)
ggg = (g
1
; g
2
; : : : ; g
n
)
yyy = (y
(1)
; y
(2)
; : : : ; y
(n)
; )
x
x
x = ggg(yyy) = ggg(yyy
i
) +
m+1
X
j=1
1
j!
d
j
ggg(yyy
i
; yyy
¡ yyy
i
)
+
1
(m + 2)!
d
m+2
ggg(»»»; yyy
¡ yyy
i
)
»»»
2 [yyy; yyy
i
]
d
j
h(x
x
x; sss) =
n
X
i
1
=1
n
X
i
2
=1
: : :
n
X
i
j
=1
D
i
1
;i
2
;:::;i
j
h(x
x
x)s
i
1
s
i
2
: : : s
i
j
D
i
1
;i
2
;:::;i
j
h(x
x
x)
sss = (s
i
1
; s
i
2
; : : : ; s
i
j
)
x
x
x
i+1
= F
F
F (x
x
x
i
; x
x
x
i
¡1
; : : : ; x
x
x
i
¡n+1
)
17
Szukane rozwiązanie ma postać
Po odrzuceniu reszty w rozwinięciu Taylora i
uwzględnieniu powyższego warunku otrzymujemy
n-wymiarowy odpowiednik metody Newtona.
Dla m=0 (
metoda jednokrokowa
)
Pochodne funkcji g można wyrazic poprzez
pochodne funkcji f. Dla n=2 otrzymujemy
Rząd zbieżności metody wynosi 2. Zazwyczaj
zbieżność uzyskujemy tylko jeśli startujemy już z
dobrym przybliżeniem rozwązania.
®
®
® = ggg(000)
) yyy = 000
Problem poszukiwania rozwiązań układu równań
nieliniowych można sformułować jako problem
poszukiwania minimum poniższej fukcji
Funkcja osiąga minimum globalne dla dokładnego
rozwiązania x. Do jego znalezienia można użyć
metody największego spadku (minimalizacja
wartości funkcji)
.
©(x
x
x) =
n
X
i=1
f
2
i
(x
x
x)
x
x
x
i+1
= x
x
x
i
¡
1
J
2
4
@f
2
@x
(2)
@f
1
@x
(2)
¡
@f
2
@x
(1)
@f
1
@x
(1)
3
5
2
4
f
1
f
2
3
5
x
x
x=x
x
x
i
J =
2
4
@f
1
@x
(1)
@f
1
@x
(2)
@f
2
@x
(1)
@f
2
@x
(2)
3
5
x
x
x
i+1
= x
x
x
i
+ dggg(yyy
i
;
¡yyy
i
) =
= x
x
x
i
¡
n
X
j=1
@ggg(yyy
i
)
@y
j
y
(j)
i
18
Wyznaczanie zer wielomianów
Szukamy zer rzeczywistych i zespolonych
wielomianu
Metoda Lehmera-Schura
Dla pierwotnego wielomianu f(z) definiujemy
wielomian
(kreska pozioma – sprzężenie zespolone)
i wprowadzamy operator T
dla z=0
f (z) = a
n
z
n
+ a
n
¡1
z
n
¡1
+ : : : + a
0
= 0
z
2 C
a
i
2 R; (i = 0; 1; : : : ; n)
f
¤
(z) = z
n
¹
f (¹
z
¡1
) = ¹
a
n
+ ¹
a
n
¡1
z + : : : + ¹
a
0
z
0
T [f (z)] = ¹
a
0
f (z)
¡ a
n
f
¤
(z)
T [f (0)] = ¹
a
0
a
0
¡ ¹a
n
a
n
=
ja
0
j
2
¡ ja
n
j
2
2 R
Operator T działając na f(z) obniża stopień
wielomianu o 1. Działając nim wielokrotnie na f(z)
otrzymamy ciąg wielomianów corza niższego
stopnia.
Tw. Jeśli dla
istnieje takie h, że
to f(z) ma co najmniej jedno zero wewnątrz
koła jednostkowego.
Jeśli
to wewnątrz koła jednostkowego nie leży
żadne zero f(z).
T
j
[f (z)] = T
£
T
j
¡1
[f (z)]
¤
f (0)
6= 0
T
h
[f (0)] < 0
0 < h < k; h; k
2 Z
k = min
f1; 2; : : : ; ng $ T
k
[f (0)] = 0
T
i
[f (0)] > 0; 1
· i < k
T
k
¡1
[f (z)] = const
19
T [f (0)] < 0
T
j
[f (z)](j = 1; 2; : : :)
T
j
[f (0)] < 0 (j < k)
T
k
[f (0)] = 0
Jeśli f(z) ma zero wewnątrz koła
to wielomian
ma zero wewnątrz koła jednostkowego.
Algorytm lokalizacji zer metodą LS:
1. Jeśli f(0)=0 to z=0 jest zerem. Jeśli nie to
przechodzimy do 2.
2. Obliczamy T[f(z)]. Jeśli
to wewnątrz koła jednostkowego leży
pierwiastek. Jeśli nie to przechodzimy do 3.
3. Obliczamy
aż do uzyskania
(w kole jednostkowym leży pierwiastek)
lub
(jeśli T
k-1
[f(0)]=const to w kole nie ma
pierwiastka)
jz ¡ cj = ½
4. Jeśli wewnątrz koła jednostkowego nie ma
zera to sprawdzamy funkcję g(2z) (wewnątrz
koła jednostkowego)
5. Zgodnie z punktami 3 i 4 lokalizujemy zero w
pierścieniu
(jeśli zero jest w kole to połowimy jego
promień tak długo aż zero znajdzie się w
pierścieniu).
6. Znaleziony pierścień można pokryć 8 kołami
badając każde koło znajdziemy na pewno
zero w jednym z nich.
7. W wybranym kole (C
j
) stosujemy kroki 3-4
(stosując połowienie promienia) i
lokalizujemy zero w pierścieniu
8. Następnie powtarzamy kroki 6-7
R = 2
j
· jzj < 2
j+1
= 2R
r =
4
5
R
(promien)
C
i
=
3R
2cos(¼=8)
e
¼
4
ik
; k = 0; 1; : : : ; 7
R
1
=
4
5
R2
¡j
1
· jz ¡ C
j
j <
4
5
R2
¡(j
1
¡1)
= 2R
1
g(z) = f
µ
z
¡ c
½
¶
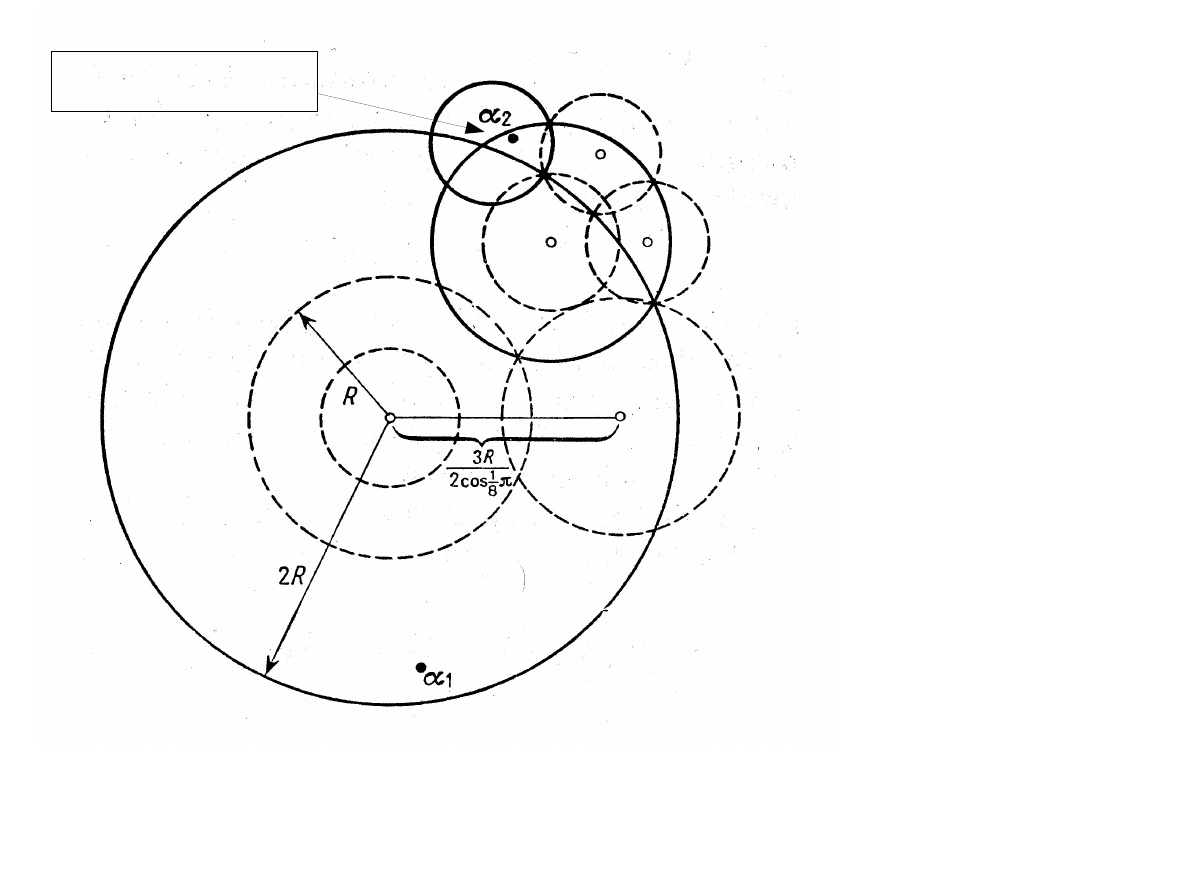
20
Rys. Lokalizacja zer w metodzie Lehmera-Schura.
Inne zero leżące blisko
pierwotnego koła
21
Po k krokach zero leży w kole o promieniu 2R
k
Własności metody Lehmera-Schura:
1) Szybkość zbieżności metody jest niewielka
ale nie zależy od krotności pierwiastka
równania
2) Pozwala lokalizować zera rzeczywiste i
zespolone z zadaną dokładnością
3) Po znalezieniu pierwiastka można go
wyrugować z równania dzieląc wielomian
przez odpowiedni dwumian i szukać jego
kolejne zera
R
k
·
µ
2
5
¶
k
R
Metoda Łobaczewskiego (Graeffego)
Dla wielomianu n-tego stopnia w postaci
można zdefiniować wielomian stopnia 2n
Zera wielomianu f
1
są kwadratami zer f
0
(
rozdzielamy zera
). Ogólnie można to zapisać
Pomiędzy współczynnikami wielomianów f
r+1
oraz f
r
zachodzi związek
W metodzie Łobaczewskiego współczynniki
wielomianu f
r
wykorzystujemy do obliczenia jego
zer.
f
0
(z) = (z
¡ ®
1
)(z
¡ ®
2
) : : : (z
¡ ®
n
)
f
1
(w) = (
¡1)
n
f
0
(z)f
0
(
¡z) =
= (w
¡ ®
2
1
)(w
¡ ®
2
2
) : : : (w
¡ ®
2
n
)
w = z
2
f
r+1
(w) = (
¡1)
n
f
r
(z)f
r
(
¡z); (r = 0; 1; : : :)
a
(r+1)
j
= (
¡1)
n
¡j
0
@
³
a
(r)
j
´
2
+ 2
min
fn¡j;jg
X
k=1
(
¡1)
k
a
r
j
¡k
a
(r)
j+k
1
A
22
Związek współczynników wielomianu z jego
zerami:
gdzie S
k
(x
1
,x
2
,...,x
n
) jest k-tą funkcją
symetryczną zmiennych x
1
,x
2
,...,x
n
np.: dla j=n-1, k=n-j=1
Zera wielomianu możemy zapisać w postaci
i załóżmy, że pierwiastki mają różne moduły
Wówczas dla j=n-1 otrzymujemy
a
r
j
= (
¡1)
n
¡j
S
n
¡j
(®
2
r
1
; ®
2
r
2
; : : : ; ®
2
r
n
; )
j = 0; 1; : : : ; n
¡ 1
S
k
(x
1
; x
2
; : : : ; x
n
) =
=
X
1
·r
1
<r
2
<:::<r
k
·n
x
r
1
x
r
2
: : : x
r
k
a
(r)
n
¡1
=
¡S
1
³
®
2
r
1
; ®
2
r
2
; : : : ; ®
2
r
n
´
=
¡
n
X
k=1
®
2
r
k
®
k
= ½
k
e
i'
k
; k = 1; 2; : : : ; n
½
1
> ½
2
> : : : ½
n
>
a
(r)
n
¡1
=
¡®
2
r
1
"
1 +
n
X
k=2
µ
®
k
®
1
¶
2
r
#
I w granicy
Dla dostatecznie dużego r możemy oszacować
moduł zera (
1
)
Dla j=n-2 mamy
i analogicznie dla pozostałych modułów
lim
r
!1
ja
(r)
n
¡1
j
1=2
r
=
j®
1
j
½
1
¼ ja
(r)
n
¡1
j
1=2
r
a
(r)
n
¡2
=
X
1
·r
1
<r
2
·n
®
2
r
r
1
®
2
r
r
2
=
= ®
2
r
1
®
2
r
2
2
6
41 +
X
1
·r1<r2·n
(r1;r2)6=(1;2)
µ
®
r
1
®
r
2
®
1
®
2
¶
2
r
3
7
5
½
2
¼
1
½
1
ja
(r)
n
¡2
j
1=2
r
¼
¯
¯
¯
¯
¯
a
(r)
n
¡2
a
(r)
n
¡1
¯
¯
¯
¯
¯
1=2
r
½
k
¼
¯
¯
¯
¯
¯
a
(r)
n
¡k
a
(r)
n
¡k+1
¯
¯
¯
¯
¯
1=2
r
; k = 2; 3; : : : ; n
23
Wartość r określa się empirycznie badając
stabilizację cyfr znaczących wyznaczanych
modułów.
Znaki zer wyznacza się określają znak wartości
wielomianu po podstawieniu do niego
odpowiedniego modułu.
Przykład. Wyznaczyć zera wielomianu
z
3
¡ 5z
2
¡ 17z + 21 = 0
r
1
1
-59
499
-441
2
1
-2483
196963
-194481
3
1
-5771363 37828630723
-37822859361
a
(r)
3
a
(r)
2
a
(r)
1
a
(r)
0
r
1
7.68
2.91
0.94
2
7.06
2.98
0.997
3
7.001
2.999
0.99998
½
1
½
2
½
3
Dokładne wartości:
®
1
= 7
®
2
=
¡3
®
3
= 1
a) Metodę modyfikuje się dla zer zespolonych
oraz przypadku gdy pierwiastki równania mają
identyczne moduły.
b) Szybki wzrost wartości współczynników
eliminuje się normalizując współczynniki.
Do wyznaczania zer wielomianów stosuje się też
metody Bernoulliego oraz Laguerre'a.
Metoda Laguerre'a jest zbieżna dla zer
rzeczywistych i wielokrotnych, a rząd zbieżności
wynosi 2. W przypadku pojedynczych zer
zespolonych rząd metody wynosi 3.
Metody dzielenia wielomianów
Aby wyznaczyć zera zespolone konieczne jest
przeprowadzenie dzielenia wielomianów
a) przez czynniki liniowe (dwumian)
b) przez czynniki kwadratowe (trójmian)
Dzielenie wielomianu przez czynnik liniowy
Wielomian
dzielimy przez dwumian:
f (z) = a
n
z
n
+ a
n
¡1
z
n
¡1
+ : : : + a
0
= 0
(z
¡ z
j
)
24
Wynikiem dzielenia jest
Z porównania współczynników przy jednakowych
potęgach otrzymujemy zależności
Zatem współczynnki nowego wielomianu można
obliczać rekurencyjnie
a
n
=
b
n
¡1
a
n
¡1
=
b
n
¡2
¡ z
j
b
n
¡1
..
.
a
1
=
b
0
¡ z
j
b
1
a
0
=
R
j
¡ z
j
b
0
b
n
=
0
b
k
=
a
k+1
+ z
j
b
k+1
k
=
n
¡ 1; n ¡ 2; : : : ; 0
R
j
=
a
0
+ z
j
b
0
Dzieląc jeszcze raz wielomian otrzymamy
Wartości współczynników c
i
wyznaczamy
analogicznie jak w poprzednim przypadku.
Obliczanie zer za pomocą iterowanego
dzielenia
Zera wielomianu możemy wyznaczyć
iteracyjnie stosując zmodyfikowane wzory
jednokrokowe np.. metodę siecznych czy
Newtona.
Kolejne przybliżenia w metodzie siecznych
wyznaczamy ze wzoru
oraz w metodzie Newtona
z
j+1
= z
j
¡
R
j
(z
j
¡ z
j
¡1
)
R
j
¡ R
j
¡1
z
j+1
= z
j
¡
R
j
R
0
j
f (z)
=
(z
¡ z
j
)
¡
b
n
¡1
z
n
¡1
+ b
n
¡2
z
n
¡2
+
: : : + b
0
) + R
j
f (z)
=
(z
¡ z
j
)
2
¡
c
n
¡2
z
n
¡2
+ c
n
¡3
z
n
¡3
+
: : : + c
0
) + R
0
j
(z
¡ z
j
) + R
j
25
Metodę Newtona można jeszcze zmodyfikować
jeśli zauważymy, że R
j
=0 gdy z
j
jest
pierwiastkiem równania. Wtedy kolejne
przybliżenie ma postać
Wzór
określa
metodę Lina
, która jest wolniej
zbieżna od metody Newtona (rząd zbieżności
p=1). W jednym kroku wymaga ona wykonania
mniej działań niż metoda Newtona. Może być
tez rozbieżna.
Chcąc wyznaczyć pierwiastek zespolony należy
wykonywać działana na liczbach zespolonych.
Ponadto pierwotne przybliżenie pierwiastka
powinno być zespolone
.
Postępowanie w przypadku zer
zespolonych
z
j+1
=
¡
a
0
b
0
= z
j
¡ z
j
¡
a
0
b
0
=
=
z
j
¡
b
0
z
j
+ a
0
b
0
= z
j
¡
R
j
b
0
z
j+1
= z
j
¡
R
j
b
0
z
j
= x
j
+ iy
j
b
k
= °
k
+ i±
k
c
k
= "
k
+ i´
k
°
n
=
±
n
= 0
°
k
=
a
k+1
+ x
j
°
k+1
¡ y
j
±
k+1
;
(k = n
¡ 1; n ¡ 2; : : : ; 0)
±
n
¡1
=
"
n
¡1
= ´
n
¡1
= 0
±
k
=
x
j
±
k+1
+ y
j
°
k+1
;
(k = n
¡ 2; n ¡ 3; : : : ; 0)
"
k
=
°
k+1
+ x
j
"
k+1
¡ y
j
´
k+1
´
n
¡2
=
0
´
k
=
±
k+1
+ x
j
´
k+1
+ y
j
"
k+1
;
(k = n
¡ 3; n ¡ 4; : : : ; 0)
R
j
= b
¡1
= °
¡1
+ i±
¡1
R
0
j
= c
¡1
= "
¡1
+ i´
¡1
x
j+1
= x
j
¡
"
¡1
°
¡1
+ ´
¡1
±
¡1
"
2
¡1
+ ´
2
¡1
y
j+1
= y
j
¡
±
¡1
"
¡1
¡ °
¡1
´
¡1
"
2
¡1
+ ´
2
¡1
26
Wpływ błędów współczynników
wielomianu podczas wyznaczania zer
wielomianów.
Dokładny wielomian (współczynniki bez błędów)
oraz wielomian ze współczynnikami
zaburzonymi
błędy współczynników
Z
0
(dokładne zero) i z
0
(obliczone zero) łączy
zależność
Po podstawieniu
i
oraz Z
0
do F(z) otrzymujemy
Oszacowanie traci sens gdy pochodna jest
bliska 0.
F (z) = A
n
z
n
+ A
n
¡1
z
n
¡1
+ : : : + A
0
Z
0
= z
0
+ "
±
i
= A
i
¡ a
i
(i = 0; 1; : : : ; n)
Okazuje się, że istnieją wielomiany (wysokiego
stopnia) dla których nawet niewielkie zaburzenie
współczynników powoduje duże zmiany wartości zer
(np.. zera rzeczywiste staja się zespolonymi).
Przykład: wielomian Wilkinsona.
Wielomiany takie nazywamy źle uwarunkowanymi.
Uzyskanie dokładniejszych przybliżeń zer wielomianu
mozliwe jest wówczas tylko jeśli obliczenia
wykonywane przy użyciu silniejszej arytmetyki.
f (z) = a
n
z
n
+ a
n
¡1
z
n
¡1
+ : : : + a
0
n
X
i=1
±
i
z
i
0
+ "f
0
(z
0
)
¼ 0
" =
¯
¯P
n
i=1
±
i
z
i
0
¯
¯
jf
0
(z
0
)
j
Document Outline