Fizyka statystyczna

• Fizyka stanów równowagi

• Fizyka stanów nierówności

(zjawiska transportu)

Fizyka statystyczna stanów

równowagi

Układy złożone z dużej liczby cząsteczek
wymagają innego opisu teoretycznego, niż
układy z niewielką liczbą cząsteczek. W
pomiarach interesujące są wielkości
makroskopowe takie jak ciśnienie, ciepło
właściwe, namagnesowanie, przewodnictwo
cieplne i elektryczne.

W opisie teoretycznym wprowadza się
procedurę uśredniania po stanach
mikroskopowych.

Stany mikroskopowe układu - określony

przez podanie stanów wszystkich jego

cząstek.

• klasyczny stan określony przez trzy współrzędne
wektora położenia r i trzy współrzędne wektora
pędu p.

• W fizyce kwantowej stan układu określony przez
zbiór liczb kwantowych (elektrony w atomie) i
wektorów falowych k i spinów (elektrony
swobodne)

Q - zbiór liczb charakteryzujących stany
wszystkich cząstek, m

s,

(s) - magnetyczna liczba

spinowa

}

,..

,

,

,...

,

{

2

1

2

1

N

N

p

p

p

r

r

r

Q















}

,..

,

,

,...

,

{

2

1

2

1

N

s

s

s

N

m

m

m

k

k

k

Q









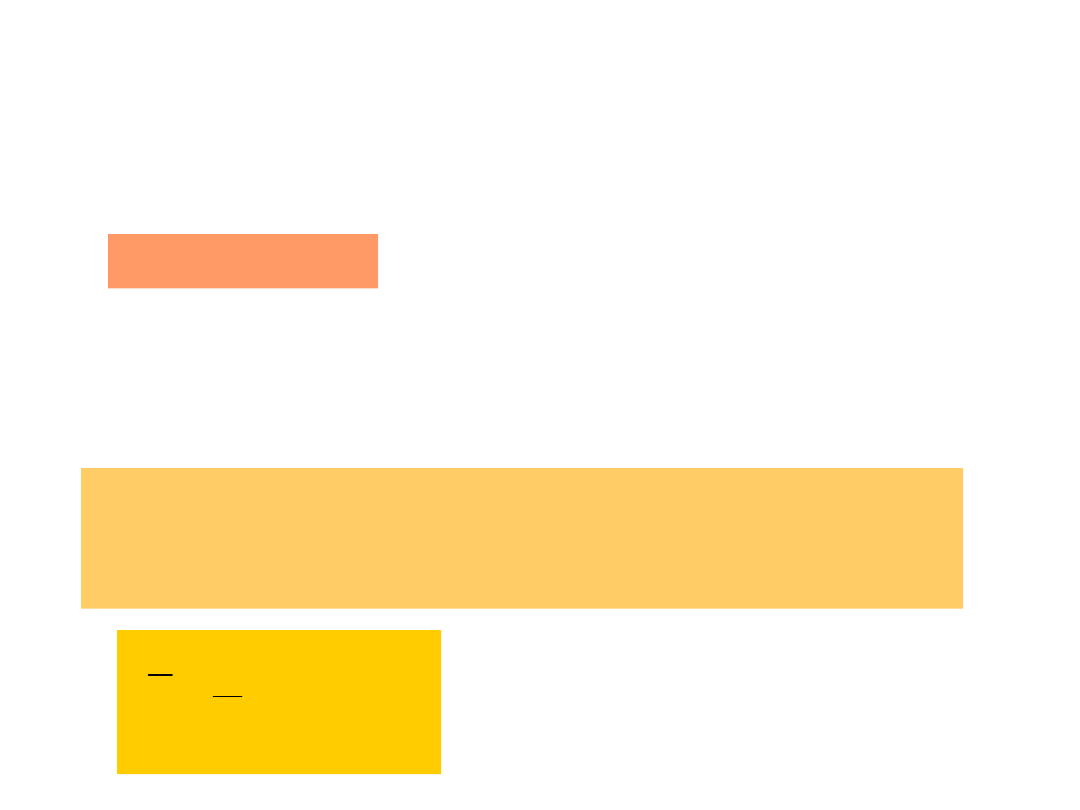
N - liczba cząsteczek w układzie i jest rzędu 10

23

.

Stany makroskopowe układu cząsteczek
wynikają ze stanów mikroskopowych.

X = X{Q(t)}

X - wielkość
makroskopowa

t - czas

Parametry makroskopowe (X) określają stan
makroskopowy układu. Parametry X są
uśredniane w trakcie pomiaru, np. w czasie T.





dt

t

Q

X

T

X

T





0

)

(

1

Jeżeli <X> nie zmienia się w czasie mówimy, że
układ jest w stanie równowagi. Obliczenie <X> jest
praktycznie niemożliwe (całka z 10

23

zmiennych!).

Obliczanie wartości średniej <X> realizuje się po
wprowadzeniu prawdopodobieństwa P(Q)
wystąpienia odpowiedniego stanu
mikroskopowego. Następnie wielkość X jest
uśredniana po różnych stanach Q, wziętych z
odpowiednimi prawdopodobieństwami.









Q

Q

X

Q

P

X

X

)

(

)

(

Obliczanie jest uwarunkowane znajomością
funkcji P(Q), W fizyce statystycznej stosuje się
trzy typy takich funkcji rozkładu, zwanych
rozkładami,

Funkcje rozkładu

•

Rozład mikrokanoniczny

- wszystkie stany

układu są jednakowo prawdopodobne P(Q) =
const. Rozkład mikrokanoniczny stosuje się do
opisu układów odizolowanych, ustalona energia,
liczba cząstek itp...

•

Rozład kanoniczny

- układ znajduje się w

kontakcie cieplnym z otoczeniem, ale nie zmienia
swoich innych parametrów (rozkład Maxwella).

•

Rozład wielki kanoniczny

- rozkład opisuje

układy, które wymieniają nie tylko energię z
otoczeniem, ale i cząsteczki (rozkład Fermiego-
Diraca, rozkład Bosego-Einsteina).

Kinetyczna teoria gazów

Ten sam zakres zagadnień jak w klasycznej
termodynamice. Przyjmuje się istnienie atomów i
cząsteczek. Podstawowymi prawami są prawa
mechaniki, zastosowane do atomów tworzących
układ.

Wielkości makroskopowe - ciśnienie, temperatura,
objętość.

Kinetyczna teoria gazów posługuje się stosunkowo
prostymi technikami uśredniania.

Gaz doskonały - opis

makroskopowy

• Cząstki poruszają się chaotycznie i podlegają
prawom Newtona.

• Całkowita liczba cząstek jest bardzo duża.
• Objętość cząstek jest bardzo małą częścią
objętości całego gazu, można ją pominąć.

• Poza momentem zderzenia na cząstki nie
działają żadne siły.

• Zderzenia są sprężyste i czas zderzenia można
pominąć.

Obliczanie ciśnienia na

podstawie kinetycznej teorii

gazów

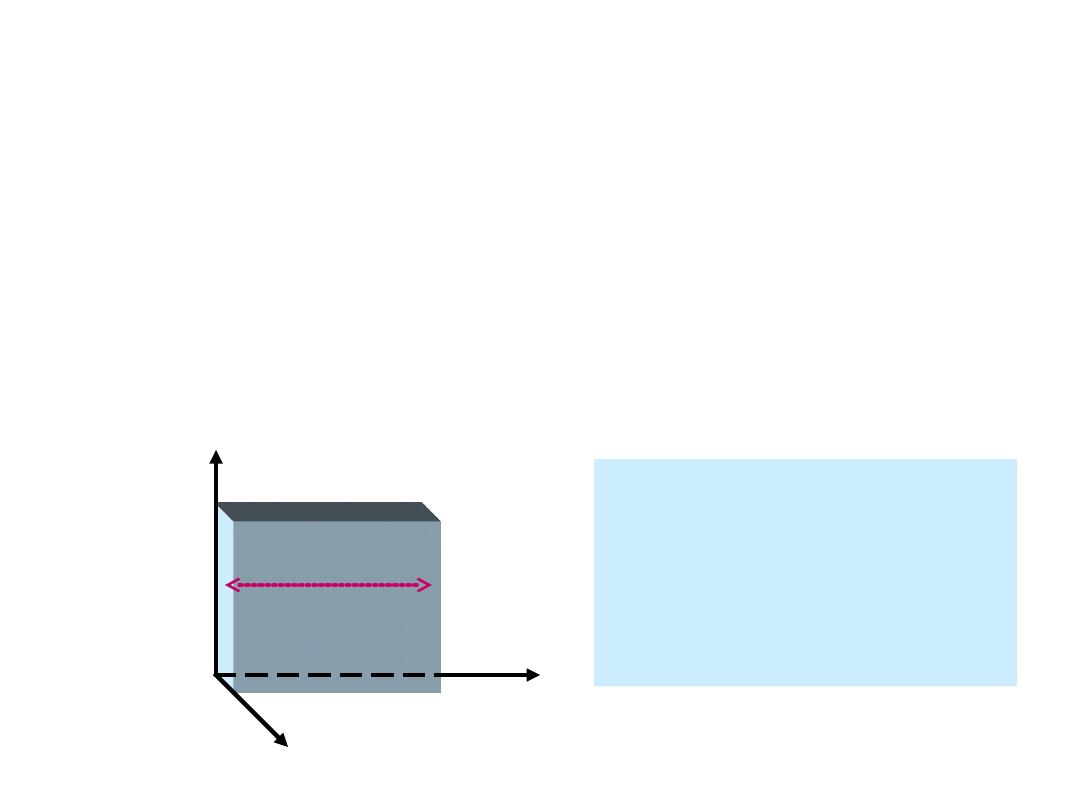
Rozważamy gaz doskonały zamknięty w
sześciennym pudełku o boku l, którego ścianki są
doskonale sprężyste. Po zderzeniu ze ścianką
zmiana pędu

P = -mv

x

- mv

x

= -2 mv

x

l

l

l

x

y

z

Zakładamy, że
cząstka zderza się ze
ścianką pudełka nie
zderzając się z innymi
ściankami po drodze.

Czas przelotu cząstki od ścianki do ścianki:
l/v

x

Liczba zderzeń w jednostce czasu: v

x

/2l

Szybkość przekazywania pędu ściance przez
cząstkę o masie m:

l

mv

l

v

mv

x

x

x

2

2

2



Ciśnienie wywierane przez cząstki na
ściankę:





...

2

2

2

1

3







x

x

v

v

l

m

p

N - liczba cząstek w naczyniu

n

o

- koncentracja cząstek

0

3

n

N

l 























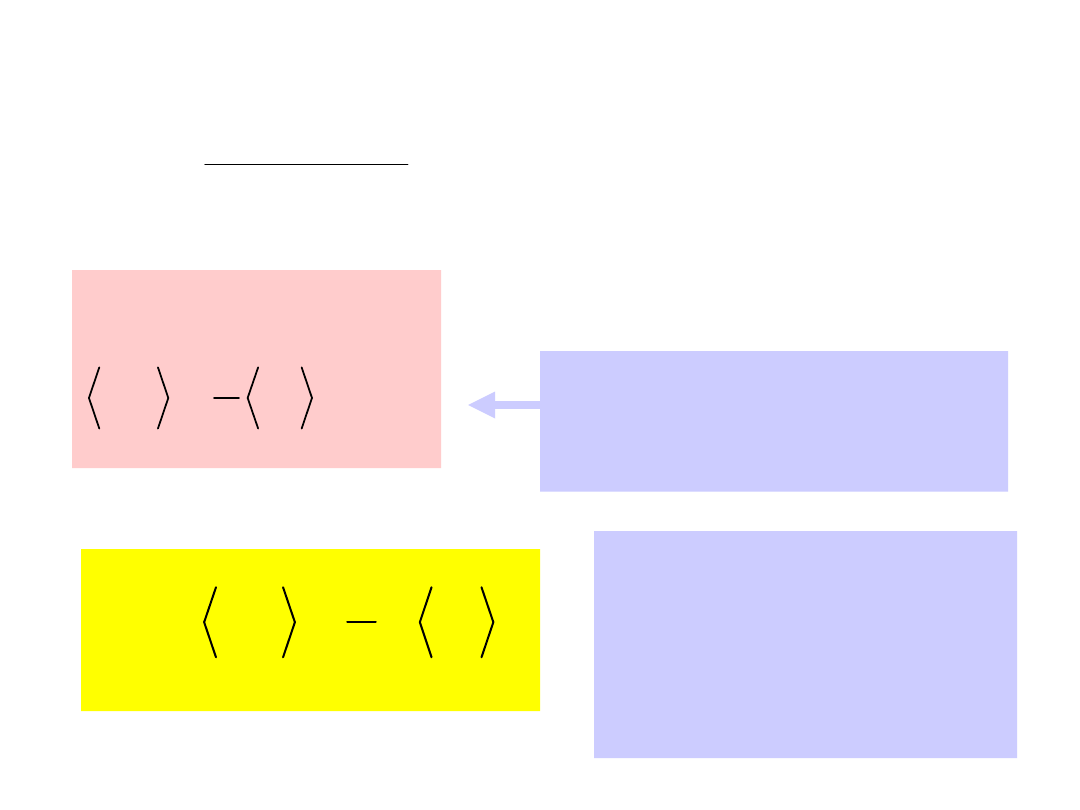
0

2

2

2

1

0

,

...

mn

N

v

v

mn

p

x

x

 - gęstość

2

2

2

2

2

2

v

3

1

v

v

v

v

v

x

z

y

x









Wszystkie kierunki
prędkości są
równoważne

2

2

v

3

1

v

p

x









Z prawa Pascala
wynika, że ciśnienie
wywierane na
wszystkie ścianki jest
jednakowe

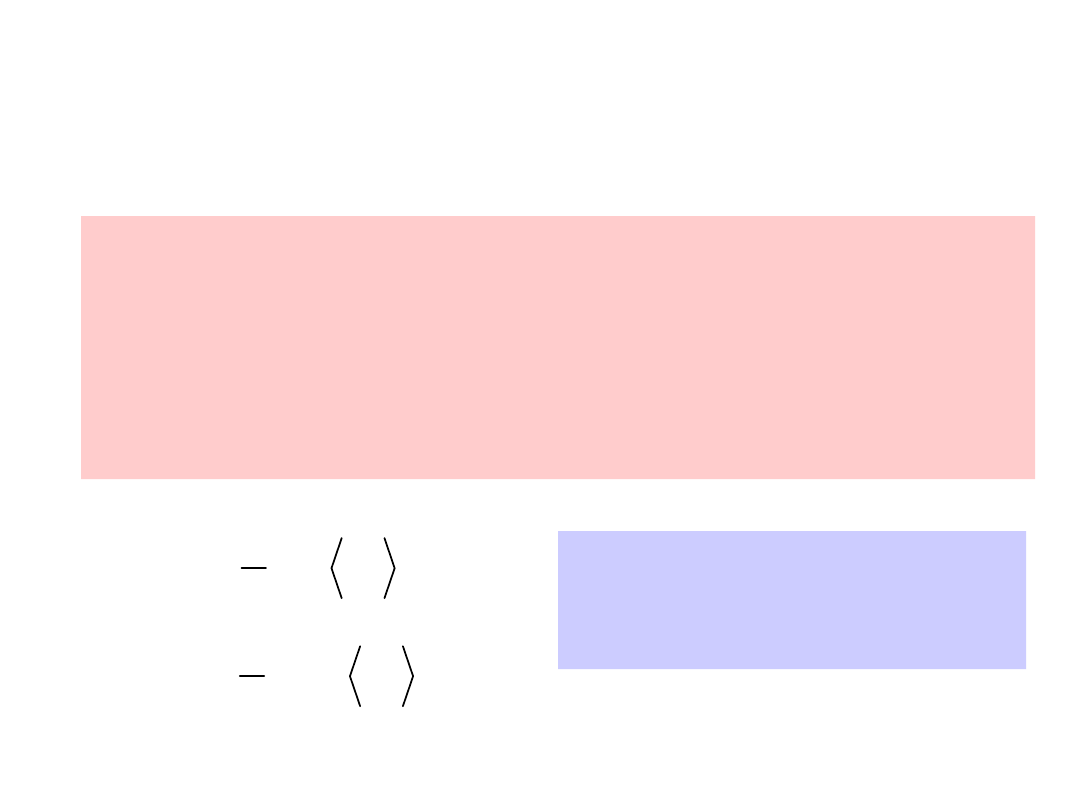
Kinetyczna interpretacja

temperatury

Jeżeli obie strony ostatniego równania
pomnożymy przez objętość V, a następnie
skorzystamy z równania gazu doskonałego,
to otrzymamy związek temperatury z
energią kinetyczną cząsteczek.

2

v

V

3

1

pV





2

v

V

n

3

1

pV





n - liczba moli

 - masa molowa

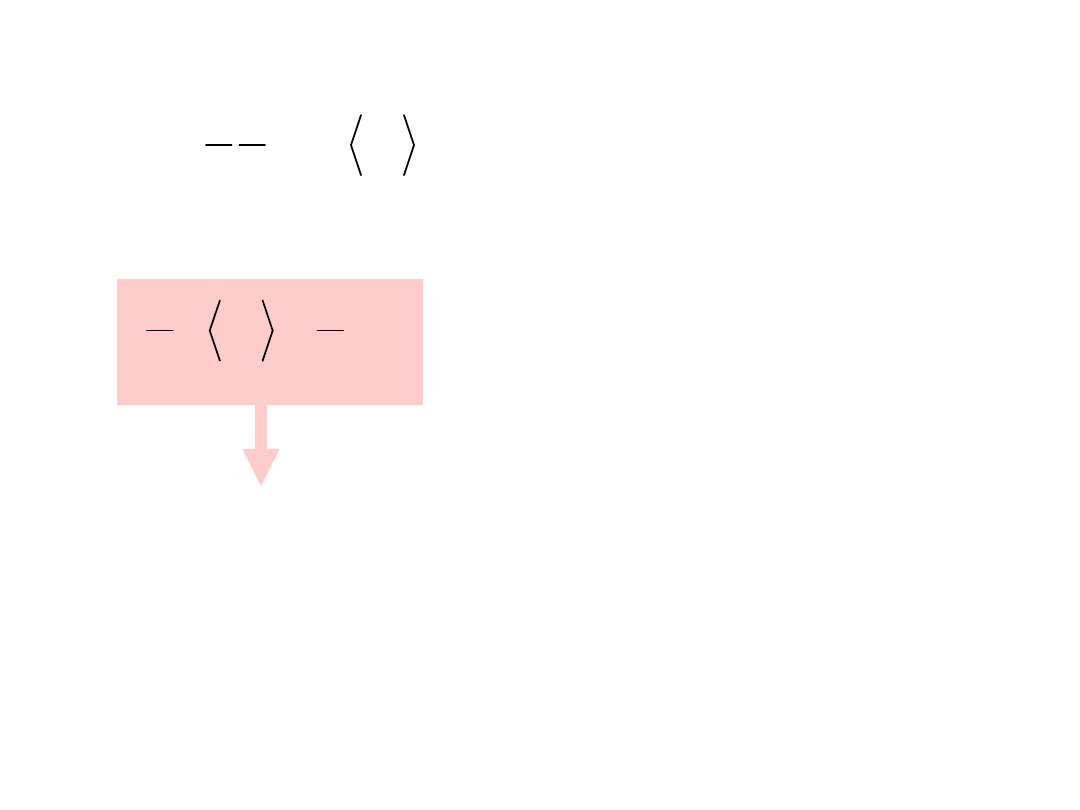
2

v

V

n

2

1

3

2

pV





RT

2

3

v

2

1

nRT

pV





2



Def. Temperatury: Całkowita energia
kinetyczna

ruchu postępowego jednego

mola gazu jest proporcjonalna do
temperatury.

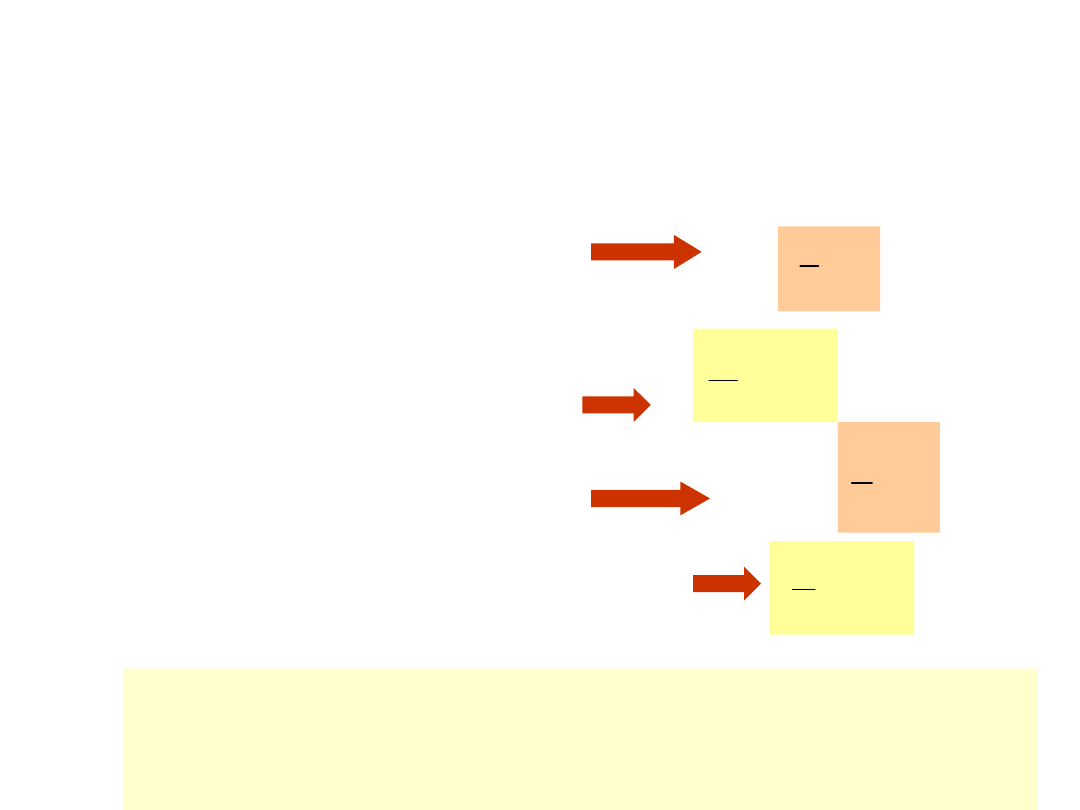
Zasada ekwipartycji energii

Energia cząsteczek gazu:

• Energia kinetyczna ruchu

postępowego opisana
wyrazami typu:

• Kinetyczna energia rotacji -
• Kinetyczna energia drgań

atomów tworzących
cząsteczkę -

• Energia potencjalna drgań

atomów tworzących
cząsteczkę -

2

x

mv

2

1

2

x

I

2

1



2

v

2

1



2

kx

2

1

k – stała sprężystości, µ - masa
zredukowana,  - prędkość kątowa I –

moment bezwładności

Dostępna energia zależy tylko od
temperatury i rozkłada się w
równych porcjach na sposoby, w
jakie cząsteczki mogą ją absorbować.

Każdy z niezależnych sposobów absorpcji
energii nazywany jest stopniem swobody.

Na każdy składnik energii przypada

½

RT

Clerc Maxwell:

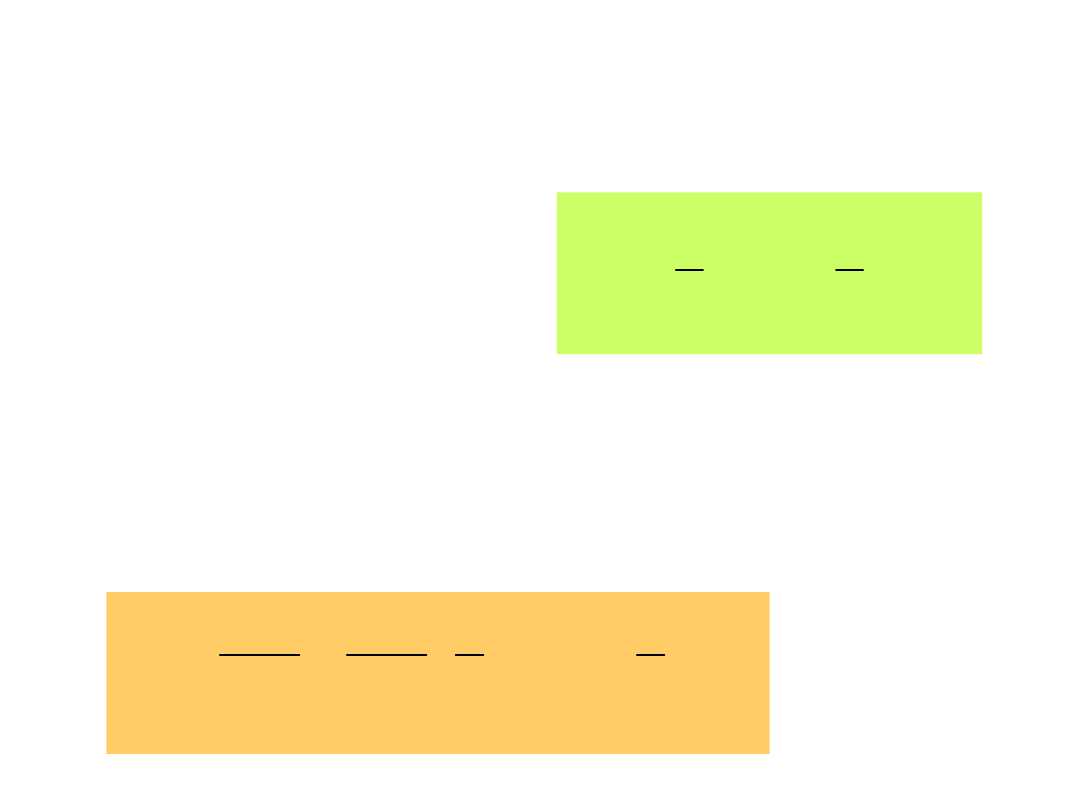
Ciepło właściwe

nRT

2

3

NkT

2

3

U





Energia wewnętrzna U
gazu doskonałego

N – liczba cząsteczek, n liczba moli

Ciepło właściwe gazu doskonałego w stałej
objętości

R

2

3

nRT

2

3

ndT

d

ndT

dU

c

v



















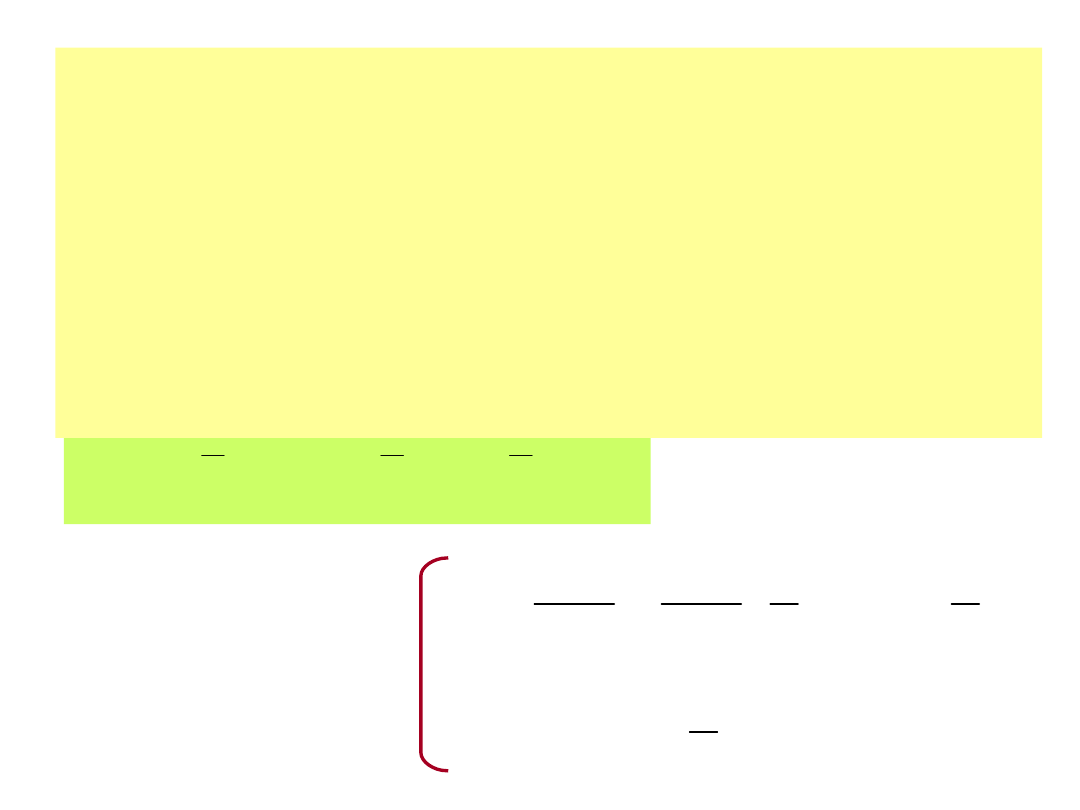
Dla gazów dwuatomowych, lub o jeszcze
bardziej złożonej strukturze energia
wewnętrzna jest sumą wszystkich rodzajów
energii. Przy obliczaniu ciepła właściwego
należy to uwzględniać.

Na przykład dla dla gazu dwuatomowego
(ruch postępowy i rotacyjny):

nRT

2

RT

2

1

n

RT

2

1

n

U

5

2

3































R

2

7

R

c

c

R

2

nRT

2

ndT

d

ndT

dU

c

v

p

v

























5

5

Obliczanie ciepła
właściwego w
stałej objętości c

v

i

przy stałym
ciśnieniu c

p

Rozkład Maxwella prędkości

cząsteczek

Prędkości poszczególnych cząsteczek gazu
są różne. Dla danego gazu istnieje
charakterystyczny rozkład prędkości, który
zależy od temperatury.

Podane przez Maxwella prawo rozkładu
prędkości cząsteczek ma postać:

 

kT

mv

e

v

kT

m

N

v

N

2

2

2

3

2

2

4





















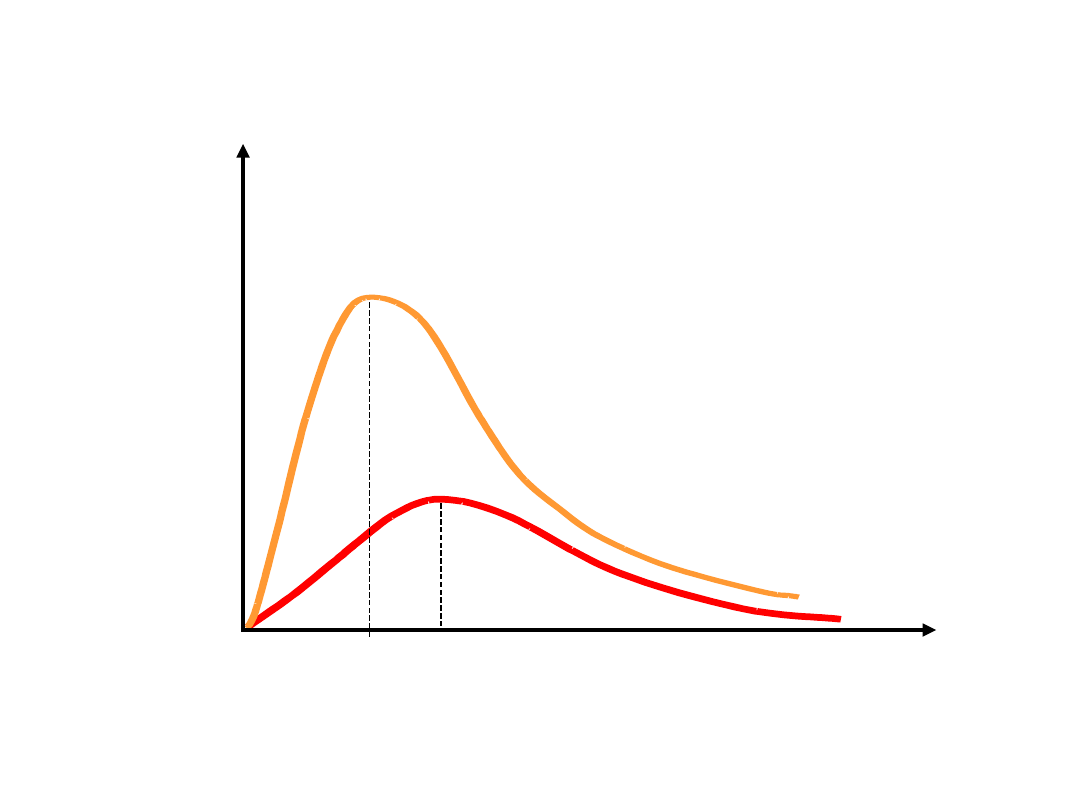
v

N(v
)

T

1

T

2

T

2

> T

1

v

p1

v

p2

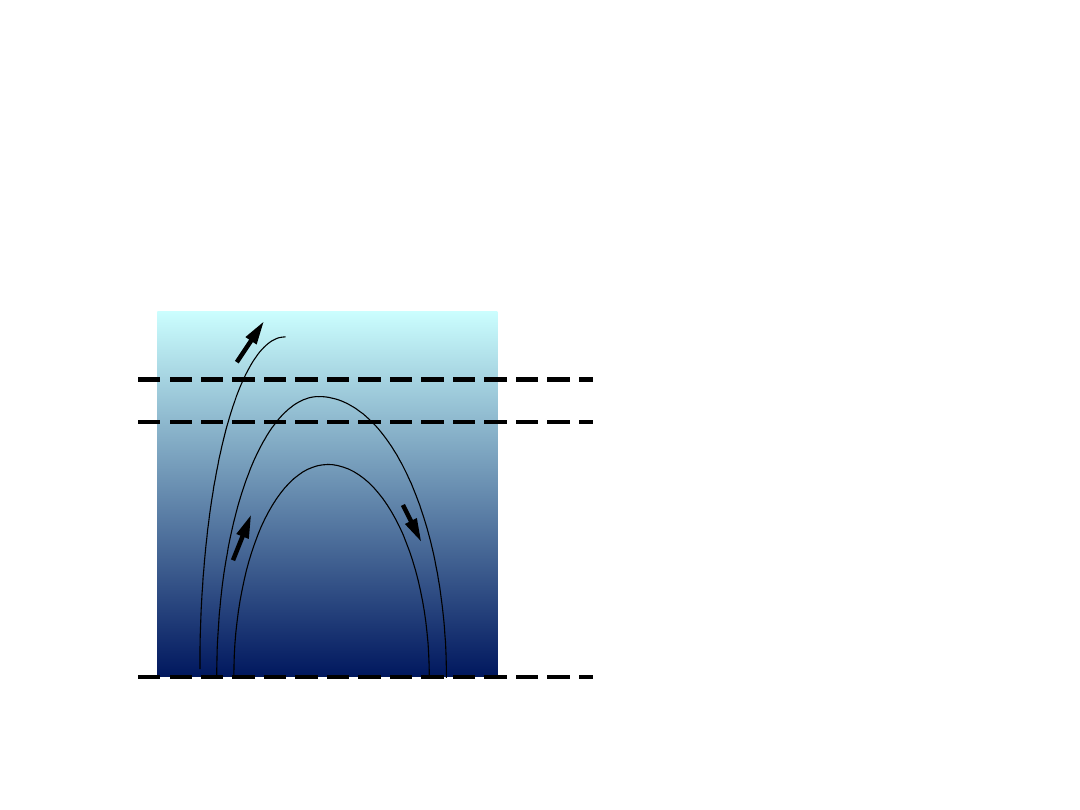
Boltzmann (1876 r.) wyprowadził prawo
rozkładu prędkości analizując zachowanie
cząsteczek gazu doskonałego w stałej
temperaturze T i w jednorodnym polu
grawitacyjnym.

z = 0

z

z + dz

n

v

– liczba cząstek gazu w jednostce

objętości, maleje ze wzrostem z

Ciężar gazu na jednostkę powierzchni w
warstwie o grubości dz równy różnicy ciśnień

dp

dz

mg

n

v





Na podstawie równania gazu doskonałego
można napisać:

kT

n

p

nRT

pV

v





0

N

V

n

n

v



0

N

V

n

n

v



objętość

Liczba

Avogadra

Liczba

moli

dz

kT

mg

n

dn

p

dp

v

v







Na podstawie poprzednich równań
otrzymujemy:

Po scałkowaniu otrzymujemy

kT

mgz

v

e

const

n





Zmiana n

v

po przejściu przez warstwę o

grubości dz:

dz

e

const

dn

kT

mgz

v







n

v

 gdy z 

Koncentracja maleje z wysokością.

 

2kT

mv

z

z

z

z

z

z

e

const

dv

v

n

mgdz

dv

mv

2







W warstwie o grubości dz część cząsteczek
gazu nie jest w stanie wydostać się wyżej.
Dla tych cząstek spełniony jest warunek:

mgz

mv

2

1

z



2

stąd

po
wyeliminowaniu z
i dz

Liczba cząstek na jednostkę
objętości o prędkościach w
przedziale v

z

, (v

z

+ dv

z

)

Otrzymany rozkład jest słuszny nawet przy
braku pola grawitacyjnego, stosować go
można dla cząsteczek poruszających się w
kierunku y i x. Można więc napisać:

 

 

2kT

mv

y

y

y

2kT

mv

x

x

x

y

x

e

const

dv

v

n

e

const

dv

v

n

2

2









Aby znaleźć rozkład prędkości N(v)
wprowadzamy przestrzeń prędkości.

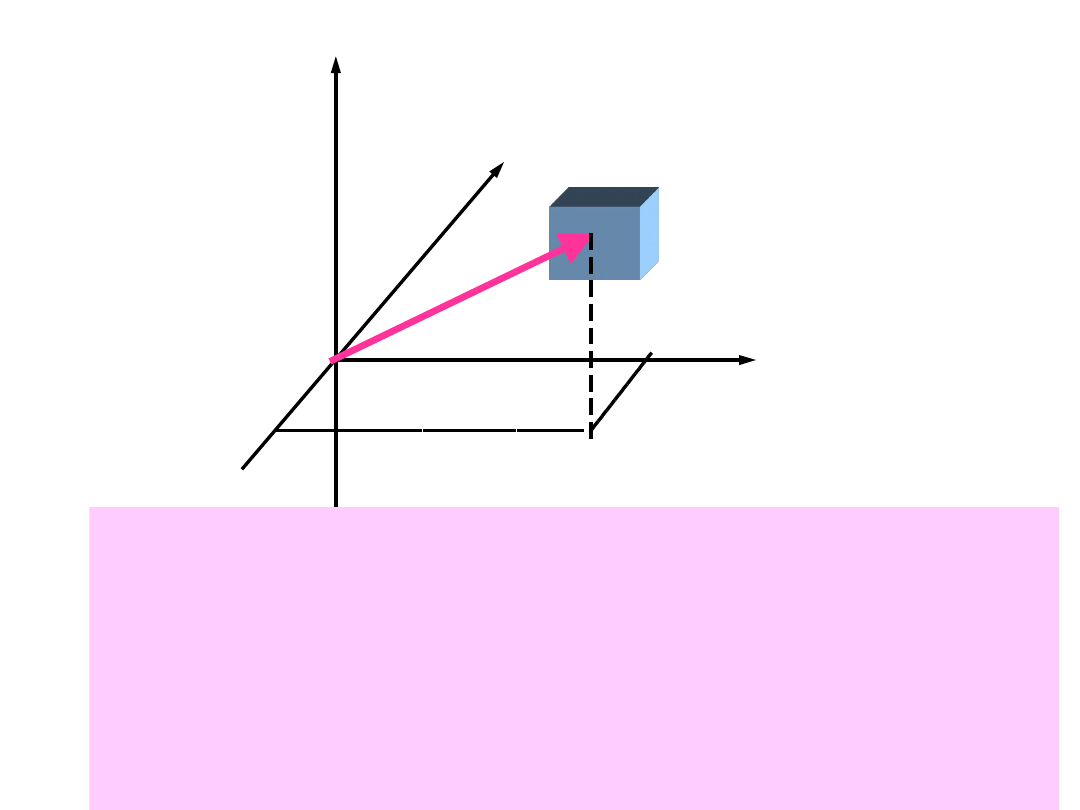
v

y

v

z

v

v

x

v

y

dv

x

dv

y

dv

z

v

x

Przestrzeń
prędkości

Dowolny punkt leżący wewnątrz elementu o
objętości dv

x

dv

y

dv

z

odpowiada cząstce, której

prędkości zawarte są w przedziale v

x

, v

x

+ dv

x

, v

y

, v

y

+ dv

y

, v

z

, v

z

+ dv

z

. Wyrażenie n

v

(v

x

) przedstawia

prawdopodobieństwa tego, że dana cząstka będzie
miała prędkości w przedziale (v

x

, v

x

+ dv

x

).

Podobnie n

v

(v

y

), n

v

(v

z

).

Prawdopodobieństwo tego, że dana
cząstka będzie miał trzy składowe
prędkości w konkretnych przedziałach
jest iloczynem trzech niezależnych
prawdopodobieństw, czyli

z

y

x

kT

mv

kT

mv

kT

mv

dv

dv

dv

e

e

e

const

z

y

x

2

2

2

2

2

2







ale

2

2

2

2

z

y

x

v

v

v

v











z

y

x

kT

mv

dv

dv

dv

e

const

2

2



stą
d

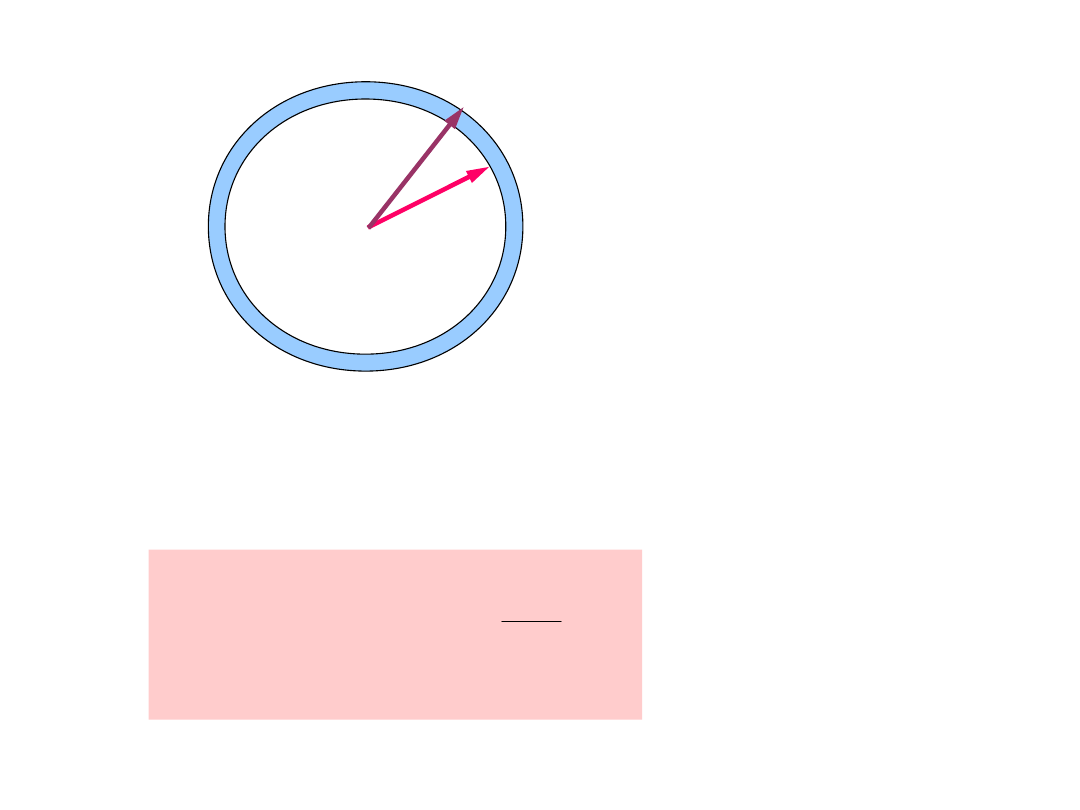
v

v +
dv

Równoważny
sześcianowi element
objętości w przestrzeni
prędkości - obszar
zawarty między dwiema
powierzchniami
kulistymi o objętości V.

dv

v

4

dv

dv

dv

V

z

y

x

2







 

dv

e

v

C4

dv

v

n

kT

mv

2

2

2







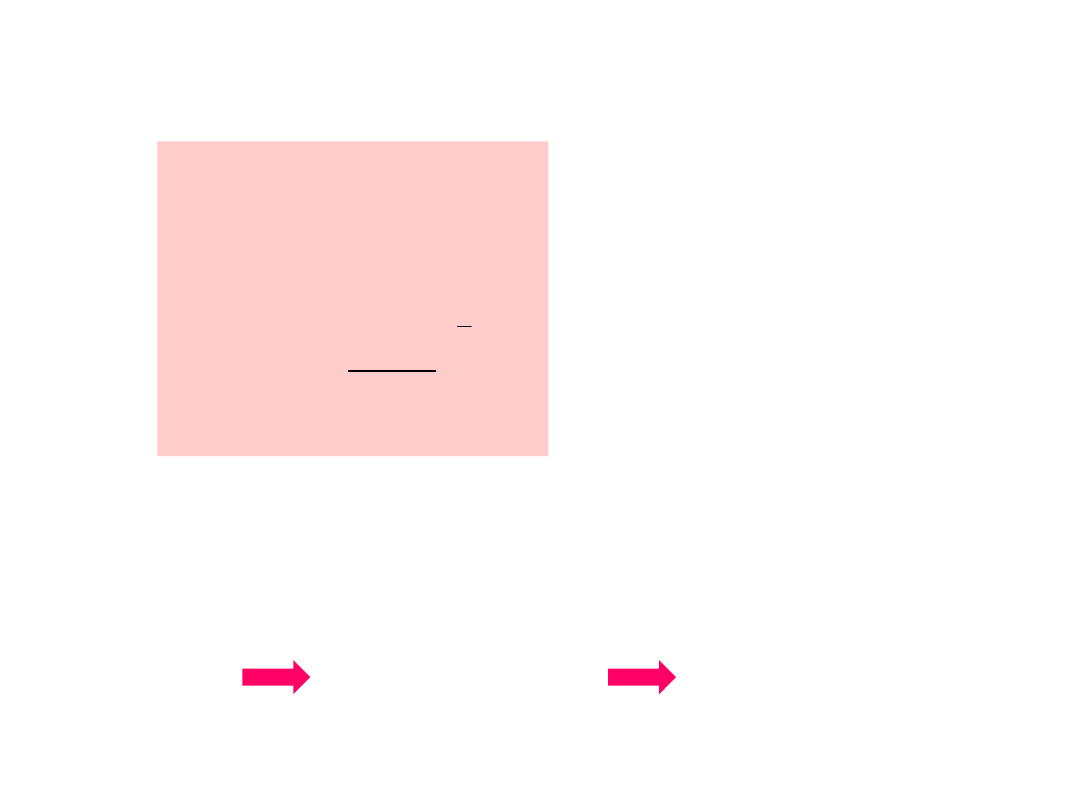
Stałą C wyznaczamy z warunku:

 

2

3

0

2





















kT

m

n

4

C

n

dv

v

n

v

v

v





Następnie koncentracje zastępujemy
liczbą cząstek w pewnym
rozpatrywanym obszarze.

n

v

V N

n

v

(v)V N(v)

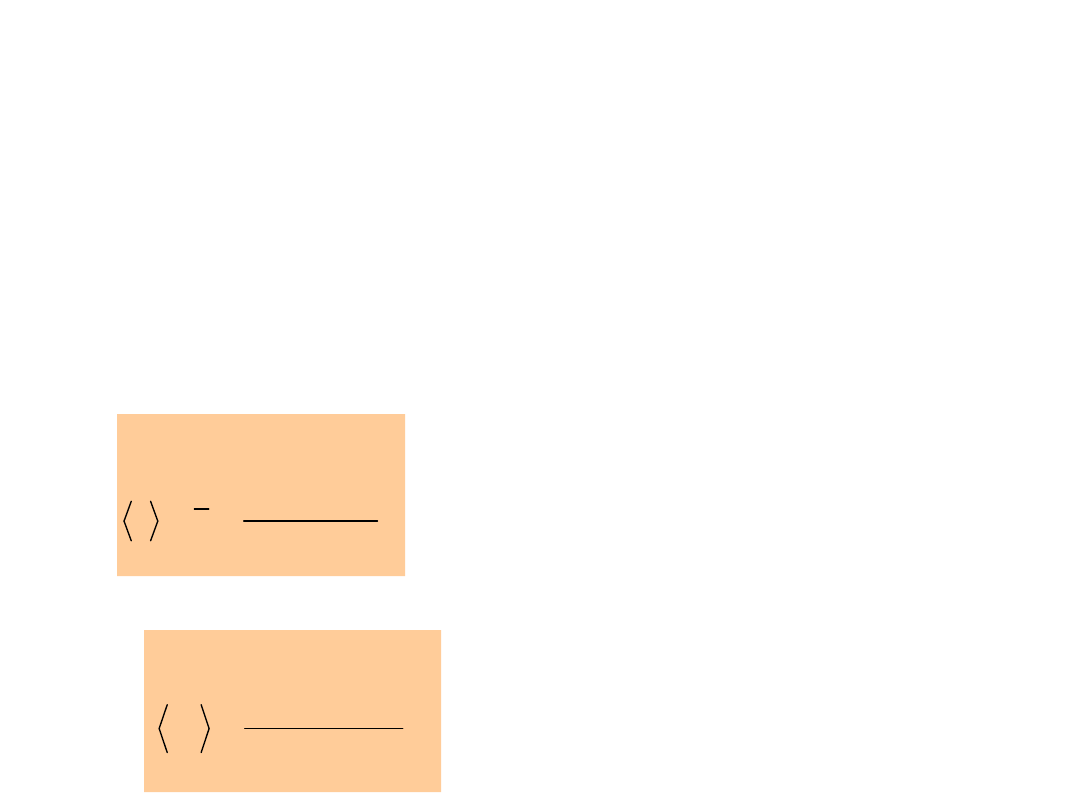
N

dv

v

v

N

v







0

2

2

)

(

Na postawie rozkładu Maxwella dla danej

temperatury obliczyć można:

1.

prędkość najbardziej

prawdopodobną v

p

- odpowiadająca

położeniu maksimum krzywej

2.

prędkość średnią <v>

3.

średni kwadrat prędkości <v

2

>

N

vdv

v

N

v

v









0

)

(

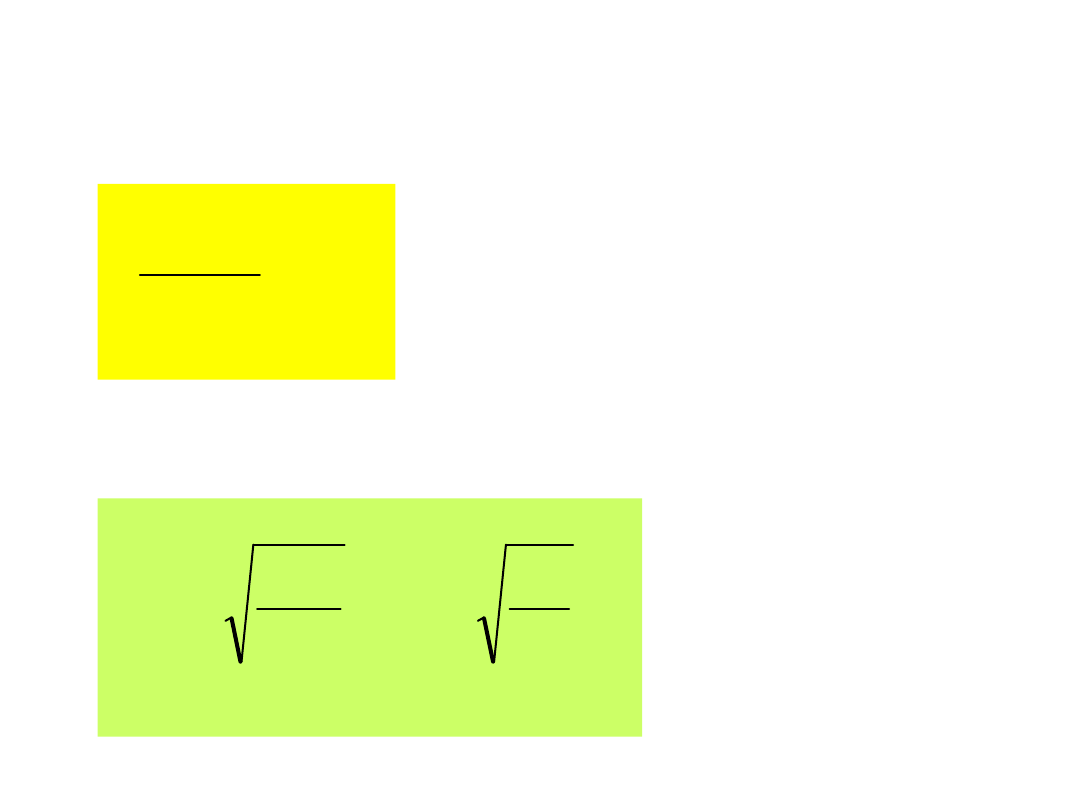
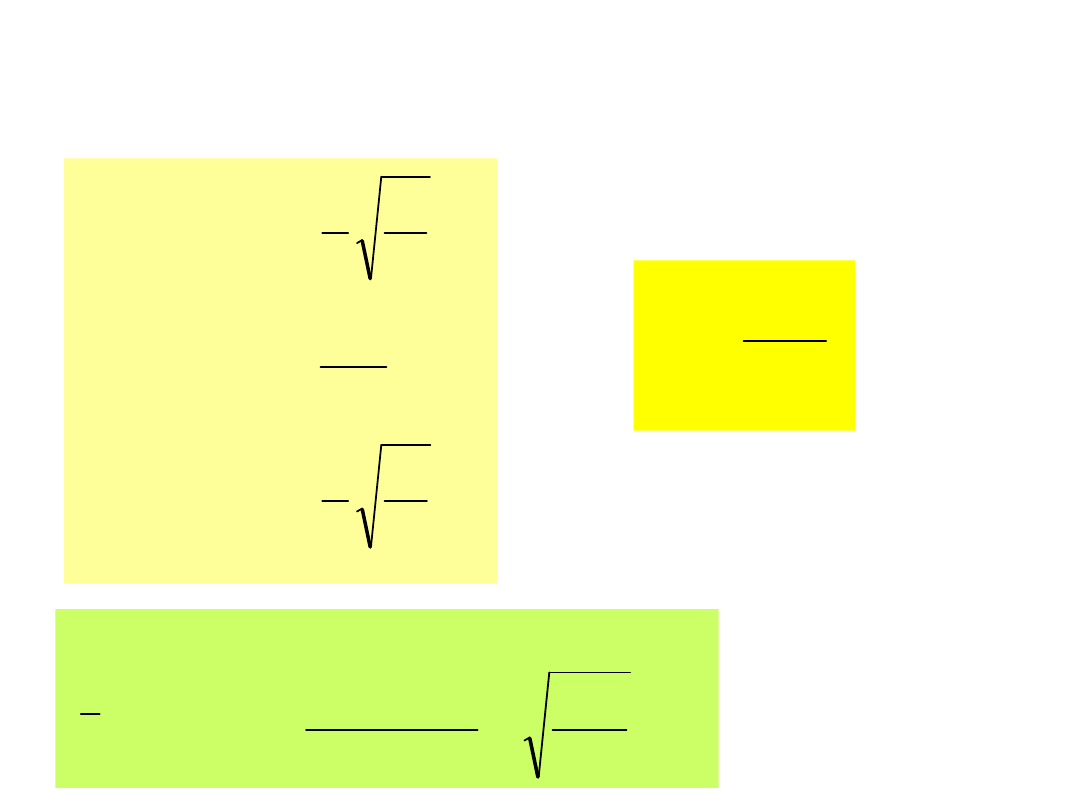
Ad 1. v

p

obliczamy żądając aby

 

0

dv

v

dN



otrzymujemy

m

kT

1.41

m

2kT

v

p





5

0

4

2

0

3

3

0

2

2

2

2

















8

3

dv

e

v

2

1

dv

e

v

4

1

dv

e

v

v

v

v

























Ad 2 . <V> obliczamy korzystając z
tablic całek

 

m

8kT

N

vdv

v

N

v

v

















0

gdzie

2kT

m





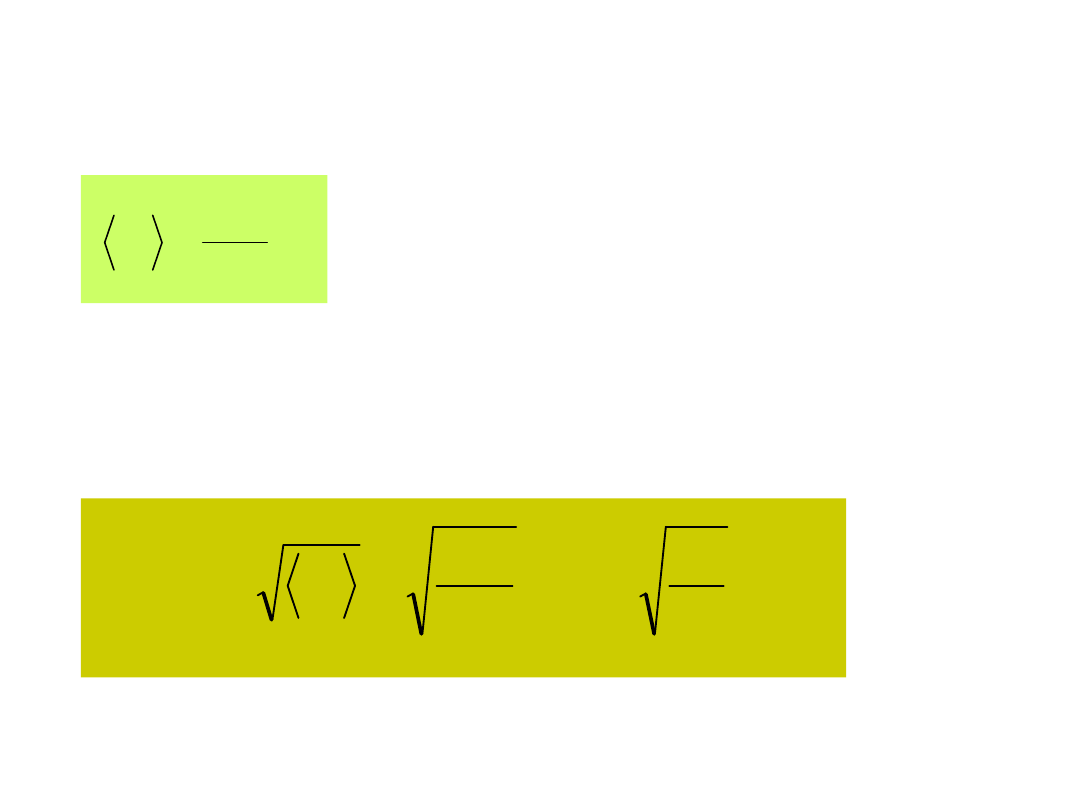
Ad 3 . <V

2

> obliczamy analogicznie

m

3kT

v 

2

Następnie obliczamy prędkość średnią
kwadratową v

śr.kw

m

kT

1.73

m

3kT

v

v

kw

śr







2

.