Proste zastosowania mechaniki kwantowej:
Cząstka swobodna:
Cząstka swobodna to obiekt o masie m poruszający się swobodnie.
Termin „swobodna” oznacza, że na cząstkę nie działa żaden
potencjał. Całkowita energia cząstki (E) jest sumą energii
kinetycznej (T) i potencjalnej (V), wobec tego:
E = T + V , ale ponieważ (dla cząstki swobodnej) V = 0 , to E = T
Dla uproszczenia rozpatrujemy przypadek jednowymiarowy, czyli
cząstkę o masie m poruszającą się wzdłuż osi x. Energia kinetyczna
(a zarazem całkowita) tego układu jest dana przez:
gdyż
Operator Hamiltona dla takiego wyrażenia na energię ma postać:
(dowód na ćwiczeniach), natomiast równanie Schrödingera dla
cząstki swobodnej jest następujące:
m
p
T
E
x
2
2
m
p
m
v
m
m
v
m
m
m
mv
mv
T
x
x
x
x
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ˆ
dx
d
m
H
n
n
n
E
dx
d
m
2
2
2
2
Pomnóżmy to równanie obustronnie przez
, otrzymamy
wówczas:
Przenosząc następnie prawą stronę i podstawiając k
n2
= 2m
E
n
/ ħ
2
otrzymujemy:
Okazuje się, iż rozwiązaniem powyższego równania są funkcje:
φ
+
=N
+
exp(ik
n
x) oraz φ
–
=N
–
exp(–ik
n
x) ,
natomiast rozwiązaniem ogólnym jest ich liniowa kombinacja,
czyli
ψ
n
= a
1
N
+
exp(ik
n
x) + a
2
N
–
exp(–ik
n
x)
2
2
m
n
n
n
E
m
dx
d
2
2
2
2
0
2
2
2
n
n
n
k
dx
d
Współczynniki normalizacyjne N
+
i N
–
można łatwo wyznaczyć z
warunku normalizacyjnego funkcji ψ
n
(jeżeli założymy, że cząstka
może się poruszać w ograniczonym obszarze (patrz podręcznik
Kołosa).
Funkcja falowa dla cząstki swobodnej reprezentuje falę materii
(falę de Broglie’a), co można wykazać porównując wyrażenie na
ψ
n
z równaniem fali znanym z fizyki.
Można sprawdzić (dowód na ćwiczeniach), że operator Hamiltona
dla cząstki swobodnej komutuje z operatorem pędu oraz z
operatorem kwadratu pędu
(czyli oraz ).
Ponieważ operatory przemienne posiadają wspólne funkcje
własne (dowód na ćwiczeniach), to funkcje własne hamiltonianu
(φ
+
oraz φ
–
) są także funkcjami własnymi operatora pędu i
operatora kwadratu pędu, czyli zapisujemy:
oraz
x
pˆ
2
ˆ
x
p
x
x
p
pˆ
2
2
ˆ
x
x
p
p
Po wstawieniu operatora pędu (lub kwadratu pędu) do tych równań i
zróżniczkowaniu (patrz ćwiczenia) otrzymamy następujące wartości
własne dla pędu:
p
x
= ħk
n
(w przypadku funkcji φ
+
) oraz p
x
= – ħk
n
(w przypadku
funkcji φ
–
).
Dla kwadratu pędu otrzymujemy natomiast następujące wartości własne
(patrz ćwiczenia):
p
x2
= ħ
2
k
n2
(w przypadku funkcji φ
+
) oraz p
x2
= ħ
2
k
n2
(w przypadku
funkcji φ
–
).
W obu stanach (φ
+
oraz φ
–
) wartość własna operatora kwadratu pędu jest
jednakowa, natomiast wartości własne operatora pędu różnią się znakiem.
Interpretacja: funkcja φ
+
opisuje stan cząstki poruszającej się w
dodatnim kierunku osi x, natomiast funkcja φ
–
opisuje stan cząstki
poruszającej się w ujemnym kierunku osi x.
Cząstka w pudle potencjału:
(inaczej: cząstka w studni potencjału o nieskończonej głębokości).
Cząstka poruszająca się w pewnej ograniczonej przestrzeni
(obszar jest ograniczony barierą potencjału o nieskończonej
wysokości, przez którą cząstka nie może się przedostać).
Rozpatrujemy (dla uproszczenia) przypadek jednowymiarowy
(kierunek x). Rozmiar pudła: od x=0 do x=L:
Energia potencjalna (V) cząstki wynosi:
W obrębie pudła cząstka porusza się swobodnie (nie działa na nią
żaden potencjał). Obszar gdzie V=∞ jest dla niej niedostępny.
V =
8
V =
8
|
|
|
|
x
0
L
L
x
dla
L
x
dla
x
dla
V
0
0
0
W obszarze dla cząstki niedostępnym, funkcja falowa układu ψ =
0. Wewnątrz pudła ψ ≠ 0, ale ponieważ funkcja ψ musi być ciągła,
to musi ona znikać na brzegach (krańcach) pudła, czyli dla x=0
oraz dla x=L (są to tzw. warunki brzegowe)
Wewnątrz pudła cząstka zachowuje się tak, jak cząstka swobodna,
a więc rozwiązaniem równania Schrödingera jest funkcja:
ψ
n
= a
1
N
+
exp(ik
n
x)+a
2
N
–
exp(–ik
n
x)
Sprowadzenie równania do postaci rzeczywistej (wzory Eulera) i
nałożenie
dodatkowych
warunków
(brzegowych)
oraz
normalizacja prowadzi ostatecznie do
funkcji falowej dla cząstki w jednowymiarowym pudle potencjału:
(gdzie (2/L)
½
jest współczynnikiem normalizacyjnym, który zależy
od rozmiaru pudła potencjału).
x
L
n
L
n
sin
2
Rozwiązanie ψ
n
oraz warunki brzegowe (znikanie ψ
n
dla x=0 i
x=L) są dla cząstki w pudle identyczne jak w przypadku drgającej
struny, zamocowanej w punktach x=0 i x=L.
Znikanie funkcji ψ
n
dla x=0 jest spełnione gdyż sin(nπx/L)=0 dla
x=0.
Aby funkcja ψ
n
znikała również dla x=L musi być sin(nπL/L)=0,
a więc sin(nπ)=0, co jest prawdziwe tylko dla n=1, 2, 3,...
Pamiętając, że k
n2
= 2m E
n
/ ħ
2
(tak, jak dla cząstki swobodnej),
otrzymujemy wyrażenie na energię całkowitą cząstki w pudle:
a ponieważ dla drgającej struny funkcja falowa jest następująca:
φ
n
=A∙sin(k
n
x), więc czynnik k
n2
=(nπ/L)
2
.
Wobec tego:
m
k
E
n
n
2
2
2
,...
3
,
2
,
1
8
)
2
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
n
dla
mL
h
n
mL
h
n
L
m
n
E
n
x
L
n
L
n
sin
2
Energia cząstki w pudle jest więc skwantowana (może przyjmować
tylko określone wartości), w przeciwieństwie do energii cząstki
swobodnej.
Kwantowanie energii jest w tym przypadku (oraz w wielu
innych sytuacjach) konsekwencją uwzględnienia warunków
brzegowych.
Wykorzystując wzór na energię cząstki w pudle można znaleźć
odpowiednie wartości liczbowe (E
1
, E
2
, E
3
, itd.), czyli poziomy
energetyczne, oraz stwierdzić, że odstępy między poziomami
energetycznymi maleją wraz ze wzrostem rozmiarów pudła.
W granicy, kiedy rozmiar pudła dąży do nieskończoności (L→∞),
odstępy między poziomami energetycznymi dążą do zera, czyli
dyskretne widmo energii przechodzi w widmo ciągłe.
Widmo
ciągłe
energii
(czyli
brak
kwantowania)
jest
charakterystyczne dla cząstki swobodnej, co jest zrozumiałe, gdyż
rozsunięcie do nieskończoności ścian pudła (L→∞) prowadzi do
„oswobodzenia” uwięzionej w nim cząstki.
(Wykresy funkcji falowych dla cząstki w pudle – patrz podręcznik
Kołosa).
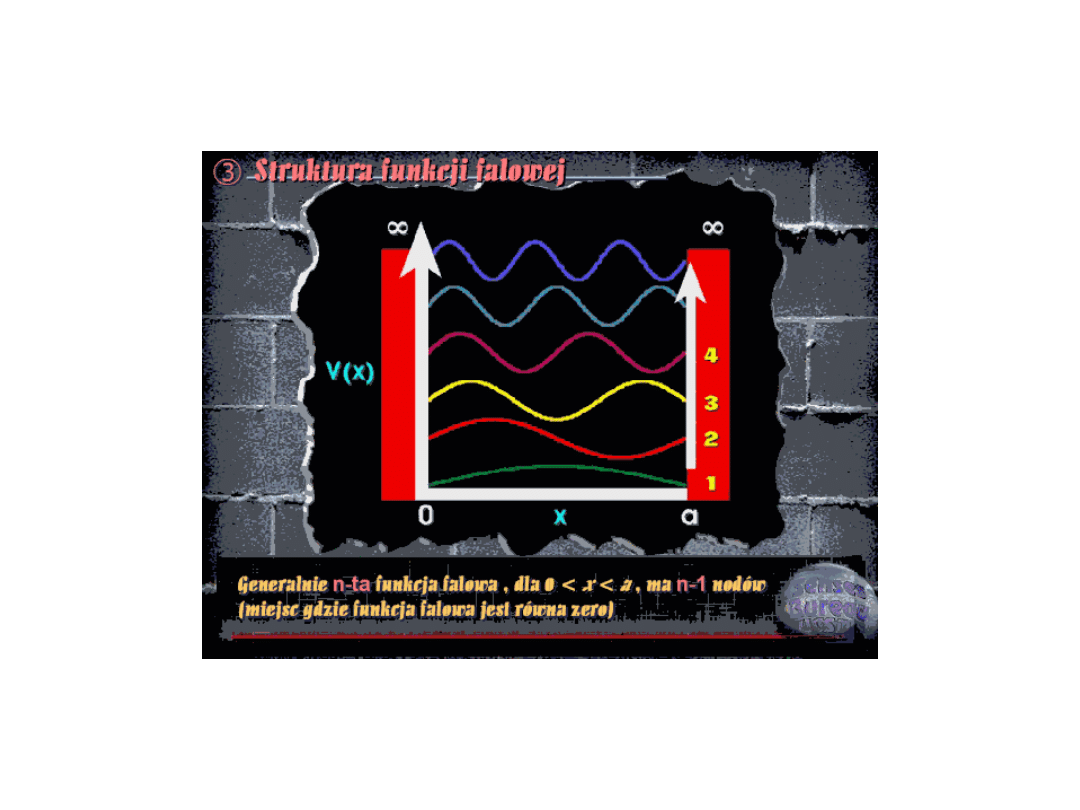
Wykresy funkcji falowych dla cząstki w pudle
0
L
Dygresja: najważniejsze operatory (wyrażone we
współrzędnych kartezjańskich):
Operator wektorowo-różniczkowy „nabla” (symbol ),
nazywany także „operatorem gradientu”
Operator różniczkowy „nabla kwadrat” (symbol )
(nazywany także operatorem Laplace’a lub laplasjanem –
symbol Δ)
Operator Laplace’a występuje bardzo często w równaniu
Schrödingera, np. dla cząstki swobodnej, zamiast pisać
możemy napisać
natomiast dla cząstki swobodnej poruszającej się w trzech
wymiarach (x,y,z) mamy
albo
z
k
y
j
x
i
2
2
2
2
2
2
2
x
y
z
�
�
�
D=
+
+
�
�
�
E
dx
d
m
2
2
2
2
E
m
x
2
2
2
2
2
2
2
2
2
2
E
m
x
y
z
y
�
�
�
�
�
-
�
+
+
=
�
�
�
�
�
�
�
h
E
m
2
2
OSCYLATOR HARMONICZNY
Oscylatorem harmonicznym nazywamy układ, w którym na cząstkę o
masie m poruszającą się wzdłuż prostej działa siła F proporcjonalna
do wychylenia i skierowana do położenia równowagi.
Rozważamy przypadek jednowymiarowy (kierunek x).
Siła F jest proporcjonalna do wychylenia x (przeciwnie skierowana), a
współczynnik proporcjonalności k nazywamy stałą siłową.
Jak wiadomo z kursu fizyki, siła to ujemny gradient potencjału, czyli
F= –dV/dx,
a zatem mamy –kx = –dV/dx, i dalej dV = kx∙dx
Całkując to równanie: ∫ dV = ∫ kx∙dx otrzymujemy V = ½kx
2
czyli wyrażenie na energię potencjalną oscylatora harmonicznego.
Ponieważ energia kinetyczna oscylatora wynosi T=p
x2
/2m, to
całkowita energia oscylatora jest dana przez:
0
X
0
X
m
m
F = k x
2
2
2
1
2
kx
m
p
V
T
E
x
Utworzony zgodnie z regułami Jordana operator Hamiltona dla
oscylatora harmonicznego ma postać:
Natomiast odpowiednie równanie Schrödingera jest następujące:
Pomnóżmy obie strony przez -2m/ħ
2
i przenieśmy prawą stronę:
czyli inaczej zapisując
Podstawmy teraz
2
=km/ħ
2
; λ=2mE/ħ
2.
Stosując te oznaczenia
możemy przepisać równanie jako:
czyli
Wprowadzamy następnie nową zmienną: , otrzymując:
Ponieważ:
(pochodna funkcji uwikłanej), więc:
a zatem:
2
2
2
2
2
1
2
ˆ
kx
dx
d
m
H
E
kx
dx
d
m
2
2
2
2
2
1
2
2
2
2
2
2
2
0
d
m
m
kx
E
dx
y
y
y
-
+
=
h
h
0
2
2
2
2
2
2
mE
x
km
dx
d
0
2
2
2
2
x
dx
d
0
)
(
2
2
2
2
x
dx
d
x
0
)
(
)
(
2
2
2
d
d
dx
d
d
dx
dx
d
d
x
d
1
])
[
(
2
2
2
2
1
1
])
[
(
dx
d
d
dx
dx
dx
d
d
d
x
d
2
2
2
2
d
d
dx
d
Mamy więc teraz równanie względem nowej zmiennej ζ
(związanej z dotychczasową zmienną x poprzez wyrażenie:
Zbadajmy najpierw rozwiązania równania
dla dużych wartości | x |. Duże wartości | x | oznaczają zarazem
duże wartości | ξ |. Jeżeli | ξ | jest duże, to w powyższym równaniu
można pominąć λ/α. Otrzymamy wówczas asymptotyczną postać
równania,
którego
rozwiązania
będą
rozwiązaniami
asymptotycznymi (prawdziwymi w obszarze dużych wartości | ξ |).
Równanie to spełnia w przybliżeniu (dla dużych | ξ |) funkcja ψ
as
=
exp( ±ξ
2
/ 2), co można łatwo pokazać (przez podstawienie):
x
0
)
(
)
(
2
2
2
d
d
0
2
2
2
as
as
d
d
Zapiszmy równanie podstawiając funkcję ψ
as
= exp( ξ
2
/ 2) :
czyli,
;
czyli,
Widać, że równanie asymptotyczne jest (w przybliżeniu) spełnione
dla funkcji
ψ
as
= exp( ±ξ
2
/ 2) – dla dużych wartości | ξ | element +1
w nawiasie jest zaniedbywalny.
Wyrażenie ψ
as
= exp( ±ξ
2
/2) opisuje w rzeczywistości dwie funkcje
(jedna z dodatnim, a druga z ujemnym wykładnikiem).
0
2
2
2
as
as
d
d
as
as
d
d
2
2
2
2
/
2
2
/
2
/
2
2
2
1
e
e
e
2
/
2
2
/
2
2
2
2
e
e
d
d
2
/
2
2
/
2
2
e
e
d
d
2
/
2
2
2
/
2
2
1
e
e
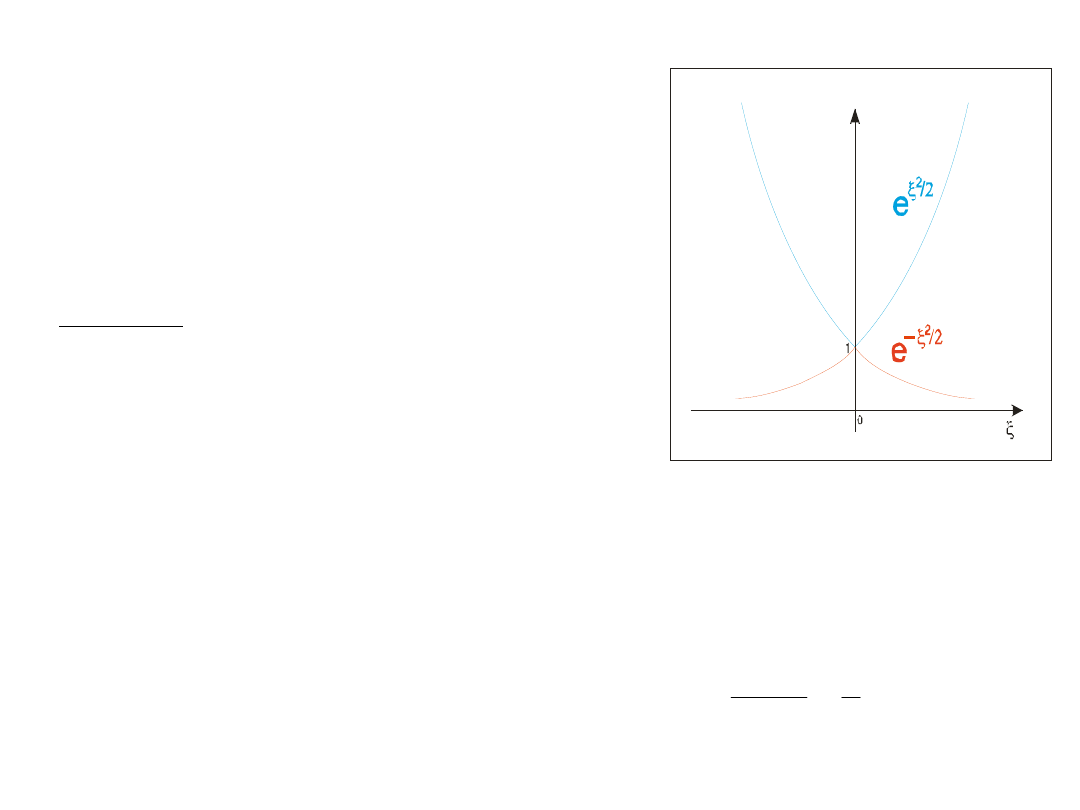
Funkcję ψ
as
= exp( ξ
2
/ 2) (z dodatnim
wykładnikiem) odrzucamy, gdyż nie jest to
funkcja klasy Q (nie znika w nieskończoności).
Funkcja
ψ
as
= exp( –ξ
2
/ 2) jest natomiast funkcją
klasy Q.
Wniosek: asymptotyczne zachowanie funkcji
falowej dla oscylatora harmonicznego opisuje
funkcja ψ
as
= exp( –ξ
2
/ 2)
Rozwiązanie asymptotyczne jest poprawne dla
dużych | ξ | (czyli dla dużych | x | ). Szukamy
teraz rozwiązania dla wszystkich wartości x.
Rozwiązanie
to
znajdziemy
poprzez
„poprawienie” funkcji asymptotycznej tak, aby
była poprawna w całym zakresie x.
Poprawiamy funkcję asymptotyczną mnożąc ją
przez pewną nową funkcję f (ξ ), czyli
szukamy rozwiązań postaci ψ = ψ
as
∙ f (ξ ).
Podstawiamy funkcję ψ = exp(–ξ
2
/2) ∙ f (ξ )
do równania
.
0
)
(
)
(
2
2
2
d
d
Otrzymujemy:
Funkcja exp(–ξ
2
/2) jest zawsze różna od zera, więc równanie to może
być spełnione tylko wtedy gdy
Okazuje się, że powyższe równanie należy do pewnej klasy równań
różniczkowych, których rozwiązaniami są tzw. wielomiany Hermite’a
zdefiniowane wzorem:
przy czym spełniony musi być warunek
, v=0, 1, 2, …
aby pełna funkcja falowa ψ była funkcją klasy Q.
Jak łatwo zauważyć,
H
0
=1;
H
1
=2 ξ ;
H
2
=4 ξ
2
–2 ;
H
3
= 8 ξ
3
–12 ξ , i tak dalej.
(rzeczywiście są to wielomiany stopnia v zmiennej ξ )
0
1
2
2
/
exp
2
2
2
f
d
df
d
f
d
0
1
2
2
2
f
d
df
d
f
d
v
v
v
v
d
d
H
)
exp(
)
exp(
)
1
(
)
(
2
2
v
2
1
Ostatecznie, funkcja falowa będąca dokładnym rozwiązaniem
równania Schrödingera dla oscylatora harmonicznego jest
następująca:
przy czym kwantowanie energii będzie wynikało z konieczności
spełnienia warunku :
gdzie v=0, 1, 2, ...).
Jeżeli w powyższym równaniu rozpiszemy zdefiniowane wcześniej
symbole
λ i α, ( pamiętamy, że α
2
=km/ħ
2
; λ=2mE/ħ
2
), dostaniemy:
i dalej:
(*)
Korzystając z klasycznego wzoru na częstość drgań oscylatora:
wyznaczamy:
)
(
)
2
/
exp(
2
v
v
v
H
N
v
m
k
mE
v
2
1
2
2
v
k
m
E
v
2
1
2
m
k
2
1
0
0
2
1
k
m
v
2
1
Wstawiając ostatnie równanie do równania (*) otrzymujemy
; i dalej
Stąd
wyrażenie
na
energię
kwantowego
oscylatora
harmonicznego:
Ostatecznie:
v
E
v
2
1
2
1
2
0
1
2
0
v
E
v
0
0
0
2
1
2
)
1
2
(
)
1
2
(
h
v
h
v
v
E
v
0
2
1
h
v
E
v
0
2
1
h
v
E
v
(v = 0, 1, 2,
...)
Widać, że energia oscylatora jest skwantowana. Indeks v
jest liczbą kwantową.
Liczbę tę nazywamy liczbą kwantową oscylacji.
Energia oscylatora zależy od liczby v oraz od częstości ν
0
i
może przyjmować tylko wartości:
E
0
=
1
/
2
∙hν
0
(dla v=0);
E
1
=
3
/
2
∙hν
0
(dla v=1);
E
2
=
5
/
2
∙hν
0
(dla v=2), i tak dalej.
Widać, że odległość między sąsiednimi poziomami energetycznymi
oscylatora jest stała i wynosi hν
0
Energia oscylatora kwantowego nie może być nigdy równa zeru.
Stan o najniższej możliwej energii (dla v=0) ma energię ½∙hν
0
Energia E
0
=½∙hν
0
nosi nazwę zerowej energii oscylacji.
Oscylacje atomów lub jonów w kryształach zależą od
temperatury (im wyższa temperatura tym większa energia
oscylacji).
Widać, że nawet w temperaturze 0 K (zero bezwzględne)
oscylacje atomów (jonów) w sieci krystalicznej nie ustają
(energia oscylatora jest większa od zera nawet w
temperaturze T=0 K).
Oscylator harmoniczny jest stosowany w chemii jako
model drgającej cząsteczki dwuatomowej (zamiast
ruchu dwóch mas rozważa się wtedy ruch jednej masy,
tzw. masy zredukowanej).
Oscylator klasyczny i oscylator kwantowy
(i)
Energia oscylatora klasycznego może być równa zeru, natomiast energia
oscylatora kwantowego jest zawsze większa od zera.
(ii) Oscylator klasyczny może być w stanie spoczynku (masa nie porusza się).
Oscylator kwantowy nie może być w stanie spoczynku
(oscylacje zachodzą zawsze).
(iii) Największe prawdopodobieństwo znalezienia drgającej masy
w oscylatorze
klasycznym jest w pobliżu punktów zwrotu (maksymalne
wychylenie), a w
oscylatorze kwantowym w położeniu równowagi (dla małych
wartości liczby
kwantowej oscylacji).
(iv) Wraz ze wzrostem liczby kwantowej oscylacji, oscylator kwantowy staje się
coraz bardziej podobny do oscylatora klasycznego (drgająca masa najczęściej
przebywa w pobliżu punktów zwrotu).
(v) W oscylatorze kwantowym drgająca masa (cząstka) może
penetrować
obszary klasycznie niedostępne (dalsze niż punkty
maksymalnego
wychylenia), co w oscylatorze klasycznym jest niemożliwe.
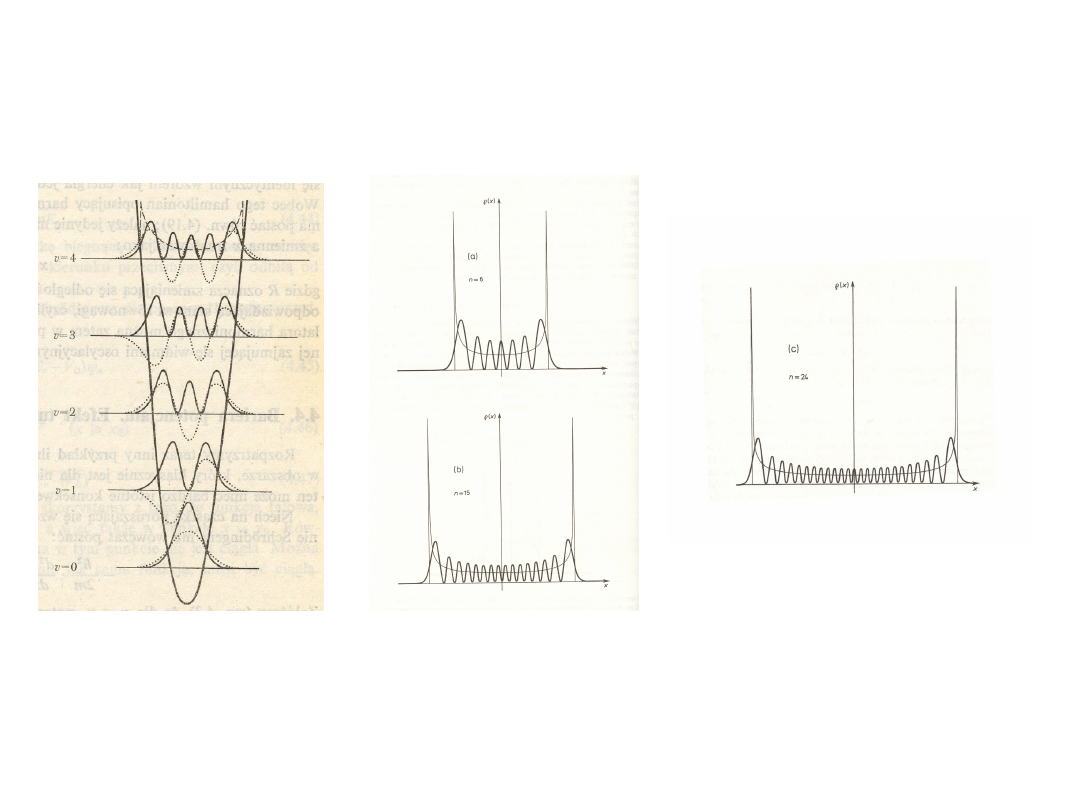
Poziomy energetyczne oscylatora kwantowego oraz odpowiadające im
kwadraty funkcji falowych (linie ciągłe):
(oscylator kwantowy i klasyczny dla v=0-4, 6, 15, 24)
Document Outline