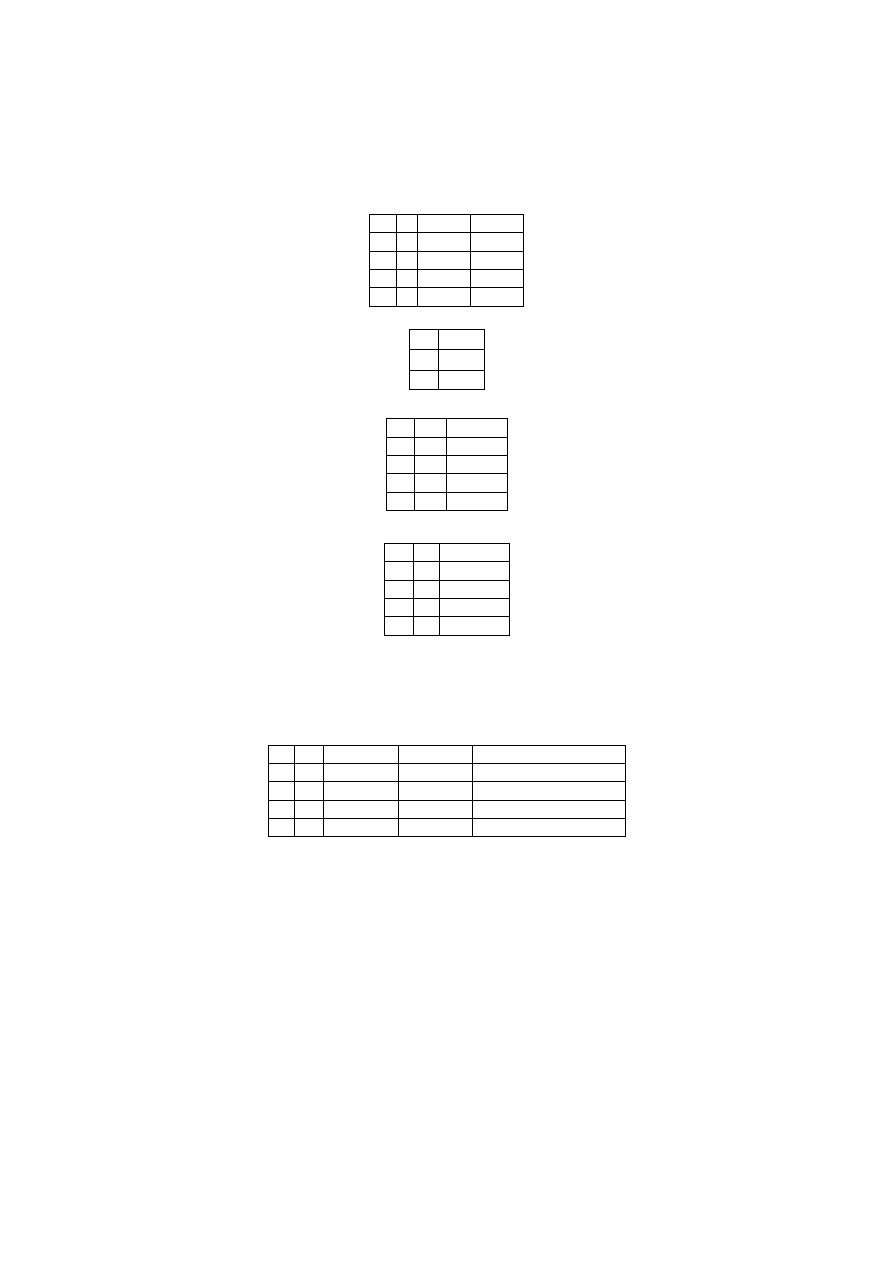
Strona 1 z 19
Analiza matematyczna 1
KRÓTKI KURS LOGIKI
–> Zdanie w logice (p, q) jest prawdziwe lub fałszywe. Zdanie, któremu możemy przypisać wartość 0 lub 1.
–> Zdania złożone przez spójniki:
o
∩ (i) – koniunkcja
o
∪ (lub) – alternatywa
o
∼ (zaprzeczenie) – nieprawda, że
p ∼ p
0 1
1 0
o
⟹ implikacja (jeżeli p to q)
p
q
p ⟹ q
1
1
1
1
0
0
0
1
1
0
0
1
o
⟺ równoważność (p jest równoważne q)
p q
p ⟺ q
1 1
1
1 0
0
0 1
1
0 0
1
(p ⟺ q) ⟺ [(p ⟹ q) ∩ (q ⟹ p)]
o
tautologia
– zadanie, które jest zawsze prawdziwe bez względu na to jakie wartości logiczne mają zdania
pojedyncze.
(p ⟹ q) ⟺ (∼ p ∪ q)
Sprawdzanie za pomocą tabelki:
p q
p ⟹ q
∼ p ∪ q
(p ⟹ q) ⟺ (∼ p ∪ q)
1 1
1
1
1
1 0
0
0
1
0 1
1
1
1
0 0
1
1
1
–> Dowody nie wprost
o
∼ (p ⟹ q) ⟺ ∼[(∼ p) ∪ q]
∼ [(∼ p) ∪ q] ⟺ [∼ (∼ p) ∩ (∼ q)] ⟺(p ∩ ∼ q)
∼ (p ⟹ q) ⟺ (p ∩ ∼ q)
o
[(p ∪ q) ∩ (∼ p)] ⟹ q
Załóżmy, że to nie jest tautologia, tzn. to zdanie może być fałszywe, a to jest wtedy gdy (p ∪ q) ∩ (∼ p) jest prawdziwe
i q jest fałszywe. (p ∪ q) ∩ (∼ p) ma wartość 1 ⟺ p ∪ q jest prawdziwe oraz ∼ p jest prawdziwe, ⟹ p jest fałszywe, ale
wiemy, że q też jest fałszywe ⟹ p ∪ q jest fałszywe, ⟹ p ∪ q nie jest prawdą.
KWANTYFIKATORY
–>
∧
(dla każdego)
∀
–>
∨
(istnieje)
∃
–>
∨
! (istnieje tylko jeden)
–> ⋀ g(x) ⋁ f(x)
x∊X
x∊X
–> ∼[⋀ g(x)] ⟺ ⋁ [∼ f(x)]
x∊X
x∊X
–> ∼[⋁ f(x)] ⟺ ⋀ [∼ g(x)]
x∊X
x∊X
p q p ∩ q p ∪ q
1 1 1
1
0 1 0
1
1 0 0
1
0 0 0
0

Strona 2 z 19
1. ⋁ [ f(x) ∩ g(x)] ⟹ ⋁ f(x) ∩ ⋁ g(x) } dobre wnioskowanie
x∊X x∊X x∊X
2. [⋁ f(x) ∩ ⋁ g(x)] ⟹ ⋁ [ f(x) ∩ g(x)] } złe wnioskowanie
x∊X x∊X x∊X
–> Reguły wnioskowania
przesłanki (zakładam, że są prawdziwe)
wnioski (z prawdziwych przesłanek ma wynikać prawdziwy wniosek)
ZBIORY
–> Rachunek zbiorów:
o
A ∪ B = {x: x ∊ A ∪ x ∊ B}
o
A ∩ B = {x: x ∊ A ∩ x ∊ B}
o
A \ B = {x: x ∊ A ∩ x ≠ B}
o
A’ = {x: x ≠ A ; x ∊ X}
o
A ∆ B = {x: x ∊ (A \ B) ∪ x ∊ (B \ A)} różnica
A ÷ B = { (A \ B) ∪ (B \ A) = (A ∪ B) \ (A ∩ B)} symetryczna
o
A × B = { (x, y): x ∊ A ∩ y ∊ B} <----- iloczyn kartezjański
(x, y) – zbiór par uporządkowanych
FUNKCJE JEDNEJ ZMIENNEJ
X, Y – podzbiory zbioru liczb rzeczywistych
Oznaczenia:
N = {1;2;3;…} – zbiór liczb naturalnych
Z = {…;-2;-1;0;1;2;…} – zbiór liczb całkowitych
Q = {
p ∊ Z ; q ∊ N} – zbiór liczb wymiernych
R – zbiór liczb rzeczywistych
N ⊂ Z ⊂ Q ⊂ R
X ⊆ Y tzn. albo X ⊂ Y (jest podzbiorem zbioru Y)
albo X = Y podzbiór właściwy
⊆ – zawiera się albo równa się
Funkcją f(x) nazywamy przyporządkowanie każdemu elementowi ze zbioru X dokładnie jednego
elementu ze zbioru Y.
X, Y ⊆ R
y = f(x)
Dziedziną funkcji f(x) /oznaczenie D
f
/ jest zbiór X
Wykres funkcji
<-- jest to wykres funkcji
{(x, y): x ∊ D
f
; y = f(x)}
Zbiór wartości
{y ∊ R: y = f(x); x ∊ D
f
}
FUNKCJE
Podstawowe własności:
D
f
– dziedzina funkcji f(x)
f(x) = y ; x ∊ D
f
; y ∊ Y
D
f
⊂ x ⊆ R
Funkcja f(x) może być parzysta lub nieparzysta (lub ani taka ani taka)
f(x) jest parzysta ⟺ ∀ f(x) = f(-x)
x∊D
f
Strona 3 z 19
np. f(x) = cos (x) (symetria wspólna osi OY)
f(x) jest nieparzysta ⟺ ∀ f(-x) = - f(x)
x∊D
f
np. f(x) = sin (x) [symetria wzg. pkt (0;0)]
funkcja ani parzysta ani nieparzysta
Przykłady:
1. f(x) = |x
3
+ x|
f(-x) = |(-x
3
) + (-x)| = |-(x
3
+ x)| = |x
3
+ x|
2. g(x) = x
3
+ x = x(x
2
+ 1)
g(-x) = -g(x)
Strona 4 z 19
Monotoniczność
f(x) jest rosnąca ⟺ ∀
x
1
,x
2
∊D
f
f(x) jest malejąca ⟺ ∀
x
1
,x
2
∊D
f
x
1
< x
2
⟹ f(x
1
) < f(x
2
)
x
1
< x
2
⟹ f(x
1
) > f(x
2
)
f(x) jest nierosnąca ⟺ ∀
x
1
,x
2
∊D
f
f(x) jest niemalejąca ⟺ ∀
x
1
,x
2
∊D
f
x
1
> x
2
⟹ f(x
1
) ⩽ f(x
2
)
x
1
> x
2
⟹ f(x
1
) ⩾ f(x
2
)
Przykład:
f(x) =
x ∊ [0; ∞)
x
1
x
2
⩾ 0 x
1
> x
2
f(x
1
) – f(x
2
) =
–
=
=
< 0
f(x
1
) < f(x
2
)
funkcja malejąca
WNIOSEK:
f(x) =
; x ∊ [0; ∞) <-------- jest funkcją malejącą
Różnowartościowość
f(x) jest różnowartościowa ⟺ ∀
x
1
,x
2
∊D
f
x
1
≠ x
2
⟹ f(x
1
) ≠ f(x
2
)
Przykład:
f(x) = ; x ⩾ -1
x
1
≠ x
2
x
1
x
2
⩾ -1
f(x
1
) – f(x
2
) = - =
≠ 0
Więc,
f(x) jest różnowartościowa bo x
1
≠ x
2
⟹ f(x
1
) ≠ f(x
2
)
Strona 5 z 19
Złożenie funkcji
f, g ⟹ (f o g)(x) = f[g(x)]
x ∊ D
f
oraz g(x) ∊ D
f
Przykład:
f(x) = x
2
+ 1; g(x) =
(f ∘ g) = f[g(x)] = f( ) = ( )
2
+ 1 = x + 1 + 1 = x + 2; x ⩾ -1
(g ∘ f) = g[f(x)] = g(x
2
+ 1) =
=
; x ∊ R
Funkcja odwrotna
f(x); x ∊ D
f
Funkcją odwrotną do funkcji f(x) jest taka funkcja g(x), że (f o g)(x) = (g o f)(x) = x, dla x ∊ D
f
Oznaczenie funkcji odwrotnej f
-1
(x), czyli (f o f
-1
)(x) = (f
-1
o f)(x)
Nie dla każdej funkcji istnieje funkcja odwrotna!
Funkcja f(x) musi być różniczkowalna, by była funkcją odwrotną
Przykład:
f(x) =
; x ≠ 0
y =
⟹ x =
; y ≠ 0
f
-1
(x) =
(f ∘ f
-1
)(x) = f(
) =
= x
(f
-1
∘ f)(x) = f(
) =
= x
Wykresy f(x) i f
-1
(x) są symetryczne względem prostej y = x
Funkcja SGN(x)
sgn(x) =
Stąd f
-1
(x) można napisać podobnym wzorem.
f
-1
(x) = sgn(x) ∙ ; x ∊ R
FUNKCJE POTĘGOWE, WYKŁADNICZE, LOGARYTMICZNE
Funkcje potęgowe
f(x) = x
n
n – liczba rzeczywista
Dziedzina funkcji f(x) zależy od n
1
o
n > 0, naturalne
n- parzyste to D
f
=R, zbiór wartości- liczby nieujemne y ⩾ 0
n – nieparzyste to D
f
= R, zbiór wartości y = R
parzyste
nieparzyste
Strona 6 z 19
2
o
n < 0 0 ∉ D
f
D
f
= R\{0}
np. f(x) =
= x
-1
np. f(x) =
= x
-2
nieparzyste
parzyste
3
o
n =
> 0 p, q – względnie pierwsze
q – parzyste
q – nieparzyste
Funkcja wykładnicza
f(x) = a
x
a – ustalona, a > 0, a ≠ 1
x ∊ R – funkcja wykładnicza
a > 1; f(x) = a
x
: R --> D
f
0 < a < 1
Funkcja logarytmiczna
f(x) =
np. c =
a
c
= b
b > 0, a ≠ 1, a > 1
a > 1,
a < 1,
Własności logarytmów:
(a)
+
=
(b)
–
=
(c) log
a
b
r
= r
(d)
=
Strona 7 z 19
FUNKCJE CYKLOMETRYCZNE
Są to funkcje odwrotne do funkcji trygonometrycznych na odpowiednich przedziałach.
1)
f(x) = sinx
dla x ∊ [-
] f
-1
(x) = arcsinx x ∊ [-1; 1]
arcsinx = y ⟺ siny = x x ∊ [-1; 1] y ∊ [-
]
Przykład:
arcsin
=
arcsin(-
) = -
2) f(x) = cosx
dla x ∊ [0; ]
f
-1
(x) = arccosx
x ∊ [-1; 1]
arccosx = y ⟺ cosy = x x ∊ [-1; 1] y ∊ [0 ]
Zależność między arcsinx, a arccosx
arcsinx + arccosx =
x ∊ [-1; 1]
3) f(x) = tgx
dla x ∊ (-
)
f
-1
(x) = arctgx
x ∊ R
4) f(x) = ctgx
dla x ∊ (0; )
f
-1
(x) = arcctgx
x ∊ R
Zależność między arctgx, a arcctgx
arctgx + arcctgx =
x ∊ R
Strona 8 z 19
Przykład:
Znaleźć funkcję odwrotną do sinx dla x ∊ [-
]
x = t +
sinx = sin (t + ) = - sint
arcsinx = - arcsint = arcsin(-t)
- arcsinx + = arcsin(-x) +
y = sinx = sin(t + ) = - sint
t ∊ [-
]
-y = sint
arcsin(-y) = arcsin(sint) = t
t = x – = arcsin(-y)
x = arcsin(-y) +
FUNKCJE HIPERBOLICZNE
shx
– sinus hiperboliczny
chx
– cosinus hiperboliczny
shx =
chx =
x ∊ R
CIĄGI LICZBOWE
f(n) = a
n
; n ∊ N
Ciągi to są funkcje, których zbiorem argumentów (dziedziną) jest zbiór liczb naturalnych.
a
n
= (-1)
n
n ∊ N
a
n
=
1) Rekurencyjna (np. ciąg zdefiniowany rekurencyjnie)
a
1
= 1, a
2
= 1, a
n
= a
n-1
+ a
n-2
n > 2
1, 1, 2, 3, 5, 8, 13, 21 ciąg Fibonacciego
2) Ograniczoność ciągu
a) Mówimy, że ciąg a
n
jest ograniczony z dołu
⋁ ⋀ a
n
⩾ M
M n ∊ N
b) Mówimy, że ciąg a
n
jest ograniczony z góry
⋁ ⋀ a
n
⩽ m
m n ∊ N
c) Mówimy, że ciąg a
n
jest ograniczony
⋁ ⋀ a
n
⩽ m
M, m n ∊ N
Strona 9 z 19
Przykład:
5sin(n! + 1)
-5 ⩽ 5sin(n! +1) ⩽ 5
ciąg jest ograniczony z dołu m = -5, a z góry M = 5
3) Monotoniczność ciągu
(a) ciąg rosnący
a
n+1
> a
n
lub
> 1 dla każdego n ∊ N
(b) ciąg niemalejący
a
n+1
⩾ a
n
dla każdego n ∊ N
(c) ciąg malejący
a
n+1
< a
n
lub
< 1 dla każdego n ∊ N
(d) ciąg nierosnący
a
n+1
⩽ a
n
dla każdego n ∊ N
(e) ciąg stały
a
n+1
= a
n
dla każdego n ∊ N
Przykład:
a
n
=
a
n+1
=
=
=
∙
= (n+1)(
)
n
=
=
> 1
= e 2 ⩽
< 3
Czyli a
n
jest rosnące
4) Granice ciągów
Definicja ciąg a
n
ma granicę g, |g| <
wtedy i tylko wtedy gdy
⋀ ⋁ ⋀
Ɛ>0 N n⩾N
|a
n
– g| < Ɛ
-Ɛ < a
n
– g < Ɛ
g – Ɛ < a
n
< g + Ɛ
n(Ɛ) – n zależy od Ɛ
Przykład:
= 0
Bierzemy dowolny Ɛ > 0
|
| < Ɛ
„wyliczamy” z tej nierówności n
+1 >
>
– 1
1
o
– 1 ⩽ 0 ⟺ Ɛ ⩾ 1
Wtedy
>
– 1 zachodzi dla każdego n ∊ N, N = 1
2
o
– 1 > 0 ⟺ 0 < Ɛ < 1
>
– 1 ⟺ n >
- 1)
N = [
- 1)] + 1
Definicja a
n
ma granicę +
⋀ ⋁ ⋀
M N n⩾N
Strona 10 z 19
Przykład:
= ∞
=
= [
] = ∞
5) Twierdzenie : Jeżeli ciąg a
n
ma granicę (skończoną lub nieskończoną) to każdy podciąg tego ciągu ma
tą samą granicę (podciąg – czyli co któryś wyraz danego ciągu).
np.
a
1
, a
2
, a
3
, a
4
, a
5
, a
6
, a
7
, a
8
, a
9
Przykład:
= ∞
podciąg ciągu
6) Twierdzenie o arytmetyce granic
Załóżmy, że a
n
, b
n
mają granice właściwe, wtedy:
a)
=
+
b)
=
–
c)
=
d)
=
; gdy b
n
≠ 0,
≠ 0
e)
= (
)
m
; m – ustalone
f)
=
; k – ustalone
Szczególne przypadki:
= 1
= 1 ; a > 0
7) Twierdzenie
Jeżeli
= 0 , to
= 0
Przykład:
Uzasadnij, że
= 0
|
| =
0
8) Twierdzenie o trzech ciągach
Jeżeli ciągi a
n
, b
n
, c
n
spełniają taki warunek
⋀ c
n
⩽ a
n
⩽ b
n
oraz
=
= g , to
= g
n ∊ N
g g g
Przykład:
3
n
⩽
⩽ 5
n
∞ ∞
∞
9) Twierdzenie o dwóch ciągach
a) Jeżeli c
n
⩽ a
n
= ∞ , to
= ∞
b) Jeżeli a
n
⩽ b
n
= - ∞ , to
= - ∞
10)
Twierdzenie
a, b > 0
= max {a, b}
Przykład:
3, bo
3 =
<
<
= 3
3
11) Twierdzenie
Jeżeli ciąg an jest monotoniczny (od pewnego miejsca) i ograniczony to ten ciąg jest zbieżny.
Przykład:
a
n
=
a
1
=
; a
2
=
; a
3
=
[
= 0
[
] = 0
Strona 11 z 19
1
o
Badamy monotoniczność a
n+1
– a
n
n+1
=
n+1
–
n
=
) =
=
> 0
bo
2n+1 < 2n+2
0 < 1
⟹
n
rośnie
0 <
n
< ?
n
=
<
< 1 , bo n < n+1
0 < 1
⟹ 0 <
n
< 1, czyli a
n
jest ciągiem ograniczonym
z twierdzenia o ciągu monotonicznym i ograniczonym wynika, że a
n
jest zbieżny
12)
Ciąg zadany rekurencyjnie
b
n+1
=
b
n
= b
n
> 0
b
1
= b
2
= b
3
=
b
n+1
– b
n
=
- b
n
=
> 0
rozkład na czynniki
= 0
– t
2
+ t + 2 = 0
∆ = 9 = 3
t
1
= 2 t
2
= 1
stąd
b
n+1
– b
n
=
> 0
Założenie, że
0 < b
n
< 2
Sprawdzamy czy prawdą jest ⋀ 0 < b
n
< 2
n ∊ N
indukcyjnie
1
o
n = 1 b
1
= 0 <
2
o
0 < b
n
< 2
0 <
< 2
0 <
< 4
-2 < b
n
< 2 co prawdą jest z założenia 0 < b
n
< 2
Stąd b
n
, ograniczony ⟹ zbieżny
b
n+1
=
,
= g , 0 < b
n
< 2 ⟹ 0 ⩽ g ⩽ 2
⩽ g ⩽ 2
=
= g
Stąd
g =
g
2
= 2 + g ⟹ g
2
– g – 2 = (g + 1)(g - 2)= 0 ⟺
, więc wybieramy g = 2, bo g [ ; 2]
Stąd
= 2
13) Liczba e
e ≈ 2,72
14) Wyrażenia nieoznaczone
∞ – ∞, np. n ∙ n = 0 → 0 ; 2n – n = n → ∞
0 ∙ ∞, np.
∙ n = 1 ;
∙ n =
→ 0 ;
∙
= n → ∞
, np.
= 1 ;
=
→ 0 ;
= n → ∞
, np.
= 1 ;
= n → ∞ ;
=
→ 0
= np.
= e ;
=
, np.
= 1
, np.
=
→ 1
Strona 12 z 19
15) Wyrażenia oznaczone
+ ∞ = ∞ –∞ < ⩽ ∞
∙ ∞ = ∞ ∞ ⩾ > 0
= 0 –∞ < < 0
= ∞ 0 < ⩽
= 0
⩽ < 1
= o –∞ ⩽ < 0
= ∞ 1 < ⩽ ∞
= ∞ 0 < ⩽ ∞
16) Punkty skupienia ciągów
Punktem skupienia ciągu
nazywamy taką liczbę g (g – skończone lub nieskończone) jeżeli istnieje podciąg tego ciągu,
który ma granicę równą g.
=
= – 1
= 1
S = {-1; 1}
⟵
zb ór punktów skup en a
= 1
= – 1
= snpS (największy element ze zbioru punktów skupienia)
= infS (najmniejszy element ze zbioru punktów skupienia)
Przykład:
= cos
S = {
; 0; -
; -1; 1}
cos(
) = cos(
) =
cos(
) = cos(
) = 0
cos(
)
cos(
)
s
= 1
s
= -1
GRANICA FUNKCJI
1) Definicja Heinego
= g ⟺ ⋀
{
} ⊂ S
) ⟵ pewne otoczenie punktu x
0
x
n
≠
0
=
= g
x
0
może być liczbą równą , tak samo g (g – liczba lub )
Przykład:
Z definicji pokaż, że
=
Bierzemy dowolny ciąg {x
n
}
x
n
- 1 x
n
≠ - 1
f(x
n
) =
,
=
=
=
=
=

Strona 13 z 19
2) Granica funkcji f(x), gdy x dąży do
nie istnieje
⟺ ⋁ {
} ≠ {
}
} wa ró ne
}
}
≠
Fakt
Jeżeli
jest skończone, to
istnieje
⟺
=
granica prawostronna = granica lewostronna
Przykład:
f(x) =
; x → 0
→
(
> 0)
=
f(
) =
= n
∞
→
(
< 0)
= -
f(
) =
= - n
- ∞
Granice jednostronne istnieją, ale są różne, zatem nie istnieje
3) Arytmetyka granic funkcji
Założenie
,
istnieją i skończone
(a)
=
(b)
=
(c)
=
; g(x) ≠ 0 ,
≠ 0
(d)
=
4) Ważne granice
a)
= 1
= 1
b)
= 1
c)
= , > 0 , w szczególności
= 1
d)
=
, 1≠ > 0 , w szczególności
= 1
e)
=
=
f)
=
g)
= ;
5) Twierdzenie o trzech funkcjach
Dla h(x) ⩽ f(x) ⩽ g(x) oraz
=
= g
= g
Przykład:
Oblicz
E(x) = [x] ⟵ część wspólna
x – 1 < [x] ⩽ x
< [
] ⩽
<
⩽
=
= 1
=
= 1
Więc…
= 1
6) Asymptoty
a) Pionowe (w punktach skończonych na końcach dziedzin funkcji)
np. y =
D = R\{0}
( ) (0; )
x
o
= 0 w tym punkcie sprawdzamy czy istnieje asymptota pionowa
x
o
≠ D
– asymptota lewostronna ;
– asymptota prawostronna
Strona 14 z 19
A jeśli
oraz
asymptota x = x
o
pionowa obustronna
b) Poziome w
= b
b – skończone
c) Ukośne w
Taka prosta y = ax +b, dla której zachodzi warunek
(mogą być dwie różne asymptoty ukośne; inna w )
a =
, a – stałe
b =
, b – stałe
7) Funkcja ciągła
Funkcją ciągłą f(x) jest funkcja w punkcie x
o
⟺
= f(x
o
)
ciągła w x
o
nie ciagła w x
o
może być ciągłość jednostronna
Jeżeli
f(x
o
) , to f(x) jest ciągła w punkcie x
o
Jeżeli
≠ f(x
o
) , to f(x) nie jest ciągła w punkcie x
o
(tzw. nieciągłość I rodzaju)
Może być jeszcze nieciągłość II rodzaju
Tak jak wtedy gdy któraś z granic
nie istnieje lub jest równa
Strona 15 z 19
Funkcja jest ciągła na przedziale (a, b) jeżeli jest ciągła w każdym punkcie wewnętrznym tego przedziału oraz istnieją
granice
oraz
.
Funkcja jest ciągła na przedziale [a, b) jeżeli dodatkowo
= f( )
Działania na funkcjach ciągłych:
f, g ciągłe w x
o
, wtedy
(f g)(x
o
) ciągłe w x
o
(f ∘ g)(x
o
) ciągłe w x
o
ciągłe w x
o
; g(x
o
) ≠ 0
Założenie: Jeżeli f(x) jest ciągłe w x
o
oraz funkcja g(x) jest ciągła y
o
= f(x
o
), wtedy (g ∘ f)(x
o
) jest ciągłe w x
o
.
Własności funkcji ciągłych:
Załóżmy, że f(x) jest ciągła w przedziale [a; b] (ograniczony przedział)
Wtedy funkcja f(x) jest ograniczona na tym przedziale
Domkniętość przedziału [a; b] ma znaczenie
Funkcja ciągła na przedziale domkniętym osiąga swoje kresy
tzn.
⋁
n
a
⋀
⩾
⋀
⩽
8) Własność Darboux
Niech f(x): funkcja określana na [a; b]
Ma własność Darboux
⟺ ⋀ ⋁ taki, że f(x
o
) = c
x
o
∊ [a, b]
Funkcja ciągła na [a; b] ma własność Darboux
(czyli z f(a) dochodzimy do f(b) przez wszystkie wartości pośrednie)
Szczególny przypadek:
f(a) ∙ f(b) < 0
W szczególności jeżeli f(x) jest monotoniczna na danym przedziale (ciągła na [a; b], f(a) ∙ f(b) < 0)
Wtedy ⋁ f(x
o
) = 0 (istnieje dokładnie jeden taki punkt, w którym funkcja się zeruje)
x
o
∊ [a; b]
Przykład:
Pokaż, że równanie ma dokładnie jedno rozwiązanie w danym przedziale lnx = 2 – x ; x ∊ [1; 2]
f(x) = lnx – 2 + x ciągła w [1; 2]
(suma funkcji ciągłych jest funkcją ciągłą)
f(1) = ln1 + 1 – 2 = -1 < 0
f(2) = ln2 + 2 – 2 = ln2 > 0
}
lnx + x ⟹ lnx + x - 2
f ⟹ ⋁ f(x
o
) = 0 tzn. lnx
o
+ x
o
– 2 = 0
x
o
∊ [1; 2] lnx
o
= 2 – x
o
; x
o
∊ [1; 2]
Strona 16 z 19
POCHODNA FUNKCJI
Mówimy, że istnieje pochodna f ’(x
o
) funkcji f(x) w punkcie x
o
jeżeli istnieje granica (skończona lub nieskończona)
f ’(x
o
) =
(ta granica = pochodna funkcji w punkcie x
o
) ; x ≠ x
o
Można to też napisać tak:
f ’(x
o
) =
∆x = x – x
o
(
)
WARUNKIEM KONIECZNYM istnienia pochodnej funkcji w danym punkcie jest
ciągłość w tym punkcie
Funkcja może być ciągła w danym punkcie, ale może nie być pochodnej w tym punkcie.
Przykład:
f(x) =
f ’(x
o
) =
=
=
=
= 2x
o
(
)’= 2x , x ∊ R
Pochodna funkcji istnieje w danym punkcie ⟺
f ’(x
o
) =
=
f ’(
) = f ’(
) pochodna jednostronna
pochodna prawostronna = pochodna lewostronna
(Może być tak, że nie istnieją pochodne jednostronne)
Podstawowe funkcje i ich pochodne
= nx
n-1
n ∊ N s n s
=
∊ R s s n
= s n
= 0 s
= -
t
t
=
t
t
)
(
=
t
=
∙ ln t
=
s n
s n s
=
s
s s n
=
Podstawowe działania:
1.
2.
3.
4.
⟹ g(x) ≠ 0
5.
6.
Pochodna funkcji odwrotnych
f(x) ⟹ f
-1
(x)
Ciągła, istnieje pochodna
; f(x) – różniczkowalna (rosnąca malejąca)
Wtedy f
-1
(x) =
Przykład:
(arctg x)’ = ? (tg x)’ =
y = tg x ⟹ x = arctg y = g(y) ⟹
s
y =
s
(arctg x)’ =
Strona 17 z 19
Zastosowanie pochodnej
(a)
Styczna do funkcji f(x) w punkcie x
o
ma równanie
(b)
Kąt przecięcia się krzywych
(dla f(x), g(x) takich, że istnieje
pochodna w punkcie przecięcia)
- to jest taki kąt między stycznymi
w punkcie przecięcia
⟹
Pod warunkiem, że
≠ .
Jeżeli jednak
≠ , to znaczy, że krzywe g(x) i f(x) przecinają się pod kątem prostym w punkcie
(c)
Przybliżone wartości funkcji
Różniczka:
Błąd pomiaru
Twierdzenie Rolle’a
f(x) jest okreslona w [a; b] ciągła na [a; b], różniczkowalna na (a; b)
f(a) = f(b) i a, b ∊ D
f
to istnieje x
o
∊ (a; b), wtedy
Czyli istnieje co najmniej jeden taki punkt wykresu, że styczna do y = f(x) w tym
punkcie jest pozioma.
Twierdzenie Lagrange’a
f(x) ciągła na [a; b], różniczkowalna wewnątrz tego przedziału.
Wówczas istnieje taki punkt c ∊ [a; b]
Czyli istnieje taka prosta przechodząca przez x
o
styczna do siecznej.
Strona 18 z 19
Monotoniczność funkcji
f(x) ciągła, różniczkowalna w pewnym przedziale P
1. ⋀
2. ⋀
3. ⋀
⩾
4. ⋀
⩽
Wzór Taylora
Niech f(x) jest określona na pewnym przedziale jest różniczkowalne n-krotnie na tym przedziale; f
n-1
(x) ciągła;
f
n
(x) właściwa w punkcie x
o
.
Wtedy dla każdego x
o
∊ [a; b] istnieje taki punkt c ∊ [a; b], że
f(x) =
gdzie
Reszta Lagrange’a
Wzór Maclaurina
x
o
= 0
f(x) =
gdzie
Reguła de L’Hospitala
Dla nieoznaczoności typu:
Jeżeli spełnione są warunki
1.
są określone w sąsiedztwie punktu x
o
2.
3. Jeżeli istnieje granica
to
Ekstrema funkcji
Twierdzenie Fermata
Warunek konieczny istnienia ekstremum funkcji.
f(x) różniczkowalna w xo i ma w tym punkcie lokalne ekstremum to
(loklne ekstremum może nie być związane z isniejącą (zerową) pochodną).
Wypukłość funkcji
Funkcję f(x) nazywamy wypukłą w przedziale [a; b] ⊆ D
f
(lub wklęsłą) jeśli każdy odcinek siecznej wykresu tej funkcji
położony między punktami wykresu, przez które przechodzi sieczna, leży nad wykresem (pod wykresem dla funkcji
wklęsłej)
Ścisła wypukłość (wklęsłość) – brak mozliwości pokrycia siecznej z wykresem funkcji
f(x) jest ściśle wypukła f(x) jest ściśle wklęsła
Punkt przegięcia funkcji
Punkt, w którym funkcja zmienia rodzaj wypukłości
Warunek konieczny dla istnienia punktu przegięcia
Jeśli f(x) ma dwie pochodne to f ’’(x) = 0
Strona 19 z 19
CAŁKA
Całka nieoznaczona funkcji jednej zmiennej
⟺ (F(x) + C)’ = [F(x)]’ = f(x)
Podstawowe całki
s s n
s n s
n
Własności całkowania
a.
b.
c.
Całkowanie przez części
Przykład:
=
–
–
n
n
Całkowanie przez podstawienie
Przykład:
n
n
n
Całkowanie funkcji wymiernych
Funkcja wymierna właściwa; stopień [P(x)] < stopień [W(x)]
Gdy w liczniku występuje x
n
Gdy w liczniku nie występuje x
Wyszukiwarka
Podobne podstrony:
WYKLAD ANALIZA MATEMATYCZNA
Analiza matematyczna, lista analiza 2008 6 szeregi
Analiza Matematyczna 1 Gewert Skoczylas zadania
Analiza Matematyczna Twierdzenia
Praca domowa 2a Analiza Matematyczna
Zadania z Analizy Matematycznej, Matematyka
zestaw9, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
Analiza matematycza opracowanie pytań
Kolos 3 Analiza matematyczna
analiza matematyczna 7
Analiza matematyczna 2 Przyklady i zadania
cw 13 Analiza Matematyczna (calki) id
Analiza matematyczna 1, tab
,analiza matematyczna 2, elemen Nieznany (2)
zestaw10, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
a2k, WTD, analiza matematyczna
CALY E -TRAPEZ, PWR, Analiza Matematczna
więcej podobnych podstron