
DRGANIA I FALE
• Ruchem drgający – ruch lub zmianę stanu, które charakteryzuje powtarzalność w czasie
wartości wielkości fizycznych, określających ten ruch lub stan.
• Fale – różnego rodzaju zaburzenia stanu materii lub pola rozchodzące się w przestrzeni.
• Wspólną cechą wszystkich zjawisk falowych jest zdolność przenoszenia energii.
Drganie harmoniczne
Jeżeli układ, na który nie działają zmienne siły zewnętrzne, zostaje wprawiony w drgania na
skutek jakiegokolwiek początkowego odchylenia od położenia równowagi, to takie drgania
nazywamy swobodnymi.
Ruch drgający nazywamy okresowym (periodycznym), jeżeli wartości wielkości fizycznych
zmieniające się podczas drgań, powtarzają się w pewnych odstępach czasu.
Dla drgań harmonicznych zależność drgań wielkości fizycznej od czasu t opisujemy
)
t
cos(
A
s
o
φ
ω
+
=
(8.1)
gdzie
A
– amplituda,
ω
ο
– częstość kątowa,
ϕ
– faza początkowa drgań,
ω
ο
t +
ϕ – faza drgań w chwili czasu t.
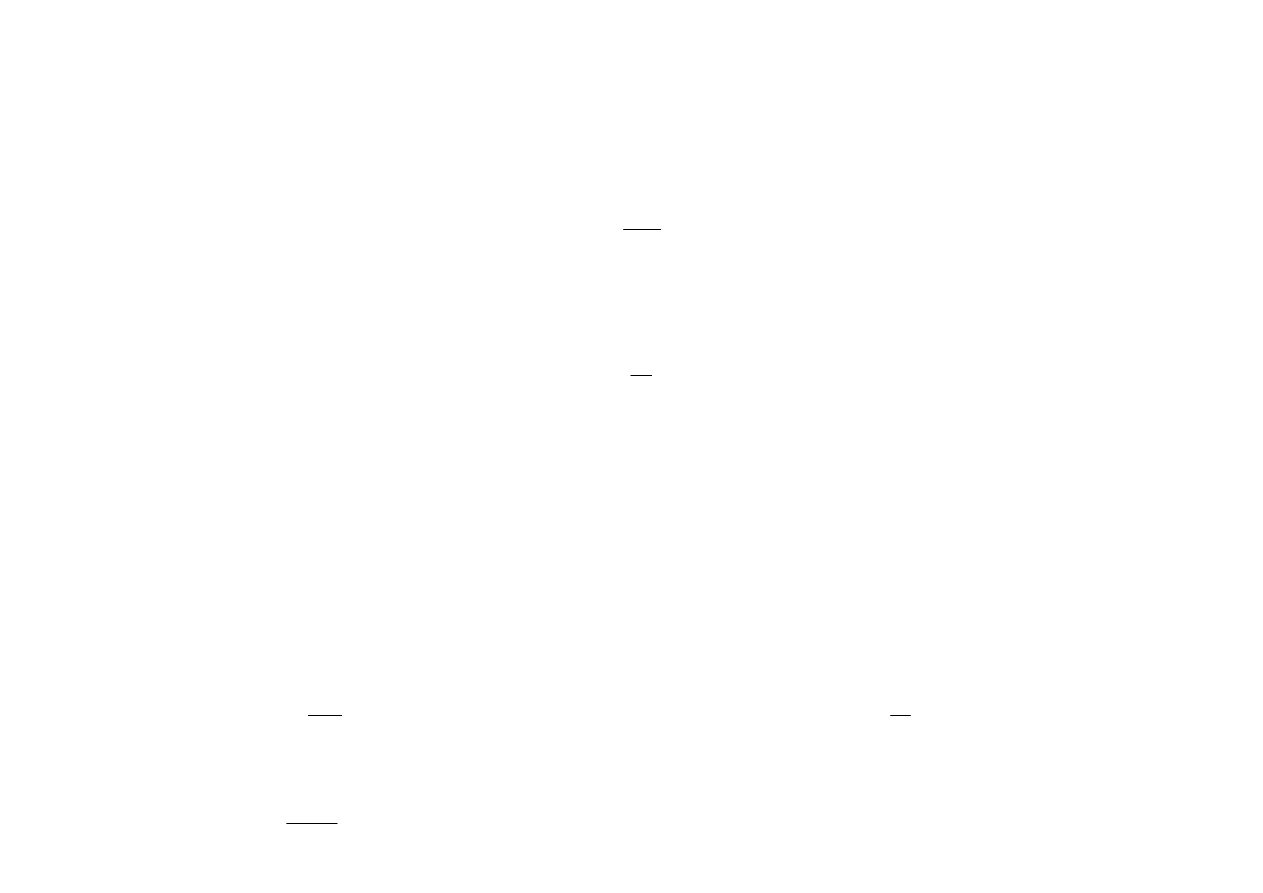
Określone stany układu powtarzają się w odstępie czasu T nazywanym okresem drgań
, w
którym faza drgań wzrasta o 2
π, t.j.
π
φ
ω
φ
ω
2
+
+
=
+
+
)
t
(
)
T
t
(
o
o
stąd
o
T
ω
π
2
=
(8.2)
Częstotliwość drgań
T
1
=
ν
(8.3)
Porównując (8.2) i (8.3) otrzymujemy
ν
π
ω
o
2
=
(8.4)
Jednostką częstotliwości jest hertz (1Hz) – jest to częstotliwość periodycznych drgań w których jeden
cykl wykonywany jest w 1s.
Pierwszą i druga pochodna po czasie wielkości s
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
+
−
=
2
π
ϕ
ω
ω
φ
ω
ω
t
cos
A
)
t
sin(
A
dt
ds
o
o
o
o
(8.5)
(
)
π
ϕ
ω
ω
ϕ
ω
ω
+
+
−
=
+
−
=
t
cos
A
)
t
cos(
A
dt
s
d
o
o
o
o
2
2
2
2
(8.6)
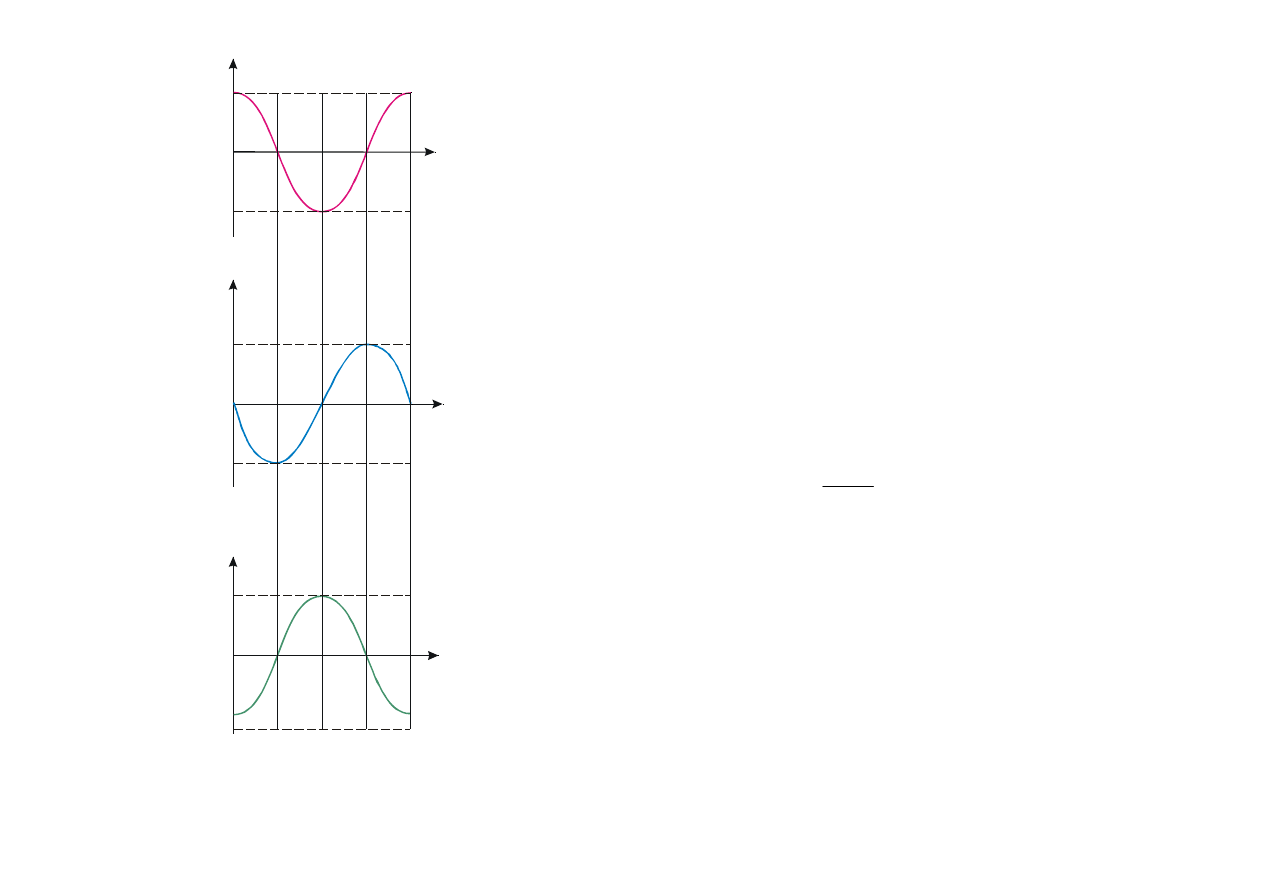
+A
+A
ω
o
+A
ω
o
+A
ω
o
-A
ω
o
-A
s
ds/dt
ds /dt
2
2
t
t
t
2
2
Rys. 8.1. Zależność s, ds/dt i
2
2
dt
/
s
d
od t dla
drgań harmonicznych o okresie
o
/
T
ω
π
2
=
.
Faza prędkości (8.5) różni cię od fazy
wychylenia o
π/2, a faza przyśpieszenia o π.
W chwili czasu gdy s = 0, ds/dt przyjmuje
największą wartość; podczas gdy s przyjmuje
maksymalną ujemną wartość, to
2
2
dt
/
s
d
przyjmuje największą dodatnią wartość (rys.
8.1).
Ze związku (8.6) wynika równanie różniczkowe
drgań harmonicznych
0
2
2
2
=
+
s
dt
s
d
o
ω
(8.7)
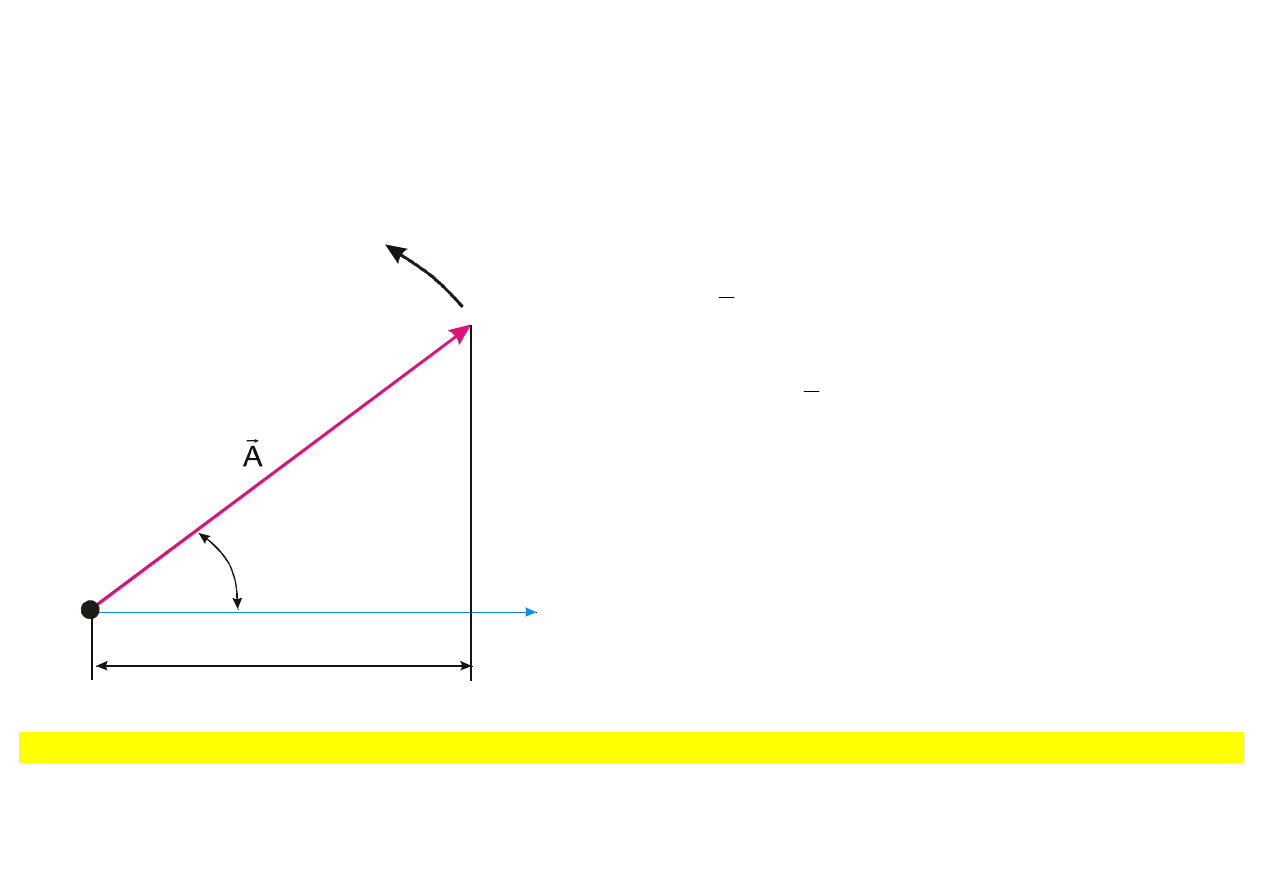
Metoda wykresów fazowych
ϕ
ω
o
0
s
x
Rys. 8.2. Metoda wykresów fazowych.
Druga metoda opisu drgań harmonicznych
(liczby zespolone).
(
)
ϕ
ω
+
=
t
i
o
Ae
s
(8.8)
Część rzeczywista tego wyrażenia
s
)
t
cos(
A
s
Re
o
=
+
=
ϕ
ω
przedstawia drganie harmoniczne.
Przyjmuje się, że
drgająca wielkość s równa jest
części rzeczywistej wyrażenia zespolonego
(8.8),
czyli
(
)
ϕ
ω
+
=
t
i
o
Ae
s
(8.9)

Mechaniczne drgania harmoniczne
Oscylatorem harmonicznym nazywamy układ opisywany równaniem (8.7).
Przykłady oscylatora harmonicznego:
• wahadło sprężynowe, fizyczne i matematyczne,
• drgające obwody elektryczne.
Wahadło sprężynowe wykonuje drgania harmoniczne pod wpływem siły sprężystości F = –kx, gdzie k
jest współczynnikiem sprężystości.
Równanie ruchu dla wahadła
kx
dt
x
d
m
−
=
2
2
czyli
0
2
2
=
+
x
m
k
dt
x
d
Porównując to wyrażenie do równania (8.7) wynika, że wahadło sprężynowe wykonuje drgania
harmoniczne
)
t
cos(
A
x
o
ϕ
ω
+
=
z częstością kołową
m
k
o
=
ω
(8.10)
i okresem
m
k
T
π
2
=
(8.11)
Wzór (8.11) jest słuszny dla drgań sprężystych w których spełnione jest prawo Hooke'a, kiedy masa
sprężyny jest mała w porównaniu z masą ciała.

Siła działająca na masę m wynosi
x
m
)
t
cos(
mA
F
o
o
o
2
2
ω
ϕ
ω
ω
−
=
+
−
=
i jest proporcjonalna do przesunięcia x z położenia równowagi i skierowana w przeciwną stronę.
Energia kinetyczna
(
)
(
)
[
]
ϕ
ω
ω
ϕ
ω
ω
+
−
=
+
=
=
t
cos
mA
t
sin
mA
mv
K
o
o
o
o
2
1
4
2
2
2
2
2
2
2
2
(8.12)
Energia potencjalna
(
)
2
2
2
2
2
2
2
0
2
2
kx
t
cos
mA
x
m
Fdx
U
o
o
x
o
=
+
=
=
−
=
∫
ϕ
ω
ω
ω
czyli
(
)
[
]
ϕ
ω
ω
+
+
=
t
cos
mA
U
o
o
2
1
4
2
2
(8.13)
Energię całkowita
2
2
2
o
mA
U
K
W
ω
=
+
=
U
i K zmieniają się z częstością
o
ω
2
. Ponieważ wartości średnie
α
2
sin
i
α
2
cos
są równe 1/2,
więc
2
W
U
K
=
=
.
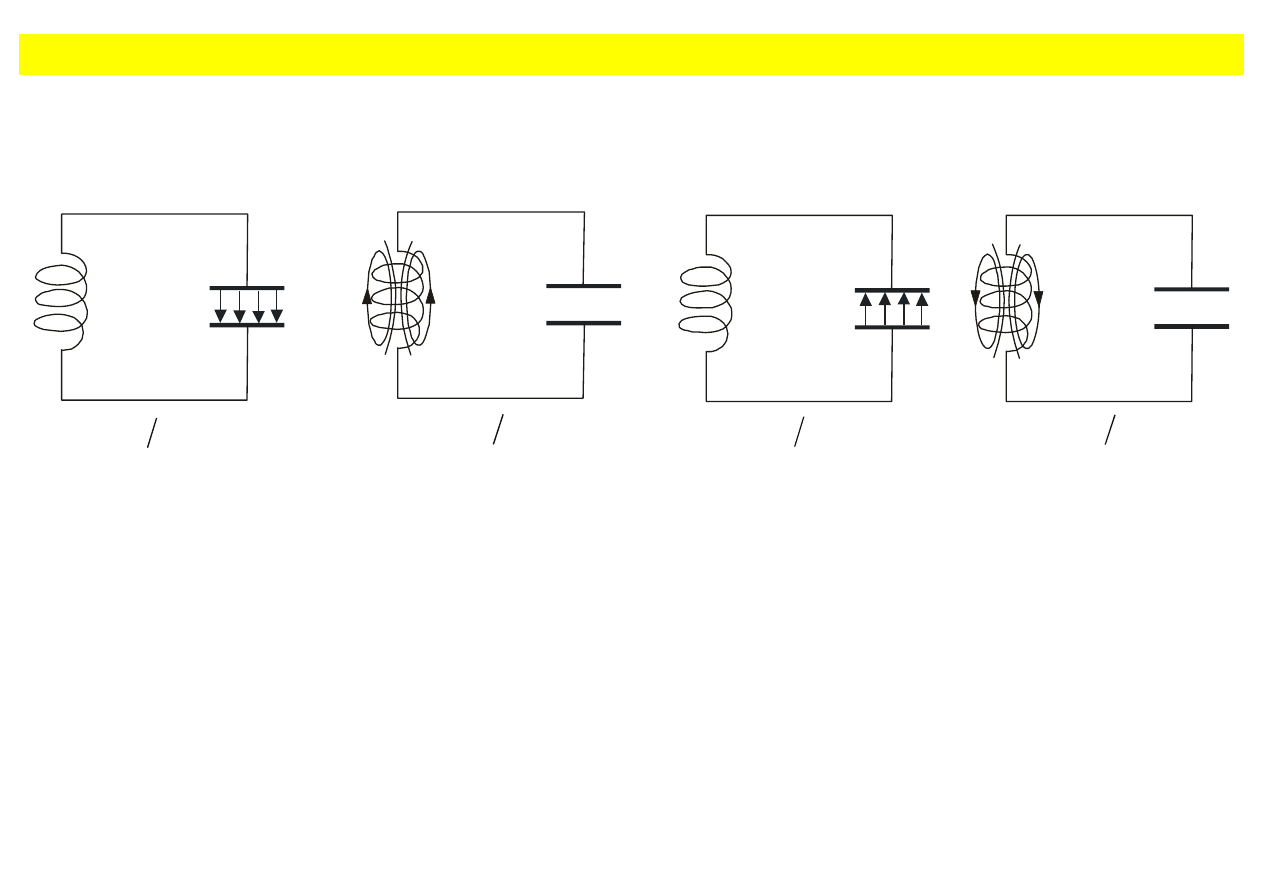
Elektryczne drgania harmoniczne
-Q
-Q
+Q
+Q
t = 0
t = (1/4)T
t = (1/2)T
t = (3/4)T
(a) (b) (c) (d)
(
)
2
Q
C
2
1
W
=
(
)
2
Q
C
2
1
W
=
( )
2
o
LI
2
1
W
=
( )
2
o
LI
2
1
W
=
Rys. 8.3. Przebieg drgań elektrycznych w obwodzie LC.
Rozważmy obwód elektryczny RLC zawierający cewkę o indukcyjności L, kondensator o pojemności
C
i rezystor o rezystancji R. Z prawa Kirchoffa mamy
s
c
E
V
IR
=
+
gdzie:
IR
– napięcie na rezystorze,
C
/
Q
V
c
=
– napięcie na kondensatorze, a
dt
/
LdI
E
s
−
=
SEM indukcji.

Więc
0
=
+
+
C
Q
IR
dt
dI
L
A ponieważ I = dQ/dt oraz
2
2
dt
/
Q
d
dt
/
dI
=
, otrzymujemy
0
1
2
2
=
+
+
Q
LC
dt
dQ
L
R
dt
Q
d
(8.15)
Jeżeli R = 0 to otrzymujemy równanie różniczkowe swobodnych drgań harmonicznych
0
1
2
2
=
+
Q
LC
dt
Q
d
Ładunek wykonuje drgania harmoniczne
(
)
ϕ
ω
+
=
t
cos
Q
Q
o
o
(8.16)
Częstość drgań własnych
LC
o
1
=
ω
(8.17)
Okres drgań
LC
T
π
2
=
(8.18)

Natężenie prądu
(
)
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
+
−
=
=
2
0
π
ϕ
ω
ϕ
ω
ω
t
cos
I
t
sin
Q
dt
/
dQ
I
o
o
o
o
(8.19)
gdzie
o
o
o
Q
I
ω
=
– amplituda natężenia prądu.
Napięcie na kondensatorze
(
)
(
)
ϕ
ω
ϕ
ω
+
=
+
=
=
t
cos
V
t
cos
C
Q
C
Q
V
o
o
o
o
c
(8.20)
gdzie
C
/
Q
V
o
o
=
– amplituda napięcia.
Z wyrażeń (8.16) i (8.19) wynika, że
drgania prądu I wyprzedzają w fazie drgania ładunku Q o
π/2:
kiedy prąd osiąga maksymalną wartość, ładunek (napięcie) przyjmuje zerową wartość i na odwrót
.
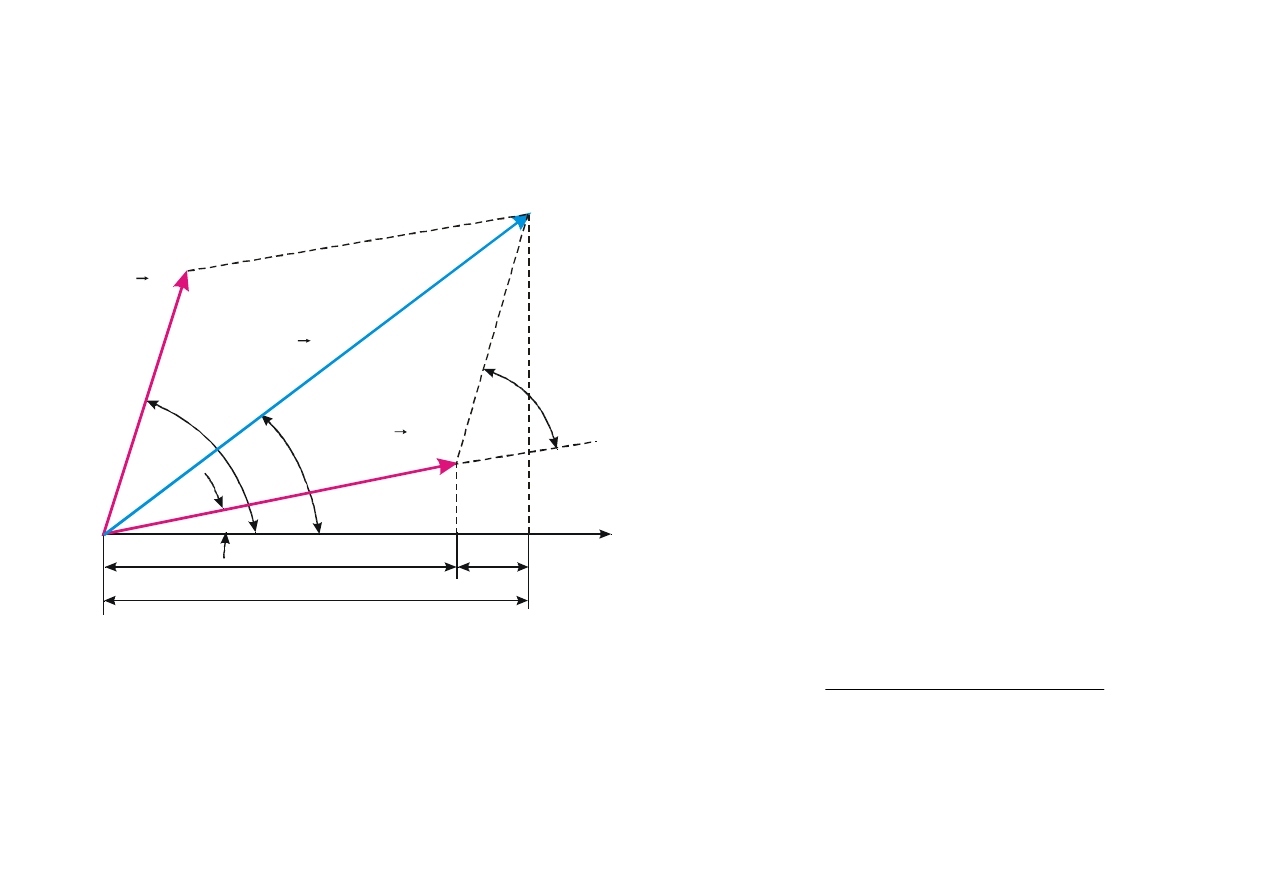
Składanie drgań harmonicznych równoległych
o jednakowej częstości. Dudnienie
x
x
1
x
2
x
1
A
2
A
A
O
ϕ
1
ϕ ϕ
1
2
-
ϕ
2
ϕ
Rys. 8.4. Wektorowa metoda składania drgań.
Dokonamy złożenia drgań harmonicznych o
jednakowych częstotliwościach
(
)
1
1
1
ϕ
ω
+
=
t
cos
A
x
o
(
)
2
2
2
ϕ
ω
+
=
t
cos
A
x
o
Równanie drgania wypadkowego ma postać
(
)
ϕ
ω
+
=
+
=
t
cos
A
x
x
x
o
2
1
(8.21)
gdzie amplituda A i faza
ϕ
są określone
wyrażeniami
(
)
1
2
2
1
2
2
2
1
2
2
ϕ
ϕ
−
+
+
=
cos
A
A
A
A
A
(8.22)
2
2
1
1
2
2
1
1
ϕ
ϕ
ϕ
ϕ
ϕ
cos
A
cos
A
sin
A
sin
A
tg
+
+
=
(8.23)

Ciało biorące udział w dwóch drganiach harmonicznych o jednakowych kierunkach wykonuje także
drgania harmoniczne w tym kierunku i o tej samej częstotliwości co drgania składowe.
Amplituda drgania wypadkowego:
• gdy
...)
,
,
m
(
m
2
1
0
2
1
2
=
±
=
−
π
ϕ
ϕ
, wówczas
2
1
A
A
A
+
=
• gdy
...)
,
,
m
(
1)
+
m
(
2
1
0
2
1
2
=
±
=
−
π
ϕ
ϕ
, wówczas
2
1
A
A
A
+
=
Dudnienie
Rozważymy dwa dodawane drgania równoległe nieznacznie różniące się częstotliwościami drgań.
Niech amplitudy składanych drgań będą równe A, a ich częstości kołowe
ω
i
ω
+
Δω
przy czym
Δω
<<
ω
.
Przyjmijmy, że fazy początkowe drgań są zerowe, wówczas
t
cos
A
x
ω
=
1
t
)
cos(
A
x
ω
Δ
ω
+
=
2
Uwzględniając że
ω
ω
Δ
<<
2
/
, znajdujemy
t
cos
t
cos
A
x
ω
ω
Δ
⎟
⎠
⎞
⎜
⎝
⎛
=
2
2
(8.24)
Otrzymane wyrażenie jest iloczynem modulowanej amplitudy
t
cos
A
A
~
2
2
ω
Δ
=
(8.25)
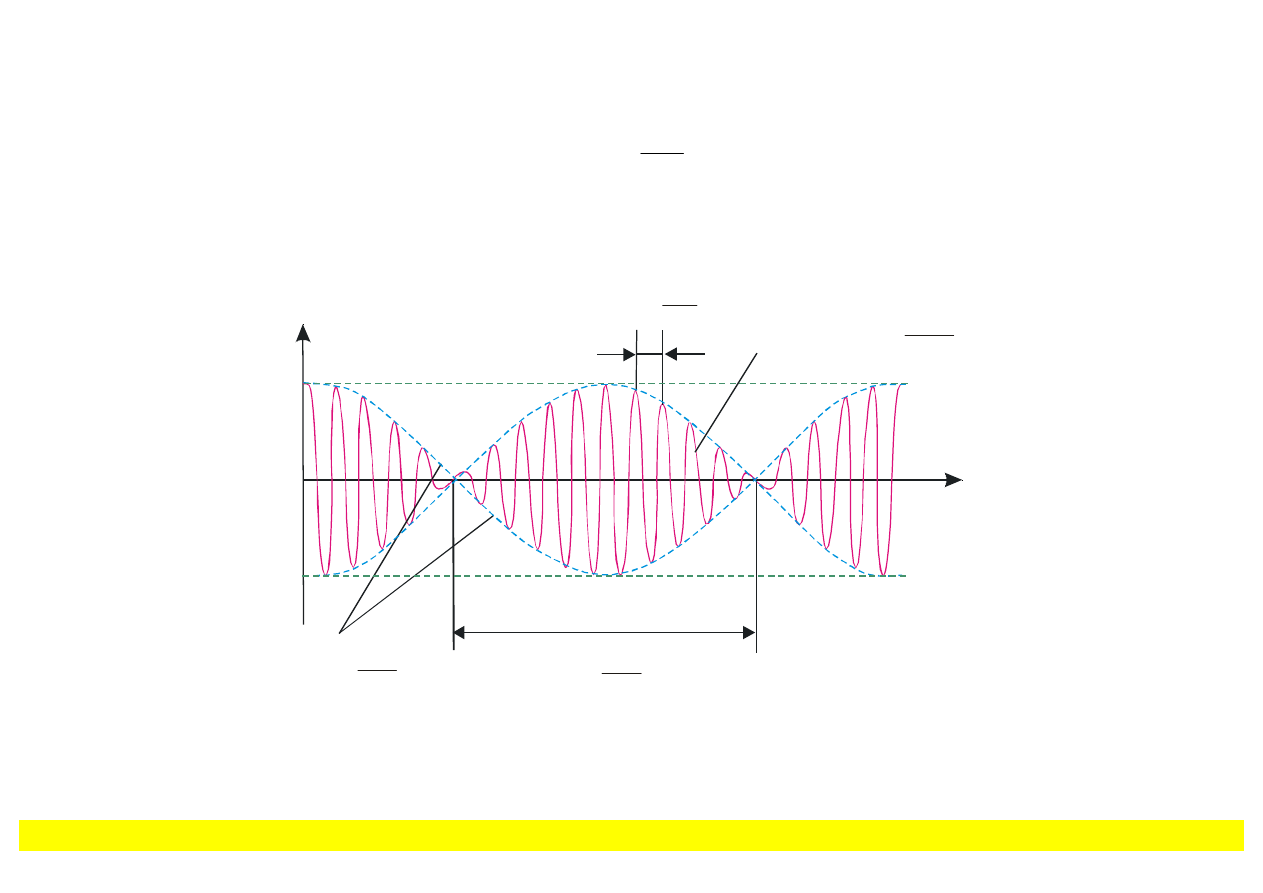
o okresie dudnień
ω
Δ
π
2
=
o
T
i szybko zmieniającego się członu cos
ω
t
.
ω
π
=
2
T
o
ω
Δ
π
=
2
T
t
cos
2
t
cos
A
2
x
ω
⎟
⎠
⎞
⎜
⎝
⎛
ω
Δ
=
t
2
cos
A
2
A
~
ω
Δ
=
t
2A
-2A
~
A
,
x
Rys. 8.5. Nałożenie się drgań harmonicznych o zbliżonych częstościach kołowych daje w
wyniku dudnienie.

Składanie drgań wzajemnie prostopadłych
Rozważmy złożenie dwóch drgań harmonicznych o jednakowej częstości
ω
, zachodzących w
kierunkach wzajemnie prostopadłych wzdłuż osi x i y. Dla prostoty przyjmiemy, że faza początkowa
pierwszego drgania jest zerowa:
)
t
cos(
B
y
t
cos
A
x
ϕ
ω
ω
+
=
=
(8.26)
Zapisując drganie składowe w postaci
ϕ
ω
ϕ
ω
ω
sin
t
sin
cos
t
cos
B
y
;
t
cos
A
x
−
=
=
i uwzględniając, że
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−
=
A
x
t
sin
ω
otrzymujemy po prostych przekształceniach równanie elipsy
ϕ
2
2
2
2
2
2
sin
B
y
AB
xy
A
x
=
+
−
(8.27)
Otrzymaliśmy przypadek tak zwanych drgań eliptycznie spolaryzowanych.
Orientacja osi elipsy i jej rozmiary zależą od amplitud drgań składowych i różnicy faz
ϕ
.
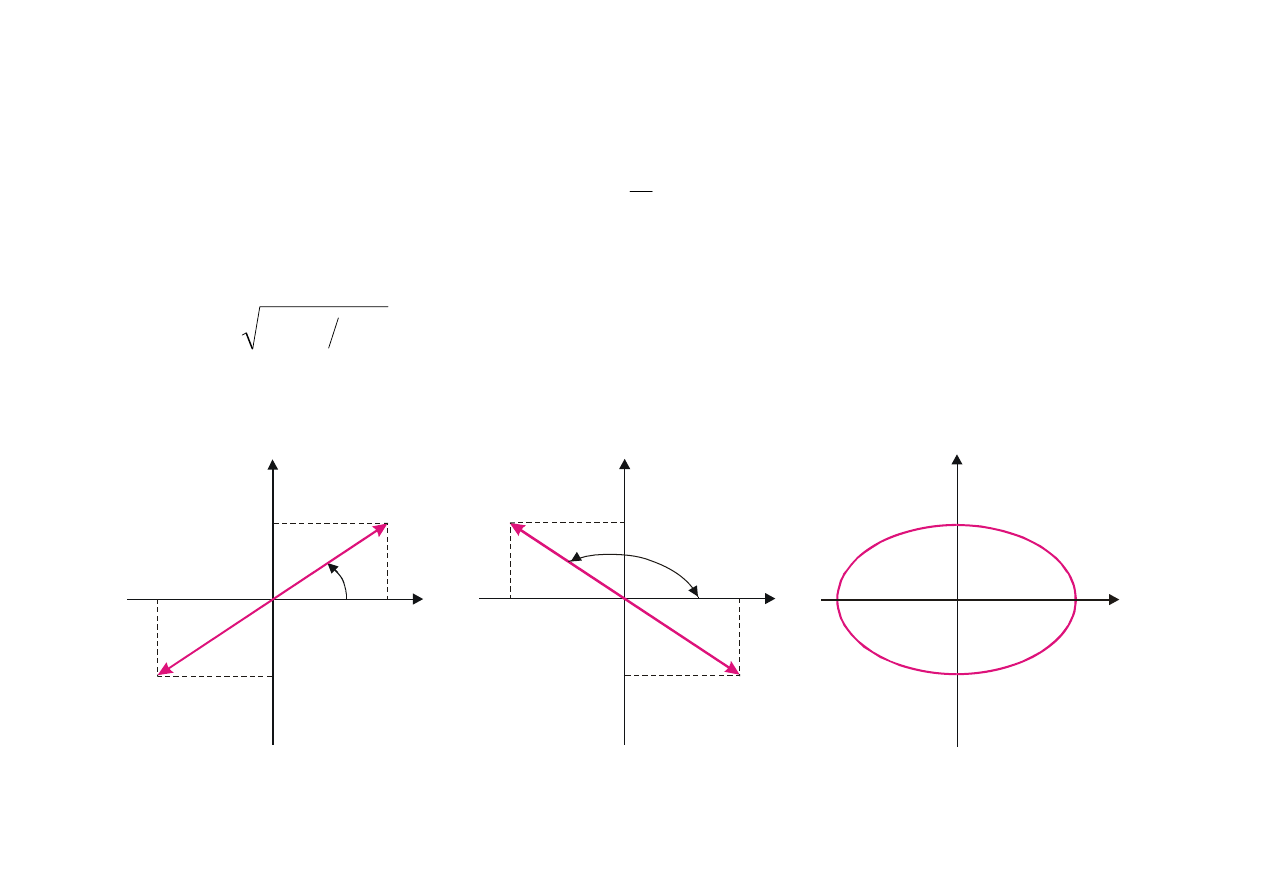
Rozpatrzymy niektóre szczególe przypadki:
•
(
)
,...
,
,
m
m
2
1
0
±
±
=
=
π
ϕ
w tym przypadku elipsa degeneruje się do odcinka prostej
x
A
B
y
±
=
(8.28)
gdzie znak + odpowiada zeru i parzystym wartościom m (rys. 8.6a), a znak – nieparzystym
wartościom m (rys. 8.6b). Wypadkowe drganie stanowi drganie harmoniczne o częstości
ω
i
amplitudzie
(
)
2
1
A
x
−
zachodzące wzdłuż prostej nachylonej pod kątem
(
)
[
]
π
ϕ
m
cos
A
/
B
arctg
=
. W tym przypadku mamy drgania liniowo spolaryzowane.
(a) (b) (c)
A
A
A
-A
-A
-B
-B
B
B
B
ϕ
ϕ
x
x
x
y
y
y
,...
4
,
2
,
0
m
±
±
=
,...
5
,
3
,
1
m
±
±
±
=
O
Rys. 8.6. Superpozycja drgań harmonicznych wzajemnie prostopadłych o różnych amplitudach
i jednakowych częstościach.
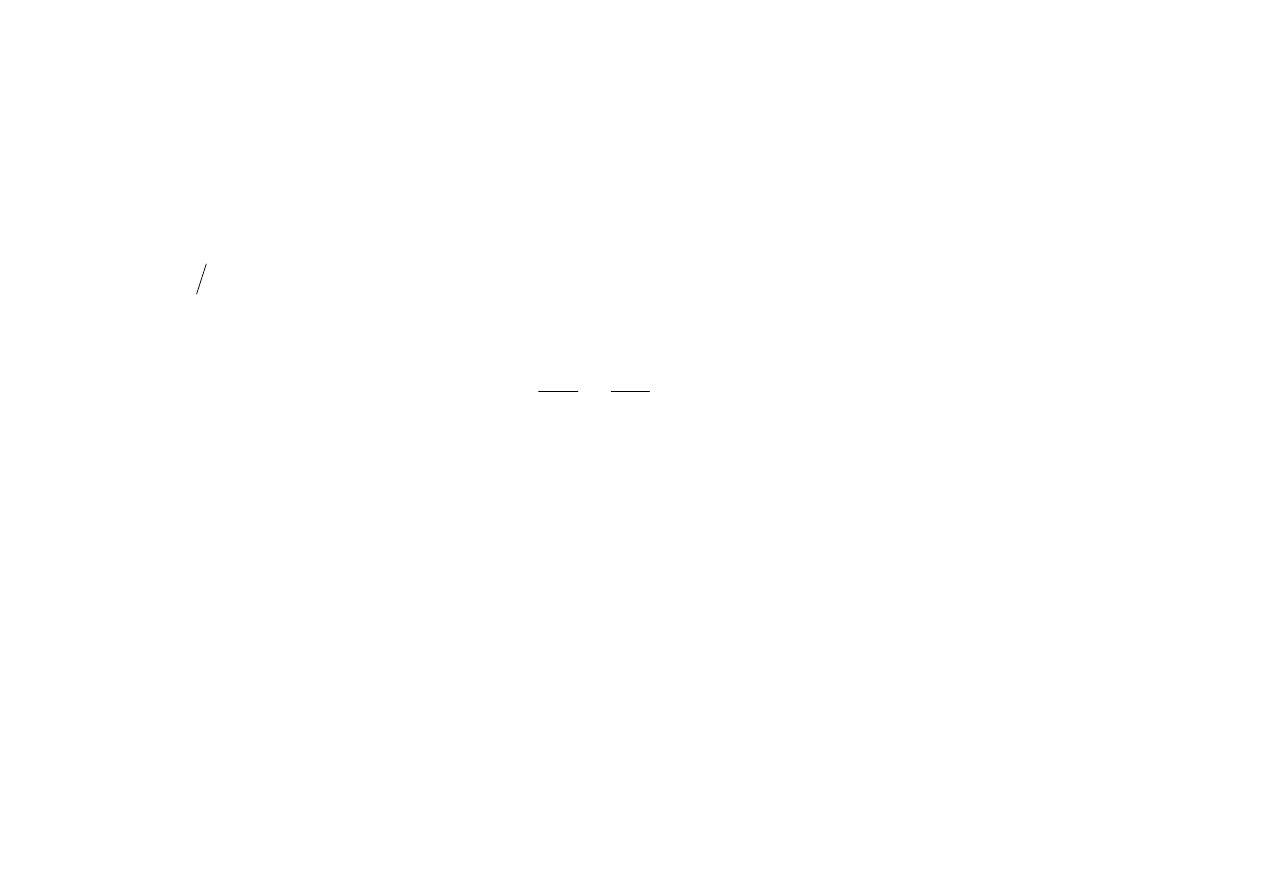
(
)
(
)
2,...
1,
0,
m
m
±
±
=
+
=
2
1
2
π
ϕ
w tym przypadku otrzymujemy
1
2
2
2
2
=
+
B
y
A
x
(8.29)
Jest to równanie elipsy, której osie pokrywają się z osiami współrzędnych, a jej półosie są równe
odpowiednim amplitudom (rys. 8.6c).
Złożenie drgań harmonicznych o różnych częstościach daje w wyniku skomplikowane krzywe, zwane
krzywymi Lissajous. Kształt tych krzywych zależy od stosunku amplitud, częstości i początkowych faz
drgań.
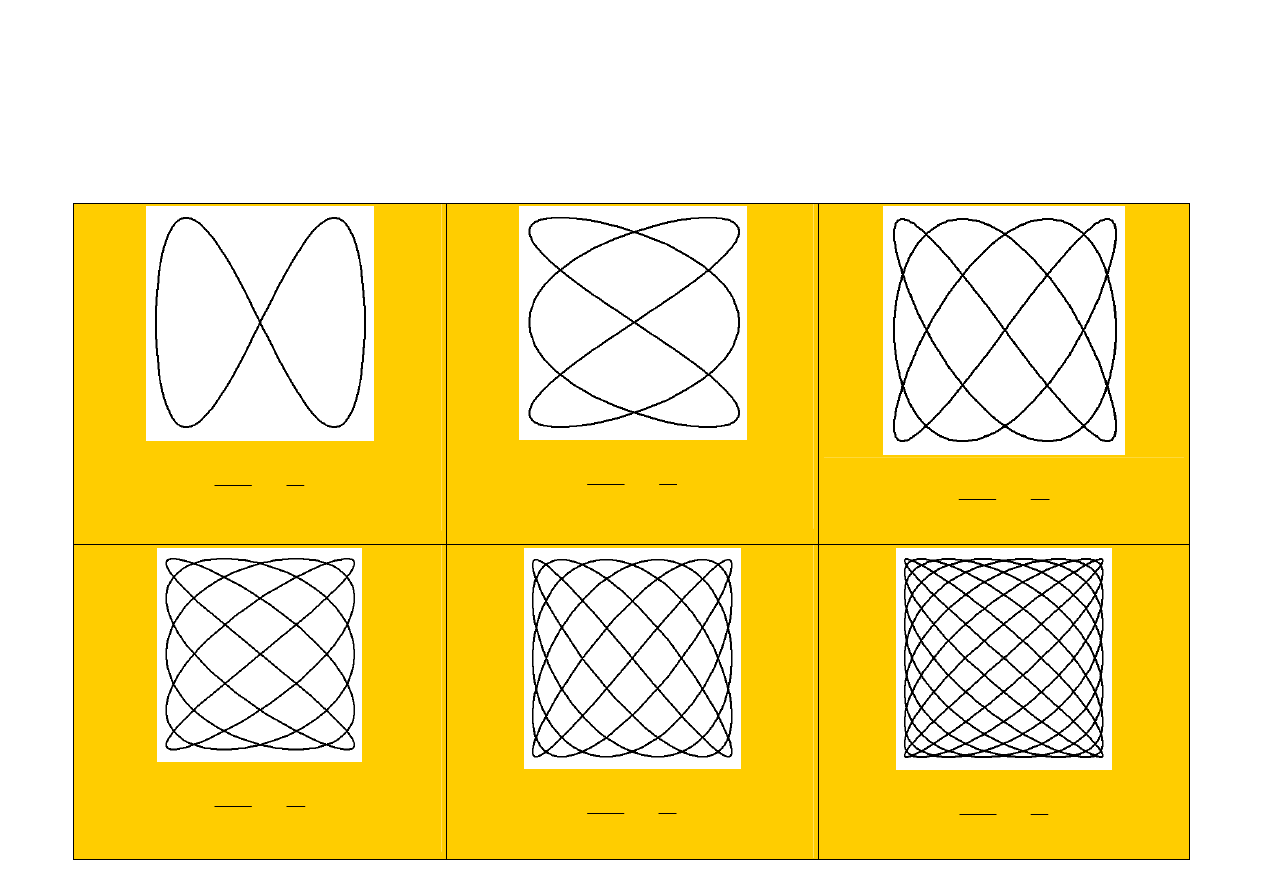
Krzywe Lissajous: przykład
(
)
ϕ
ω
+
=
t
sin
A
x
1
( )
t
sin
A
y
2
ω
=
Poniżej zamieszczono przykłady krzywych Lissajous o parametrach
ϕ = π/2.
1
2
2
1
=
ω
ω
3
2
2
1
=
ω
ω
3
4
2
1
=
ω
ω
5
4
2
1
=
ω
ω
5
6
2
1
=
ω
ω
9
8
2
1
=
ω
ω

Drgania swobodne tłumione
Wszystkie rzeczywiste układy drgające są układami rozpraszającymi energię. W wielu przypadkach
zanikania drgań mechanicznych siły tarcia są proporcjonalne do prędkości
rv
F
t
−
=
gdzie r jest współczynnikiem oporu. Wówczas równanie ruchu
dt
ds
r
ks
dt
s
d
m
−
−
=
2
2
gdzie m jest masą ciała drgającego, ks siłą zwrotną sprężyny a r(ds/dt) siłą tarcia. Otrzymujemy więc
0
2
2
=
+
+
s
m
k
dt
ds
m
r
dt
s
d
(8.30)
czyli
0
2
2
2
2
=
+
+
s
dt
ds
dt
s
d
o
ω
δ
(8.31)
gdzie
const
=
δ
jest współczynnikiem pochłaniania,
o
ω
częstością nietłumionych drgań swobodnych układu (
δ
= 0).

Rozwiązaniem równania (8.31) jest
u
e
s
t
δ
−
=
(8.32)
Po znalezieniu pierwszej i drugiej pochodnej wyrażenia (8.32) i podstawieniu do (8.31) otrzymujemy
(
)
0
2
2
2
2
=
−
+
u
dt
u
d
o
δ
ω
(8.33)
Kiedy ten współczynnik
)
(
o
2
2
δ
ω
−
jest dodatni
(
)
2
2
2
δ
ω
ω
−
=
o
(8.34)
to rozwiązaniem równania (8.33) jest
(
)
ϕ
ω
+
=
t
cos
A
u
o
Wobec tego rozwiązaniem równania (8.33) w przypadku małego tłumienia
(
)
2
2
o
ω
δ
<
jest
)
t
cos(
e
A
s
t
o
ϕ
ω
δ
+
=
−
(8.35)
gdzie
t
o
e
A
A
δ
−
=
(8.36)
jest amplitudą drgań tłumionych, a A
o
– amplitudą początkową.
Okres czasu
δ
τ
/
1
=
w ciągu którego amplituda drgań tłumionych zmniejsza się e razy,
nazywamy czasem relaksacji
.
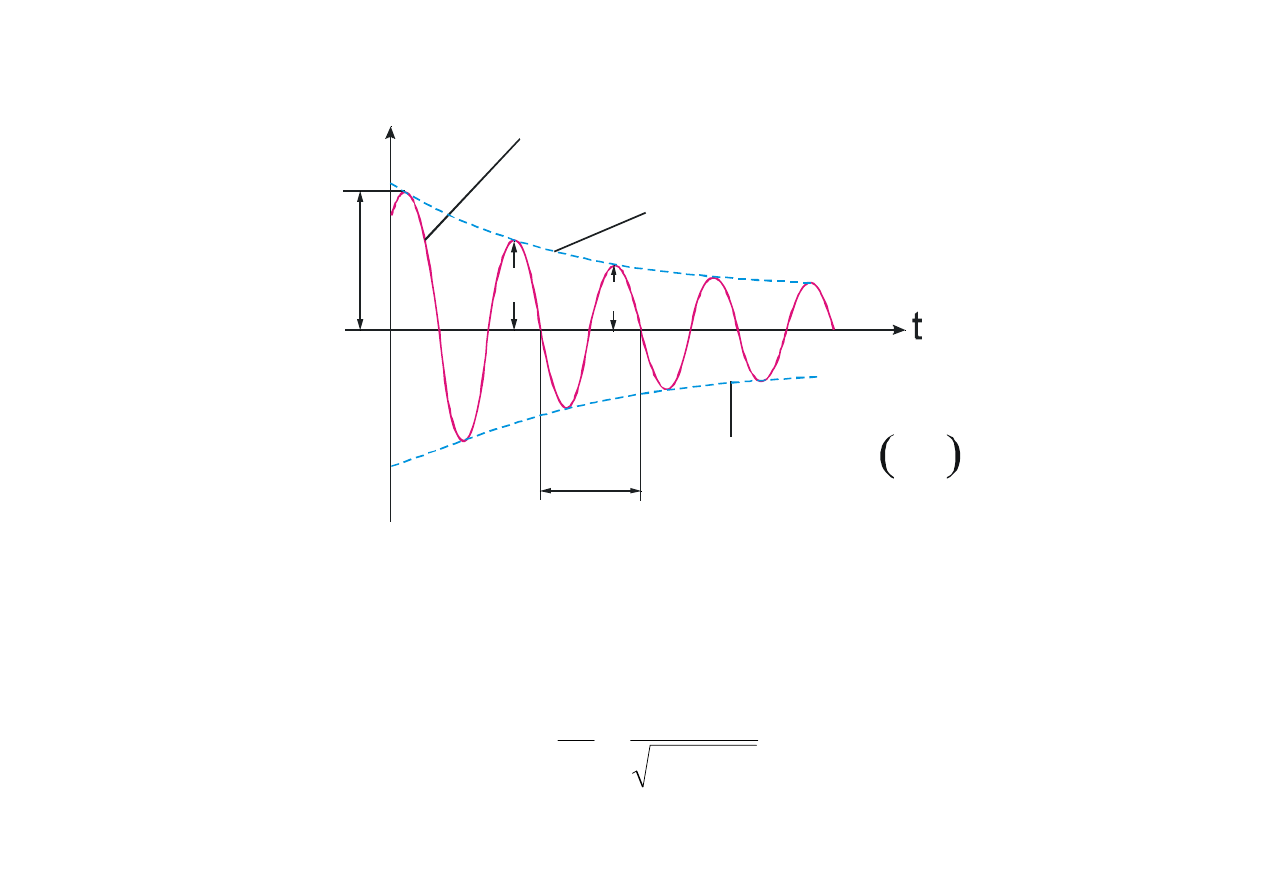
A
o
A
1
A
2
t
exp
A
A
o
δ
−
−
=
t
o
e
A
A
δ
−
−
=
(
)
ϕ
+
ω
=
δ
−
t
cos
e
A
s
t
o
s, A
T
Rys. 8.7. Drgania swobodne tłumione.
Drgania tłumione nie są harmonicznymi, ponieważ drgania nie powtarzają się. Dlatego wielkość
ω
możemy tylko umownie nazwać częstością kołową drgań tłumionych
2
2
2
2
δ
ω
π
ω
π
−
=
=
o
T

Jeżeli A(t) i A(t+T) są amplitudami dwóch kolejnych drgań odpowiadających chwilom czasu
różniących się o umowny okres drgań, to stosunek
T
e
)
T
t
(
A
)
t
(
A
δ
=
+
nazywamy
dekrementem tłumienia
, a jego logarytm
τ
δ
Θ
T
T
)
T
t
(
A
)
t
(
A
ln
=
=
+
=
(8.37)
logarytmicznym dekrementem tłumienia
.
W celu scharakteryzowania drgającego układu wprowadzono pojęcie dobroci Q, która dla małych
wartości logarytmicznego dekrementu tłumienia jest równa
δ
ω
δ
π
Θ
π
2
o
o
T
Q
=
=
=
(8.38)
Dla wahadła sprężynowego, porównując równanie (8.30) z równaniem (8.31) mamy
m
r
2
=
δ
(8.39)
oraz
)
t
cos(
e
A
s
t
o
ϕ
ω
δ
+
=
−
gdzie
2
2
2
4m
r
o
−
=
ω
ω
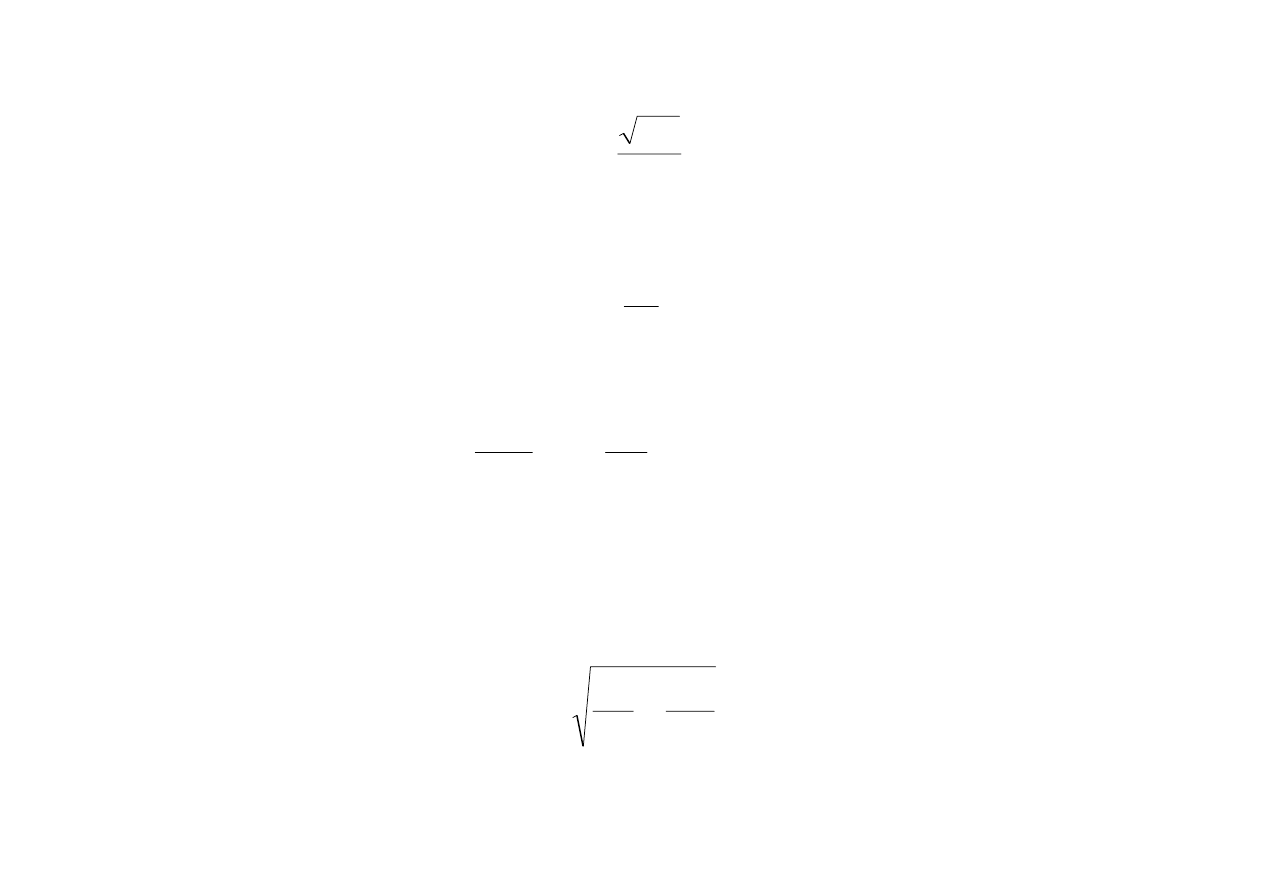
Dobroć wahadła sprężynowego zgodnie z (8.38) wnosi
r
r
km
Q
=
Analogiczne wyrażenie możemy otrzymać dla swobodnych tłumionych drgań ładunku w obwodzie
RLC
. Równanie to ma postać (8.15), w związku z tym współczynnik tłumienia
L
R
2
=
δ
(8.40)
Równanie różniczkowe (8.15) możemy zapisać w sposób analogiczny do (8.31)
0
2
2
2
2
=
+
+
Q
dt
dQ
dt
Q
d
o
ω
δ
Drgania ładunku zachodzą według prawa
(
)
ϕ
ω
δ
+
=
−
t
cos
e
Q
Q
t
o
z częstością kołową
2
2
4
1
L
R
LC
−
=
ω
(8.41)
mniejszą od częstości drgań swobodnych (porównaj z (8.17)). Dla R = 0 wyrażenie (8.41) przechodzi
w (8.17). Dobroć obwodu drgającego

C
L
R
Q
1
=
(8.42)
Gdy
δ
wzrasta, to okres drgań tłumionych również rośnie i przy
o
ω
δ
=
przyjmuje wartość
nieskończoną, tj. ruch drgający przestaje być periodycznym. W tym przypadku wielkość drgająca
asymptotycznie zbliża się do zera, kiedy
∞
→
t
. Proces ten nazywamy
aperiodycznym
.

Drgania wymuszone
Ażeby w układzie drgającym otrzymać drgania nietłumione, należy kompensować straty energii.
Czynnik wymuszający
t
cos
X
X
o
ω
=
W przypadku drgań mechanicznych rolę X(t) odgrywa siła wymuszająca
t
cos
F
F
o
ω
=
(8.43)
Z uwzględnieniem siły (8.43) prawo ruchu dla wahadła sprężynowego zapiszemy w postaci
t
cos
F
dt
ds
r
ks
dt
s
d
m
o
ω
+
−
−
=
2
2
Stąd otrzymujemy równanie w bardziej ogólnej formie
t
cos
m
F
s
dt
ds
dt
s
d
o
o
ω
ω
δ
=
+
+
2
2
2
2
(8.44)
W przypadku elektrycznego obwodu drgającego, to rolę X(t) odgrywa periodycznie zmieniająca się
SEM
lub zmienne napięcie
V = V
o
cos
ω
t
.
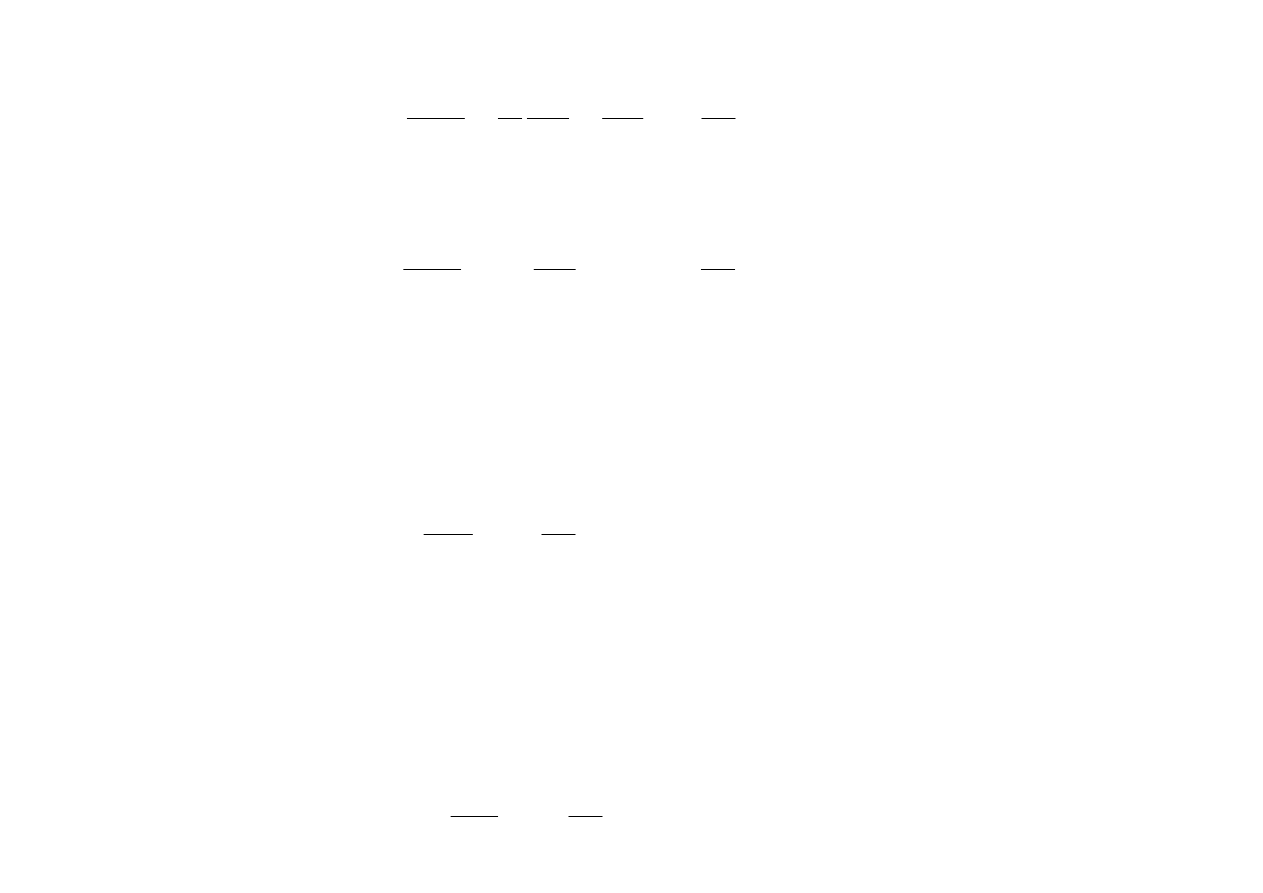
Wówczas równanie (8.15) możemy napisać w postaci
t
cos
L
V
Q
LC
dt
dQ
L
R
dt
Q
d
o
ω
=
+
+
1
2
2
(8.45)
Stosując (8.17) i (8.40) otrzymujemy
t
cos
L
V
Q
dt
dQ
dt
Q
d
o
o
ω
ω
δ
=
+
+
2
2
2
2
(8.46)
Drgania powstające pod wpływem zewnętrznej, periodycznie zmieniającej się siły, lub pod
wpływem periodycznie zmieniającej się SEM, nazywamy odpowiednio wymuszonymi
drganiami mechanicznymi lub elektrycznymi.
Równania (8.44) i (8.46) można sprowadzić do liniowego niejednorodnego równania różniczkowego
t
cos
x
s
dt
ds
dt
s
d
o
o
ω
ω
δ
=
+
+
2
2
2
2
(8.47)
Rozwiązanie tego równania stanowi suma ogólnego rozwiązania (8.35) równania jednorodnego (8.31)
i szczególnego rozwiązania równania niejednorodnego.
W celu rozwiązania równania (8.47), zamienimy prawą stronę równania na wielkość zespoloną
t
i
o
e
s
s
η
=
t
i
o
o
e
x
s
dt
ds
dt
s
d
ω
ω
δ
=
+
+
2
2
2
2
(8.48)
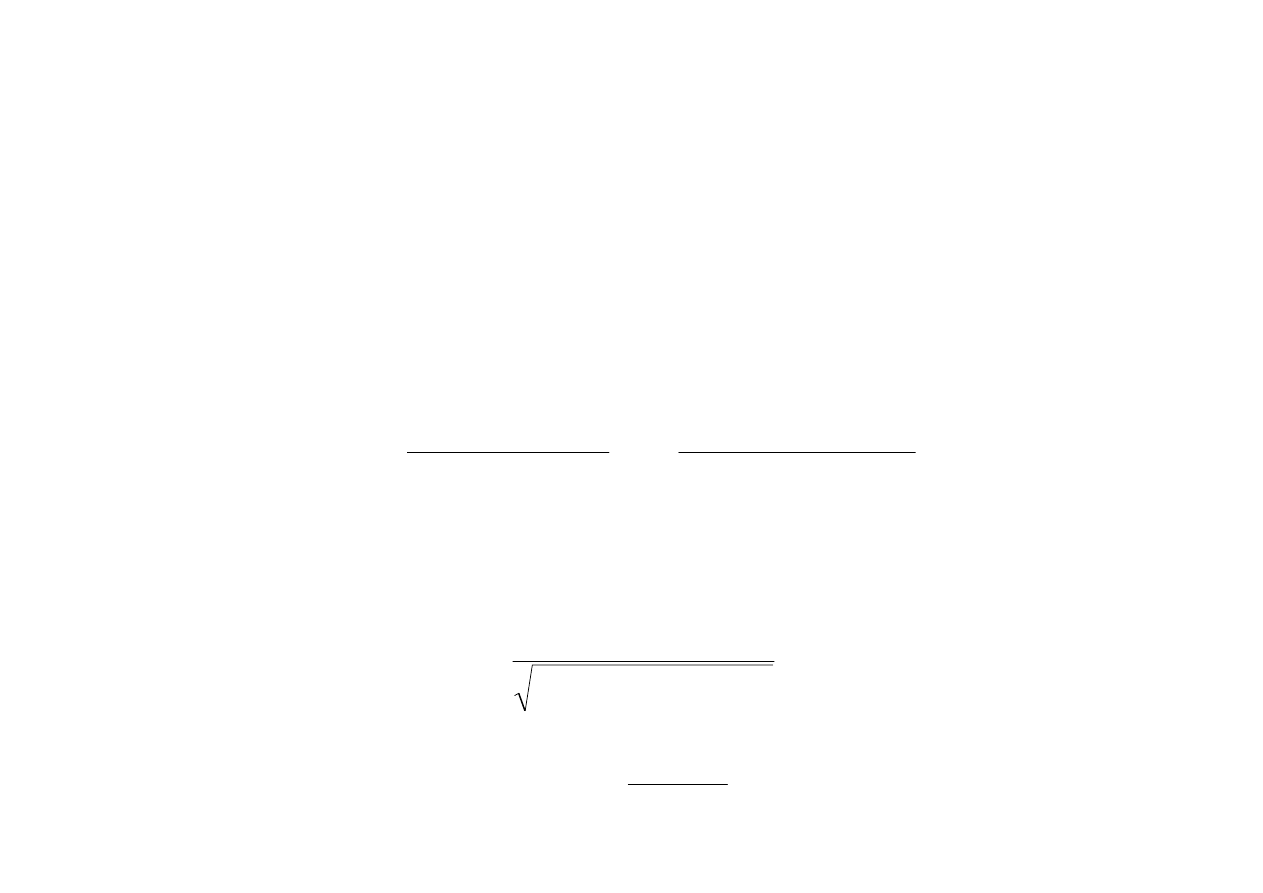
Szczególnego rozwiązania tego równania będziemy poszukiwać w postaci
t
i
o
e
s
s
η
=
Podstawiając wyrażenia dla s i jego pochodnych do równania (8.48), otrzymujemy
(
)
t
i
o
o
t
i
o
e
x
i
e
s
s
ω
η
ω
δη
η
=
+
+
−
=
2
2
2
Ponieważ równość ta musi być spełniona dla każdej chwili czasu, więc
ω
η
=
. Z równania tego
również można określić s
o
. Mnożąc licznik i mianownik wyrażenia s
o
przez
(
)
δω
ω
ω
i
o
2
2
2
−
−
,
otrzymujemy
(
)
(
)
(
)
2
2
2
2
2
2
2
2
2
4
2
2
ω
δ
ω
ω
δω
ω
ω
δω
ω
ω
+
−
−
−
=
+
−
=
o
o
o
o
o
o
i
x
i
x
s
To złożone wyrażenie wygodniej jest przedstawić w formie
ϕ
i
o
Ae
s
−
=
gdzie
(
)
2
2
2
2
2
4
ω
δ
ω
ω
+
−
=
o
o
x
A
(8.49)
oraz
2
2
2
ω
ω
δω
ϕ
−
=
o
arctg
(8.50)
Tak więc rozwiązanie równania (8.48) w postaci zespolonej ma postać
(
)
ϕ
ω
−
=
t
i
Ae
s
natomiast jego rzeczywista część jest równa
(
)
ϕ
ω
−
=
t
cos
A
s
(8.51)
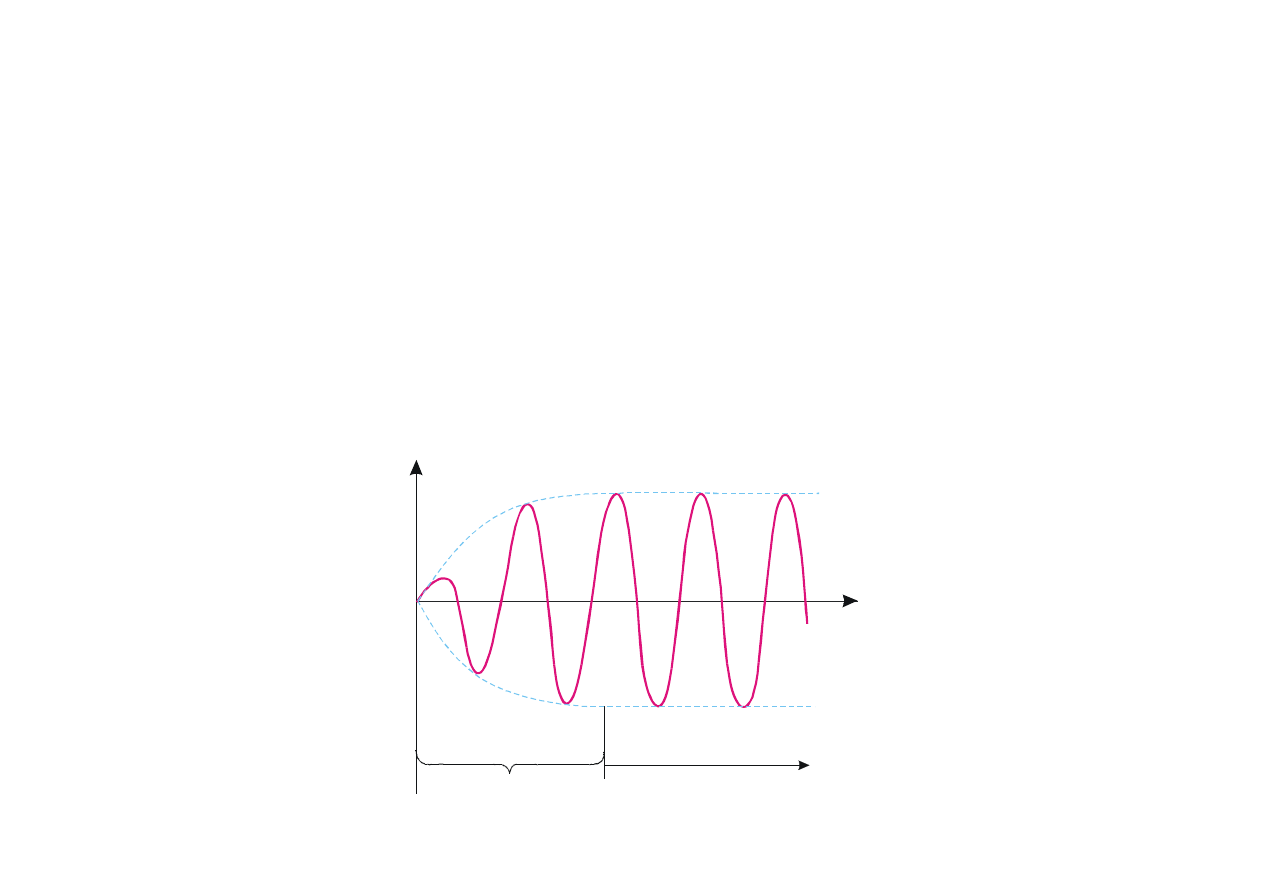
Składowa ogólnego rozwiązania równania (8.48) stanowiąca ogólne rozwiązanie równania
jednorodnego [patrz (8.31)] odgrywa istotną rolę tylko w początkowym stadium procesu (przy
ustalaniu się drgań) do chwili kiedy amplituda drgań wymuszonych osiąga wartość (8.49).
W stanie ustalonym, drgania wymuszone przebiegają z częstością
ω
i są drganiami harmonicznymi, a
ich amplituda i faza określone są wzorami (8.49) i (8.50) zależnymi od
ω
.
Drgania ustalone
Drgania
nieustalone
s
t
Rys. 8.8. Drgania wymuszone

W przypadku drgań elektromagnetycznych uwzględniając, że
LC
o
1
2
=
ω
[zob. (8.17)]
L
R
2
=
δ
[zob. (8.40)]
wyrażenia (8.49), (8.50) i (8.51) mają postać
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
C
L
R
V
Q
o
o
ω
ω
(8.52)
L
)
C
/(
R
tg
ω
ω
ϕ
−
=
1
(8.53)
Różniczkując
(
)
ϕ
ω
−
=
t
cos
Q
Q
o
względem t, otrzymamy natężenie prądu w obwodzie dla drgań ustalonych
(
)
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
−
−
=
2
π
α
ω
α
ω
ω
t
cos
I
t
sin
Q
I
o
o
o
(8.54)

gdzie
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
=
C
L
R
V
Q
I
o
o
o
ω
ω
ω
ω
(8.55)
Wyrażenie (8.54) można zapisać w postaci
(
)
ϕ
ω
−
=
t
cos
I
I
o
gdzie
2
/
π
α
ϕ
−
=
oznacza przesunięcie fazowe pomiędzy prądem i napięciem. Zgodnie z
wyrażeniem (8.53)
(
)
R
C
/
L
tg
tg
tg
ω
ω
α
π
α
ϕ
1
1
2
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛ −
=
(8.56)
Z wyrażenia (8.56) wynika, że prąd opóźniony jest w fazie względem napięcia (
ϕ
> 0) gdy
)
C
/(
L
ω
ω
1
>
i wyprzedza napięcie (
ϕ
< 0) gdy
)
C
/(
L
ω
ω
1
<
.

Amplituda i faza drgań wymuszonych. Rezonans
Z wyrażenia (8.49) wynika, że amplituda może przyjąć pewną maksymalną wartość. Maksimum
funkcji uzyskamy różniczkując to wyrażenie względem
ω i przyrównując do zera
(
)
0
8
4
2
2
2
=
+
−
−
ω
δ
ω
ω
ω
o
Równość ta jest spełniona dla
ω
= 0 i
2
2
2
δ
ω
ω
−
±
=
o
.
Tak więc, częstotliwość rezonansowa
2
2
2
δ
ω
ω
−
=
o
rez
(8.57)
Zjawisko silnego wzrastania amplitudy drgań wymuszonych przy zbliżaniu się częstości siły
wymuszającej do częstości
rez
ω
nazywamy rezonansem.
Podstawiając (8.57) do (8.49), otrzymujemy
2
2
2
δ
ω
δ
−
=
o
o
rez
x
A
(8.58)
Jeżeli
0
→
ω
, to wszystkie krzywe przyjmują jedną wartość, różną od zera
2
o
o
/
x
ω
nazywaną
odchyleniem statycznym.
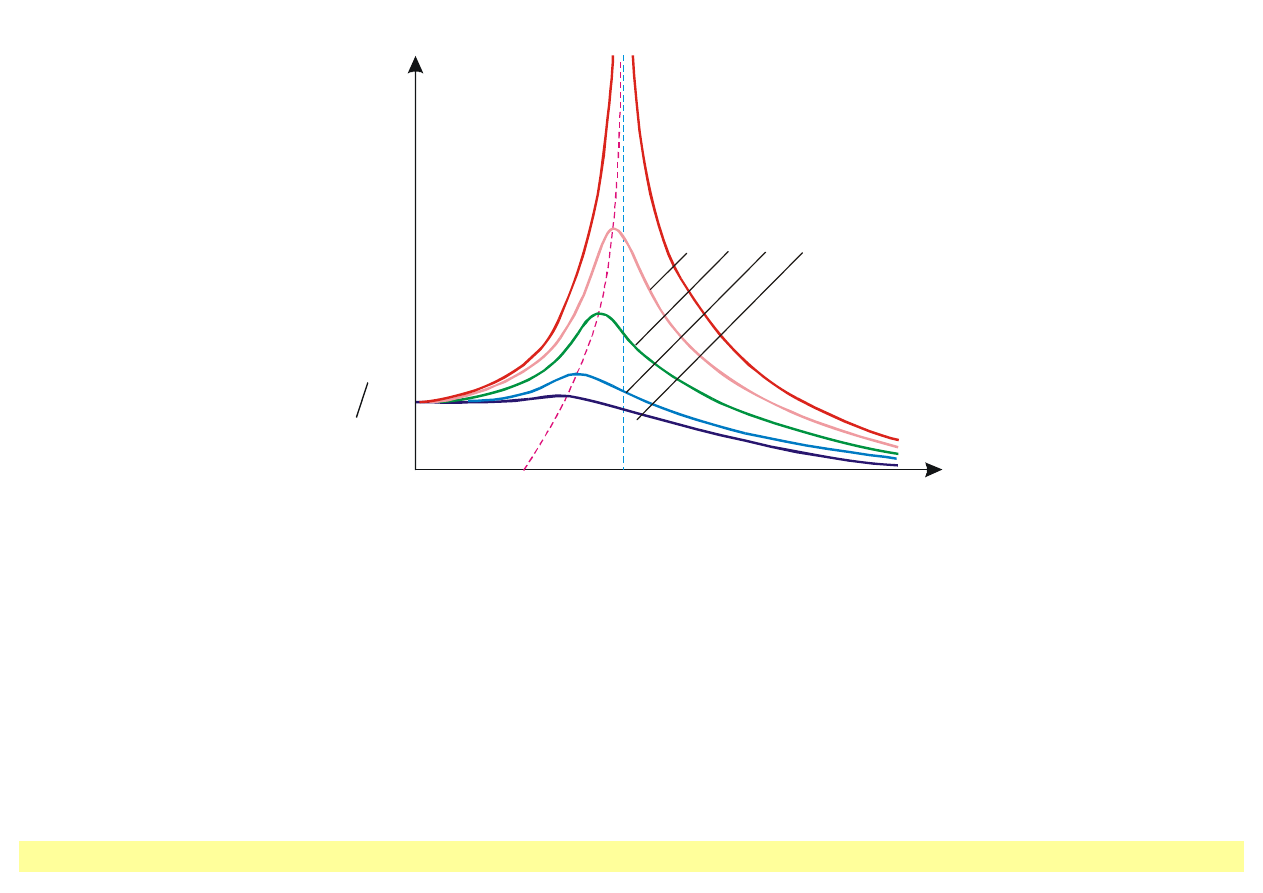
2
o
o
x
ω
A
rez
ω
o
ω
ω
δ <δ <δ <δ
1
2
3
4
δ=0
Rys. 8.9. Krzywe rezonansu dla różnych wartości współczynnika tłumienia.
Zjawisko rezonansu może być zjawiskiem pożytecznym jak i szkodliwym.
Przykłady zastosowań:
• akustyka
(instrumenty)
•
odbiorniki radiowe i telewizyjne
Katastrofy

Katastrofa mostu w Tacoma
(USA, 7 listopada 1940)
http://pl.wikipedia.org/wiki/Most_Tacoma
Most ten był mostem wiszącym, którego główne przęsło miało 840 m długości, przy szerokości
jedynie 12 m, co było powodem jego niebywałej wiotkości. Już w trakcie budowy, pracujący robotnicy
doznawali mdłości wynikających z dużych ugięć mostu. Po oddaniu do eksploatacji, stał się on
prawdziwą atrakcją turystyczną, ze względu na niesamowite wrażenia towarzyszące przejazdowi
przez most, tak iż nazwany został potocznie "galopującą Gertie".
Po czterech miesiącach istnienia, rano 7 listopada 1940 r. huraganowy wiatr wiejący od oceanu (56-
67 km/h), spowodował wprowadzenie mostu w drgania, odpowiadające ruchowi falowemu.
Początkowo (godz. 7:00), był to ruch pomostu w płaszczyźnie pionowej (podnoszenie i opadanie o
amplitudzie ok. 90 cm z częstością 36 razy na minutę), później ok. godz. 10:00 rytmiczne wznoszenie
i opadanie zamieniło się w dwufalowy ruch skręcający 14 cykli na minutę z wychyleniem do 8,4 m,
przy skręceniu dochodzącym do 45 stopni. Ok. 10:30 nastąpiło pierwsze załamanie jednej z płyt
pomostu, a ok. 11:00 most rozpadł się ostatecznie.

Prąd zmienny
Rozważymy wymuszone drganie elektromagnetyczne zachodzące w obwodzie RLC.
Prąd zmienny można traktować jako kwasistacjonarny, co oznacza, że chwilowe wartości natężenia
prądu we wszystkich przekrojach obwodu są praktycznie jednakowe; spełnione jest prawo Ohma i
prawa Kirchhoffa.
Napięcie zmienne
t
cos
V
V
o
ω
=
(8.59)
Obwód zawierający rezystancję
(a)
(b)
I
o
V =RI
o
o
R
V
Rys. 8.10. (a) schemat obwodu; (b) wykres
fazowy.
Prąd płynący przez rezystor określony jest
prawem Ohma
t
cos
I
t
cos
R
V
R
V
I
o
o
ω
ω
=
=
=
gdzie
R
V
I
o
o
=
Przesunięcie fazowe pomiędzy I
o
i V
o
jest
zerowe
.

Obwód zawierający indukcyjność
SEM
samoindukcji
dt
dI
L
E
s
−
=
Wówczas prawo Ohma dla rozważanego obwodu ma postać
0
=
−
dt
dI
L
t
cos
V
o
ω
stąd
t
cos
V
dt
dI
L
o
ω
=
(8.60)
Tak więc spadek napięcia na cewce indukcyjnej
dt
dI
L
V
L
=
(8.61)
Z równania (8.60) wynika, że
tdt
cos
L
V
dI
o
ω
=
lub po scałkowaniu
(
)
(
)
2
2
π
ω
π
ω
ω
ω
ω
−
=
−
=
=
t
cos
I
t
cos
L
V
t
sin
L
V
I
o
o
o
(8.62)
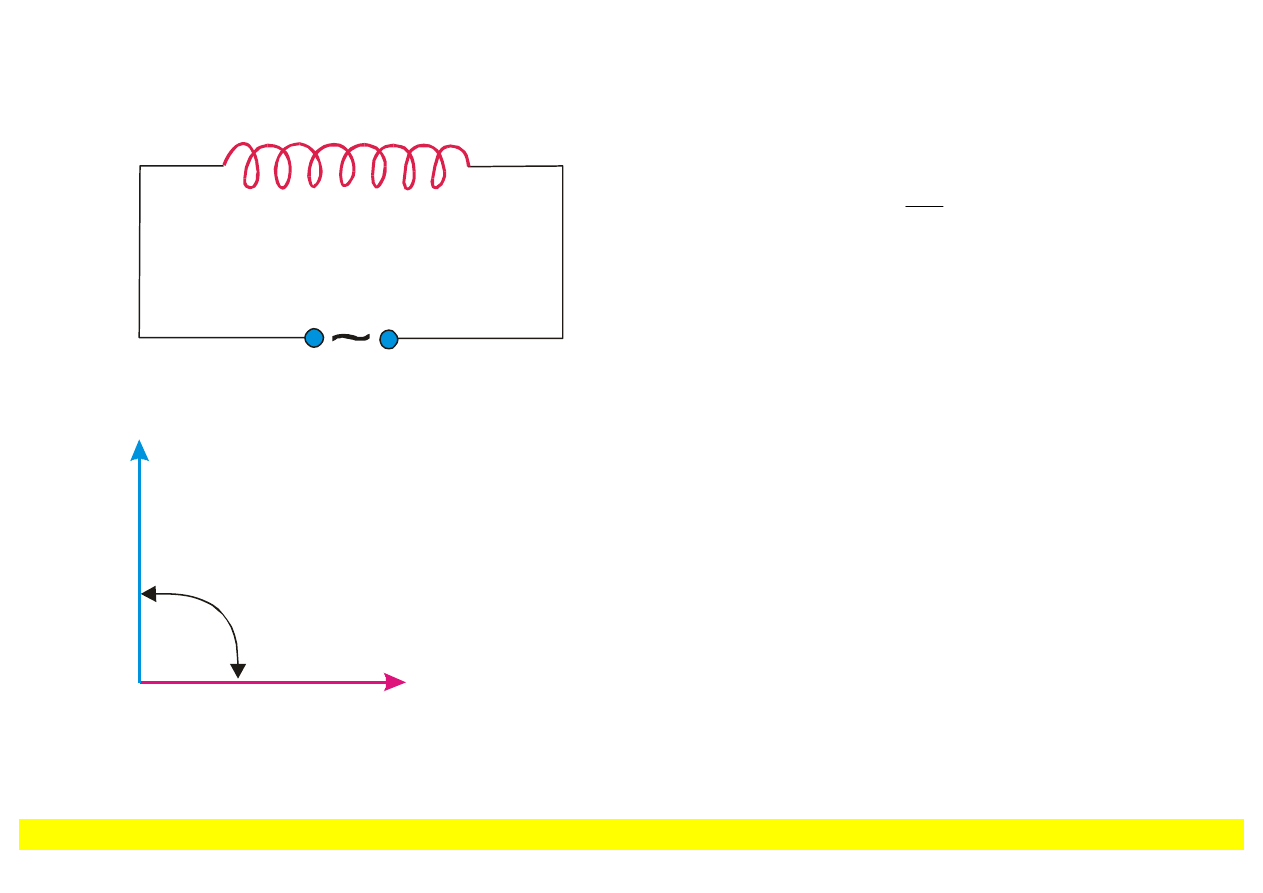
V
L
V = LI
L
o
ω
I
o
(a)
(b)
π/2
Rys. 8.11. Obwód zawierający
indukcyjność: (a) schemat obwodu; (b)
wykres fazowy.
gdzie
L
V
I
o
o
ω
=
Wielkość
L
R
L
ω
=
(8.63)
nazywamy reaktancją indukcyjną
.
Podstawiając
o
o
LI
V
ω
=
w wyrażenie (8.60) i
uwzględniając (8.61), otrzymujemy spadek
napięcia na cewce indukcyjnej
t
cos
LI
V
o
L
ω
ω
=
(8.64)
Spadek napięcia V
L
wyprzedza w fazie prąd I
płynący przez cewkę o kąt
π/2
, co pokazano na
wykresie fazowym (rys. 8.11b).
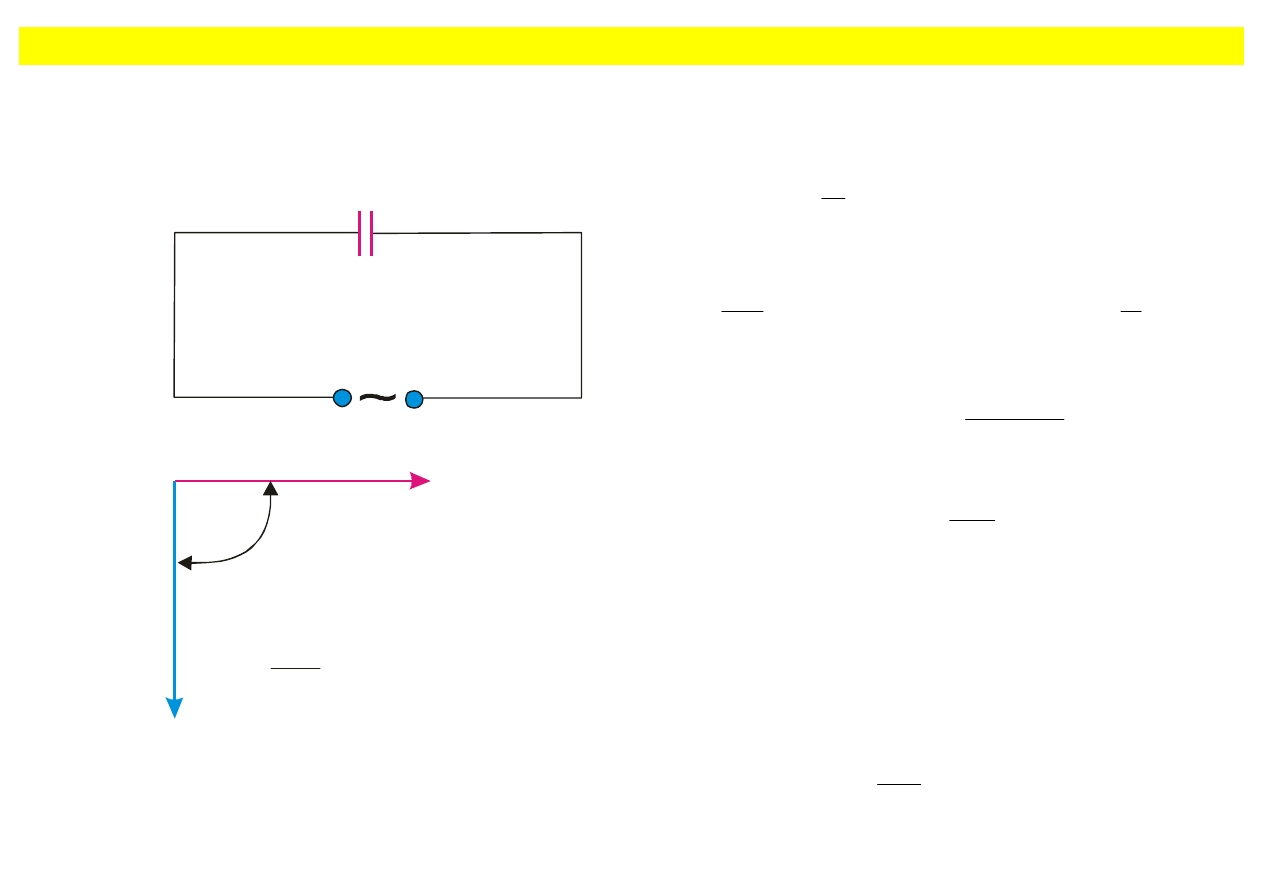
Obwód zawierający pojemność
Jeżeli napięcie zmienne (8.59) przyłożymy do kondensatora, to z upływem czasu kondensator będzie
przeładowywał się a w obwodzie popłynie prąd zmienny.
V
C
I
o
(a)
(b)
π/2
o
C
I
C
1
V
ω
=
Rys. 8.12. Obwód zawierający kondensator: (a)
schemat obwodu, (b) wykres fazowy.
t
cos
V
V
C
Q
o
c
ω
=
=
Natężenie prądu
(
)
2
π
ω
ω
ω
+
=
=
=
t
cos
I
t
sin
CV
dt
dQ
I
o
o
(8.65)
gdzie
( )
[
]
C
/
1
V
CV
I
o
o
o
ω
ω
=
=
Wielkość
C
1
R
C
ω
=
nazywamy reaktancją pojemnościową
.
Dla prądu stałego (
ω
= 0) R
C
=
∞, co oznacza, że
prąd stały nie płynie przez kondensator.
Spadek napięcia na kondensatorze
t
cos
I
C
V
o
c
ω
ω
1
=
(8.66)
Spadek napięcia
c
V
opóźniony jest w fazie o
π/2 w porównaniu z prądem I.
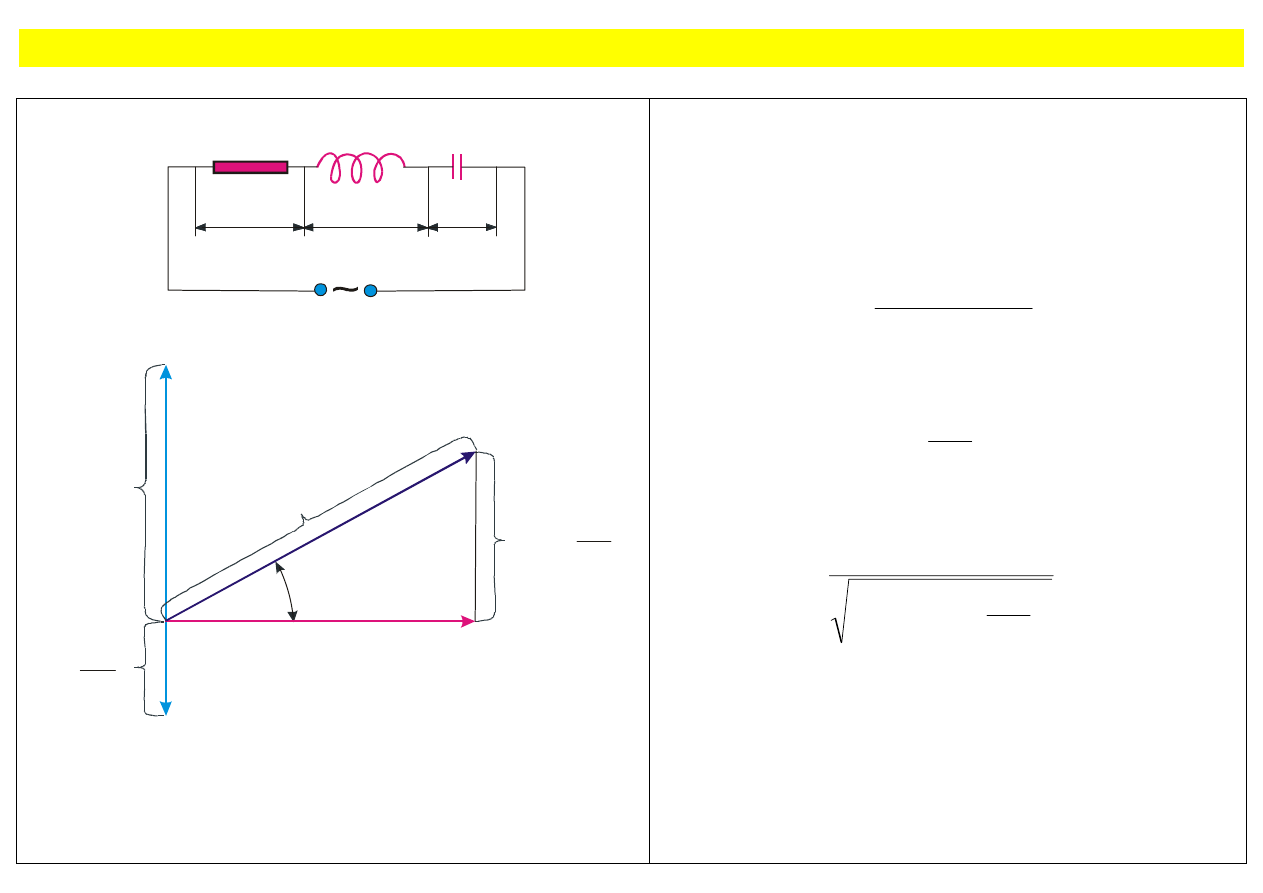
Obwód RLC
V
R
L
C
V = LI
L
o
ω
o
I
C
1
L
⎟
⎠
⎞
⎜
⎝
⎛
ω
−
ω
(a)
(b)
V
o
RI
o
ϕ
o
C
I
C
1
V
ω
=
Rys. 8.13. Obwód RLC: (a) schemat obwodu; (b)
wykres fazowy.
Amplituda przyłożonego napięcia V
o
jest równa
sumie geometrycznej amplitud tych spadków
napięć.
Z rysunku wynika, że
( )
R
C
/
L
tg
ω
ω
ϕ
1
−
=
(8.67)
Z trójkąta prostokątnego otrzymujemy
( )
(
)
[
]
2
2
2
1
o
o
o
V
I
C
L
RI
=
−
+
ω
ω
stąd amplituda prądu ma wartość
(
)
2
2
1
C
L
R
V
I
o
o
ω
ω
−
+
=
(8.68)
co jest zgodne z (8.55).
Tak więc, jeżeli napięcie w obwodzie zmienia się
według prawa
t
cos
V
V
o
ω
=

to w obwodzie płynie prąd
(
)
ϕ
ω
−
=
t
cos
I
I
o
(8.69)
gdzie
ϕ
i Io określone są wzorami (8.67) i (8.68). Wielkość
(
)
(
)
2
2
2
2
1
C
L
R
R
R
C
L
R
Z
−
+
=
−
+
=
ω
ω
(8.70)
nazywamy impedancją obwodu, a
wielkość
C
L
R
R
X
C
L
ω
ω
1
−
=
−
=
nazywamy reaktancją
.
Zauważmy, że impedancja obwodu RLC osiąga minimum, gdy
0
1
=
−
C
L
ω
ω
czyli gdy
LC
o
1
=
ω
(8.71)
Częstość tę nazywamy rezonansową i oznaczamy przez
ω
o
.
Moc wydzielana w obwodzie prądu zmiennego
Chwilowa wartość mocy rozpraszanej w obwodzie
( )
( ) ( )
t
I
t
V
t
P
=
gdzie
V(t)
=
V
o
cos
ω
t
a I(t) = I
o
cos(
ω
t –
ϕ
)
( )
(
)
(
)
ϕ
ω
ω
ϕ
ω
ω
ϕ
ω
sin
t
cos
t
sin
cos
t
cos
V
I
t
cos
t
cos
V
I
t
P
o
o
o
o
+
=
−
=
2
Uwzględniając, że
2
1
2
=
t
cos
ω
,
0
=
t
cos
t
sin
ω
ω
,
otrzymamy
ϕ
cos
V
I
P
o
o
2
1
=
(8.72)
Z wykresu fazowego (rys. 8.13) wynika, że V
o
cos
ϕ
= RI
o
, dlatego
2
2
1
o
RI
P
=
Taką moc wydziela prąd stały
2
o
I
I
=

Wielkości
2
o
I
I
=
;
2
o
V
V
=
nazywamy odpowiednio wartościami skutecznymi prądu i napięcia.
Uwzględniając to
ϕ
cos
IV
P
=
(8.73)
gdzie czynnik cos
ϕ
nazywamy ”współczynnikiem mocy”.
Moc wydzielana w obwodzie prądu zmiennego zależy nie tylko od natężenia prądu i napięcia,
ale również od przesunięcia fazowego między nimi.

Procesy falowe
Falami nazywamy różnego rodzaju rozchodzące się w przestrzeni zaburzenia stanu materii lub
pola
.
Fale akustyczne – drgania ciśnienia
Fale elektromagnetyczne – drgania natężeń pola elektrycznego i magnetycznego.
Fale sprężyste – mechaniczne zaburzenia (odkształcenia) rozchodzące się w ośrodku sprężystym
Fala sprężysta nazywa się podłużną, jeżeli drgania cząstek ośrodka są równoległe do kierunku
rozchodzenia się fal. Jeżeli cząsteczki ośrodka drgają w płaszczyznach prostopadłych do
kierunku rozchodzenia się fali, to fala taka nazywa się poprzeczną.
• Fale poprzeczne propagują się tylko w ośrodku który charakteryzuje się sprężystością postaci
(ciała stałe).
• Fale podłużne związane są z odkształceniem objętościowym ośrodka i dlatego mogą się
rozchodzić zarówno w ciałach stałych, jak i w cieczach i gazach.
• Rozchodzenie się fal sprężystych nie jest związane z przenoszeniem materii.
Miejsce geometryczne punktów do których dochodzą drgania w danej chwili t, nazywamy
czołem fali
.
Miejsce geometryczne punktów drgających w jednakowej fazie nazywamy powierzchnią
falową
.

Powierzchni falowych można przeprowadzić bardzo dużo, natomiast w danej chwili czasu jest to tylko
jedno czoło fali.
Powierzchnie falowe mogą mieć dowolne kształty: fala płaska, kulista.
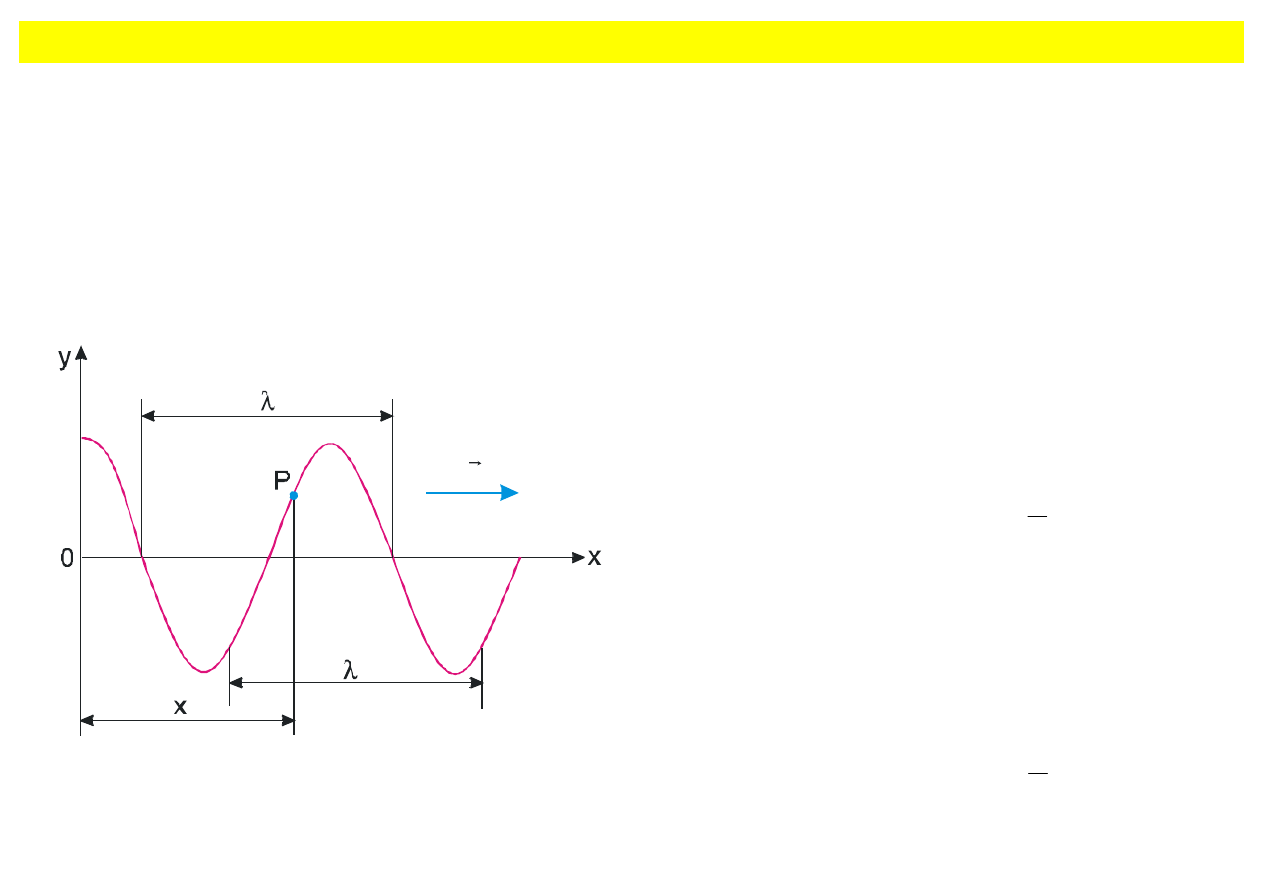
Fale biegnące
Falami biegnącymi nazywamy fale, które (w odróżnieniu od fal stojących) przenoszą energię.
Fala na strunie
• zakładamy, że oś x jest zgodna z kierunkiem propagacji fali,
•
powierzchnie falowe są prostopadłe do osi x,
• przemieszczenie
y = y(x, t)
.
u
Rys. 8.14. Fala biegnąca po strunie.
Jeżeli drganie w płaszczyźnie x = 0 opiszemy
funkcją y = Acos
ω
t
, to drganie punktu P jest
opóźnione o czas
τ
= x/u
potrzebny dla
przemieszczenia fali. Wówczas równanie drgań
cząstek leżących w odległości x ma postać
( )
⎟
⎠
⎞
⎜
⎝
⎛ −
=
u
x
t
cos
A
t
,
x
y
ω
(8.74)
Jest to równanie fali biegnącej
.
Jeżeli fala płaska propaguje się w kierunku
przeciwnym, to
( )
⎟
⎠
⎞
⎜
⎝
⎛ +
=
u
x
t
cos
A
t
,
x
y
ω

W ogólnym przypadku równanie płaskiej sinusoidalnej fali, ma postać
( )
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛ −
=
o
u
x
t
cos
A
t
,
x
y
ϕ
ω
(8.75)
gdzie:
A
– amplituda fali,
ω
– częstość kołowa,
ϕ
o
– faza początkowa, natomiast
[
ω
(t – x/u)+
ϕ
o
] oznacza całkowitą fazę fali.
Liczba falowa
u
uT
k
ω
π
λ
π
=
=
=
2
2
(8.76)
Uwzględniając to
( )
(
)
o
kx
t
cos
A
t
,
x
y
ϕ
ω
+
−
=
(8.77)
W postaci funkcji zespolonej
( )
(
)
o
kx
t
i
Ae
t
,
x
y
ϕ
ω
+
−
=
gdzie sens fizyczny ma jedynie część rzeczywista.
Załóżmy, że w procesie falowym faza jest stała, to jest
const
u
x
t
o
=
+
⎟
⎠
⎞
⎜
⎝
⎛ −
ϕ
ω
(8.78)
Różniczkując to wyrażenie otrzymujemy dt – (1/u)dx = 0, skąd
u
dt
dx =
(8.79)
Prędkość u propagacji fali jak prędkością przemieszczania się fazy fali. Z tego powodu prędkość tę
nazywamy prędkością fazową.
Z wyrażenia (8.76) wynika, że
k
u
ω
=
(8.80)
co oznacza, że
prędkość fal sinusoidalnych zależy od ich częstości. To zjawisko nazywamy
dyspersją fal, a ośrodek w którym obserwowana jest dyspersja fal nazywamy ośrodkiem
dyspersyjnym.
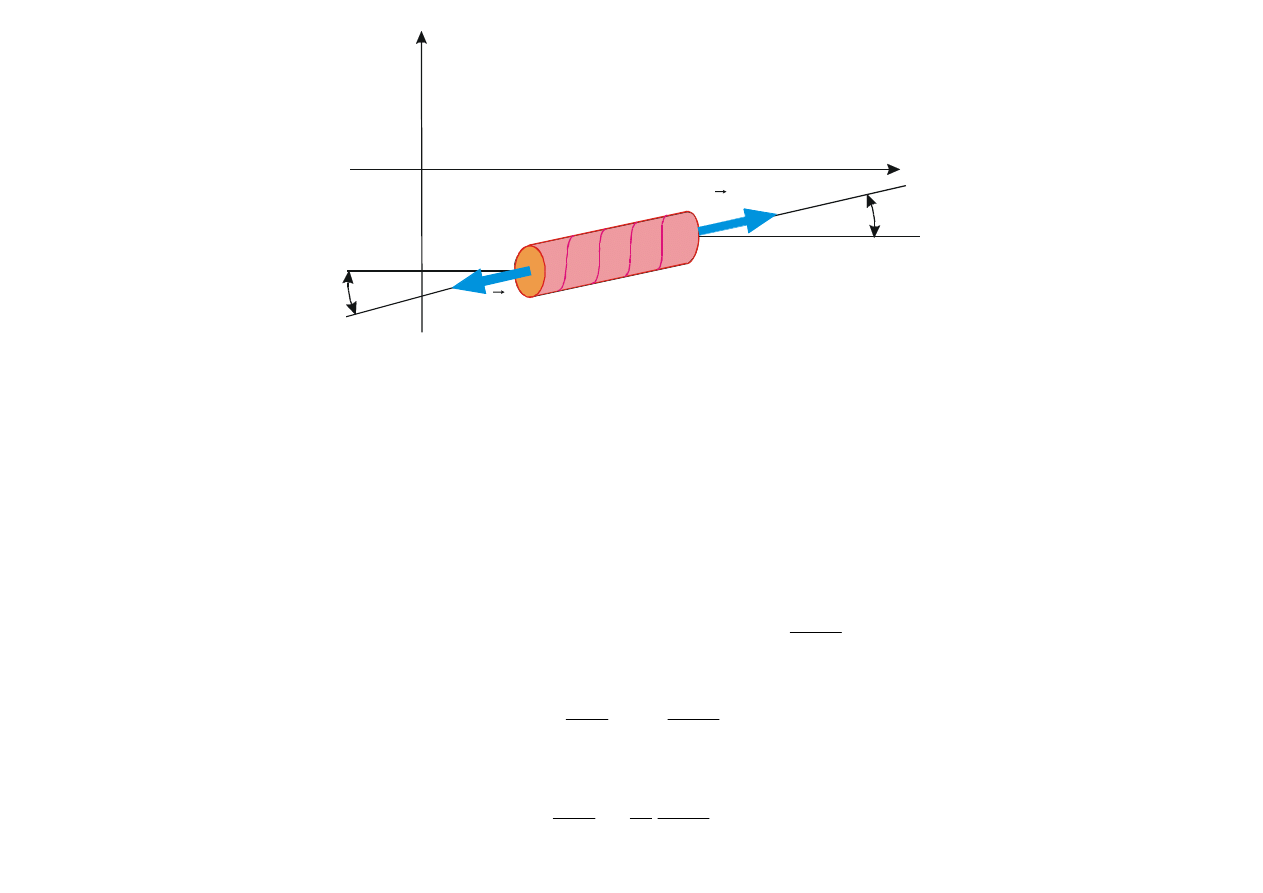
Δx
α
2
α
1
T
T
y
x
Rys. 8.15. Siły działające na element
Δ
x struny.
Teraz znajdziemy relację określającą zależność prędkości fali na strunie od T i
μ
. Dla małych kątów
sin
α
=
α
=
∂
y/
∂
x
.
Siła wypadkowa działająca na element struny w kierunku pionowym jest równa iloczynowi masy
elementu struny
μΔ
x
przez przyśpieszenie pionowe
2
2
t
/
y
∂
∂
. Wobec tego
(
)
2
2
2
1
t
y
x
T
T
F
wyp
∂
∂
Δ
μ
α
α
=
−
=
2
2
t
y
x
T
∂
∂
μ
Δ
α
Δ
=
2
2
t
y
T
x
∂
∂
μ
Δ
α
Δ
=

Podstawiając
α
=
∂
y/
∂
x
, otrzymamy
2
2
2
2
t
y
T
x
y
∂
∂
μ
∂
∂
=
(8.81)
Jest to różniczkowe równanie falowe struny
.
Prędkość fali można określić podstawiając w (8.81) odpowiednie pochodne funkcji y(x, t) określonej
równaniem (8.77).
(
)
0
2
2
2
ϕ
ω
∂
∂
+
−
−
=
kx
t
cos
Ak
x
y
(
)
0
2
2
2
ϕ
ω
ω
∂
∂
+
−
−
=
kx
t
cos
A
t
y
Uwzględniając te wyrażenia w (8.81), mamy
2
2
ω
μ
T
k
=
skąd znajdujemy
μ
T
u
=
(8.82)
Podstawiając do równania (8.81) w miejsce wyrażenia
μ
/T
parametr
2
1
u
/
, otrzymamy
2
2
2
2
2
1
t
y
u
x
y
∂
∂
∂
∂
=
(8.83)
Jest to równanie falowe
. Jego rozwiązaniem jest wyrażenie (8.77)
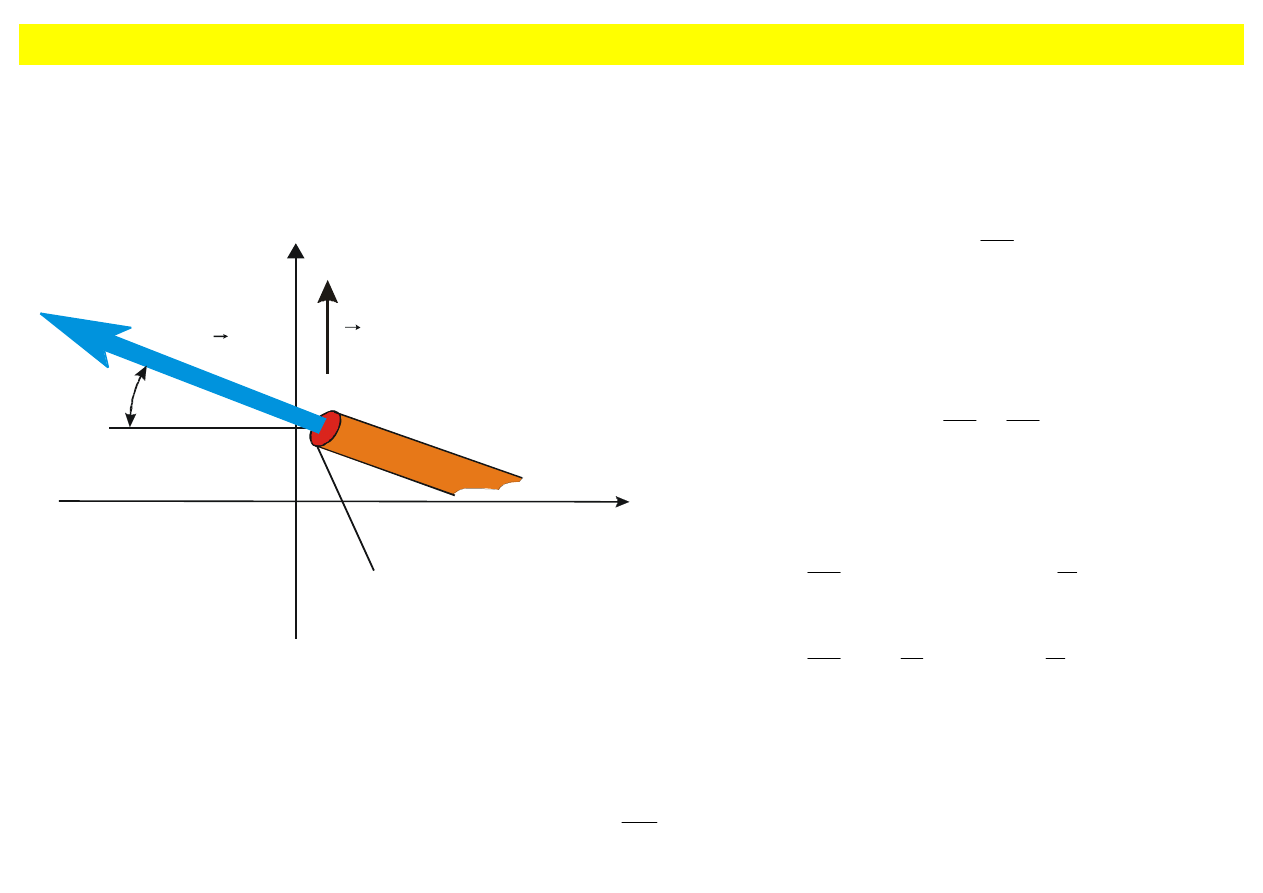
Przenoszenie energii przez fale
Energia dostarczona do jednego końca struny, przenoszona z prędkością fali może być przyjęta i
pochłonięta na drugim końcu.
T
α
v
Koniec struny
O
x
y
Rys. 8.16. Koniec struny odciągnięty do góry
celem wzbudzenia fali biegnącej.
Moc
α
∂
∂
sin
t
y
T
v
F
P
⎟
⎠
⎞
⎜
⎝
⎛
=
⋅
=
r
r
kładąc
t
/
y
v
∂
∂
=
. Dla małego kąta
x
/
y
sin
∂
∂
α
−
=
. Tak więc
x
y
t
y
T
P
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
=
∂
∂
∂
∂
a ponieważ
(
)
u
/
x
t
cos
A
y
−
=
ω
, więc
⎟
⎠
⎞
⎜
⎝
⎛ −
=
⎟
⎠
⎞
⎜
⎝
⎛ −
−
=
u
x
t
sin
u
A
x
y
u
x
t
sin
A
t
y
ω
ω
∂
∂
ω
ω
∂
∂
Chwilowa moc przekazywana w chwili czasu t w punkcje x = 0
t
sin
u
TA
P
ω
ω
2
2
2
=

Średnia wartość mocy jest dwukrotnie mniejsza (
2
1
2
/
t
sin
=
〉
〈
ω
)
2
2
2
A
u
T
P
ω
=
〉
〈
(8.84)
Średnia wartość przenoszonej mocy nazywana jest natężeniem fali
.
Natężenie fali jest proporcjonalne do kwadratu jej amplitudy.
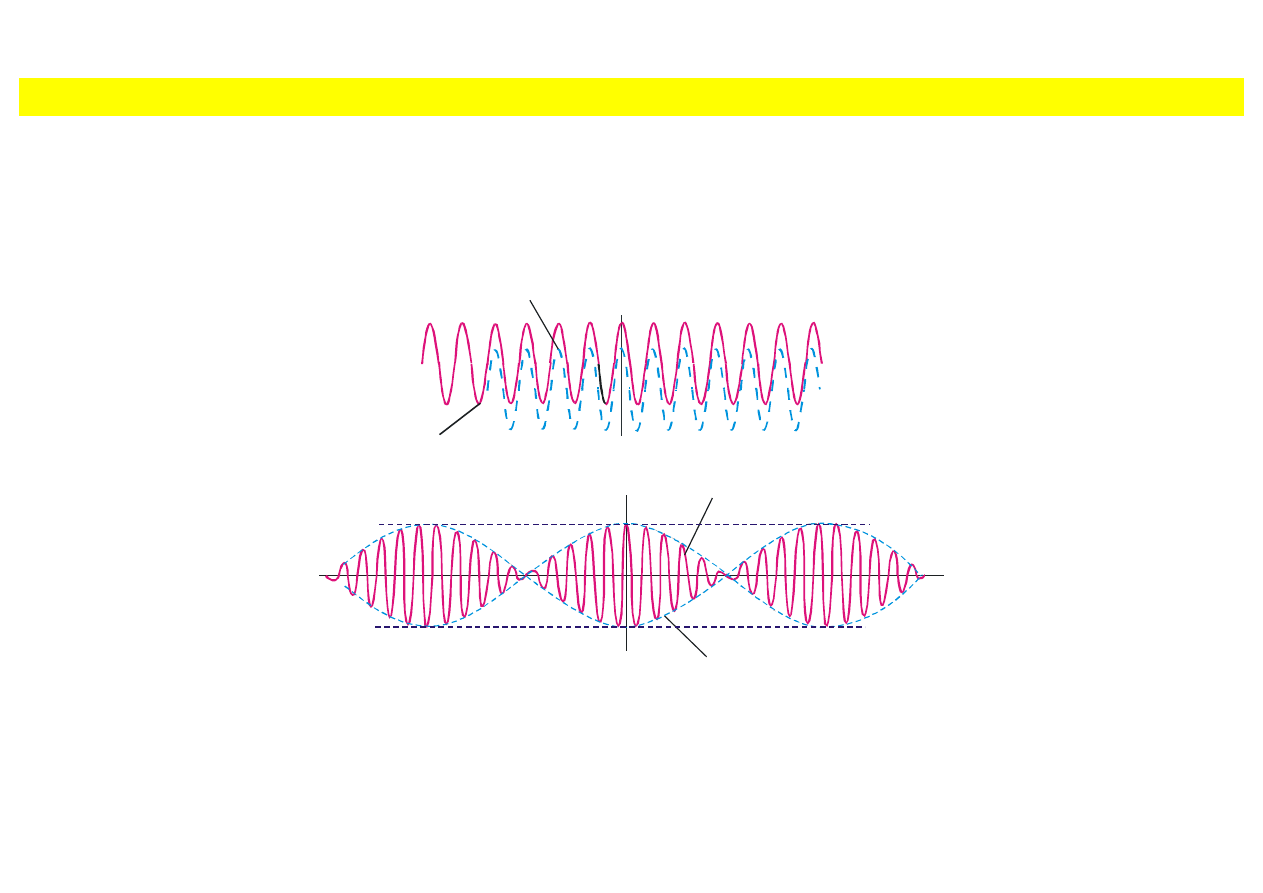
Paczka falowa. Prędkość grupowa
Jeżeli ośrodek jest liniowy, to spełniona jest zasada superpozycji (nakładania) fal:
wypadkowe
wzbudzenie w dowolnym punkcie ośrodka liniowego przy jednoczesnej propagacji kilku fal
jest równe sumie wzbudzeń wywołanych przez każdą z tych fal z osobna.
Obwiednia
(a)
(b)
Acos t
ω
2
Acos t
ω
1
A(cos t + cos t)
ω
ω
1
2
Rys. 8.17. (a) Dwie fale monochromatyczne o nieznacznie różniących się częstościach,
będących w fazie w początku układu współrzędnych. (b) Suma dwóch fal
monochromatycznych.
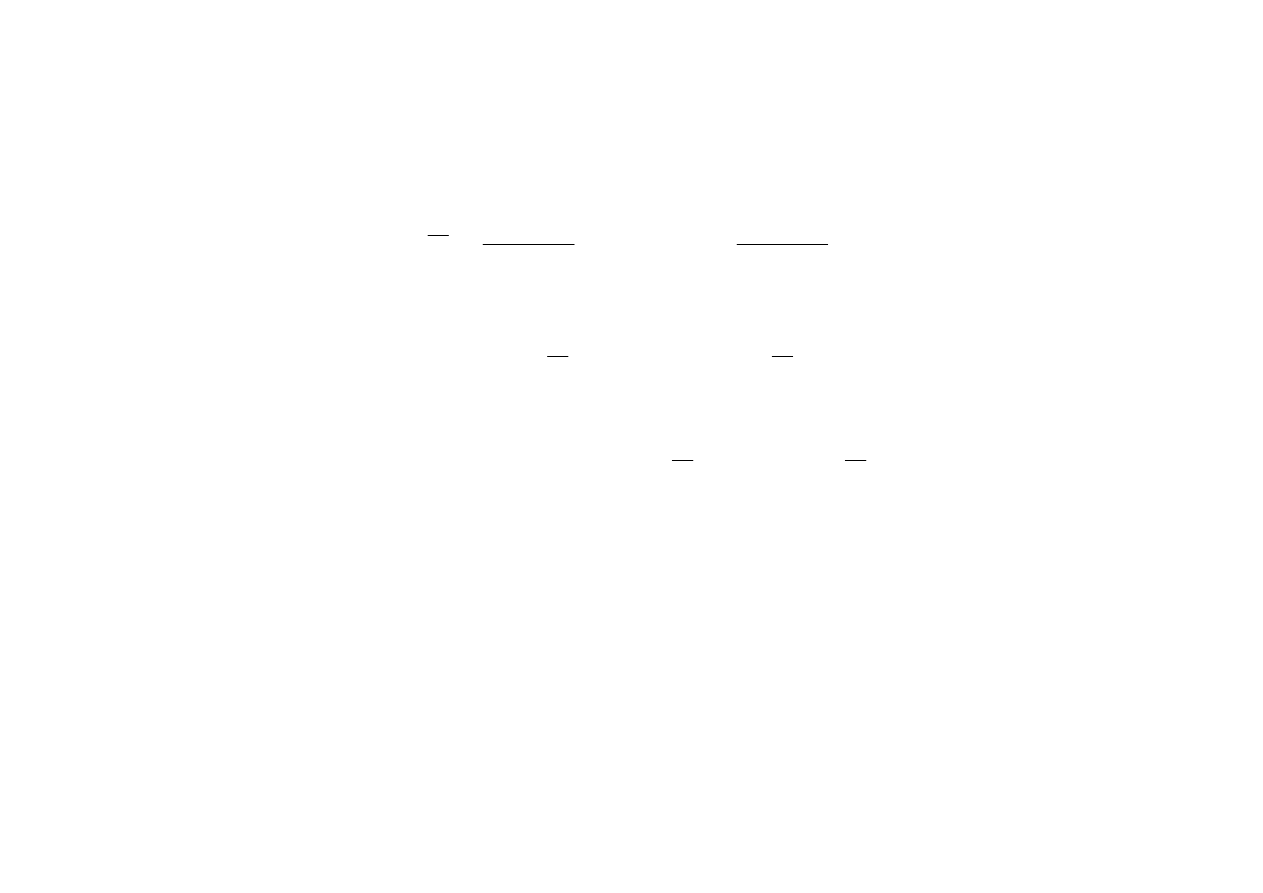
Dodawanie fal monochromatycznych o różnych lecz zbliżonych częstościach. Z upływem czasu fale
będą ”rozbiegać się” fazowo jedna względem drugiej. Przyjmijmy
2
2
1
2
2
1
ω
ω
ω
Δ
ω
ω
ω
−
=
+
=
,
.
Wówczas suma
( )
(
)
(
)
t
cos
A
t
cos
A
t
S
ω
Δ
ω
ω
Δ
ω
−
+
+
=
Wyrażenie to możemy przekształcić
( )
( )
[
]
( )
t
cos
t
A
t
cos
t
cos
A
t
S
ω
ω
ω
Δ
=
= 2
(8.85)
gdzie
( )
( )
t
cos
A
t
A
ω
Δ
2
=
jest obwiednią, czyli funkcją modelującą
.
Dodamy większą liczbę fal monochromatycznych o nieznacznie różniących się częstościach.
Poprzez dobór fal monochromatycznych o zbliżonych częstościach można zbudować paczkę falową.
ω
G( )
ω
Δω
(a)
(b)
ω
t
Rys. 8.18. (a) Suma trzech fal monochromatycznych. (b) Względny rozkład amplitud.
Funkcja
( )
ω
G
charakteryzuje względne intensywności trzech sumowanych fal monochromatycznych.
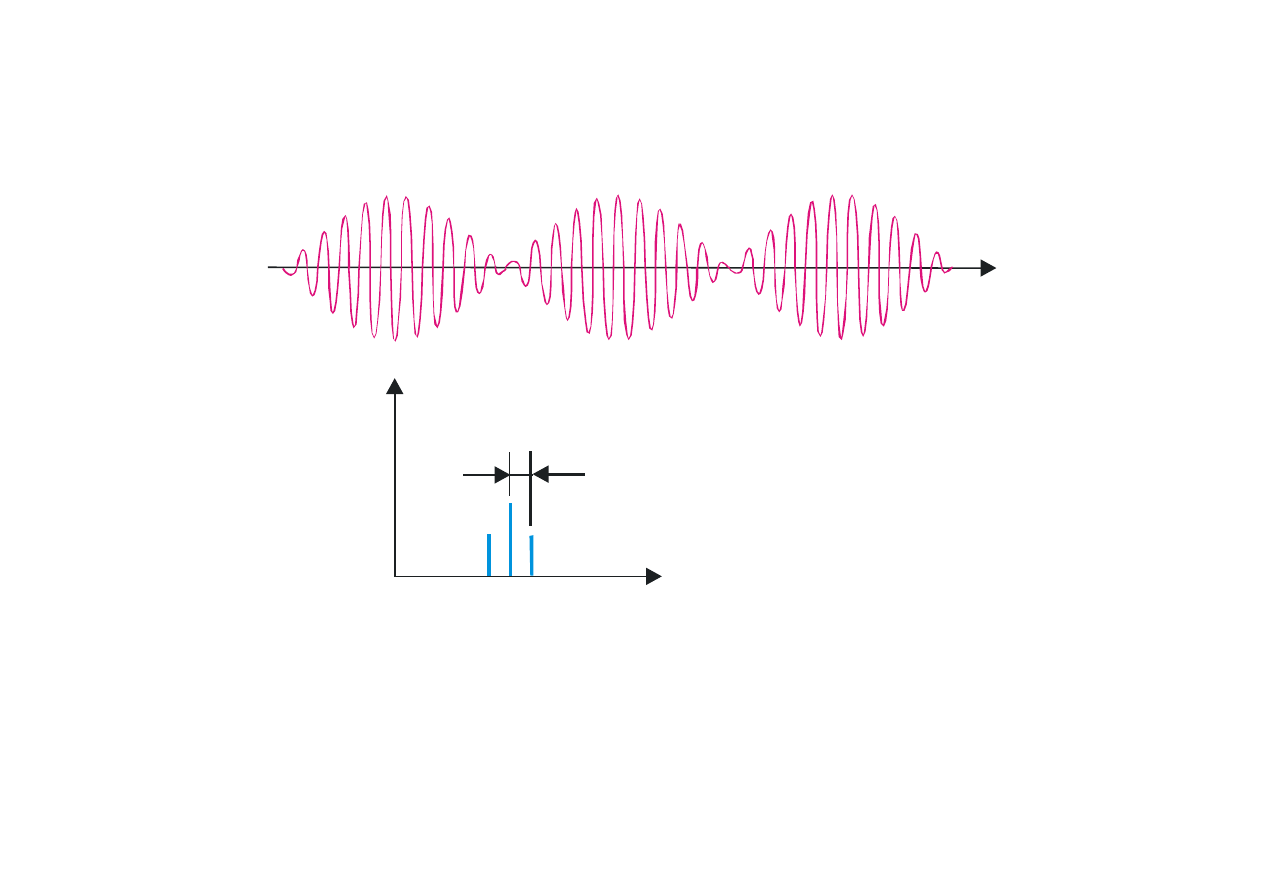
G( )
ω
Δω
ω
(a)
(b)
t
ω
Rys. 8.19. (a) Suma pięciu fal monochromatycznych. (b) Względny rozkład amplitud.
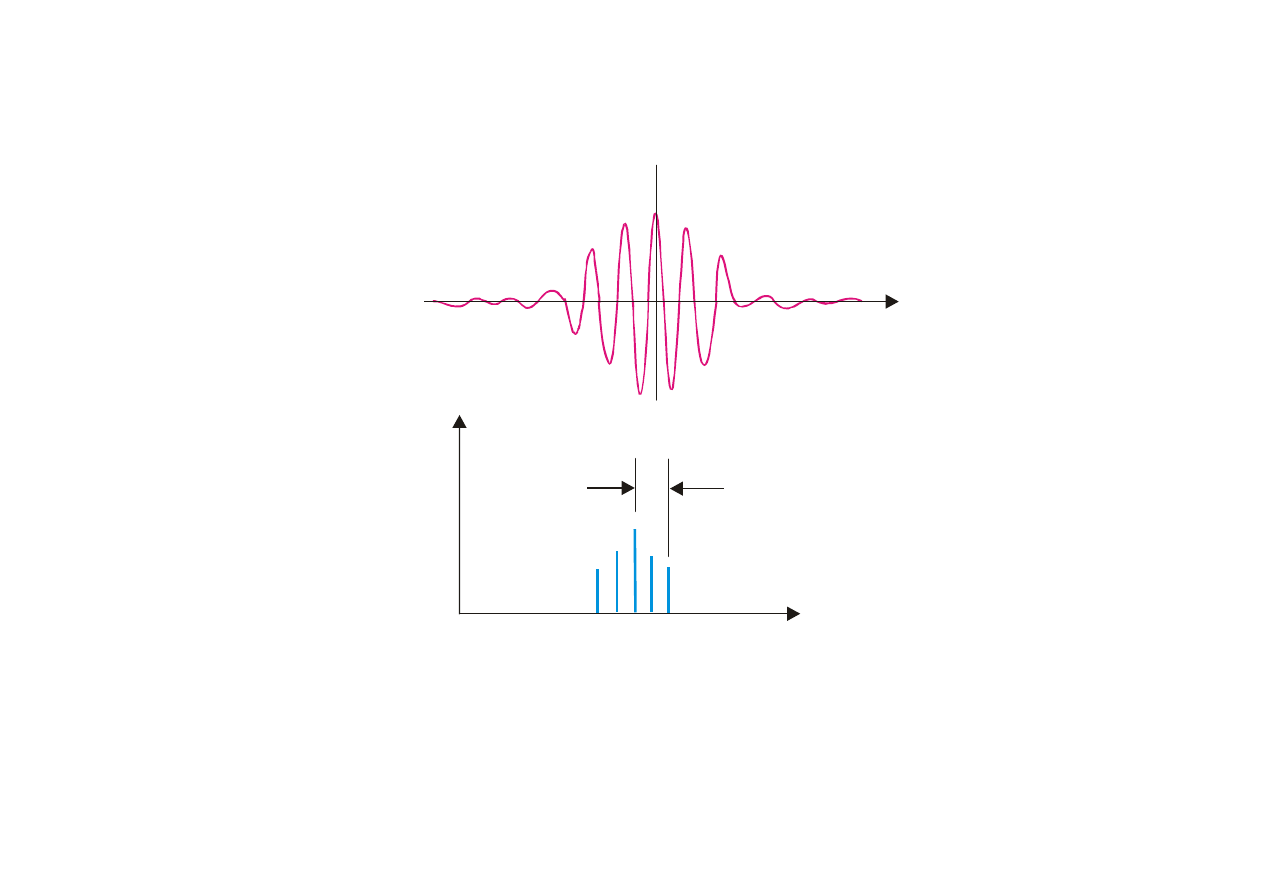
W celu uformowania pojedynczej paczki falowej dokonuje się sumowania nieskończenie wielu fal
monochromatycznych o zbliżonych częstościach.
G( )
ω
Δω
ω
ω
t
(a)
(b)
Rys. 8.20. (a) Suma nieskończonej liczby fal monochromatycznych. (b) Względny rozkład
amplitud.
( )
ω
G
- funkcja gaussowska ze średnią wartością
ω
i odchyleniem
średniokwadratowym
ω
Δ
.
Funkcja gaussowska
( )
ω
G
charakteryzuje względne amplitudy pojedynczych składowych
monochromatycznych
( )
(
)
( )
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
2
2
2
ω
Δ
ω
ω
ω
exp
G
(8.87)
gdzie
ω
Δ
odchylenie średniokwadratowe – rozrzut częstości.
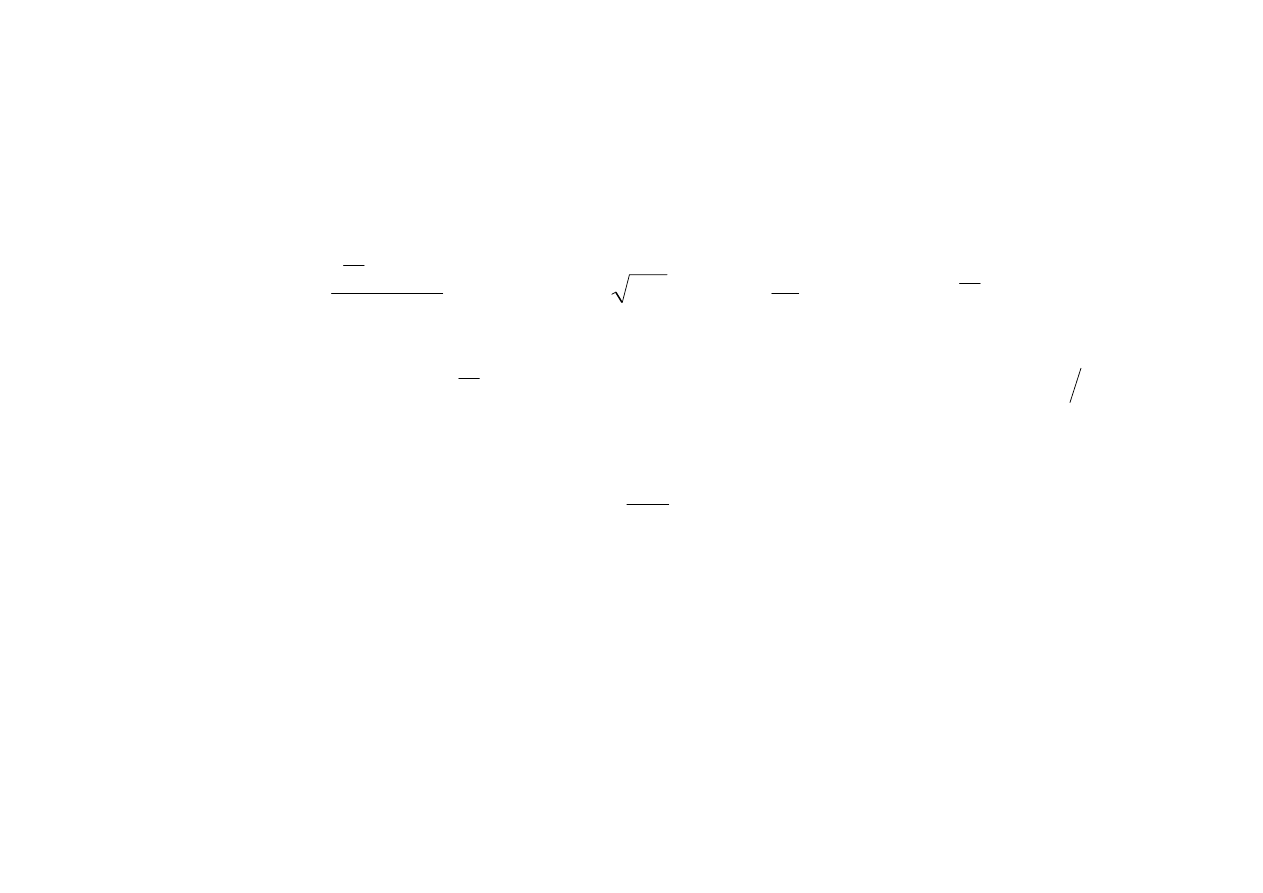
Aby obliczyć całkę
( )
ω
ω
ω
td
cos
G
∫
(8.88)
skorzystamy z tablic całek
(
)
( )
( )
t
cos
t
exp
td
cos
exp
ω
ω
Δ
π
ω
ω
ω
Δ
ϖ
ω
⎥
⎦
⎤
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
∫
2
2
2
2
2
2
2
(8.89)
Jest to fala monochromatyczna
t
cos
ω
zmodulowana gaussowską obwiednią
( )
( )
[
]
2
2
2
ω
Δ
t
exp
−
.
Odchylenie średniokwadratowe dla tej funkcji
ω
Δ
Δ
1
=
t
(8.90)
nazywane jest szerokością paczki falowej
Rozrzut częstości składowych monochromatycznych równy jest odwrotności szerokości
paczki falowej. Funkcja
( )
ω
G
nazywana jest transformatą (obrazem) Fouriera paczki falowej.
Prędkość paczki falowej, czyli prędkość obwiedni, nazwana jest prędkością grupową. Prędkość
grupowa może znacznie różnić się od prędkości fazowej, z którą rozchodzą się składowe
monochromatyczne.
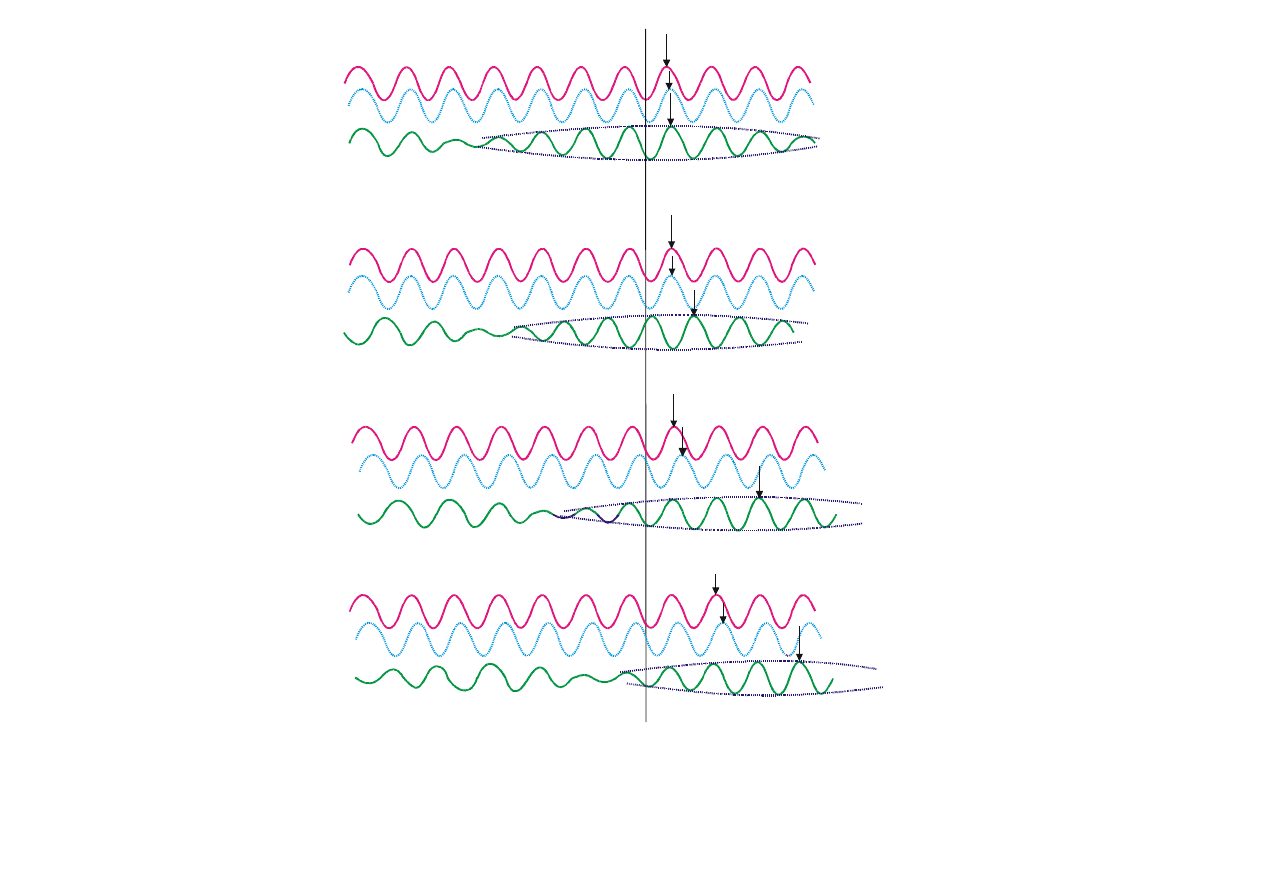
y
1
t
1
t
2
t
3
t
4
(y +y )
1
2
y
2
Rys. 8.21. Dwie fale monochromatyczne y
1
i y
2
poruszają się w prawo z nieznacznie różniącymi
się prędkościami. Obwiednia sumy y
1
i y
2
przemieszcza się w prawo z podwójną prędkością.
Przytoczono cztery kolejne położenia odpowiadające chwilom czasu t
1
,....,t
4
. Strzałkami
zaznaczono położenie grzbietów w różnych chwilach czasu.
Superpozycja dwóch fal biegnących
( )
(
)
(
)
[
]
(
)
(
)
[
]
x
k
k
t
cos
A
x
k
k
t
cos
A
t
,
x
y
Δ
ω
Δ
ω
Δ
ω
Δ
ω
−
−
−
+
+
−
+
=
gdzie
λ
π
/
k
2
=
jest średnią liczbą falową.
Stosując dla
β
α
cos
cos
+
trygonometryczną formę dodawania,
( )
( ) ( )
[
]
(
)
x
k
t
cos
x
k
t
cos
A
t
,
x
y
−
−
=
ω
Δ
ω
Δ
2
Obwiednie możemy opisać w postaci
( )
( ) ( )
[
]
x
k
t
cos
A
t
,
x
A
Δ
ω
Δ
−
= 2
.
Maksimum funkcji jest przyjmowane gdy
( ) ( )
0
=
−
x
k
t
Δ
ω
Δ
to jest przy
k
t
x
Δ
ω
Δ
=
Jest to prędkość przemieszczania się grzbietu obwiedni czyli prędkość grupowa.
Jeżeli mamy zbiór fal monochromatycznych o zbliżonych częstościach, przy czym
( )
k
ω
ω
=
, to
prędkość grupowa
dk
d
v
g
ω
=
(8.91)

( )
λ
λ
λ
λ
d
du
k
k
u
dk
d
d
du
k
u
dk
du
k
u
dk
uk
d
v
g
⎟
⎠
⎞
⎜
⎝
⎛−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
=
λ
λ
d
du
u
v
g
−
=
(8.92)
g
v
może być mniejsze jak i większe od u w zależności od znaku
λ
d
/
du
.
W ośrodkach niedyspersyjnych
0
=
λ
d
/
du
i v
g
= u.
W teorii względności udowadnia się, że prędkość grupowa
c
v
g
≤
, podczas gdy dla prędkości
fazowej nie ma ograniczenia.
Przykłady rozchodzenia się fali z prędkością grupową:
• przechodzenie
światła przez dielektryk,
• paczki
falowe.
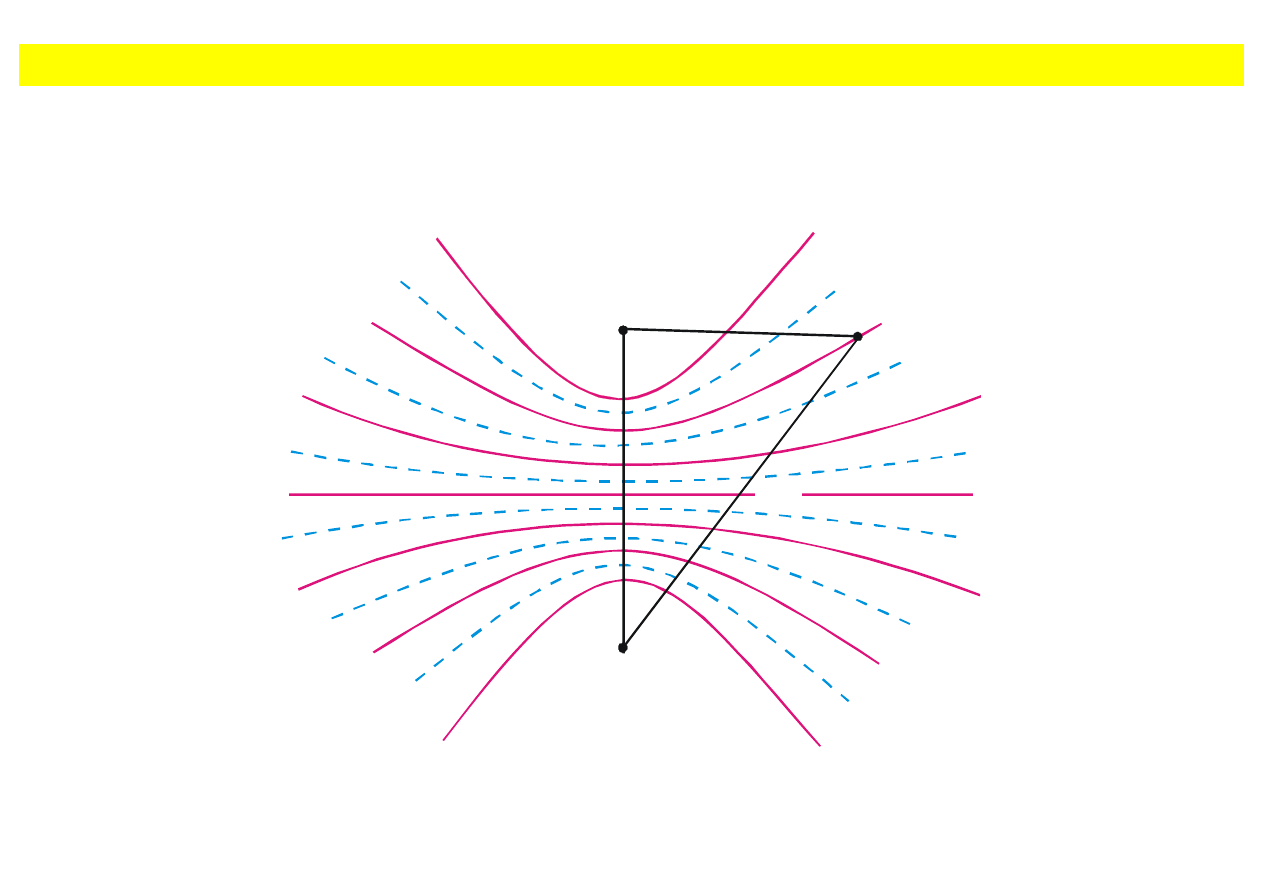
Interferencja fal
Fale nazywamy koherentnymi jeżeli różnica ich faz pozostaje stała w czasie
.
Superpozycja dwóch koherentnych fal sferycznych wzbudzonych źródłami punktowymi.
r
2
r
1
S
1
S
2
P
Rys. 8.22. Interferencja koherentnych fal sferycznych.
Równanie fali sferycznej
( )
(
)
o
o
kr
t
cos
r
A
t
,
r
S
ϕ
ω
+
−
=
(8.93)
Amplituda fali sferycznej maleje jak 1/r (gdy nie ma miejsca dysypacja energii). W wyniku
superpozycji dwóch fal
( )
(
)
1
1
1
1
ϕ
ω
+
−
=
kr
t
cos
r
A
t
,
r
S
o
( )
(
)
2
2
2
2
ϕ
ω
+
−
=
kr
t
cos
r
A
t
,
r
S
o
Amplituda fali wypadkowej w punkcie P
(
) (
)
[
]
⎩
⎨
⎧
⎭
⎬
⎫
−
+
−
+
+
=
2
1
2
1
2
1
2
2
2
1
2
2
2
1
1
ϕ
ϕ
r
r
k
cos
r
r
r
r
A
A
o
Dla źródeł koherentnych
ϕ
1
–
ϕ
2
= const, więc wynik interferencji fal zależy od wielkości
2
1
r
r
−
=
Δ
nazywanej różnicą dróg fal.

W punktach gdzie
(
) (
)
π
ϕ
ϕ
m
r
r
k
2
2
1
2
1
±
=
−
−
−
(8.94)
(m = 0, 1, 2,...) obserwuje się
maksima interferencyjne
, a amplituda wypadkowa wynosi
2
1
r
A
r
A
A
o
o
+
=
W punktach gdzie
(
) (
)
π
ϕ
ϕ
)
m
(
r
r
k
1
2
2
1
2
1
+
±
=
−
−
−
m
= 1, 2,
(8.95)
obserwuje się
minima interferencyjne
; amplituda wypadkowa
⎥
⎦
⎥
⎢
⎣
⎢
−
=
2
1
r
A
r
A
A
o
o
m
= 0, 1, 2,... nazywamy odpowiednio
rzędem interferencyjnego maksimum lub minimum
.
Warunki (8.94) i (8.95) sprowadzają się do tego, że
const
r
r
=
−
2
1
(8.96)
Jest to równanie hiperboli o ogniskach w punktach
1
S
i
2
S
.

Fale stojące
Szczególnym przypadkiem interferencji są fale stojące.
Dwie fale sinusoidalne propagujące się w przeciwnych kierunkach wzdłuż osi x mają jednakowe
amplitudy i częstości.
(
)
kx
t
cos
A
y
−
=
ω
1
(
)
kx
t
cos
A
y
+
=
ω
2
Dodając te równania, otrzymamy
(
)
t
cos
/
x
cos
A
t
cos
kx
cos
A
y
y
ω
λ
π
ω
2
2
2
2
1
=
=
+
(8.97)
W każdym punkcie fali stojącej zachodzą drgania o tej samej częstości
ω
z amplitudą
(
)
λ
π
/
x
cos
A
A
st
2
2
=
.
W punktach (
strzałki
) gdzie
π
λ
π
m
x
±
=
2
(m = 0,1,2,...)
amplituda fali stojącej osiąga maksimum równe 2A.
W punktach (węzły) gdzie
π
λ
π
⎟
⎠
⎞
⎜
⎝
⎛ +
±
=
2
1
2
m
x
(m = 0,1,2,...)
amplituda fali stojącej jest zerowa.
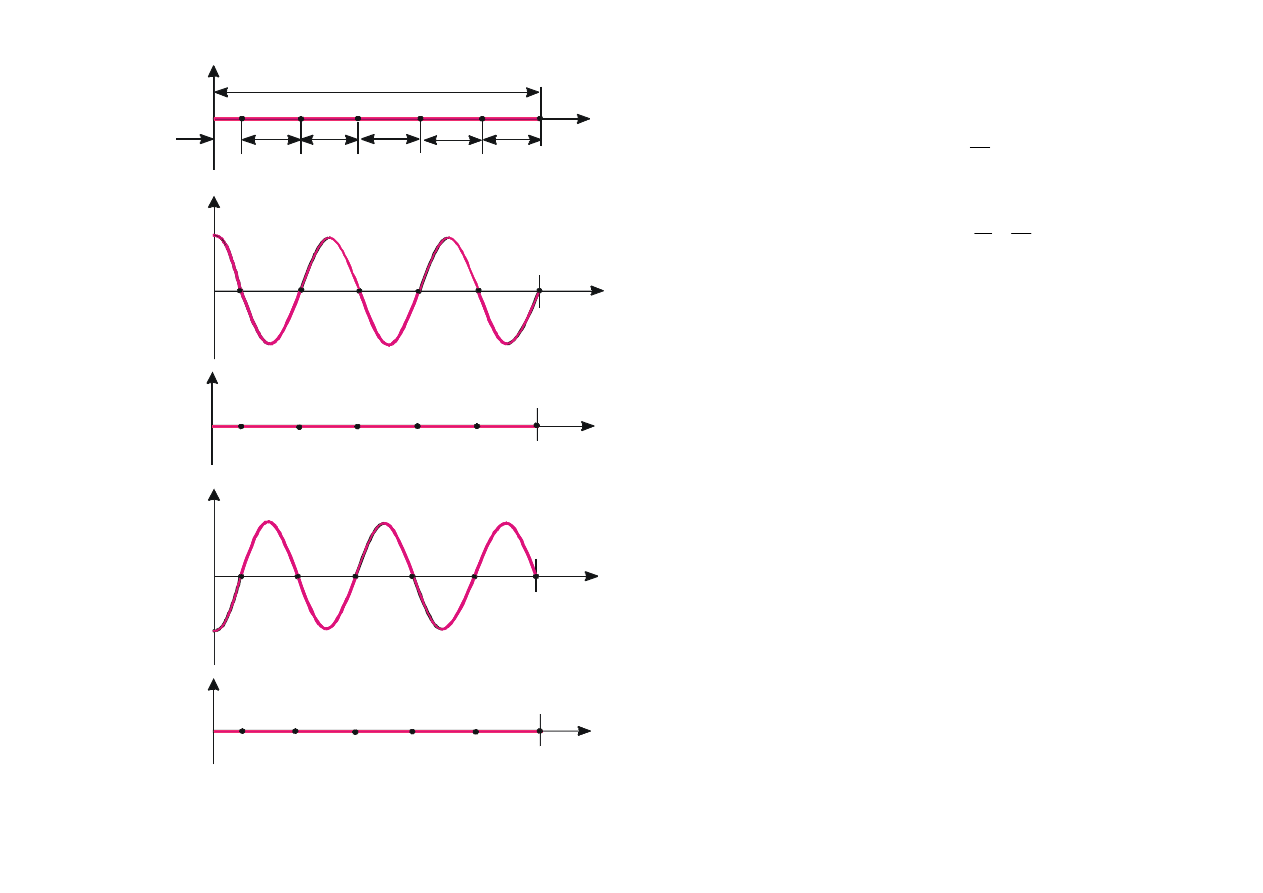
s
s
s
s
s
0
0
0
0
0
N
N
N
N
N
x
x
x
x
x
t=t
0
t=t +T/4
0
t=t +T/2
0
l
0
0
0
x
x
t=t +3T/4
0
t=t +T
0
λ/2 λ
λ
λ
λ
λ
Rys. 8.23. Fala stojąca.
Współrzędne strzałek i węzłów
2
λ
m
x
s
±
=
(m = 0, 1, 2,...)
2
2
1
λ
⎟
⎠
⎞
⎜
⎝
⎛ +
±
=
m
x
w
(m = 0, 1, 2,...)
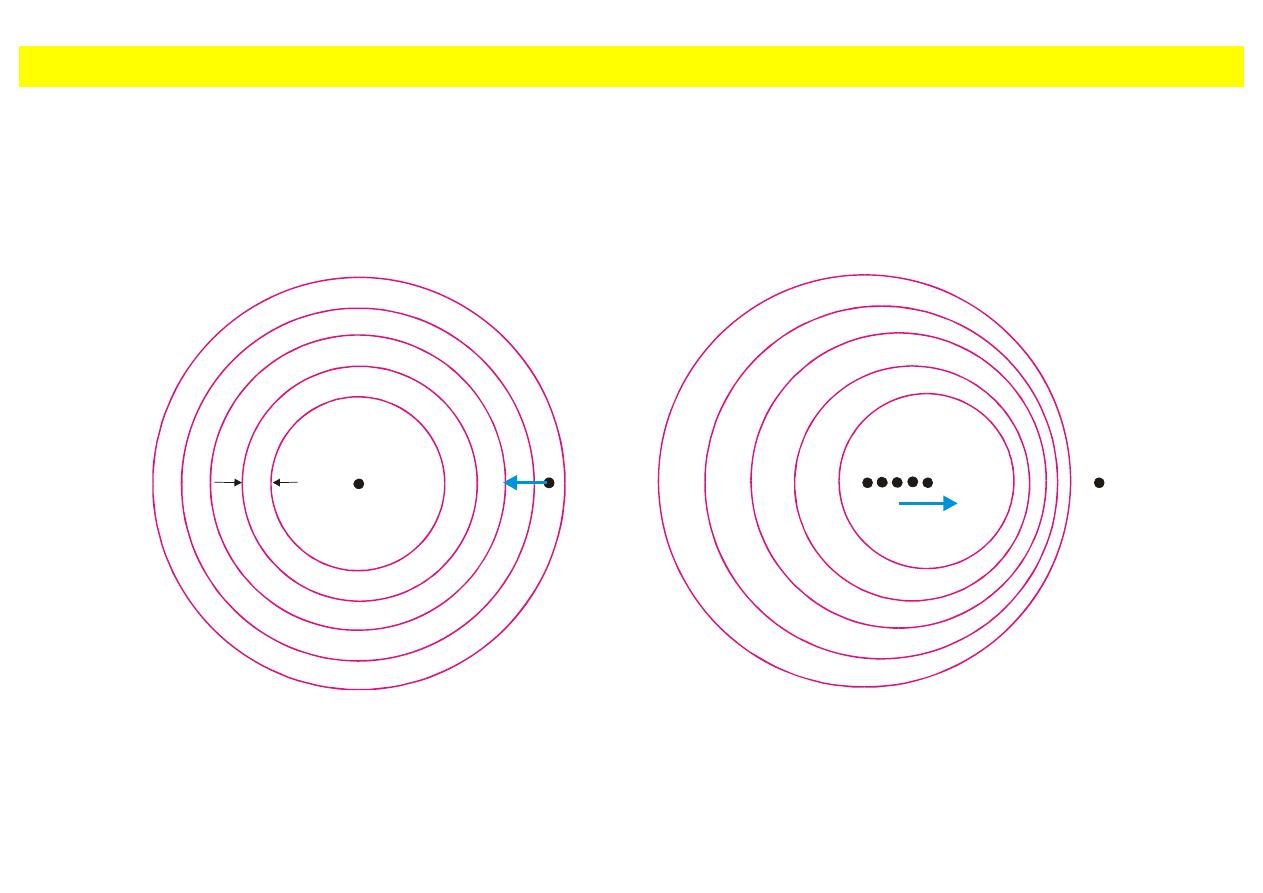
Zjawisko Dopplera
Zmiana częstości wynikająca z wzajemnego ruchu obserwatora i źródła nazywa się zjawiskiem
Dopplera.
Typowy przykład: dźwięk gwizdka zbliżającego się pociągu.
(a) (b)
λ
Z
O
O
Z
v
z
v
o
1
1 2 3 4 5
2
3
4
5
Rys. 8.24. Zjawisko Dopplera: a) źródło jest nieruchome (zbliżający się obserwator odbiera fale
o większej częstotliwości), b) źródło zbliża się do obserwatora (fala ma mniejszą długość z
przodu, a większą z tyłu).

Gdyby obserwator nie poruszał się, to w ciągu czasu t rejestrowałby ut/
λ
fal. Ponieważ jednak
porusza się w kierunku źródła z prędkością v
o
, to w tym samym czasie t odbiera on v
o
/t
dodatkowych
fal. Z tego powodu częstotliwość f’ odbierana przez obserwatora
(
)
⎟
⎠
⎞
⎜
⎝
⎛ +
=
+
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
u
v
f
u
f
v
u
v
u
t
t
v
ut
'
f
o
o
o
o
1
1
λ
λ
λ
(8.98)
Częstotliwość odbierana przez obserwatora jest większa od częstotliwości źródła. Gdy obserwator
oddala się, to we wzorze (8.98) należy zmienić znak prędkości v
o
, co powoduje, że częstotliwość
ulega zmniejszeniu.
Gdy źródło porusza się względem nieruchomego obserwatora, występuje efekt skrócenia długości fali
w kierunku obserwatora oraz wydłużenia długości fali w kierunku przeciwnym, co pokazano na rys.
8.24b.
Jeżeli częstotliwość źródła jest f, a jego prędkość v
z
, to w czasie jednego okresu drgań źródło to
przesuwa się o odcinek v
z
/f
i każda długość fali ulega skróceniu o ten odcinek. Długość fali
dochodzącej do obserwatora wynosi więc
f
v
f
u
'
z
−
=
λ
A stąd częstotliwość odbierana przez obserwatora
(
)
u
v
f
v
u
uf
'
f
u
'
f
z
z
−
=
−
=
=
1
1
(8.99)
Mamy więc efekt podobny jak w przypadku ruchu obserwatora; zbliżanie się źródła powoduje wzrost
częstotliwości, a oddalanie (v
z
< 0) zmniejszenie się częstotliwości.

W przypadku gdy porusza się zarówno źródło dźwięku jak i obserwator, to należy traktować, że ruch
źródła odbywa się niezależnie od ruchu obserwatora.
W przypadku fal akustycznych, stosunek prędkości obserwatora (lub źródła) do prędkości fazowej fali
nazywa się liczbą Macha
u
v
m
=
Gdy źródło porusza się z prędkością przewyższającą prędkość dźwięku, to wytwarza ono falę
uderzeniową o właściwościach odmiennych od poprzednio omawianych fal.
Zjawisko Dopplera dla fal elektromagnetycznych ma liczne praktyczne zastosowania, np.:
• w fizyce atomowej,
• w astronomii do określenia prędkości odległych świecących ciał niebieskich,
• w radiolokacji do pomiaru prędkości i odległości ruchomych obiektów.
Wyszukiwarka
Podobne podstrony:
Fizyka dla liceum Drgania i fale mechaniczne
fizyka drgania i fale pr klucz
Drgania i fale elektromagnetyczne
Sprawdzian z drgań, biologia operon testy sprawdzające, sprawdziany, Sprawdziany, Drgania i Fale
III Drgania i fale rut(1)
1 21 03 2014Czytanka Drgania i Fale
fizyka drgania i fale pr
Drgania i fale elektromagnetyczne
Zestaw11 drgania,fale
drgania i fale pp
Drgania i fale mechaniczne klucz poziom podstawowy
drgania, biologia operon testy sprawdzające, sprawdziany, Sprawdziany, Drgania i Fale
drgania i fale, egzamin fizyka
elaktro drgania, biologia operon testy sprawdzające, sprawdziany, Sprawdziany, Drgania i Fale
Drgania i fale mechaniczn1, nauka, nauka dla każdego, fizyka różne, fizyka gimnazjum
Drgania - zadania, Fizyka, 06.Drgania i fale
Dyktando z drgań, biologia operon testy sprawdzające, sprawdziany, Sprawdziany, Drgania i Fale
05-drgania i fale, ▬ Studia Elektrotechnika - Politechnika, Fizyka
więcej podobnych podstron