Opracowała: K. Sokołowska
56
14. FUNKCJE DWÓCH ZMIENNYCH
14.1.
Podstawowe pojęcia
•
Def.
Funkcją dwóch zmiennych x i y określoną w zbiorze
2
R
D
⊂
nazywamy
przyporządkowanie każdej parze
( )
D
y
x
∈
,
dokładnie jednej liczby
R
z
∈
, co zapisujemy:
( )
( )
R
y
x
f
z
D
y
x
f
∈
=
→
∈
,
,
:
.
x, y – zmienne niezależne (argumenty funkcji)
z – zmienna zależna (wartość funkcji)
PRZYKŁAD 46
Ze wzoru z=2x-3y+5 można obliczyć z dla dowolnej pary liczb (x,y) np. dla x=1, y=2: z=1.
•
Def.
Dziedziną funkcji f nazywamy zbiór tych par (x,y) dla których wzór opisujący daną funkcję
ma sens liczbowy.
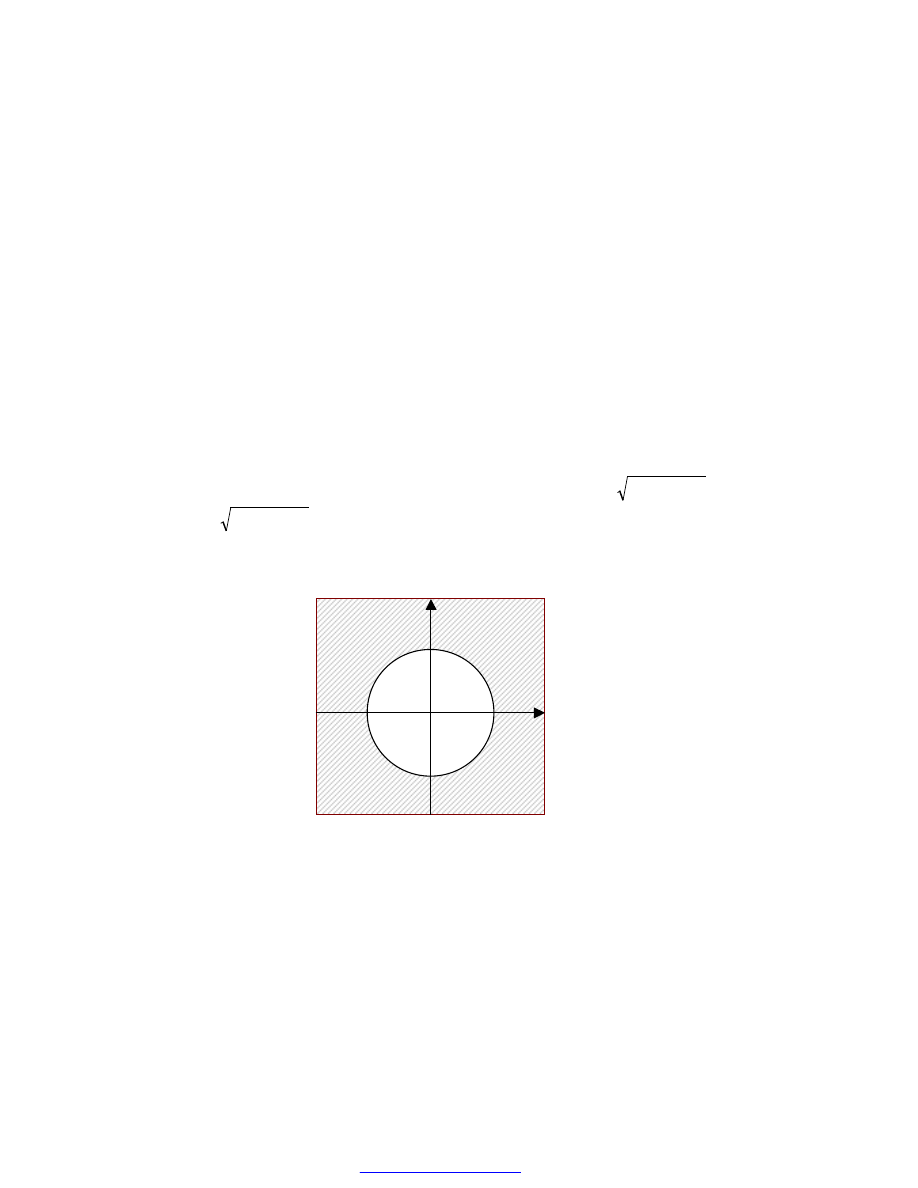
PRZYKŁAD 47
Określ i zilustruj w
2
R
dziedzinę funkcji określonej wzorem:
( )
16
,
2
2
−
+
=
y
x
y
x
f
Wyrażenie
16
2
2
−
+
y
x
ma sens, gdy:
0
16
2
2
≥
−
+
y
x
, czyli
16
2
2
≥
+
y
x
. Dziedziną funkcji
jest więc zewnętrze koła o promieniu r=4 i środku (0,0) wraz z brzegiem:
( )
{
}
16
:
,
2
2
2
≥
+
∈
=
y
x
R
y
x
D
•
Def.
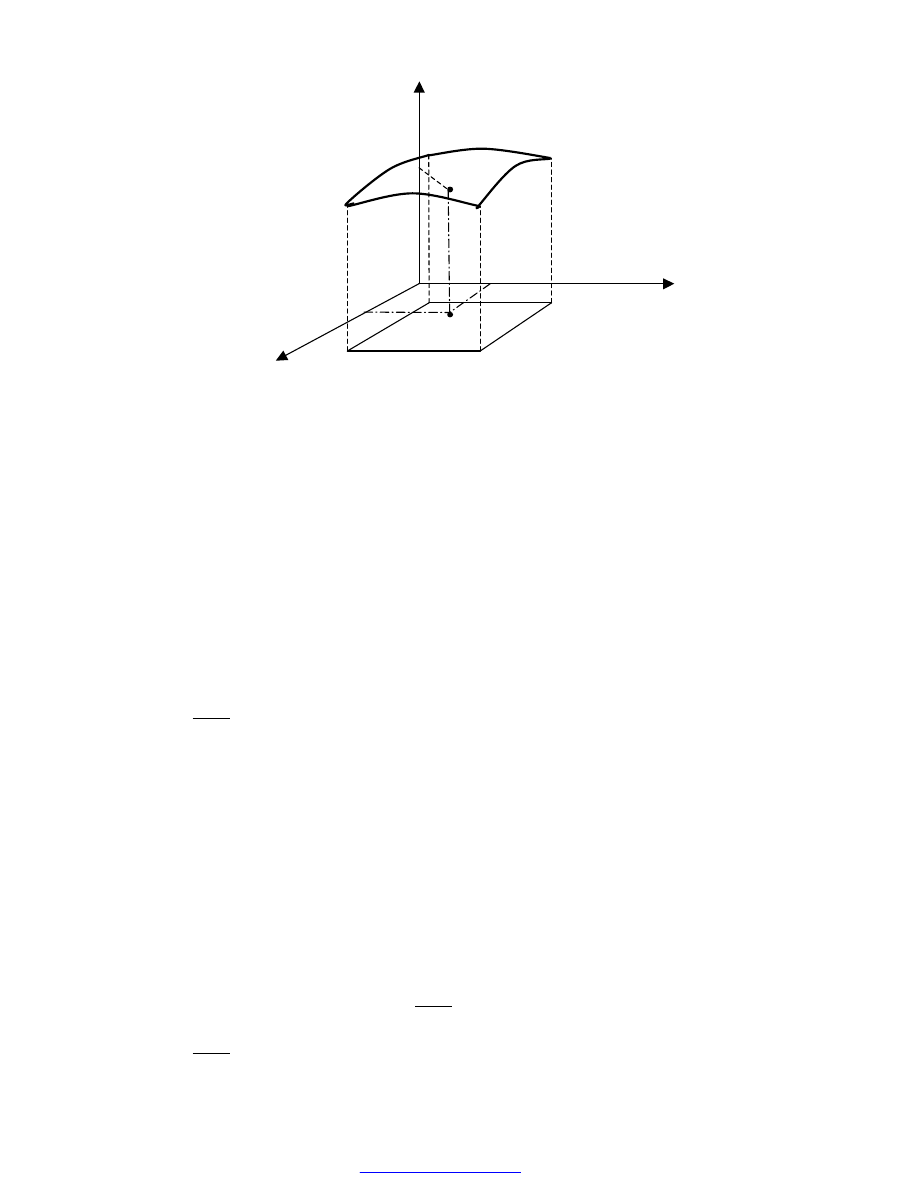
Wykresem funkcji dwóch zmiennych
( )
y
x
f
z
,
=
nazywamy zbiór wszystkich punktów
(x,y,z) w przestrzeni trójwymiarowej
3
R , dla których
( )
y
x
f
z
,
=
. (Na ogół jest więc to
pewna powierzchnia w przestrzeni trójwymiarowej, którą znajdujemy przyporządkowując
określonym wartościom zmiennych x i y punkt P(x,y) na płaszczyźnie XY, a następnie punkt
R o tych samych współrzędnych x,y i o współrzędnej
( )
y
x
f
z
,
=
).
4
0
4
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
57
14.2.
Granica i ciągłość funkcji
•
Def.
Ciąg punktów płaszczyzny
(
)
n
n
y
x ,
jest zbieżny do punktu
(
)
0
0
, y
x
, gdy
0
x
x
n
n
∞
→
→
,
0
y
y
n
n
∞
→
→
.
•
Def.
Liczbę g nazywamy granicą funkcji f w punkcie
(
)
0
0
, y
x
, jeżeli dla każdego ciągu
punktów
(
)
(
)
n
n
y
x ,
, takich, że
(
)
D
y
x
n
n
∈
,
,
(
) (
)
0
0
,
,
y
x
y
x
n
n
≠
i zbieżnego do
(
)
0
0
, y
x
,
odpowiadający mu ciąg wartości funkcji
(
)
n
n
y
x
f
,
jest zbieżny do g, co zapisujemy:
(
) (
)
(
)
g
y
x
f
n
n
y
x
y
x
n
n
=
→
,
lim
0
0
,
,
.
PRZYKŁAD 48
Obliczymy granicę:
2
lim
2
1
−
=
−
→
→
y
x
xy
y
x
•
Def.
Funkcja
( )
y
x
f
z
,
=
jest ciągła w punkcie
(
)
D
y
x
P
∈
0
0
0
,
jeżeli:
ma granicę w punkcie
(
)
0
0
, y
x
istnieje wartość funkcji w punkcie
(
)
0
0
, y
x
granica jest równa wartości funkcji w punkcie
(
)
0
0
, y
x
,
co zapisujemy:
( ) (
)
0
0
,
,
lim
0
0
y
x
f
y
x
f
y
y
x
x
=
→
→
PRZYKŁAD 49
Zbadajmy ciągłość funkcji
( )
y
x
xy
y
x
f
−
=
,
w punkcie
( )
2
,
1
0
=
P
.
2
lim
2
1
−
=
−
→
→
y
x
xy
y
x
,
( )
2
2
,
1
−
=
f
, więc funkcja f jest ciągła w punkcie (1,2).
P(x,y)
z=f(x,y)
y
x
z
R(x,y,z)
z
y
x
D
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
58
14.3.
Pochodne cząstkowe
•
Def.
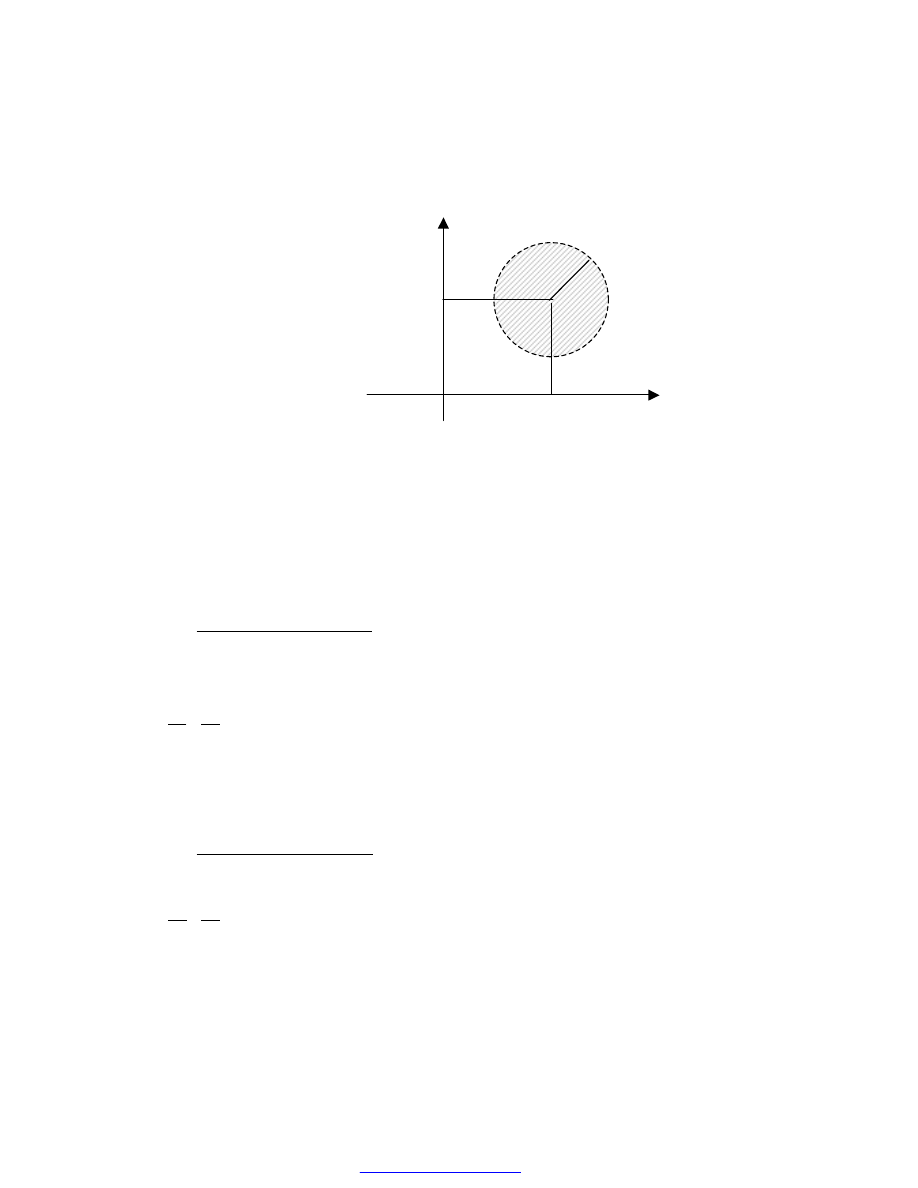
Otoczeniem punktu
(
)
0
0
0
, y
x
P
o promieniu R>0 nazywamy zbiór punktów
płaszczyzny, których współrzędne (x,y) spełniają nierówność
(
) (
)
2
2
0
2
0
R
y
y
x
x
<
−
+
−
i
oznaczamy
(
)
R
P
Q
,
0
.
Niech f będzie funkcją określoną w pewnym otoczeniu punktu
(
)
0
0
, y
x
.
Jeżeli we wzorze
( )
y
x
f
z
,
=
jednej ze zmiennych przypiszemy konkretną wartość
liczbową, np. w miejsce y wstawimy liczbę
0
y , to otrzymamy funkcję jednej zmiennej
(
)
0
, y
x
f
z
=
.
•
Def.
Jeśli tak utworzona funkcja ma pochodną w punkcie
0
x , tzn. jeżeli istnieje granica :
(
) (
)
x
y
x
f
y
x
x
f
x
∆
−
∆
+
→
∆
0
0
0
0
0
,
,
lim
,
to nazywamy ją pochodną cząstkową pierwszego rzędu funkcji
( )
y
x
f
z
,
=
względem
zmiennej x w punkcie
(
)
0
0
, y
x
i oznaczamy:
x
z
∂
∂
,
x
f
∂
∂
,
x
f
′
w punkcie
(
)
0
0
, y
x
.
•
Def.
Pochodną cząstkową funkcji
( )
y
x
f
z
,
=
względem zmiennej y w punkcie
(
)
0
0
, y
x
definiujemy analogicznie:
(
) (
)
y
y
x
f
y
y
x
f
y
∆
−
∆
+
→
∆
0
0
0
0
0
,
,
lim
i oznaczamy:
y
z
∂
∂
,
y
f
∂
∂
,
y
f
′
w punkcie
(
)
0
0
, y
x
.
14.4.
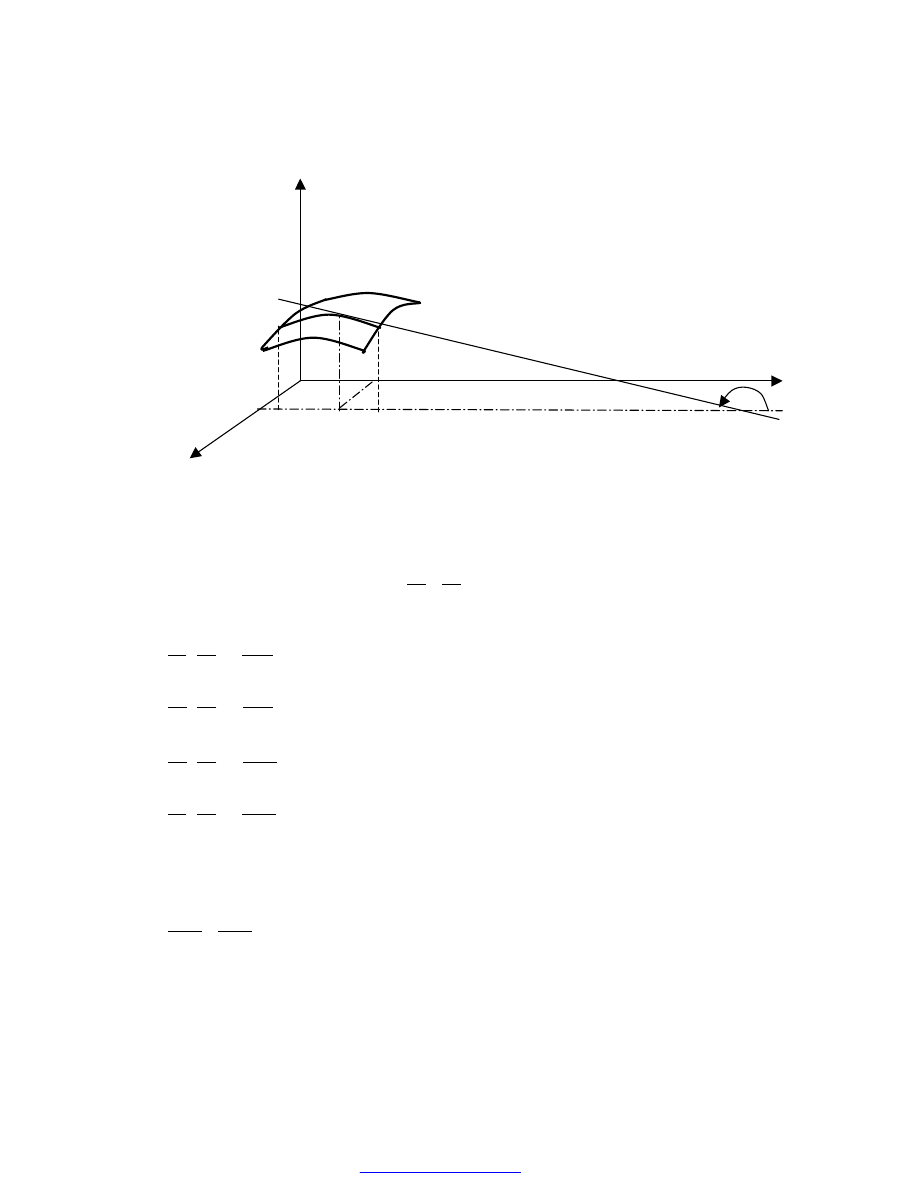
Interpretacja geometryczna pochodnej cząstkowej
•
W interpretacji geometrycznej pochodna cząstkowa
x
f
′
w punkcie
(
)
0
0
, y
x
jest równa
tangensowi kąta między styczną do krzywej
(
)
0
, y
x
f
z
=
, a dodatnim kierunkiem osi
0
x
0
y
R
(
)
R
P
Q
,
0
0
P
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
59
0X, tzn. równa tangensowi kąta miedzy styczną w punkcie
(
)
0
0
0
,
,
z
y
x
, gdzie
(
)
0
0
0
, y
x
f
z
=
, a osią równoległą do osi 0X przechodzącą przez punkt
(
)
0
,
,
0
0
y
x
.
14.5.
Pochodne cząstkowe wyższych rzędów
•
Def.
Pochodne cząstkowe pochodnych:
x
f
∂
∂
,
y
f
∂
∂
nazywamy pochodnymi cząstkowymi rzędu
drugiego i oznaczamy:
′′
=
∂
∂
=
∂
∂
∂
∂
′′
=
∂
∂
=
∂
∂
∂
∂
yy
xx
f
y
f
y
f
y
f
x
f
x
f
x
2
2
2
2
pochodne cząstkowe jednorodne rzędu drugiego funkcji f(x,y)
′′
=
∂
∂
∂
=
∂
∂
∂
∂
′′
=
∂
∂
∂
=
∂
∂
∂
∂
yx
xy
f
x
y
f
y
f
x
f
y
x
f
x
f
y
2
2
pochodne cząstkowe mieszane rzędu drugiego funkcji f(x,y)
•
Tw. Schwarza
Jeżeli funkcja
( )
y
x
f
z
,
=
ma w pewnym obszarze D ciągłe pochodne mieszane rzędu
drugiego, to pochodne te są sobie równe:
y
x
f
∂
∂
∂
2
=
x
y
f
∂
∂
∂
2
w każdym punkcie
( )
D
y
x
∈
,
.
PRZYKŁAD 50
Obliczyć pochodne cząstkowe pierwszego i drugiego rzędu dla funkcji:
( )
5
4
3
4
3
5
,
xy
xy
y
x
y
x
f
+
−
+
=
(
)
0
0
, y
x
z=f(x,y)
0
y
x
(
)
0
, y
x
f
z
=
α
z
y
0
x
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
60
x
f
∂
∂
=
5
2
4
3
15
y
y
x
+
−
,
y
f
∂
∂
=
4
3
20
3
4
xy
x
y
+
−
,
2
2
x
f
∂
∂
=
x
30 ,
2
2
y
f
∂
∂
=
3
2
80
12
xy
y
+
,
y
x
f
∂
∂
∂
2
=
4
20
3
y
+
−
,
x
y
f
∂
∂
∂
2
=
4
20
3
y
+
−
.
14.6.
Różniczka funkcji
Niech
( )
y
x
f
z
,
=
będzie określona w otoczeniu punktu
(
)
0
0
, y
x
i różniczkowalna w tym
punkcie.
•
Def.
Różniczką zupełną rzędu pierwszego funkcji f w punkcie
(
)
0
0
, y
x
nazywamy wyrażenie
postaci:
(
)
(
)
(
)
dy
y
x
y
f
dx
y
x
x
f
y
x
df
0
0
0
0
0
0
,
,
,
∂
∂
+
∂
∂
=
•
Def.
Różniczką zupełną rzędu drugiego funkcji f w punkcie
(
)
0
0
, y
x
nazywamy wyrażenie
postaci:
(
)
(
)
(
)
(
)
dxdy
y
x
y
x
f
dy
y
x
y
f
dx
y
x
x
f
y
x
df
0
0
2
2
0
0
2
2
2
0
0
2
2
0
0
,
2
,
,
,
∂
∂
∂
+
∂
∂
+
∂
∂
=
,
gdzie
dxdx
dx
=
2
PRZYKŁAD 51
Wyznaczyć różniczkę zupełną drugiego rzędu dla funkcji:
( )
5
4
3
4
3
5
,
xy
xy
y
x
y
x
f
+
−
+
=
Ponieważ pochodne cząstkowe drugiego rzędu wynoszą:
2
2
x
f
∂
∂
=
x
30
,
2
2
y
f
∂
∂
=
3
2
80
12
xy
y
+
,
y
x
f
∂
∂
∂
2
=
4
20
3
y
+
−
,
x
y
f
∂
∂
∂
2
=
4
20
3
y
+
−
.
Więc różniczka zupełna drugiego rzędu przyjmuje postać:
(
)
(
)
dxdy
y
dy
xy
y
xdx
df
4
2
3
2
2
20
3
2
80
12
30
+
−
+
+
+
=
.
Różniczka zupełna drugiego rzędu w punkcie (1,2) przyjmuje zaś postać:
( )
dxdy
dy
dx
df
634
688
30
2
,
1
2
2
+
+
=
14.7.
Ekstrema lokalne funkcji dwóch zmiennych
Niech dana będzie funkcja
( )
y
x
f
z
,
=
określona w pewnym otoczeniu punktu
(
)
0
0
0
, y
x
P
.
•
Def.
Mówimy, że funkcja posiada w punkcie
(
)
0
0
, y
x
maksimum (minimum) lokalne, jeżeli
istnieje otoczenie punktu
(
)
0
0
, y
x
takie, że dla każdego punktu
( )
y
x,
należącego do tego
otoczenia spełniona jest nierówność:
( ) (
)
0
0
,
,
y
x
f
y
x
f
≤
( ) (
)
(
)
0
0
,
,
y
x
f
y
x
f
≥
Maksima i minima lokalne łącznie nazywamy ekstremami lokalnymi.
•
Warunek konieczny i wystarczający istnienia ekstremum lokalnego funkcji dwóch
zmiennych:
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
61
Jeżeli dana jest funkcja dwóch zmiennych z=f(x,y) mająca w otoczeniu punktu
(
)
0
0
0
, y
x
P
wszystkie drugie pochodne cząstkowe ciągłe oraz jeżeli spełnione są następujące warunki:
−
x
y
x
f
∂
∂
)
,
(
0
0
=0,
y
y
x
f
∂
∂
)
,
(
0
0
=0, (warunek konieczny)
−
0
)
,
(
)
,
(
)
,
(
)
,
(
2
0
0
2
2
0
0
2
2
0
0
2
0
0
>
∂
∂
∂
−
∂
∂
⋅
∂
∂
=
y
x
y
x
f
y
y
x
f
x
y
x
f
y
x
W
, (warunek wystarczający)
to w punkcie
(
)
0
0
0
, y
x
P
funkcja ma ekstremum, przy czym:
−
w punkcie
(
)
0
0
0
, y
x
P
jest minimum lokalne, jeżeli
2
0
0
2
)
,
(
x
y
x
f
∂
∂
>0
−
w punkcie
(
)
0
0
0
, y
x
P
jest maksimum lokalne, jeżeli
2
0
0
2
)
,
(
x
y
x
f
∂
∂
<0.
UWAGA:
Jeżeli spełnione są warunki:
−
x
y
x
f
∂
∂
)
,
(
0
0
=0,
y
y
x
f
∂
∂
)
,
(
0
0
=0,
ale:
•
)
,
(
0
0
y
x
W
<0 to funkcja nie ma ekstremum w punkcie
(
)
0
0
0
, y
x
P
•
)
,
(
0
0
y
x
W
=0 to ekstremum w punkcie
(
)
0
0
0
, y
x
P
może istnieć lub nie
PRZYKŁAD 52
Wyznacz, jeżeli istnieją ekstrema lokalne funkcji
( )
3
2
6
3
,
y
xy
y
x
y
x
f
+
−
=
.
−
Dla funkcji
( )
3
2
6
3
,
y
xy
y
x
y
x
f
+
−
=
mamy:
y
xy
x
f
6
6
−
=
∂
∂
,
2
2
3
6
3
y
x
x
y
f
+
−
=
∂
∂
,
y
x
f
6
2
2
=
∂
∂
,
y
y
f
6
2
2
=
∂
∂
,
6
6
2
−
=
∂
∂
∂
x
y
x
f
−
Sprawdzamy warunek konieczny
(
)
=
+
−
=
∨
=
⇔
=
+
−
=
−
⇔
=
+
−
=
−
⇔
=
∂
∂
=
∂
∂
0
3
6
3
1
0
0
3
6
3
0
1
6
0
3
6
3
0
6
6
0
)
,
(
0
)
,
(
2
2
2
2
2
2
0
0
0
0
y
x
x
x
y
y
x
x
x
y
y
x
x
y
xy
y
y
x
f
x
y
x
f
1.
( )
( )
⇒
=
∨
=
=
⇔
=
−
=
⇔
=
−
=
0
,
2
0
,
0
2
0
0
0
)
2
(
3
0
0
6
3
0
2
1
2
P
P
x
x
y
x
x
y
x
x
y
2.
( )
( )
−
⇒
−
=
∨
=
=
⇔
=
=
⇔
=
+
−
=
1
,
1
1
,
1
1
1
1
1
1
0
3
3
1
4
3
2
2
P
P
y
y
x
y
x
y
x
.
−
Sprawdzamy warunek dostateczny:
−
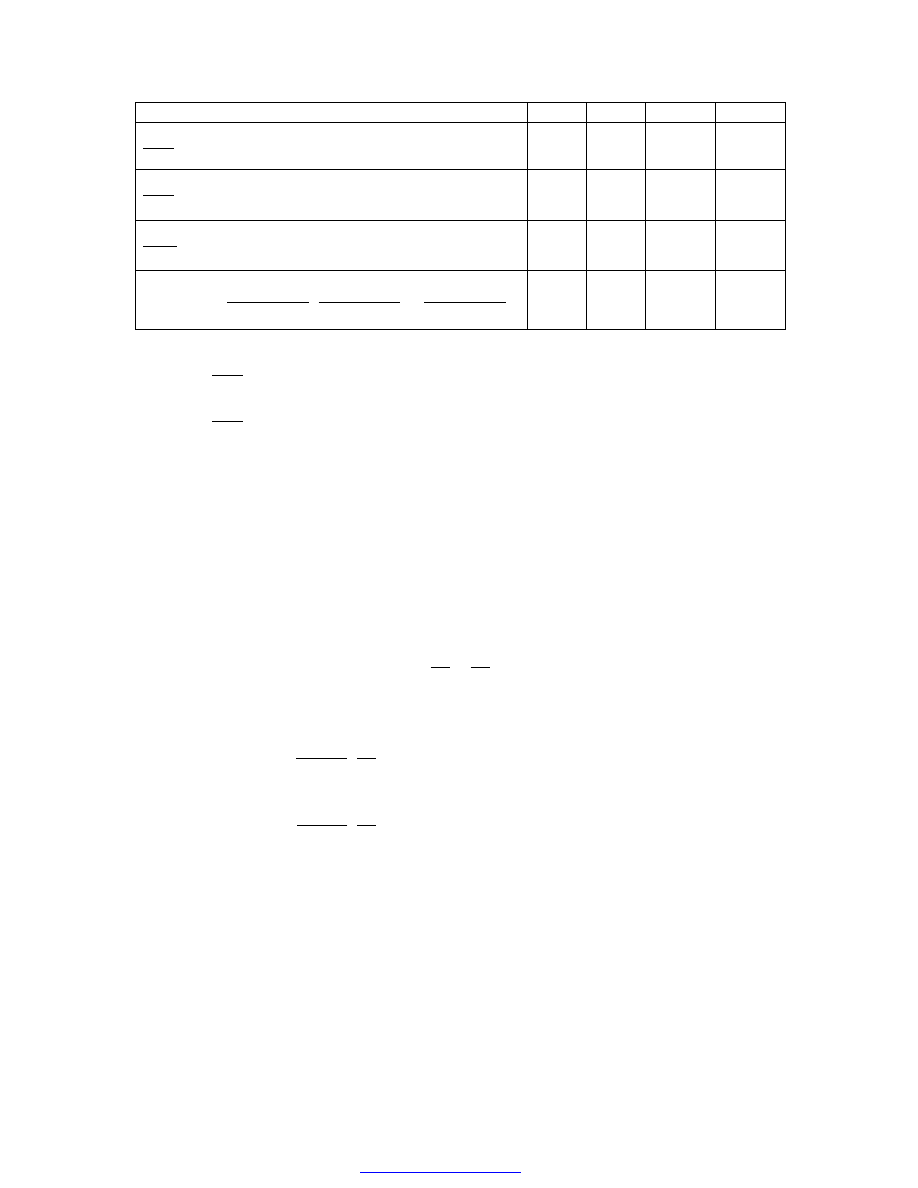
Wartości poszczególnych pochodnych oraz wyróżniki dla każdego z 4 otrzymanych
punktów zestawimy w tabeli:
PDF created with pdfFactory trial version
Opracowała: K. Sokołowska
62
(0,0)
(2,0)
(1,1)
(1,-1)
y
x
f
6
2
2
=
∂
∂
0
0
6
-6
y
y
f
6
2
2
=
∂
∂
0
0
6
-6
6
6
2
−
=
∂
∂
∂
x
y
x
f
-6
6
0
0
2
0
0
2
2
0
0
2
2
0
0
2
0
0
)
,
(
)
,
(
)
,
(
)
,
(
∂
∂
∂
−
∂
∂
⋅
∂
∂
=
y
x
y
x
f
y
y
x
f
x
y
x
f
y
x
W
-36<0
brak
ekstr.
-36<0
brak
ekstr.
36>0
min
lokalne
36>0
max
lokalne
Ponieważ
0
6
)
1
,
1
(
2
2
>
=
∂
∂
x
f
, więc w punkcie (1,1) istnieje minimum.
Ponieważ
0
6
)
1
,
1
(
2
2
<
−
=
−
∂
∂
x
f
, więc w punkcie (1,-1) istnieje maksimum.
−
( )
2
1
,
1
min
−
=
f
,
( )
2
1
,
1
max
=
−
f
.
14.8.
Zastosowanie rachunku różniczkowego dwóch zmiennych w ekonomii
•
Elastyczność funkcji
Elastyczności cząstkowe funkcji dwóch zmiennych definiuje się analogicznie jak
elastyczność funkcji jednej zmiennej.
Jeżeli istnieją pochodne cząstkowe
x
f
∂
∂
i
y
f
∂
∂
, to elastycznością cząstkową funkcji
( )
y
x
f
z
,
=
:
−
względem zmiennej x nazywamy wyrażenie :
x
f
y
x
f
x
E
y
x
xf
∂
∂
⋅
=
)
,
(
)
,
(
−
względem zmiennej y nazywamy wyrażenie :
y
f
y
x
f
y
E
y
x
yf
∂
∂
⋅
=
)
,
(
)
,
(
Interpretacja elastyczności
)
,
(
y
x
xf
E
określa w przybliżeniu o ile procent wzrośnie wartość funkcji z, gdy zmienna
niezależna x wzrośnie o 1% przy ustalonej wartości zmiennej y.
)
,
(
y
x
yf
E
określa w przybliżeniu o ile procent wzrośnie wartość funkcji z, gdy zmienna
niezależna y wzrośnie o 1% przy ustalonej wartości zmiennej x.
PRZYKŁAD 53
Obliczyć
elastyczności
cząstkowe
funkcji
produkcji
typu
Cobba-Douglasa
5
,
0
1
,
0
4
)
,
(
y
x
y
x
z
=
, gdzie z - wielkość produkcji, x – wielkość majątku produkcyjnego, y –
wielkość zatrudnienia.
Obliczamy:
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
63
- pochodną
cząstkową
rzędu
pierwszego
funkcji
)
,
(
y
x
z
względem
x
:
x
f
∂
∂
=
5
,
0
9
,
0
1
,
0
4
y
x
−
⋅
- pochodną
cząstkową
rzędu
pierwszego
funkcji
)
,
(
y
x
z
względem
y
:
y
f
∂
∂
=
5
,
0
1
,
0
5
,
0
4
−
⋅
y
x
Zatem elastyczności cząstkowe wynoszą:
1
,
0
1
,
0
4
4
)
,
(
5
,
0
9
,
0
5
,
0
1
,
0
)
,
(
=
⋅
⋅
=
∂
∂
⋅
=
−
y
x
y
x
x
x
f
y
x
f
x
E
y
x
xf
5
,
0
5
,
0
4
4
)
,
(
5
,
0
1
,
0
5
,
0
1
,
0
)
,
(
=
⋅
⋅
=
∂
∂
⋅
=
−
y
x
y
x
y
y
f
y
x
f
y
E
y
x
yf
Jak można zauważyć, elastyczności te są stałe (nie zależą od wyjściowych wartości
wielkości majątku produkcyjnego i zatrudnienia).
Interpretacja:
Wzrost wielkości majątku trwałego o 1% (przy nie zmienionej wielkości
zatrudnienia) powoduje wzrost wielkości produkcji w przybliżeniu o 0,1
%.
Wzrost wielkości zatrudnienia o 1% (przy nie zmienionej wielkości majątku
trwałego) powoduje
wzrost wielkości produkcji w
przybliżeniu o 0,5
%.
•
Wielkości krańcowe
Wielkości krańcowe funkcji dwóch zmiennych definiuje się analogicznie jak wielkości
krańcowe funkcji jednej zmiennej.
Interpretacja wielkości krańcowej
Wielkość krańcowa funkcji f(x,y) w punkcie (x,y) względem zmiennej x mówi, o ile
jednostek w przybliżeniu zmieni się (wzrośnie lub spadnie) wartość funkcji f(x,y) jeśli
argument x wzrośnie o jedną jednostkę (przy nie zmienionej wartości argumentu y).
Obliczamy ją licząc wartość pochodnej funkcji z=f(x,y) w punkcie (x,y) -
x
f
∂
∂
.
Wielkość krańcowa funkcji f(x,y) w punkcie (x,y) względem zmiennej y mówi, o ile
jednostek w przybliżeniu zmieni się (wzrośnie lub spadnie) wartość funkcji f(x,y) jeśli
argument y wzrośnie o jedną jednostkę(przy nie zmienionej wartości argumentu x).
Obliczamy ją licząc wartość pochodnej funkcji z=f(x,y) w punkcie (x,y) -
y
f
∂
∂
.
PRZYKŁAD 54
Wyznacz krańcową wydajność (w mln zł) majątku produkcyjnego i zatrudnienia dla funkcji
produkcji Cobba-Douglasa
5
,
0
1
,
0
4
)
,
(
y
x
y
x
f
=
, dla wartości majątku produkcyjnego x=9 mln
zł i wielkości zatrudnienia y=30 osób.
Obliczamy:
- pochodną cząstkową rzędu pierwszego funkcji
)
,
(
y
x
f
względem x :
x
f
∂
∂
=
5
,
0
9
,
0
1
,
0
4
y
x
−
⋅
- pochodną cząstkową rzędu pierwszego funkcji
)
,
(
y
x
f
względem y :
y
f
∂
∂
=
5
,
0
1
,
0
5
,
0
4
−
⋅
y
x
- wartość pochodnej
x
f
∂
∂
dla (x,y)=(9,30):
x
f
∂
∂
(9,30)=
≈
⋅
⋅
⋅
−
5
,
0
9
,
0
30
9
1
,
0
4
0,303251
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
64
- wartość pochodnej
y
f
∂
∂
dla (x,y)=(9,30):
y
f
∂
∂
(9,30)=
≈
⋅
⋅
⋅
−
5
,
0
1
,
0
30
9
5
,
0
4
0,454877
Interpretacja:
Przybliżony wzrost wartości produkcji, gdy wartość majątku produkcyjnego wzrasta o 1 mln
zł (przy wartości majątku produkcyjnego x=9 mln zł i wielkości zatrudnienia y=30 osób)
wynosi 0,303251mln zł, przy założeniu, że wielkość zatrudnienia nie ulegnie zmianie.
Przybliżony wzrost wartości produkcji, gdy wielkość zatrudnienia wzrasta o 1 osobę (przy
wartości majątku produkcyjnego x=9 mln zł i wielkości zatrudnienia y=30 osób) wynosi
0,454877mln zł, przy założeniu, że wartość majątku produkcyjnego nie ulegnie zmianie.
•
Wielkości optymalne
Znalezienie wielkości optymalnej dla danej funkcji w danym przedziale podobnie jak dla
funkcji jednej zmiennej, sprowadza się do wyznaczenia wartości najmniejszej lub największej
w tym przedziale.
PRZYKŁAD 55
Przypuśćmy, że przedsiębiorstwo wytwarza dwa wyroby. Wielkość produkcji pierwszego
wyrobu oznaczmy przez x, drugiego wyrobu oznaczmy przez y. Pomiędzy zyskiem f(x,y)
osiąganym ze sprzedaży tych wyrobów (który jest zależny od wielkości ich produkcji), a
wielkością produkcji tych wyrobów zachodzi zależność:
2
2
3
2
4
)
,
(
y
x
y
x
y
x
y
x
f
−
−
=
.
Wyznaczyć takie wielkości produkcji, aby osiągnięty zysk był maksymalny.
Zakładamy, że zmienne x i y spełniają warunki: x>0, y>0
Dla funkcji
2
2
3
2
4
)
,
(
y
x
y
x
y
x
y
x
f
−
−
=
mamy:
2
2
2
3
8
xy
y
x
xy
x
f
−
−
=
∂
∂
,
y
x
x
x
y
f
2
3
2
2
4
−
−
=
∂
∂
,
2
2
2
2
6
8
y
xy
y
x
f
−
−
=
∂
∂
,
2
2
2
2x
y
f
−
=
∂
∂
,
xy
x
x
y
x
f
4
3
8
2
2
−
−
=
∂
∂
∂
Sprawdzamy warunek konieczny
(
)
(
)
=
−
−
∨
=
=
−
−
∨
=
∨
=
⇔
=
−
−
=
−
−
⇔
=
−
−
=
−
−
⇔
=
∂
∂
=
∂
∂
0
2
4
0
0
2
3
8
0
0
0
2
4
0
2
3
8
0
2
4
0
2
3
8
0
)
,
(
0
)
,
(
2
2
3
2
2
2
0
0
0
0
y
x
x
y
x
x
y
y
x
x
y
x
xy
y
x
x
x
xy
y
x
xy
y
y
x
f
x
y
x
f
Ponieważ z zadania wynika, że x>0, y>0, więc pod uwagę bierzemy tylko poniższe równania
( )
1
,
2
2
4
2
1
2
3
8
3
8
4
2
3
8
2
4
2
3
8
0
2
4
0
2
3
8
1
P
x
x
y
y
x
x
x
y
x
y
x
y
x
y
x
y
x
=
⇒
=
=
⇒
=
−
⇒
−
=
−
=
−
⇔
=
−
=
−
⇔
=
−
−
=
−
−
.
Sprawdzamy warunek dostateczny:
Wartości poszczególnych pochodnych oraz wyróżniki dla każdego z 4 otrzymanych
punktów zestawimy w tabeli:
PDF created with pdfFactory trial version

Opracowała: K. Sokołowska
65
(2,1)
2
2
2
2
6
8
y
xy
y
x
f
−
−
=
∂
∂
-6
2
2
2
2x
y
f
−
=
∂
∂
-8
xy
x
x
y
x
f
4
3
8
2
2
−
−
=
∂
∂
∂
-4
2
0
0
2
2
0
0
2
2
0
0
2
0
0
)
,
(
)
,
(
)
,
(
)
,
(
∂
∂
∂
−
∂
∂
⋅
∂
∂
=
y
x
y
x
f
y
y
x
f
x
y
x
f
y
x
W
32>0
max
lokalne
Ponieważ
0
6
)
1
,
2
(
2
2
<
−
=
∂
∂
x
f
, więc w punkcie (2,1) istnieje maksimum.
( )
4
1
,
2
max
=
f
.
Wynika stąd, że optymalnymi wielkościami produkcji obu wyrobów są x=2, y=1. Przy takiej
wielkości produkcji zysk wynosi 4.
PDF created with pdfFactory trial version
Wyszukiwarka
Podobne podstrony:
4 6 Różniczki funkcji dwóch zmiennych
1 funkcje dwoch zmiennych
09 Rozdział 07 Więcej o całce funkcji dwóch zmiennych
4 5 Ekstrema funkcji dwoch zmiennych
funkcje dwoch zmiennych
6 Funkcja dwóch zmiennych 2 zadania
Ekstrema lokalne funkcji dwóch zmiennych, Ekstrema lokalne funkcji dwóch zmiennych
sciaga18 ekstrema lokalne funkcji dwoch zmiennych, AGH górnictwo i geologia, I SEM, matematyka
Funkcje dwóch zmiennych
6 funkcje dwoch zmiennych
sciaga18 ekstrema lokalne funkcji dwoch zmiennych[1], Analiza
8 Funkcje dwóch zmiennych
RACHUNEK?LKOWY FUNKCJI DWOCH ZMIENNYCH
Funkcje dwóch zmiennych
sciaga20 rozniczka zupelna funkcji dwoch zmiennych, Księgozbiór, Studia, Pozostałe
E3 Funkcje dwóch zmiennych rozwiązywanie zadań
AM23 w08 Ekstrema funkcji dwóch zmiennych
więcej podobnych podstron