Funkcje dwóch zmiennych
Pojęcie funkcji dwóch zmiennych
Dany jest niepusty podzbiór D płaszczyzny Oxy.
Funkcję f, która każdemu punktowi
)
,
(
y
x
P
należącemu
do zbioru D przyporządkowuje dokładnie jedną liczbę
rzeczywistą
)
,
(
y
x
f
z
nazywamy funkcją dwóch
zmiennych rzeczywistych x i y.
Przykład 1. Niech
3
)
,
(
2
xy
x
y
x
f
. Dziedziną funkcji
f jest cała płaszczyzna Oxy.
Wartość tej funkcji w punkcie
)
3
,
2
(
P
wynosi:
13
3
3
2
2
)
3
,
2
(
2
f
Przykład 2. Niech
x
y
y
x
f
1
)
,
(
. Dziedziną funkcji f jest
płaszczyzna Oxy z usuniętą prostą
x
y
.
Wartość tej funkcji w punkcie
)
4
,
1
(
P
wynosi:
3
1
1
4
1
)
4
,
1
(
f
.
Pochodne cząstkowe
Pochodną cząstkową funkcji f względem zmiennej x
oznaczamy symbolem:
'
x
f
albo
x
f
i określamy wzorem:
h
y
x
f
y
h
x
f
y
x
f
h
x
)
,
(
)
,
(
lim
)
,
(
0
'
Pochodną cząstkową funkcji f względem zmiennej y
oznaczamy symbolem:
'
y
f
albo
y
f
i określamy wzorem:
h
y
x
f
h
y
x
f
y
x
f
h
y
)
,
(
)
,
(
lim
)
,
(
0
'
Obliczanie pochodnych cząstkowych wykonujemy
według tych samych reguł, co dla funkcji jednej zmiennej
z tym, że:
- obliczając
'
x
f
zmienną y uważamy za stałą,
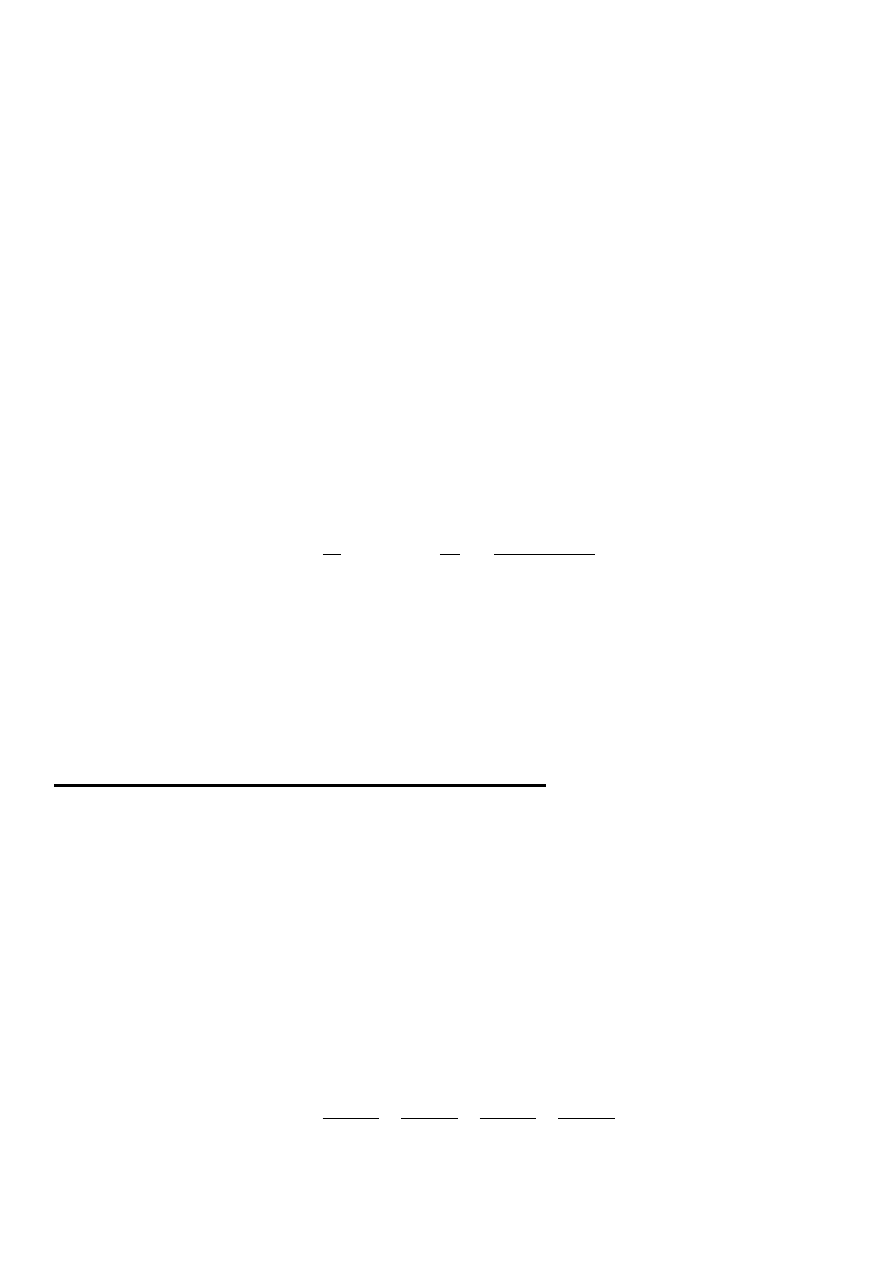
- obliczając
'
y
f
zmienną x uważamy za stałą.
Przykład 3.
x
xy
y
x
y
x
f
2
3
2
3
5
)
,
(
.
1
3
10
1
1
3
2
5
)
,
(
2
3
2
3
'
y
xy
y
x
y
y
x
f
x
xy
y
x
y
x
y
x
y
x
f
y
6
15
0
2
3
3
5
)
,
(
2
2
2
2
'
Przykład 4.
x
y
xe
y
x
f
y
ln
)
,
(
x
y
xe
x
y
e
x
y
e
y
x
f
y
y
y
x
1
1
)
,
(
'
x
e
x
y
x
f
y
y
ln
)
,
(
'
Pochodne cząstkowe drugiego rzędu
Są to pochodne cząstkowe obliczone z pochodnych
cząstkowych
'
x
f
i
'
y
f
.
Oznaczamy je symbolami:
''
''
''
''
,
,
,
yy
yx
xy
xx
f
f
f
f
albo:
2
2
2
2
2
2
,
,
,
y
f
yx
f
xy
f
x
f
Pochodne:
''
''
,
yy
xx
f
f
nazywamy czystymi.
Pochodne:
''
''
,
yx
xy
f
f
nazywamy mieszanymi.
Przykład 5. Obliczyć pochodne cząstkowe drugiego rzędu
funkcji
3
5
3
4
)
,
(
x
y
x
y
x
y
x
f
Rozwiązanie. Obliczmy pochodne rzędu pierwszego:
2
4
3
3
2
4
3
3
'
3
5
4
3
5
4
)
,
(
x
y
x
y
x
x
x
y
x
y
y
x
f
x
5
2
4
5
2
4
'
3
0
1
3
)
,
(
x
y
x
x
y
x
y
x
f
y
Teraz obliczamy pochodne rzędu drugiego:
x
y
x
y
x
x
x
y
x
y
y
x
f
xx
6
20
12
6
4
5
3
4
)
,
(
3
3
2
3
2
3
''
4
2
3
4
2
3
''
5
12
0
1
5
3
4
)
,
(
x
y
x
x
y
x
y
x
f
xy
4
2
3
4
3
2
''
5
12
5
4
3
)
,
(
x
y
x
x
x
y
y
x
f
yx
y
x
y
x
y
x
f
yy
4
4
''
6
0
2
3
)
,
(
Zauważmy, że w powyższym przykładzie jest:
)
,
(
)
,
(
''
''
y
x
f
y
x
f
yx
xy
. Nie jest to przypadek. Pochodne
mieszane – jeśli istnieją – są sobie równe (twierdzenie
Schwarza).
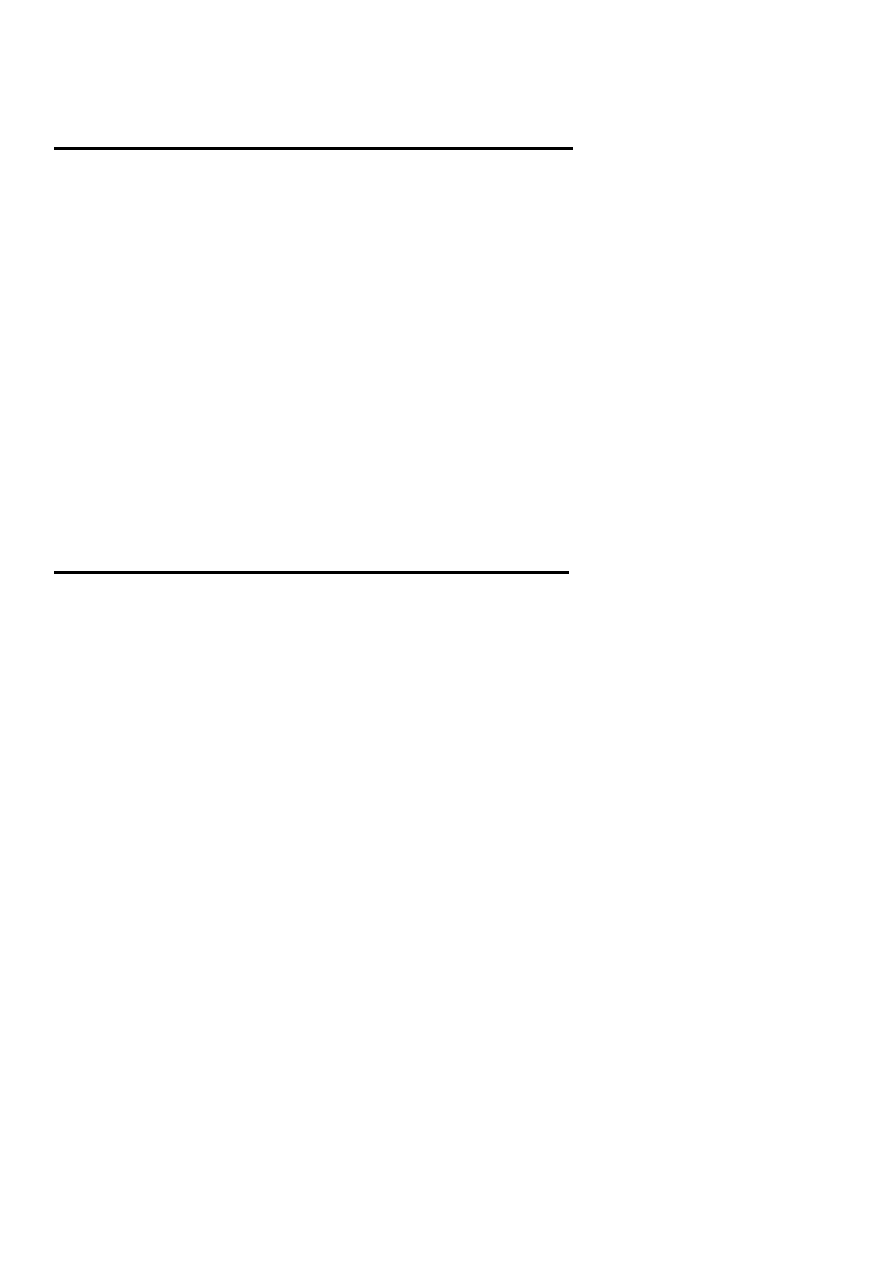
Otoczenie punktu na płaszczyźnie Oxy Otoczeniem o
promieniu
punktu
)
,
(
0
0
y
x
na płaszczyźnie Oxy
nazywamy wnętrze koła o środku
)
,
(
0
0
y
x
i promieniu
.
Założenie. W dalszym ciągu będziemy zakładać, że
istnieją wszystkie pochodne cząstkowe rozważanej funkcji
w pewnym otoczeniu punktu
)
,
(
0
0
y
x
.
Ekstremum funkcji dwóch zmiennych
Mówimy, że funkcja f ma w punkcie
)
,
(
0
0
y
x
maksimum,
gdy istnieje otoczenie U punktu
)
,
(
0
0
y
x
zawarte w
dziedzinie funkcji f i takie, że dla każdego
U
y
x
)
,
(
jest:
)
,
(
)
,
(
0
0
y
x
f
y
x
f
Mówimy, że funkcja f ma w punkcie
)
,
(
0
0
y
x
minimum,
gdy istnieje otoczenie U punktu
)
,
(
0
0
y
x
zawarte w
dziedzinie funkcji f i takie, że dla każdego
U
y
x
)
,
(
jest:
)
,
(
)
,
(
0
0
y
x
f
y
x
f
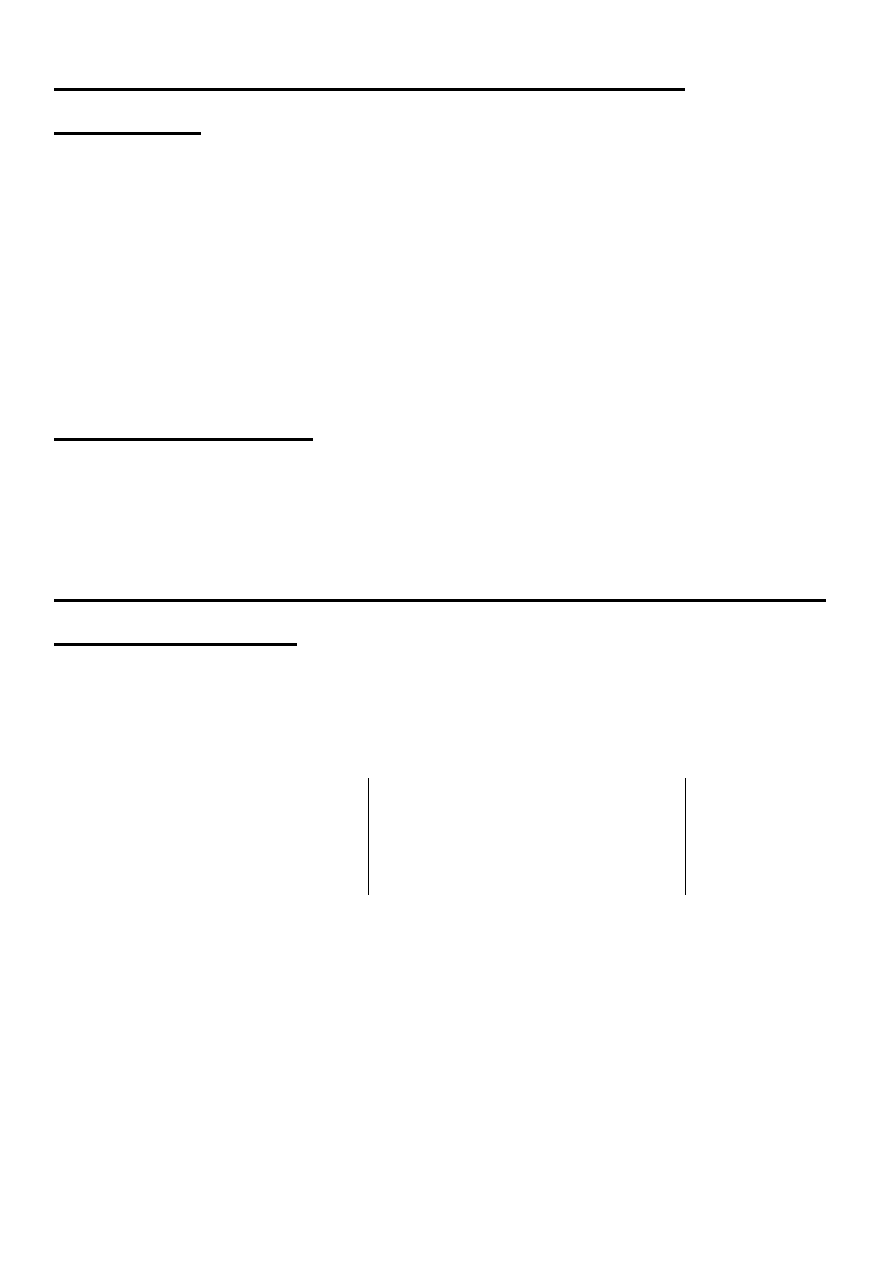
Warunek konieczny ekstremum funkcji dwóch
zmiennych
Jeżeli funkcja f ma w punkcie
)
,
(
0
0
y
x
ekstremum, to obie
pochodne cząstkowe
'
x
f
i
'
y
f
są w tym punkcie równe
zeru:
0
)
,
(
)
,
(
0
0
'
0
0
'
y
x
f
y
x
f
y
x
Punkt stacjonarny funkcji f jest to punkt, w którym obie
pochodne cząstkowe tej funkcji są równe zero.
Warunek dostateczny (wystarczający) ekstremum funkcji
dwóch zmiennych
Jeżeli
)
,
(
0
0
y
x
jest punktem stacjonarnym funkcji f i
wyrażenie
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
0
0
''
0
0
''
0
0
''
0
0
''
0
0
y
x
f
y
x
f
y
x
f
y
x
f
y
x
W
yy
yx
xy
xx
jest dodatnie, to funkcja f ma w punkcie
)
,
(
0
0
y
x
ekstremum.
Gdy
0
)
,
(
0
0
''
y
x
f
xx
jest to maksimum, zaś gdy
0
)
,
(
0
0
''
y
x
f
xx
jest to minimum.
Warunek wykluczający ekstremum funkcji dwóch
zmiennych
Jeżeli
)
,
(
0
0
y
x
jest punktem stacjonarnym funkcji f i
wyrażenie
)
,
(
0
0
y
x
W
jest ujemne, to funkcja f nie ma w
punkcie
)
,
(
0
0
y
x
ekstremum.
Przykład 6. Wyznaczyć ekstrema funkcji
xy
y
x
y
x
f
3
)
,
(
3
3
Rozwiązanie. Dziedzina – cała płaszczyzna.
Obliczamy pochodne cząstkowe:
x
y
y
x
f
y
x
y
x
f
y
x
3
3
)
,
(
,
3
3
)
,
(
2
'
2
'
Punkty stacjonarne:
0
3
3
0
3
3
2
2
x
y
y
x
, stąd
0
0
2
2
x
y
y
x
Z pierwszego równania wyznaczamy:
2
x
y
i wstawiamy
do drugiego równania:
0
4
x
x
Stąd:
0
)
1
(
3
x
x
1
,
0
2
1
x
x
Zatem:
1
1
,
0
0
2
2
2
1
y
y
.
Są dwa punkty stacjonarne:
)
1
,
1
(
,
)
0
,
0
(
2
1
P
P
Obliczamy pochodne cząstkowe rzędu drugiego:
y
y
x
f
y
x
f
y
x
f
x
y
x
f
yy
yx
xy
xx
6
)
,
(
,
3
)
,
(
)
,
(
,
6
)
,
(
''
''
''
''
Wyznacznik
9
36
6
3
3
6
)
,
(
xy
y
x
y
x
W
Badamy punkt
)
0
,
0
(
1
P
:
0
9
9
0
0
36
)
0
,
0
(
W
W punkcie
)
0
,
0
(
1
P
funkcja nie ma ekstremum.
Badamy punkt
)
1
,
1
(
2
P
:
0
27
9
1
1
36
)
1
,
1
(
W
W punkcie
)
1
,
1
(
2
P
funkcja ma ekstremum. Ponieważ
0
6
1
6
)
1
,
1
(
''
xx
f
więc jest to minimum.