Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (10)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (50)

Dyskretna Transformata Fouriera – DFT

Analiza częstotliwościowa sygnałów czasu dyskretnego jest zwykle

przeprowadzana przy pomocy cyfrowych procesorów sygnałowych, którymi mogą

być zwykłe komputery lub też specjalizowane układy DSP. Aby przeprowadzić

analizę częstotliwościową takiego sygnału należy dokonać jego konwersji do

postaci częstotliwościowej, danej transformatą Fouriera czasu dyskretnego DTFT

X(ω) = F(x[n]).

Funkcja X(ω) jest jednak funkcją ciągłą zmiennej rzeczywistej ω i jako taka jest

niewygodną obliczeniowo reprezentacją sygnału x[n].

Dyskretna Transformata Fouriera DFT zawiera próbki DTFT pobierane

w określonych interwałach częstotliwościowych, stanowiąc podstawowe narzędzie

analizy cyfrowych układów LTI.

2 (50)

Próbkowanie widma częstotliwości

i rekonstrukcja sygnału czasu dyskretnego

Transformata DTFT sygnału czasu dyskretnego o skończonej energii jest funkcją

ciągłą postaci:

X =

∑

n=−∞

∞

x [n]e

−

i n

Przyjmijmy, że widmo X(ω) próbkujemy okresowo z rozdzielczością Δω pomiędzy

kolejnymi próbkami, przy czym – ponieważ X(ω) jest funkcją okresową –

wystarczy, że pobierzemy próbki z podstawowego zakresu częstości [0, 2π). Jeśli

pobierzemy N równoodległych próbek widma, wówczas:

 =

2

N

3 (50)

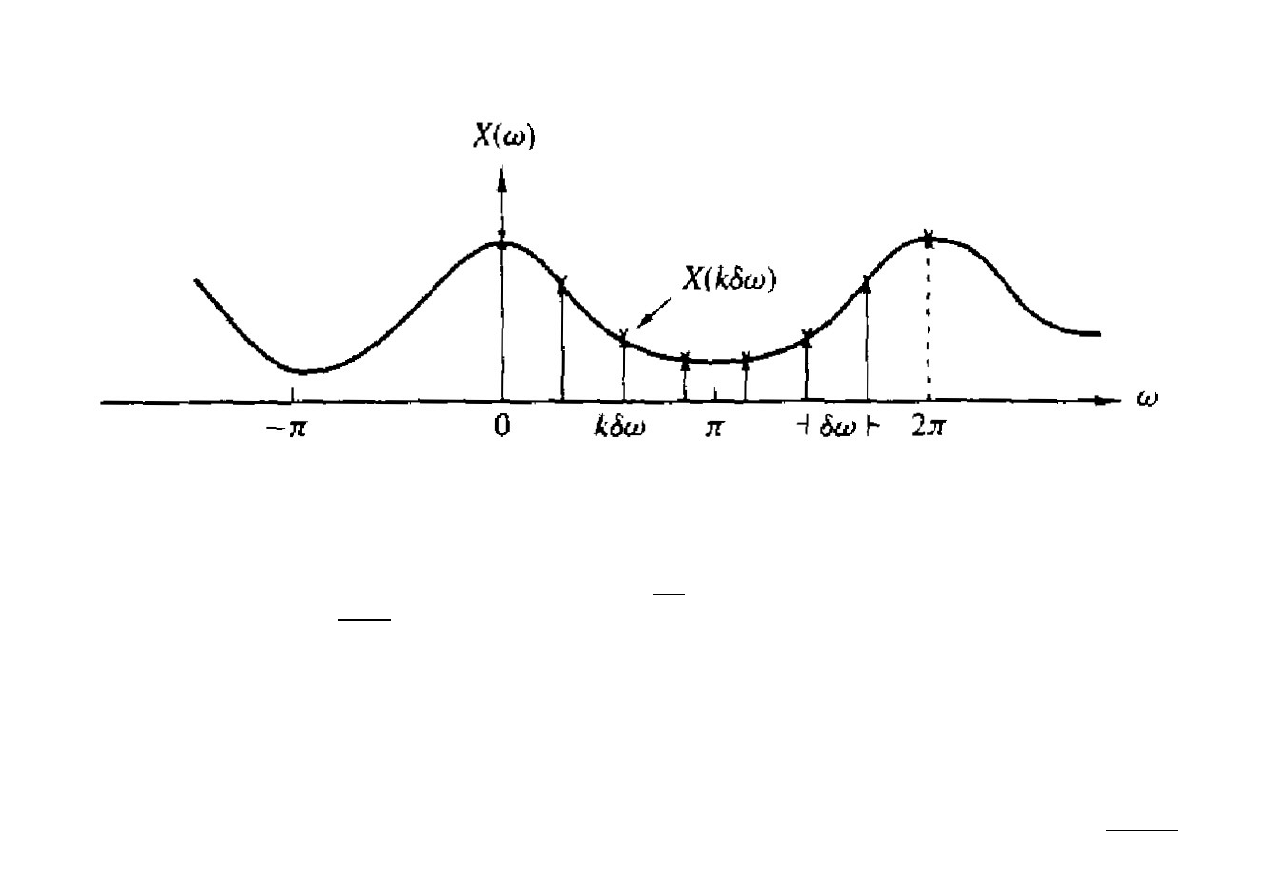
Obliczmy wartości próbek widma w wybranych punktach:

X



2 

N

⋅

k



=

∑

n=−∞

∞

x [n]e

−

i

2

N

k⋅n

; k =0,1,... , N −1

Zauważmy jednak, że z uwagi na okresowość widma (sygnał dyskretny!):

4 (50)

X



2 

N

⋅

k



=

...

∑

n=−N

−

1

x [n]e

−

i

2 

N

k⋅n



∑

n=0

N −1

x[n]e

−

i

2 

N

k⋅n



∑

n= N

2N−1

x [n]e

−

i

2 

N

k⋅n



...=

...=

∑

m=−∞

∞

∑

n=m N

m N  N −1

x[n]e

−

i

2
N

k⋅n

Jeśli zmienimy indeks sumacyjny: n → (n-mN) oraz zamienimy kolejność

sumowania, to:

X



2 

N

⋅

k



=

∑

n=0

N −1



∑

m=−∞

∞

x [n−mN ]



e

−

i

2 

N

k⋅n

5 (50)

Zauważmy jednak, że sygnał:

x

p

[

n]=

∑

m=−∞

∞

x [n−mN ]

otrzymany przez okresowe powtarzanie sygnału x[n] co N-próbek jest sygnałem

okresowym o okresie podstawowym N. Może być on zatem przedstawiony

w postaci szeregu Fouriera czasu dyskretnego DTFS:

x

p

[

n]=

∑

k=0

N −1

c

k

e

i 2  k

n

N

; n=0,1, 2, ... , N −1

gdzie współczynniki rozwinięcia dane są jako:

c

k

=

1

N

∑

n=0

N −1

x

p

[

n]e

−

i 2  k

n

N

; k =0,1, 2,... , N −1

6 (50)

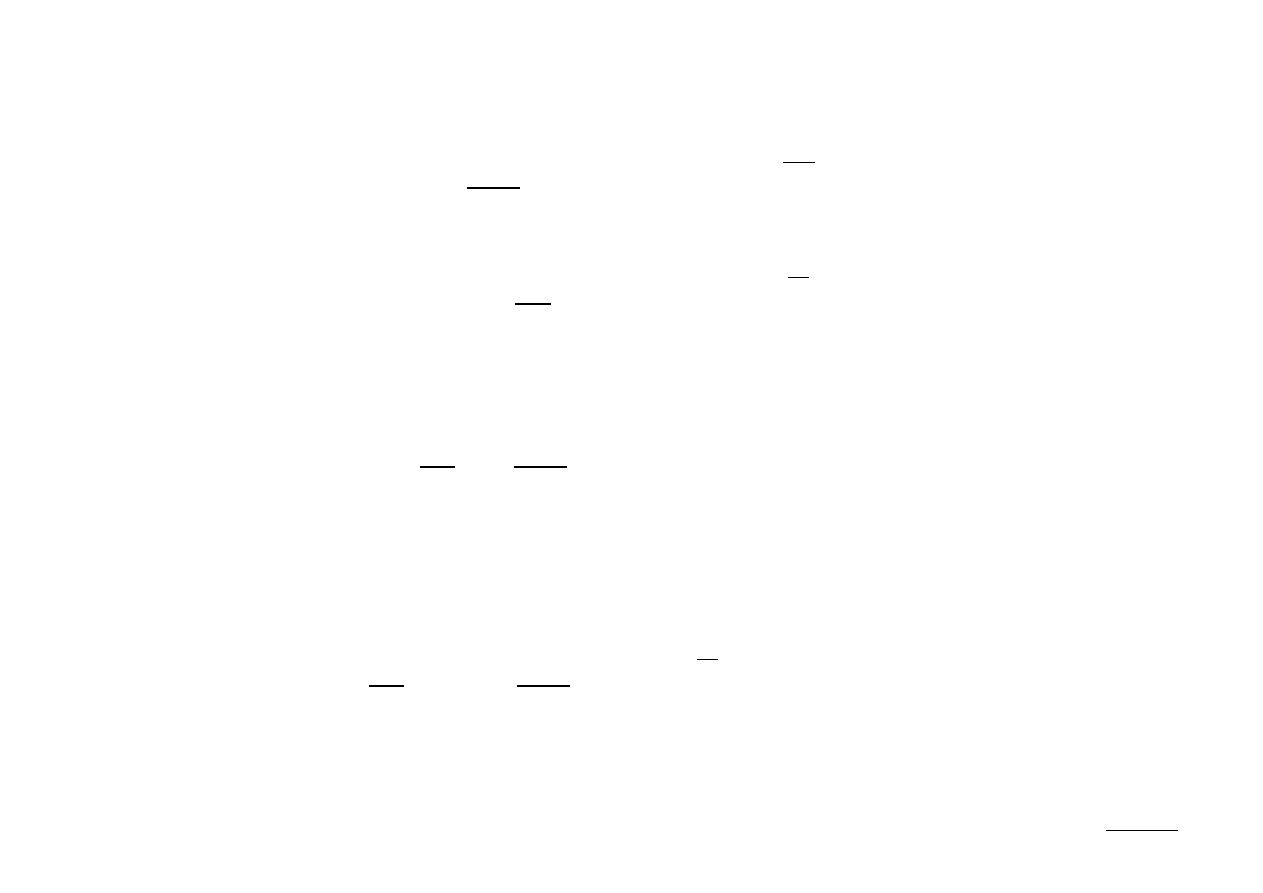
Mamy więc:

X



2 

N

⋅

k



=

∑

n=0

N −1

x

p

[

n] e

−

i

2 

N

k⋅n

c

k

=

1

N

∑

n=0

N −1

x

p

[

n]e

−

i 2 k

n

N

Z porównania wynika, że:

c

k

=

1

N

X



2 

N

⋅

k



; k =0,1, 2,... , N −1

Otrzymujemy w ten sposób równanie syntezy sygnału okresowego x

p

[n]:

x

p

[

n]=

1

N

∑

k=0

N −1

X



2

N

⋅

k



e

i 2 k

n

N

; n=0,1, 2,... , N −1

7 (50)

Otrzymaliśmy wynik, że:

x

p

[

n]=

1

N

∑

k=0

N −1

X



2

N

⋅

k



e

i 2 k

n

N

; n=0,1, 2,... , N −1

Powyższa zależność pozwala zrekonstruować sygnał okresowy x

p

[n] mając próbki

widma X(2πk/N). Ponieważ jednak widmo sygnału okresowego jest z natury

dyskretne, to znajomość X(2πk/N) i tak nie pozwala odtworzyć ani widma ciągłego

X(ω), ani tym bardziej odtworzyć sygnału x[n].

Ponieważ x

p

[n] jest okresowym rozszerzeniem x[n]:

x

p

[

n]=

∑

m=−∞

∞

x [n−mN ]

zatem x[n] może zostać odtworzony z próbek x

p

[n] tylko wówczas, gdy nie

występuje aliasing w dziedzinie czasu, a więc, gdy czas trwania L sygnału x[n] jest

krótszy niż okres N sygnału x

p

[n]:

8 (50)

9 (50)

Zauważmy, że przy braku aliasingu:

x

p

[

n]= x [n] ; n=0,1, 2, ... , N −1

tak więc sygnał x[n] może być odtworzony jednoznacznie, co nie jest możliwe,

gdy L > N. Wynika stąd, że widmo nieokresowego sygnału czasu dyskretnego x[n]

o czasie trwania L może być jednoznacznie wyznaczone na podstawie próbek

pobranych z rozdzielczością:



k

=

2

N

⋅

k ⇔ L≤N

10 (50)

Procedura odtwarzania widma ciągłego X(ω) obejmuje wyznaczenie sygnału x

p

[n]

na podstawie próbek widma X(ω

k

) = X[k]:

x

p

[

n]=

1

N

∑

k=0

N −1

X [k ]e

i 2 k

n

N

; n=0, 1, 2,... , N −1

W następnej kolejności należy odtworzyć sygnał x[n]:

x [n]=

{

x

p

[

n]⇔ n=0,1, 2, ... , N −1

0⇔ dla pozostałych n

}

W ostatnim kroku wyznaczamy widmo ciągłe X(ω) korzystając z:

X =

∑

n=−∞

∞

x [n]e

−

i  n

11 (50)

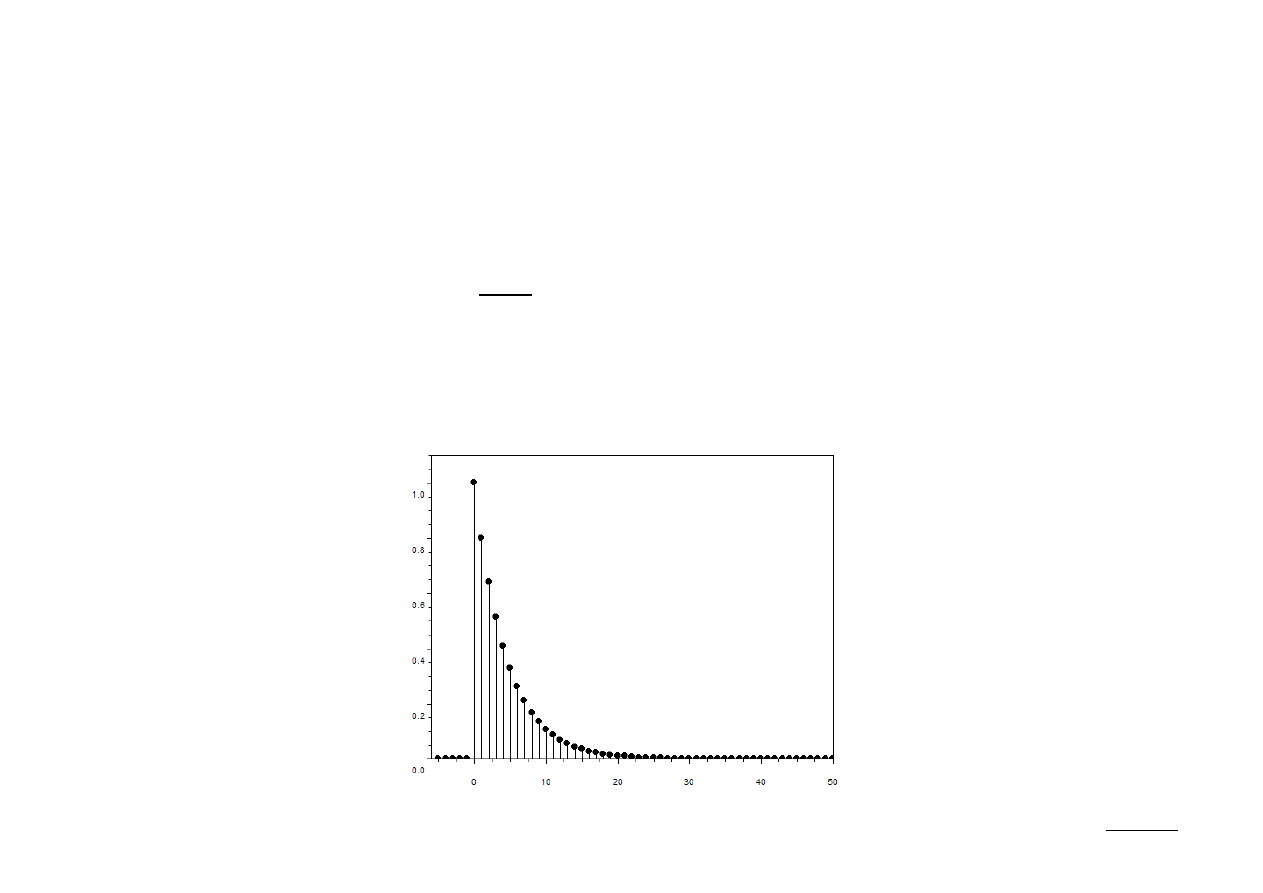
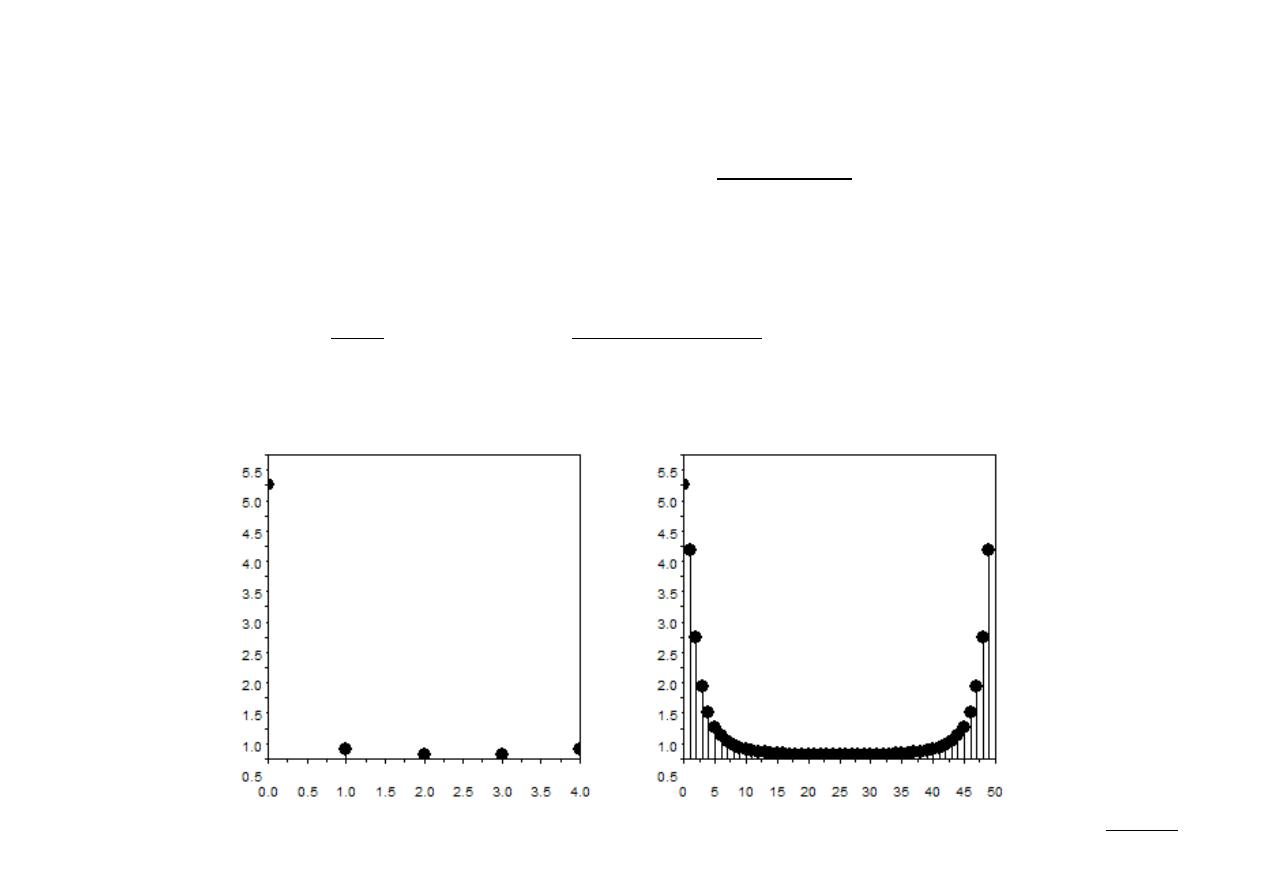
Ex.: Dany jest sygnał:

x [n]=a

n

u[n] ; a=0.8

Znając wartości próbek jego widma pobranych z rozdzielczością:



k

=

2

N

⋅

k ; k =0, 1, 2,... , N −1

wyznaczyć ciągłe widmo DTFT X(ω) dla: (a) N=5, oraz (b) N=50.

12 (50)

DTFT sygnału x[n] ma postać:

X =

∑

n=0

∞

a

n

e

−

i  n

=

1

1−a e

−

i 

Załóżmy, że znamy próbki tego widma pobrane z rozdzielczością ω

k

:

X 

k

=

2 

N

⋅

k = X [k ]=

1

1−a e

−

i 2 k / N

; k =0,1, 2,... , N −1

13 (50)

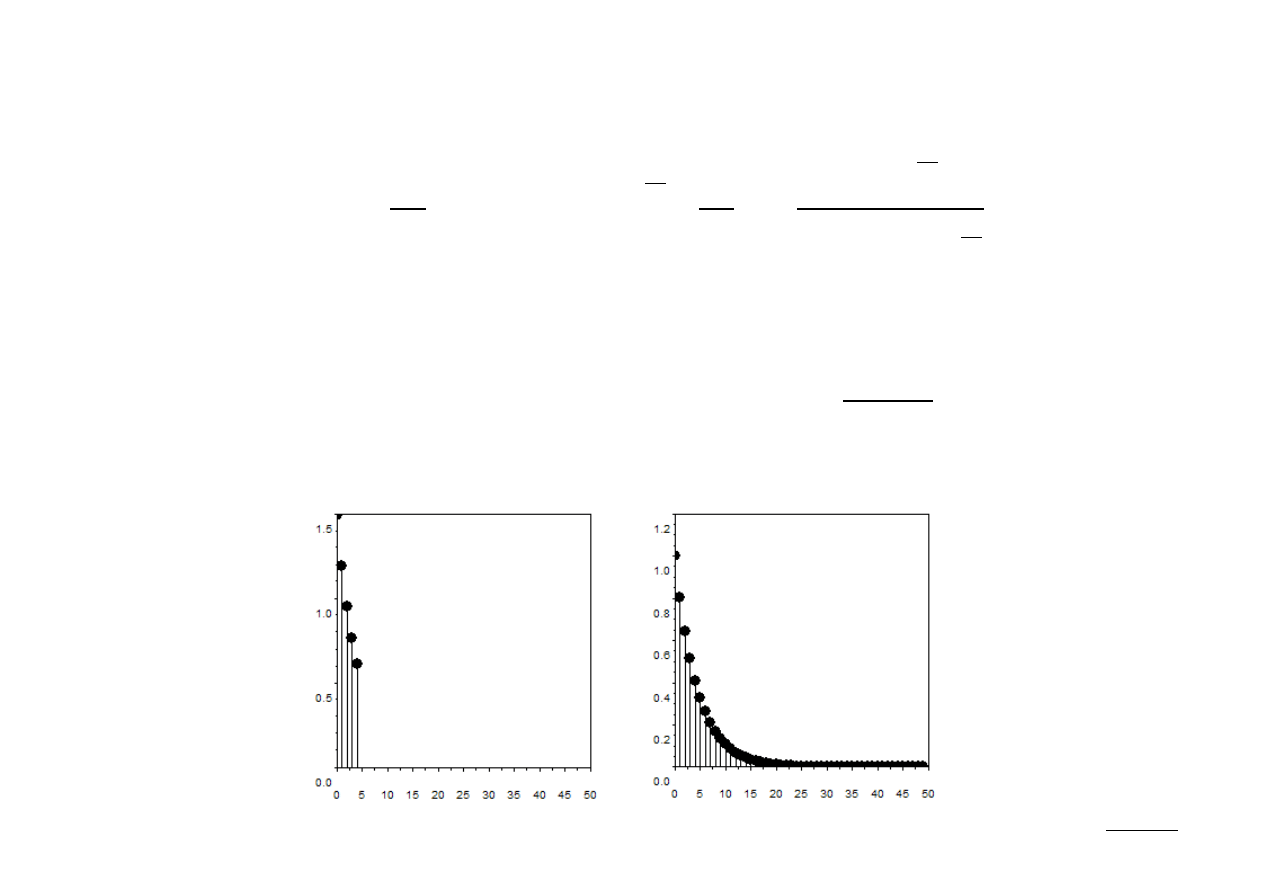
Sygnał okresowy x

p

[n] można utworzyć korzystając z próbek widma X[k]:

x

p

[

n]=

1

N

∑

k=0

N −1

X [k ]e

i 2 k

n

N

=

1

N

∑

k =0

N −1

e

i 2  k

n

N

1−a e

−

i 2 k

n

N

bądź też korzystając ze wzoru:

x

p

[

n]=

∑

m=−∞

∞

x [n−m N ]=

∑

m=−∞

0

a

n−m N

=

a

n

∑

m=0

∞

a

m N

=

a

n

1−a

N

; n=0,1,... , N −1

14 (50)

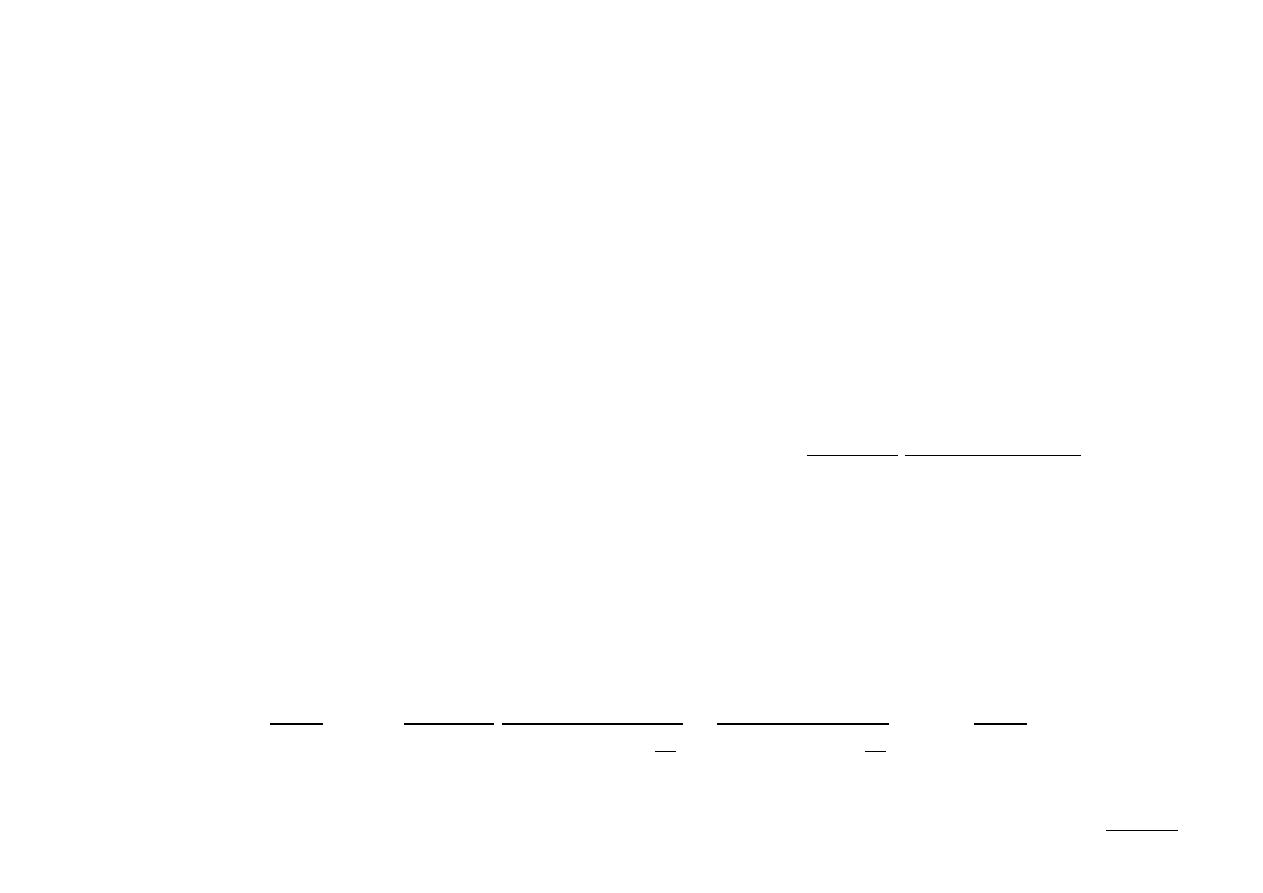
Czynnik 1/(1 – a

N

) reprezentuje tutaj wpływ aliasingu i dla |a| < 1 maleje do zera,

gdy N → ∞.

Zdefiniujmy sygnał o skończonym czasie trwania N:

x

apr

[

n]=

{

x

p

[

n]⇔n=0,1,... , N −1

0⇔dla pozostałych n

}

Wówczas jego widmo DTFT ma postać:

X

apr

=

∑

n=0

N −1

x [n]e

−

i  n

=

∑

n=0

N −1

x

p

[

n]e

−

i  n

=

1

1−a

N

1−a

N

e

−

i  N

1−a e

−

i 

Zauważmy, że mimo różnicy między X(ω) a X

apr

(ω) ich wartości dla ω

k

= 2πk/N są

identyczne:

X

apr



2

N

⋅

k



=

1

1−a

N

1−a

N

e

−

i 2 k

1−a e

−

i 2 

k

N

=

1

1−a e

−

i 2

k

N

=

X



2 

N

⋅

k



15 (50)

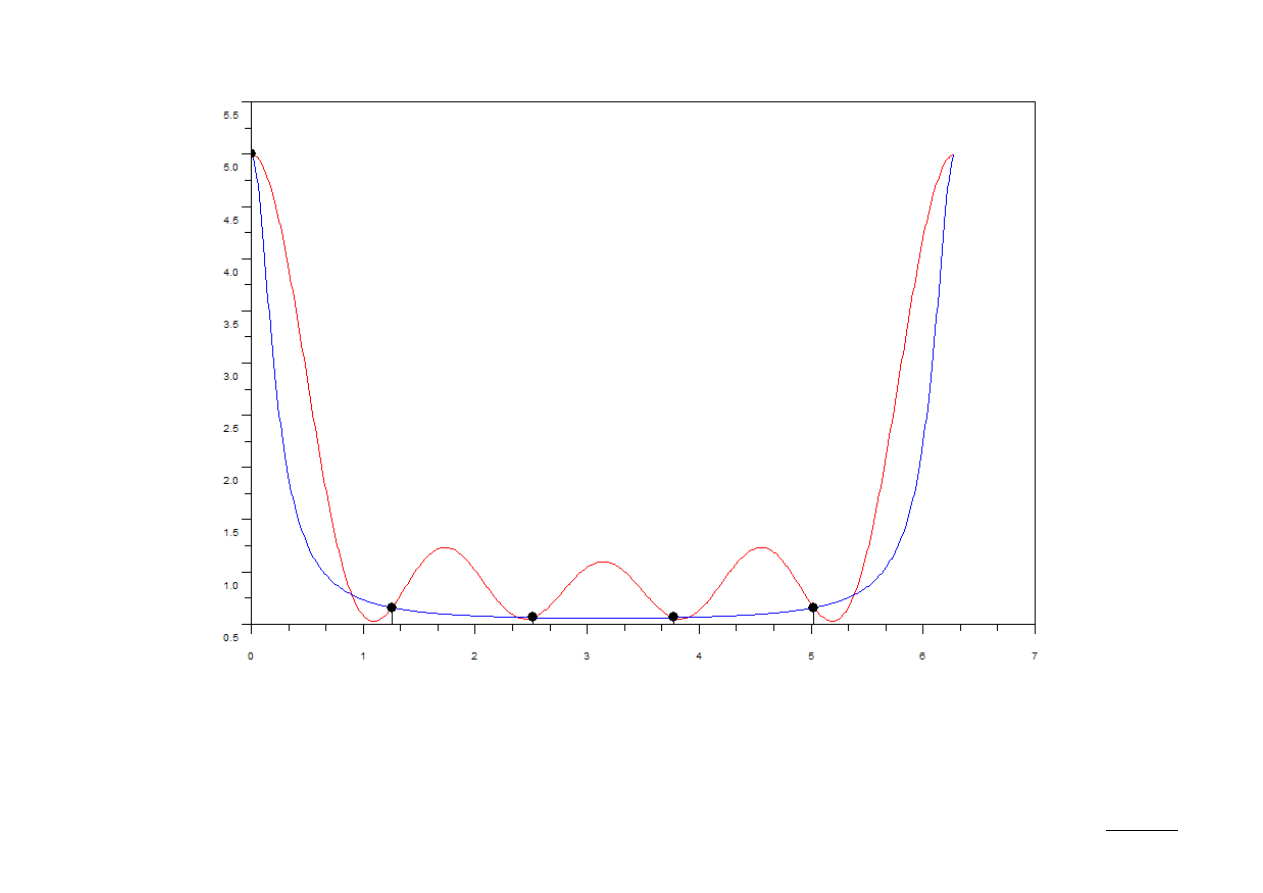
Wykresy odtworzonych widm X

apr

(ω) dla N=5 (czerwony) oraz N=50 (niebieski)

razem z próbkami widma X(ω

k

= 2πk/5)

16 (50)

Dyskretna Transformata Fouriera (DFT)

Z dotychczasowych rozważań widać, że równoodległe próbki widma X[2πk/N],

k = 0, 1, ..., N-1 nie tworzą jednoznacznego odwzorowania sygnału x[n], gdy

sygnał ten posiada nieskończony czas trwania. Zamiast tego, powyższe próbki

widma odpowiadają okresowemu sygnałowi x

p

[n] o okresie N, który jest aliasem

x[n] w myśl relacji:

x

p

[

n]=

∑

m=−∞

∞

x [n−mN ]

Jeśli sygnał x[n] ma czas trwania L ≤ N, wówczas x

p

[n] jest okresowo

zwielokrotnioną kopią x[n] zgodnie ze wzorem:

x

p

[

n]=

{

x [n]⇔ n=0,1,... , L−1

0⇔ n=L , L1,... , N −1

}

Próbki widma DTFT jednoznacznie odwzorowują wówczas ciąg x[n] pozwalając

na jego bezbłędną rekonstrukcję.

17 (50)

Zauważmy, że uzupełnienie sygnału x

p

[n] zerami (zero-padding) nie wnosi żadnej

dodatkowej informacji o widmie X(ω) sygnału x[n]. L-równoodległych próbek tego

widma wystarcza, aby zrekonstruować całe widmo DTFT X(ω). Uzupełnienie

sygnału zerami wpływa jednak na rozdzielczość uzyskanego widma dyskretnego.

Transformata sygnału czasu dyskretnego x[n] na dyskretny ciąg próbek widma

Fouriera X[k] liczonych dla równoodległych częstości ω

k

= 2πk/N to tzw.

dyskretna transformata Fouriera (DFT):

X [ k ]=

∑

n=0

N −1

x [n]e

−

i 2  k

n

N

Odwrotna dyskretna transformata Fouriera (iDFT) ma postać:

x [n]=

1

N

∑

n=0

N −1

X [k ]e

i 2  k

n

N

18 (50)

Dyskretna transformata Fouriera (DFT) jest zatem spróbkowaną wersją

transformaty Fouriera czasu dyskretnego (DTFT), pobieraną w równoodległych

punktach ω

k

= 2πk/N.

Pomimo jednak tego, że L-punktowa DFT jednoznacznie odwzorowuje sygnał x[n]

w dziedzinie częstotliwości, przy małej liczbie punktów nie oddaje ona

wystarczająco szczegółowo charakterystyki widmowej x[n], dlatego też w celu

zwiększenia rozdzielczości DFT sygnał x[n] uzupełnia się zerami (zero-padding):

19 (50)

20 (50)

DFT jako przekształcenie liniowe

Transformaty DFT oraz iDFT można zapisać w zwięzłej postaci jako:

X [ k ]=

∑

n=0

N −1

x [n]W

N

k n

; k =0,1,... , N −1

x [n]=

∑

k=0

N −1

X [k ]W

N

−

k n

; n=0,1,... , N −1

gdzie współczynnik:

W

N

=

e

−

i 2 

N

jest N-tym pierwiastkiem z jedności.

Zauważmy, że obliczenie 1 punktu DFT wymaga N-zespolonych mnożeń oraz

(N-1) zespolonych dodawań, a więc złożoność obliczeniowa całej N-punktowej

DFT jest rzędu N

2

.

21 (50)

Obliczenia DFT oraz iDFT można traktować jak liniowe przekształcenia wektorów

x[n] oraz X[k], a więc w szczególności można jest zapisać w postaci macierzowej.

Niech x

N

będzie n-punktowym wektorem próbek sygnału, X

N

– N-punktowym

wektorem próbek widma tego sygnału, zaś macierz W

N

– macierzą

przekształcenia (symetryczną) postaci:

x

N

=

[

x [0]
x [1]

...

x [ N ]

]

, X

N

=

[

X [0]
X [1]

...

X [ N ]

]

W

N

=

[

1

1

...

1

1

W

N

...

W

N



N −1

⋮

⋮

⋱

⋮

1 W

N



N −1

... W

N



N −1⋅N −1

]

22 (50)

Przy takich oznaczeniach DFT przyjmuje postać macierzową:

X

N

=

W

N

⋅

x

N

Zakładając, że macierz przekształcenia W

N

jest nieosobliwa (odwracalna),

wówczas iDFT wyraża się jako:

x

N

=

W

N

−

1

⋅

X

N

Z drugiej strony, definicja iDFT wymaga, aby:

x

N

=

1

N

W

N

∗

⋅

x

N

gdzie: W

N

* jest macierzą sprzężoną do W

N

.

Porównanie obu wyników prowadzi do wniosku, że:

W

N

−

1

=

1

N

W

N

∗

23 (50)

Powyższe równanie można zapisać także jako:

W

N

⋅

W

N

∗

=

N⋅I

N

gdzie: I

N

jest macierzą jednostkową wymiaru NxN.

Wynika stąd, że macierz przekształcenia W

N

jest macierzą ortogonalną (unitarną),

co znacznie upraszcza obliczenia macierzy odwrotnej.

24 (50)

Ex.: Wyznaczyć DFT sygnału 4-punktowego: x[n] = [0,1,2,3].

Macierz W

4

ma w tym przypadku postać:

W

4

=

[

W

4

0

W

4

0

W

4

0

W

4

0

W

4

0

W

4

1

W

4

2

W

4

3

W

4

0

W

4

2

W

4

4

W

4

6

W

4

0

W

4

3

W

4

6

W

4

9

]

=

[

1

1

1

1

1 −i −1

i

1 −1

1

−

1

1

i

−

1 −i

]

DFT ma zatem postać:

X

N

=

W

4

⋅

x

4

' =

[

6

−

22 i

−

2

−

2−2 i

]

iDFT daje się wyznaczyć przez sprzężenie elementów macierzy W

4

i przemnożenie przez próbki widma DFT.

25 (50)

Związki DFT z innymi transformatami

(1) DFT a DTFS – sygnały okresowe czasu dyskretnego:

Przypomnijmy, że dowolny sygnał okresowy x

p

[n] o okresie podstawowym N może

być przedstawiony w postaci:

x

p

[

n]=

∑

k=0

N −1

c

k

e

i 2  k

n

N

;

c

k

=

1

N

∑

n=0

N −1

x

p

[

n]e

−

i 2 k

n

N

Po porównaniu ze wzorami na DFT widać, że przy założeniu, iż x

p

[n] = x[n]

współczynniki szeregu Fouriera c

k

są równe:

X [ k ]=N⋅c

k

Z drugiej strony, rozwinięcie na szereg Fouriera jest równe iDFT, tak więc

N-punktowa DFT dokładnie odtwarza widmo liniowe sygnału okresowego

o okresie podstawowym N.

26 (50)

(2) DFT a DTFT – sygnały nieokresowe czasu dyskretnego:

Jeśli x[n] jest nieokresowym sygnałem czasu dyskretnego o widmie DTFT X(ω),

próbkowanym w równych przedziałach częstotliwości ω

k

= 2πk/N, to prążki:

X [ k ]= X 

k

 ∣



k

=

2 k / N

=

∑

n=−∞

∞

x [n]e

−

i 2  k

n

N

są równe współczynnikom DFT sygnału okresowego x

p

[n] o okresie N

utworzonego przez cykliczne powtarzanie x[n]:

x

p

[

n]=

∑

m=−∞

∞

x [n−m N ]

Z tego względu dokładność DFT jest uzależniona od aliasingu sygnału x[n]

w przedziale 0 ≤ n ≤ N-1. Warunkiem powracalności iDFT do pierwotnej postaci

x[n] jest, aby czas trwania L sygnału x[n] był nie dłuższy niż okres N sygnału x

p

[n].

27 (50)

(3) DFT a z-transformata:

Niech dany jest sygnał x[n], którego z-transformata ma postać:

X  z =

∑

n=−∞

∞

x [n] z

−

n

Przy czym ROC zawiera okrąg jednostkowy.

Okazuje się wówczas, że DFT jest równoważne z-transformacie liczonej na

okręgu jednostkowym w N-równoodległych punktach:

X [ k ]= X  z

k

 ∣

z

k

=

e

i 2 k n/ N

=

∑

n=−∞

∞

x [n]e

−

i 2  k

n

N

28 (50)

Jeśli długość sygnału x[n] nie przekracza N, wówczas może on być odtworzony

z N-punktowego widma DFT. Oznacza to, że i z-transformata jest jednoznacznie

definiowana przez DFT. Z-transformata daje się bowiem wyrazić jako:

X  z =

∑

n=0

N −1

x [n] z

−

n

=

...=

1−z

−

N

N

∑

k=0

N −1

X [k ]

1−e

i 2

k

N

z

−

1

z-transformata liczona po okręgu jednostkowym prowadzi do wzoru

interpolacyjnego na DTFT w funkcji próbek widma DFT:

X =

1−e

−

N

N

∑

k=0

N −1

X [k ]

1−e

−

i



−

2 

k

N



29 (50)

Własności DFT

(1) Okresowość DFT:

Jeśli x[n] oraz X[k] są parą transformat DFT, to:

x [ nN ]=x [n]

X [ k N ]= X [k ]

(2) Liniowość DFT:

Jeśli {x

1

[n], X

1

[k]}, {x

2

[n], X

2

[k]} są parami transformat DFT, to:

DFT a

1

x

1

[

n]a

2

x

2

[

n]=a

1

X

1

[

k ]a

2

X

2

[

k ]

30 (50)

(3) Cykliczna symetria sygnału:

Dowiedliśmy wcześniej, że N-punktowa DFT sygnału x[n] o skończonym czasie

trwania L ≤ N jest równa N-punktowej DFT sygnału okresowego x

p

[n] o okresie N,

otrzymanego przez okresowe rozszerzanie x[n]:

x

p

[

n]=

∑

m=−∞

∞

x [n−m N ]

Załóżmy teraz, że sygnał x

p

[n] przesuwamy o k-próbek w prawo:

x

p

' [n]=x

p

[

n−k ]=

∑

m=−∞

∞

x [ n−k −m N ]

Odtworzenie sygnału x'[n] na podstawie znajomości x

p

'[n]:

x ' [n]=

{

x

p

' [n]⇔0≤n≤N −1

0 dla pozostałych N

}

prowadzi do wniosku, że x'[n] także jest przesunięte względem x[n] o k-próbek,

wykazując przy tym cykliczność przesunięcia.

31 (50)

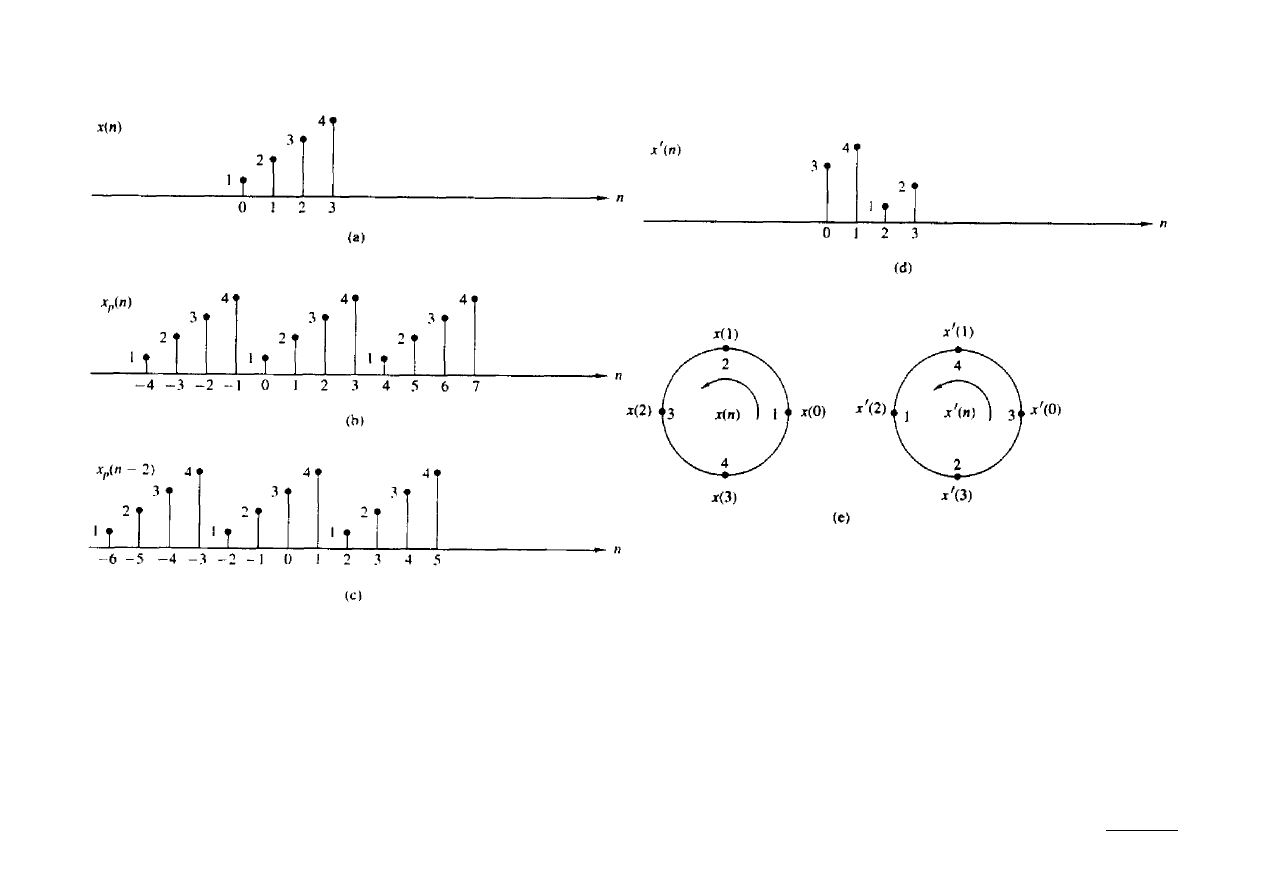
Kołowe przesunięcie N-punktowego sygnału skończonego w czasie (przesunięcie

modulo N) jest zatem równoważne liniowemu przesunięciu jego rozszerzenia

okresowego i vice versa.

32 (50)

Powyższa własność nakazuje przedefiniować pojęcie parzystości sygnału:

N-punktowy sygnał jest kołowo parzysty wtedy i tylko wtedy gdy:

x [ N −n]=x [n]; n=1, 2,... , N −1

N-punktowy sygnał jest kołowo nieparzysty wtedy i tylko wtedy gdy:

x [ N −n]=−x [ n]; n=1, 2, ... , N −1

33 (50)

Własności symetrii DFT

Załóżmy, że N-punktowy sygnał x[n] oraz jego widmo DFT X[k] są ciągami

zespolonymi. Można je zatem wyrazić jako:

x [n] x

R

[

n]i x

I

[

n]; n=0, 1,... , N −1

X [ k ]= X

R

[

k ]i X

I

[

k ]; k =0,1,... , N −1

Korzystając ze wzorów DFT otrzymujemy, że:

X

R

[

k ]=

∑

n=0

N −1



x

R

[

n]cos



2  k n

N





x

I

[

n]sin



2 k n

N





X

I

[

k ]=−

∑

n=0

N −1



x

R

[

n]sin



2 k n

N



−

x

I

[

n]cos



2 k n

N





x

R

[

k ]=

1

N

∑

n=0

N −1



X

R

[

n]cos



2 k n

N



−

X

I

[

n]sin



2 k n

N





x

I

[

k ]=

1

N

∑

n=0

N −1



X

R

[

n]sin



2  k n

N





X

I

[

n]cos



2  k n

N





34 (50)

Jeśli x[n] jest sygnałem rzeczywistym, wówczas:

X [ N −k ]= X

∗

[

k ]= X [−k ]

Jeśli x[n] jest dodatkowo sygnałem parzystym, tzn.: x[N-n] = x[n], to X

I

[k] = 0,

wtedy DFT redukuje się do widma rzeczywistego, parzystego:

X [ k ]= X

R

[

k ]=

∑

n=0

N −1

x [ n]cos



2  k n

N



iDFT również ulega redukcji do postaci:

x [n]=

1

N

∑

k=0

N −1

X [k ]cos



2 k n

N



35 (50)

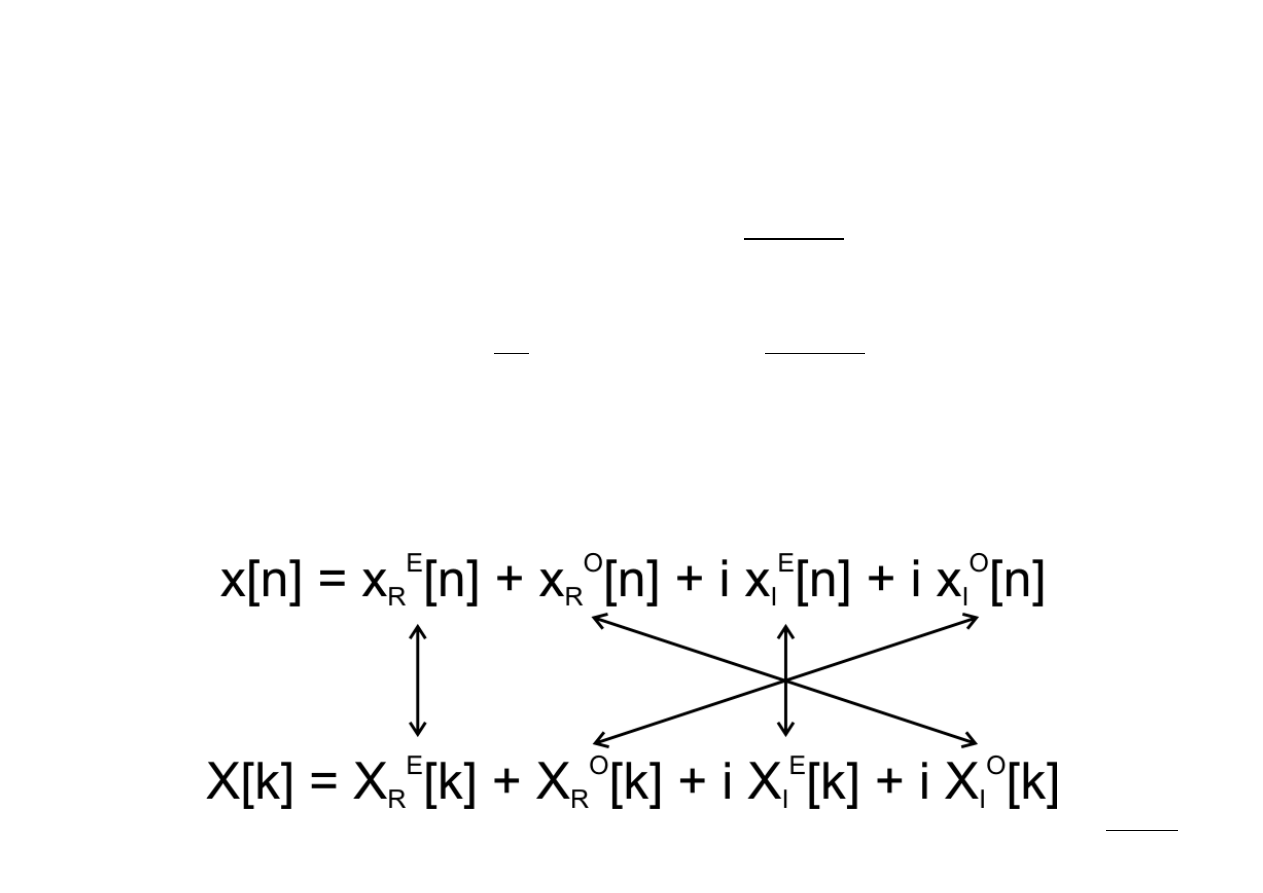
W przypadku, gdy x[n] jest sygnałem rzeczywistym, parzystym, tzn.: x[N-n] = -x[n],

otrzymujemy, że X

R

[k] = 0 oraz widmo DFT jest urojone, nieparzyste:

X [ k ]=−i

∑

n=0

N −1

x [n]sin



2  k n

N



x [n]=i

1

N

=

∑

k =0

N −1

X [k ]sin



2  k n

N



Powyższe własności symetrii DFT można podsumować następująco:

36 (50)

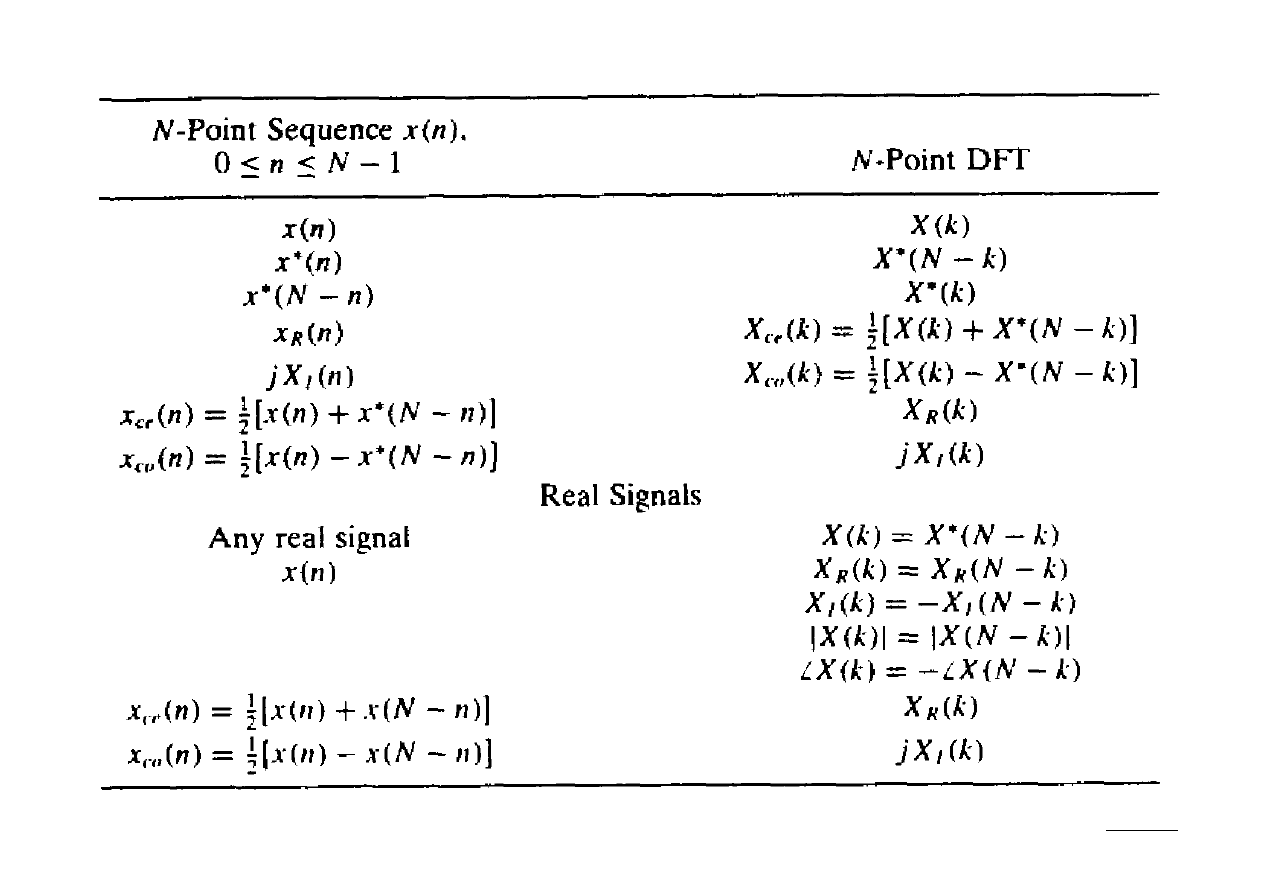
37 (50)

Mnożenie transformat DFT i splot kołowy

Niech dane są dwa ciągi skończone o długości N: x

1

[n] oraz x

2

[n], których DFT

mają postać:

X

1

[

k ]=

∑

n=0

N −1

x

1

[

n]e



−

i 2  k n

N



X

2

[

k ]=

∑

n=0

N −1

x

2

[

n]e



−

i 2 k n

N



Po wymnożeniu obu widm DFT dostajemy widmo X

3

[k] ciągu x

3

[n] o długości N

takiego, że:

X

3

[

k ]= X

1

[

k ]⋅X

2

[

k ]

x

3

[

m]=

1

N

∑

k =0

N −1

X

3

[

k ]e



i 2 k m

N



=

1

N

∑

k=0

N −1

X

1

[

k ]⋅X

2

[

k ]e



i 2 k m

N



38 (50)

Rozpiszmy wyjściowe wyrażenie:

x

3

[

m]=

1

N

∑

k =0

N −1

[

∑

n=0

N −1

x

1

[

n]e

−

i 2  k

n

N

][

∑

l=0

N −1

x

2

[

l ]e

−

i 2 k

l

N

]

e

i 2  k

m
N

=

...

...=

1

N

∑

n=0

N −1

x

1

[

n]

∑

l=0

N −1

x

2

[

l ]

[

∑

k =0

N −1

e

i 2 k



m−n−l 

N

]

Zauważmy jednak, że:

∑

k =0

N −1

a

k

=

{

N ⇔ a=1

1−a

N

1−a

⇔

a≠1

}

gdzie zdefiniowano:

a=e

i 2



m−n−l 

N

39 (50)

W powyższym przypadku analizowany szereg ulega redukcji do:

∑

k =0

N −1

a

k

=

{

N ⇔m−n−l = p⋅N , p∈ℤ

0 ⇔w pozostałych przypadkach

}

Szereg pozostaje więc niezerowy tylko wówczas, gdy:

l=m−n p⋅N =m−nmod N

Końcowe wyrażenie na x

3

[m] przyjmuje zatem postać:

x

3

[

m]=

∑

n=0

N −1

x

1

[

n]⋅x

2

[

m−nmod N ]= x

1

[

n]∗

N

x

2

[

n]; m=0,1,... , N −1

Powyższe wyrażenie nazywane jest splotem kołowym i w dziedzinie czasu jest

ono równoważne mnożeniu widm DFT.

40 (50)

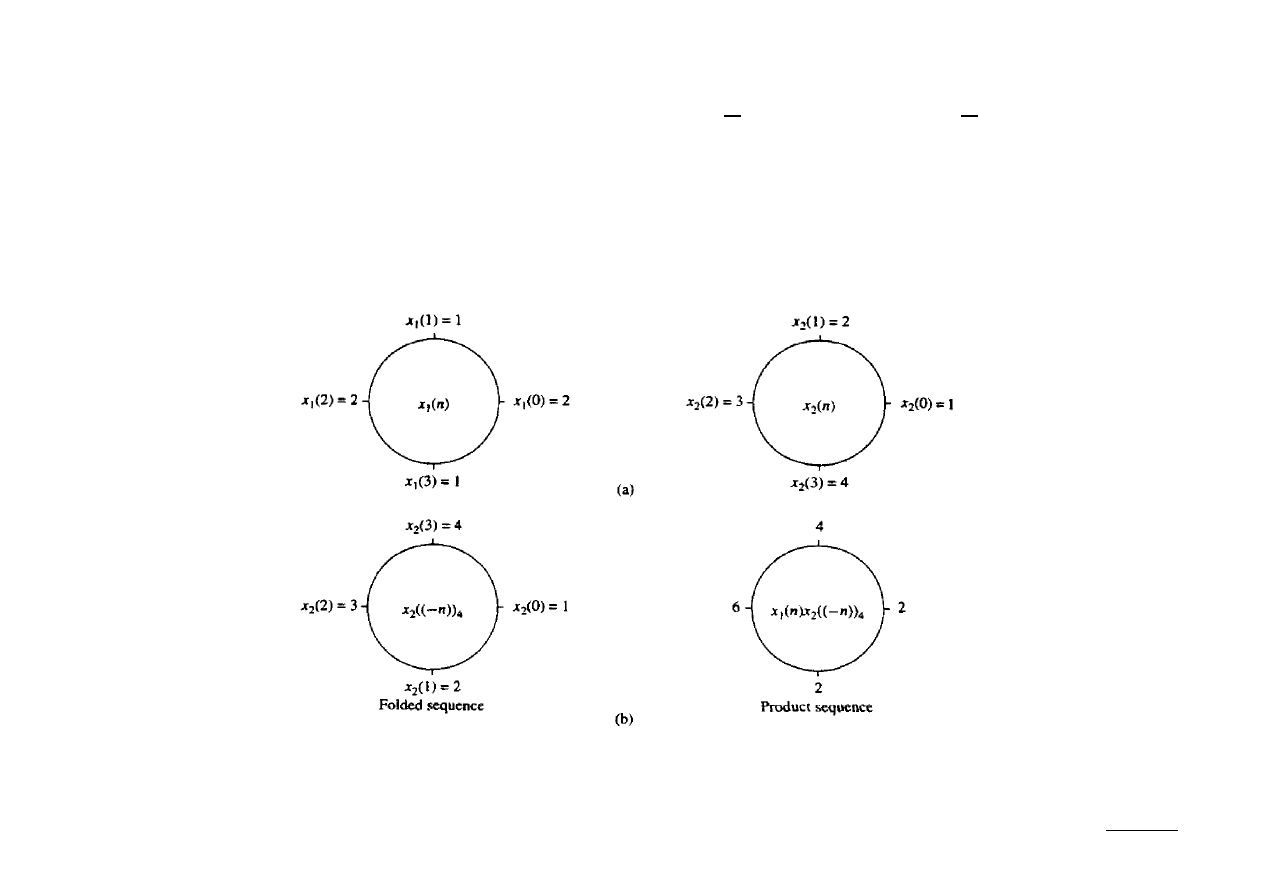
Ex.: Wyznaczyć splot kołowy sygnałów: x

1

[n] = {2, 1,2,1,}, x

2

[n] = {1, 2, 3, 4}.

Przedstawmy oba sygnały w postaci wykresów kołowych (zwrot dodatni przyjęto

jako przeciwny do ruchu wskazówek zegara):

41 (50)

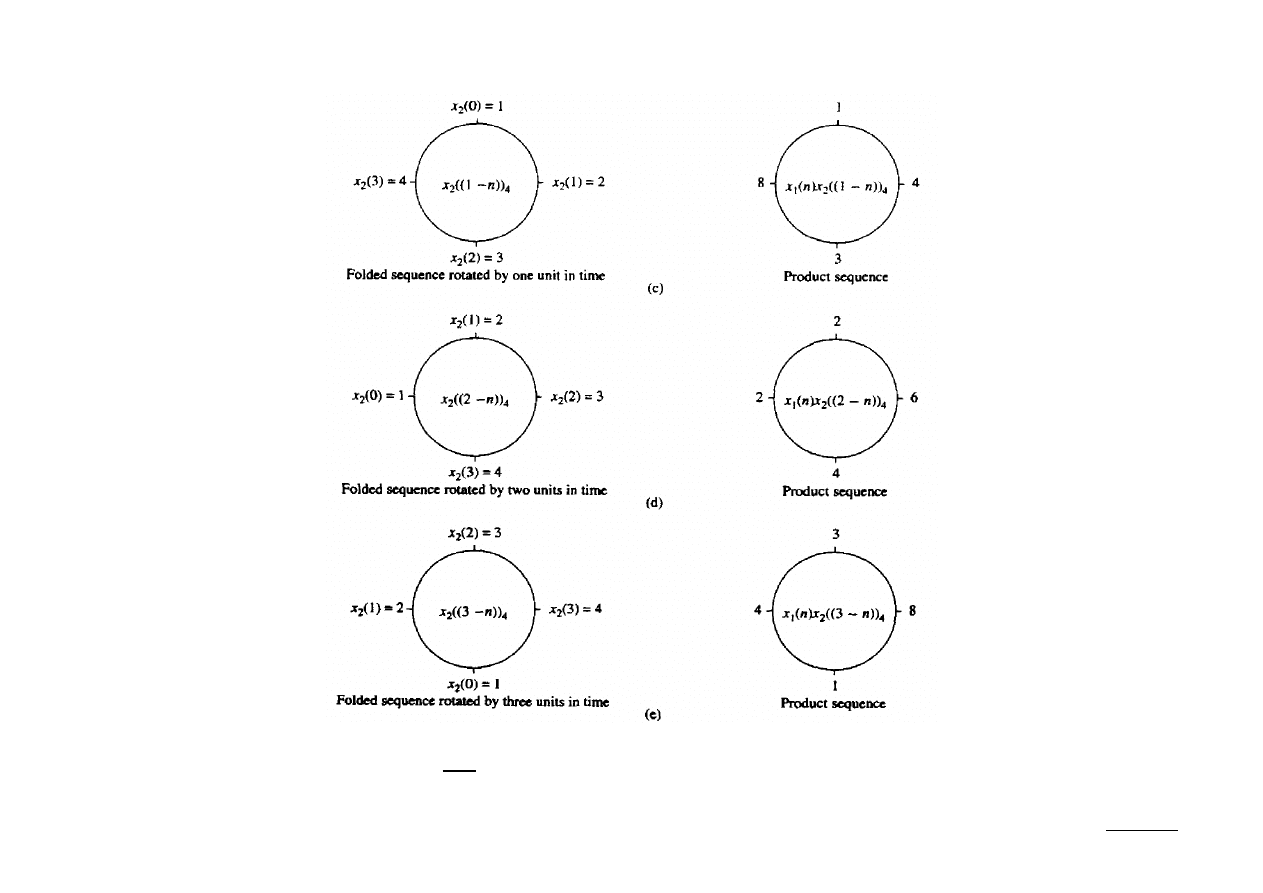
Końcowy wynik to: x

3

[n] = {14, 16, 14, 16}.

42 (50)

Dodatkowe własności DFT

Zawijanie sygnału w czasie:

Jeśli X[k] = DFT(x[n]) to:

x [−n] mod N = x [−n]

N

=

x [ N −n] ⇔

DFT

X [−k ]

N

=

X [ N −k ]

Kołowe przesunięcie sygnału w czasie:

Jeśli X[k] = DFT(x[n]) to:

x [n−m]

N

⇔

DFT

X [k ] e

−

i 2 k

m

N

Kołowe przesunięcie sygnału w dziedzinie częstotliwości:

Jeśli X[k] = DFT(x[n]) to:

x [n]e

i 2 m

n

N

⇔

DFT

X [ k −m]

N

43 (50)

Mnożenie sygnałów:

Jeśli X

1

[k] = DFT(x

1

[n]) oraz X

2

[k] = DFT(x

2

[n]), to:

x

1

[

n]⋅x

2

[

n] ⇔

DFT

X

1

[

k ]∗

N

X

2

[

k ]

Pozostałe własności DFT zebrano w formie tabeli:

44 (50)

Analiza częstotliwościowa sygnałów z użyciem DFT

Każdy badany sygnał jest z natury rzeczy ograniczony czasowo, co powoduje, że

widmo takiego sygnału jest liczone na podstawie skończonej ilości próbek.

Skończony czas obserwacji sygnału wpływa nie tylko na kształt wyliczonego

widma, ale również na jego rozdzielczość, przez co istotnym problemem

w procesie przetwarzania sygnału staje się zbudowanie odpowiedniej funkcji

bramkującej (funkcji okna).

45 (50)

Niech x[n] oznacza badany sygnał czasu dyskretnego, zawierający L-próbek,

co jest równoważne przemnożeniu sygnału x[n] przez funkcję okna prostokątnego

w[n] o długości L:

x [n]= x [n]⋅w [n]

gdzie:

w [n]=

{

1⇔0≤n≤ L−1

0 dla pozostałych n

}

Załóżmy, że x[n] jest sygnałem sinusoidalnym:

x [n]=cos2 f

0

⋅

n

Transformata Fouriera ma postać:



X =

1
2

[

W −

0



W 

0



]

46 (50)

gdzie W(ω) jest transformatą funkcji okna:

W =

sin  L/ 2

sin / 2

e

−

i  L−1

2

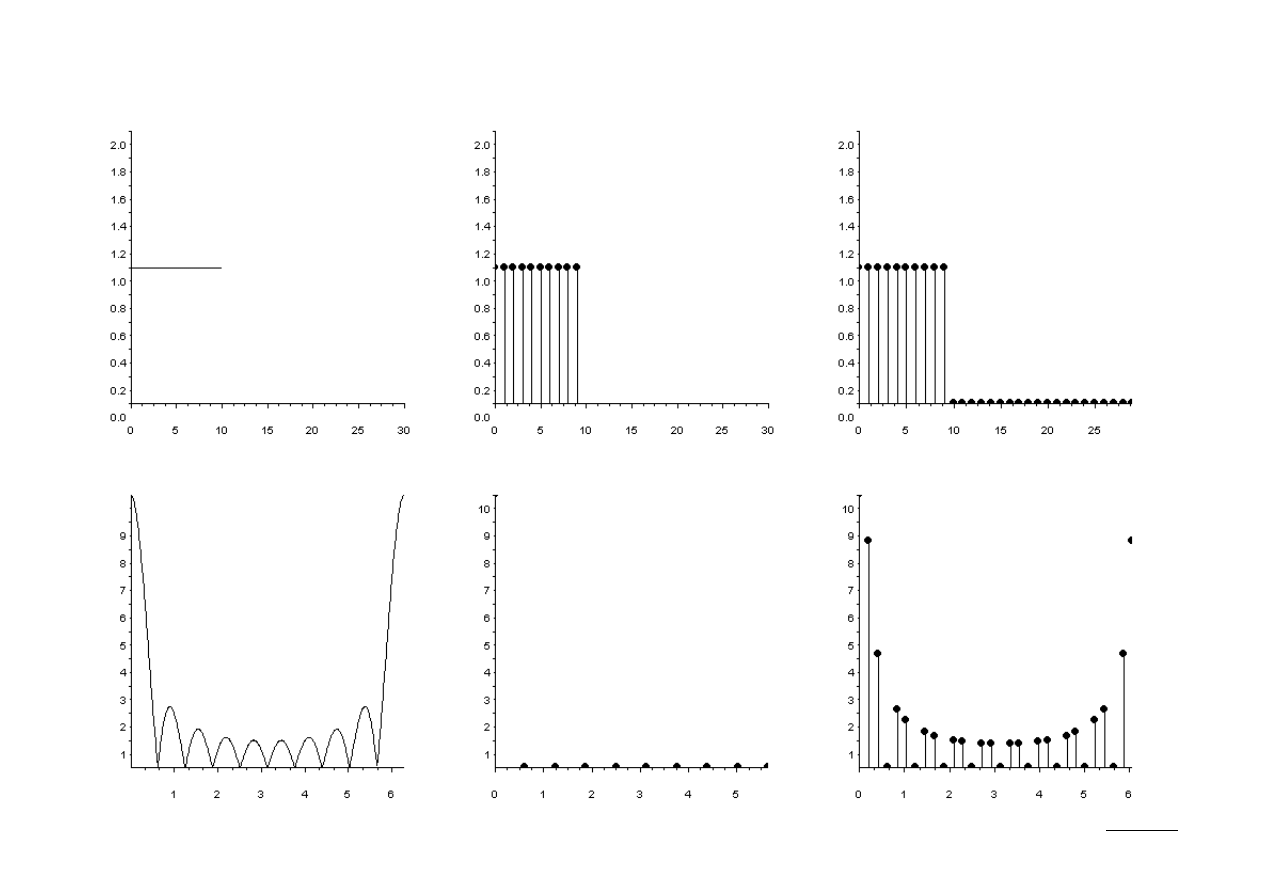
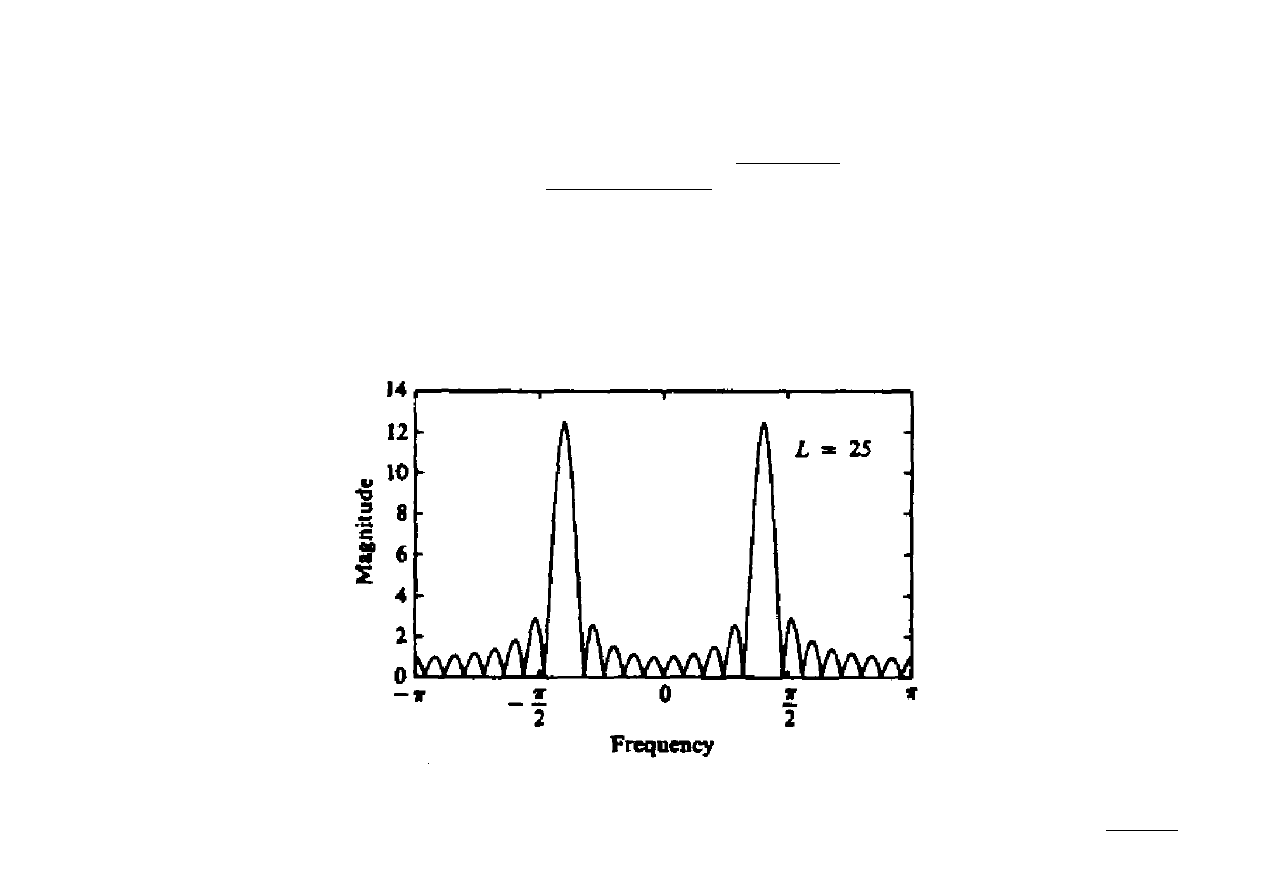
Do obliczenia X(ω) posłużymy się DFT. Uzupełniwszy sygnał x[n] (N-L)-zerami

możemy wyznaczyć jego N-punktową DFT (np. dla L=25, N=2048 jak na rys.):

47 (50)

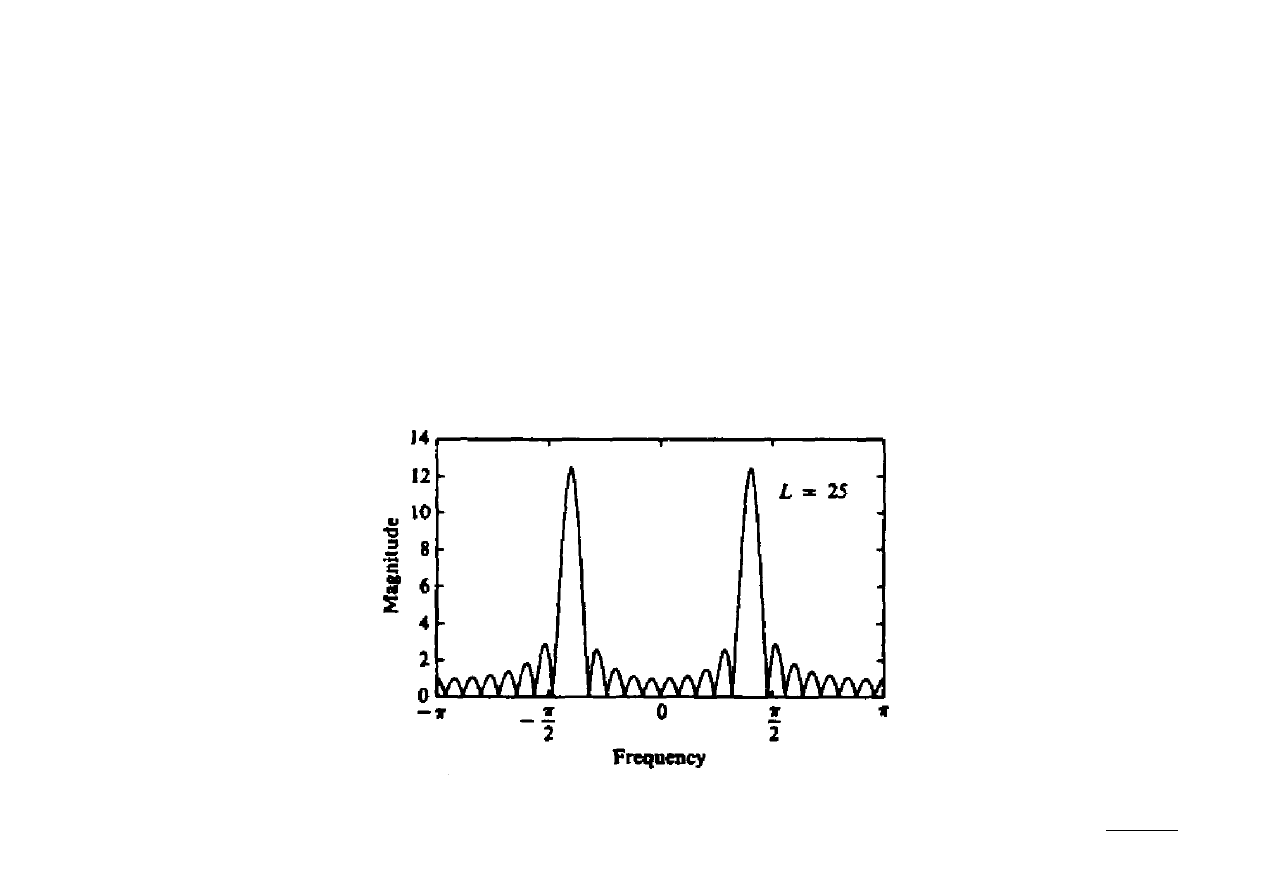
Przeciekanie sygnału

Obserwacja widma sygnału okienkowanego prowadzi do wniosku, że nie jest

zlokalizowane dla jednej częstotliwości, ale rozmywa się w różnym stopniu po

całym przedziale częstotliwości. Mówi się, że widmo przecieka z listków głównych

do pozostałych częstotliwości widma, określając ten proces mianem przeciekania

(leakage).

48 (50)

Rozdzielczość widma

Wpływ funkcji okna nie tylko powoduje przeciekanie energii widma do listków

bocznych, ale także zmienia rozdzielczość widma.

Niech sygnał x[n] składa się z 2 sygnałów sinusoidalnych:

x [n]=sin 2 f

1

nsin 2  f

2

n

Obcięcie sygnału do L-próbek powoduje, że jego widmo ma postać:



X =

1
2

[

W −

1



W −

2



W 

1



W 

2



]

Jeśli:

∣

1

−

2

∣

2 

L

wówczas transformaty funkcji okien W(ω – ω

k

) zachodzą na siebie i oba prążki

zlewają się w jeden.

49 (50)

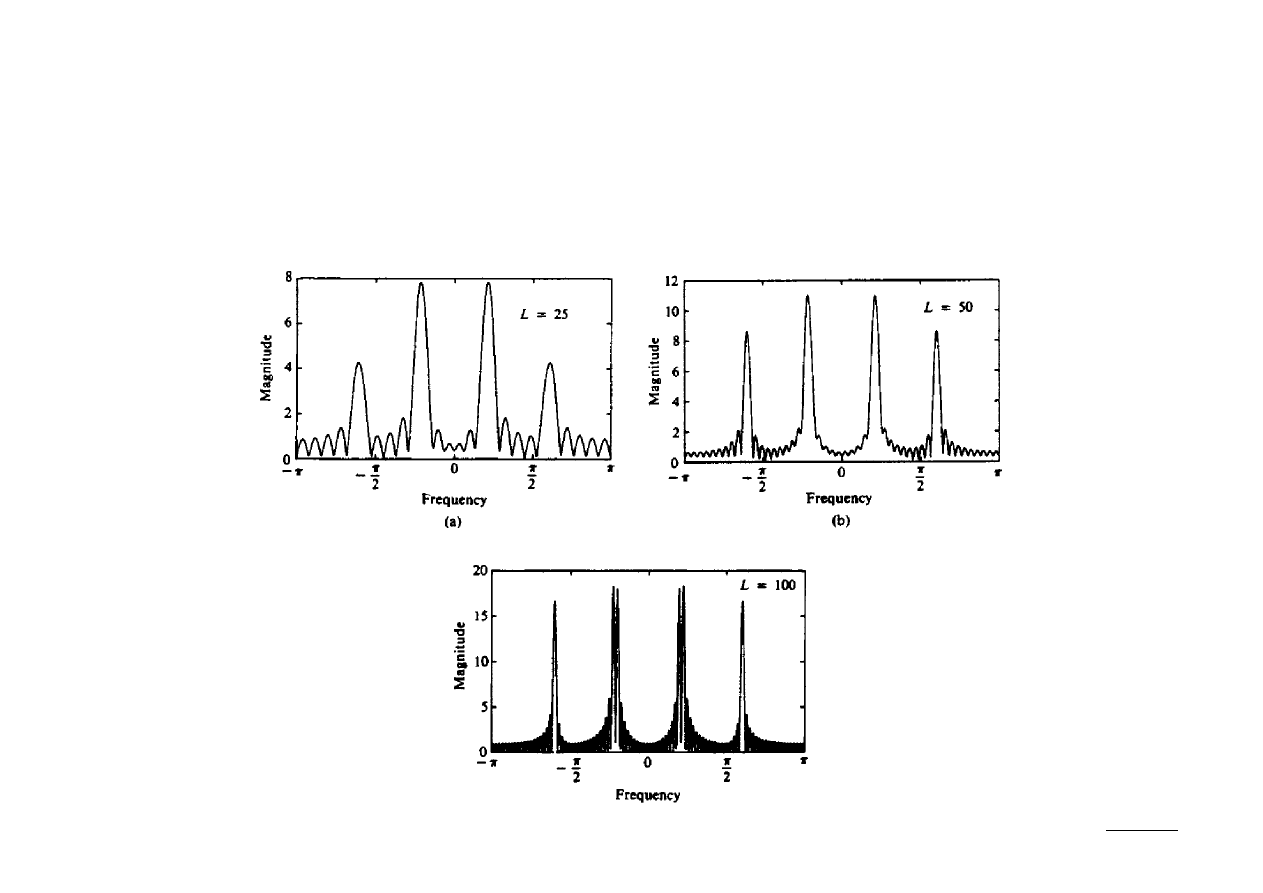
Poniżej przedstawiono wyniki obliczeń widma amplitudowego sygnału:

x [n]=cos0.2  ncos0.22  ncos0.6  n

Długość okna wynosi odpowiednio: L = 25, 50 oraz 100 próbek:

50 (50)