Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (2)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

Sygnały jako elementy przestrzeni funkcyjnych

W celu sformalizowania opisu sygnałów pozwalającego na ich późniejszą analizę

tworzy się matematyczne modele sygnałów (zwane w uproszczeniu sygnałami),

będące funkcjami:

gdzie:

f – jest badanym sygnałem, T – jego dziedziną (zbiorem argumentów), zaś

S - przeciwdziedziną (zbiorem wartości).

f : T  S

Zwykle żąda się, aby S była przestrzenią liniową, tzn., aby zdefiniowane w niej

było dodawanie elementów (wektorów) oraz mnożenie wektorów przez skalar

spełniające następujące warunki:

–

przemienność: x + y = y + x;

–

łączność: (x + y) + z = x + (y + z);

–

element neutralny dodawania: x + 0 = x;

–

rozdzielność mnożenia względem dodawania: a(x + y) = ax + ay;

–

łączność mnożenia przez skalar: a(b(x)) = (ab)x.

Wymagane jest przy tym, aby żadna z powyższych operacji nie wyprowadzała

wyniku poza przestrzeń S.

W teorii sygnałów przestrzenią S jest zwykle przestrzeń Hilberta H.

Traktowanie sygnałów jako elementów przestrzeni liniowej pozwala na formalne

zdefiniowanie miary odległości między sygnałami (przez analogię do euklidesowej

odległości między wektorami w zwykłej przestrzeni wektorowej), która jest

użyteczna do oceny podobieństwa dwóch sygnałów oraz do rozwiązania

problemu aproksymacji danego sygnału. Przez analogię do wektorów, możliwe

staje się także rozwinięcie danego sygnału w bazie sygnałów podstawowych

(kombinacja liniowa sygnałów bazowych w przestrzeni S), co oznacza kompresję

sygnału z nieprzeliczalnego (w ogólności) zbioru jego chwilowych wartości na

skończony lub przynajmniej przeliczalny zbiór współczynników jego rozwinięcia.

Baza przestrzeni liniowej: zbiór niezależnych liniowo elementów {s

k

: k

∈

K}

tej przestrzeni takich, że:

Metryka przestrzeni liniowej: odwzorowanie przyporządkowujące dowolnej

parze elementów x, y

∈

H nieujemną liczbę rzeczywistą

ρ

(x, y) taką, że:

-  x , y =0⇔ x= y ;

-  x , y = y , x ;

-  x , y  y , z  x , z .

Metryka stanowi miarę odległości między elementami danej przestrzeni.

∑

k ∈K



k

⋅

s

k

=

0 ⇔ ∀

k ∈ K



k

=

0

Norma przestrzeni liniowej: odwzorowanie przyporządkowujące danemu

elementowi x

∈

H nieujemną liczbę rzeczywistą x taką, że:

- ∥x∥=0⇔ x=0 ;

- ∥⋅x∥=∣∣⋅∥x∥ ;

- ∥x y∥≤∥x∥∥y∥ .

Norma definiuje 'wielkość' sygnału w przestrzeni H.

Iloczyn skalarny w przestrzeni liniowej: odwzorowanie przyporządkowujące

parze elementów x, y

∈

H liczbę zespoloną (x, y) taką, że:

-  x , y= y , x ;

- ⋅x⋅y , z=⋅ x , z⋅ y , z ;

-  x , x≥0∧ x , x =0⇔ x=0

Zauważmy, że (x, x)

1/2

= x

.

spełnia warunki normy

,

Przez analogię do wektorów w zwykłych przestrzeniach wektorowych iloczyn

, :

skalarny definiuje kąt między sygnałami x y

cos 

xy

=



x , y



x , x⋅ y , y

;

w przestrzeni sygnałów rzeczywistych

cos 

xy

=

ℜ

x , y 



x , x⋅ y , y

.

w przestrzeni sygnałów zespolonych

,

Zauważmy także iż iloczyn skalarny zdefiniowany jako  x , y=

∫

−∞

∞

x t⋅y t dt

,

= :

jest równy funkcji korelacji wzajemnej wektorów x y dla przesunięcia

0



x , y=

∫

−∞

∞

x t⋅y t dt=R

xy



0

,

( , ) = ,

,

W takim przypadku jeśli x y

0 to sygnały x y nazywamy

(

),

( , ) > ,



nieskorelowanymi ortogonalnymi jeśli zaś x y

0 to kąt

xy

jest

.

współczynnikiem korelacji tychże sygnałów

Bazę ortogonalną

{

przestrzeni H stanowi zbiór sygnałów s

k

: k

∈

K} jeżeli są

one wzajemnie ortogonalne (nieskorelowane) oraz nie istnieje w tej przestrzeni

niezerowy wektor x który jest ortogonalny do każdego x

k

z osobna.

Baza ortogonalna unormowana, tzn. s

k

 = {

1 k

∈

}

K nazywana jest bazą

ortonormalną (

jk

–

)

delta Kroneckera :



s

j

, s

k

=

jk

=

{

1⇔ j=k
0⇔ j≠k

}

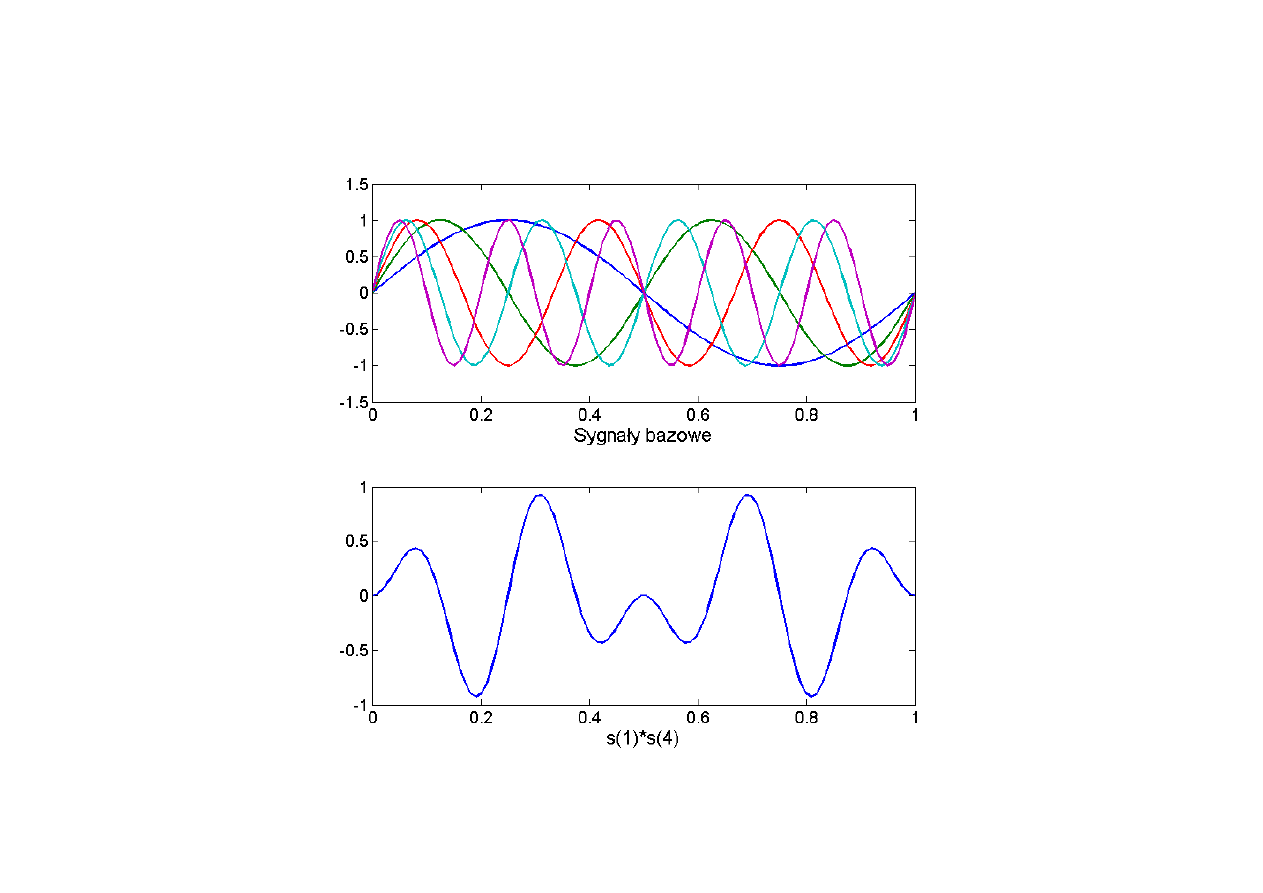
Przykłady baz ortogonalnych

Niech w przestrzeni sygnałów H iloczyn skalarny zdefiniowany będzie

następująco:

Sprawdźmy, że baza sygnałów {s

m

= sin(2mt)} jest bazą ortogonalną:



x , y=

∫

0

1

x t⋅y t dt



s

j

, s

k

=

∫

0

1

sin2 jt ⋅sin 2 ktdt=

1

2

∫

0

1

cos j−k 2t dt

1

2

∫

0

1

cos jk 2t dt=0



s

j

, s

j

=

∫

0

1

sin

2



2 jt dt =

[

1
2

t−

1

8j

sin4 j t

]

0

1

=

1

2

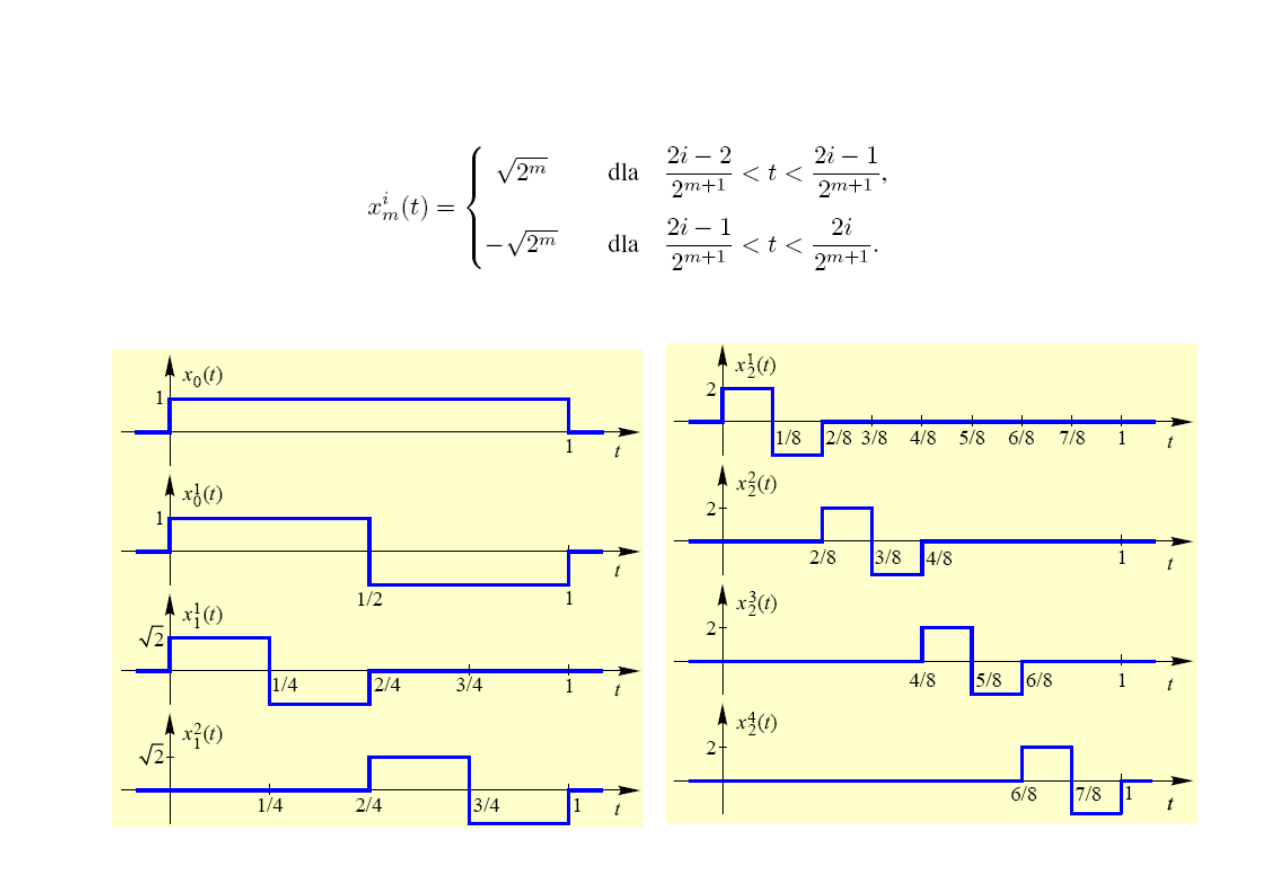
Baza funkcji Haara (ortonormalna)

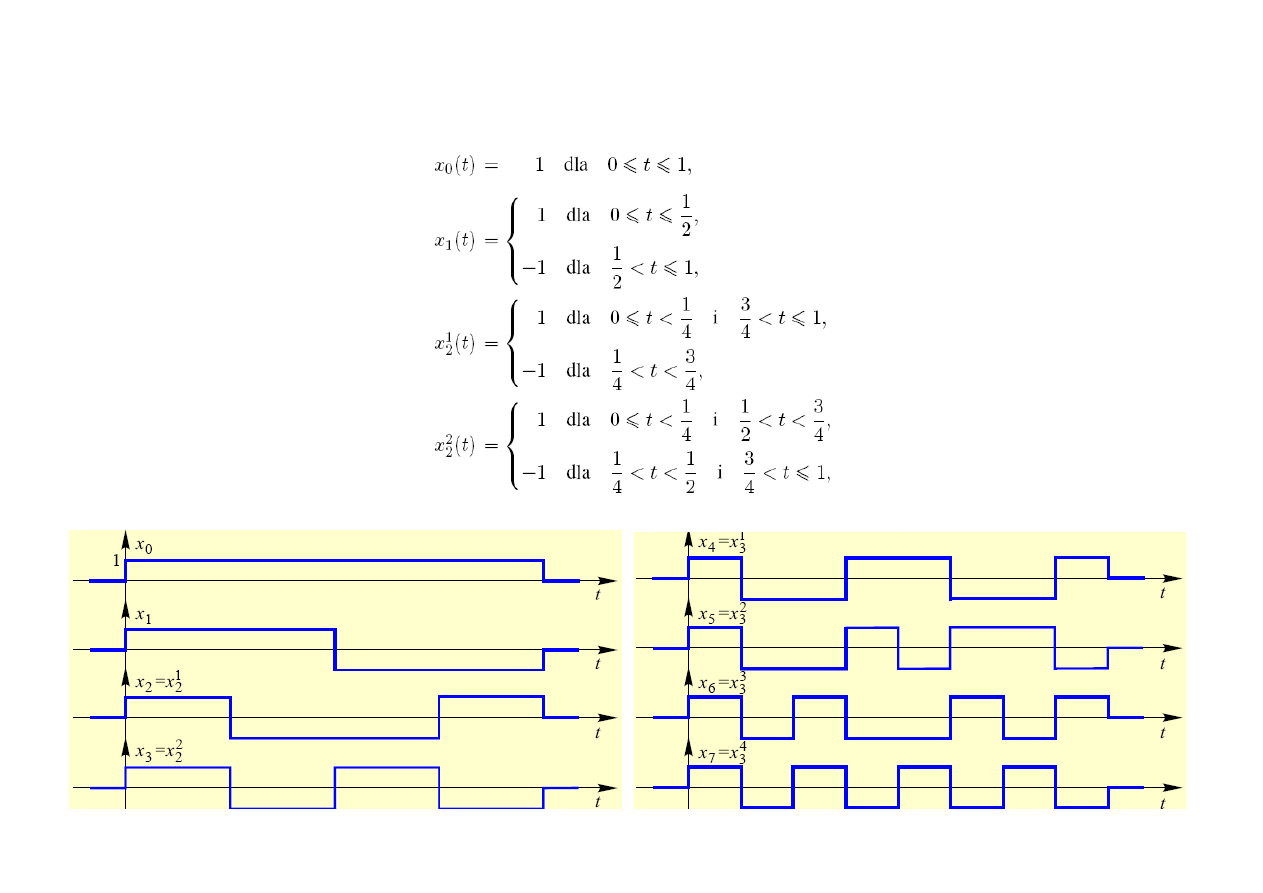
Baza funkcji Walsha (ortonormalna)

Uogólniony szereg Fouriera

Niech {s

k

: k

∈

K}

.

będzie ortonormalną bazą w przestrzeni H Dla zadanego

sygnału x

∈

H szukamy sygnału x

ap

w postaci:

stanowiącego najlepsze przybliżenie sygnału x w tej przestrzeni. Jest to tzw.

zagadnienie aproksymacji liniowej sygnału x, które polega na wyznaczeniu

współczynników {

k

} takich, aby błąd aproksymacji (odległość między sygnałami

x oraz x

ap

) była najmniejsza:

x

ap

=

∑

k ∈K



k

⋅

s

k

∥

x−x

ap

∥=∥

x−

∑

k ∈K



k

⋅

s

k

∥=

min

W celu wyznaczenia współczynników rozwinięcia obliczmy iloczyny skalarne:

Lub macierzowo:

Gdzie G jest macierzą Grama, która w przypadku bazy ortonormalnej jest

macierzą jednostkową. Powyższy układ równań ma nietrywialne rozwiązania

wówczas, gdy wyznacznik macierzy Grama jest niezerowy.



x , s

j

=

∑

k ∈K



k

⋅

s

k

, s

j

=

∑

k ∈K



k

⋅

s

k

, s

j

=

j

G⋅

[



1



2

...

]

=

[



x , s

1





x , s

2



...

]

Twierdzenie o rzucie

W oparciu o twierdzenie o rzucie konstruuje się rozwiązanie zagadnienia

najlepszej aproksymacji wektora x w bazie {s

k

}.

Twierdzenie o rzucie mówi, że błąd aproksymacji  -

x x

ap



,

osiąga minimum gdy

współczynniki rozwinięcia danego wektora w bazie są równe współczynnikom

uogólnionego szeregu Fouriera:

,

Z twierdzenia tego wynika ponadto iż sygnał błędu aproksymacji jest

{

ortogonalny do każdego elementu bazy s

k

} (

i

vice versa

).

x=

∑

k ∈K



k

⋅

s

k

=

∑

k ∈K



x , s

k

⋅

s

k

Twierdzenie Parsevala

Norma sygnału przedstawionego w postaci uogólnionego szeregu Fouriera jest

równa sumie kwadratów modułów współczynników rozwinięcia tego sygnału

w

{

bazie ortonormalnej s

k

}:

∥

x∥= x , x=

∑

k ∈K



k

⋅

s

k

, x=

∑

k ∈K



k

⋅

s

k

, x =

∑

k ∈K



k

⋅

k

=

∑

k ∈K

∣

k

∣

2

–

Aproksymacja sygnałów

przykłady

( ) = { , ∈ [ , . ); - , ∈ [ . , )},

Dany jest sygnał x t

1 t

0 0 5

1 t

0 5 1

który należy

{

rozwinąć w bazie s

k

( ) =

(

 ), = , , }.

t

sin 2k t k

1 2 3 Iloczyn skalarny

.

zdefiniowany jak wyżej

: (

Poszukiwane współczynniki macierzy Grama s

k

,

s

k

) = . ; (

0 5 s

j

,

s

k

) = .

0

Zatem G = . *

0 5 .

I

{

Współczynniki rozwinięcia

k

}:

:

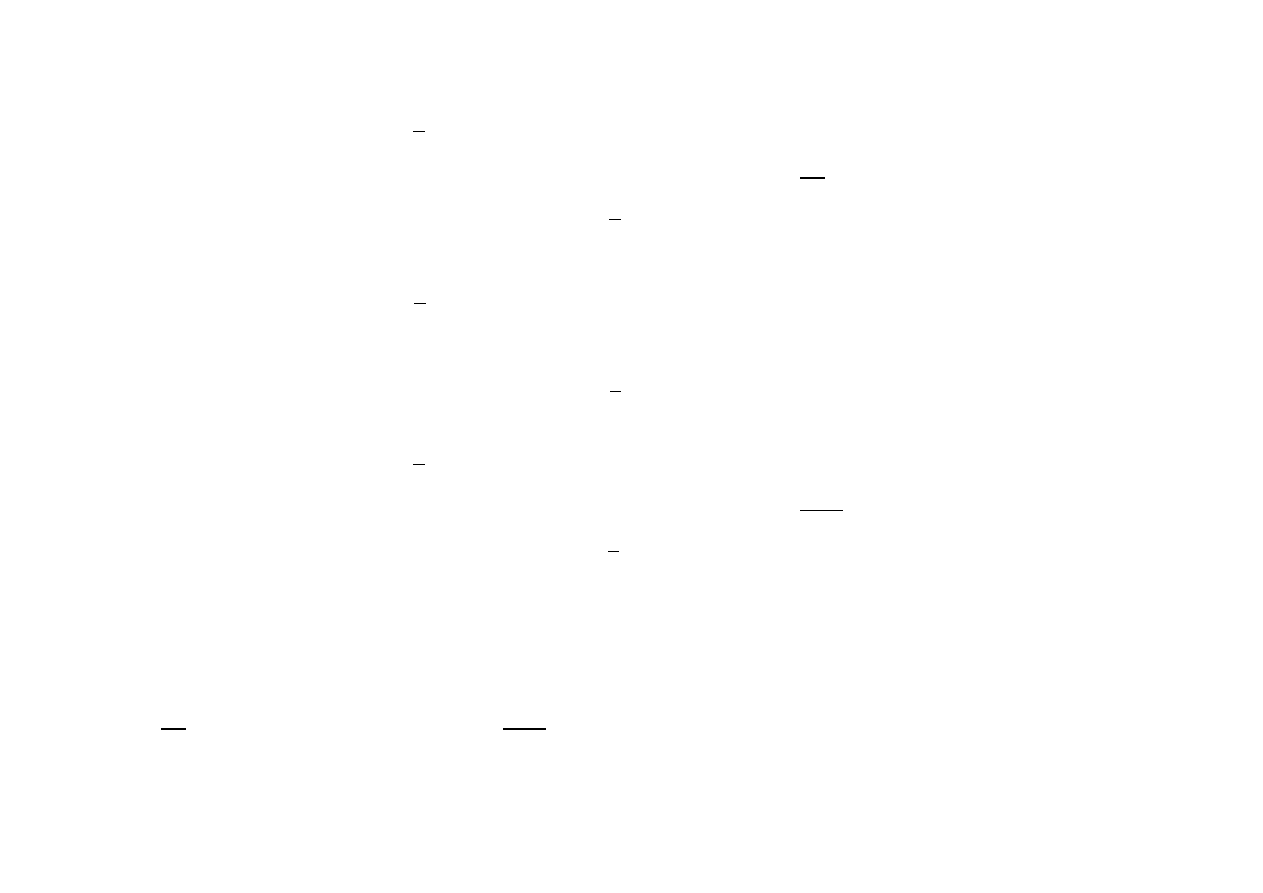
Zatem



x , s

1

=

∫

0

1

x t⋅s

1



T dt=

∫

0

1
2

sin2 t dt−

∫

1
2

1

sin2t dt=

2





x , s

2

=

∫

0

1

x t ⋅s

2



T dt =

∫

0

1

2

sin4t dt−

∫

1
2

1

sin4t dt=0



x , s

3

=

∫

0

1

x t ⋅s

3



T  dt=

∫

0

1
2

sin6 t dt−

∫

1

2

1

sin6 t dt=

2

3

x

ap

=

2



⋅

sin2 t0⋅sin 4 t 

2

3

⋅

sin 6 t 

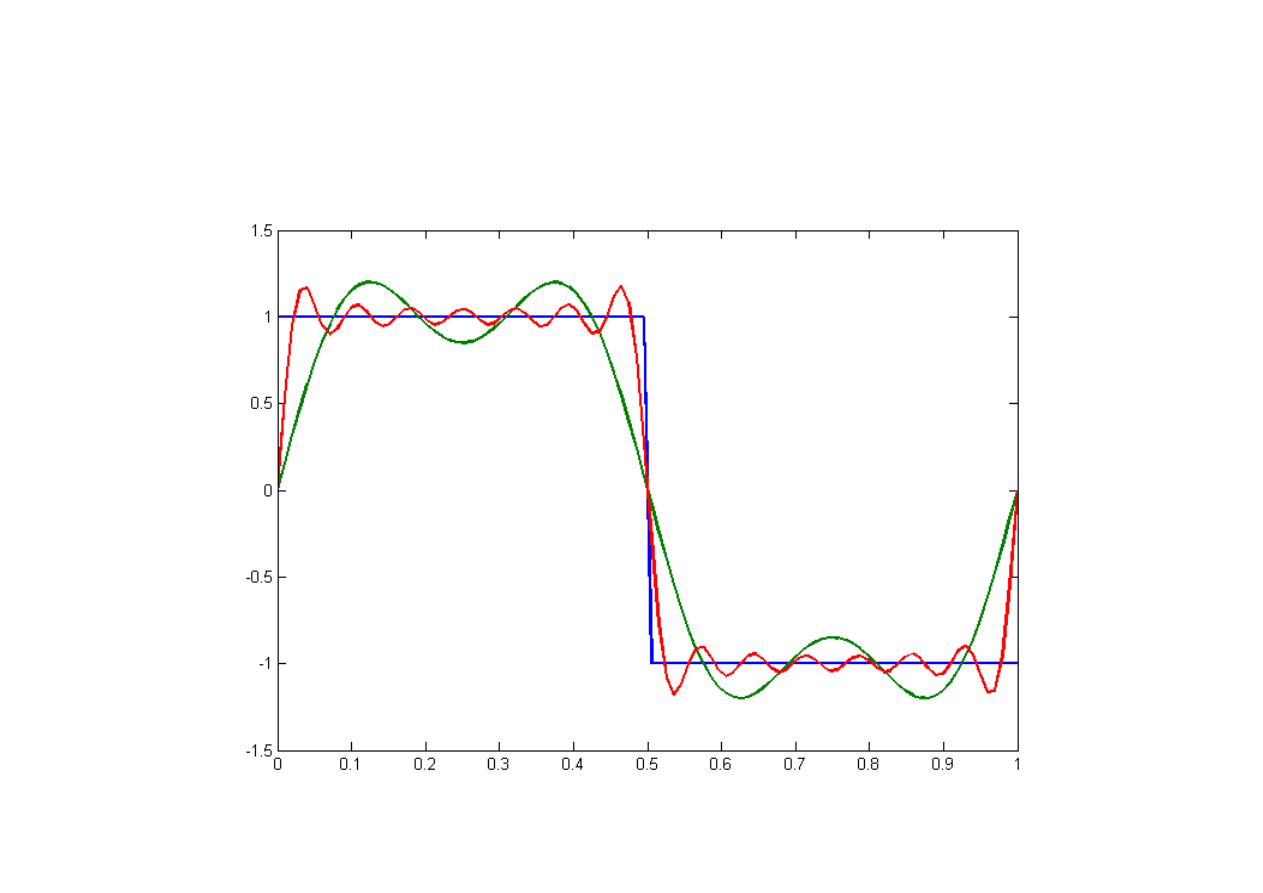
Wyniki aproksymacji

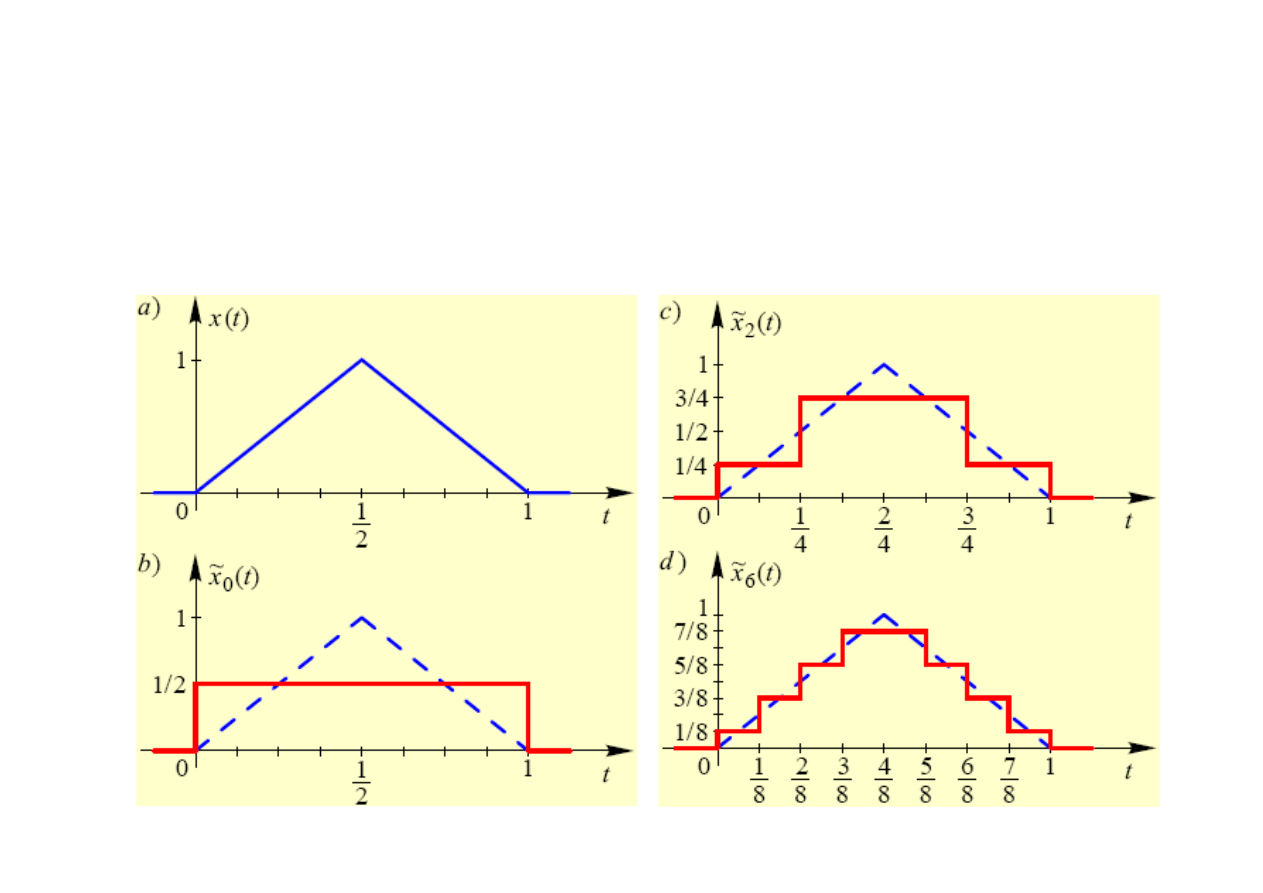
Aproksymacja impulsu trójkątnego w bazie funkcji Walsha

:

Współczynniki rozwinięcia

( ,

x s

0

) = . ; ( ,

0 5 x s

1

) = ; ( ,

0 x s

2

) = - .

; ( ,

0 25 x s

3

) =

.

0 itd

Analiza widmowa sygnałów

∈

Sygnały są funkcjami przyporządkowującymi chwilom czasu t R określone

(

).

wartości liczby Z tego punktu widzenia sygnały można analizować pod

,

,

.

kątem ich zmian czasowych kształtu ciągłości itd Metody analizy sygnałów

w

dziedzinie czasu są więc określane

metodami czasowymi.

Alternatywną dziedziną opisu i analizy sygnałów jest dziedzina ich

,

częstotliwości która polega na wydzielaniu z badanego sygnału sygnałów

,

prostszych i badaniu ich wkładu co określa się mianem analizy

(

)

częstotliwościowej widmowej .

,

,

Istotne jest iż obie dziedziny opisu są sobie równoważne zaś relacje między

nimi zdefiniowane są przy pomocy

przekształcenia Fouriera.

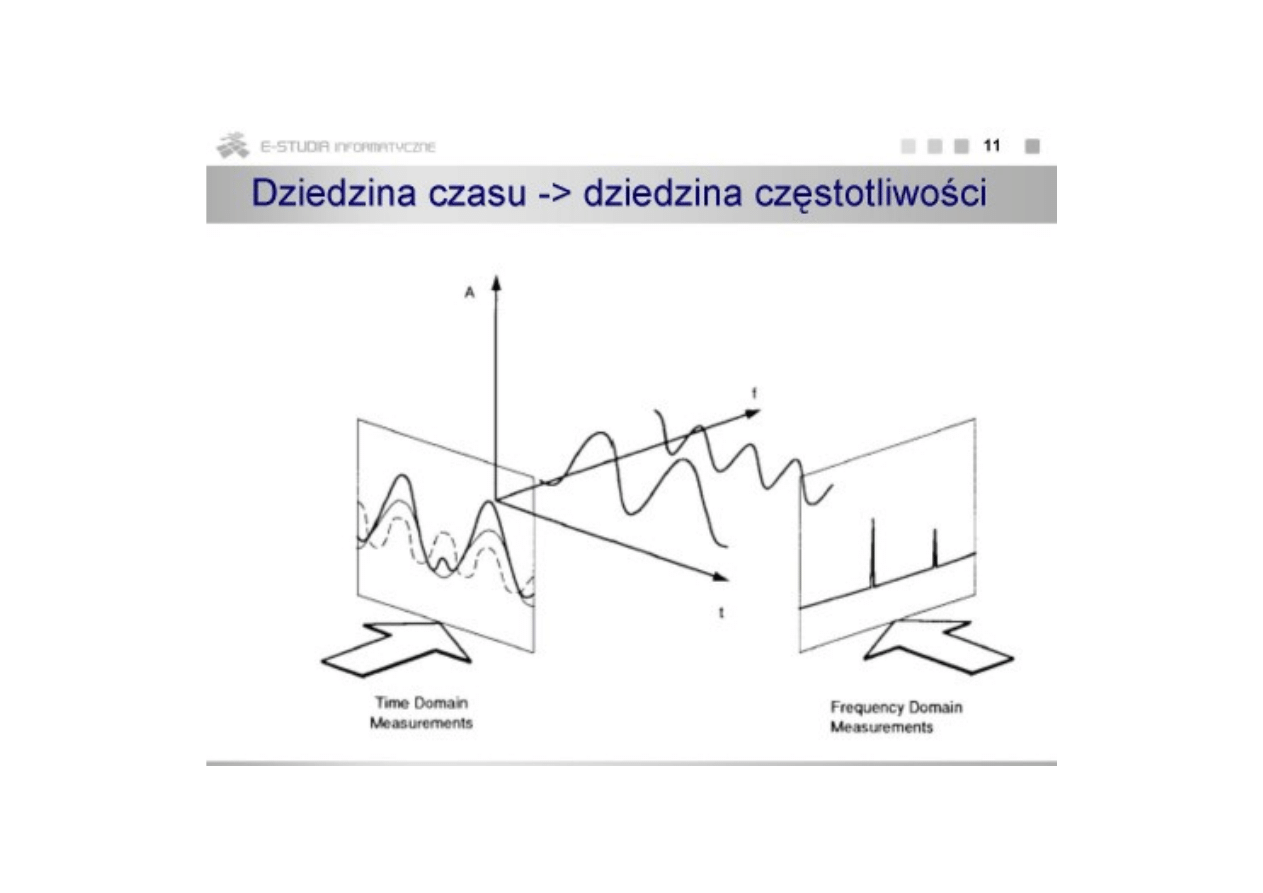
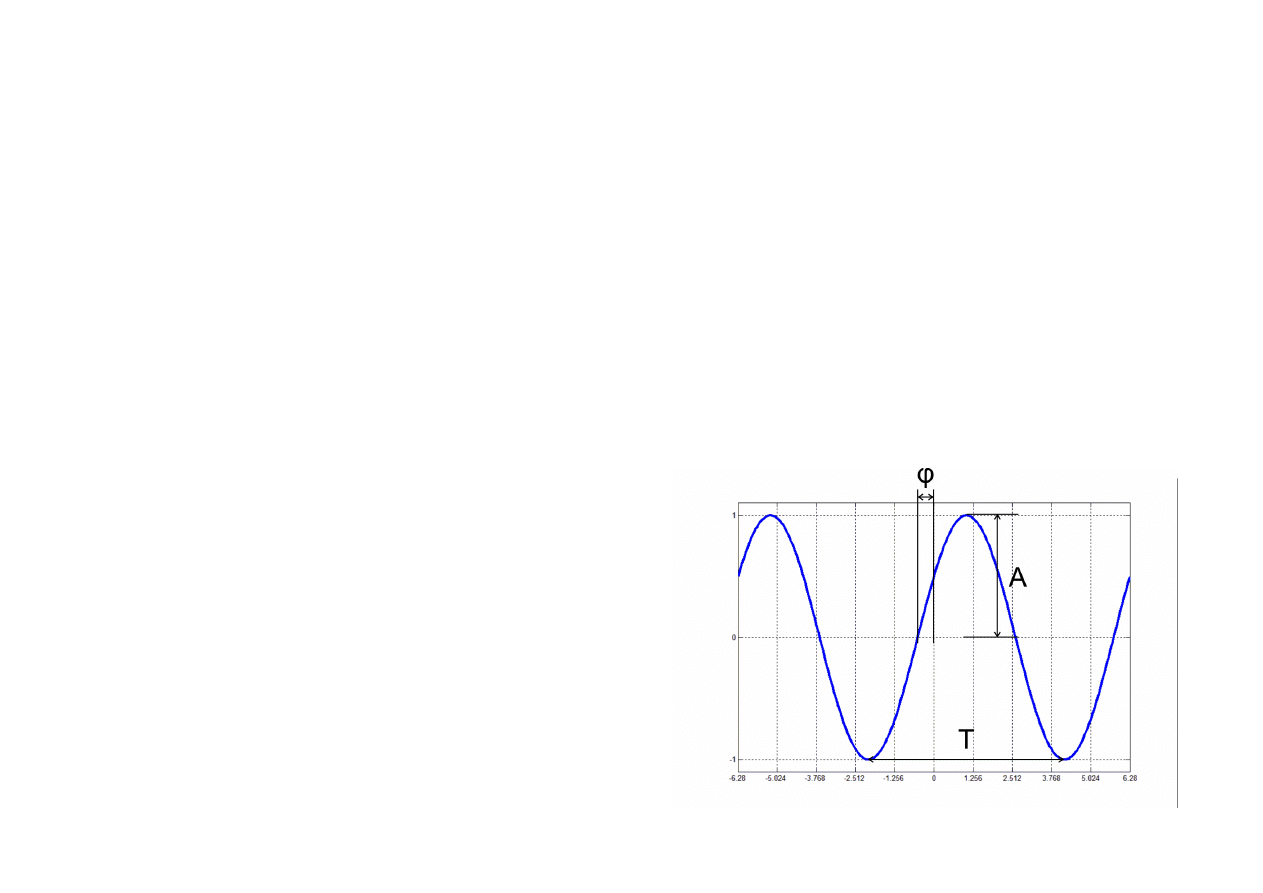
Analiza widmowa sygnałów okresowych czasu ciągłego

( ) : 

,

Sygnał s t

R

S jest sygnałem okresowym wtedy gdy ∀

t∈R

stT =st 

,

=

gdzie T jest okresem sygnału zaś f

T

-

1

–

.

jego częstotliwością Sygnał taki

.

jest sygnałem nieskończonym

.

Sygnałem okresowym jest np

sygnał sinusoidalny:

( ) =

s t

A·

(

sin ω +

t φ)

Twierdzenie o rzucie

W oparciu o twierdzenie o rzucie konstruuje się rozwiązanie zagadnienia

najlepszej aproksymacji wektora x w bazie {s

k

}.

Twierdzenie o rzucie mówi, że błąd aproksymacji  -

x x

ap



,

osiąga minimum gdy

współczynniki rozwinięcia danego wektora w bazie są równe współczynnikom

uogólnionego szeregu Fouriera:

,

Z twierdzenia tego wynika ponadto iż sygnał błędu aproksymacji jest

{

ortogonalny do każdego elementu bazy s

k

} (

i

vice versa

).

x=

∑

k ∈K



k

⋅

s

k

=

∑

k ∈K



x , s

k

⋅

s

k

:

Zwykle wygodniej jest posługiwać się sygnałami w postaci zespolonej

s(t) = A·e

j(ω +

t φ)

= A·[cos(ω +

t φ)+j·

(

sin ω +

t φ)] = A(φ)·e

jωt

:

gdzie A(φ) jest amplitudą zespoloną sygnału.

W celu analizy, sygnał okresowy s(t) rozwija się w trygonometryczny szereg

Fouriera s

F

(t):

s

F



t =

1
2

⋅

C

0



∑

k=1

∞



C

k

⋅

cosk⋅⋅tS

k

⋅

sink⋅⋅t



;=

2

T

Na gruncie uogólnionego szeregu Fouriera, funkcje cos (parzyste) oraz sin

(nieparzyste) w powyższym przykładzie łącznie z funkcją stałą tworzą bazę

ortogonalną przestrzeni sygnałów, zatem współczynniki C

k

oraz S

k

wyznacza się

następująco:

C

0

=

2

T

∫

t

0

t

0



T

stdt

C

k

=

2
T

∫

t

0

t

0



T

st ⋅cosk⋅⋅t dt

S

k

=

2

T

∫

t

0

t

0



T

st ⋅sink⋅⋅t dt

W przypadku gdy s(t) = s

F

(t), mówimy, że sygnał s(t) daje się rozwinąć

w trygonometryczny szereg Fouriera.

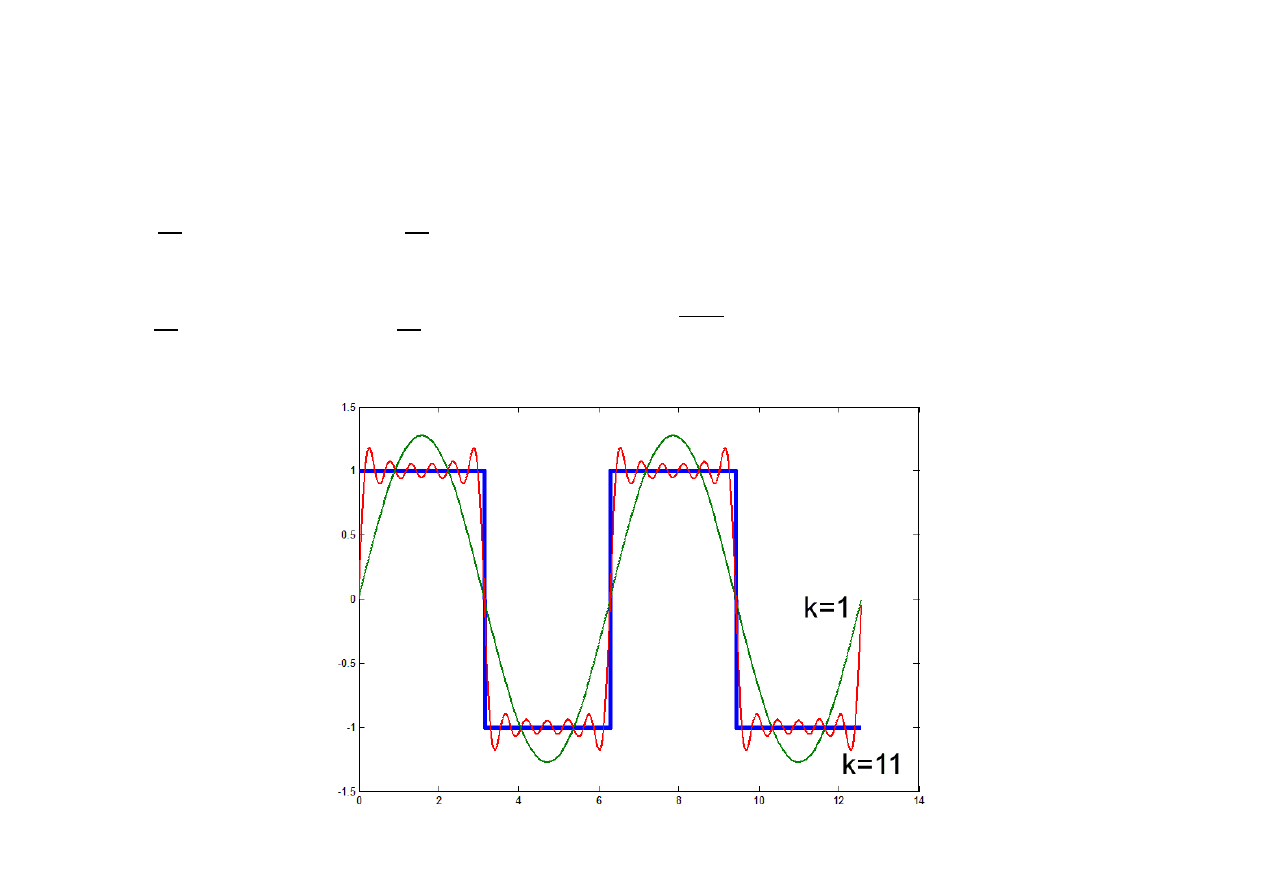
Przykład 1:

Rozwinąć w szereg Fouriera falę prostokątną o amplitudzie jednostkowej.

C

k

=

2
T

∫

0



cosk⋅⋅t dt−

2

T

∫



2



cosk⋅⋅t dt=0

S

k

=

2

T

∫

0



sin k⋅⋅t dt−

2

T

∫



2



sink⋅⋅t dt=

{

4
k 

, k −nieparzyste

0, k − parzyste

}

Rozwinięcie trygonometryczne na funkcje parzyste i nieparzyste równoważne jest

rozwinięciu na funkcje jednego tylko typu, za to przesunięte w fazie o kąt φ

k

:

C

k

⋅

cosk⋅⋅tS

k

⋅

sin k⋅⋅t =A

k

⋅

cosk⋅⋅t

k



gdzie: A

k

=



C

k

2



S

k

2

; 

k

=−

arc tg



S

k

C

k



Wyrazy A

k

·cos(kΩt) nazywa się składowymi harmonicznymi, przy czym dla k=1

mamy składową podstawową, zaś wyraz ½A

0

wyznacza składową stałą.

Wówczas trygonometryczny szereg Fouriera przyjmuje postać:

st =

1
2

C

0



∑

k =1

∞

A

k

⋅

cosk⋅⋅t

k



Dalsze uproszczenie rachunków możliwe jest dzięki zastosowaniu liczb

zespolonych. Zauważmy, że:

cos=

1

2



e

j⋅



e

−

j⋅



Wówczas:

s

F



t =

1
2

A

0



1
2

∑

k =1

∞



A

k

⋅

e

j k t



A

−

k

⋅

e

−

j k t



; A

k

=

A

k

⋅

e

j⋅

k

Ostatecznie:

st =

1
2

∑

k =−∞

∞

A

k

⋅

e

j k  t

Otrzymaliśmy w ten sposób zespolony szereg Fouriera (rozwinięcie ciągłego

w czasie sygnału okresowego na sumę nieskończonej ilości harmonicznych).

Współczynnik A

k

jest amplitudą zespoloną k-tej harmonicznej, zaś ciąg wartości

rzeczywistych {|A

k

|} tworzy widmo amplitudowe sygnału, podczas gdy ciąg {φ

k

} – widmo

fazowe.

Można pokazać, że A

k

= C

k

– jS

k

, a więc:

A

k

=

2

T

∫

t

0

t

0



T

st ⋅e

−

j⋅k⋅⋅t

dt

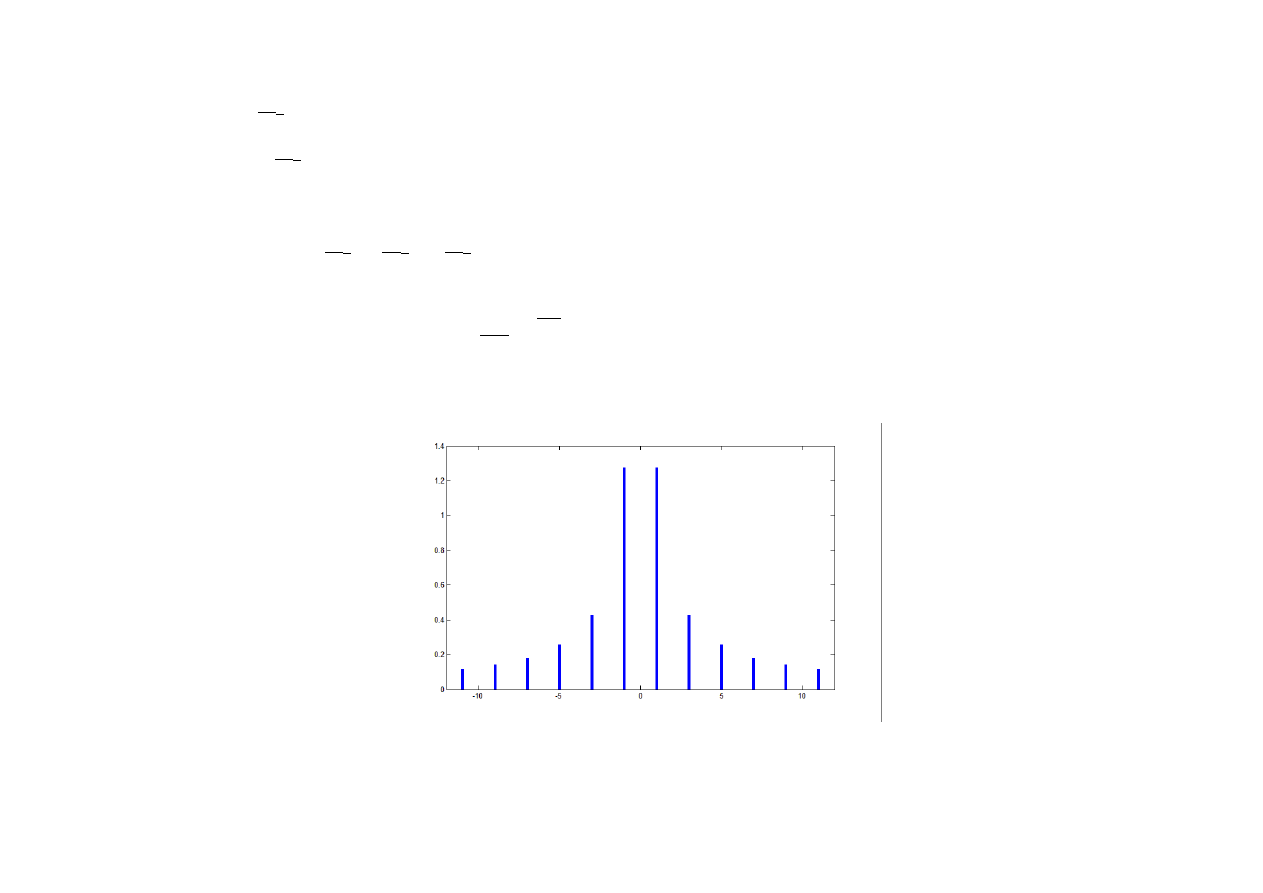
Widmo amplitudowe fali prostokątnej z wcześniejszego przykładu:

Prążek o numerze k odpowiada tutaj składowej o częstotliwości k/T.

Analiza częstotliwościowa sygnałów nieciągłych – efekt Gibbsa

W przypadku, gdy analizowany sygnał posiada punkty nieciągłości (np. zbocza fali
prostokątnej), wówczas jego aproksymacja przy pomocy funkcji ciągłych
(np. sinus) objawia się powstaniem silnych oscylacji sygnału aproksymującego
w punktach nieciągłości – efekt Gibbsa.

Analiza częstotliwościowa sygnałów nieokresowych czasu ciągłego

Częstotliwościowe metody analizy sygnałów ciągłych x(t) oparte są na całkowych

przekształceniach Fouriera zdefiniowanych parą transformat:

proste przekształcenie Fouriera

odwrotne przekształcenie Fouriera

Przekształcenia Fouriera wzajemnie jednoznacznie odwzorowują sygnał x(t) na

funkcję amplitudy zespolonej X() zależną od rzeczywistych wartości pulsacji.

Wzajemną jednoznaczność transformat Fouriera prostej ℱ i odwrotnej ℱ

-

1

zapisuje się jako:

x(t) ↔ X()

X =

∫

−∞

∞

x te

−

j t

dt

x t =

1

2

∫

−∞

∞

X e

j t

d 

Przykład 2: Wyznaczyć widmo amplitudowe sygnału x(t) = exp(-0.5*t), t≥0.

Proste przekształcenie Fouriera prowadzi do wyrażenia:

X =

∫

0

∞

e

−

1

2

t

e

−

j t

dt=

∫

0

∞

e

−

1
2



j t

dt =−

1

1
2



j 

e

−

1
2



j  t

0

∞

=

1

1
2



j 

Na poniższych rysunkach przedstawiono przebieg sygnału x(t) oraz jego

transformaty (widma) X():

Własności całkowych transformat Fouriera

–

Transformaty X() sygnałów rzeczywistych x(t) są hermitowskie: X() = X(-)

*

,

co oznacza, że widma amplitudowe są funkcjami parzystymi, zaś widma fazowe

– nieparzystymi.

–

Transformaty zachowują liniowość: ax(t) + by(t) ↔ aX() + bY().

–

Transformaty są symetryczne: x(t) ↔ X() ⇒ X(t) ↔ 2x(-).

–

Transformaty są skalowalne: x(t/a) ↔ aX(a), a∈R

+

- nieoznaczoność.

–

Transformata splotu w dziedzinie czasu odpowiada mnożeniu widm:

x(t)⊗y(t) ↔ X()*Y() - filtracja.

–

Transformata splotu w dziedzinie częstotliwości odpowiada mnożeniu

sygnałów: x(t)*y(t) ↔ [

2 X()⊗Y()] - próbkowanie.

–

Transformata ciągłego sygnału okresowego jest równa jego rozwinięciu

na zespolony szereg Fouriera.

Zasada nieoznaczoności w teorii sygnałów

Z własności skalowalności transformat Fouriera wynikało, iż rozciągnięcie sygnału

w jednej dziedzinie skutkowało jego zwężeniem w drugiej. Formalną zależność

liczbową tej obserwacji nadaje zasada nieoznaczoności.

Zdefiniujmy równoważny czas trwania sygnału t oraz równoważną szerokość

widma :



t=

∫

−∞

∞

x t dt

x 0

; =

∫

−∞

∞

X d 

X 0

:

Wówczas iloczyn



t⋅ =2⋅

jest wartością stałą, co oznacza m.in., że wymagania dotyczące zwiększania

szybkości transmisji sygnałów (krótkie impulsy) oraz zwiększania pojemności

kanałów transmisji (wąskie widma) są wzajemnie sprzeczne.