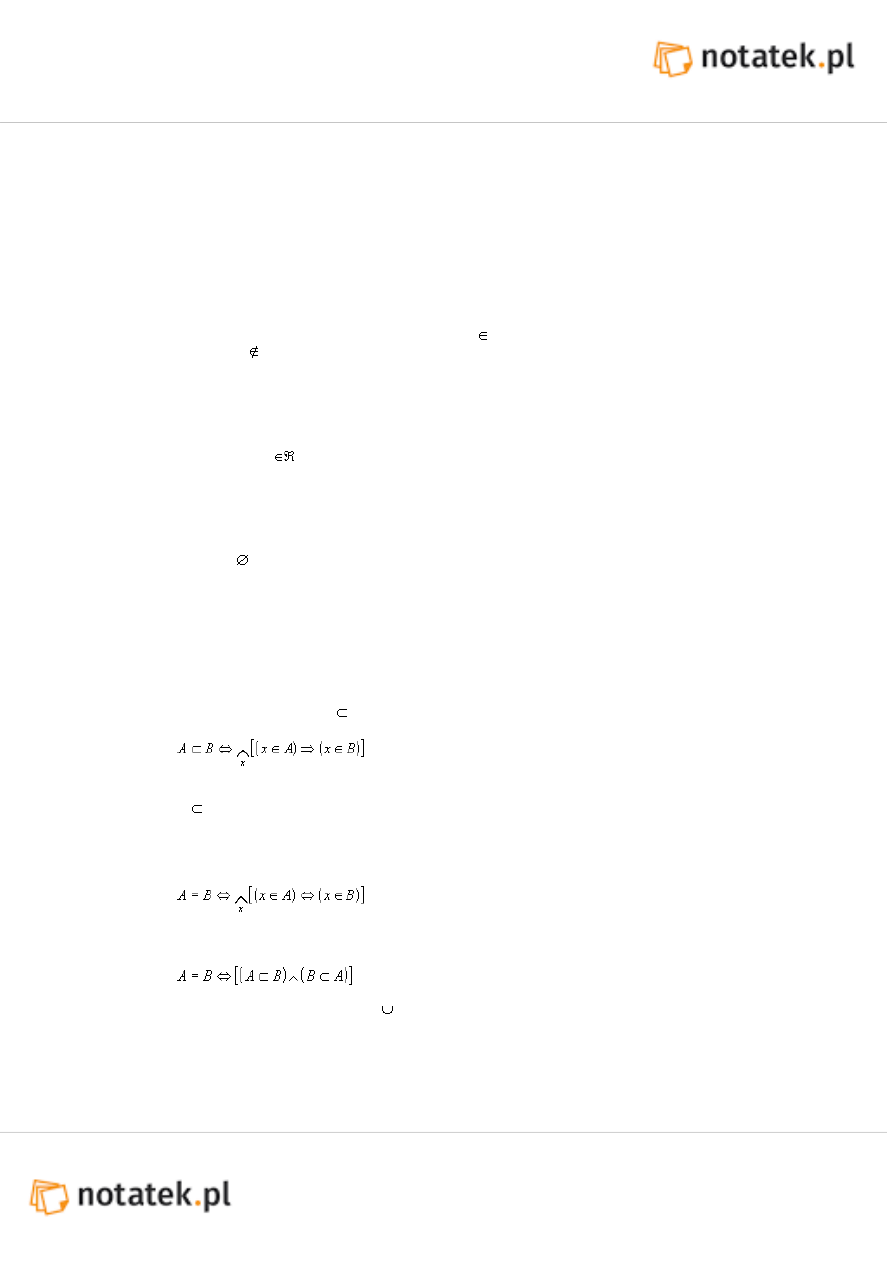
Algebra zbiorów. Iloczyn kartezjański zbiorów.

Jednym z pojęć pierwotnych matematyki jest pojęcie zbioru.

Dużymi literami alfabetu oznaczamy zbiory, małymi ich elementy, czyli przedmioty należące
do zbioru.

Jeżeli element a należy do zbioru A, to zapiszemy a A, jeżeli a nie jest elementem zbioru A,
to piszemy a A.

Zbiory są opisywane jednym z dwóch sposobów:

a. poprzez wymienienie wszystkich elementów zbioru np.: A={1,3,7}, lub
b. opisanie własności, którą posiadają wszystkie elementy tego zbioru i tylko one

np.:B={x

:2

≤

x

≤

5}.

Jeżeli wszystkimi elementami zbioru są a

1

, a

2

,..., a

n

, to taki zbiór nazywamy zbiorem

skończonym, i oznaczamy symbolem {a

1

,a

2

,..., a

n

}.

Jeżeli do zbioru nie należy żaden element, to zbiór nazywamy zbiorem pustym, i oznaczamy
symbolem .

Natomiast zbiór, który nie jest skończony i nie jest pusty, nazywamy zbiorem
nieskończonym.

Zatem zbiorem nieskończonym, jest na przykład zbiór liczb naturalnych czy zbiór liczb
całkowitych.

Definicja: Jeżeli każdy element zbioru A, jest elementem zbioru B, to mówimy, że zbiór A
zawiera się w zbiorze B. (A B).

Np.:dla dwóch zbiorów A={1,3,5,7} i B={0,1,2,3,4,5,6,7,8} zbiór A zawiera się w zbiorze B
(A B lub inaczej zbiór A jest podzbiorem zbioru B).

Definicja: Mówimy, że zbiór A jest równy zbiorowi B (A=B),jeżeli każdy element zbioru A
jest elementem zbioru B i każdy element zbioru B jest elementem zbioru A.

Możemy zauważyć, że

Definicja: Sumą zbiorów A i B (A B) nazywamy zbiór tych elementów, które należą do
zbioru A lub bo zbioru B.

Przykład: niech będą dane zbiory: A={3,5,8,12,23} i B={2,4,5,8,9,13,23} wówczas

A B={2,3,4,5,8,9,12,13,23}.

Definicja: Iloczynem (częścią wspólną zbiorów A i B (A B) nazywamy zbiór tych
elementów, które należą do zbioru A i do zbioru B.

Przykład: Niech będą dane zbiory

A={15, 18, 40, 43} i B={10, 11, 18, 20, 40, 52}

to A B={18, 40}.

Definicja: Różnicą zbiorów A i B (A\B) nazywamy zbiór tych elementów, które należą do
zbioru A i nie należą do zbioru B.

Przykład: Dane są zbiory: A={-4, -2, 0, 5, 8, 10, 13}

B={-1, 0, 7, 12, 13, 18}

To A\B={-4, -2, 5, 8, 10}

Definicja: Zbiory A i B nazywamy zbiorami rozłącznymi, gdy ich iloczyn jest zbiorem
pustym (to znaczy nie mają ani jednego wspólnego elementu).

Wszystkie rozważane zbiory należą do pewnego ustalonego zbioru X. Zbiór ten nazywamy
przestrzenią.

Definicja: Dopełnieniem

zbioru A do przestrzeni X nazywamy zbiór X\A.

Przykład: Jeżeli traktujemy zbiór liczb rzeczywistych jako przestrzeń, to dopełnieniem
zbioru liczb dodatnich jest zbiór liczb rzeczywistych niedodatnich.

Niektóre prawa algebry zbiorów

Prawa przemienności

a)

b)

Prawa łączności

c)

d)

Prawa rozdzielności

e)

f)

Prawa tautologii

g)

h)

i)

j)

Prawa de Morgana:

k)

l)

Iloczyn kartezjański zbiorów

Rozważmy teraz zbiór dwuelementowy {a, b} gdzie a

≠

b.

Z określenia równości zbiorów wynika, że {a, b}={b, a}

Jeśli jednak jeden z elementów tego zbioru np. a uznamy za pierwszy element, a b za drugi, to
otrzymamy parę uporządkowaną (a, b)

a – pierwszy element pary nazywamy poprzednikiem

b – drugi element – następnikiem.

Definicja: Iloczynem kartezjańskim zbiorów A i B

nazywamy zbiór wszystkich par

uporządkowanych (a, b) takich, że

.

http://notatek.pl/algebra-zbiorow-iloczyn-kartezjanski-zbiorow?notatka