przygotowa la Joanna Grabowska na podstawie Szyma´

nski, Dr´

obka “Ma-

tematyka w szkole ´sredniej. Powt´orzenie i zbi´or zada´

n” oraz Leksi´

nski, Na-

bia lek, ˙Zakowski “Matematyka, definicje, twierdzenia, przyk lady, zadania”

1

Badanie przebiegu zmienno´

sci funckji

1.1

Algorytm badania wykresu funkcji

1) Wyznaczamy dziedzine funkcji f;
2) wyznaczamy granice funkcji na ko´

ncach przedzia l´

ow, z kt´

orych sk lada sie

dziedzina;
3) znajdujemy miejsca zerowe funkcji f i punkt, w kt´

orym wykres przecina

o´s y;
4) wyznaczamy pochodna funkcji f i znajdujemy miejsca zerowe pochodnej;
5) znajdujemy przedzia ly monotoniczno´sci funkcji i jej ekstrema (je´sli ist-
nieja);
6) badamy, czy istnieja asymptoty wykresu funkcji i znajdujemy ich r´

onania;

7) wykorzystujac dane zebrane w pkt 1-6 budujemy tabele zmienno´sci i szki-
cujemy wykresy funkcji f

1.2

Asymptoty wykresu funkcji

Je´sli funkcja f jest okre´slona w przedziale (α, +∞) i istnieje sko´nczone gra-
nica lim

x→

+

f (x) = b, to prosta o r´

ownianiu y = b nazywamy asymp-

tota pozioma wykresu funkcji f w plus niesko´

nczono´sci.

Podobnie je´sli

funkcja f jest okre´slona w przedzxiale (−∞, α) i istnieje sko´nczona gra-
nica lim

x→−

f (x) = b to prosta o r´

ownaniu y = b nazywamy asymptota

pozioma funkcji f w minus niesko´

nczono´sci. Je´sli prosta o r´

ownaniu y = b

jest asymptota pozioma wykresu funkcji f zar´owno w plus, jak i w minus
nieko´

nczono´sci, to nazywamy ja asymptota pozioma obustronna. Je´sli pro-

sta o r´

ownaniu y = b jest asymptota pionowa wykresu funkcji f, to wykres

funkcji zbili˙za sie do tej prostej, gdy x da˙zy do niesko´

nczono´sci.

Je´sli funkcja f jest okre´slona w przedziale (α, +∞) i istnieje sko´nczone

granica lim

x→a

+

f (x) = b, lub lim

x→a

+

f (x) = −∞ to prosta o r´ownianiu

x = a nazywamy asymptota prawostronna pionowa wykresu funkcji f w plus
niesko´

nczono´sci. Podobnie okre´slamy asymptote lewostronna. Je´sli prosta

jest jednocze´snie asymptota pionowaprawo i lewostronnato jest asymptota
pionowa obustronna.

1.3

Monotoniczno´

s´

c funkcji

Je´sli funkcja f jest okre´slona i r´

o˙zniczkowalna w przedziale (a,b) i przy tym

jest funkcja rosnaca w tym przedziale, to jej pochodna f’ jest w ka˙zdym

1

punkcie przedzia lu (a,b) nieujemna.

Je´sli funkcja f jest okre´slona i r´

o˙zniczkowalna w przedziale (a,b) i przy

tym jest funkcja malejaca w tym przedziale, to jej pochodna f’ jest w ka˙zdym
punkcie przedzia lu (a,b) niedodatnia.

Je´sli funkcja f jest okre´slona i r´

o˙zniczkowalna w przedziale (a,b), a jej

pochodna f’ przyjmuje co najwy˙zej sko´

nczonej liczbie punkt´

ow przedzia lu

warto´s´c zero, a we wszystkich pozosta lych punktach przedzia lu jest dodat-
nia, to funkcja f jest w przedziale (a,b) rosnaca.

Je´sli funkcja f jest okre´slona i r´

o˙zniczkowalna w przedziale (a,b), a jej

pochodna f’ przyjmuje co najwy˙zej sko´

nczonej liczbie punkt´

ow przedzia lu

warto´s´c zero, a we wszystkich pozosta lych punktach przedzia lu jest ujemna,
to funkcja f jest w przedziale (a,b) malejaca.

1.4

Ekstremum funkcji

Za l´

o˙zmy, ˙ze funkcja f jest okre´slona w przedziale (a, b) i x

0

∈ (a, b). M´owimy,

˙ze funkcja f osiaga w punkcie x

0

maksimum, je´sli istnieje taki przedzia l

(a

1

, b

)

⊂ (a, b) o ´srodku w punkcie x

0

to dla ka˙zdego x ∈ (a

1

, b

)

ix 6= x

0

za-

chodzi nier´owno´s´c f (x) < f (x

0

). Analogicznie okre´slamy minimum funkcji.

Ekstrema funkcji to minimum lub maksimum funkcji.

2

Przyk lad badania zmienno´

sci funkcji

2.1

Zadanie 1

Zbadamy przebieg zmienno´scio funkcji f okre´slanej wzorem f (x) =

x

3

+4

x

2

1) df = (−∞, 0) i (0, +∞) 2) lim

x→

+∞

(

x

3

+4

x

2

) = lim

x→

+∞

(x+

4

x

2

) = +∞

lim

x→−∞

(

x

3

+4

x

2

) = −∞

lim

x→

0

+

(

x

3

+4

x

2

) lim

x→

0

−

(

x

3

+4

x

2

) = lim

x→

+∞

(x +

4

x

2

) = +∞

3) f (x) = 0 ⇔ x

3

+ 4 = 0 i X

2

6= 0 ⇔ x = −

√

3

4, a poniewa˙z 0 /

∈ Df,

wiec wykres funkcji nei przecina osi y;

4) f

′

(x) =

(x

3

+4)

′

x

2

−

(x

3

+4)(x

2

)

′

x

4

=

x

4

−

8x

x

4

f

′

(x) = 0 ⇔ x

4

− 8x = 0 i x

4

6= 0 ⇔ x = 2

5) przedzia ly monotoniczno´sci funkcji f:

2

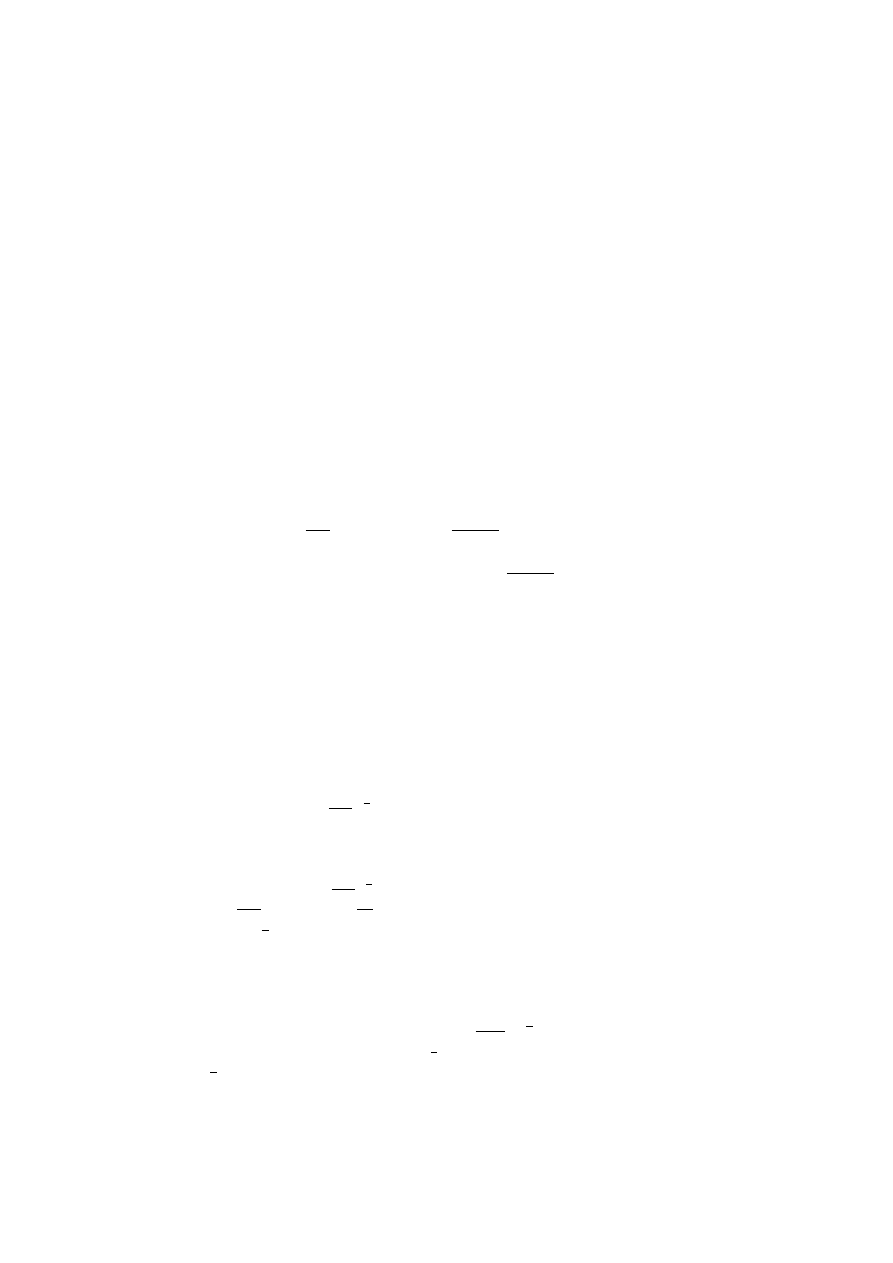
f

′

(x) > 0 ⇔ x(x − 2) > 2 i x 6= 0

f

′

(x) < 0 ⇔ x(x − 2) < 2 i x 6= 0

stad otrzymujemy:
f

′

(x) > 0 ⇔ x ∈ (−∞, 0) i x ∈ (2, ∞)

f

′

(x) < 0 ⇔ x ∈ (0, 2)

Zatem funkcja ro´snie w przedzia lach (−∞, 0) i (2, ∞) i maleje w prze-

dziale (0, 2). W takim razie wynika,˙ze f osiaga maksimum w punkcie x

0

= 2

i f

min

= 3

6) Poniewqa˙z nie istnieje sko´

nczona granica funkcji w niesko´

nczono´sci ani

granica w minus niesko´

nczono´sci, to nie istnieje pozioma asymptota wykresu

funkcji f.

Istnieje natomiast asymptota pionowa, jest nia prosta o r´

ownaniu x = 0.

Aby zbada´c istnienie asymptoty pochy lej, najpierw badamy istnbienie

granicy lim

x→−∞

f

(x)

x

, czyli lim

x→−∞

f

(x

3

+4)

x

3

. Granica ta istnieje i wynosi

1. Znaczy to, ˙ze wsp´

o lczynnik kierunkowy ewentualnej asymptoty jest r´

owny

1. Teraz badamy istnienie granicy lim

x→−∞

(

f

(x

3

+4)

x

2

− x). Granica ta wy-

nosi zero. W takim razie asymptota pochy la jest prosta o r´

ownianiu x=y.

7) Wykorzystujac zebrane o funkcji wiadomo´sci, budujemy tabele zmienno´sci

funkcji, a nastepnie szkicujemy wykres.

|x

(−∞, 0) 0 (0, 2) 2 (2, ∞)

f

′

(x)

(+)

x

(−)

0

(+)

f

′

(x)

(↑)

x

(↓)

3

(↑)

2.2

Zadanie 2

Zbada´c funkcje: y =

x−

1

x

e

1

x

Rozwiazanie: Dziedzina funkcji: Df = (−∞, 0) i (0.∞) Mamy nastepnie

y → 1, gdy x → −∞ lub x → ∞, y → −∞, gdy x → 0

−

oraz

lim

x→

0

+

y = lim

x→

0

+

x−

1

x

e

1

x

lim

u→∞

1−u

e

u

=

H

lim

u→∞

−

1

e

u

= 0

, gdzie u =

1

x

Z przeprowadzonych oblicze´

n granic wynika, ˙ze wykres funkcji ma lewo-

stronna asymptote pionowa o r´

ownaniu x= 0, oraz obustronna asymptote

pozioma y = 1. Wynika stad, ˙ze nie istnieje ˙zadna asymptota uko´sna.

Obliczamy pierwsza pochodna y

′

=

2x−1

x

3

e

−

1

x

. Poniewa˙z Df

′

= Df ,

y

′

= 0 wtedy i tylko wtedy, gdy x =

1
2

oraz pochodna zmienia znak w punkcie

x =

1
2

z ujemnego na dodatni, wiec funkcja w tym punkcie ma ekstremum,

3

minimum; y

m

in = y(

1
2

) =

−

1

e

2

. Poniewa˙z y

′

> 0 na przedziale (−∞, 0) i na

przedziale (

1
2

, ∞), wiec funkcja jest na tych przedzia lach rosnaca. Poniewa˙z

y

′

< 0 na przedziale (0,

1
2

), wiec funkcja jest malejaca na tym przedziale.

na podstawie uzyskanych informacji sporzadzamy tabelke zmienno´sci

funkcjii sporzadzamy wykres.

|x

(−∞, 0) 0 (0,

1
2

)

(

1
2

)

(

1
2

, ∞)

f

′

(x)

(+)

x

(−)

0

(+)

f

′

(x)

(↑)

x

(↓)

(

−

1

e

2

)

(↑)

4