FALE ELEKTROMAGNETYCZNE
Teoria Maxwella – cztery równania
Przy
śpieszony ładunek emituje pola elektryczne i magnetyczne propagujące się z prędkością
o
o
c
µ
ε
=
.
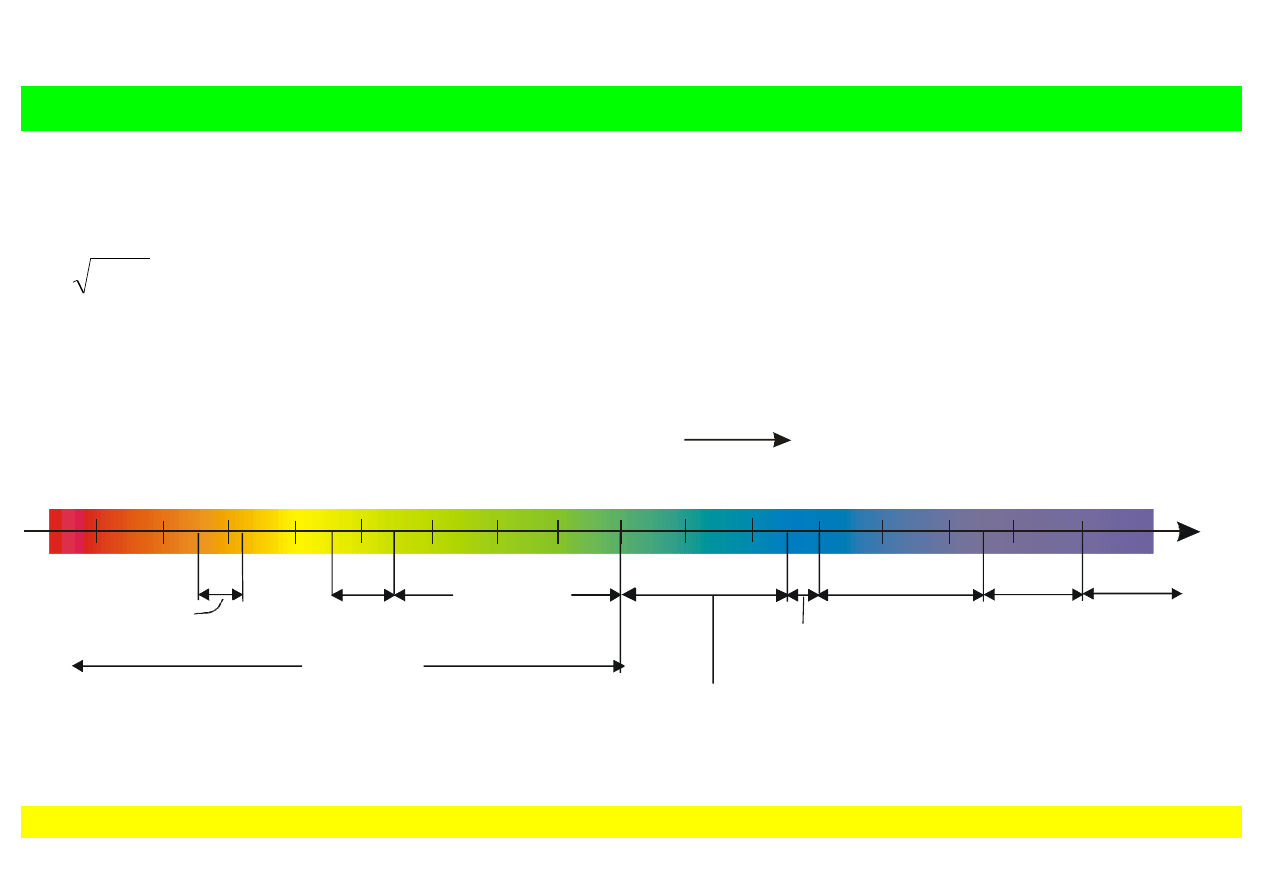
Fale elektromagnetyczne – zakres cz
ęstotliwości (4–7)
×
10
14
Hz
W wi
ększości zjawisk fizycznych występują oddziaływania elektromagnetyczne
10
10
10
4
10
16
10
10
10
5
11
17
10
10
10
6
12
18
10
10
10
7
13
19
10
10
8
14
10
10
9
15
Cz
ęstotliwość Hz
Fale
średnie
Fale
krótkie
Fale
radiowe
Promieniowanie
podczerwone
Zakres
widzialny
Ultrafiolet
Promieniowanie
Mikrofale
TV
X
γ
Rys. 9.1. Widmo fal elektromagnetycznych
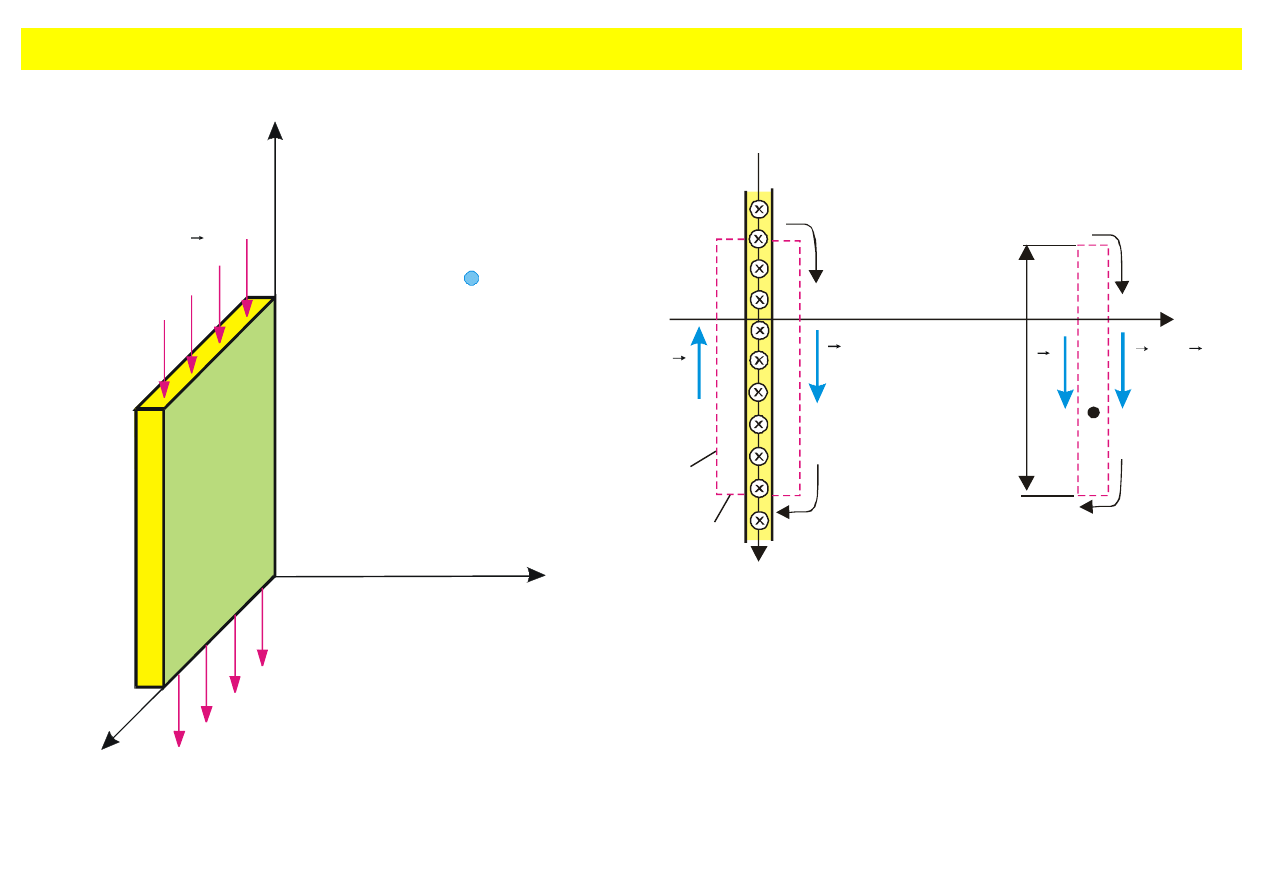
Równanie ró
żniczkowe fali elektromagnetycznej
O
P
x
y
z
J
Rys. 9.2. Prostok
ątny element nieskończonej
powierzchni z pr
ądem powierzchniowym J.
Widok z góry
P
x
B
B
B
B
B
a
z
b
b
+d
Rys. 9.3. Widok z góry elementu pr
ądu
przedstawionego
na
rys.
9.2.
Ca
łki
krzywoliniowe liczone s
ą w kierunku ruchu
wskazówek zegara wokó
ł prądu i wokół
punktu P.

Uogólnione prawo Ampera
S
d
t
E
c
S
d
j
s
d
B
S
S
C
o
r
v
r
r
r
r
⋅
∂
∂
+
⋅
=
⋅
∫
∫
∫
2
1
µ
(7.16)
Kontur obchodzimy zgodnie z kierunkiem wskazówek zegara. Równanie (7.16) napiszemy w postaci
Jb
s
d
B
o
µ
=
⋅
∫
r
r
lub
Jb
Bb
o
µ
=
2
St
ąd znajdujemy B w pobliżu płaskiego prądu
2
J
B
o
µ
=
(9.1)
Pr
ąd J zmienia się w czasie, a otrzymany wynik słuszny jest jedynie w pobliżu źródła.
Teraz pos
łużymy się prostokątnym konturem całkowania wokół punktu P. Wektor
S
d
r
jest skierowany
za p
łaszczyznę rysunku w ujemnym kierunku osi y. Wówczas
bdx
E
dS
E
S
d
E
y
y
−
=
−
=
⋅
r
r
.
a równanie (7.16) przyjmie posta
ć
S
d
t
E
c
s
d
B
C
r
r
r
∫
∫
+
=
⋅
∂
∂
2
1
0

lub
(
)
(
)
bdx
t
E
c
b
B
b
dB
B
y
z
z
z
∂
∂
2
1
−
=
−
+
Wobec tego
dx
t
E
c
dB
y
z
∂
∂
2
1
−
=
dx
t
E
c
dx
dB
y
const
t
z
∂
∂
2
1
−
=
=
t
E
c
x
B
y
z
∂
∂
∂
∂
2
1
−
=
(9.2)
Z uogólnionego prawa Faradaya
∫
∫
∂
−
=
⋅
S
C
S
d
dt
B
s
d
E
r
r
r
r
mo
żna otrzymać jeszcze jeden związek między polami B i E.
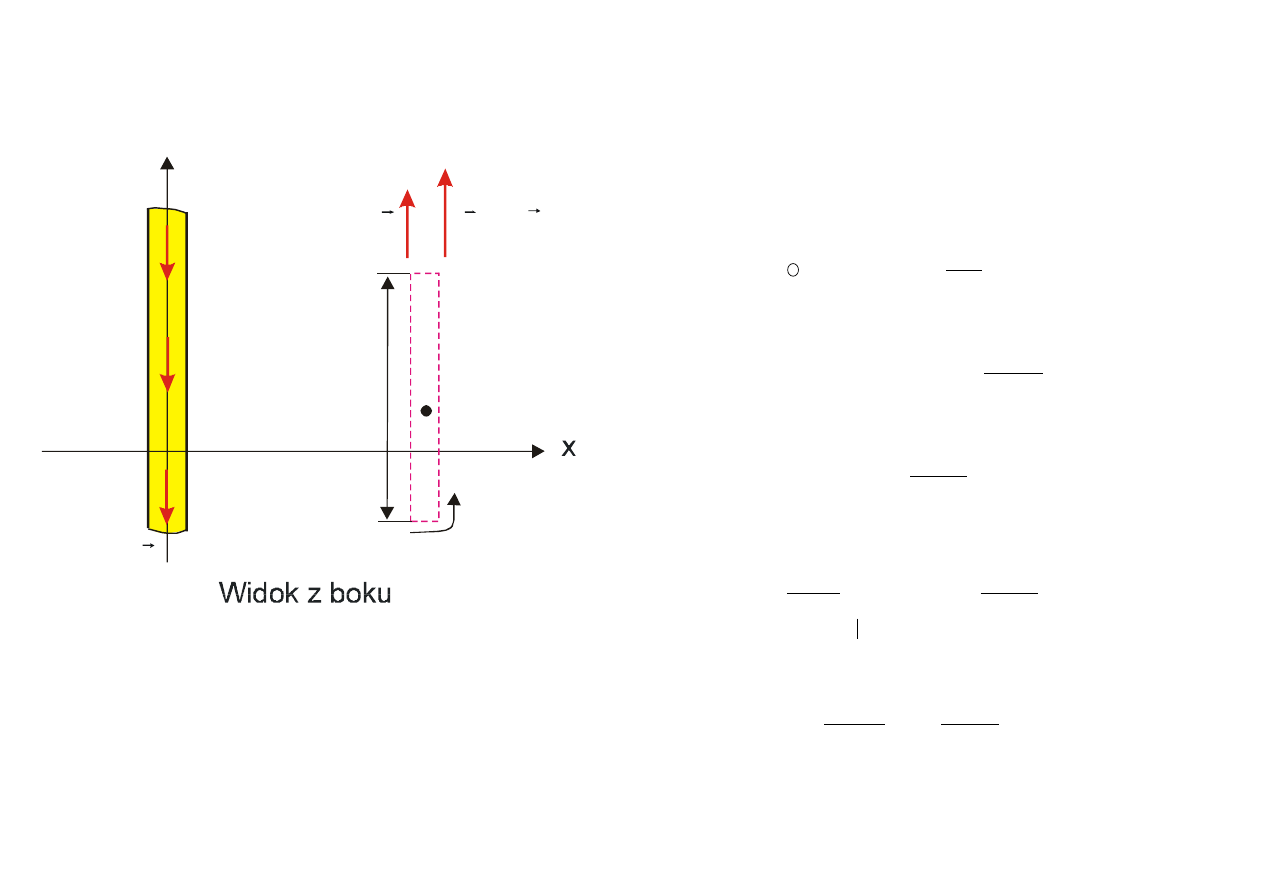
P
y
h
dx
J
E
)
E
d
E
(
+
Rys. 9.4. Widok z boku na element p
łaskiego
pr
ądu przedstawionego na rys. 9.2.
Ca
łkujemy w kierunku przeciwnym do ruchu
wskazówek zegara po prostok
ątnym konturze
wokó
ł punktu P w płaszczyźnie Oxy
∫
∫
−
=
⋅
C
S
d
t
B
s
d
E
r
r
r
r
∂
∂
)
hdx
(
t
B
h
E
h
)
dE
E
(
z
y
y
y
∂
∂
−
=
−
+
czyli
dx
t
B
dE
z
y
∂
∂
−
=
a dalej
t
B
dx
dE
z
const
t
y
∂
∂
−
=
=
i ostatecznie
t
B
x
E
z
y
∂
∂
∂
∂
−
=
(9.3)

Mamy dwa równania, (9.2) i (9.3), z dwiema niewiadomymi B
z
i E
y
. Ró
żniczkując równanie (9.2) po x,
a równanie (9.3) po t, mo
żna wyłączyć E
y
−
=
t
E
c
x
x
B
x
y
z
∂
∂
∂
∂
∂
∂
∂
2
1
t
x
E
c
x
B
y
z
∂
∂
∂
∂
∂
2
2
2
2
1
−
=
(9.4)
Podobnie
2
2
2
t
B
t
x
E
t
B
t
x
E
t
z
y
z
y
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
−
=
=
Podstawiaj
ąc to wyrażenie w prawą stronę równania (9.4), mamy
2
2
2
2
2
1
t
B
c
x
B
z
z
∂
∂
∂
∂
=
(9.5)
Jest to s
łynne równanie różniczkowe równanie falowe Maxwella. Rozwiązanie tego równania
przedstawia fal
ę biegnącą propagującą się z prędkością c.
Równanie (9.3) zawiera uzupe
łniającą informację wskazującą, że wielkość pola elektrycznego
jest równa E = cB i
że pola
E
r
i
B
r
s
ą wzajemnie prostopadłe.
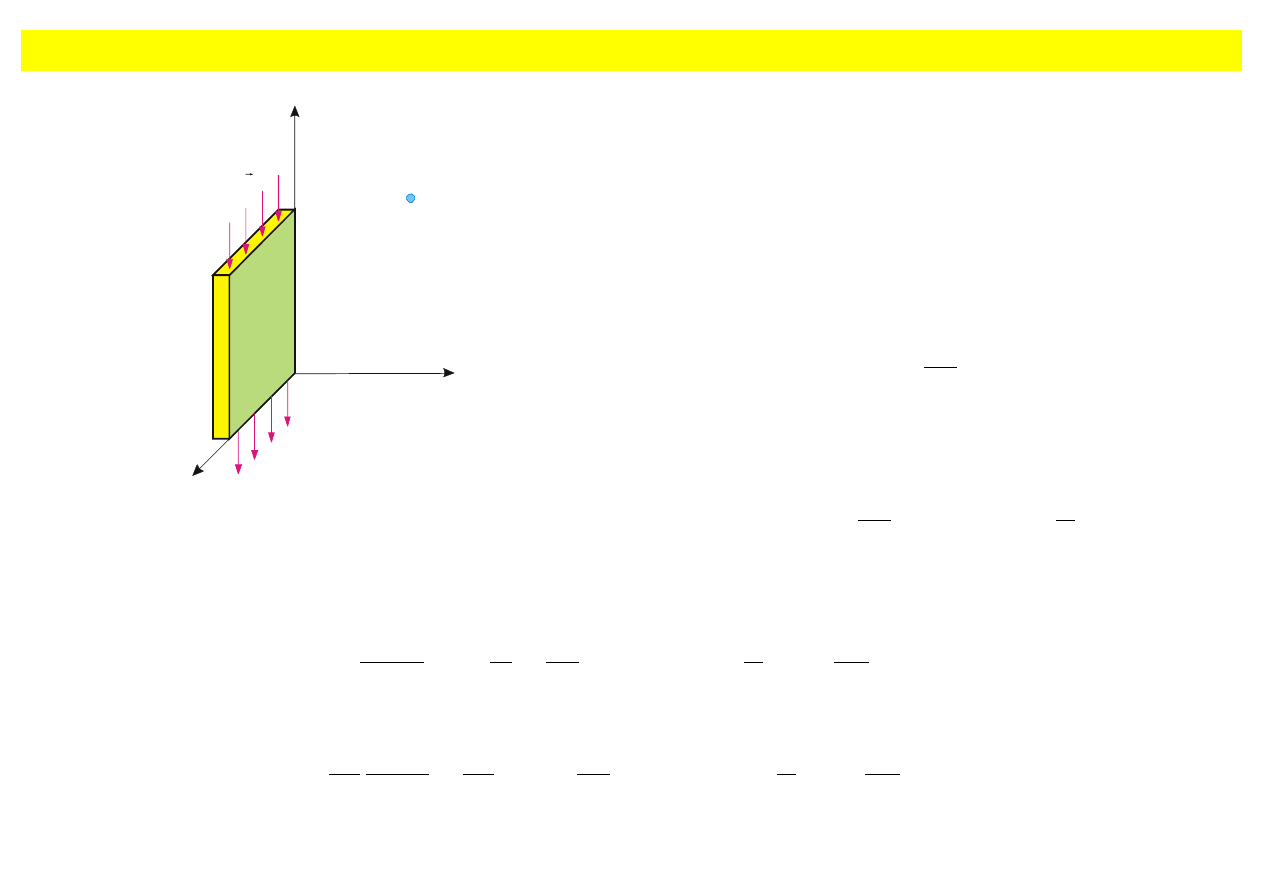
Promieniowanie p
łaskiego prądu
O
P
x
y
z
J
Rys. 9.2. Prostok
ątny element nieskończonej
powierzchni z pr
ądem powierzchniowym J.
Za
łóżmy, że prąd powierzchniowy (rys. 9.2) ma
posta
ć
t
cos
J
J
o
ω
=
,
pr
ąd J
o
p
łynie w kierunku przeciwnym do osi y.
Przy ma
łych wartościach x rozwiązanie
okre
ślone jest wyrażeniem (9.1)
( )
t
cos
J
t
,
x
B
o
o
z
ω
µ
2
=
W
przypadku
du
żych
warto
ści
x
jednoznacznym rozwi
ązaniem jest
( )
−
=
c
x
t
cos
J
t
,
x
B
o
o
z
ω
µ
2
(9.6)
Pdstawiaj
ąc to rozwiązanie do lewej strony równania (9.5) mamy
z
o
o
z
B
c
c
x
t
cos
J
c
x
B
2
2
2
2
2
2
ω
ω
µ
ω
∂
∂
−
=
−
−
=
a do prawej
( )
z
o
o
z
B
c
c
x
t
cos
J
c
t
B
c
2
2
2
2
2
2
2
2
1
1
ω
ω
µ
ω
∂
∂
−
=
−
−
=
czyli równanie falowe (9.5) jest spe
łnione.

Zauwa
żmy, że dla
0
→
x
otrzymujemy
t
cos
J
)
/
(
B
o
o
z
ω
µ 2
=
. Rozwi
ązanie to spełnia warunek
brzegowy i jest jednoznacznym rozwi
ązaniem problemu.
Teraz znaj
ąc B możemy obliczyć pole E podstawiając rozwiązanie na B do równania (9.3)
−
=
−
−
=
c
x
t
sin
B
c
x
t
cos
B
t
x
E
o
o
y
ω
ω
ω
∂
∂
∂
∂
st
ąd
const
c
x
t
cos
cB
dx
c
x
t
sin
B
E
o
o
y
+
−
=
−
=
∫
ω
ω
ω
Sta
ła całkowania jest równa zeru, ponieważ ładunki tworzące stałe pole elektryczne nie występują.
Tak wi
ęc
−
=
=
c
x
t
cos
J
c
cB
E
o
o
z
y
ω
µ
2
(9.7)
Jest to pole promieniowania.
Za dodatni kierunek pr
ądu J
o
przyj
ęto kierunek przeciwny do kierunku osi y. Dlatego dodatnie znaki
wielko
ści
y
E i
z
B oznaczaj
ą, że w pobliżu źródła pole E
y
skierowane jest przeciwnie do pr
ądu J.
Wygodnie jest to zapami
ętać w następujący sposób: dodatnie ładunki będą gromadzić się na dolnej
kraw
ędzi, a ujemne na górnej. Linie sił pola skierowane są z dołu do góry, tj. przeciwnie do kierunku
pr
ądu.
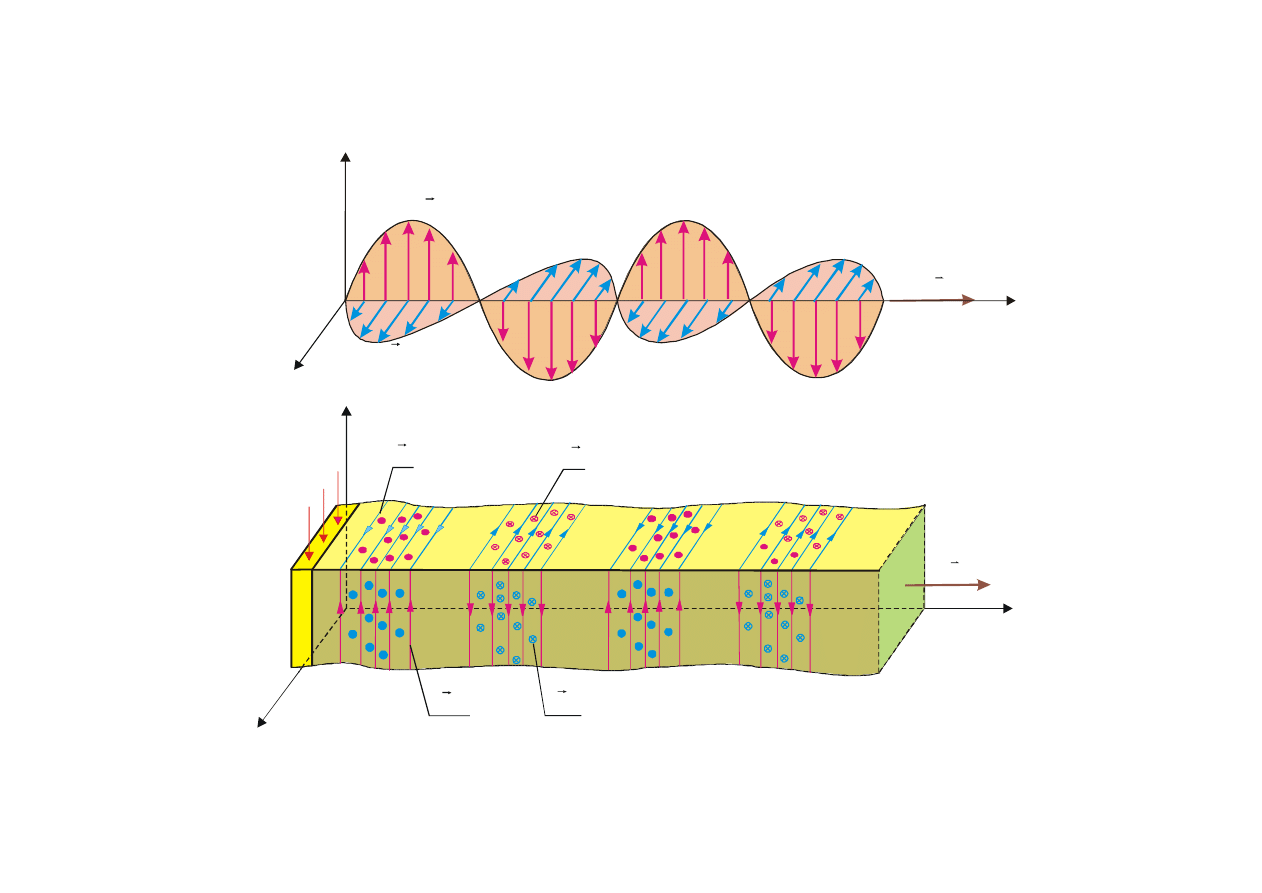
Wykazali
śmy, że E = cB a także, że pola elektryczne i magnetyczne są wzajemnie prostopadłe.
B
B
B
E
E
E
y
y
z
z
x
x
J
c
c
Rys. 9.5. P
łaska fala monochromatyczna propagująca się w prawo z prędkością c. Fala
emitowana jest przez sinusoidalny pr
ąd J płynący w płaszczyźnie yz.

Rozk
ład Fouriera periodycznej funkcji F(t
Rozwa
żmy przypadek, kiedy prąd powierzchniowy określany jest funkcją piłokształtną o okresie
τ.
Wówczas
τ
π
ω 2
=
.
Funkcj
ę piłokształtną można przedstawić w postaci sumy nieskończonej liczby fal sinusoidalnych
(
)
∑
∞
=
=
1
1
n
t
n
sin
n
)
t
(
F
ω
Jest to rozk
ład Fouriera periodycznej funkcji F(t).
W ogólnym przypadku dowoln
ą funkcję periodyczną o częstości 1/
τ można zapisać w postaci sumy fal
monochromatycznych o cz
ęstościach n(1/
τ), gdzie n przyjmuje liczby całkowite od 1 do
∞
.
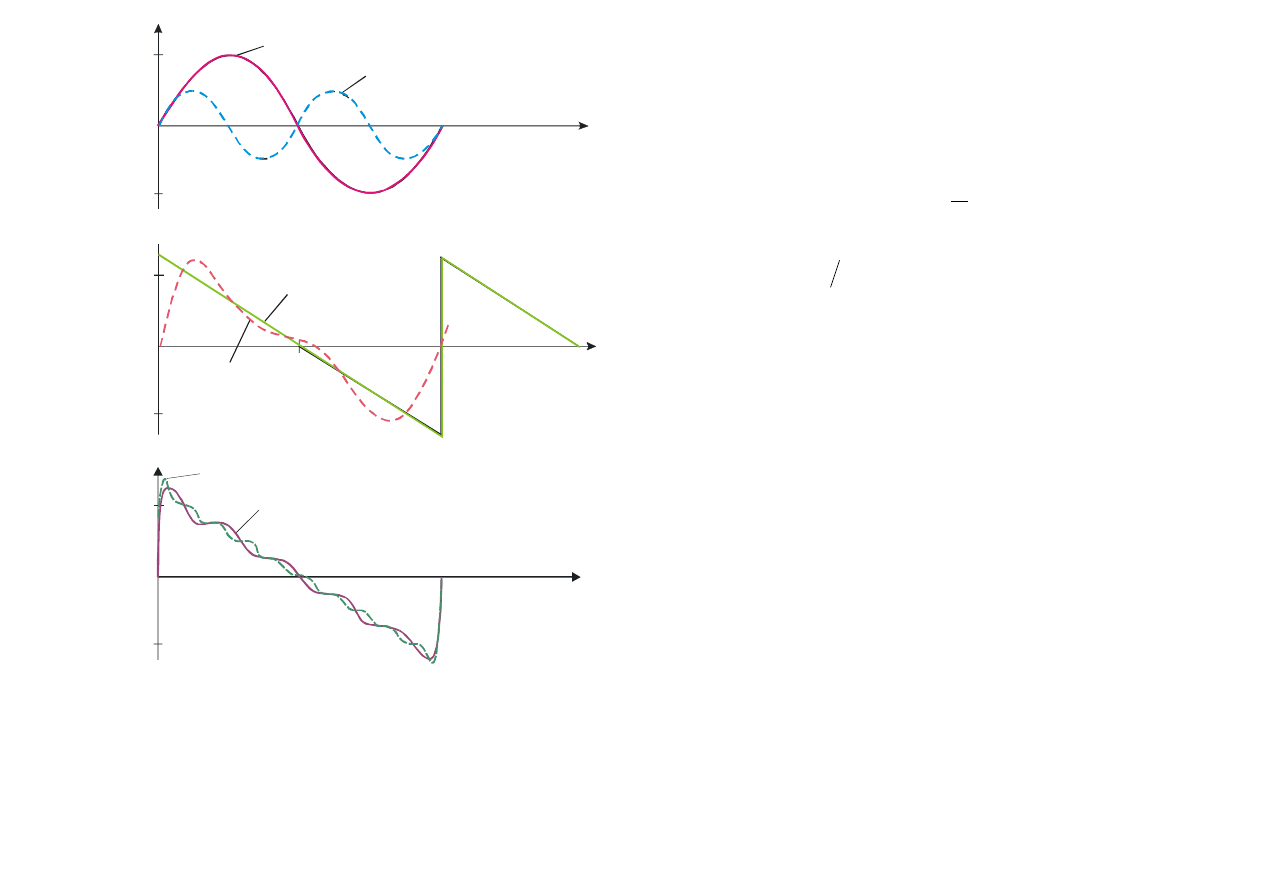
(a)
(b)
(c)
19 fal
9 fal
2 fale
t
t
t
τ
τ
τ
1
0
1
0
1
0
-1
-1
-1
t
2
sin
2
1
ω
sin t
ω
ω
+
ω
t
2
sin
2
1
t
sin
( )
( )
∑
∞
=
ω
=
1
n
t
n
sin
n
1
t
F
Rys. 9.6. Przedstawienie pi
łokształtnej funkcji
w postaci sumy niesko
ńczonej liczby fal
sinusoidalnych: (a) dwie fale sinusoidalne; (b)
wynik z
łożenia dwóch fal sinusoidalnych; (c)
suma pierwszych dziewi
ęciu i dziewiętnastu
fal sinusoidalnych.
Dla
generacji
pi
łokształtnej
fali
elektromagnetycznej
pr
ąd powierzchniowy
okre
ślany jest wzorem
(
)
∑
∞
=
=
1
n
o
t
n
sin
n
1
J
J
ω
gdzie
τ
π
ω 2
=
.
Poniewa
ż równania Maxwella są liniowe
odno
śnie E, B i J, więc pełne rozwiązanie jest
równe sumie oddzielnych rozwi
ązań.
Oddzia
ływanie promieniowania z materią
Dobry przewodnik odbija fal
ę ze 100% efektywnością. Przez dielektryk fala propaguje się nie
doznaj
ąc pochłaniania; jednakże propagacja fali zachodzi wolniej niż w próżni. Te pozorne paradoksy
rozwi
ązuje się stosując podejście mikroskopowe z uwzględnieniem budowy atomowej materii.
Energia promieniowania
z
o
y
o
∆
x
E
∆
E
∆
j
pad
E
pad
B
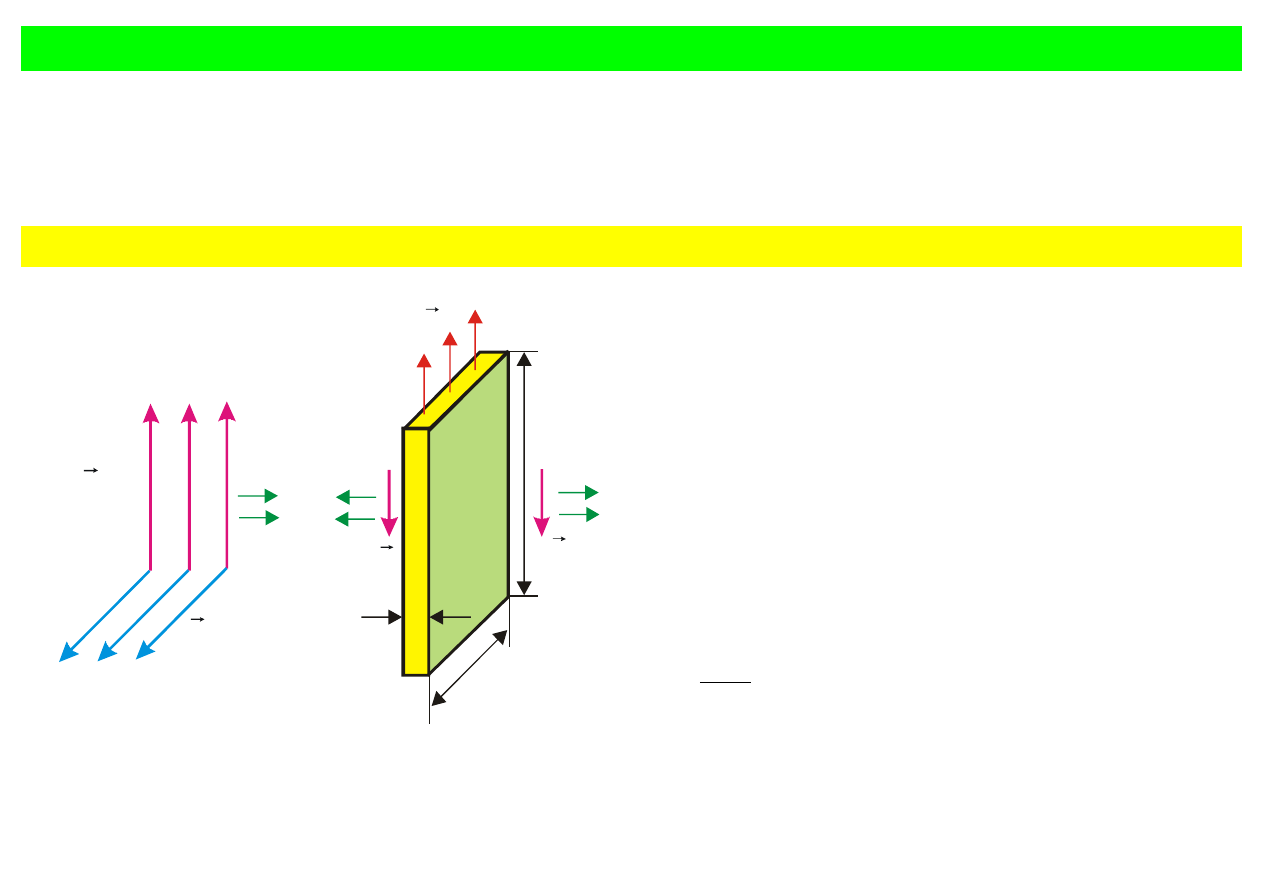
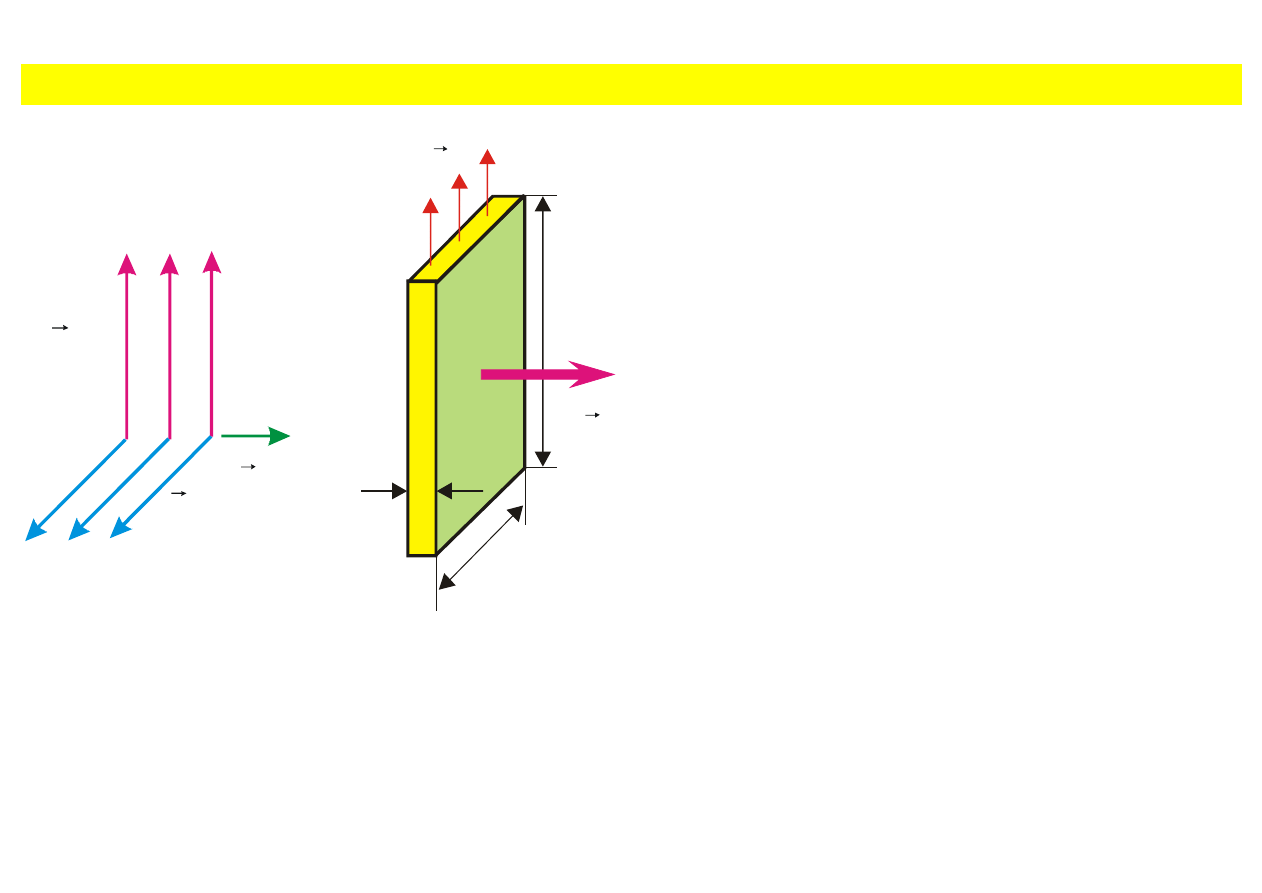
Rys. 9.7. Fala padaj
ąca
pad
E
r
przemieszcza
si
ę w prawo i pada na płytkę indukując
pr
ąd, który na prawo i na lewo od płytki
promieniuje w
łasne pole
E
r
∆
.
Na rys. 9.7 pokazano fal
ę elektromagnetyczną
padaj
ącą na prostokątny element płytki o
niesko
ńczonych rozmiarach. Jeżeli gęstość
pr
ądu indukowanego jest równa j, to w
prostok
ątnym elemencie będzie płynął prąd
x
jz
I
o
∆
=
Ró
żnica potencjałów pomiędzy górną a dolną
kraw
ędzią wynosi
o
Ey
V
=
, a energia tracona
w jednostce czasu na ciep
ło Joule'a wynosi
(
)
(
)
x
z
y
jE
Ey
x
jz
IV
dt
dW
o
o
o
o
∆
∆
=
=
=
gdzie
x
z
y
o
o
∆
oznacza obj
ętość elementu
p
łytki.
Moc
tracona
w
jednostce
obj
ętości
przewodnika wynosi jE
.

Je
żeli na przewodzącą płytkę pada płaska fala monochromatyczna, to przy tym nie tylko wydziela się
ciep
ło z szybkością jE w jednostce objętości, lecz indukowany prąd j także promieniuje falę
elektromagnetyczn
ą.
Je
żeli prąd powierzchniowy
x
j
J
∆
=
, to zgodnie z (9.7)
x
j
c
E
o
∆
µ
∆
2
−
=
(9.8)
Znak minus wskazuje,
że wewnątrz płytki pole
E
r
∆
skierowane jest przeciwnie do pr
ądu
j
r
.
Niech
S
P
∆
oznacza straty mocy na jednostkow
ą powierzchnię. W przypadku cienkiej płytki o grubości
x
∆
x
jE
dt
dW
z
y
P
o
o
S
∆
∆
=
=
1
(9.9)
czyli
E
E
c
P
o
S
∆
µ
∆
2
−
=
(9.10)
Rozpatrzmy teraz stos takich cienkich p
łytek. Jeżeli stos płytek jest nieskończenie gruby, to pole
pad
E
r
zostanie ca
łkowicie pochłonięte i całkowitą moc promieniowania z jednostki powierzchni wynosi
pad
pad
pad
pad
E
S
B
E
E
c
EdE
c
P
0
2
0
0
0
1
1
2
µ
µ
µ
=
=
−
=
∫
Moc promieniowana przez jednostkow
ą powierzchnię charakteryzowana jest wektorem
Poytinga
. Jego warto
ść oznaczana jest przez P
S
. Poniewa
ż kierunek strumienia energii określany
jest iloczynem wektorowym
B
E
r
r
×
, to
S
P
r
mo
żemy wyrazić
B
E
P
o
S
r
r
r
×
=
µ
1
(9.11)
Sprawdzimy czy otrzymany wzór nie przeczy otrzymanemu wcze
śniej wyrażeniu dla energii
przypadaj
ącej na jednostkę objętości pola [wzór (7.14)]. Rozpatrzymy falę płaską padającą na
powierzchni
ę A. Zgodnie z określeniem P
S
, strumie
ń energii w czasie dt wynosi
Adt
P
dW
S
=
gdzie dW oznacza energi
ę w objętości dV = Adx. Ponieważ
c
dx
dt
=
, st
ąd
dV
c
P
c
dx
A
P
dW
S
S
=
=
czyli
c
P
dV
dW
S
=
Stosuj
ąc teraz wyrażenie (9.11) otrzymamy
EB
c
dV
dW
o
µ
1
=
Zamieniaj
ąc E na cB
o
o
B
B
dV
dW
µ
µ
2
2
2
2
+
=
czyli
+
=
=
o
o
B
E
dV
dW
w
µ
ε
2
2
2
1
P
ęd promieniowania
c
m
F
z
o
y
o
∆
x
j
pad
E
pad
B
Rys. 9.8. Padaj
ąca fala wywołuje w płytce
pr
ąd
x
jz
I
o
∆
=
. Na ten pr
ąd działa siła
magnetyczna
B
y
I
F
o
m
r
r
r
=
.
Wyka
żemy teraz, że płaska fala z rys. 9.7
przekazuje p
łytce o grubości
∆x nie tylko
energi
ę, ale i pęd. Rozważmy prostokątny
element
niesko
ńczonej
p
łytki,
którego
powierzchnia wynosi
o
o
z
y
(rys. 9.8).
Poniewa
ż jEdt jest ilością ciepła Joule’a
wydzielaj
ącego się w jednostce objętości w
czasie dt, to ilo
ść ciepła wydzielającego się w
elemencie p
łytki o objętości y
o
z
o
∆x wynosi
(
)(
)
x
z
y
jEdt
dW
o
o
∆
=
Zamieniaj
ąc E na cB
Bdt
y
x
cjz
dW
o
o
∆
=
Poniewa
ż prąd płynący przez rozważany
element p
łytki wynosi
(
)
x
z
j
I
o
∆
=
, wi
ęc
Bdt
cIy
dW
o
=

Na element pr
ądu długości y
o
, prostopad
ły do padającego pola magnetycznego, działa siła
B
y
I
F
o
m
r
r
r
×
=
w kierunku
B
E
r
r
×
zgodnie z kierunkiem fali padaj
ącej. Zamieniając Iy
o
B na F
m
otrzymujemy
dt
cF
dW
m
=
P
ęd przekazywany elementowi płytki dp = F
m
dt, czyli
cdp
dW
=
, a st
ąd
dW
c
dp
1
=
(9.12)
Tak jak poprzednio, ca
łkując po grubości płytki x otrzymujemy p = W/c. Wobec tego
p
ęd
przekazywany p
łytce przez padającą falę równy jest wielkości 1/c pomnożonej przez energię
rozproszon
ą w płytce
.
W dowolnym elemencie obj
ętości pola promieniowania dV zawarta energia wynosi
dV
E
dW
o
2
ε
=
a jego p
ęd jest równy energii podzielonej przez c.
Element obj
ętości dV charakteryzuje się wektorem pędu (z uwzględnieniem związku
c
dV
P
dW
S
=
)
=
dV
c
P
c
p
d
S
r
r
1
(9.13)
Energi
ę promieniowania łatwo odczuć umieszczając rękę w strumieniu światła. Jednakże pomiar pędu
strumienia
świetlnego jest utrudniony na skutek tego, że wartość 1/c jest mała.
Odbicie promieniowania od przewodnika
P
łytka
pad
E
E
∆
E
∆
J
Rys. 9.9. Padaj
ąca fala wywołuje w płytce
nadprzewodz
ącej prąd J, który promieniuje
pole
E
r
∆
równe co do warto
ści z
pad
E
r
.
W
przypadku
przewodnika
o
wysokiej
konduktywno
ści
σ, fala elektromagnetyczna nie
jest poch
łonięta całkowicie; częściowo jest
odbijana.
Rozwa
żymy
skrajny
przypadek
∞
=
σ
(nadprzewodnik). Pole elektryczne wewn
ątrz
nadprzewodnika zawsze przyjmuje warto
ść
zerow
ą
(w
przeciwnym
przypadku
nieograniczenie wzrós
łby prąd). Tak więc
indukowany pr
ąd powierzchniowy okazuje się
takim,
że pole promieniowania
pad
E
E
−
=
∆
.
Wówczas wewn
ątrz płytki wypadkowe pole
0
=
+
=
E
E
E
pad
r
r
r
∆
Na lewo od p
łytki pole uwarunkowane jest
dwoma
falami
monochromatycznymi
o
jednakowym
nat
ężeniu,
biegn
ącymi
w
przeciwnych kierunkach (fala stoj
ąca).
Oddzia
ływanie promieniowania z dielektrykiem
Zewn
ętrzne elektrony atomów dielektryka ulegają przemieszczaniu pod wpływem zewnętrznego pola
elektrycznego.
R
x
o
Chmura
elektronowa
Proton
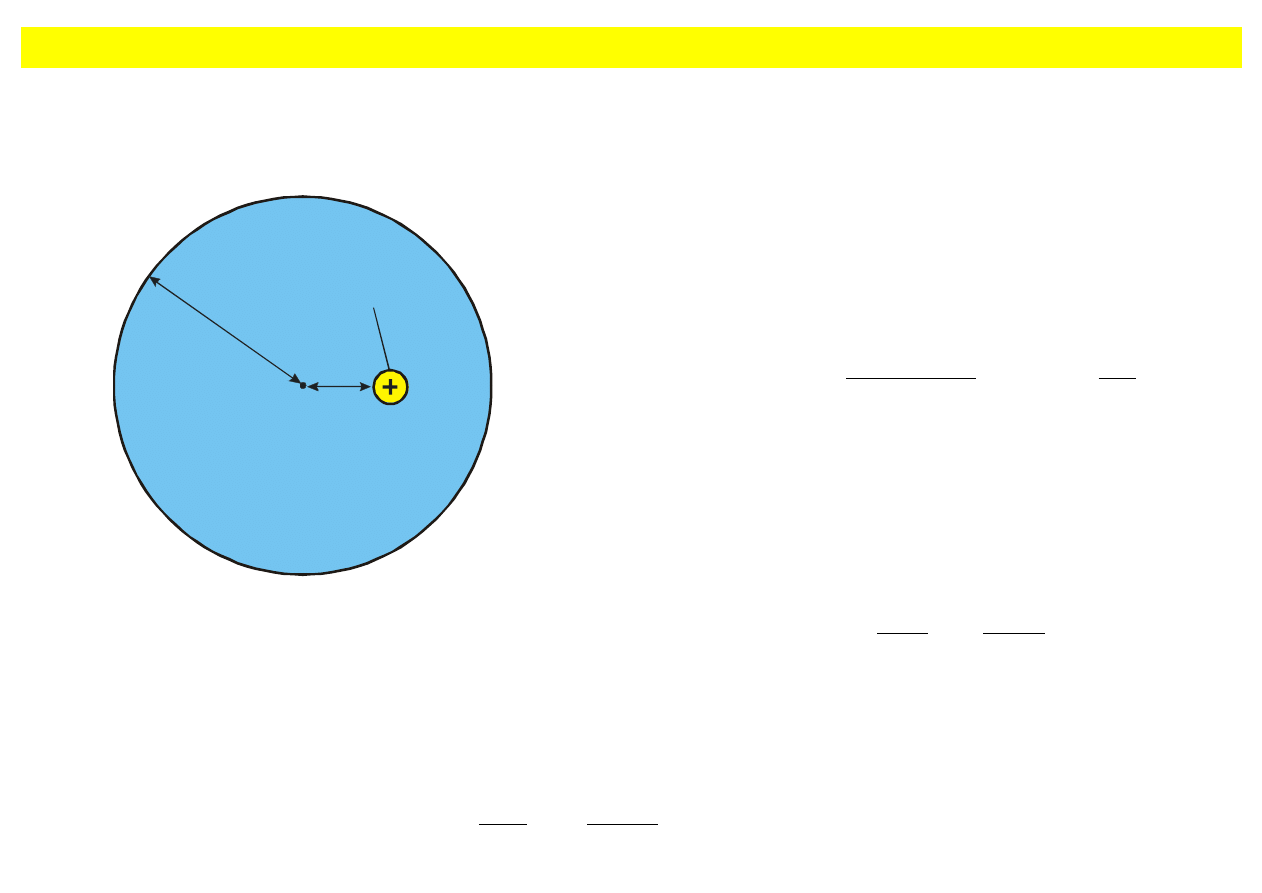
Rys. 9.10. Elektron traktowany jako
jednorodna na
ładowana kula przesunięty
na odleg
łość x
o
wzgl
ędem protonu.
Zewn
ętrzny elektron atomu traktujemy w postaci
kulistego ob
łoku o promieniu R. Przyjmiemy, że
g
ęstość ładunku jest stała.
Si
ła działająca na proton zgodnie z równaniem
(4.16) wynosi
x
R
e
k
x
R
e
e
eE
F
o
r
o
3
2
3
4
−
=
−
=
=
ε
ε
π
gdzie
r
o
o
/
k
ε
πε
4
1
=
.
Zgodnie z III prawem Newtona, identyczna si
ła
dzia
ła na elektron
x
R
e
k
dt
x
d
m
o
e
3
2
2
2
−
=
Z powy
ższego równania otrzymamy
x
x
R
m
e
k
dt
x
d
2
o
3
e
2
o
2
2
ω
−
=
−
=

gdzie
3
2
R
m
e
k
e
o
o
=
ω
Si
ła działająca na zewnętrzną chmurę elektronową wynosi
x
m
F
o
atom
2
ω
−
=
(9.14)
gdzie
ω
o
cz
ęstość kołowa drgań własnych elektronu.
Je
żeli na chmurę elektronową działa pole E
pad
padaj
ącej fali, to wypadkową siłę zapiszemy w postaci
( )
pad
atom
wyp
E
e
F
F
−
+
=
st
ąd otrzymamy następujące równanie
pad
o
E
e
y
m
dt
y
d
m
−
−
=
2
2
2
ω
Rozpatrujemy przypadek, kiedy
pad
E
r
skierowane jest wzd
łuż osi y. Falę padającą w odległości x od
źródła zapisujemy jako
( )
c
x
o
pad
t
cos
E
E
−
=
ω
Wówczas
−
−
−
=
c
x
t
cos
m
eE
y
dt
y
d
o
o
ω
ω
2
2
2

Rozwi
ązaniem tego równania różniczkowego jest
(
)
−
−
−
=
c
x
t
cos
m
eE
y
o
o
ω
ω
ω
2
2
(9.15)
W powy
ższy sposób wykazaliśmy jak oddziaływuje pojedynczy atom z falą elektromagnetyczną.
Teraz rozwa
żymy oddziaływanie fali z dużą ilością takich atomów zawartych w płytce ciała stałego lub
w warstwie gazu.

Wspó
łczynnik załamania. Dyspersja
o
na p
łytkę o grubości
∆x pada fala płaska,
o
pole elektryczne fali padaj
ącej E
pad
wymusi drganie harmoniczne elektronów,
o
drgaj
ący elektron promieniuje falę elektromagnetyczną,
o
powstaje fala odbita i przechodz
ąca, lecz teraz nie ma strat na ciepło Joule’a,
o
energia zachowuje si
ę w postaci promieniowania elektromagnetycznego, a wobec tego płytka
okazuje si
ę przezroczystą dla promieniowania,
o
fala elektromagnetyczna propaguje si
ę wewnątrz płytki z prędkością u < c.
Chcemy wyja
śnić, że fala elektromagnetyczna propaguje się z prędkością u < c.
Pole wewn
ątrz płytki jest superpozycją pola fali padającej i pól promieniowania wszystkich
elektronów. Ka
żde z pól z osobna będzie propagować się z prędkością u = c, lecz pole
wypadkowe mo
że propagować się tak, jakby jego prędkość była mniejsza.
Stosuj
ąc wzór (9.15) wykażemy, że pole promieniowania każdego elektronu atomowego opóźnia się
w fazie o
π
/2 wzgl
ędem pola fali padającej, która wywołuje ruch elektronów.
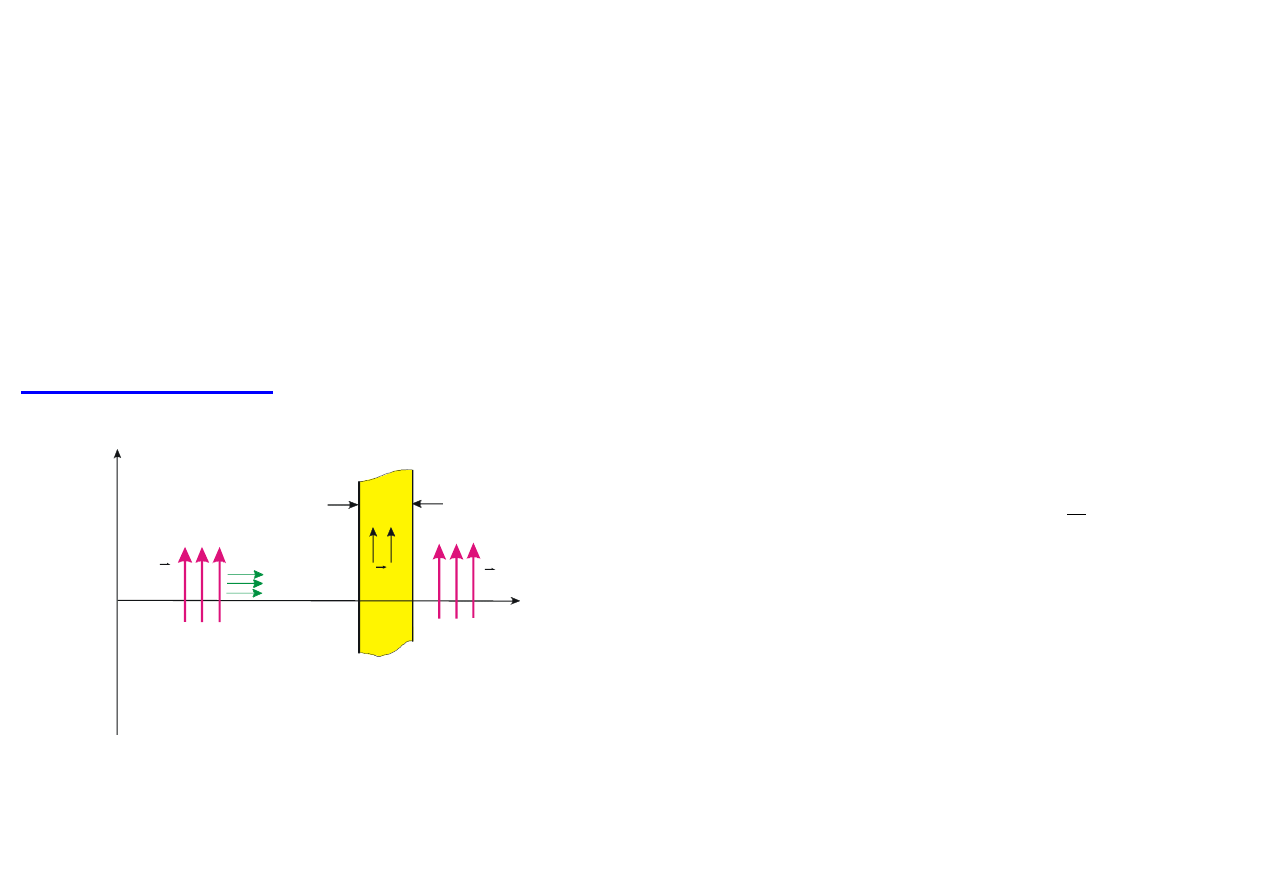
Wyprowadzimy wzór dla wspó
łczynnika załamania korzystając z rys. 9.11 i postępując w następujący
sposób:
1. Zadamy pole elektryczne fali padaj
ącej.
2. Obliczymy pr
ędkość elektronów atomowych w płytce uwarunkowaną wpływem pola
elektrycznego fali padaj
ącej.
3. Maj
ąc tą prędkość (lub gęstość pola elektrycznego), obliczymy wtórne promieniowanie
emitowane przez elektrony.
4. Zsumujemy fal
ę padającą i fale wtórne w celu otrzymania wypadkowej emitowanej fali.
5. Znajdziemy zwi
ązek pomiędzy fazą fali emitowanej a współczynnikiem załamania.
Ad.1. Fala padaj
ąca
∆
x
Pró
żnia Płytka Próżnia
y
x
E
'
E
J
Rys. 9.11 Fala padaj
ąca
pad
E
r
wytwarza w p
łytce
pr
ąd o gęstości j, którego promieniowanie
wnosi wk
ład w wypadkową falę
'
E
r
.
Pole elektryczne fali padaj
ącej ma postać
−
=
c
x
t
cos
E
E
o
pad
ω

Ad.2. Pr
ędkość elektronu
Ró
żniczkując wzór (9.15) otrzymujemy wyrażenie na prędkość słabo związanych elektronów:
(
)
−
−
=
=
c
x
t
sin
m
eE
dt
dy
v
o
o
y
ω
ω
ω
ω
2
2
G
ęstość prądu w płytce wynosi
( )
y
v
e
N
j
−
=
gdzie N jest liczb
ą drgających elektronów w jednostce objętości. Czyli
(
)
−
−
−
=
c
x
t
sin
m
E
Ne
j
o
o
ω
ω
ω
ω
2
2
2

Ad.3. Promieniowanie emitowane przez elektrony
Pole promieniowania emitowane przez elektrony p
łytki, zgodnie z (9.7), zapiszemy w postaci
x
j
2
c
=
E
o
∆
µ
∆
−
gdzie znak ”–” wskazuje,
że prąd j i wytwarzane przezeń pole promieniowania charakteryzują się
przeciwnymi kierunkami.
Podstawiaj
ąc wyrażenie dla j, mamy
(
)
x
c
x
t
sin
m
E
Ne
c
E
o
o
o
∆
ω
ω
ω
ω
µ
∆
−
−
−
−
=
2
2
2
2
Przepiszemy to wyra
żenie w postaci
(
)
2
kx
t
cos
E
=
E
o
π
ω
∆
∆
−
−
(9.16)
gdzie k =
ω/c, oraz
(
)
x
E
m
Ne
c
E
o
o
o
o
∆
ω
ω
ω
µ
∆
2
2
2
2
−
=
(9.17)
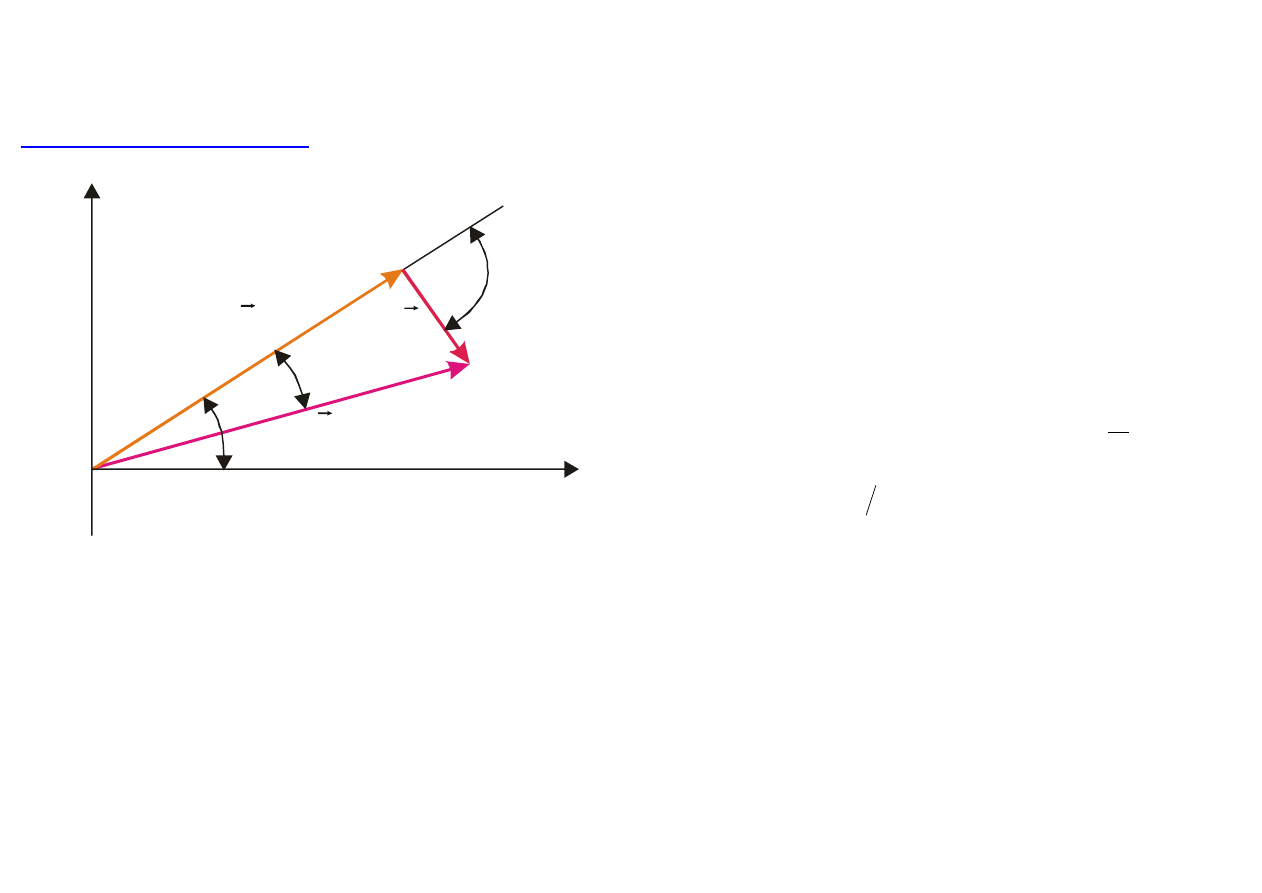
Ad.4. Fala wypadkowa
π
/2
ϕ
θ
o
E
∆
o
E
'
o
E
x
y
Rys. 9.12. Wykres fazowy dla przypadku
dodawania dwóch fal monochromatycznych
θ
cos
E
o
i
(
)
2
/
cos
E
o
π
θ
∆
−
.
Wypadkowe pole elektryczne emitowanej fali
stanowi superpozycj
ę pola fali padającej i pola
emitowanego przez elektrony atomowe
E
E
'
E
pad
∆
+
=
Uwzgl
ędniając wyrażenie (9.16) otrzymamy
( )
2
π
θ
∆
θ
−
+
=
cos
E
cos
E
'
E
o
o
gdzie
(
)
c
x
t
−
=
ω
θ
.
Chocia
ż
θ
rośnie z czasem, jednakże obie fale
monochromatyczne zachowuj
ą stałą różnicę
faz równ
ą
π
/2.
Z rys. 9.12 mo
żna zauważyć, że wektor wypadkowy
'
o
E
r
przesuni
ęty jest w fazie względem fali
padaj
ącej o kąt
o
o
E
/
E
∆
ϕ
=
(przyj
ęto przy tym małe kąty zakładając, że
1
<<
o
o
E
/
E
∆
).
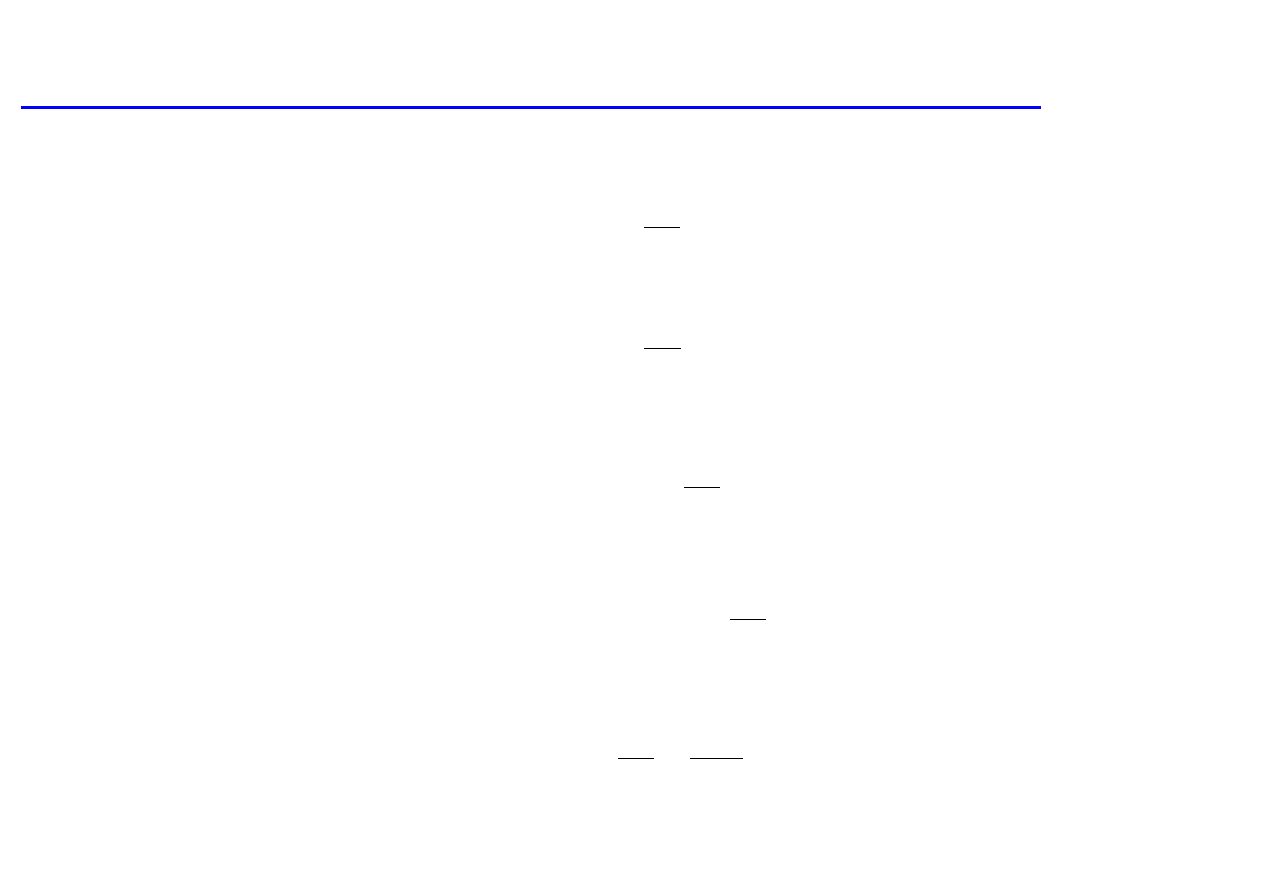
Ad.5. Zwi
ązek pomiędzy przesunięciem fazowym a współczynnikiem załamania
Fala padaj
ąca przechodzi przez płytkę w ciągu czasu
c
x
t
∆
=
,
podczas gdy fala rozchodz
ąca się z prędkością u = c/n potrzebuje więcej czasu
c
x
n
'
t
∆
=
.
Czo
ło wypadkowej fali przy przejściu przez płytkę opóźni się o
(
)
c
x
n
'
t
∆
∆
1
−
=
.
Odpowiada to przesuni
ęciu fazowemu
(
)
[
]
c
x
n
t
∆
ω
∆
ω
ϕ
1
−
=
=
Poniewa
ż
E
/
E
o
∆
ϕ
=
, to
(
)
o
o
E
E
c
x
n
∆
∆
ω
=
−
1
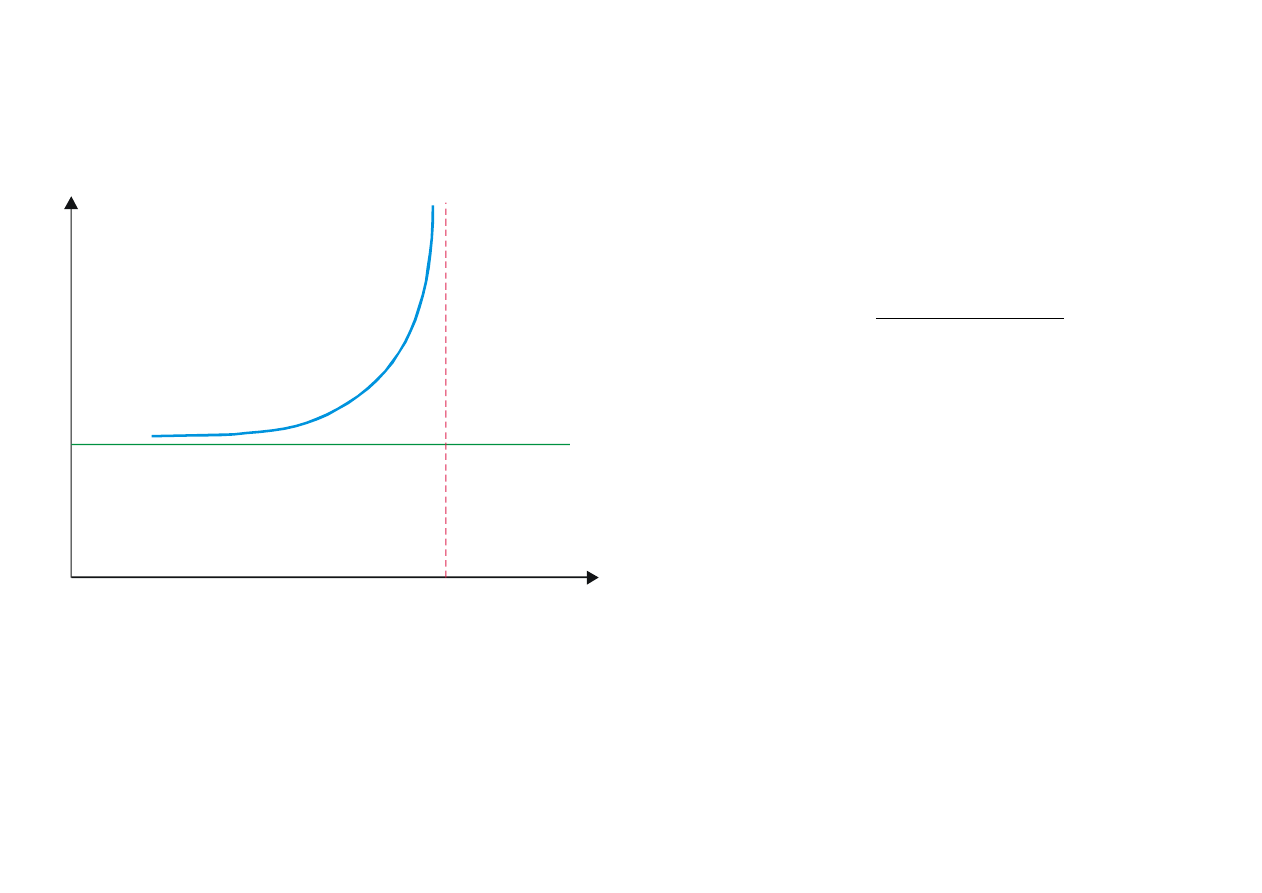
1
n
ω
ω
o
Rys. 9.13. Krzywa dyspersji normalnej
wykre
ślona zgodnie ze wzorem (9.18).
Podstawiaj
ąc wyrażenie (9.17) dla
∆E
o
i
rozwi
ązując względem n, znajdujemy
(
)
2
2
2
2
1
ω
ω
ε
−
+
=
o
o
m
Ne
n
(9.18)
Jest to wzór okre
ślający współczynnik
za
łamania płytki.
Zauwa
żmy także, że stosowaliśmy przybliżenie
zgodnie z którym pole fali padaj
ącej zmienia się
s
łabo, tj.
o
o
E
E
<<
∆
i st
ąd (n – 1) << 1.
W przypadku du
żych n, pole E
pad
wewn
ątrz
p
łytki należy zmienić na wypadkowe pole.
Komplikuje to obliczenia i nie b
ędziemy ich tutaj
przytacza
ć.

Otrzymany wynik poprawnie okre
śla zależność współczynnika załamania od częstości padającego
promieniowania (rys. 9.13).
o
Dla wi
ększości atomów
2
2
ω
ω
>
o
, gdzie
ω odnosi się do widzialnego zakresu widma. Odpowiada
temu wspó
łczynnik załamania większy od 1, czyli prędkość światła mniejsza od c.
o
Przy przej
ściu od zakresu czerwonego do zakresu fioletowego widma widzialnego, współczynnik
za
łamania wzrasta i wzrasta również odchylenie promieni świetlnych przechodzących przez
pryzmat, tj. ma miejsce dyspersja normalna.
o
Fala elektromagnetyczna propaguje si
ę wewnątrz płytki z prędkością u < c.
o
Stosunek c/u = n nazywamy wspó
łczynnikiem załamania.
o
Dla wi
ększości ciał stałych, współczynnik załamania równy jest w przybliżeniu 1.5; oznacza to, że
pr
ędkość światła w tych ciałach jest niższa o około 33
%
.

Pole promieniowania
ładunków punktowych
Za
łóżmy, że w jednostce objętości znajduje się N ładunków. Jeżeli każdy ładunek q drga według
prawa
t
sin
y
y
o
ω
=
,
to g
ęstość prądu wynosi
t
cos
y
Nq
j
o
ω
ω
=
,
a pr
ąd w warstwie o grubości
∆x wynosi
t
cos
)
x
y
q
N
(
x
j
J
o
ω
∆
ω
∆
=
=
Wówczas stosuj
ąc wyrażenie (9.7), pole promieniowania jest określone wzorem
)
kx
t
cos(
x
y
Nq
c
E
o
o
y
−
=
ω
∆
ω
µ
2
(9.19)
Za
łóżmy teraz, że zamiast rozkładu ładunków mamy pojedynczy ładunek q drgający według prawa
t
sin
y
y
o
ω
=
. Korzystaj
ąc z równania Maxwella można pokazać, że w odległości r od ładunku q pole
promieniowania okre
ślone jest wyrażeniem
θ
ω
π
ω
µ
sin
c
r
t
sin
r
y
q
E
o
o
−
=
4
2
(9.20)
gdzie
θ jest kątem pomiędzy wektorem przyśpieszenia a wektorem wodzącym (rys. 9.14).
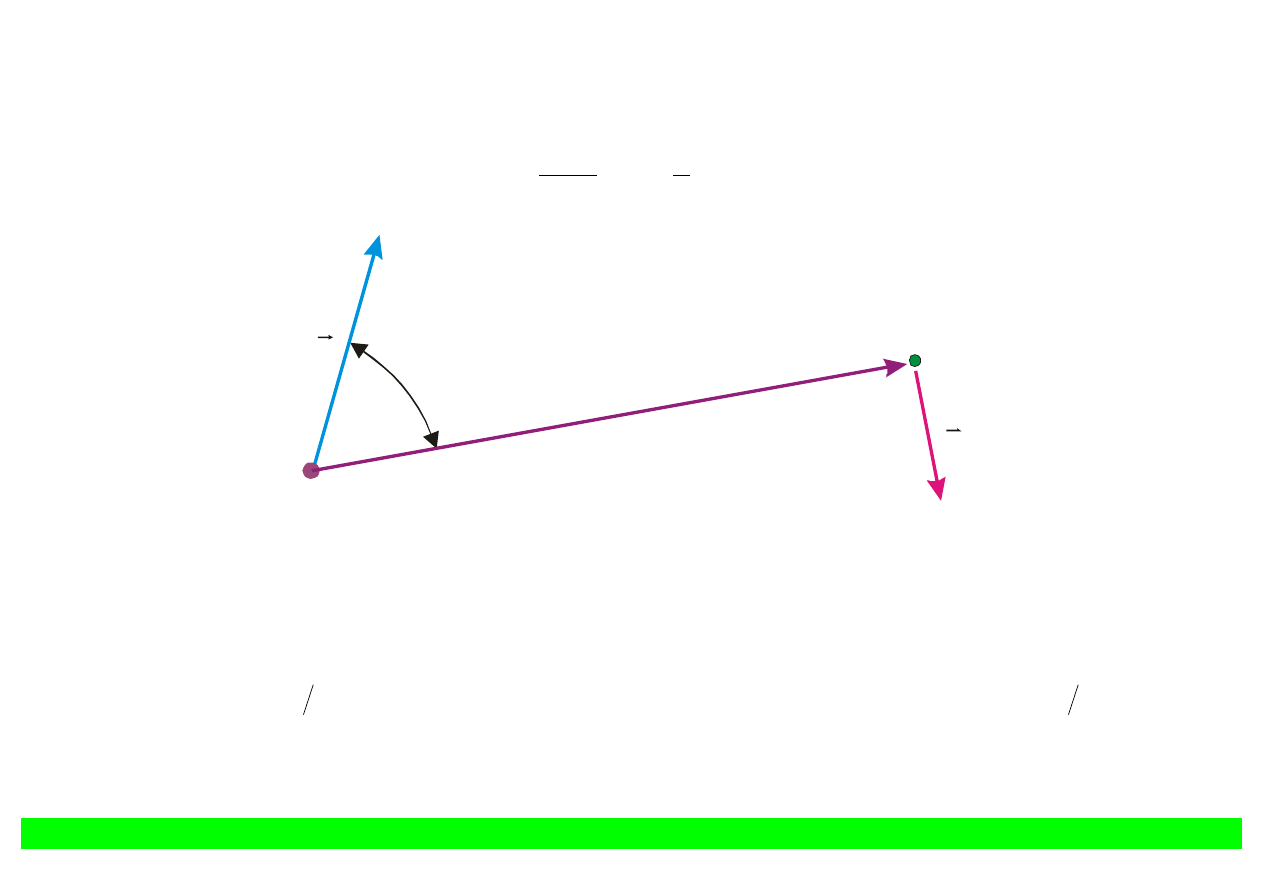
Uwzgl
ędniając, że przyśpieszenie
t
sin
y
a
o
ω
ω
2
−
=
, mamy
θ
π
µ
sin
c
r
t
a
r
q
E
o
−
−
=
4
(9.21)
q
P
q
E
a
θ
Rys. 9.14. Kierunek pola promieniowania
E
r
wytwarzanego przez
ładunek punktowy q
poruszaj
ący się z przyśpieszeniem
a
r
.
We wzorze tym
(
)
c
r
t
a
−
oznacza przy
śpieszenie z wcześniejszej chwili czasu
c
r
t
−
. Wektor
E
r
skierowany jest prostopadle do wektora wodz
ącego
r
r
(rys. 9.14). Wzór (9.21) jest poprawny gdy
c
v
<<
. Kierunek pola B
r
jest prostopad
ły do
E
r
i
r
r
i tak jak poprzednio B = E/c.
Interferencja fal elektromagnetycznych
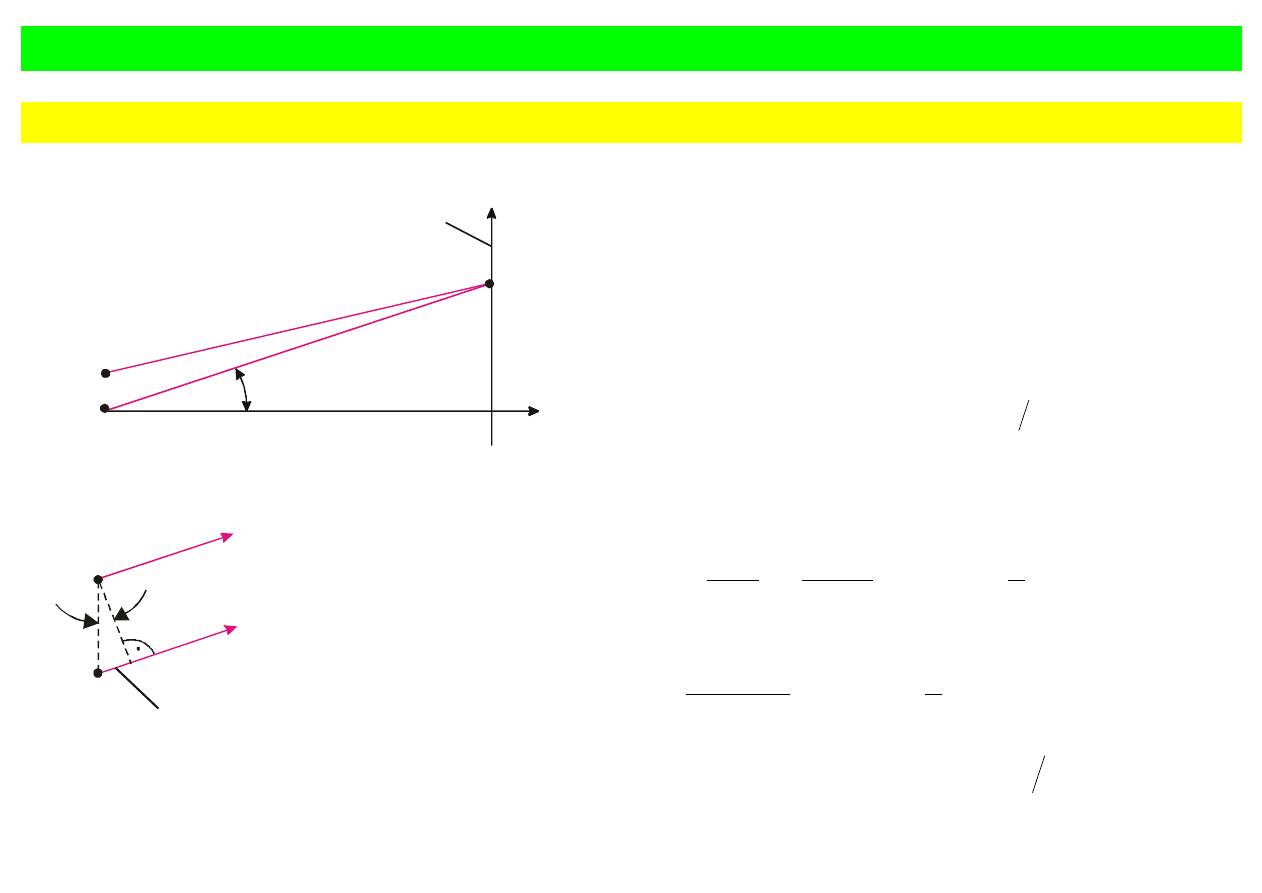
Interferencja fal promieniowanych przez dwa
źródła punktowe
(a)
(b)
d
O
Ekran
x
y
P
S
1
S
1
S
2
S
2
r
1
r
1
r
2
r
2
dsin
θ
θ
θ
Rys. 9.15. (a) Dwa
źródła S
1
i S
2
w
odleg
łości d od siebie. (b) Powyższe
źródła w powiększeniu. Różnica dróg
θ
sin
d
r
r
≈
−
1
2
.
Rozwa
żmy dwa dipole elektryczne S
1
i S
2
drgaj
ące
w fazie w kierunku osi z (rys. 9.15). Przyjmijmy,
że
moment dipolowy okre
ślony jest wzorem
t
cos
p
t
cos
qz
qz
p
o
o
ω
ω
=
=
=
.
Wówczas przy
śpieszenie ładunku dipola
(
)
t
cos
q
p
t
cos
z
a
o
o
ω
ω
ω
ω
2
2
−
=
−
=
Podstawiaj
ąc to wyrażenie do (9.21) znajdujemy
pole promieniowania dipola w postaci
(
)
t
kr
cos
E
c
r
t
cos
r
p
c
r
t
cos
q
p
r
q
E
o
o
o
o
o
ω
ω
π
ω
µ
ω
ω
π
µ
−
=
−
=
−
−
−
=
4
4
2
2
poniewa
ż
1
=
Θ
sin
i
r
p
E
o
o
π
ω
µ
4
2
=
.
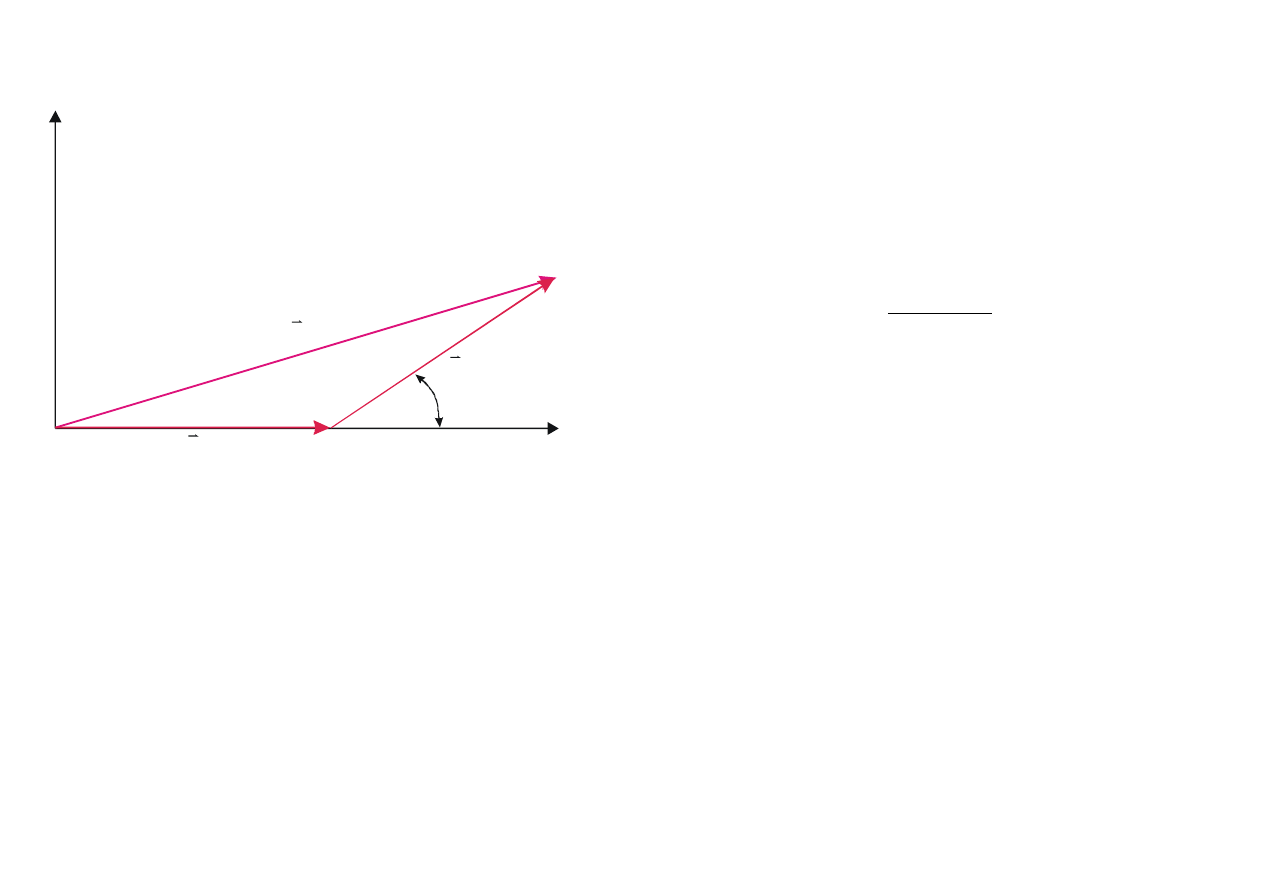
ϕ
E
1
E
2
E
x
y
O
Rys. 9.16. Wykres fazowy dla przypadku
dwóch
źródeł o różnicy faz
ϕ.
Zgodnie z tym wyra
żeniem, pole elektryczne w
punkcie P
(
)
(
)
t
kr
cos
E
t
kr
cos
E
E
E
E
o
o
ω
ω
−
+
−
=
+
=
2
1
2
1
gdzie
r
p
E
o
o
o
π
ω
µ
4
2
=
K
ąt
ϕ
mi
ędzy wektorami jest równy różnicy faz pól
1
E
r
i
2
E
r
(
) (
) (
)
1
2
1
2
r
r
k
t
kr
t
kr
−
=
−
−
−
=
ω
ω
ϕ
Pole wypadkowe
)
cos
(
E
cos
E
E
E
E
o
o
o
o
2
ϕ
ϕ
+
=
+
+
=
1
2
2
2
2
2
2
Nat
ężenie fali, I, jest proporcjonalne do kwadratu amplitudy, dlatego
(
)
[
]
1
2
1
2
r
r
k
cos
I
I
o
−
+
=
.
Ró
żnica dróg
θ
sin
d
r
r
=
−
1
2
, je
żeli odległość od ekranu jest dostatecznie duża.
Warunek, dla którego ró
żnica dróg jest równa dsin
θ, nazywany jest przybliżeniem Fraunhofera
.
W tym przypadku
[
]
)
sin
kd
cos(
I
I
o
θ
+
=
1
2
(9.22)
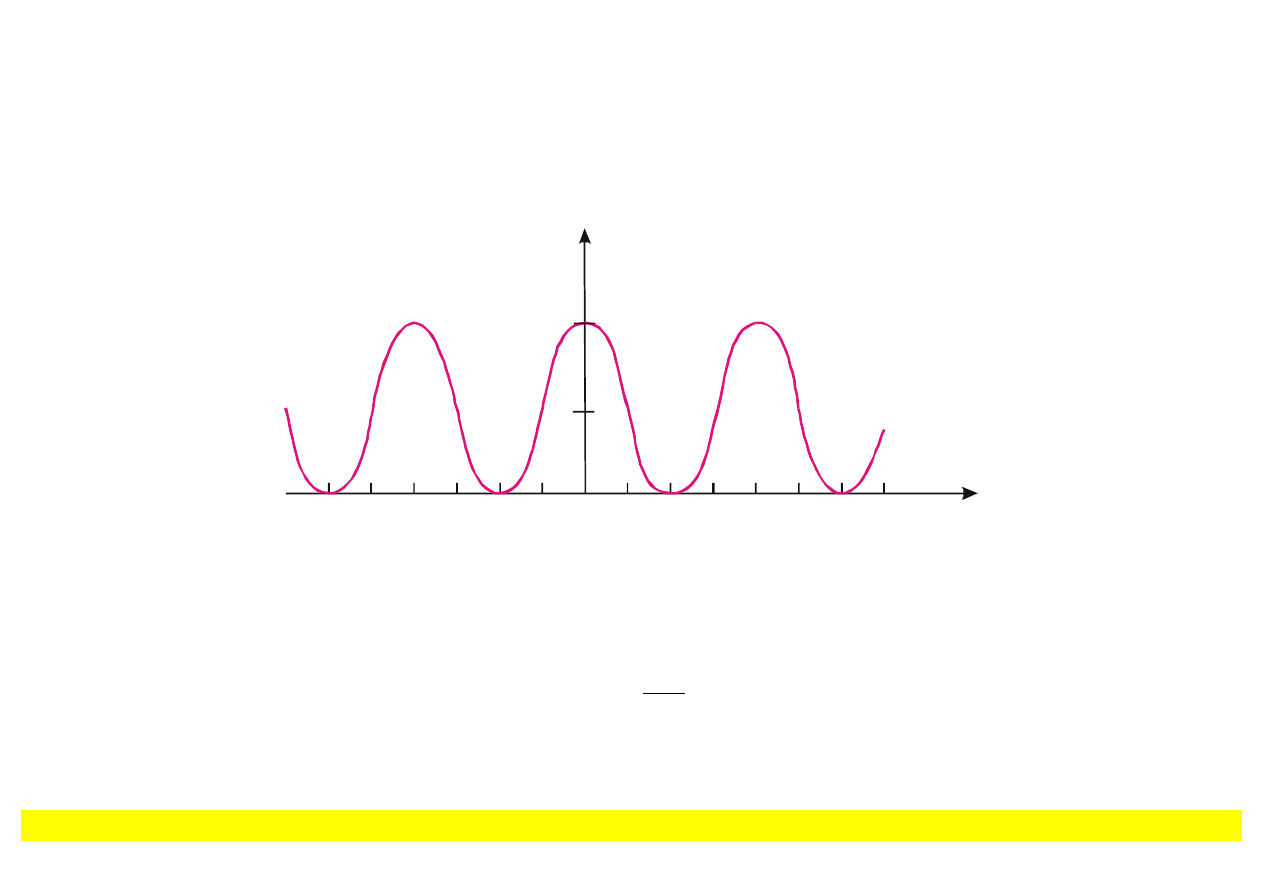
I
4I
o
0
sin
θ
λ
/2d
λ
/d
Rys. 9.17. Obraz interferencyjny od dwóch
źródeł. Pokazano zależność intensywności od sin
θ.
Maksimum intensywno
ści obserwuje się zawsze, gdy
π
θ 2
=
sin
kd
, czyli gdy
d
n
sin
λ
θ
=
(9.23)
W tym przypadku ró
żnica dróg, która zgodnie z (9.23) jest równa dsin
θ, wynosi nλ.
Interferencja fal od wi
ększej liczby źródeł
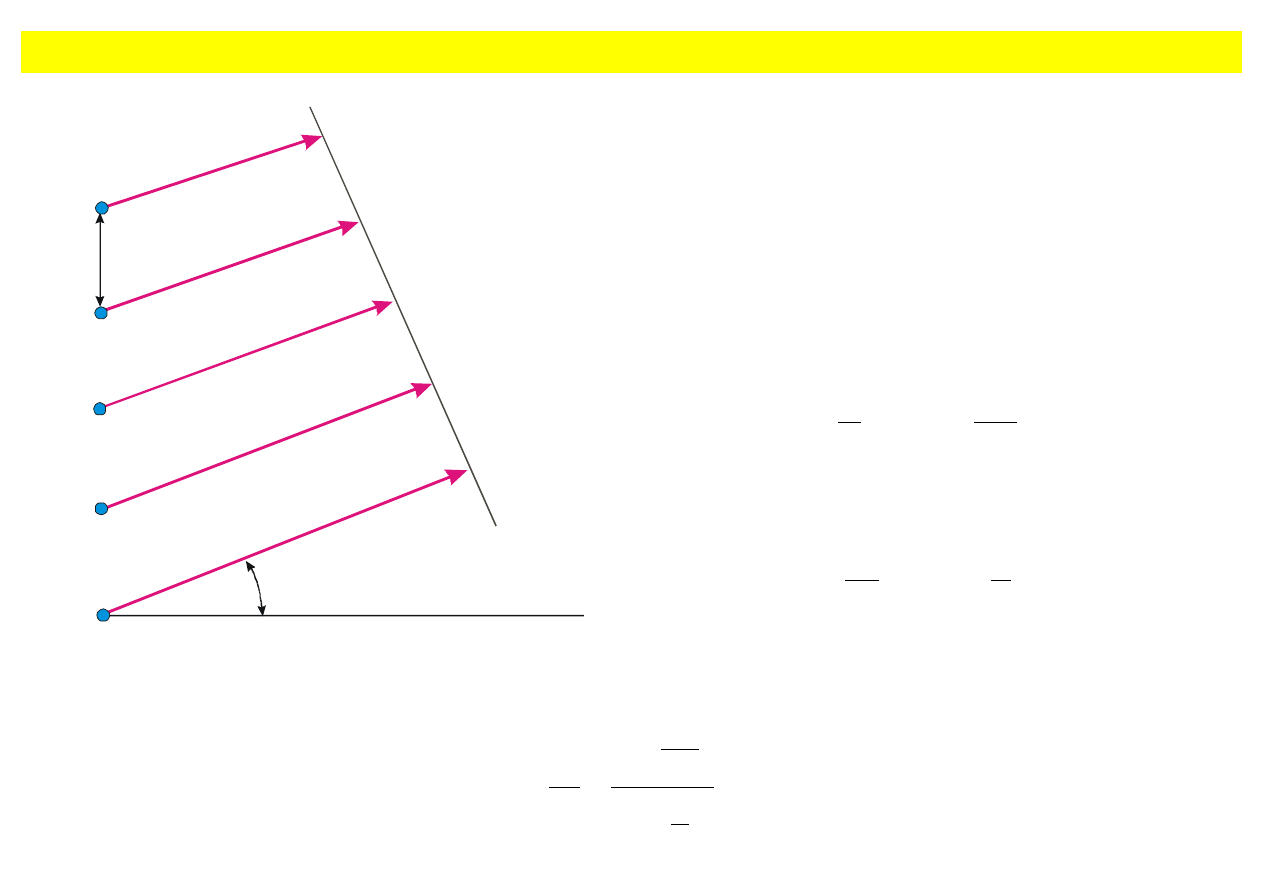
r
1
S
1
S
2
S
3
S
N
r
2
r
3
r
N
d
θ
Rys. 9.18. N
źródeł we wzajemnej odległości d.
Za
łóżmy, że obserwator położony jest pod
k
ątem
θ względem normalnej do linii łączącej N
równomiernie rozmieszczonych
źródeł (rys.
9.18). Dla obserwatora ró
żnica faz pomiędzy
s
ąsiednimi źródłami jest równa
(
)
θ
ϕ
sin
kd
r
r
k
=
−
=
1
2
.
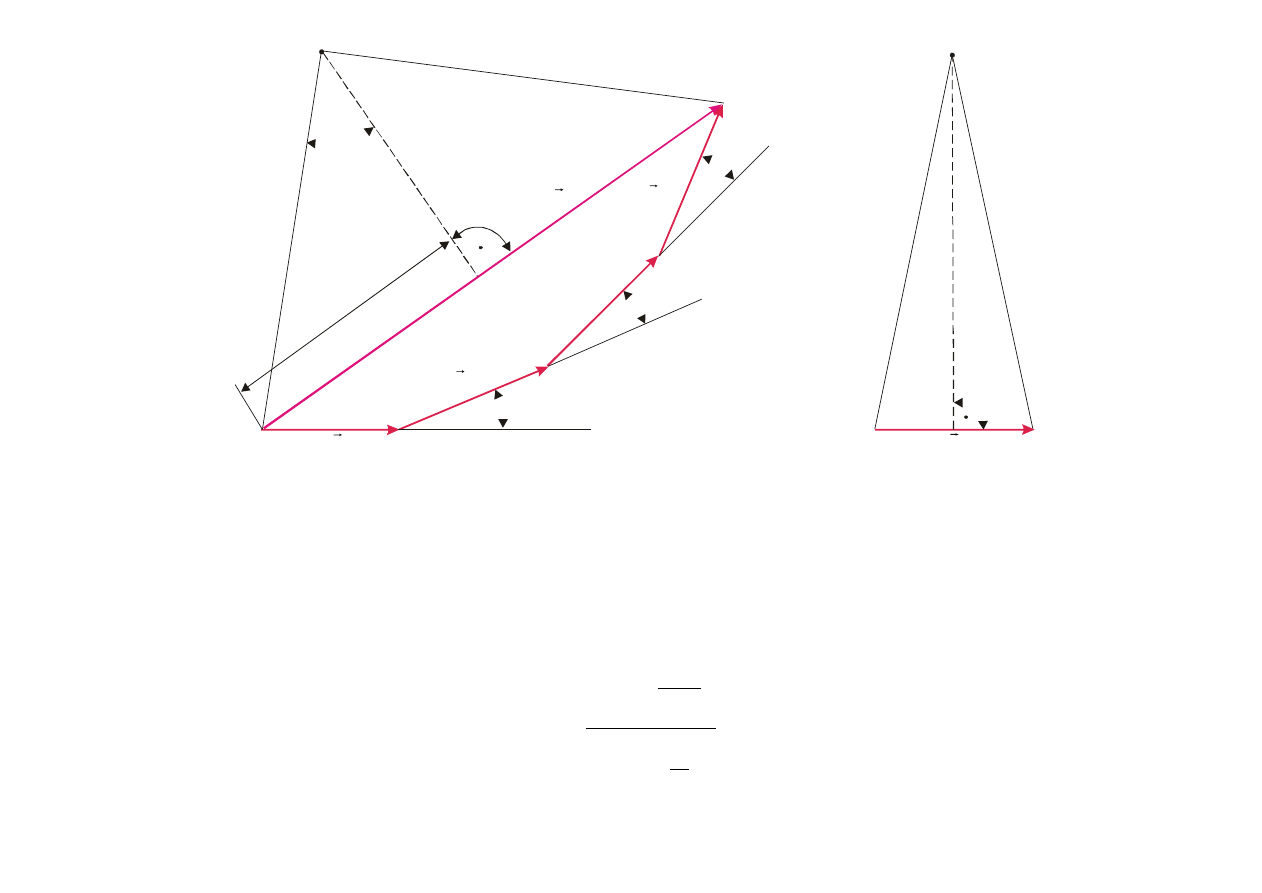
Z trójk
ąta równoramiennego z rys. 9.19a mamy
=
2
2
ϕ
N
sin
R
E
Z kolei z trójk
ąta prostokątnego na rys. 9.19b
mamy
=
2
2
1
ϕ
sin
R
E
Dziel
ąc stronami dwa ostatnie równania
=
2
sin
2
N
sin
E
E
1
ϕ
ϕ
E’
/2
ϕ
ϕ
ϕ
R
R
0
0
R
N /2
ϕ
(a) (b)
1
E
1
E
2
E
N
E
E
2
ϕ
Rys. 9.19. (a) Wykres fazowy dla przypadku N
źródeł przedstawionych na rys. 9.18, końce
wektorów po
łożone są na okręgu o promieniu R. (b) Wykres dla pierwszego źródła.
i po podniesieniu do kwadratu
=
2
2
2
2
ϕ
ϕ
sin
N
sin
I
I
o
(9.24)
gdzie I
o
jest nat
ężeniem fali pojedynczego źródła, a
θ
ϕ
sin
kd
=
.
sin
θ
λ
/d
−λ
/d
2λ
/d
0
10I
o
I
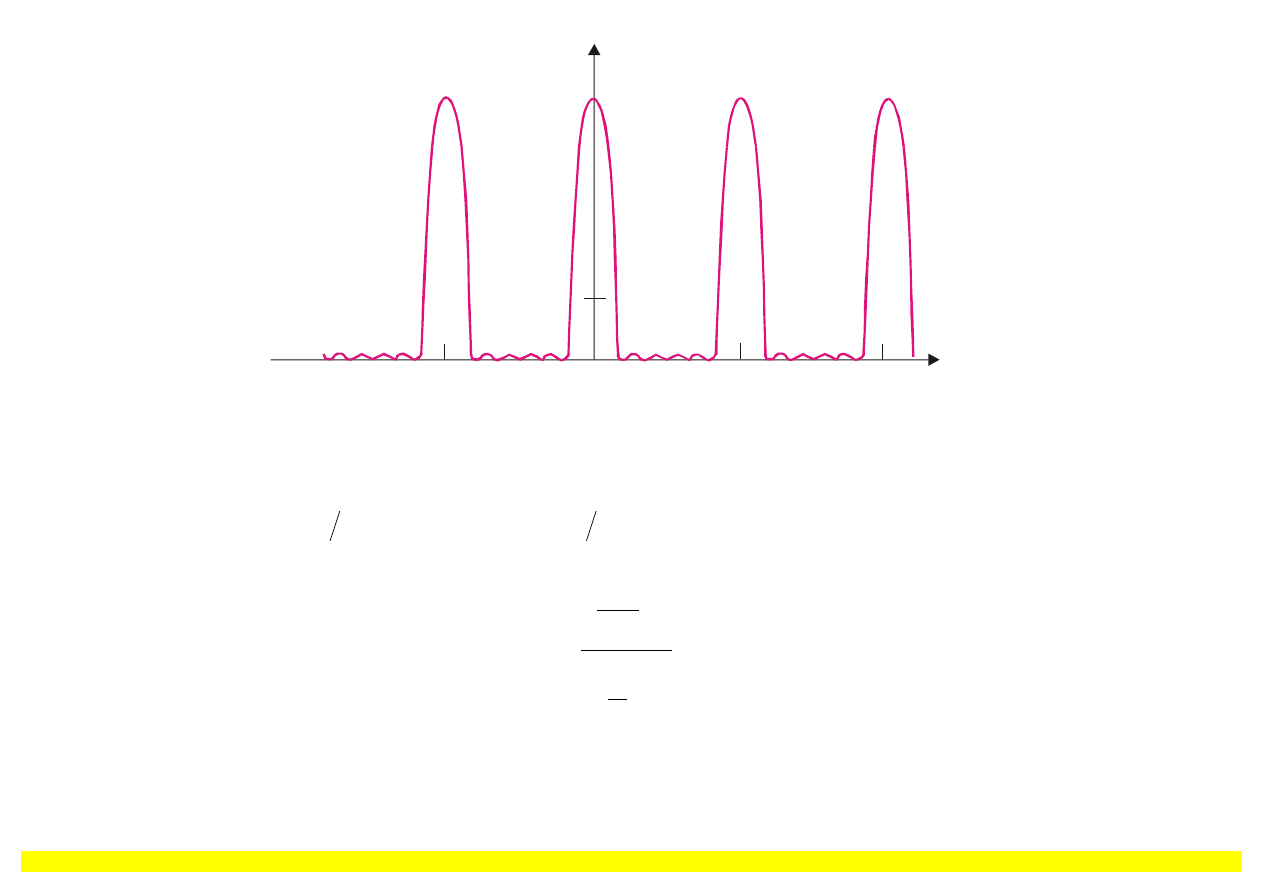
Rys. 9.20. Obraz interferencyjny od sze
ściu źródeł położonych w jednej linii.
Na rys. 9.20 pokazano rozk
ład natężenia określony wzorem (9.24). Należy zaznaczyć, że dla
0
→
ϕ
mamy
(
)
2
2
ϕ
ϕ
N
/
N
sin
→
, a
(
)
2
2
ϕ
ϕ
→
/
sin
, wtedy zwi
ązek (9.24) można napisać w postaci
o
o
I
N
N
I
I
2
2
2
2
2
=
→
ϕ
ϕ
Wobec tego nat
ężenie fali wytworzonej przez N źródeł okazuje się N
2
razy wi
ększe od natężenia fali
pojedynczego
źródła.

Siatka dyfrakcyjna
Dla siatki dyfrakcyjnej rozk
ład natężenia na ekranie określa wzór
=
2
2
2
2
ϕ
ϕ
sin
N
sin
I
I
o
gdzie
θ
ϕ
sin
kd
=
.
Nat
ężenie przyjmuje wartość
o
I
N
I
2
=
w tych przypadkach, kiedy mianownik przyjmuje warto
ść
zerow
ą, czyli kiedy
n
n
π
ϕ
2
=
lub
n
sin
kd
n
π
θ
2
=
st
ąd
d
n
sin
n
λ
θ
=
(9.25)
θ
0
I
Do
ekranu
Od
źródła
dsin
θ
(a) (b)
θ
θ
1
θ
2
−θ
2
−θ
1
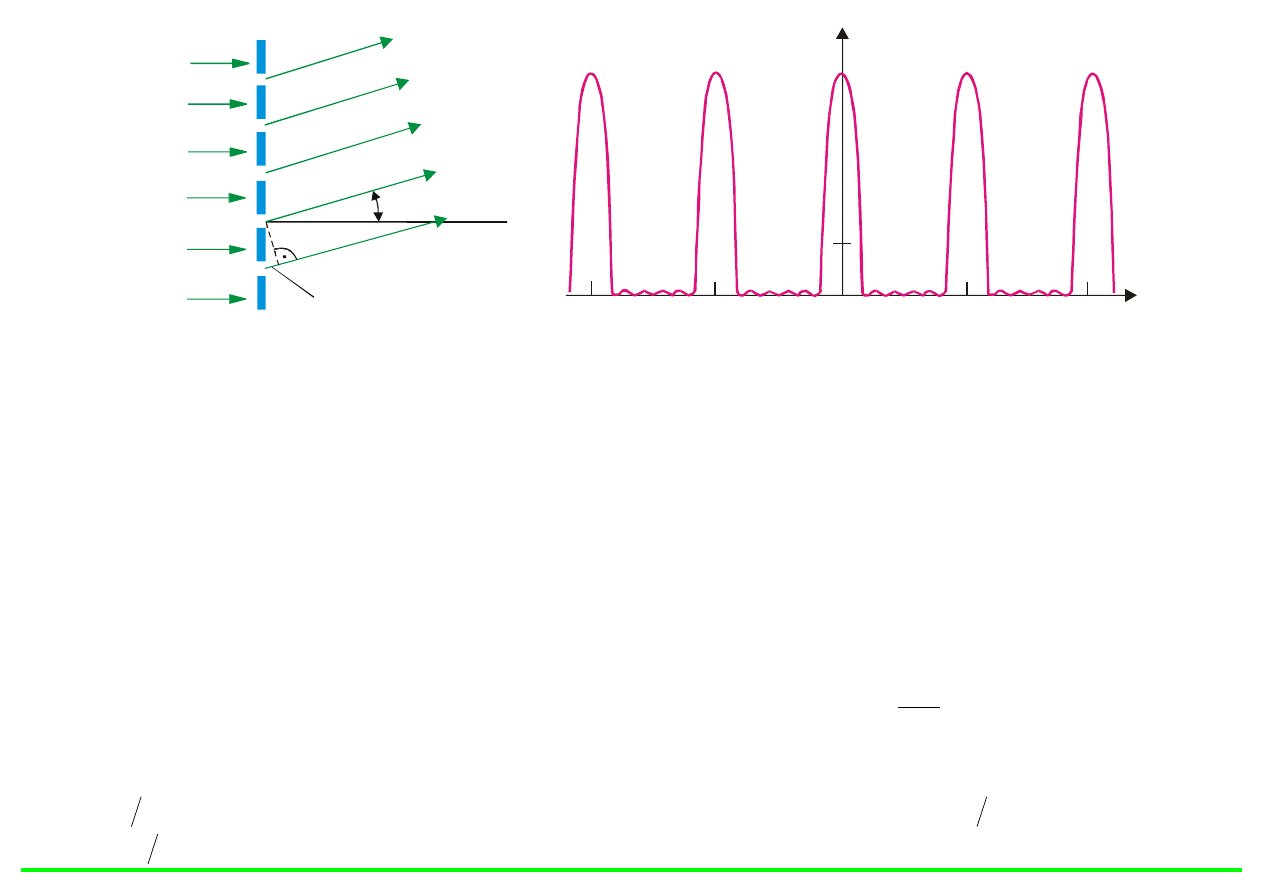
Rys. 9.21. (a) Cz
ęść siatki dyfrakcyjnej w powiększonej skali. (b) Rozkład natężenia na ekranie.
Dla pozosta
łych kątów
θ natężenie I w przybliżeniu jest równe I
o
, tj. oko
ło N
2
razy mniejsze.
W typowych siatkach dyfrakcyjnych warto
ść N wynosi kilka tysięcy.
Z pomoc
ą rys. 9.21a nietrudno otrzymać warunek (9.25); różnica dróg dla każdej pary sąsiednich
promieni musi wynosi
ć n
λ. Ponieważ ta różnica dróg wynosi dsinθ, otrzymamy
λ
θ n
sin
d
=
lub
d
n
sin
λ
θ
=
Linia spektralna odpowiadaj
ąca długości fali
λ jest obserwowana pod kątem określonym związkiem
d
sin
λ
θ
=
. Obraz linii drugiego rz
ędu będzie odpowiadać
d
sin
λ
θ 2
=
, trzeciego rz
ędu
d
sin
λ
θ 3
=
, itd.
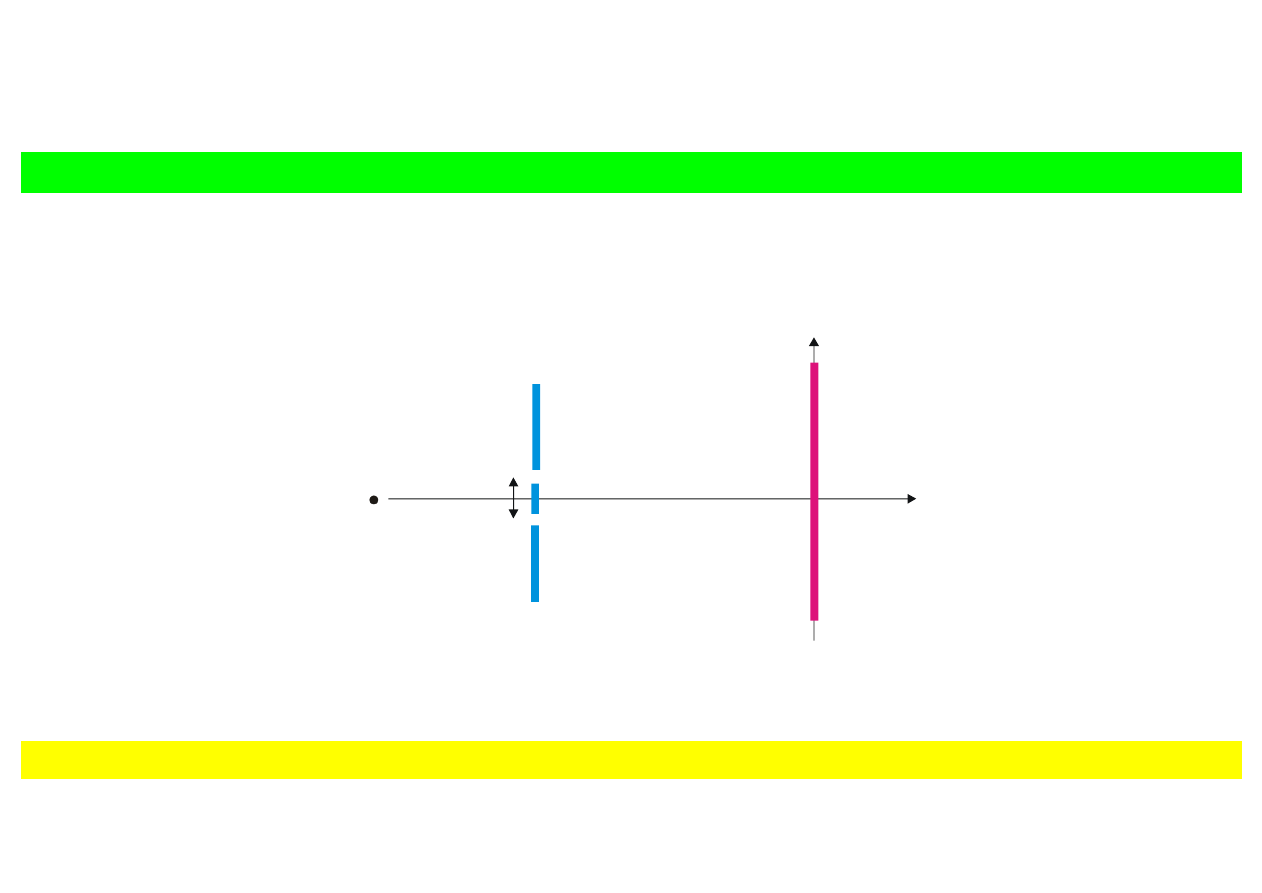
Dyfrakcja
światła
Dwie szczeliny o
świetlone są pojedynczym źródłem światła. Rozkład natężenia światła na ekranie
opisany jest wzorem (9.22) i przedstawia taki obraz jakby szczeliny by
ły zastąpione przez dwa źródła
światła. Pierwszy taki eksperyment przeprowadził Thomas Young w 1803 r.
d
Źródło
Ekran
Przys
łona
y
x
0
Rys. 9.22. Schemat do
świadczenia interferencji światła z dwóch szczelin.

Zasada Huygensa
W XVIII w. Christian Huygens sformu
łował następującą zasadę, nie dowodząc jej:
je
żeli czoło fali
przechodzi przez jeden lub kilka otworów, ka
żdy element czoła fali zachowuje się tak jakby był
źródłem fali
.
Na pierwszy rzut oka mo
że to wydawać się dziwne, gdy odniesiemy to do np. siatki dyfrakcyjnej. W
otworach nie mamy
źródeł prądu; prądy mogą indukować się w dowolnym miejscu ekranu za
wyj
ątkiem otworów.
Wyka
żemy matematycznie, że promieniowane przez źródło prądu pole zapełniające otwór w
ekranie jest zgodne z polem fali padaj
ącej na ekran z otworami
.
Oznaczamy pole promieniowane przez pr
ądy indukowane w ekranie jako E
ekr
. Wówczas na prawo od
ekranu wypadkowe pole zapiszemy w postaci
ekr
pad
wyp
E
E
E
+
=
(9.26)
gdzie E
pad
jest polem wytwarzanym przez
źródło w nieobecności ekranu.
Teraz zakryjmy otwory dodatkowymi ekranami, których rozmiary s
ą zgodne z rozmiarami otworów.
Niech E
otw
oznacza pole promieniowane przez pr
ądy w ekranach zakrywających otwory. Wówczas
mamy
0
=
+
+
=
otw
ekr
pad
wyp
E
E
E
E
na prawo od ekranu, st
ąd

2
2
ekr
pad
otw
ekr
pad
otw
E
E
E
E
E
E
+
=
+
=
−
Prawa strona tego równania jest zgodna z polem odpowiadaj
ącym realnej sytuacji fizycznej [wzór
(9.26)]; a lewa
świadczy o tym, że sytuacja ta jest matematycznie równoważna rozkładowi
intensywno
ści promieniowania wywołanego źródłami prądów położonych w otworach i emitujących
promieniowanie niezale
żnie od siebie.
Wykazali
śmy, że jeżeli każdy element frontu falowego przechodzącego za ekran traktować jako
nowe punktowe
źródło, to rozkład intensywności będzie identyczny jak w przypadku ekranu i
oddzielnego
źródła
.
Jednak
że rozważania należy nieznacznie skorygować ze względu na efekty graniczne
(przeprowadzony przez nas dowód zak
ładał, że indukowane prądy mogą przecinać krawędzie
otworów).
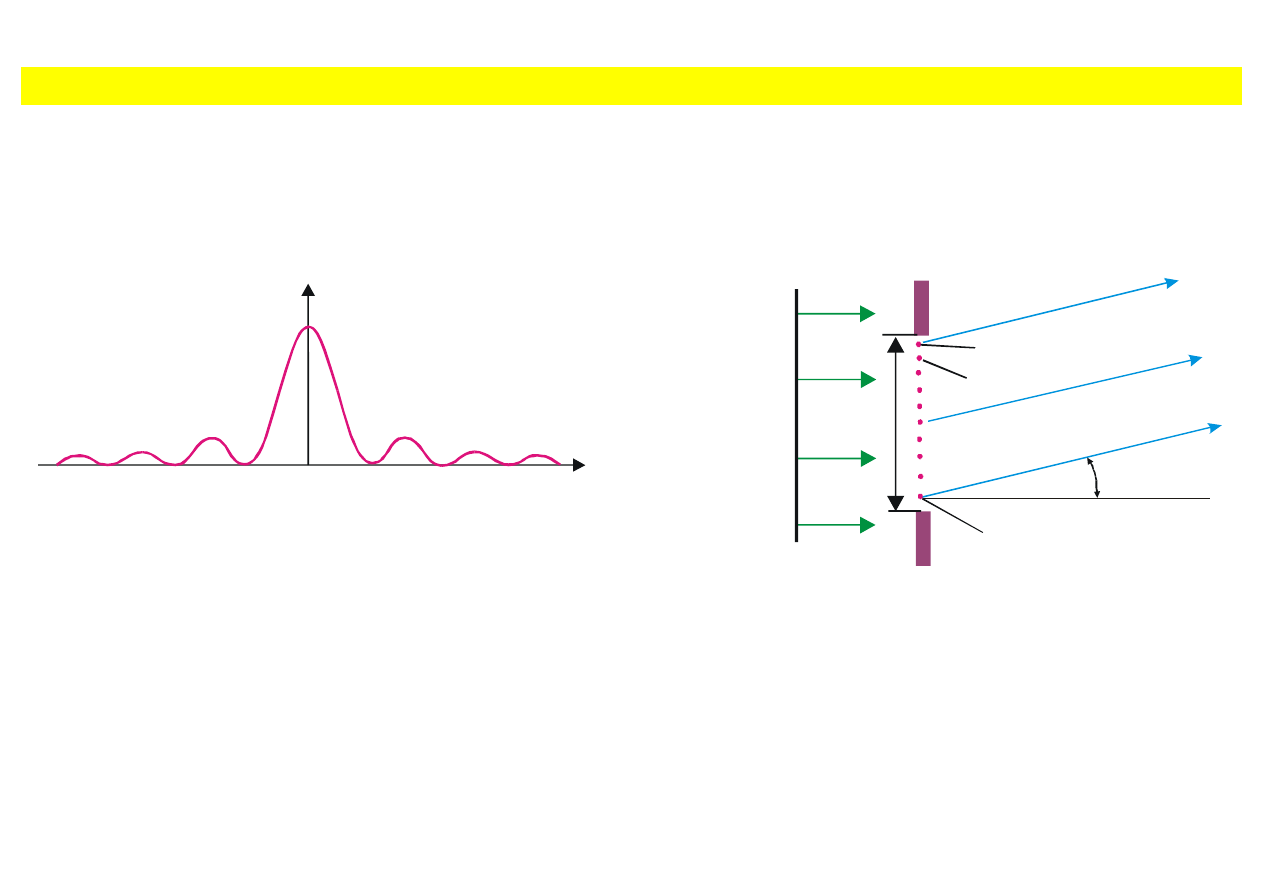
Dyfrakcja na pojedynczej szczelinie
Równoleg
ła wiązka światła monochromatycznego padając na pojedynczą szczelinę o szerokości a
tworzy na oddalonym ekranie obraz interferencyjny pokazany na rys. 9.23. Podobna interferencja
powstaj
ąca od pojedynczej szczeliny lub od krawędzi ekranu nazywana jest dyfrakcją.
θ
I
Rys. 9.23. Rozk
ład intensywności na
oddalonym ekranie przy dyfrakcji na
pojedynczej szczelinie.
S
1
S
2
S
N
a
θ
1
2
3
Padaj
ący
front falowy
Rys. 9.24. Promieniowanie od pojedynczej
szczeliny. Promienie 1 i 3 wychodz
ą od
kraw
ędzi, a promień 2 ze środka szczeliny.
Korzystaj
ąc z rys. 9.24 łatwo można określić kąt
θ, przy którym obserwuje się pierwsze minimum
nat
ężenia. Zgodnie z zasadą Huygensa szczelinę możemy traktować jako zbiór pojedynczych źródeł
N
2
1
S
,.....
S
,
S
.
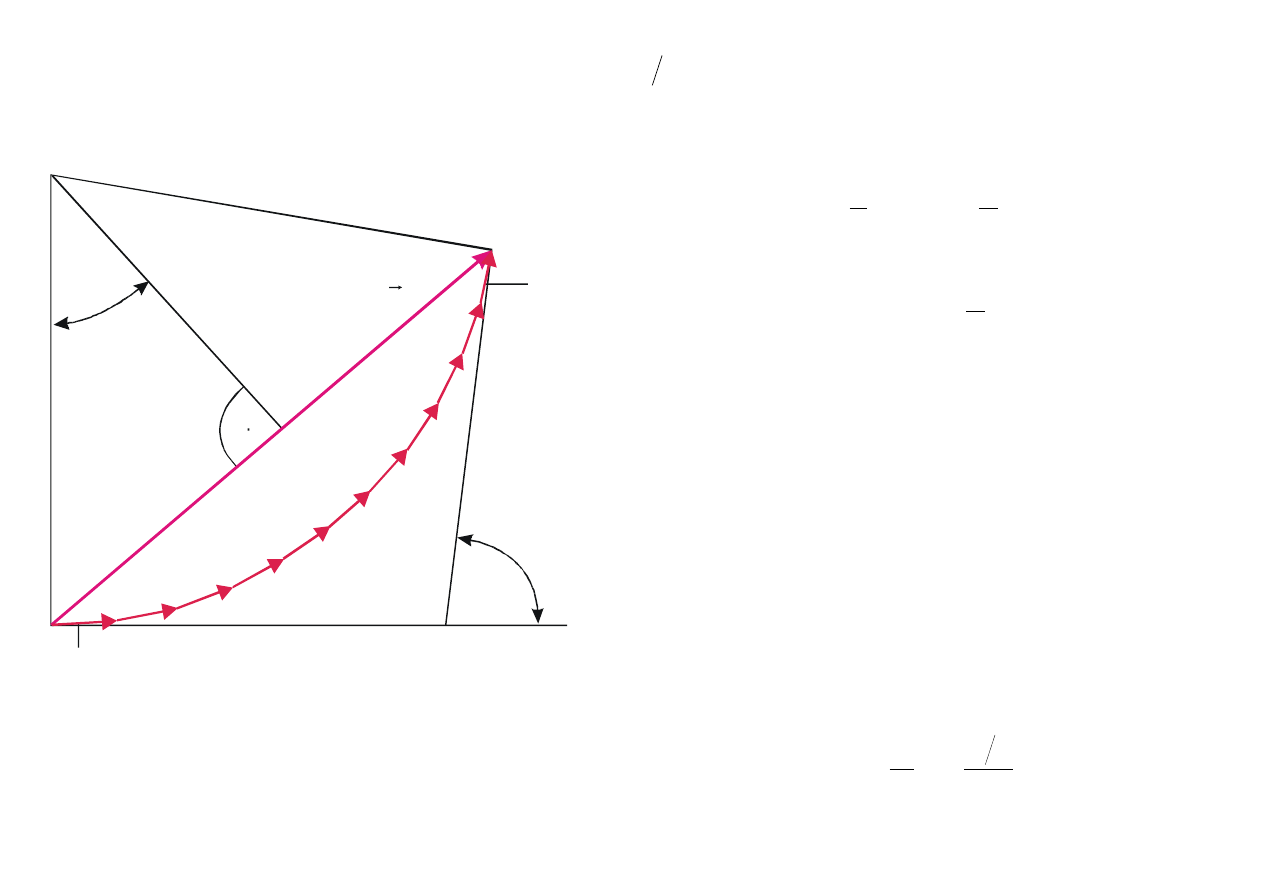
Ró
żnica dróg między promieniami 1 i 2 wynosi
( )
θ
sin
a 2
. Aby uzyska
ć różnicę faz między nimi
wynosz
ącą
π
, ró
żnica dróg powinna wynosić
λ/2. Kąt odpowiadający pierwszemu minimum natężenia
okre
ślony jest z równania
Φ
/2
Φ
R
R
A/2
od S
1
od S
N
A
Rys. 9.25. Wektor
A
r
stanowi sum
ę wektorową
sygna
łów od N źródeł przedstawionych na
rys. 9.18.
Φ oznacza różnicę faz pomiędzy
pierwszym a ostatnim
źródłem.
2
2
1
λ
θ
=
sin
a
czyli
a
sin
λ
θ
=
1
(9.27)
Warto
ść natężenia dla dowolnego kąta
θ
otrzymuje si
ę w wyniku zsumowania wkładów
niesko
ńczenie małych źródeł (rys. 9.25).
Odpowiednie wektory tworz
ą łuk, dla którego
wypadkowa ró
żnica faz dla skrajnych promieni
1 i 3 wynosi
θ
Φ
sin
ka
=
Wypadkow
ą amplitudę A można znaleźć z
trójk
ąta prostokątnego
R
A
sin
2
2
=
Φ
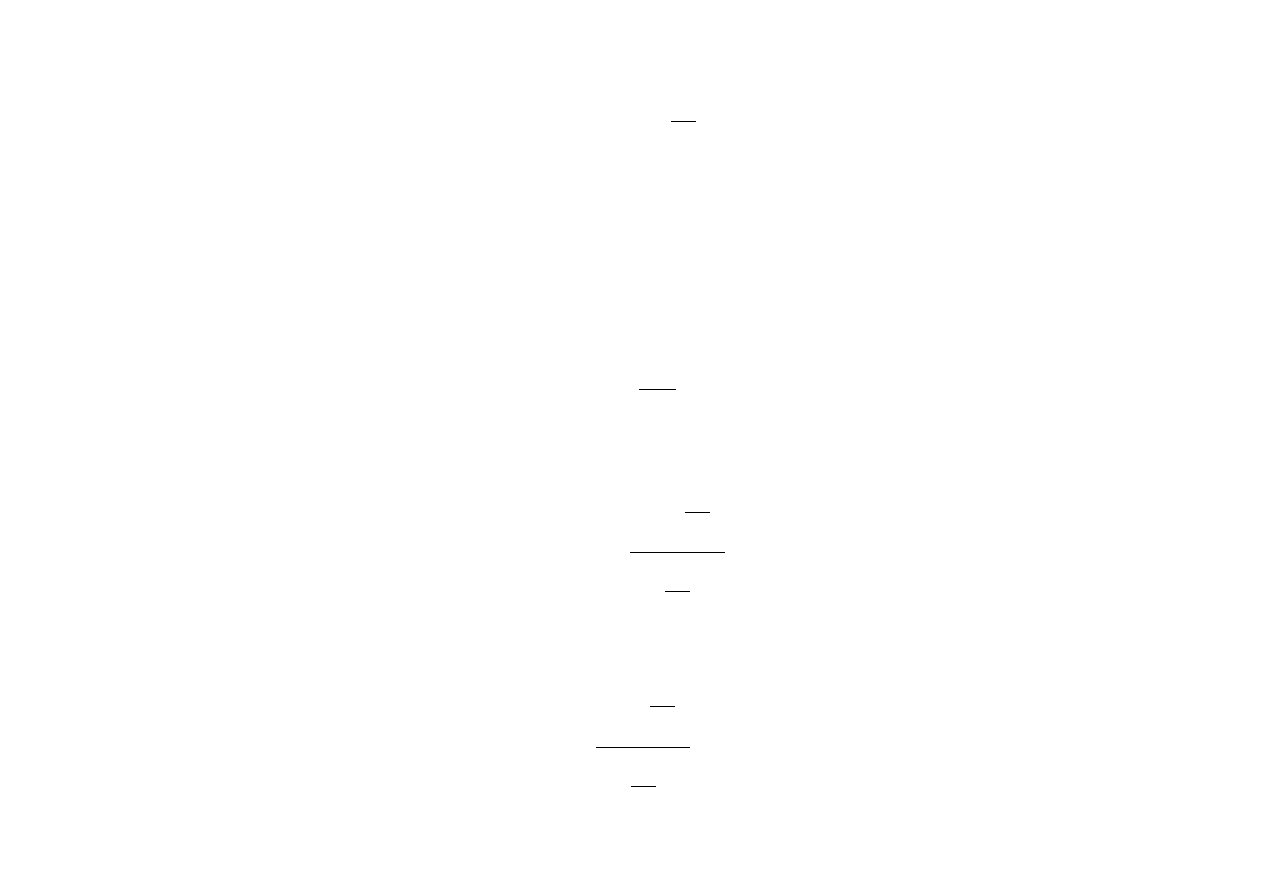
st
ąd
=
2
2
Φ
sin
R
A
(9.28)
D
ługość łuku równa jest A
o
. Jest to wypadkowa amplituda widziana pod k
ątem 0
°
, równa promieniowi
R pomno
żonemu przez kąt
Φ ( w radianach)
o
A
R
=
Φ
St
ąd znajdujemy
Φ
o
A
R
=
Podstawiaj
ąc tę wielkość do (9.28) mamy
2
2
Φ
Φ
=
sin
A
A
o
Rozk
ład natężenia
2
2
2
=
Φ
Φ
sin
I
I
o
(9.29)
gdzie
θ
Φ
sin
ka
=
.

Kolejne minima obserwuje si
ę przy
π
Φ
n
=
2
, lub przy
π
θ
n
sin
ka
=
2
czyli
a
n
sin
min
λ
θ
=
(n
≥
1)
Warunek ten jest zgodny z otrzymanym poprzednio.

Koherentno
ść i niekoherentność
Dotychczas badali
śmy
efekty interferencyjne wywo
łane źródłami, które znajdowały się w fazie
wzgl
ędem siebie lub z pewną stałą różnicą faz. Takie źródła nazywamy koherentnymi lub
spójnymi
.
Koherentno
ść dwu wiązek określa ich zdolność do interferowania; wiązki spójne interferują, wiązki
niespójne s
ą tej właściwości pozbawione.
Koherentne wi
ązki światła można również otrzymać stosując półprzezroczyste zwierciadła – jak w
interferometrze Michelsona. Jednak
że w przypadku, kiedy obydwa ramiona interferometru mają różną
d
ługość, obraz interferencyjny może zniknąć, jeżeli różnica dróg optycznych przekracza pewną
wielko
ść
∆L
o
odpowiadaj
ącą różnicy czasu
∆t
o
=
∆L
o
/c.
Wielko
ść
∆L
o
nazwana jest d
ługością
koherentno
ści, a
∆t
o
– czasem koherentno
ści
.
Linie emisyjne
źródła interferometru charakteryzują się szerokością
f
∆
w skali cz
ęstotliwości.
Szeroko
ść ta związana jest z czasem koherentności
o
t
∆
zwi
ązkiem
1
2
≈
o
t
f
∆
∆
π

o
Z mechaniki kwantowej wiadomo,
że światło stanowią fotony emitowane przez różne atomy.
o
Ci
ąg fal emitowanych nie jest nieskończenie długi (jest niekoherentny).
o
Wi
ązka światła niekoherentnego składa się z ciągu fal o skończonej długości, poprzedzielanych
przypadkowymi przerwami.
o
Docieraj
ące do punktu obserwacji dwie takie wiązki nakładają się na siebie, ale różnica faz ciągów
fal obu wi
ązek zmienia się chaotycznie, wskutek czego interferencja nie zachodzi.
o
Jednak
że w odcinku czasu
f
t
o
∆
π
∆
2
1
=
, gdzie
∆f jest obserwowaną szerokością linii, dowolna
para fotonów b
ędzie zachowywać względem siebie stałą fazę. Fotony te zachowują się jak paczki
falowe o d
ługości
f
c
t
c
L
o
o
∆
π
∆
2
≈
=
.
o
Cz
ęstotliwość źródła światła monochromatycznego zmienia się w przedziale
(
)
2
f
f
o
∆
−
do
(
)
2
f
f
o
∆
+
. Dwie czysto sinusoidalne fale ró
żnią się częstotliwościami o
∆f, będą się różnić w
fazie w czasie
f
t
∆
π
∆
2
1
≈
.
o
Najbardziej w
ąskim liniom widm atomowych odpowiada
≈
o
t
∆
10
–8
s.
o
W laserze dryf cz
ęstotliwości jest mniejszy i dlatego czas koherentności jest większy.
o
Koherentno
ść to najważniejsza i najcenniejsza własność światła laserowego.
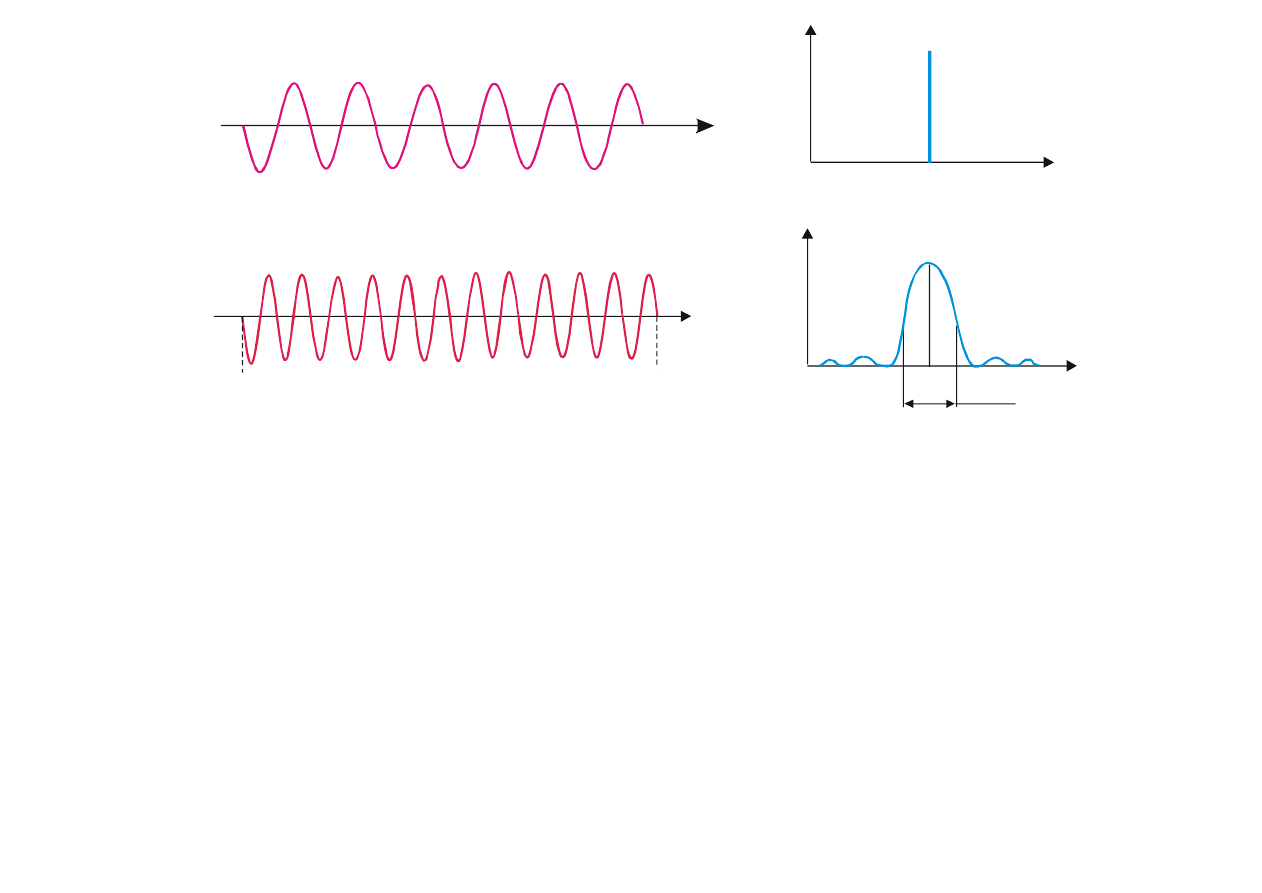
Drgania o czasie trwania t
∆
Drgania harmoniczne
N
a
tę
że
n
ie
N
a
tę
że
n
ie
Widmo
Widmo
∆ν
∆
=1/ t
o
+∆
t /2
o
−∆
t /2
o
(a)
(b)
ν
ν
Rys. 9.26. (a) Drgania harmoniczne o widmie liniowym. (b) Drgania o czasie trwania
∆t
o
i
widmie Fouriera.
Wektory
E
r
i
B
r
o niesko
ńczenie długim ciągu falowym opisujemy wzorem typu
( )
t
cos
S
t
S
o
o
ω
=
Drganie, które opisuje powy
ższy wzór jedynie przez czas trwania
o
t
∆
, a poza tym przedzia
łem czasu
S(t) = 0, nie s
ą harmonicznymi; nie charakteryzują się bowiem ściśle określoną częstotliwością, lecz
pewnym widmem cz
ęstotliwości (patrz pkt. 9.2). Drgania te opisuje wzór
( )
( )
ν
πν
ν
d
t
cos
G
t
S
2
∫
∞
∞
−
=

gdzie funkcja G(f) jest amplitud
ą drgań o częstotliwości f, zwana również widmem Fouriera, przy czym
( )
( )
(
)
[
]
(
)
o
o
o
o
o
o
t
t
sin
t
S
dt
t
cos
G
G
∆
ν
ν
π
∆
ν
ν
π
∆
πν
ν
ν
−
−
=
=
∫
∞
∞
−
2
Je
żeli
∆f oznacza szerokość widmową linii, wówczas ∆f = 1/∆t
o
.
Czas
∆t
o
nazywamy czasem
koherentno
ści, a długość
∆L
o
= c
∆t
o
d
ługością koherentności.

Polaryzacja
światła
Za kierunek polaryzacji wybrano kierunek wektora
E
r
.
P
łaszczyzną polaryzacji określa się płaszczyznę, w której leżą wektor
E
r
i wektor kierunku propagacji
fali.
Promieniowanie elektromagnetyczne, którego kierunek pola
E
r
jest sta
ły nazywamy
p
łaskospolaryzowanym, lub spolaryzowanym
liniowo.
W wi
ązce światła żródła niekoherentnego, kierunek pola elektrycznego zmienia się chaotycznie
w przestrzeni pozostaj
ąc jednak prostopadłym do kierunku propagacji fali. Taką wiązkę
nazywamy niespolaryzowan
ą.
Polaryzacja ko
łowa
Wi
ązka 1 spolaryzowana jest pionowo (wektor
1
E
r
po
łożony jest w płaszczyźnie xy), a wiązka 2
spolaryzowana jest poziomo (wektor
2
E
r
po
łożony jest w płaszczyźnie xz).
y
x
z
Strumie
ń
zmieszany
Strumie
ń 1
Strumie
ń 2
Pó
łprzezroczyste
zwierciad
ło
1
E
2
E
Rys.
9.27.
Dwie
wi
ązki
światła
spolaryzowanego
liniowo
zmieszane
za
pomoc
ą
zwierciad
ła
pó
łprzezroczystego.
Pole
2
E
r
skierowane jest na czytelnika z
p
łaszczyzny rysunku równolegle do osi z.
α
y
z
O
o
1
)
E
(
o
2
)
E
(
E
Rys. 9.28. Rzut na p
łaszczyznę yz pól
pokazanych na rys. 9.27.
Obydwie fale opisujemy
(
)
kx
t
cos
E
E
−
=
ω
10
1
;
(
)
kx
t
cos
E
E
−
=
ω
20
2
przy czym kierunki pól E
10
i E
20
tworz
ą kąt prosty (rys. 9.28).
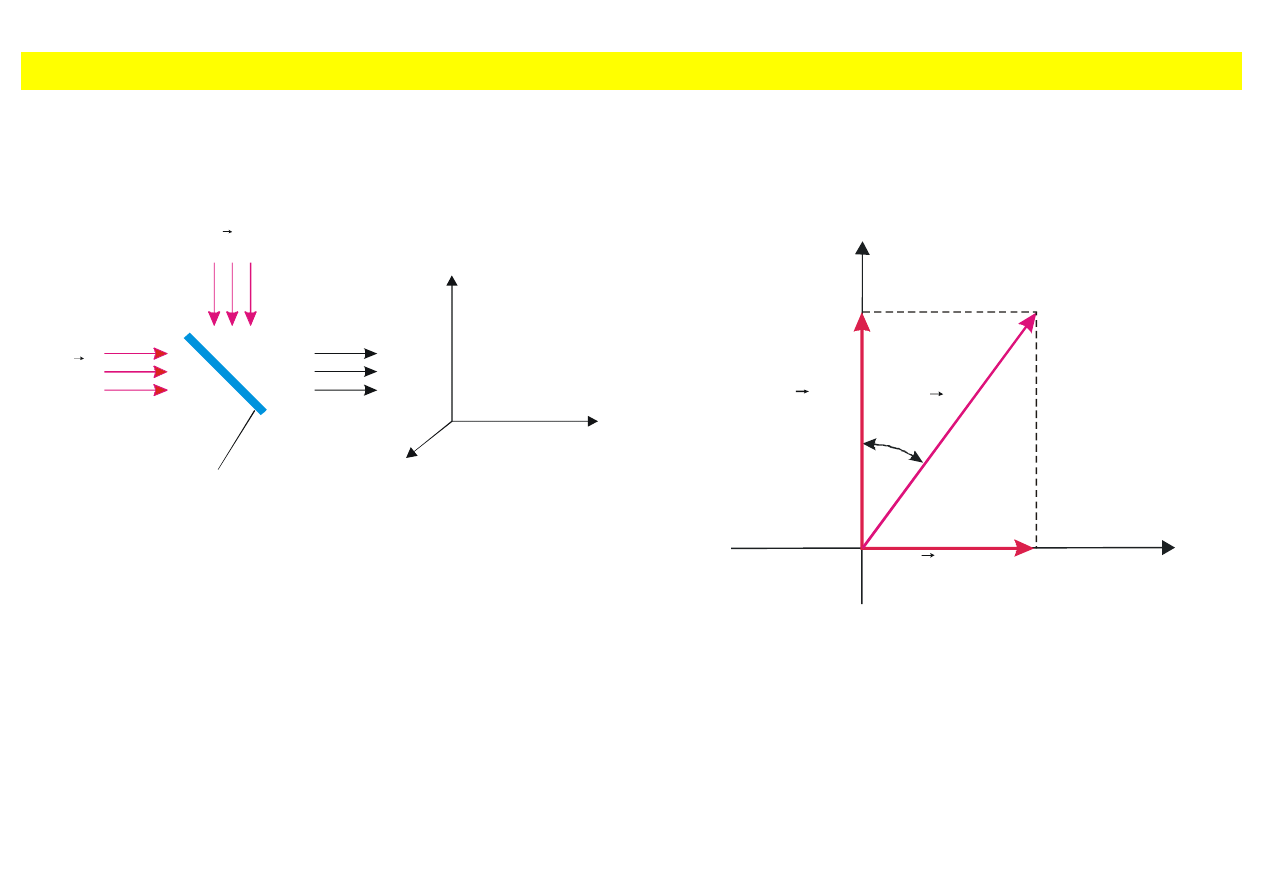
Wektor wypadkowego pola elektrycznego zawsze po
łożony jest w płaszczyźnie, która tworzy kąt
α z
pionem, przy czym
10
20
E
E
tg
=
α
.
Je
żeli
20
10
E
E
=
, to
°
=
45
α
. Wypadkowa wi
ązka światła jest płaskospolaryzowana, przy czym
p
łaszczyzna polaryzacji tworzy kąt 45
°
z pionem.
Je
żeli dwie wiązki przesunięte są w fazie o
π
/2, to przy x = 0 mamy
t
cos
E
E
y
ω
10
=
i
(
)
2
20
2
π
ω
−
=
t
cos
E
E
.
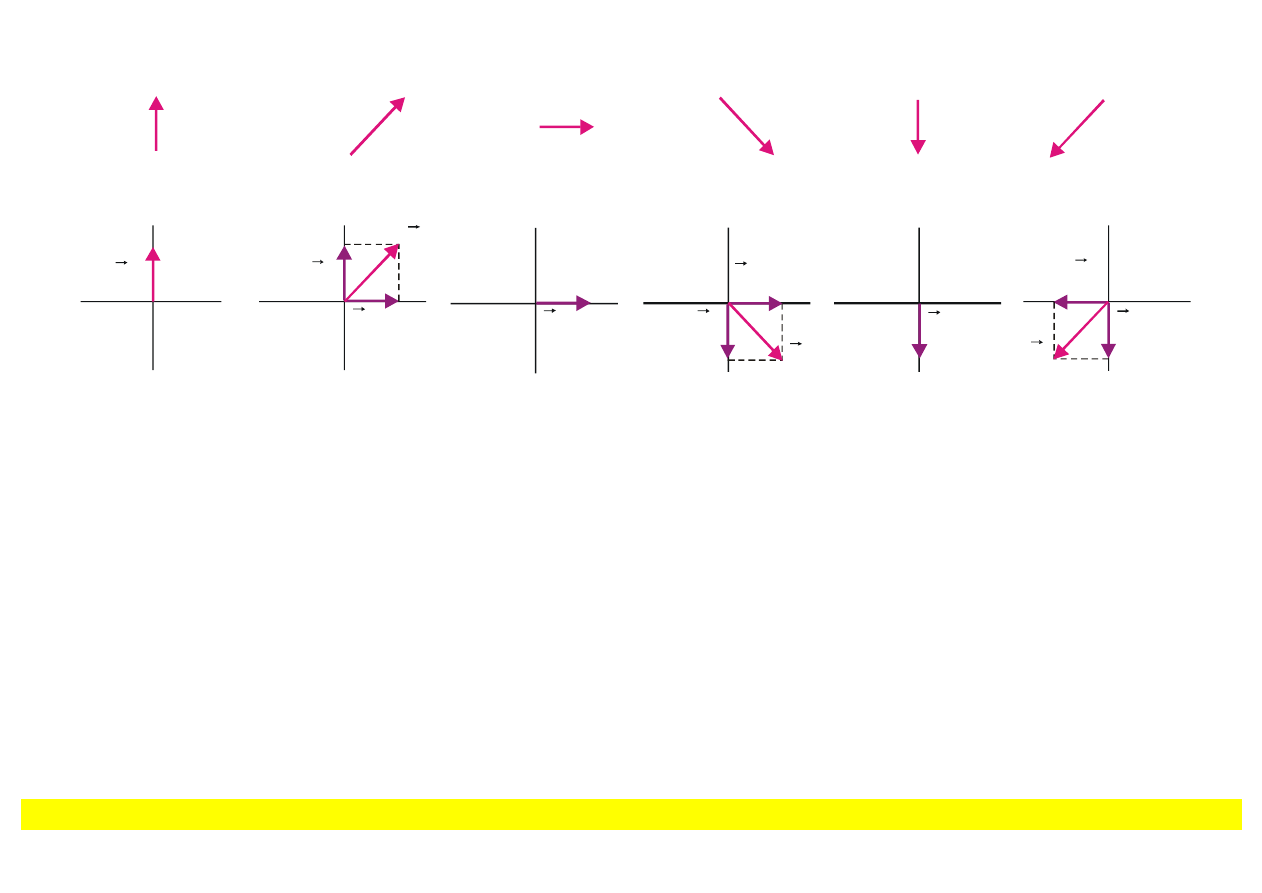
z
z
z
z
z
z
y
y
y
y
y
y
t=0 t=(1/8)T t=(1/4)T t=(3/8)T t=T/2 t=(5/8)T
1
E
1
E
1
E
1
E
1
E
2
E
2
E
2
E
2
E
E
E
E
Rys. 9.29. Pole wypadkowe w p
łaszczyźnie yz w kolejnych chwilach czasu dla przypadku kiedy
wi
ązka 2 opóźnia się w fazie w stosunku do wiązki 1 o kąt
π/2. Wypadkowe pole
E
r
obraca si
ę
zgadnie ze wskazówk
ą zegara. E
y
i E
z
maj
ą jednakowe amplitudy.
o
Wypadkowy wektor
E
r
(sta
ły co do wartości) obraca się zgodnie ze wskazówką zegara
wokó
ł osi x wykonując jeden obrót w okresie drgań T. Taką polaryzację fali nazywamy lewą
polaryzacj
ą kołową.
o
Je
żeli wektor
E
r
obraca si
ę w kierunku przeciwnym do wskazówek zegara (kiedy patrzymy w
kierunku propagacji wi
ązki), to taką polaryzację nazywamy prawą polaryzacją kołową.
o
Je
żeli zmieszać wiązki o jednakowym natężeniu, z których jedna jest spolaryzowana kołowo
w lewo a druga – w prawo, to w rezultacie otrzymamy wi
ązkę płaskospolaryzowaną.
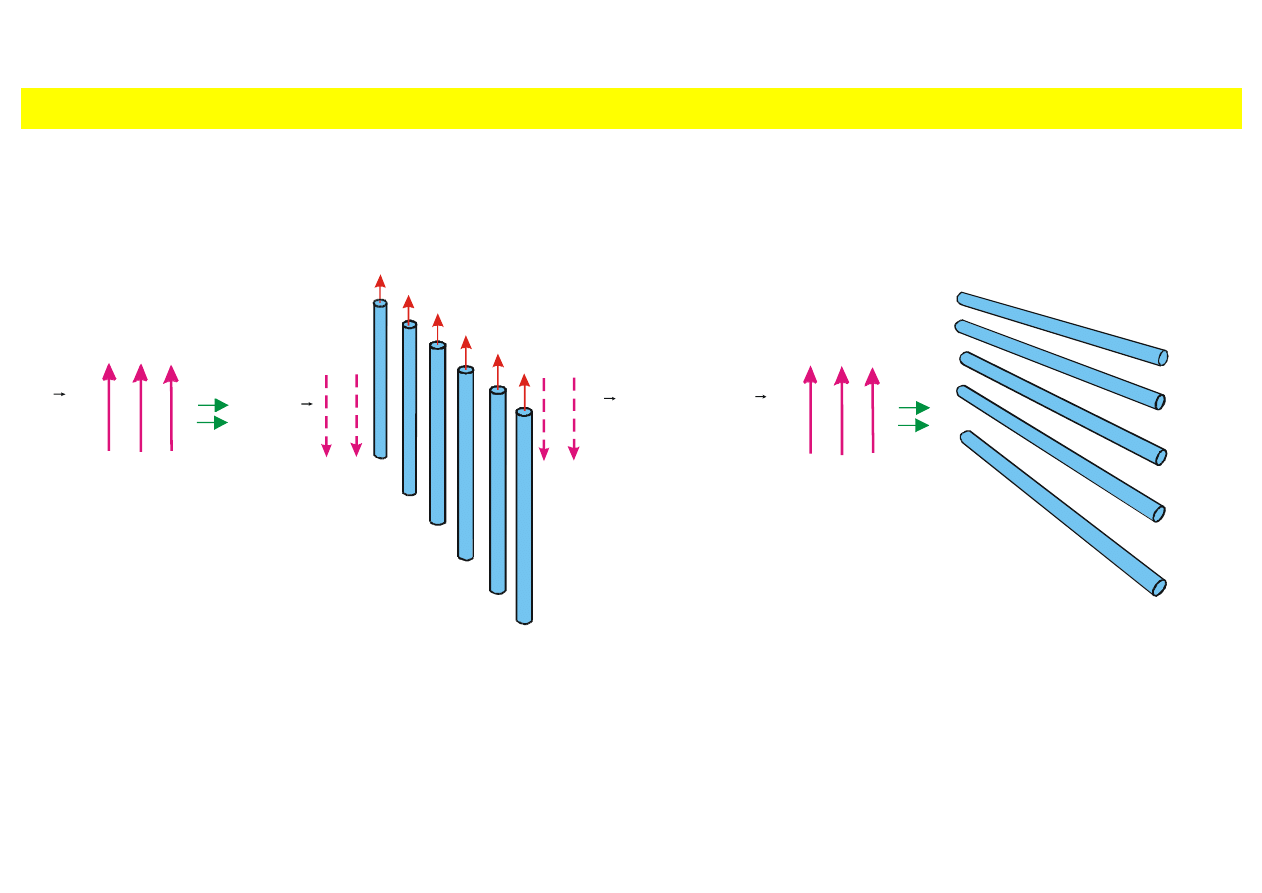
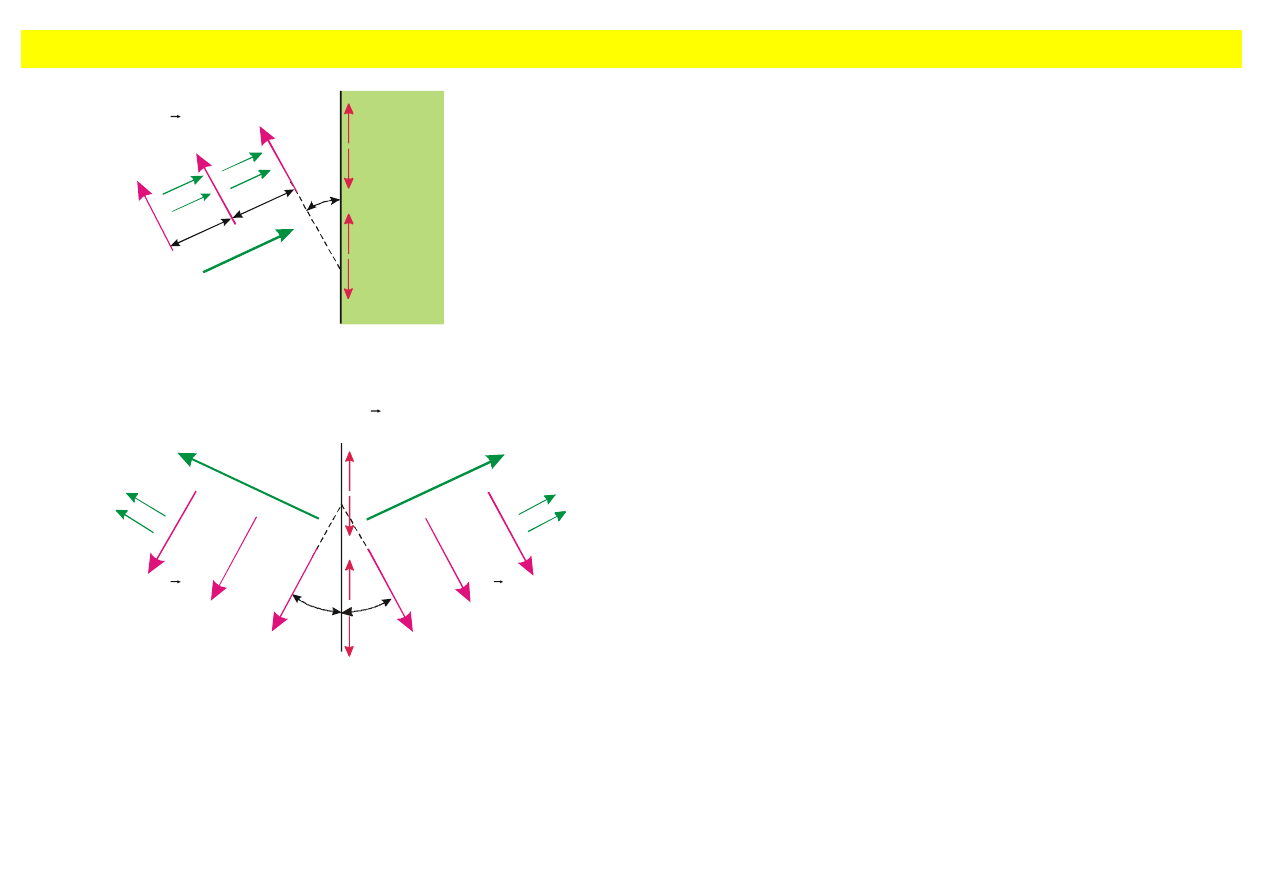
Polaryzatory
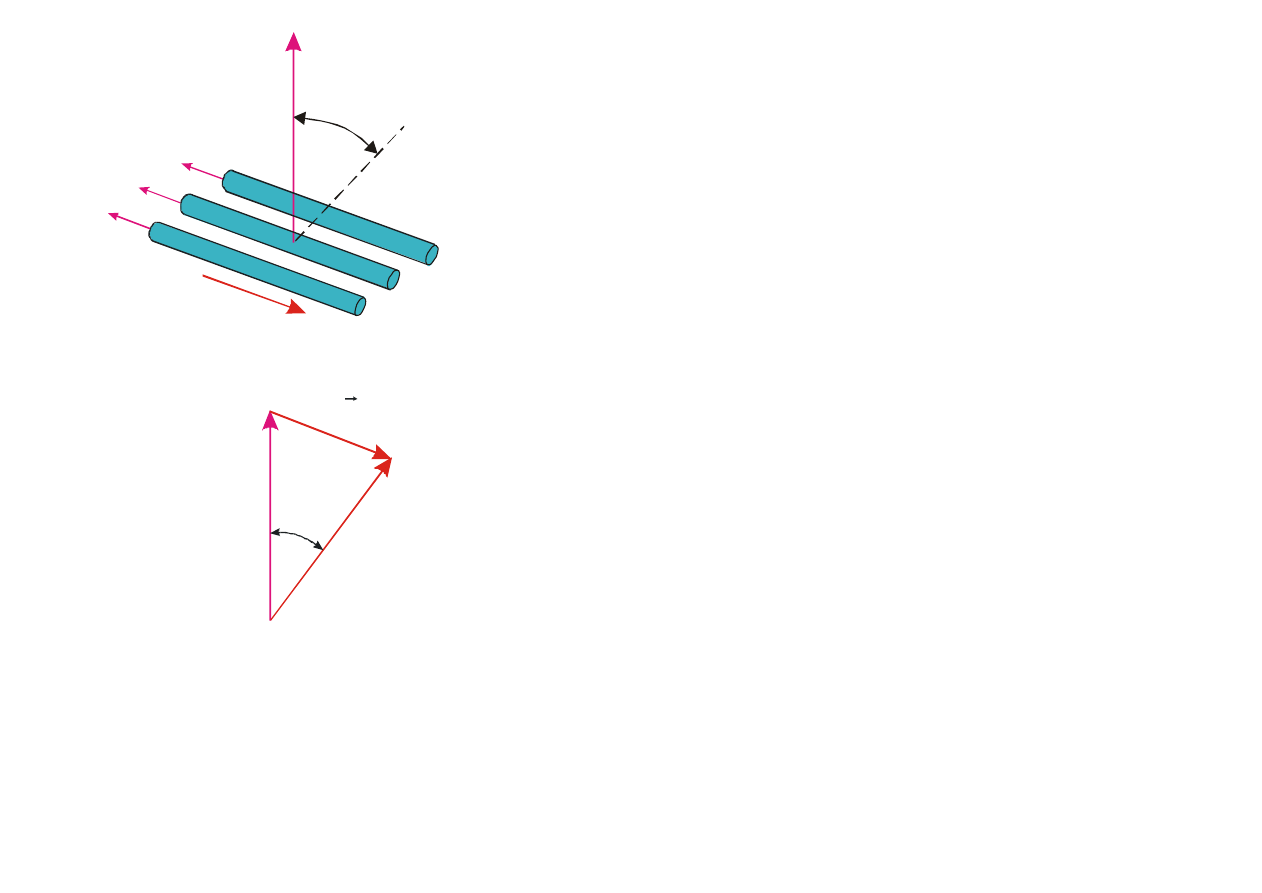
Wi
ązkę światła niespolaryzowanego można spolaryzować, jeżeli przepuścić ją przez polaryzator.
Ekran wykonany z cienkich równoleg
łych drucików jest pięknym przykładem polaryzatora dla fal
milimetrowych (mikrofal); pokazano to na rys. 9.30.
(a) (b)
E
∆
E
∆
I
I=0
pad
E
pad
E
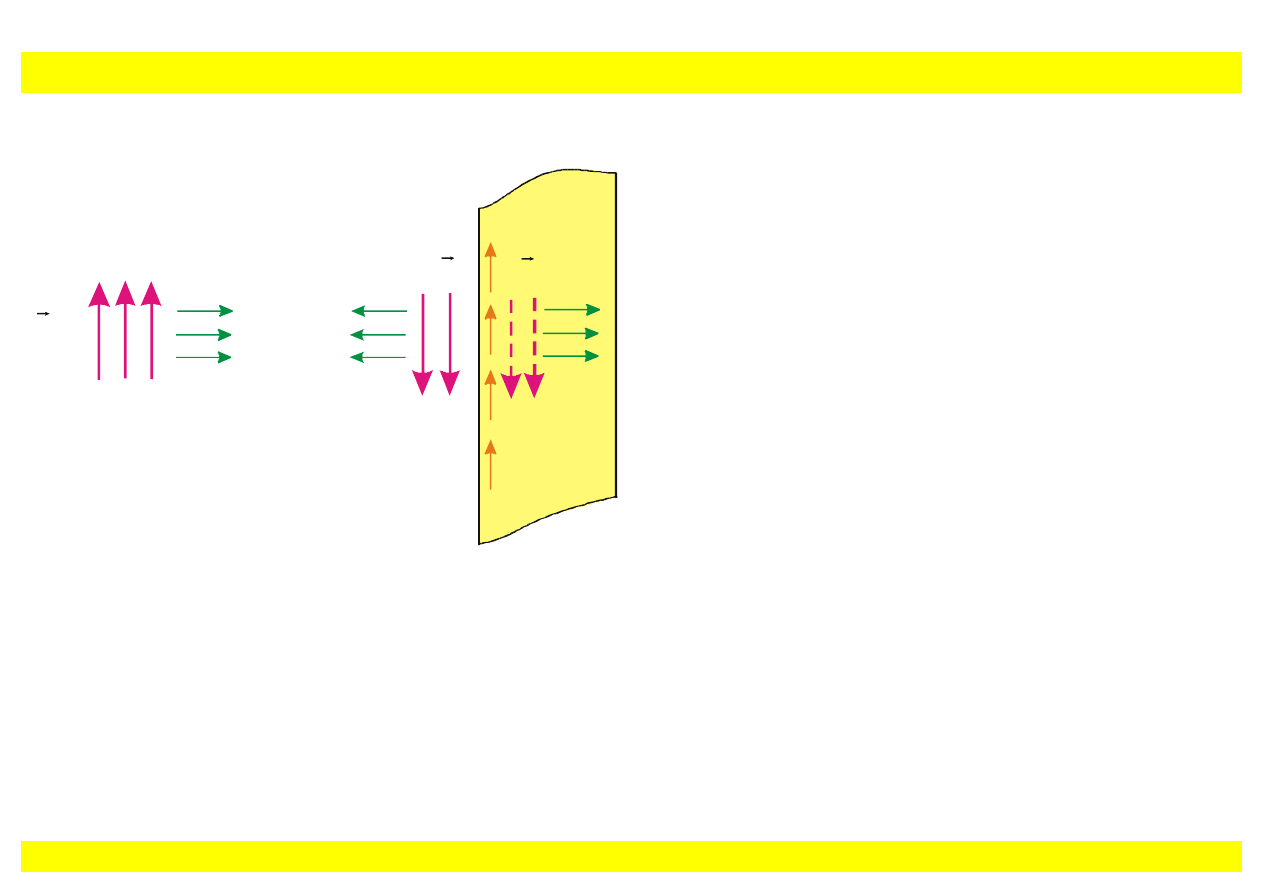
Rys. 9.30. Fala elektromagnetyczna z polaryzacj
ą pionową padająca na ekran równoległych
drucików (a) Ekran z pionowymi drucikami odbija fal
ę. (b) Ekran z poziomymi drucikami nie
odbija fali; fala przechodzi przez ekran bez os
łabienia.

Je
żeli wiązka promieniowania mikrofalowego spolaryzowana jest pionowo i druciki także ułożone są
pionowo, to w ka
żdym druciku indukuje się prąd I. Indukowany prąd emituje pole
pad
E
E
r
r
−
=
∆
.
Na prawo od polaryzatora, wypadkowe pole
0
=
+
=
E
E
E
pad
r
r
r
∆
.
Przy takiej orientacji, polaryzator zachowuje si
ę analogicznie do idealnego zwierciadła, które nie
przepuszcza wi
ązki.
Je
żeli druciki są prostopadłe do
pad
E
r
to pionowe pr
ądy nie indukują się, nie powstaje dodatkowe
promieniowanie i padaj
ąca fala przechodzi bez strat.
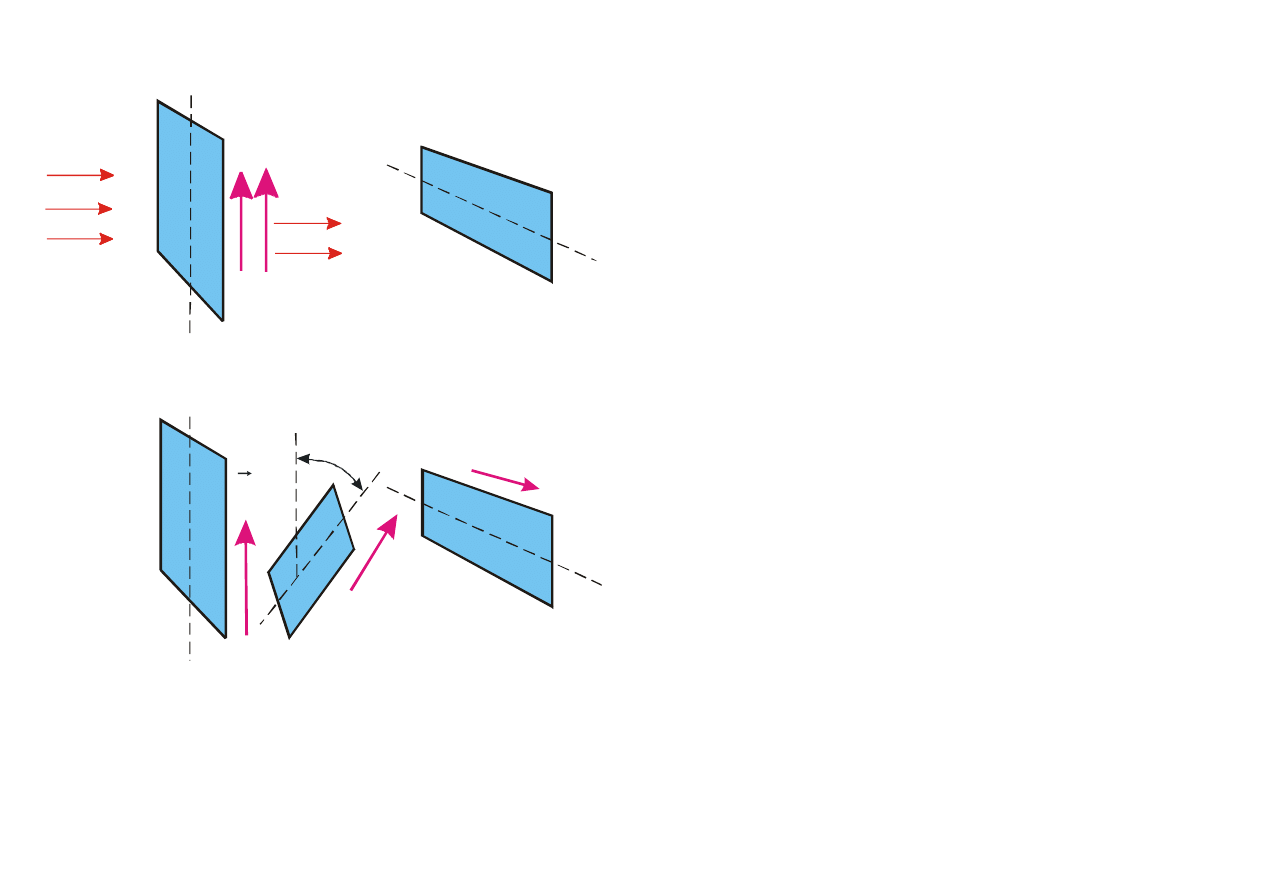
Za o
ś polaryzatora przyjmujemy linię prostopadłą do linii, w której kierunku położone są
druciki
(rys. 9.31).
E
E
'
E
pad
r
r
r
∆
+
=
E
r
∆
r
pad
E
r
pad
E
r
'
+
=
∆
E
α
α
Druciki
(a)
(b)
O
ś polaryzatora
I
Rys. 9.31. (a) Widok przekroju poprzecznego
wi
ązki (wiązka wnika w płaszczyznę rysunku);
wektor pionowej polaryzacji wi
ązki tworzy kąt
α z osią polaryzatora stanowiącego druciki
promieniuj
ące pole
E
r
∆
. (b) Wypadkowe pole
'
E
r
za drucikami.
Je
żeli oś polaryzatora tworzy kąt
α z kierunkiem
pad
E
r
, to polaryzator b
ędzie promieniować pole
E
r
∆
pod k
ątem prostym do osi. Ponieważ
E
r
∆
kompensuje sk
ładową
pad
E
r
w tym kierunku,
wi
ęc wypadkowe pole
'
E
r
b
ędzie przedstawiać
sk
ładową pola
pad
E
r
równoleg
łą do osi, a więc
α
cos
E
'
E
pad
=
czyli
α
2
cos
I
'I
pad
=
(9.30)
Polaryzator
przepuszcza
maksimum
nat
ężenia gdy jego oś skierowana jest
wzd
łuż płaszczyzny polaryzacji.
Dowolne promieniowanie po przej
ściu przez
polaryzator jest p
łaskospolaryzowane w
kierunku osi polaryzatora.
o
E
r
o
E
r
0
''
E
r
''
E
r
'
E
r
I
pad
o
E
O
ś
α
(a)
(b)
Rys. 9.32. (a) Dwa wzajemnie prostopad
łe
polaroidy ca
łkowicie wygaszają światło. (b)
Światło pojawia się jeżeli pomiędzy nimi
umie
ścić trzeci polaroid.
Na podobnej zasadzie oparte jest dzia
łanie
polaroidowego filtru
świetlnego:
o
W przypadku
światła niespolaryzowanego,
sk
ładowe pola E
r
równoleg
łe do łańcuchów
molekularnych ulegaj
ą pochłonięciu. Po
przej
ściu przez filtr polaroidowy pozostają
jedynie te sk
ładowe, które są równoległe do
osi polaroidu.
o
Je
żeli za pierwszym polaroidem umieścić
drugi, w taki sposób, aby ich osie by
ły
wzajemnie prostopad
łe, to wiązka ulega
ca
łkowitemu pochłonięciu i z drugiego
polaroidu
światło nie wychodzi.
o
Je
żeli teraz między dwoma skrzyżowanymi
polaroidami umiejscowi
ć trzeci polaroid, to
światło ponownie pojawi się.

Za
łóżmy, że na środkowy polaroid pada światło, którego natężenie jest równe
2
pad
o
I
I
=
. Za drugim
polaroidem
światło będzie spolaryzowane pod kątem
α i będzie charakteryzowało się natężeniem
α
2
o
cos
I
'I
=
. O
ś ostatniego polaroidu tworzy kąt
π
/2 z p
łaszczyzną polaryzacji światła. Tak więc
( )
(
)
( )
α
α
π
α
α
π
2
4
2
2
2
2
2
2
sin
I
cos
cos
I
cos
'
I
'
'I
o
o
=
−
=
−
=
Wyra
żenie to ma maksymalną wartość dla
α =
π
/4, przy czym w przypadku idealnych polaroidów
ko
ńcowe natężenie wynosi I
pad
/8.
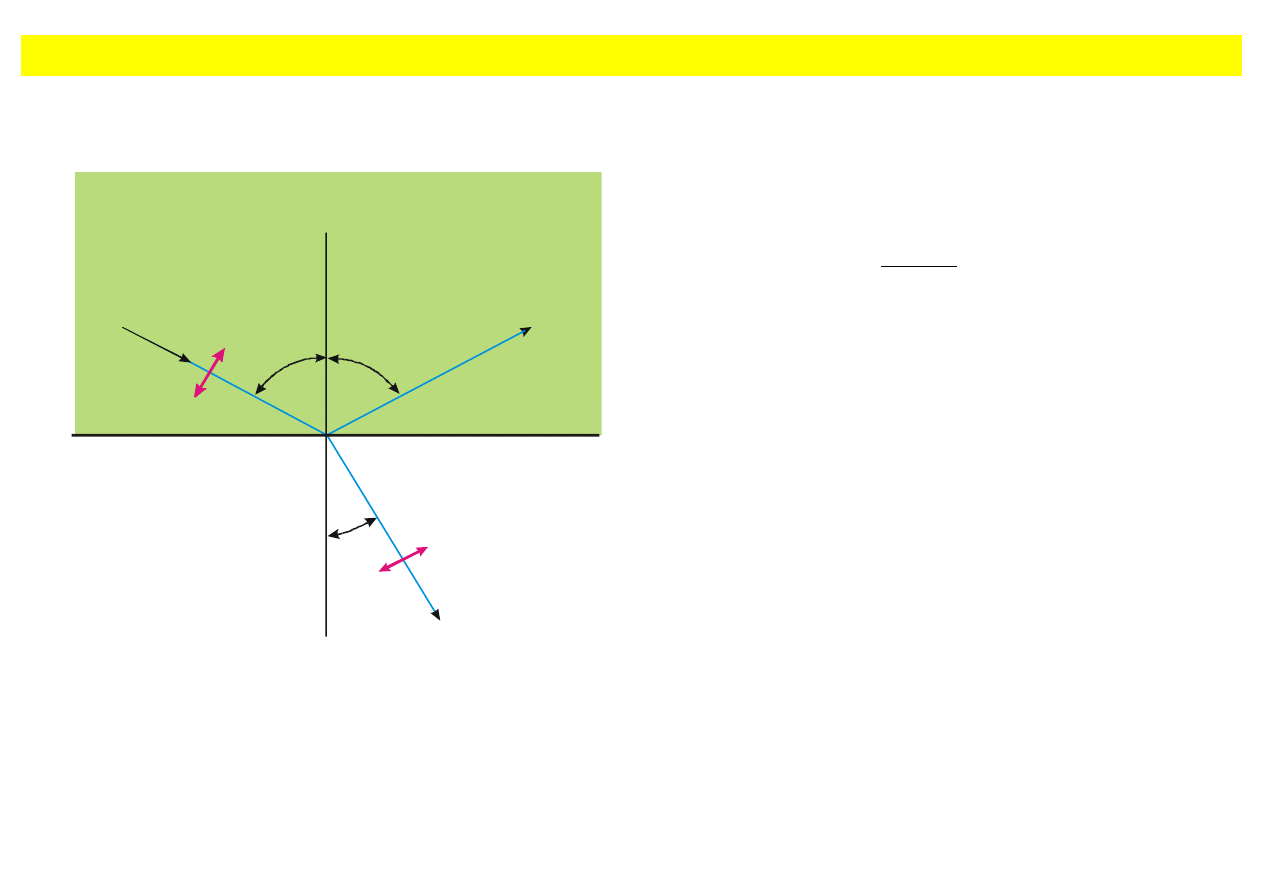
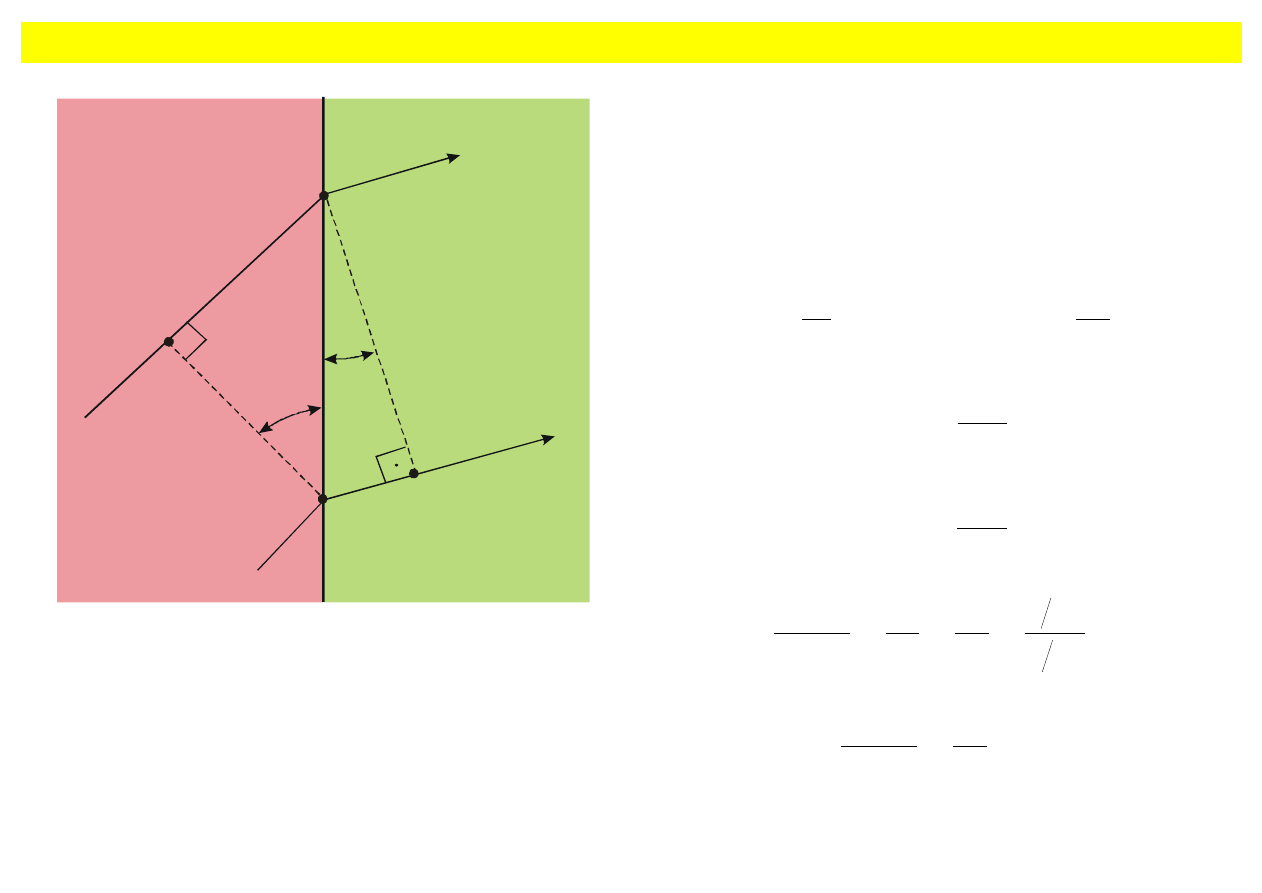
Polaryzacja przez odbicie
Niespolaryzowane
światło słoneczne staje się spolaryzowane przy odbiciu.
E
pad
E’
θ
1
θ
1
θ
2
Promie
ń
padaj
ący
Promie
ń
odbity
Promie
ń
za
łamany
Rys. 9.33. Zmiana polaryzacji przy odbiciu.
Promienie odbite i za
łamane są wzajemnie
prostopad
łe, tj. kierunek pola E' jest zgodny
z kierunkiem promienia odbitego.
Prawo Snelliusa
n
sin
sin
=
2
1
θ
θ
o
Odbite
światło może być emitowane tylko
dzi
ęki drganiom atomów nieprzewodzącego
o
środka.
o
Elektrony nie emituj
ą promieniowania w
kierunku swego ruchu.
o
Je
żeli padające światło jest spolaryzowane
jak pokazano na rys. 9.33, to elektrony b
ędą
drga
ły w kierunku
'
E
r
. W tym przypadku
światło nie będzie odbijane, ponieważ
odbijany promie
ń skierowany byłby w
kierunku ruchu elektronów.
o
Jednak
że,
je
żeli
padaj
ące
światło
spolaryzowane
jest
prostopadle
do
p
łaszczyzny rysunku, to odbicie jest
dopuszczalne.

Na rys. 9.33 mamy
2
2
1
π
θ
θ
=
+
. Podstawiaj
ąc do prawa Snelliusa
( )
1
2
2
θ
π
θ
−
=
otrzymamy
n
sin
sin
=
−
1
1
2
θ
π
θ
czyli
n
tg
=
1
θ
(9.31)
Je
żeli światło niespolaryzowane pada pod kątem Brewstera, to światło odbite jest
spolaryzowane prostopadle do p
łaszczyzny rysunku. Ten warunek powstania polaryzacji przy
odbiciu nazywamy prawem Brewstera
.
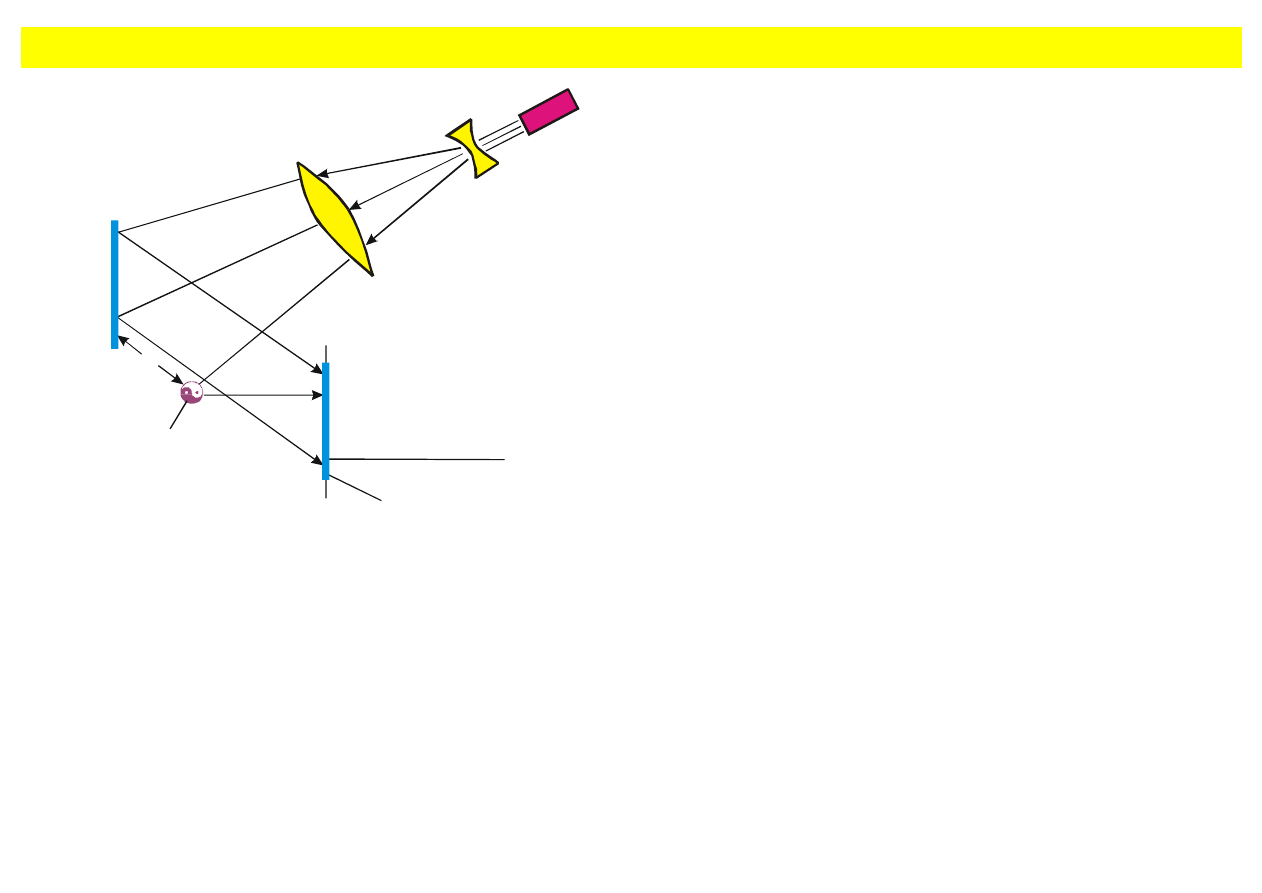
Holografia
Zwierciad
ło
Laser
Przedmiot
Warstwa
fotoczu
ła
O
x
L
y
Rys.
9.34.
Sposób
otrzymywania
hologramu. Na warstw
ę fotoczułą pada
światło laserowe odbite od przedmiotu i
wi
ązka odbita od zwierciadła.
Zasada holografii stanowi pogl
ądową ilustrację
falowej natury
światła i tego w czym tkwi istotna
ró
żnica pomiędzy światłem koherentnym, a
niekoherentnym.
Konieczna d
ługość koherentności wynosi 2L,
gdzie L jest odleg
łością pomiędzy przedmiotem a
zwierciad
łem.
Za pomoc
ą obrazu na warstwie udaje się
odtworzy
ć czoło fali z prawidłowymi wartościami
amplitud i faz wzd
łuż całej jego powierzchni
(warstwa jest jedynie czu
ła na natężenie światła).
Za
łóżmy, że warstwa fotoczuła hologramu
po
łożona jest w płaszczyźnie yz. Wówczas
amplitud
ę fali odbitej przez przedmiot w
p
łaszczyźnie yz możemy napisać w postaci
( )
( )
[
]
z
,
y
t
cos
z
,
y
a
E
Φ
ω
+
=
(9.32)
Przypu
śćmy teraz, że mając taki rozkład amplitudy fali na warstwie, oświetlamy ją płaską falą lasera.
Wówczas rozk
ład pola elektrycznego w płaszczyźnie warstwy ma postać
(
)
Φ
ω
ω
+
+
=
t
cos
a
t
cos
E
E
o
wyp
gdzie a = a(y,z) i
Φ = Φ(y,z).

Poniewa
ż natężenie jest proporcjonalne do kwadratu E
wyp
, mamy
(
)
(
)
Φ
ω
Φ
ω
ω
ω
+
+
+
+
=
t
cos
a
t
cos
t
cos
E
t
cos
E
I
o
o
2
2
2
2
2
Średnia wartość natężenia wynosi
(
)
[
]
2
2
2
2
a
t
cos
cos
a
E
I
I
o
o
+
+
+
+
=
Φ
ω
Φ
Uwzgl
ędniono tu, że
(
)
(
)
β
α
α
β
β
α
+
+
−
=
cos
)
/
(
cos
)
/
(
cos
cos
2
1
2
1
.
Średnia wartość cos(2
ωt + Φ) = 0, dlatego
( )
( )
z
,
y
cos
z
,
y
a
E
K
I
o
Φ
+
=
1
(9.33)
gdzie
(
)
2
2
1
a
I
K
o
+
=
.
W przypadku stosowania
źródła światła o długości koherentności przewyższającej 2L, udaje się
zachowa
ć informację o rozkładzie fazy
( )
z
,
y
Φ
na warstwie.
Poczernienie warstwy jest proporcjonalne do
I
.
Je
żeli skierować na negatyw wiązkę lasera o natężeniu
t
cos
'I
ω
2
, to natychmiast za negatywem
otrzymamy
(
)
[
]
Φ
ω
cos
a
E
K
K
t
cos
'I
I
o
+
−
=
1
2
2
Odpowiednie pole elektryczne proporcjonalne jest do pierwiastka kwadratowego z wyra
żenia, więc

(
)
[
]
Φ
ω
ω
Φ
ω
cos
t
cos
a
K
t
cos
K
cos
a
E
K
K
K
t
cos
E
E
/
o
4
3
2
1
2
2
1
2
1
+
≈
+
−
=
gdzie
2
1
2
1
3
K
K
K
−
=
i
4
2
4
o
E
K
K
=
Stosuj
ąc ponownie związek trygonometryczny
2cos
αcosβ = cos(α –β) + cos(α +β),
mamy
( )
( )
[
]
( )
( )
[
]
z
,
y
t
cos
z
,
y
a
K
z
,
y
t
cos
z
,
y
a
K
t
cos
K
E
Φ
ω
Φ
ω
ω
−
+
+
+
=
4
4
3
+
+
fazie
odwróconej
o
przedmiotu
od
świato
K
przedmiotu
od
odbite
świato
K
lasera
od
io
bezposredn
świato
4
4
Pierwszy cz
łon – rejestrowany jest przez oko obserwatora jako światło laserowe.
Drugi cz
łon – w postaci światła odbitego od przedmiotu jakby przedmiot faktycznie znajdował się w
swym pierwotnym po
łożeniu.
Trzeci cz
łon przejawia się w postaci jeszcze jednego realnego obrazu.
Chocia
ż holografię odkryto w 1949 r., pozostała nauką samą w sobie do początku lat
sze
śćdziesiątych. Dopiero po konstrukcji pierwszych laserów znalazła szerokie zastosowanie.

Optyka geometryczna
D
ługość fali świetlnej jest na tyle mała w porównaniu z rozmiarami większości przyrządów
optycznych,
że efekty interferencyjne nie ujawniają się.
Fale
świetlne rozprzestrzeniają się wzdłuż linii prostych prostopadłych do czoła fali.
Dowolna taka prosta wzd
łuż kierunku propagacji fal świetlnych nazywana jest promieniem świetlnym.
Stosuj
ąc prawo odbicia i załamania i zwykłe zasady geometrii euklidesowej można zbudować opis
matematyczny lub obraz geometryczny propagacji promieni
świetlnych.
Taki opis matematyczny promieni
świetlnych stanowi oddzielny dział fizyki i nosi nazwę
optyki
geometrycznej
.
Prawo odbicia
pad
E
(a)
(b)
Str
um
ień
pa
da
jąc
y
Str
um
ień
pro
mie
niu
jąc
y
Stru
mień
prom
ieniu
j
ący
Przewodnik
θ
pad
'
L
E
'
R
E
λ
λ
'
L
θ
'
R
θ
J
Rys. 9.35. (a) Trzy kolejne po
łożenia czoła fali
padaj
ącej pod kątem padania
θ
pad
;
w
przewodniku indukuje si
ę prąd powierzchniowy
J(y), którego maksima odpowiadaj
ą przecięciu
czo
ła fali z powierzchnią przewodnika. (b) Pole
promieniowania wywo
łane jedynie prądem J(y).
Pr
ąd powierzchniowy okazuje się być takim,
że pole wewnątrz przewodnika zawsze jest
równe zeru.
Oznacza to,
że promieniowane przez prąd
pole na praw
ą stronę dokładnie kompensuje
E
pad
. Tak wi
ęc
pad
'
R
E
E
−
=
i
pad
'
R
θ
θ
=
.
Warunki symetrii wymagaj
ą
'
R
'
L
E
E
=
i
'
R
'
L
θ
θ
=
Udowodnili
śmy więc, że w przypadku
powierzchni przewodz
ącej amplituda fali
odbitej zachowuje si
ę lecz jej składowa
wzd
łuż powierzchni zmienia swój kierunek na
przeciwny.
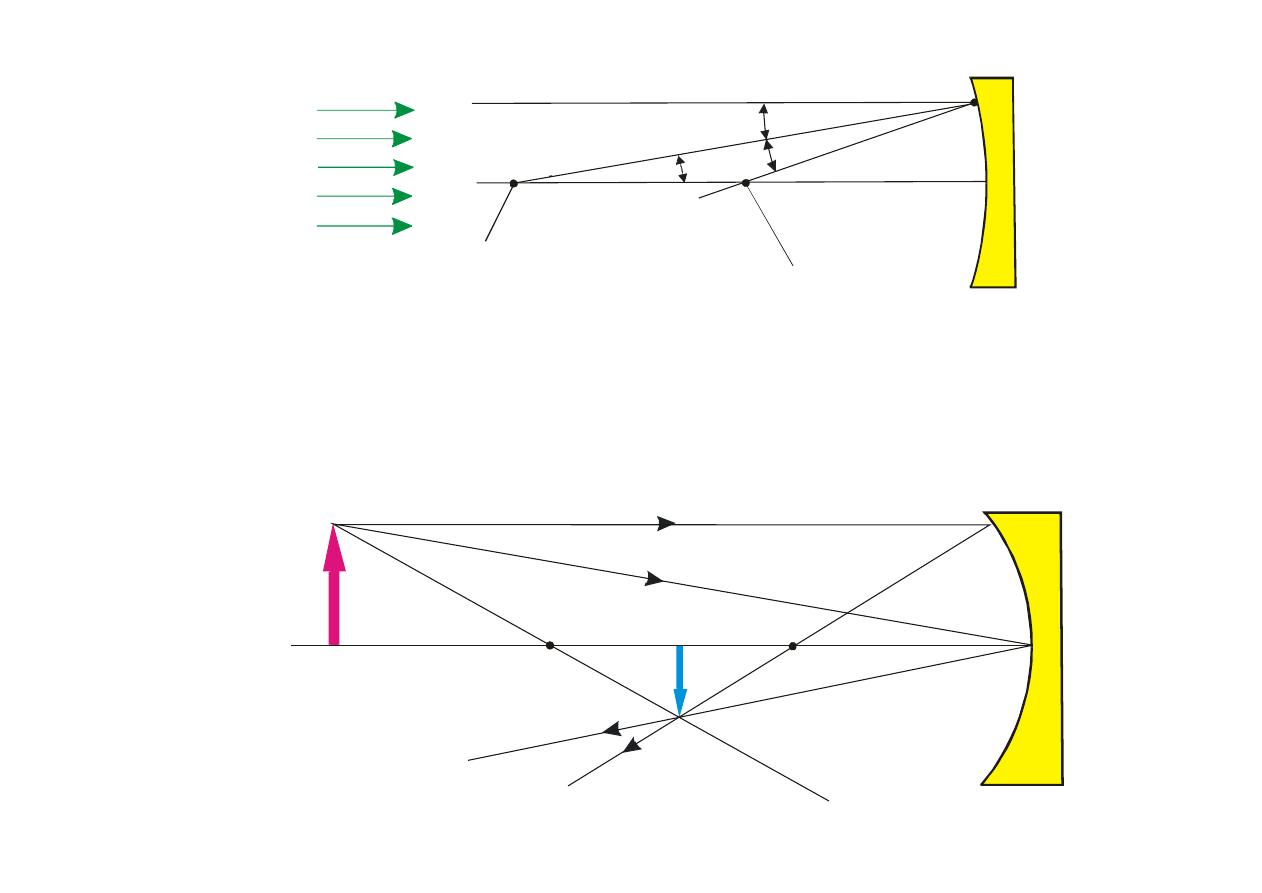
Jak wida
ć z rys. 9.36, ogniskowa zwierciadła wklęsłego równa jest połowie jego promienia krzywizny.
P
C
A
Zwierciad
ło
wkl
ęsłe
Ognisko
Strumie
ń
światła
Środek
krzywizny
F
θ
θ
θ
Rys. 9.36. Równoleg
ła wiązka światła padająca na zwierciadło wklęsłe o promieniu CP.
Na rys. 9.37 pokazano jak mo
żna graficznie zbudować obraz przedmiotu (w danym przypadku
strza
łki), jeżeli znane jest położenie ogniska F.
1
2
Przedmiot
Obraz
C
F
Rys. 9.37. Tworzenie obrazu przez zwierciad
ło wklęsłe. Za pomocą promieni 1 i 2 określa się
graficzne po
łożenie obrazu.
Prawo za
łamania
θ
1
θ
2
1
1
2
2
λ
1
λ
2
A
B
B
’
A
’
O
środek 1 Ośrodek 2
Rys. 9.38. Dwa kolejne po
łożenia czoła
falowego, kiedy fala przechodzi, przez
powierzchni
ę rozdziału szkło - powietrze.
Prawo za
łamania potwierdza, że przy przejściu z
jednego o
środka przezroczystego do drugiego,
promie
ń świetlny zmienia swój kierunek.
Na rysunku pokazano dwa kolejne po
łożenia
czo
ła falowego AB i A'B'.
f
u
1
1
=
λ
;
f
u
2
2
=
λ
Z trójk
ąta prostokątnego ABB' znajdujemy
'
AB
sin
1
1
λ
θ
=
a z trójk
ąta prostokątnego A'AB
'
AB
sin
2
2
λ
θ
=
Podzielimy pierwszy zwi
ązek przez drugi
1
2
2
1
2
1
2
1
u
c
u
c
u
u
sin
sin
=
=
=
λ
λ
θ
θ
St
ąd
1
2
2
1
n
n
sin
sin
=
θ
θ
(9.34)
gdzie
1
n i
2
n wspó
łczynniki załamania odpowiednio ośrodka 1 i 2. Jest to prawo Snelliusa.
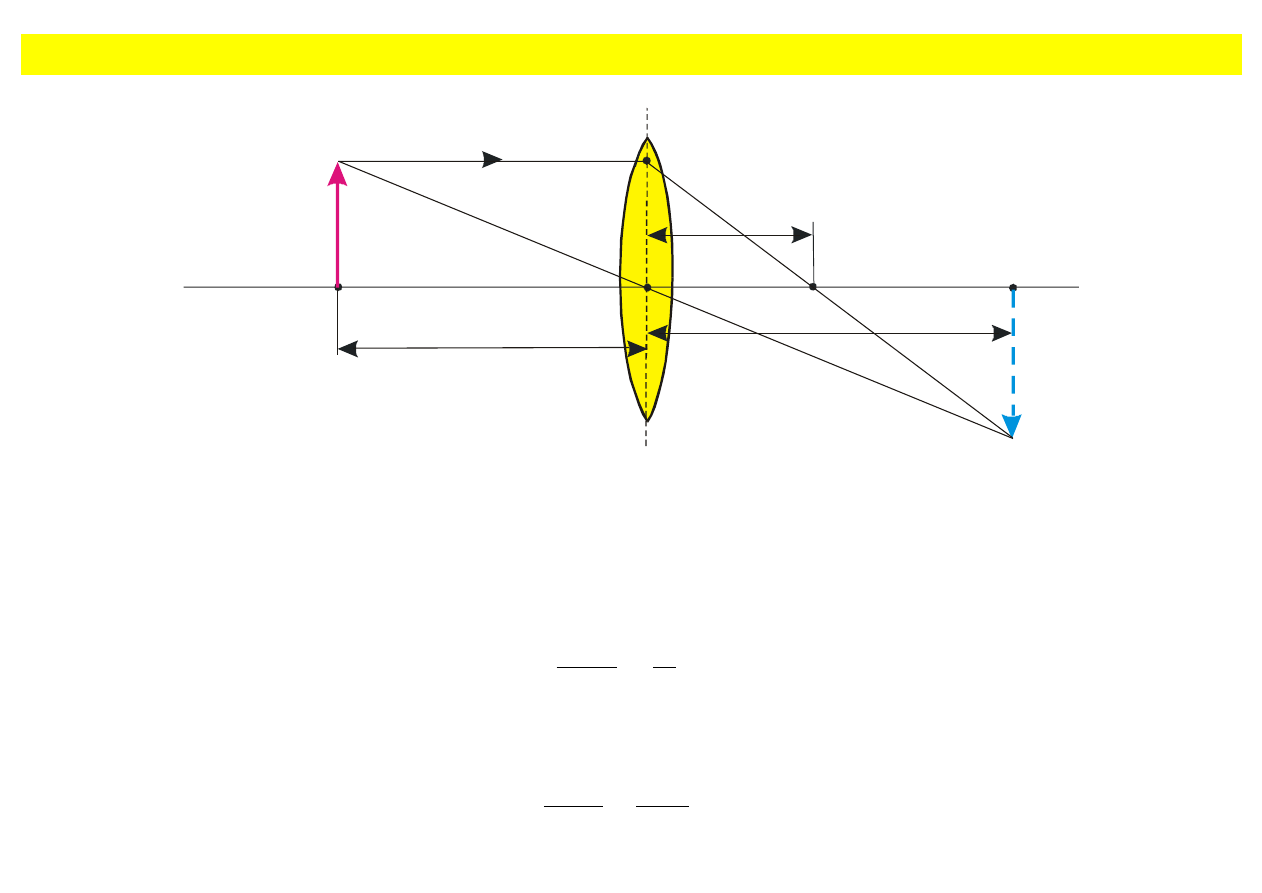
Soczewki
O
P
B
’
A
’
A
B
s
s
’
2
2
1
1
F
f
Rys. 9.39. Przedmiot AB po
łożony jest w odległości s od soczewki o ogniskowej f. Obraz A'B'
po
łożony jest w odległości s' od soczewki.
Trójk
ąt ABO jest podobny do trójkąta A'B'O. Dlatego
s
'
s
AB
'
B
'
A
=
(9.35)
Trójk
ąt POF podobny jest do trójkąta A'B'F, tak że
f
f
'
s
PO
'
B
'
A
−
=
(9.36)

Poniewa
ż PO = AB, lewe strony we wzorach (9.35) i (9.36) są równe. Przyrównując między sobą
prawe strony, otrzymujemy
'
s
s
f
1
1
1
+
=
(9.37)
Zwi
ązek ten między odległościami od przedmiotu i obrazu nazywany jest wzorem cienkiej
soczewki.
Zwykle przy rozwi
ązywaniu jakichkolwiek zadań, elementy optyczne umieszcza się w taki sposób
a
żeby światło biegło przez soczewkę z lewa na prawo. Wówczas wielkość s' traktuje się jako
dodatni
ą, jeżeli obraz położony jest na prawo od soczewki i ujemną – jeżeli obraz położony jest na
lewo od niej.
W przypadku soczewki rozpraszaj
ącej wielkość f jest ujemna.
Wielko
ść s będzie ujemna, jeżeli promienie wychodzące z soczewki schodzą się w urojony przedmiot
(mo
że to być urojony obraz wytworzony na lewo od soczewki).
Wyszukiwarka
Podobne podstrony:
Echo elektroniczne id 149974 Nieznany
Mikroskopia elektronowa id 3018 Nieznany
elektro 3 id 157863 Nieznany
elektra 4 id 157704 Nieznany
5 Pole elektrostatyczne id 397 Nieznany
elektrae1 id 157847 Nieznany
elektro 2 id 157860 Nieznany
Budowa Lampy Elektronowej id 94 Nieznany (2)
Obrobka elektroerozyjna id 3280 Nieznany
ELEKTROSTATYKA 2 id 159079 Nieznany
elektra 8 id 157752 Nieznany
O PODPISIE ELEKTRONICZNYM id 32 Nieznany
elektroliza 3 id 158085 Nieznany
Obwody elektryczne id 329051 Nieznany
angielski dla elektrykow id 640 Nieznany
elektro4 id 157939 Nieznany
elektra 9 id 157753 Nieznany
cta 105 elektryka id 108360 Nieznany
więcej podobnych podstron