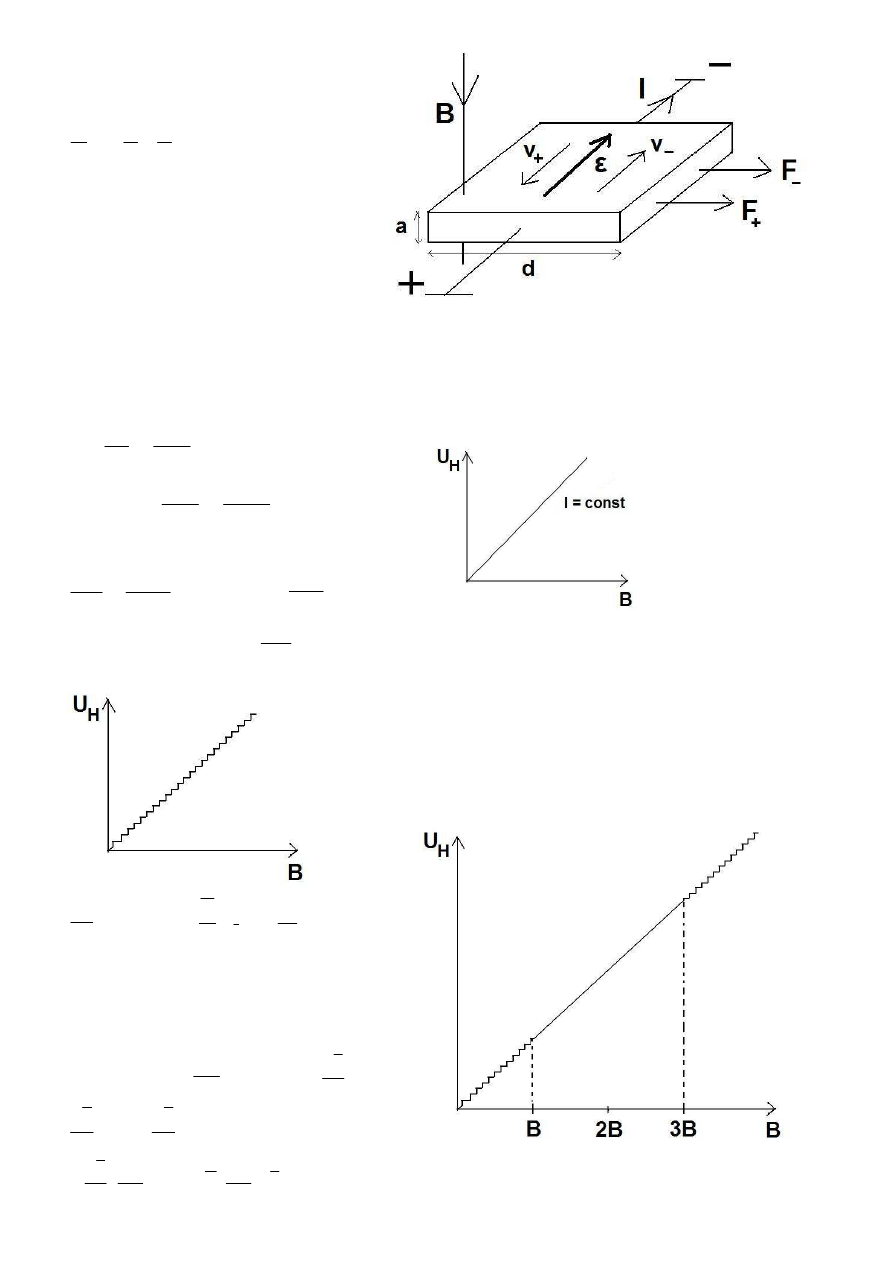
4. Efekt Holla.
Na poruszający się ładunek w polu
magnetycznym działa siła Lorenza:
B
V
q
F
×
=
Nośniki ładunku, zarówno dodatnie, jak
i ujemne, są odchylane w tą samą stronę
(bo wędrują w przeciwnych kierunkach).
Na podstawie ładunku, jaki zgromadzi
się na boku płytki można
wywnioskować, jakie cząstki przewodzą
prąd.
siła pola magnetycznego:
evB
F
B
±
=
siła pola elektrycznego, powstającego w wyniku efektu Holla:
H
e
F
H
ε
ε
=
Korzystamy ze wzoru
nev
j
=
, gdzie
u
v
v
≡
- prędkość unoszenia
neS
I
ne
j
v
=
=
,
gdzie
ad
S
=
Stąd:
neda
IB
neS
IB
H
=
=
ε
Napięcie hollowskie:
d
U
H
H
ε
=
neda
IB
d
U
H
=
→
nea
IB
U
H
=
(często pisze się:
IB
nea
U
H
1
±
=
- znak zależy od ładunku nośników)
Okazuje się, że w pewnych strukturach zachodzi tzw. kwantowy
efekt Holla (QHE).
Później dostrzeżono również ułamkowy kwantowy efekt Holla
(FQHE) – kwantowanie pojawiało się w niskich temperaturach
dla trzykrotnie wyższych B:
0
=
dt
df
0
1
=
+
∇
τ
f
f
F
k
h
1
0
f
f
f
+
=
1
0
f
f
f
k
k
k
∇
+
∇
=
∇
Jeżeli weźmiemy tylko pole elektryczne,
możemy dla tego przypadku pominąć
1
f
k
∇
:
E
E
f
f
f
k
k
k
∇
∂
∂
=
∇
≈
∇
0
0
/
h
ε
q
⋅
=
∇
≈
∇
0
f
q
f
q
k
k
h
h
ε
ε
ε
ε
q
E
f
V
E
E
f
q
k
∂
∂
=
∇
∂
∂
=
0
0
h
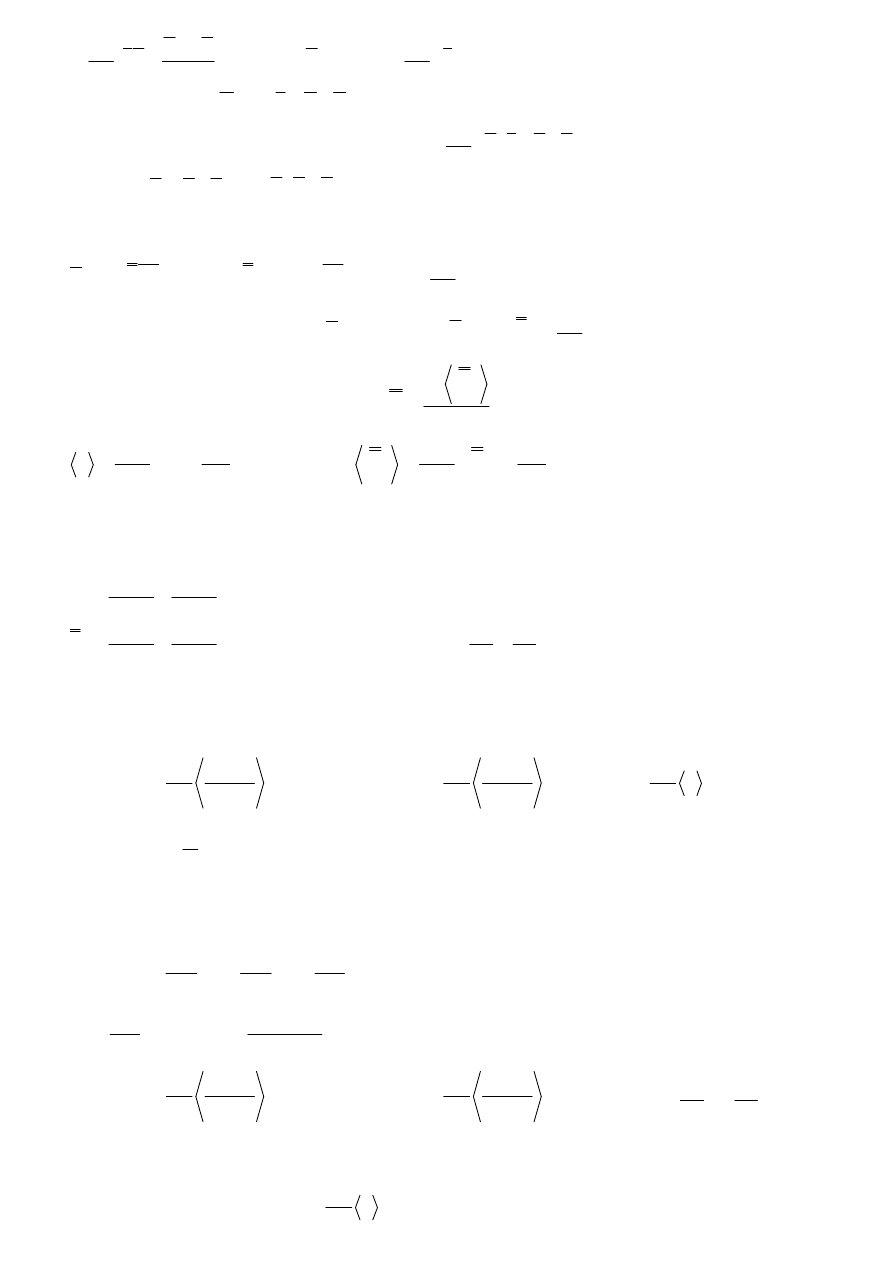
0
)
(
0
=
+
∂
∂
τ
χ
ε
V
E
V
E
f
q
, gdzie
ε
τ
χ
∂
∂
−
=
E
f
q
E
0
)
(
Wprowadzamy siłę:
(
)
B
V
q
F
×
+
=
ε
Korzystając z
0
f
f
k
k
∇
≈
∇
dostaniemy:
(
)
B
V
V
E
f
q
f
×
+
∂
∂
−
=
ε
τ
0
1
Z definicji
,
B
V
V
×
⊥
stąd
0
=
×
⋅
B
V
V
, co oznacza, że nie możemy sobie pozwolić na to przybliżenie
i musimy uwzględnić całość:
1
0
f
f
f
k
k
k
∇
+
∇
=
∇
Jest to skomplikowane i w ogólnym przypadku nie da się tego rozwiązać. Stosujemy inne przybliżenie:
)
(
)
(
0
E
S
E
χ
χ
=
, gdzie S - tensor,
ε
τ
χ
∂
∂
−
=
E
f
q
E
0
0
)
(
Pole magnetyczne zmienia funkcję
)
(E
χ
w tensor:
ε
τ
χ
∂
∂
−
=
E
f
S
q
E
0
)
(
Również przewodnictwo będzie tensorem:
*
2
m
S
e
τ
σ
=
dE
k
E
f
m
k
∫
∂
∂
−
=
0
3
0
2
3
1
τ
π
τ
, stąd:
dE
k
E
f
S
S
m
k
∫
∂
∂
−
=
0
3
0
2
3
1
τ
π
τ
Dokładna postać tensora nie jest znana, wiemy tylko co nieco o pewnych wyróżnionych kierunkach, np.
(
)
0
,
0
,
x
x
ε
ε
ε
=
=
;
(
)
z
z
B
B
B
,
0
,
0
=
=
Wówczas po skomplikowanych wyprowadzeniach:
+
+
−
+
+
=
1
0
0
0
1
1
1
0
1
1
1
2
2
2
2
S
S
S
S
S
S
S
;
τ
ω
C
S
=
, gdzie
Τ
=
=
π
ω
2
*
m
eB
C
- częstość ruchu po okręgu elektronów
Przechodzimy do współrzędnych tensora:
ij
σ
σ
→
2
*
2
22
11
1 S
m
e
+
=
=
τ
σ
σ
;
2
*
2
21
12
1 S
S
m
e
+
=
−
=
τ
σ
σ
;
τ
σ
*
2
33
m
e
=
Pozostałe:
0
=
ij
σ
Gęstość prądu:
j
ij
i
j
ε
σ
=
y
x
x
j
ε
σ
ε
σ
12
11
+
=
0
22
21
=
+
=
y
x
y
j
ε
σ
ε
σ
- w kierunku y prąd nie płynie
Stąd:
y
y
y
x
ε
σ
σ
ε
σ
σ
ε
σ
σ
ε
12
11
12
22
21
22
=
=
−
=
y
y
y
x
j
ε
σ
σ
σ
ε
σ
ε
σ
σ
12
2
12
2
11
12
12
2
11
+
=
+
=
2
*
2
22
11
1
S
m
e
+
=
=
τ
σ
σ
;
2
*
2
21
12
1
S
S
m
e
+
=
−
=
τ
σ
σ
;
τ
π
τ
τ
ω
Τ
=
=
=
2
*
m
eB
S
C
τ
- czas rozpraszania (krótki, rzędu
10
10
~
−
s)
Im wyższe pole tym większa
C
ω
i tym krótszy okres T. W słabych polach T
τ
>>
i wówczas
1
<<
S
-
możemy je pominąć i wtedy
τ
σ
*
2
11
m
e
≈
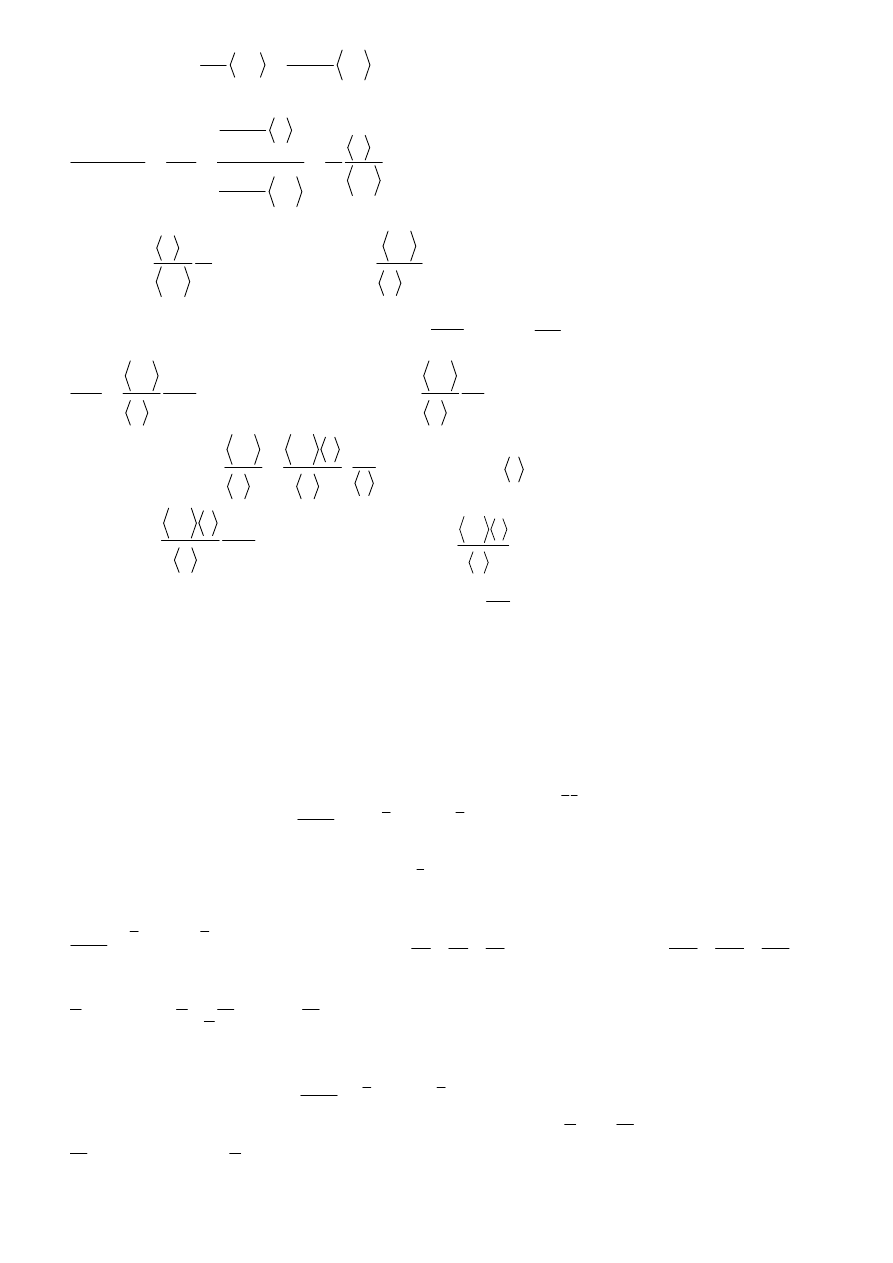
Podobnie:
( )
2
2
*
3
*
2
12
τ
τ
σ
m
B
e
S
m
e
=
≈
( )
( )
2
2
2
2
*
3
2
2
*
4
12
2
11
12
2
12
2
11
τ
τ
τ
τ
σ
σ
σ
σ
σ
B
e
m
B
e
m
e
=
=
≈
+
Stąd:
y
x
B
e
j
ε
τ
τ
2
2
=
→
B
j
e
x
y
2
2
τ
τ
ε
=
Napięcie hollowskie:
y
y
H
d
U
U
ε
=
=
;
d
U
H
y
=
ε
;
ad
I
j
x
x
=
- wstawiamy to do wzoru:
B
I
ade
d
U
x
H
1
2
2
τ
τ
=
,
ostatecznie:
B
I
ae
U
x
H
1
2
2
τ
τ
=
Stosujemy przejście:
1
1
1
2
2
2
2
⋅
=
τ
τ
τ
τ
, pamiętając, że
n
=
1
to koncentracja nośników
Stąd:
B
I
nae
U
x
H
1
1
2
2
τ
τ
=
,
gdzie wyrażenie
r
=
2
2
1
τ
τ
to tzw. współczynnik hollowski
Przewodnictwo typu n i p:
(
)
2
2
p
e
p
n
c
µ
µ
σ
+
=
, gdzie
τ
µ
~
*
m
e
=
- ruchliwość
Mierząc napięcie hollowskie nie możemy od razu obliczyć koncentracji nośników, bo jest zafałszowana
przez czynnik hollowski, który na ogół 1
≠
. Dodatkowo, gdy przewodzą nośniki dwojakiego rodzaju,
należy uwzględnić powyższy wzór. Wówczas współczynnik hollowski może zmianiać znak ze względu
na różną ruchliwość elektronów i dziur (dziury mają większą bezwładność).
5.
Poziomy Landaua.
Metoda masy efektywnej:
( )
( )
r
E
r
m
ψ
ψ
=
∇
−
2
*
2
h
;
r
k
i
e
=
ψ
Bez potencjału elektron w krysztale porusza się jak elektron swobodny z masą efektywną. W masie
efektywnej zawarta jest informacja o funkcji
( )
r
u
k
.
Landau zapisał równanie Schrödingera w postaci:
( )
( )
r
E
r
m
p
ψ
ψ
=
*
2
2
ˆ
, gdzie
∂
∂
+
∂
∂
+
∂
∂
−
=
∇
−
=
z
y
x
i
i
p
h
h
ˆ
;
∂
∂
+
∂
∂
+
∂
∂
−
=
⋅
=
2
2
2
2
2
2
2
ˆ
ˆ
ˆ
z
y
x
p
p
p
h
Mechanika klasyczna wprowadza pęd uogólniony:
p
→
A
c
e
p
+
, gdzie
A - potencjał wektorowy dla pola elektromagnetycznego
Potencjał wektorowy jest tylko zabiegiem matematycznym, nie istnieje jako wielkość fizyczna.
Wstawiamy pęd uogólniony do
( )
( )
r
E
r
m
p
ψ
ψ
=
*
2
2
ˆ
Pole magnetyczne traktujemy jako rotację potencjału wektorowego:
A
B
rot
=
(
)
0
,
0
,
yB
A
−
=
(
)
B
B
,
0
,
0
=
(skalowanie landauowskie)
( )
( )
r
E
r
A
c
e
p
m
ψ
ψ
=
+
2
*
ˆ
ˆ
2
1
( )
( )
r
E
r
z
y
By
c
e
x
i
m
ψ
ψ
=
∂
∂
−
∂
∂
−
−
∂
∂
−
2
2
2
2
2
2
2
*
2
1
h
h
h
Rozwiązanie:
( ) ( )
z
ik
x
ik
z
x
e
r
r
+
=
ϕ
ψ
Rozpisujemy i wstawiamy:
( )
( )
z
ik
x
ik
z
ik
x
ik
z
x
z
x
e
r
E
e
r
z
y
y
B
c
e
x
By
c
e
i
x
m
+
+
=
∂
∂
−
∂
∂
−
+
∂
∂
+
∂
∂
−
ϕ
ϕ
2
2
2
2
2
2
2
2
2
2
2
2
2
*
2
2
1
h
h
h
h
( )
( )
y
E
y
m
k
y
y
B
c
m
e
By
cm
e
k
m
k
z
x
x
ϕ
ϕ
=
+
∂
∂
−
+
−
−
*
2
2
2
2
2
2
2
2
*
2
*
*
2
2
2
2
2
h
h
h
h
Częstość cyklotronowa:
w układzie SI:
*
m
eB
C
=
ω
;
w układzie jednostek Gaussa:
c
m
eB
C
*
=
ω
( )
( )
r
E
r
m
x
m
ψ
ψ
ω
=
+
∂
∂
2
2
2
*
2
1
2
1
- równanie Schrödingera dla oscylatora harmonicznego
Energia drgań jest skwantowana:
+
=
2
1
n
E
ω
h
Wyłączamy przed nawias:
2
*
2
2
2
2
*
2
2
*
2
*
2
2
2
1
c
m
B
e
c
m
B
e
m
m
C
=
=
ω
( )
( )
y
m
k
E
y
m
k
B
e
c
m
By
cm
e
k
B
e
c
m
y
c
m
B
e
y
m
z
x
x
ϕ
ϕ
−
=
+
−
+
∂
∂
−
*
2
2
*
2
2
2
2
*
*
2
2
2
*
2
2
*
2
2
2
2
*
2
2
2
2
2
2
2
h
h
h
h
( )
( )
y
m
k
E
y
eB
c
k
y
eB
c
k
y
m
y
m
z
x
x
C
ϕ
ϕ
ω
−
=
+
−
+
∂
∂
−
*
2
2
2
2
2
*
2
2
*
2
2
2
2
1
2
h
h
h
h
Podstawiamy:
eB
c
k
y
x
h
−
=
η
;
y
∂
∂
=
∂
∂
η
Ostatecznie:
( )
( )
η
ϕ
η
ϕ
η
ω
η
−
=
+
∂
∂
−
*
2
2
2
2
*
2
2
*
2
2
2
1
2
m
k
E
m
m
z
C
h
h
Interpretacja:
elektron swobodny miał energię:
(
)
*
2
2
2
2
2m
k
k
k
E
z
y
x
+
+
=
h
Gdy wprowadzamy pole magnetyczne, energia ulega
skwantowaniu w płaszczyźnie prostopadłej do kierunku tego
pola.
+
→
+
2
1
2
2
n
k
k
y
x
ω
h
*
2
2
2
2
1
m
k
n
E
z
C
h
h
+
+
=
ω
W kierunku równoległym do kierunku pola nie ma
kwantowania.
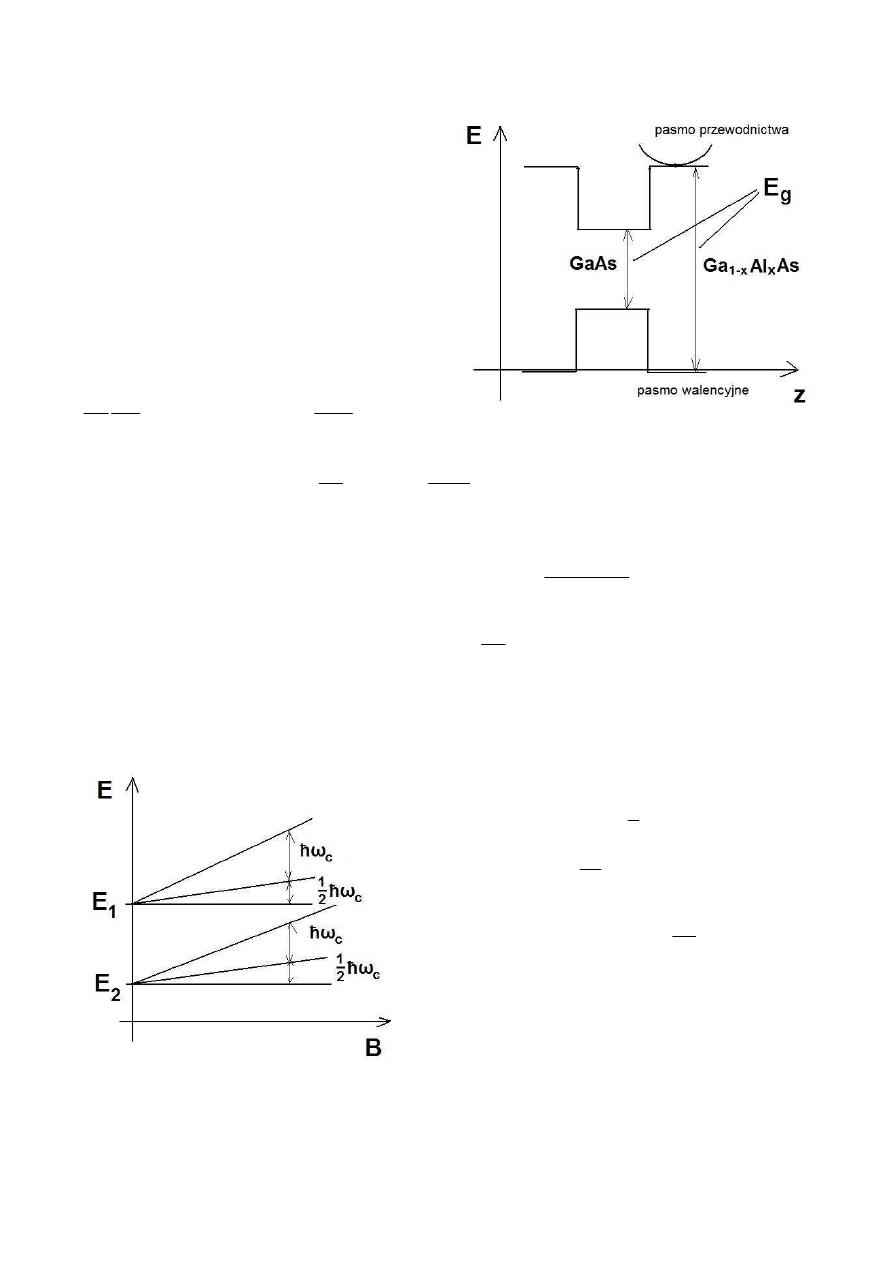
Efekty kwantowe w polu magnetycznym:
Metodą epitaksji uzyskuje się bardzo cienkie
warstwy półprzewodnika o zadanym składzie, np:
Ga
1-x
Al
x
As | GaAs | Ga
1-x
Al
x
As | GaAs ...
W ten sposób otrzymuje się studnię kwantową.
Przerwa energetyczna pomiędzy Ga
1-x
Al
x
As a
GaAs rozkłada się równo między pasmo
przewodnictwa a pasmo walencyjne.
Możemy ten układ potraktować jako
nieskończoną studnię potencjału o szerokości L
i rozwiązać równanie Schrödingera dla jednego
kierunku:
)
(
)
(
2
2
2
2
x
E
x
dx
d
m
ψ
ψ
=
−
h
m
k
E
2
2
2
h
=
Z warunków brzegowych:
π
n
kL
kL
=
→
=
0
sin
;
L
n
k
n
π
=
;
2
2
2
2
2
n
mL
E
n
π
h
=
W studni potencjału elektron zachowuje się jak fala stojąca. Jego energia jest skwantowana. W realnym
przypadku mamy studnię w paśmie przewodnictwa i paśmie walencyjnym, ale tylko w kierunku wzrostu
kryształu ( z ). Energia elektronu w rzeczywistej studni:
(
)
*
2
2
2
2m
k
k
E
E
y
x
n
+
+
=
h
Wprowadzając domieszkę (domieszkowanie modulacyjne) uzyskujemy dodatkowy elektron, który
wpada do studni i uzyskuje ogromną ruchliwość
V
cm
10
7
≈
µ
. Niestety utrzymuje się ona tylko w
niskich temperaturach (w wysokich fonony utrudniają ruch).
Zamiast tego dostajemy półprzewodnik o ściśle określonej liczbie nośników prądu.
Gdy wprowadzimy układ w pole magnetyczne, kwantowanie pojawi się również na kierunkach
x
i y .
A więc energia elektronu zostanie całkowicie
skwantowana:
+
+
=
2
1
)
,
(
B
C
n
B
z
n
E
n
n
E
z
ω
h
;
gęstość stanów:
h
eB
B
=
ρ
- rośnie wraz z polem magnetycznym
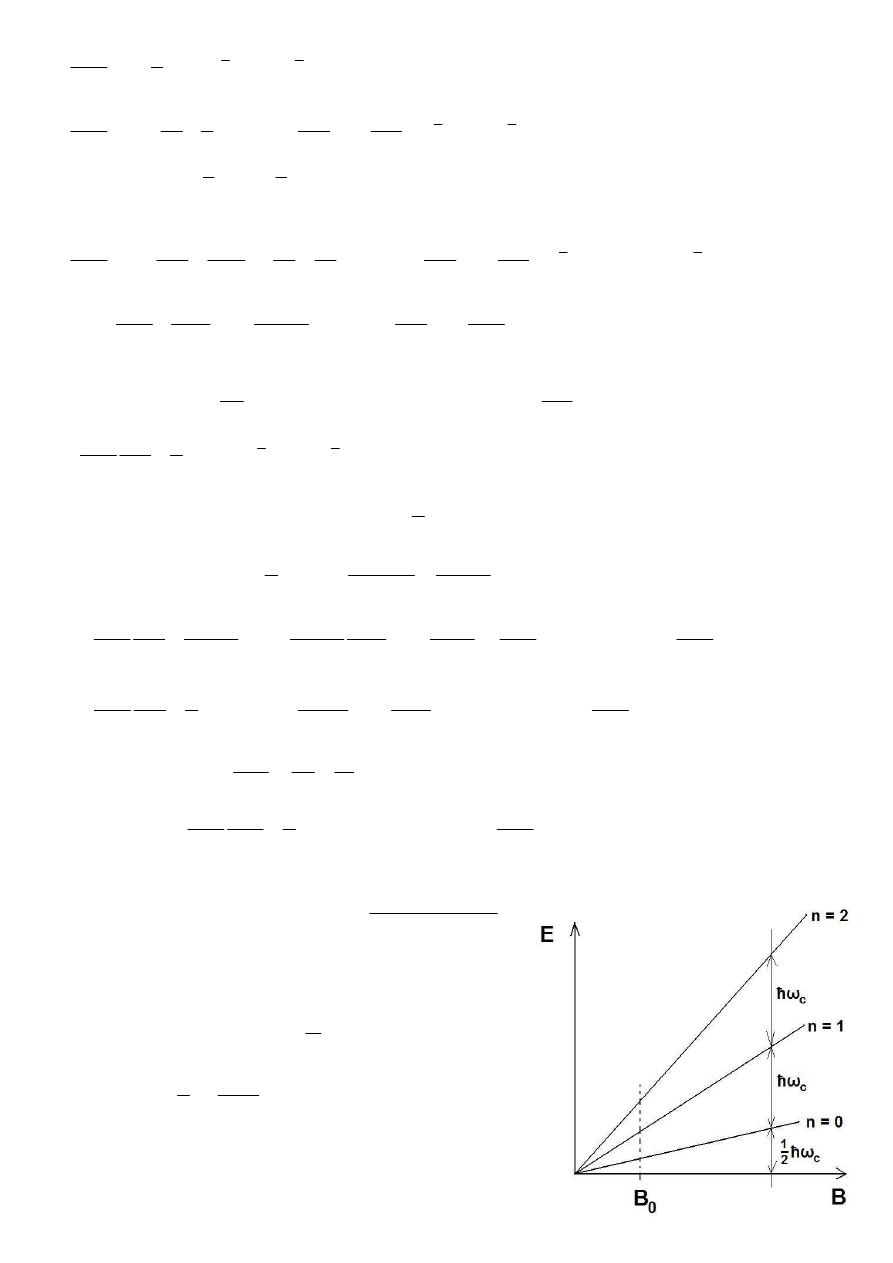
Poziomy są dosyć oddalone:
*
m
eB
C
=
ω
, i na każdym
poziomie, jeśli B jest duże, pojawia się dużo stanów.
W wysokich B wszystkie elektrony siedzą na
najniższym poziomie Landaua. Gdy zmniejszamy pole,
część elektronów będzie mogła wskoczyć na wyższe
poziomy. Stąd kwantowy efekt Holla. Warto zauważyć,
ż
e jest on w zasadzie kwantowaniem oporu elektr.