Politechnika Wrocławska	LABORATORIUM PODSTAW ROBOTYKI	Termin: piątek P 8.00-11.00
Skład grupy: Sebastian Skała Damian Tacik Sławomir Prószyński Adam Majda	Temat: Metody interpolacji.	Data:
				Ocena:

1. Wprowadzenie:

Celem naszego ćwiczenia jest zapoznanie się z metodami interpolacji oraz porównanie ich. W tym celu wykorzystujemy specjalnie do tego celu stworzoną aplikacje. Zadaniem interpolacji jest utworzenie funkcji, która przebiega przez zadane punkty. Stosuje się różne klasy funkcji do interpolowania - wielomiany algebraiczne, sklejania funkcji.

2. Przebieg ćwiczenia:

Dane wprowadzone do aplikacji jednakowe dla wszystkich metod:

L₁=5; L₂=5 -długość ramion robota

q₀=15 i 20 [st] i q_f=30 i 40 [st] - konfiguracja początkowa i końcowa podawana w stopniach;

v₀=10 i 10 [st/s] i v_f=30 i 30 [st/s] - prędkość na końcach przedziału;

a₀= 5 i 5 [st/s²] i a_f=20 i 20 [st/s²] - przyśpieszenie na końcach przedziału;

ilość węzłów 5;

• INTERPOLACJA WIELOMIANAMI TRZECIEGO STOPNIA Z CIĄGŁYM PRZYSPIESZENIEM

Gwarantuje ciągłość pochodnej toru drugiego rzędu w przestrzeni konfiguracyjnej. Wyznacza tor będący sklejeniem wielomianów stopnia trzeciego ciągłych pochodnych do rzędu drugiego w N - konfiguracjach węzłowych.

W wyniku przeprowadzonych symulacji wygenerowaliśmy następujące wykresy:

• INTERPOLACJA WIELOMIANAMI STOPNIA TRZECIEGO CIĄGŁĄ PRĘDKOŚCIĄ

Metoda ta gwarantuje ciągłość pochodnej toru pierwszego rzędu w przestrzeni konfiguracyjnej. Trzy algorytmy różniące się sposobem wyznaczania prędkości węzłowych pośrednich:

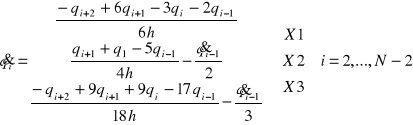
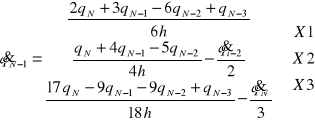
Wyznacza tor będący sklejeniem wielomianów stopnia trzeciego ciągłych pochodnych do pierwszego rzędu. Poniżej wykresy przedstawiające omówioną metodę.

• METODA KONTROLOWANEGO ODCHYLENIA OD ŚCIEŻKI PROSTOLINIOWEJ (ALGORYTM TAYLORA).

Metoda ta polega na takim wyznaczeniu ścieżki wynikowej w przestrzeni zadaniowej aby nieodbiegała ona od ścieżki zadanej na odległość większą niż założona przez użytkownika (błąd śledzenia w naszym przypadku ustawiony został na poziomie 0,5). W tym przykładzie wprowadziliśmy tylko wartości L₁ i L₂ oraz q₀ i q_f (z których wyliczane są punkty brzegowe) ponieważ tylko te były dostępne. Poniżej mamy wygenerowane wykresy.

• ZMODYFIKOWANA METODA KONTROLOWANEGO ODCHYLENIA OD ŚCIEŻKI PROSTOLINIOWEJ (ZMODYFIKOWANY ALGORYTM TAYLORA)

Ta metoda polega na takim sposobie dodawania punktów węzłowych, by błąd śledzenia osiągnął maksymalną dopuszczalną wartość. Od zwykłego algorytmy Taylora różni się właśnie mniejszą liczbą punktów węzłowych, a co za tym idzie mniejszą liczbą skoków prędkości na wynikowym torze. W tym przypadku tak jak poprzednio zadajemy jedynie długość ramion robota oraz konfigurację początkową na podstawie której zostają wyliczone punkty brzegowe.

3. Wnioski i spostrzeżenia:

W ćwiczeniu tym dokonaliśmy symulacji wykorzystując różne metody interpolacji dla tych samych wartości zadanych. Dzięki specjalnie pod tym kątem stworzonej aplikacji możemy w łatwy sposób zbadać trajektorie i określić różnice między nimi. Łatwo możemy zauważyć różnice pomiędzy wynikami naszych pomiarów, są one zobrazowane wykresami zamieszczonymi poniżej każdej wyszczególnionej metody interpolacyjnej.