POLITECHNIKA RZESZOWSKA

Im..Ignacego Łukasiewicza

WYDZIAŁ BUDOWY MASZYN

I LOTNICTWA

KATEDRA PRZERÓBKI

PLASTYCZNEJ

Marcin Kędzierski

Wydz.BMiL Spec.III MDT Gr.lab.62 sem.VI Rok akad.2002\2003

Ćwiczenie odrobiono dnia:

3.03.2003

Sprawozdanie przyjęto dnia:

Podpis:

Uwagi:

PRZERÓBKA PLASTYCZNA.LABORATORIUM Sprawozdanie z ćwiczenia nr.3 Temat: Gięcie

CEL ĆWICZENIA:

Celem ćwiczenia jest:

- wyznaczenie charakterystyki gięcia materiału ułatwiającej obliczanie momentu gnącego,

- wyznaczenie przebiegu siły wyginania pod kątem 90° w tłoczniku gnącym,

- określenie wartości sprężynowania po gięciu.

WIADOMOŚCI PODSTAWOWE

Gięcie jest procesem kształtowania przedmiotów o powierzchniach rozwijalnych, w którym zachowana zostaje prostoliniowość tworzących, a zmiana krzywizny giętego materiału zachodzi w jednej płaszczyźnie. W zależności od rodzaju ruchu narzędzi rozróżnia się:

- gięcie na prasach - narzędzie wykonuje ruch prostoliniowo-zwrotny,

- gięcie przez walcowanie,

- gięcie przez przeciąganie (przepychanie).

Stan naprężeń i odkształceń występujący przy gięciu zależy przede wszystkim od geometrycznych warunków procesu, tj. od stosunku wymiarów przekroju poprze­cznego b/g i krzywizny gięcia l/p Ze schematu przedstawionego na rysunku wynika, że w przekroju poprzecznym giętej części występuje warstwa obojętna naprężeń, na której zmienia się znak przyrostów odkształceń osiowych. Po zewnę­trznej strome tej warstwy występują osiowe naprężenia rozciągające o p a przyrost odkształceń jest dodatni, po stronie zaś wewnętrznej naprężenia osiowe są ujemne i przyrost odkształceń też jest ujemny. Po rozpatrzeniu najprostszego schematu gięcia, czyli gięcia pasów o małej krzywiźnie można przyjąć, że po stronie zewnętrznej krzywizny materiał pod wpły­wem osiowych naprężeń rozciągających jest wydłużany w kierunku osiowym oraz skracany w dwu pozostałych kierunkach, po stronie zaś wewnętrznej pod wpływem naprężeń ściskających występuje skracanie w kierunku długości oraz zwiększanie wymiarów wzdłuż szerokości i grubości.

Klasyfikacja procesów gięcia ze względu na stan naprężeń: a) gięcie o małej krzywiźnie pasów wąskich, b) gięcie o małej krzywiźnie pasów szerokich, c) gięcie o dużej krzywiźnie

Przebieg procesu gięcia

W procesie gięcia wyróżnia się następujące fazy:

l. Fazę odkształceń sprężystych materiału, dla której w skrajnych punktach przekroju poprzecznego wartość naprężeń i odkształceń wynosi odpowiednio

gdzie: g - grubość giętego pasma,

ρ- promień gięcia,

E - moduł Younga.

Rozkład naprężeń i odkształceń na przekroju pasma jest liniowy. Faza gięcia sprężystego kończy się z chwilą, gdy w skrajnych włóknach naprężenia osiągną wartość naprężeń uplastyczniających σ^o_p

2. Fazę odkształceń plastycznych; przy dalszym zwiększaniu krzywizny, już w zakresie odkształceń plastycznych zachowany zostaje w przybliżeniu prostoliniowy rozkład odkształceń przy czym w obu warstwach zewnętrznych o grubości f odkształcenie osiowe przekracza wartość graniczną σ^o_p wobec czego

warstwy te znajdują się w stanie plastycznym, podczas gdy leżąca między nimi warstwa o grubości e jest jeszcze w stanie sprężystym. Przy plastycznym zginaniu naprężenia osiowe, występujące w dowolnym punkcie przekroju poprzecznego przedstawia rysunek Jak widać, w środkowym obszarze sprężystym naprężenia wzrastają liniowo w miarę oddalania się od warstwy neutralnej, by na granicy z

obszarem uplastycznionym osiągnąć wartość σ^o_p. Dalszy ich wzrost w obszarze

plastycznym, spowodowany zjawiskiem umocnienia się odkształcanego materiału, nie jest proporcjonalny do odległości od warstwy obojętnej.

Rozkład odkształceń - a) i naprężeń - b) na przekroju giętego pasma w fazie odkształceń plastycznych

3. Fazę powrotnych odkształceń sprężystych; po całkowitym zdjęciu obciążenia w zgiętym paśmie pozostaną naprężenia własne pierwszego rodzaju. Rozkład tych naprężeń można wyznaczyć w sposób przedstawiony na rysunku, a więc przez nałożenie na rzeczywisty rozkład naprężeń w stanie obciążonym rozkładu naprężeń, jaki powstałby pod wpływem przeciwnie skierowanego obciążenia momentem -M_B, przy założeniu, że pasmo znajduje się w stanie sprężystym. Naprężenia własne, otrzymane w wyniku sumowania wymienionych rozkładów naprężeń, pokazano na rysunku. Jak widać na tym rysunku, w warstwie zewnętrznej, która w czasie gięcia była rozciągana, pojawiają się ściskające naprężenia własne i odwrotnie - w skrajnej warstwie wewnętrznej powstają naprężenia rozciągające. Jak zawsze przy napręże­niach własnych zachodzi równowaga sił i momentów.

Sposób wyznaczania naprężeń własnych pierwszego rodzaju na przekroju giętego pasma

Z przedstawionego rozkładu naprężeń własnych wynika istotna uwaga dotycząca warunków pracy tak wygiętej części. Korzystne jest bowiem, jeśli część gięta jest obciążona momentem tak samo skierowanym jak działanie momentu w procesie gięcia. Wówczas naprężenia występujące w czasie eksploatacji przedmiotu odejmują się od jego naprężeń własnych i w ten sposób zwiększa się jego nośność. Dotyczy to zwłaszcza niebezpiecznych, skrajnych warstw przekroju poprzecznego.

Schemat wyginania w matrycy w kształcie litery V.

Wykonanie ćwiczenia:

1. Zmierzyć mikrometrem grubość próbki i suwmiarką jej szerokość

2. Wygiąć próbkę, przesuwając uchwyt maszyny wytrzymałościowej. Zmierzyć za pomocą czujnika strzałkę ugięcia. Odciążyć próbkę i zmierzyć strzałkę ugięcia.

3. Ponownie wygiąć próbkę i ponowić odczyt strzałki ugięcia przy obciążeniu, oraz po odciążeniu.

4. Przy wygięciu bliskim 90^o dotłoczyć próbkę do matrycy

5. Wyjąć próbkę i porównać kąty wygięcia poszczególnych próbek

Wyniki pomiarów

Lp.	Materiał	Strzałka ugięcia		Siła gięcia	Kąt wygięcia próbki		Współczynnik sprężynowania	Wymiary próbki
				fg	fs	P[kN]	γg	γs	k	grubość [g]	szerokość [b]
	stal	4,4	3,9	0,65	8,348124	7,410669	0,887705	2	38,95
1.		7,7	7,3	0,75	14,40248	13,68312	0,950053
2.		9,8	9,2	0,75	18,09967	17,05768	0,942431
3.		12,4	11,7	0,8	22,46833	21,31659	0,948739
4.		15,3	14,4	0,8	27,03529	25,65401	0,948908
5.		17,3	16,5	0,80	29,98582	28,82541	0,961301
6.		18,1	17,1	0,8	31,11976	29,6982	0,95432
7.		19,1	18,4	0,8	32,50002	31,53817	0,970404
8.		23,8	23,6	5,3	38,44563	38,21032	0,993879
	aluminium							2	39,60
1.		3,9	2,9	0,35	7,410669	5,524237	0,745444
2.		6,9	5,8	0,4	12,95933	10,94774	0,844776
3.		10,0	9,0	0,4	18,4443	16,70771	0,905847
4.		12,8	11,7	0,4	23,11805	21,31659	0,922076
5.		16,1	14,6	0,4	28,23529	25,96381	0,919552
6.		18,4	17,1	0,4	31,53817	29,6982	0,941659
7.		20,8	18,0	0,45	34,75248	30,97946	0,891432
8.		24	23,6	5,4	38,67942	38,21032	0,987872
	mosiądz							2	39,55
1.		3,5	2,2	0,75	6,6578	4,19631	0,630285
2.		5,8	4,4	0,8	10,94774	8,348124	0,762543
3.		7,9	6,5	0,85	14,76045	12,23132	0,828655
4.		9,6	8,1	0,9	17,75367	15,11724	0,851499
5.		12,7	11,1	0,9	22,9562	20,31477	0,884936
6.		16,1	14,0	0,9	28,23529	25,02958	0,886465
7.		18,5	16,0	0,9	31,67681	28,08673	0,886665
8.		19,2	16,9	0,9	32,63579	29,40892	0,901125
9.		24	22,4	4,95	38,67942	36,76611	0,950534

- rozstaw podpór matrycy

- promień stempla

- kąt tarcia

- kąt matrycy

- współczynnik zależny od rodzaju materiału

- stała materiałowa

- wykładnik krzywej umocnienia

i
- dobrano z tablic

- długość ramienia

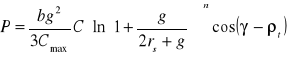
- wartość siły kształtowania plastycznego

- strzałka ugięcia

- współczynnik sprężynowania

stal	0,81	689	0,246	358,795	42,436
aluminium	0,721	127	0,258	95,944	28,89
mosiądz	0,773	710	0,480	299,94	29,97

Wykres zależności siły gięcia P[kN] od wartości kąta ugięcia w stanie obciążonym

Wykres zależności współczynnika sprężynowania odkuta ugięcia w stanie odciążonym.

Wykres zależności siły gięcia od strzałki ugięcia w stanie obciążonym

Wykres zależności strzałki ugięcia w stanie obciążonym od stanu odciążonego.

Wnioski: Pod wpływem wyginania w matrycy pod kątem 45^o, żaden z materiałów nie osiągnął tego kąta, jest to wynikiem znacznej sprężystości materiałów. Zależność strzałek ugięcia w stanie obciążonym i w stanie odciążonym jest prawie liniowa w całym zakresie. Materiału po osiągnięciu stanu plastyczności wyginają się baz znacznego przyrostu siły odkształcającej. W celu osiągnięcia żądanego kąta wygięcia próbki należy dobrać matryce o dostatecznie większym kącie roboczej części matrycy γ .

2

---