POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI
Paweł Proń	Sprawozdanie z ćwiczenia nr 9 Temat: Badanie ruchów oscylatorów sprzężonych
Wydział Elektroniki Rok I	Data: 17.03.1998	Ocena:

I. Cel ćwiczenia.

Celem ćwiczenia jest:

1. zapoznaniem się z opisem ruchu oscylatorów sprzężonych,

2. wyznaczenie częstości własnych ₁, _, częstości dudnień _d,

3. określeniem związków pomiędzy momentem kierującym D, a częstością własną ₁, a także związkiem pomiędzy momentem sprzęgającym D_s, a częstością dudnień _d.

 Wstęp teoretyczny.

Z ruchem oscylatorów sprzężonych mamy do czynienia w przypadku połączenia dwóch identycznych oscylatorów harmonicznych, w taki sposób, że dodatkowa siła (wynikająca z połączenia ) jest proporcjonalna do różnicy wzajemnych wychyleń pojedynczych oscylatorów. Równanie ruchu pojedynczego oscylatora harmonicznego, zgodnie z drugą zasadą dynamiki Newtona ma postać:

m
= -kx

gdzie : m - masa oscylatora,

x - wychylenie z położenia równowagi,

k - współczynnik proporcjonalności.

,a wielkością charakteryzującą dany oscylator jest jego częstość własna (kołowa) _,

_ 

Natomiast równanie ruchu dwóch oscylatorów sprzężonych wyrazi się:

m
₁ = -kx₁ - k_s(x₁ - x₂),

m
₂ = -kx₂ - k_s(x₂ -x₁),

Powyższe równanie można uogólnić na większą liczbę oscylatorów harmonicznych o różnych częstościach własnych.

Rozwiązując powyższe równania, otrzymamy wyrażenia określające częstości (kołowe) własne oscylatorów sprzężonych:

_ 
= _ lub _ 

W zależności od warunków początkowych, obydwa oscylatory sprzężone drgają z częstością kołową _, lub _  tak aby obydwa oscylatory drgały z częstością _, ich fazy początkowe muszą być zgodne, w przypadku gdy ich fazy są przeciwne drgają z częstością _

Badając ruch oscylatorów sprzężonych, spotykamy się ze zjawiskiem „dudnienia”. Zjawisko to występuje w przypadku gdy drgania o niewiele różniących się pulsacjach, nałożą się na siebie, tworząc drganie złożone o składowych:

x₁ = A cos _t = A cos ( 
 t

x₂ = A cos _t = A cos (   t

gdzie:

 
,  

natomiast drganie wypadkowe wyrazi się wzorem:

x =A cos ( t + A cos ( t  2Acos t cost ='cos t

Amplituda tego drgania zmienia się periodycznie w czasie z pulsacją równą 2

 Przyrządy użyte w ćwiczeniu.

• układ wahadeł sprzężonych (zestaw 4)

• stoper (Q&Q)

• przymiar (dł. - 100 cm)

IV. Wyniki pomiarów.

• Stosowane oznaczenia

n - ilość cykli

t - czas w którym te cykle wystąpiły

T - okres drgań

_,_  częstość własna (kołowa) oscylatorów sprzężonych

_d - częstość dudnień

D - moment kierujący

D_s - moment sprzęgający

Pomiary zostały przeprowadzone dla sprężyny o współczynniku sprężystości k=1

1. Wyznaczanie okresu wahań odpowiadającego częstości własnej _

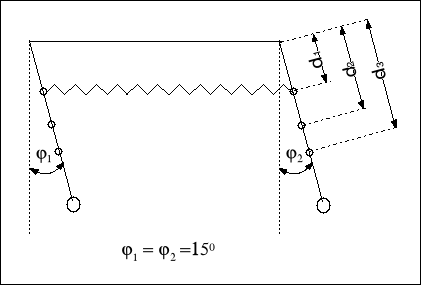
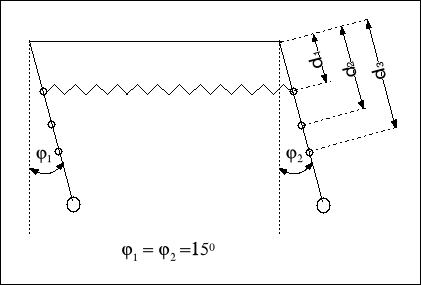
a) odległość sprężyny sprzęgającej d₁ = 0,15 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	T[s]	 ]	 
1	10	13,47	1,35	0.02	4,66	0,05
2	10	13,23	1,32	0,02	4,75	0,05

 = 1,335

0,254 [s]

 
0,19 * 100% = 19 [%]

_  ,

, 


  ,    , 

D = I_^  ,  (,^  ,

, kg*m²/s²]

b) odległość sprężyny sprzęgającej d₂ = 0,23 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	T[s]	 	  
1	10	13,36	1,34	0,01	4,7	0,02
2	10	13,49	1,35	0,01	4,66	0,02

T = 1,345
0,127 [s]

  ,    , 

_  ,
, 


  ,     

D = I_^  ,  (,^  ,
, kgm²/s²]

c) odległość sprężyny sprzęgającej d₃ =0,31 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	s	 	 
1	10	13,26	1,33	0,01	4,74	0,03
2	10	13,39	1,34	0,01	4,69	0,03

T = 1,335
0,127 [s]

  ,    , 

_  ,
, 


  ,     

D = 0,234 * (4,715)² = 5,1888 0,8653 [kgm²/s²]

2. 
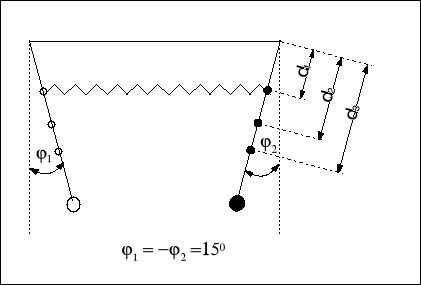
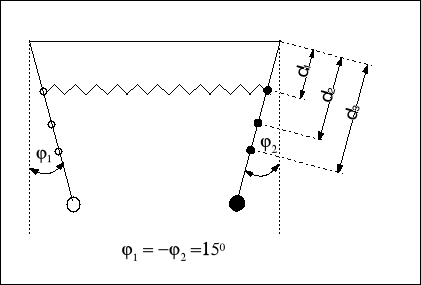
   Wyznaczanie okresu wahań odpowiadającego częstości własnej _

a) odległość sprężyny sprzęgającej d₁ = 0,15 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	s]	 	 
1	10	12,95	1,3	0,01	4,85	0,01
2	10	12,9	1.29	0,01	4,87	0,01

T = 1,295
0,127 [s]

  ,    , 

_  ,
, 


  ,    , 

b) odległość sprężyny sprzęgającej d₂ = 0,23 [m]

Lp.	n	t[s]	T[s]	s]	 	
1	10	12,59	1,26	0,02	4,99	0,06
2	10	12,29	1,23	0,02	5,11	0,06

T = 1,245
0,254 [s]

  ,   , 

_  ,
, 


  ,     

4. odległość sprężyny sprzęgającej d₃ = 0,31 [m]

Lp.	n	t[s]	T[s]	s]	 	 ]
1	10	11,87	1,19	0,01	5,29	0,04
2	10	12,06	1,21	0,01	5,21	0,04

T = 1,2
0,1 [s]

  ,     

_  ,
, 


  ,    , 

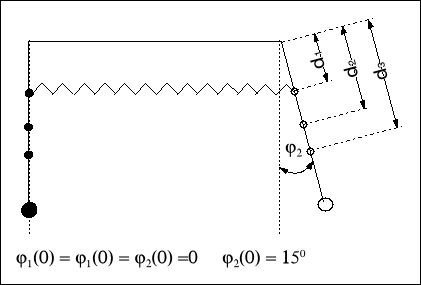
 Wyznaczanie okresu wahań odpowiadającego częstości dudnień _d

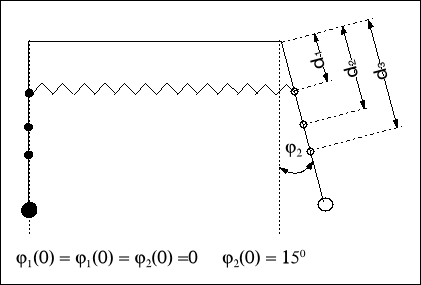
t - czas wyzerowania się amplitudy

n - ilość cykli, która w tym czasie wystąpiła

_d okres dudnień równy czterokrotnemu czasowi wyzerowania się amplitudy pojedynczego

wahadła

  różnica częstości kołowych _ i _

a) odległość sprężyny sprzęgającej d₁ = 0,15 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	s]	d [ ]	d[ ]
1	10	11,78	47,12	0,32	0,13	0,05
2	10	11,74	46,48	032	0,14	0,05

T_d = 46,8

4,1 [s]

  ,   , 

_d = 0,135

0,635 [
]

  ,     

  _  _  ,

, 


_d



D_s = _d

= 0,1483
0,7181 [kgm²]

b) odległość sprężyny sprzęgającej d₂ = 0,23 [m]

• tabela wyników

Lp.	n	t[s]	T[s]	s]	d[ ]	d[ ]
1	5	6,27	25,08	0,16	0,25	0,01
2	5	6,35	25,4	0,16	0,25	0,01

T_d = 25,24
2,03 [s]

  ,    

_d = 0,25
0,13[
]

  ,     

  _  _ ,
1,01 [
]

_d


D_s = _d
= 0,2731
0,158 [kgm²]

c) odległość sprężyny sprzęgającej d₃  , m]

• tabela wyników

Lp.	n	t[s]	T[s]	s]	d[ ]	d[ ]
1	3,5	4,83	19,32	0,12	0,33	0,05
2	3,5	4,89	19,56	0,12	0,32	0,05

T_d =19,44
1,524 [s]

  ,    , 

_d = 0,325
0,635 [
]

  ,    , 

  ,

, 


_d


D_s = _d
= 0,3577
0,7295 [kgm²]

V. Opracowanie wyników pomiarów.

• Przykłady obliczeń

• Dla IV.1 i IV.2 obliczenia wykonane są w ten sam sposób

T₁ =
[s]

T₁ =
-T₁ = 1,345 - 1,34 =
0,01 [s]

Do oszacowania błędów, ze względu na małą liczbę powtórzeń pomiarów stosuję metodę Studenta-Fishera



 ,

 

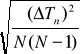
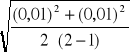
t_N,

t_{N, } współczynnik Studenta-Fishera, zależnym od liczby pomiarów N i zadanego poziomu ufności .

 = 0,95 ; t_N,  ,

  ,
(12,7 ⋅ 0,01) = 1,345
0,127 [s]

• to oznacza, że rzeczywista wartość okresu drgań znajduje się w tym przedziale z prawdopodobieństwem 95%

 
 
  , 

_ 

 , 
]

= 4,68 
]

_ 
 _  ,  , 
0,02 
]



 , 
]

 

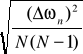
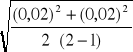
t_N,
 ,
, 
]

 
 
   

• obliczenia momentu kierującego D do IV.1

I - moment bezwładności wahadła

  , kgm²] ;   , 

I =  I =

D = I_^  ,  (,^  , 


• błąd bezwzględny dla momentu kierującego D obliczam metodą różniczki zupełnej

D = _^I + 2I__  (,^  ,    ,  ,  ,  , 


D = D
D = 5,1668
1,4212 


• obliczenie dla IV.3

T_d1 = 4 * t₁ = 4 * 4,83 = 19,32 [s]

_d1 =
= 0,32 
]

  _  _  (,
,  (,
,  (,  ,  ,  , 

 (,  ,  ,
, 
]

D_s =_d

kgm²]

Pozostałe obliczenia jak dla IV.1 i IV.2

VI. Wnioski

Ćwiczenie zostało przeprowadzone w budynku A-1 w sali na pierwszym piętrze. Ewentualny wpływ czynników zakłócających z zewnątrz na wyniki pomiarów jest mały i można go wykluczyć.

Przy wyznaczaniu okresu wahań odpowiadającego częstości własnej _, dla trzech różnych ustawień sprężyny, liczby wartości różniły się co najwyżej wartością liczby na drugim miejscu po przecinku, a błąd względny zawierał się od (9 do 19) %. Wartości częstości kołowej _ dla tych ustawień również nie odbiegały od siebie, a błąd względny zawiera się w przedziale (od 5 do 13,5) % . Ze związku między momentem kierującym D, a częstością _ widać, że moment ten jest wprost proporcjonalny do kwadratu wartości częstości _ .

Okres odpowiadający częstości _ jak i sama częstość _ podobnie jak to było wyżej, nie reagują na zmiany położenia sprężyny sprzęgającej. Ewentualne rozbieżności są wynikiem błędów pomiarów. Porównując natomiast same częstości _ i _ między sobą, można stwierdzić, że wartości częstości _ są

większe do częstości _. Różnica ta jest niewielka i równa w przybliżeniu jedności.

Dla przypadku wyznaczania częstości dudnień _d wartości okresu dudnień T_d i częstości _d zmieniają się w zależności od położenia sprężyny sprzęgającej w sposób następujący: im odległość d jest większa, tym okres jest krótszy, a wartość częstości większa. Wniosek stąd jest oczywisty: im zawieszenie sprężyny sprzęgającej jest bliższe końca wahadeł, tym wahadła lepiej przekazują sobie energię.

Wyznaczona częstość dudnień zawiera się w przedziale wartości obliczonych z różnicy częstości ₂ i ₁, jednak błędy pomiarów są bardzo duże i uniemożliwiają sprecyzowanie jak dokładnie te przedziały zamykają się w sobie.

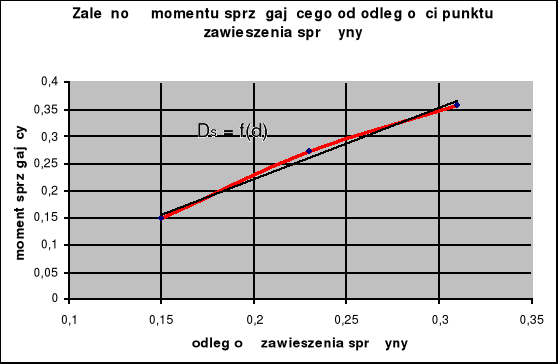
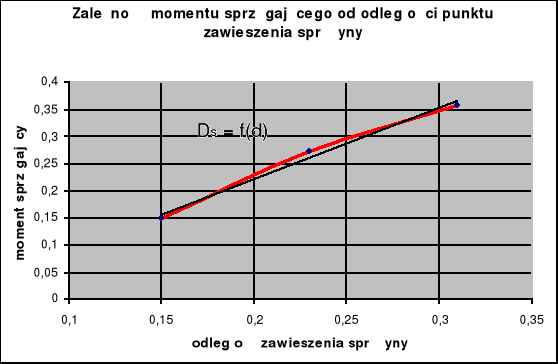
Moment sprzęgający D_s jest proporcjonalny do częstości _d , jak również do odległości zawieszenia sprężyny, co możemy odczytać z wykresu zależności tego momentu od odległości d. Zależność ta jest liniowa.

Uwaga: wykres sporządzony został na podstawie wartości średnich, gdyż błędy są zbyt duże i uniemożliwiają ich uwzględnienie, co znacznie obniża trafność ostatnich wniosków.

Błędy bezwzględne dla poszczególnych pomiarów są policzone metodą Studenta-Fishera, a otrzymane wyniki określają wartość rzeczywistą z dokładnością 95 % . Po obliczeniu błędów względnych ich wartości są przerażające i można je tłumaczyć brakiem doświadczenia w przeprowadzaniu dokładnych pomiarów, jak również przyjęciem współczynnika ufności  równego 0,95.

Instytut Fizyki - Politechnika Wrocławska ©1998

- 1 -

---