Cel ćwiczenia i opis metod pomiarowych
Zadaniem przeprowadzonego ćwiczenia było zapoznanie z metodą wyznaczenia charakterystyk elektromechanicznych silników indukcyjnych, bez konieczności używania do tego celu wyskalowanych urządzeń hamulcowych. Metoda ta jest pośrednia i zwana metodą strat poszczególnych.
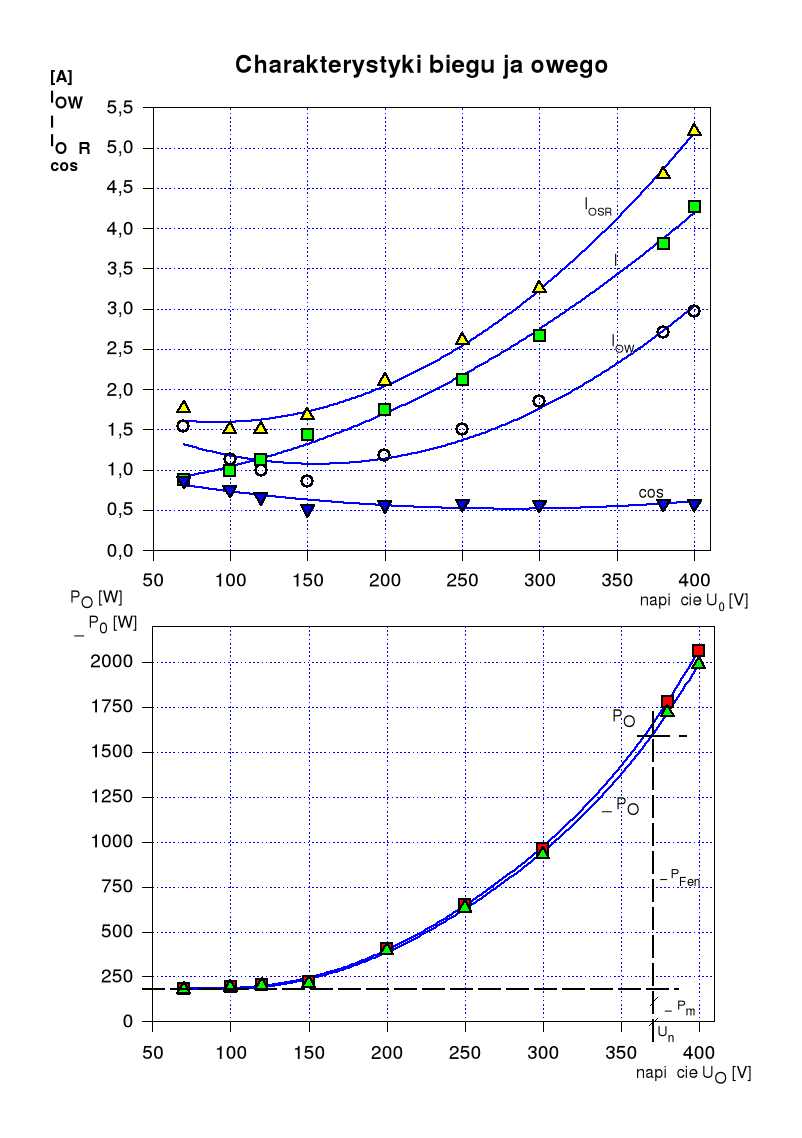
W pierwszej częsci ćwiczenia przeprowadzono pomiary podczas biegu jałowego. W tym celu nieobciążony silnik zasilono napięciem regulowanym, zmniejszając jego wartość od U=1,2Un do takiej wartości, przy której prąd pobierany przez silnik zaczyna rosnąć, tj. do U≈0,3Un. Otrzymane wyniki pozwoliły na na wyznaczenie strat mechanicznych oraz strat w żelazie silnika, na ich podstawie wykreślono charaktreystyki: Iμ , IOW =f(U0) oraz cosϕ0, I0, P0 =f(U0).
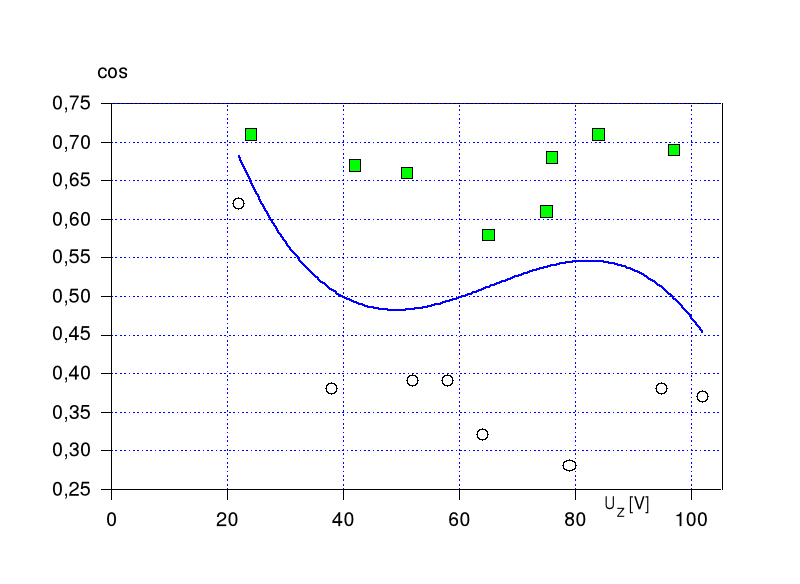
Druga część ćwiczenia obejmowała stan zwarcia (zablokowany wirnik). Pomiary przeprowadzono dla dwóch różnych położeń wirnika począwszy od wartości napięcia, przy którym wartość prądu IZ=1,2In dokonano odczytów wartości napięć i mocy. Na podstawie otrzymanych wyników wykreślono zależności cosϕz , IZ, PZ =f(UZ).
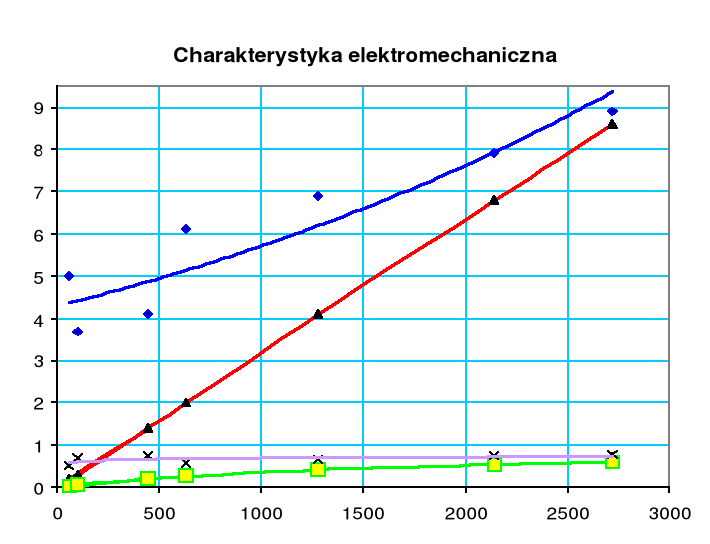
Ostatnia część ćwiczenia obejmowała pomiary w stanie bezpośredniego obciążenia. W tym celu należało obciążenie silnika zasilanego napięciem znamionowym U=Un zmniejszyć do obciążenia, przy którym I=1,2In do biegu jałowego, na podstawie wyników wykreślono charakterystyki między prądem zasilającym a mocą dostarczaną I=f(P1).
Na podstawie otrzymanych charakterystyk wyliczono pozostałe zadane wielkości.
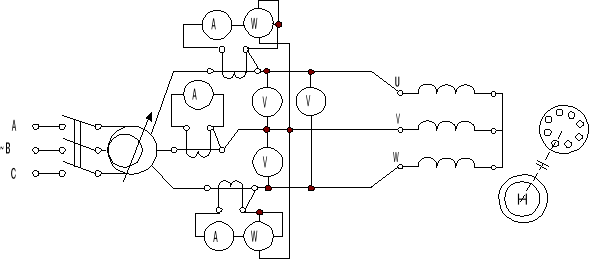
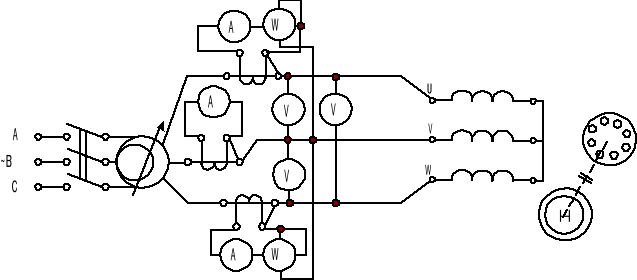
Układ pomiarowy
Tabele pomiarowe i przykłady obliczeń
3.1 Pomiar podczas biegu jałowego
Lp |
UOŚR |
IOŚR |
PO |
cosϕ0 |
ΔPobc |
ΔPO |
UO2 |
Iμ |
IOW |
|
[V] |
[A] |
[W] |
- |
[W] |
[W] |
[V] |
[A] |
[A] |
1 |
400,0 |
5,20 |
2060 |
0,57 |
77,06 |
1983,0 |
160000 |
4,27 |
2,97 |
2 |
380,0 |
4,67 |
1780 |
0,58 |
62,16 |
1718,0 |
144400 |
3,81 |
2,70 |
3 |
300,0 |
3,25 |
960 |
0,57 |
30,10 |
930,0 |
90000 |
2,67 |
1,85 |
4 |
250,0 |
2,60 |
650 |
0,57 |
19,27 |
631,0 |
62500 |
2,12 |
1,50 |
5 |
200,0 |
2,10 |
405 |
0,56 |
12,57 |
393,0 |
40000 |
1,74 |
1,17 |
6 |
150,0 |
1,67 |
220 |
0,51 |
7,95 |
212,0 |
22500 |
1,44 |
0,85 |
7 |
120,0 |
1,50 |
205 |
0,66 |
6,41 |
198,5 |
14400 |
1,13 |
0,99 |
8 |
100,0 |
1,50 |
194 |
0,75 |
6,41 |
188,1 |
10000 |
0,10 |
1,12 |
9 |
70,0 |
1,76 |
185 |
0,87 |
8,83 |
176,2 |
4900 |
0,90 |
1,53 |
Przykłady obliczeń:
-współczynnik mocy biegu jałowego
![]()
-straty obciążeniowe biegu jałowego
![]()
-straty jałowe
![]()
-skladowe prądu I0:
-składowa bierna (prąd magnesujący)
![]()
-składowa czynna
![]()
-napięcie biegu jałowego
![]()
Z otrzymanej charaktreystyki ΔP0=f(U0) odczytano wartość strat w rdzeniu ΔPFen =1350W oraz straty mechaniczne ΔPm.=200W.
3.2 Pomiar podczas stanu zwarcia
|
I położenie wirnika |
II położenie wirnika |
||||||||||
|
UZ |
IŚr |
P1 |
P2 |
P |
cosϕZ |
UZ |
IŚr |
P1 |
P2 |
P |
cosϕZ |
Lp |
[V] |
[A] |
[W] |
[W] |
[W] |
- |
[V] |
[A] |
[W] |
[W] |
[W] |
- |
1 |
102 |
9,8 |
190 |
460 |
650 |
0,37 |
97 |
9,7 |
250 |
880 |
1130 |
0,69 |
2 |
95 |
9 |
170 |
390 |
560 |
0,38 |
84 |
8,2 |
190 |
660 |
850 |
0,71 |
3 |
79 |
7,5 |
120 |
170 |
290 |
0,28 |
76 |
7,6 |
150 |
530 |
680 |
0,68 |
4 |
64 |
6,1 |
80 |
140 |
220 |
0,32 |
75 |
6,3 |
115 |
385 |
500 |
0,61 |
5 |
58 |
5,3 |
70 |
140 |
210 |
0,39 |
65 |
5,4 |
80 |
275 |
355 |
0,58 |
6 |
52 |
4,7 |
55 |
110 |
165 |
0,39 |
51 |
4,6 |
65 |
205 |
270 |
0,66 |
7 |
38 |
3,6 |
30 |
60 |
90 |
0,38 |
42 |
3,7 |
45 |
135 |
180 |
0,67 |
8 |
22 |
1,9 |
10 |
35 |
45 |
0,62 |
24 |
2,3 |
17,5 |
50 |
67,5 |
0,71 |
Przykłady obliczeń:
Na podstawie otrzymanej charakterystyki IZ=f(UZ) wyznaczono ΔUZ przydatne przy obliczeniu IZn oraz inne charakterystyczne wielkości:
-znamionowy prąd zwarcia
![]()
-krotność znamionowego prądu zwarcia
![]()
-znamionowa moc zwarcia (Un=U)
![]()
Moment obrotowy w stanie zwarcia Mzn , gdy U=Un , obliczono określając straty obciążeniowe w wirniku ΔPob2 , które dla znamionowego prądu zwarcia w przybliżeniu wynoszą :
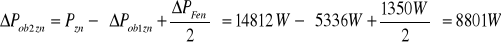
-straty obciążeniowe podstawowe
![]()
-moment obrotowy w stanie zwarcia przy U=Un
![]()
-współczynnik mocy zwarcia
![]()
3.3 Pomiar podczas obciążenia bezpośredniego
Lp |
UŚR |
IŚR |
PI |
PII |
P |
cosϕ |
ΔPOb1 |
Uwagi
|
|
[V] |
[A] |
[W] |
[W] |
[W] |
- |
[W] |
|
1 |
380 |
8,9 |
1280 |
3280 |
4560 |
0,78 |
270,9 |
R1∗=1,14Ω |
2 |
380 |
7,9 |
1000 |
2920 |
3920 |
0,75 |
213,4 |
|
3 |
380 |
6,9 |
480 |
2520 |
3000 |
0,66 |
162,8 |
|
4 |
380 |
6,1 |
280 |
2040 |
2320 |
0,58 |
127,3 |
|
5 |
380 |
5,0 |
560 |
1140 |
1700 |
0,52 |
85,5 |
|
6 |
380 |
4,1 |
560 |
1500 |
2060 |
0,76 |
57,5 |
|
7 |
380 |
3,7 |
400 |
1300 |
1700 |
0,70 |
46,8 |
|
8 |
380 |
3,3 |
240 |
1160 |
1400 |
0,64 |
37,2 |
|
3.4 Obliczanie charakterystyk elektromechanicznych
Lp |
U |
I |
PI |
PII |
P1 |
ΔPOB1 |
η |
M |
ΔPd1 |
Pel |
P2 |
UWAGI
|
|
[V] |
[A] |
[W] |
[W] |
[W] |
[W] |
- |
[Nm] |
[W] |
[W] |
[W] |
|
1 |
380 |
8,9 |
1280 |
3280 |
4560 |
270,9 |
0,60 |
8,6 |
21,4 |
2917,7 |
2718 |
Podczas ćwiczenia nie dokonano pomiaru wartości poślizgu s, z którym związany jest ΔPOB2 co unimożliwiło uwzględnienie wpływu tej wielkości na P2 |
2 |
380 |
7,9 |
1000 |
2920 |
3920 |
213,4 |
0,55 |
6,8 |
16,9 |
2339,7 |
2141 |
|
3 |
380 |
6,9 |
480 |
2520 |
3000 |
162,8 |
0,42 |
4,1 |
12,9 |
1474,3 |
1274 |
|
4 |
380 |
6,1 |
280 |
2040 |
2320 |
127,3 |
0,27 |
2,0 |
10,1 |
832,6 |
633 |
|
5 |
380 |
5,0 |
560 |
1140 |
1700 |
85,5 |
0,03 |
0,2 |
6,8 |
257,7 |
58 |
|
6 |
380 |
4,1 |
560 |
1500 |
2060 |
57,5 |
0,22 |
1,4 |
4,5 |
648,0 |
448 |
|
7 |
380 |
3,7 |
400 |
1300 |
1700 |
46,8 |
0,06 |
0,3 |
3,7 |
299,5 |
99 |
|
8 |
380 |
3,3 |
240 |
1160 |
1400 |
37,2 |
-0,14 |
-0,6 |
2,9 |
9,9 |
-190 |
|
Przykłady obliczeń:
-straty dodatkowe w uzwojeniu stojana wynikające z nierównomiernego rozkładu gęstości prądu w przekroju przewodu
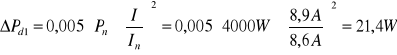
-moc elektromagnetyczna pola wirującego
![]()
-moc użyteczna na wale silnika
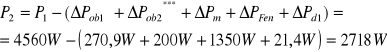
ΔPOb2***-nie uwzględniono w obliczenich (uzasadnienie we wnioskach)
-sprawnosć
![]()
-moment obrotowy na wale silnika
![]()
???????
4. Wykresy
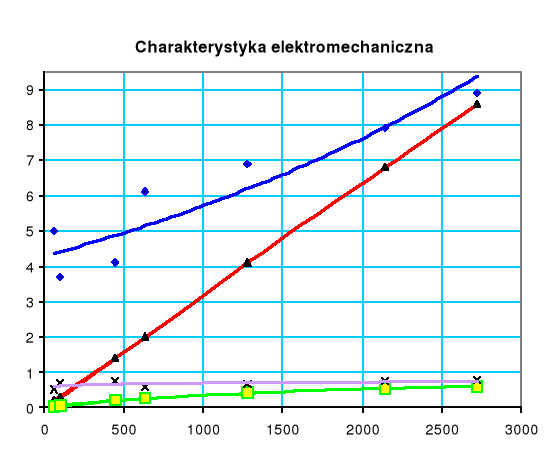
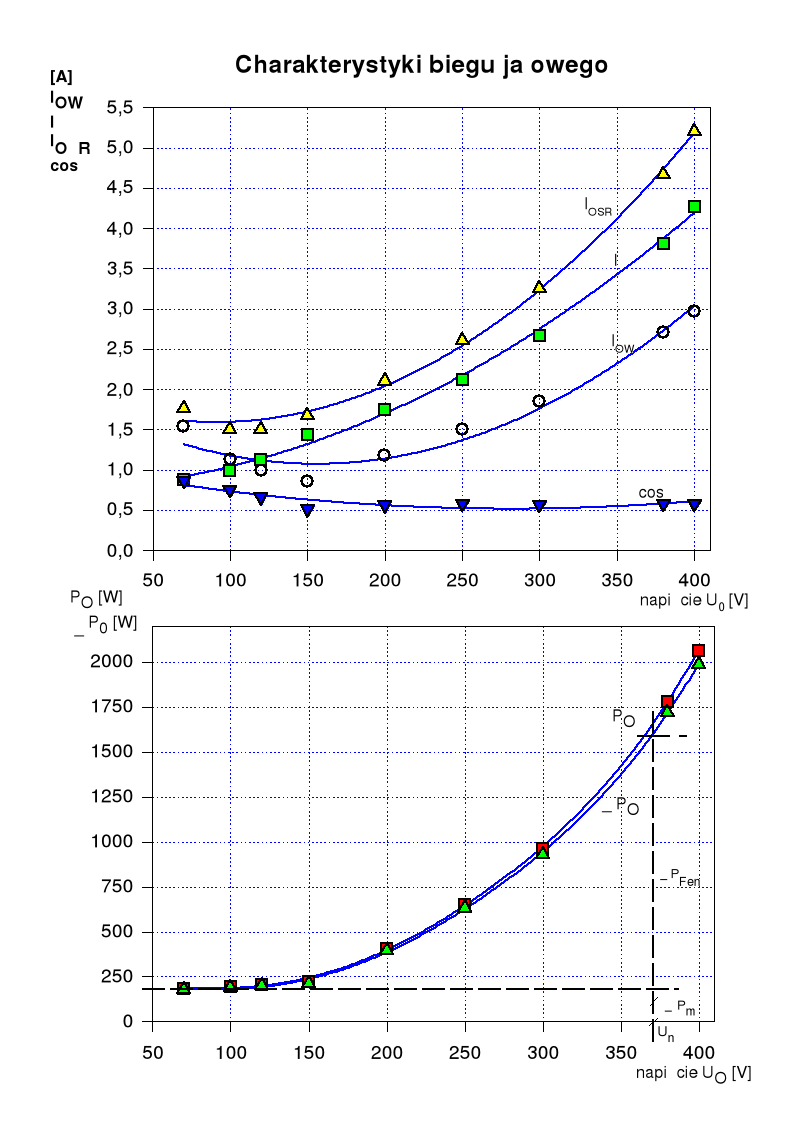
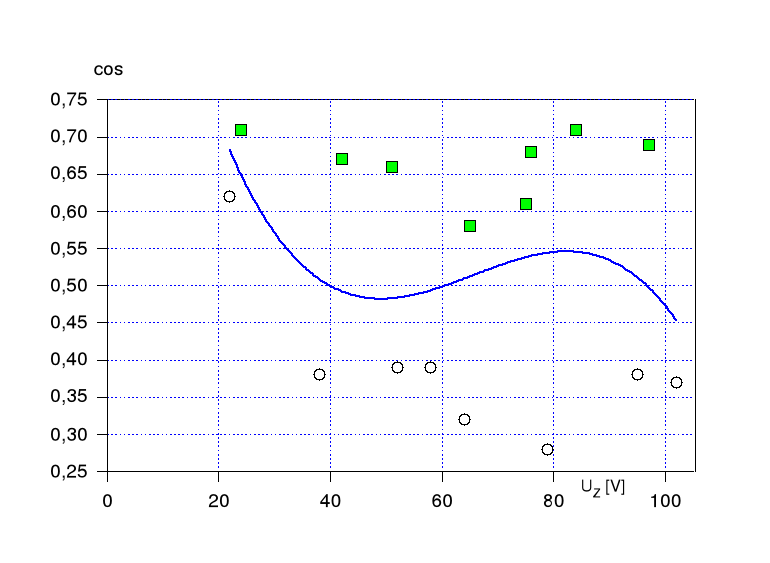
Wyszukiwarka
Podobne podstrony:
33 Wyzn.char.elektromech.silnika ind.met.strat poszczególnych(3), Politechnika Wrocławska, W-5 Wydzi
33 Wyzn.char.elektromech.silnika ind.met.strat poszczególnych(1), Politechnika Wrocławska, W-5 Wydzi
33 Wyzn char elektromech silnika ind met strat poszczególnych(5)
33 Wyzn char elektromech silnika ind met strat poszczególnych(6)
33 Wyzn char elektromech silnika ind met strat poszczególnych(3)
33 Wyzn char elektromech silnika ind met strat poszczególnych(1)
33 Wyzn char elektromech silnika ind met strat poszczególnych(6)
11 Silnik indukcyjny pierścieniowy SUHf, Szkoła, Politechnika 1- 5 sem, SEM IV, Maszyny Elektryczne.
35 Bad.silnika asynchr.jednofaz.(1), Politechnika Wrocławska, W-5 Wydział Elektryczny, Maszyny Elekt
35 Bad.silnika asynchr.jednofaz.(3)., Politechnika Wrocławska, W-5 Wydział Elektryczny, Maszyny Elek
11 Silnik indukcyjny pierścieniowy SUHf, Szkoła, Politechnika 1- 5 sem, SEM IV, Maszyny Elektryczne.
Cw88fiz, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fizy
CW84FIZ, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fizy
sprawko 5, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fi
cw 6 W1, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fizy
cw 5 wyk2, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fi
więcej podobnych podstron