Obliczanie i wyrównywanie zamkniętego ciągu sytuacyjnego, dowiązanego do dwóch punktów osnowy państwowej, przebiega w następujący sposób:

1. Wpisanie danych do formularza obliczeń.

2. Obliczenie teoretycznej sumy kątów.

Dla wieloboku zamkniętego o n kątach teoretyczna suma kątów wewnętrznych wynosi:

∑_w=(n-2)*200^g

a teoretyczna suma kątów zewnętrznych:

∑_z=(n+2)*200^g

3. Wyznaczenie praktycznej sumy kątów.

Praktyczną sumę kątów ∑a_p otrzymuje się sumując pomierzone kąty.

4. Obliczenie odchyłki kątowej ciągu.

Odchyłka kątowa ciągu f_a w ciągach poligonowych jest różna między sumą pomierzonych kątów ∑a_p a sumą teoretyczną kątów ∑a_t, zatem:

f_a=∑a_p-∑a_t

Wartość odchyłki kątowej f_a ciągu sytuacyjnego nie powinna przekraczać odchyłki maksymalnej f_{a max} obliczonej z zależności:

gdzie: m_o- średni błąd pomiaru kąta,

n_k - liczba kątów zmierzonych w ciągu.

5. Obliczanie poprawek do pomierzonych kątów.

Obliczona odchyłka kątowa f_a powinna być rozdzielona na zmierzone kąty.

Każdy pomierzony kąt otrzyma poprawkę V_a

6. Obliczenie azymutów boków ciągu sytuacyjnego.

Obliczenie azymutów boków ciągu sytuacyjnego rozpoczyna się od obliczenia ze współrzędnych azymutu boku łączącego punkty o znanych współrzędnych. Oznaczając obliczony azymut boku opartego na punktach nawiązania przez A_AB, azymuty kolejnych boków oblicza się w oparciu o wyrównane kąty wierzchołkowe. W zależności od przyjętego kierunku obliczeń przyjmuje się określenie: „kąty lewe” lub „kąty prawe”. Jako kąty lewe przyjmuje się kąty położone po lewej stronie ciągu, idąc w przyjętym kierunku obliczeń. Dla kątów prawych azymut kolejnego boku wynosi:

A_i = A_i-1 + 200^g - a_i

a dla kątów lewych:

A_i = A_i-1 + 200^g + a_i

7. Obliczanie przyrostów współrzędnych boków ciągu.

Przyrosty Δx i Δy współrzędnych boku l_i oblicza się z zależności:

Δx_i=

Δy_i=

8. Obliczenie praktycznej sumy przyrostów ∑_p

9. Obliczenie teoretycznej sumy przyrostów ∑_t

Teoretyczna suma przyrostów w ciągu zamkniętym wynosi:

∑Δx = 0 ∑Δy = 0

10. Obliczenie odchyłek sum przyrostów.

Różnice pomiędzy obliczonymi a teoretycznymi sumami przyrostów noszą nazwy odchyłek przyrostów i są oznaczone f_x i f_y:

f_x = ∑_pΔx - ∑_tΔx

f_y = ∑_pΔy - ∑_tΔy

11. Obliczanie odchyłki liniowej.

Odchyłkę liniową ciągu f_l oblicza się ze wzoru:

Odchyłka liniowa ciągu powinna być mniejsza od odchyłki dopuszczalnej:

f_l < f_{l dop}

Wartości dopuszczalnych odchyłek liniowych ciągów sytuacyjnych przedstawiono w tablicy poniżej

Długość ciągu L [m]	Dopuszczalna odchyłka fL [m]
300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000	0,15 0,16 0,17 0,18 0,20 0,22 0,23 0,24 0,26 0,27 0,29 0,31 0,33 0,34 0,36 0,38 0,40 0,42

Uwaga!

Do około 30% mierzonych ciągów można przyjąć

odchyłki dopuszczalne dwukrotnie większe od

podanych w tabeli.

12. Obliczenie poprawek i wyrównanie przyrostów do sumy teoretycznej

W obliczeniach ciągów sytuacyjnych odchyłki przyrostów rozdziela się proporcjonalnie do długości boków ciągu, stosując zależność:

VΔx_i=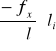

VΔy_i=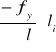

gdzie: V_Δxi, V_Δyi - poprawki do obliczonych przyrostów współrzędnych,

l_i - długość i-tego boku ciągu,

∑l - suma długości boków ciągu.

Suma przyrostów skorygowanych o obliczone poprawki V_xi i V_yi równa jest sumie teoretycznej. Wartości poprawek zaokrągla się do wartości odpowiadającej dokładności pomiaru długości boków ciągu.

13. Obliczanie współrzędnych ciągu.

Współrzędne punktów ciągu sytuacyjnego oblicza się w ten sposób, że do znanych współrzędnych punktu poprzedniego w ciągu dodaje się przyrosty Δx i Δy, otrzymując współrzędne kolejnych punktów:

X_i=X_i-1+Δx_i

Y_i=Y_i-1+Δy_i

---