POLITECHNIKA CZĘSTOCHOWSKA

W CZĘSTOCHOWIE

Instytut Fizyki

Ćwiczenie nr 17

TEMAT: Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru.

Informatyka II rok, grupa I

Borkiewicz Wojciech

Daniluk Łukasz

I. Wstęp teoretyczny

1. Dyfrakcja i interferencja fal świetlnych.

Dyfrakcja - odchylenie się biegu promieni fal świetlnych od prostoliniowości, zachodzące w pobliżu krawędzi ciał nieprzezroczystych, a także na wąskich (w porównaniu z długością fali) szczelinach.

Interferencja - wzajemne osłabianie się (niekiedy aż do całkowitego wygaszenia ) lub wzmacnianie 2 lub więcej fal świetlnych tej samej częstotliwości wskutek ich nakładania się; pierwszy przypadek następuje, gdy fazy fal są przeciwne, drugi - gdy zgodne.

Obraz interferencyjny uzyskany za pomocą dwóch szczelin różni się od obrazu dyfrakcyjnego pojedynczej szczeliny. Wygląda on tak, jak gdyby obraz pojedynczej szczeliny został dodatkowo zmodulowany szeregiem równo oddalonych prążków (trzy do pięciu) z obszaru głównego maksimum .

2. Siatka dyfrakcyjna

Siatka dyfrakcyjna - jest to płaska płytka szklana o równej grubości, posiadająca szereg równoległych rys. Rysy płytki pełnią rolę zasłon, natomiast przerwy między nimi - rolę szczelin przepuszczających światło.

Jeżeli na siatkę pada prostopadle wiązka promieni jednobarwnych, to każda jaj szczelina staje się źródłem nowych fal elementarnych .

Patrząc przez siatkę dyfrakcyjną na jednobarwny przedmiot świecący znajdujący się na tle ekranu, widać nie jeden, a kilka obrazów przedmiotu, symetrycznie położonych względem obrazu środkowego.

3. Zasada pomiaru stałej siatki dyfrakcyjnej

Włączamy lampę sodową i ustawiamy spektrometr. Lunetkę spektrometru naprowadzamy na prążek ugięty (ustawienie krzyża z nici pajęczych musi być dokładnie zgrane ze środkiem linii) i odczytujemy z możliwie największą dokładnością kąt położenia lunetki. Takie same pomiary wykonujemy dla prążków ugiętych pierwszego, drugiego i trzeciego rzędu w prawo i w lewo. Na podstawie wyników uzyskanych dla światła sodowego, obliczamy stałą d siatki z wzoru

dla k=1,2...

gdzie d- szerokość szczeliny, αk-kąt ugięcia

4. Budowa spektrometru

Spektrometr - przyrząd do wytwarzania widma optycznego i pomiaru długości fal odpowiadających poszczególnym liniom widmowym.

Spektrometr składa się z następujących części: kolimatora K, stolika T, lunetki L i kątomierza Kt. Całość zamocowana jest na silnej podstawce. Kolimator składa się z regulowanej szczeliny S i soczewki O. Długość kolimatora jest tak dobrana, że szczelina leży w ognisku soczewki, dzięki czemu otrzymujemy wiązkę równoległą. Kolimator jest nieruchomo związany z podstawką. Lunetka L połączona jest na stałe z kątomierzem Kt i może obracać się wokół osi spektrometru, a jej podłoże odczytuje się na kątomierzu Kt z dokładnością niekiedy równą jednej minucie kątowej. Tak dokładny odczyt umożliwiają noniusze N1 i N2, znajdujące się w odległości wzajemnej π. Lunetka zbiera równoległą wiązkę światła, dając tym samym ostry obraz szczeliny. W nowych goniometrach kąty odczytuje się metodą optyczną, a precyzja tego odczytu jest bardzo duża. Położenie lunetki jest równe średniej arytmetycznej wskazań l, p. obydwu noniuszy: φ=(l+p.)/2

0x01 graphic

  1. Tabela pomiarowa.

    2. Rząd widma

    Położenie kątowe n-tego prążka

    Śr wartości kąta ugięcia

    ϕ=(ϕ2+ϕ1)/2

    d

    dśr

    k

    prawo ϕ1

    lewo ϕ2

    I

    1

    2

    3

    4

    5

    7

    7

    6,5

    7

    7

    6

    6

    6

    6

    6,5

    6,5

    6,5

    6,25

    6,5

    6,75

    5,20*10-6

    5,20*10-6

    5,41*10-6

    5,20*10-6

    5,01*10-6

    II

    1

    2

    3

    4

    5

    14

    14

    14

    13,5

    13,5

    13

    13

    13,5

    13

    13

    13,5

    13,5

    13,75

    13,25

    13,25

    5,04*10-6

    5,04*10-6

    4,95*10-6

    5,13*10-6

    5,13*10-6

    5,10*10-6

    III

    1

    2

    3

    4

    5

    21

    21

    20

    21

    21

    20

    20

    20,5

    20

    20

    20,5

    20,5

    20,25

    20,5

    20,5

    5,04*10-6

    5,04*10-6

    5,10*10-6

    5,04*10-6

    5,04*10-6

    III. Opracowanie wyników pomiarów

    Stała siatki dyfrakcyjnej wynosi:

    dsinϕ=kλ

    po przekształceniu:

    0x01 graphic

    gdzie:

    d- stała siatki dyfrakcyjnej

    k- rząd widma

    λ- długość fali światła (dla lampy sodowej λ=5,89*10-7m.)

    Błąd pomiaru szacujemy metodą różniczki zupełnej

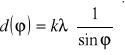
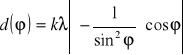
    0x01 graphic

    0x01 graphic

    0x01 graphic

    Przyjmując za Δϕ=0,02 rad (10) otrzymujemy wzór:

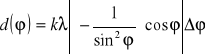
    0x01 graphic

    Błąd dla k=1

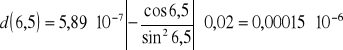
    0x01 graphic

    d%=0,00015*10-6/5,20*10-6*100%=0,0028%

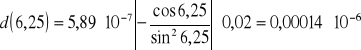
    0x01 graphic

    d%=0,00014*10-6/5,41*10-6*100%=0,0026%

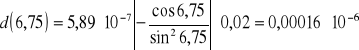
    0x01 graphic

    d%=0,00016*10-6/5,01*10-6*100%=0,0032%

    Średni błąd pomiaru (dla 5 pomiarów wg tabeli pomiarowej) wynosi 0,00015*10-6

    Błąd dla k=2

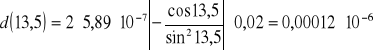
    0x01 graphic

    d%=0,00012*10-6/5,04*10-6*100%=0,0024%

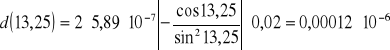
    0x01 graphic

    d%=0,00012*10-6/5,13*10-6*100%=0,0023%

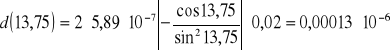
    0x01 graphic

    d%=0,00013*10-6/4,95*10-6*100%=0,0026%

    Średni błąd pomiaru (dla 5 pomiarów wg tabeli pomiarowej) wynosi 0,00012*10-6

    Błąd dla k=3

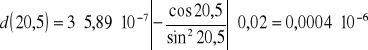
    0x01 graphic

    d%=0,0004*10-6/5,04*10-6*100%=0,0079%

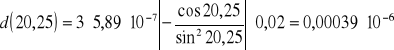
    0x01 graphic

    d%=0,00039*10-6/5,1*10-6*100%=0,0076%

    Średni błąd pomiaru (dla 5 pomiarów wg tabeli pomiarowej) wynosi 0,0004*10-6

    IV. Wnioski

    Na błędy powstałe podczas pomiaru stałej siatki dyfrakcyjnej nieznaczny wpływ miały:

    1. Błąd paralaksy (odczytu)

    2. Zbyt duża szerokość szczeliny, co wpływa na błędne odczytanie położenia mierzonego prążka

    3. Nierównoległość wiązki wychodzącej ze szczeliny

    4. Nieprostopadłe ustawienie siatki dyfrakcyjnej względem wiązki.