Katedra Algorytmów i Modelowania Systemów

Wydział Elektroniki, Telekomunikacji i Informatyki

Politechniki Gdańskiej

BADANIA OPERACYJNE

Część IC Zastosowania programowania liniowego

Materiały pomocnicze do wykładu z przedmiotu "Badania operacyjne"

Opracował: dr Tadeusz Ratajczak               

Gdańsk, 2005

Literatura:

1. Jacek Błażewicz, Wojciech Celary, Roman Słowiński, Jan Węglarz:     Badania     operacyjne dla informatyków. WNT, Warszawa 1983.

2. Saul I. Gass: Programowanie liniowe - Zastosowania. PWN,     Warszawa 1976.

3. Stanisław Krawczyk: Programowanie matematyczne. PWE,     Warszawa 1980.

4. Zbigniew Jędrzejczyk, Karol Kukuła, Jerzy Skrzypek, Anna Walkosz:     Badania     operacyjne w przykładach i zadaniach. PWN,     Warszawa 1997.

1. Zagadnienie transportowe

 dostawców posiada jednorodny towar odpowiednio w ilościach
jednostek. Całą masę towarową należy przetransportować do
 odbiorców, których zapotrzebowanie odpowiednio wynosi
jednostek. Znana jest macierz

,

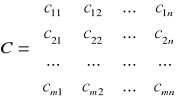
której element
oznacza koszt transportu jednostki towaru od i-tego dostawcy do j-tego odbiorcy. Należy wyznaczyć taką macierz

,

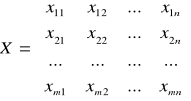
gdzie
oznacza liczbę jednostek towaru, którą należy przetransportować od i-tego dostawcy do j-tego odbiorcy, aby sumaryczny koszt transportu był najmniejszy.

Gdy
zagadnienie nazywamy zagadnieniem transportowym zamkniętym. W przypadku, gdy
problem nazywamy zagadnieniem transportowym otwartym. Zagadnienie transportowe otwarte sprowadzamy do zamkniętego w następujący sposób.

Jeśli
<
, to wprowadzamy fikcyjnego dostawcę
przyjmując
oraz
.

Jeśli
>
, to wprowadzamy fikcyjnego odbiorcę
przyjmując
oraz
.

Zad. 1.1. Trzech dostawców
posiada jednorodny towar w ilości
,
,
jednostek. Całą masę towarową należy przetransportować do pięciu odbiorców
, których zapotrzebowanie odpowiednio wynosi
,
,
,
,
. Koszty transportu jednostki towaru od poszczególnych dostawców do poszczególnych odbiorców są zestawione w poniższej macierzy

Wyznaczyć minimalny koszt transportu.

Zad. 1.2. Dwie bazy PKS:
,
wysyłają autobusy na cztery dworce:
,
,
,
położone na terenie miasta. Przejazdy między bazami i dworcami są traktowane jako puste przebiegi. Zaproponować rozdział autobusów pomiędzy dworce minimalizujący puste przebiegi.

W poniższej tablicy podano odległości pomiędzy bazami a dworcami, licznę autobusów, jakimi bazy dysponują oraz zapotrzebowanie dworców.

	Dworce
Bazy					Liczba autobusów
	15	12	10	17	100
	5	18	24	7	150
Zapotrzebowanie	40	65	45	60

2. Problemy przydziału

2.1. Problem przydziału I

wyrobów (czynności) można wykonywać na
miejscach produkcji (stanowiskach pracy, maszynach). Zakładamy, że każdy rodzaj wyrobu może być wykonany na każdym miejscu produkcji. Znane są ograniczenia na moce produkcyjne poszczególnych miejsc produkcji
(np. maksymalny dopuszczalny czas pracy) oraz plan wykonania poszczególnych wyrobów
. Ponadto dana jest macierz

,

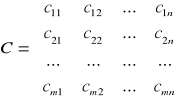
której element
oznacza koszt (czas) i-tego miejsca produkcji przy wykonywaniu jednostki j-tego wyrobu (wydajność i-tego miejsca produkcji przy wykonywaniu j-tego wyrobu).

Należy zaproponować optymalny przydział zadań produkcyjnych do poszczególnych miejsc produkcji z punktu widzenia jednego z poniższych kryteriów:

1. minimalizacja kosztów (czasu wykonania) zadań planowych,

2. maksymalizacja ilości wykonanych wyrobów.

2.2. Problem przydziału II (zagadnienie doboru)

Niech danych będzie
stanowisk i
kandydatów na te stanowiska. Każdy kandydat może być zatrudniony tylko na jednym stanowisku a każde stanowisko może być zajęte tylko przez jednego kandydata. Przydzielenie kandydata
na stanowisko
związane jest z kosztem
. Należy znaleźć takie przyporządkowanie poszczególnych kandydatów do poszczególnych stanowisk, aby łączny koszt był najmniejszy.

Zad. 2.1. W pewnej instytucji 4 sekretarkom należy przydzielić 4 różne prace biurowe. Znane są czasy (w minutach) zajmujące sekretarkom wykonanie poszczególnych rodzajów prac:

Kandydatki
	210	450	390	330
	270	390	450	330
	270	510	390	390
	330	450	330	450

Określić przydział prac sekretarkom minimalizujący łączny czas wykonania wszystkich prac. Zakładamy, że każda sekretarka będzie wykonywała tylko jedną pracę, oraz że każda praca będzie wykonywana przez jedną sekretarkę.

Algorytm węgierski

Krok 1.  Wykorzystując dwie operacje:

• od każdego wiersza macierzy
  odejmujemy minimalny element tego wiersza,

• od każdej kolumny macierzy
  odejmujemy minimalny element tej kolumny

przekształcić macierz kosztów
tak, aby w każdym wierszu i w każdej kolumnie występowało co najmniej jedno zero.

Krok 2.  W przekształconej macierzy należy skreślić wiersze i kolumny zawierające zera najmniejszą liczbą linii. Jeżeli liczba linii niezbędnych do pokrycia zer macierzy jest równa 
, to otrzymaliśmy rozwiązanie optymalne i przechodzimy do kroku 4. W przeciwnym przypadku przechodzimy do kroku 3.

Krok 3.  W przypadku, gdy liczba linii skreśleń jest mniejsza od 
w macierzy 
 należy znaleźć najmniejszy nie skreślony element i ten element:

1. odjąć od elementów nie skreślonych,

2. dodać do elementów podwójnie skreślonych.

(elementy skreślone jedną linią pozostawiamy bez zmian). Następnie powracamy do kroku 2.

Krok 4.  Konstruujemy macierz rozwiązania
biorąc pod uwagę, że

• jedynki w macierzy
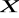
  mogą znaleźć się tylko na tych pozycjach, na których występują zera w macierzy
  ,

• w każdym wierszu macierzy
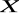
  powinna wystąpić dokładnie jedna jedynka,

• w każdej kolumnie macierzy
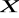
  powinna wystąpić dokładnie jedna jedynka.

Trzeba pamiętać, że

1. Metoda węgierska w opisanej postaci ma zastosowanie wyłącznie do rozwiązywania problemów minimalizacji.

2. Metoda węgierska w opisanej postaci zakłada, że macierz
   jest macierzą kwadratową, tzn. liczba kandydatów jest równa liczbie stanowisk.

3. W praktyce może się zdarzyć, że pewne przydziały są niedopuszczalne, tzn. trzeba założyć, że pewne
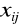
   muszą być równe zeru.

Zad. 2.2. Pewna instytucja zamierza zatrudnić trzech tłumaczy celem przetłumaczenia tekstów zapisanych w językach: angielskim, niemieckim i włoskim. W konkursie na te stanowiska wzięło udział czterech kandydatów. W poniższej tabeli podane są czasy potrzebne poszczególnym kandydatom na przetłumaczenie odpowiednich tekstów.

	Czas [w godzinach] potrzebny na przetłumaczenie tekstu
Tekst w języku:	Kandydat 1	Kandydat 2	Kandydat 3	Kandydat 4
angielskim	5	2	10	12
niemieckim	10	8	2	5
włoskim	15	1	5	5

Wybrać trzechn kandydatów do tłumaczenia tekstów w taki sposób, aby sumaryczny czas tłumaczenia był najmniejszy. Zakładamy, że każdy z trzech tekstów będzie tłumaczony tylko przez jednego tłumacza oraz że każdy tłumacz może pracować tylko nad jednym tekstem.

3. GRY MACIERZOWE

3.1. Podstawowe definicje

Podstawowym zagadnieniem teorii gier (sformułowanym przez Johna von Neumanna) jest badanie następującego problemu: Jeśli n graczy rozgrywa zadaną grę , to jak musi grać i-ty gracz , aby uzyskać najpomyślniejszy wynik ?

Zakładamy, że na końcu rozgrywki każdy gracz otrzymuje pewną ilość pieniędzy . Ilość może być liczbą dodatnią (oznacza wówczas wygraną gracza ), ujemną (oznacza wówczas przegraną gracza ) lub równe zero (oznacza wówczas wynik remisowy). W najbardziej znanych grach, jak na przykład poker, dla wszystkich rozgrywek zachodzi

.

Takie gry nazywamy grami o sumie zero. W grach o sumie zero gracze nie tworzą ani nie rozbierają puli bankowej. Przykładem gry o sumie niezerowej mógłby być poker, w którym pewien procent puli stanowi wynagrodzenie dla właściciela lokalu.

Gra macierzowa

Gra macierzowa jest grą dwuosobową, zdefiniowaną przez macierz

o elementach rzeczywistych, zwaną macierzą wypłat. W najprostszym przypadku (w przypadku wyboru przez graczy strategii czystych) zasady gry są następujące.

Najpierw gracz 
wybiera numer wiersza i macierzy wypłat, a następnie gracz
wybiera numer kolumny j. Element
oznacza sumę, którą gracz
płaci graczowi 
na zakończenie rozgrywki. Dopuszczamy oczywiście, że elementy
mogą być ujemne  i wówczas oznaczają, że
płaci graczowi
kwotę -
.

Dyskusja na temat wyboru strategii czystych przez graczy

Zgodnie ze sformułowanym we wstępie podstawowym zagadnieniem teorii gier, jedynym celem graczy jest maksymalizacja ich wygranych. Jeśli nie będziemy uwzględniali pomyłek graczy w trakcie rozgrywki, to przyjmiemy za naturalny następujący wybór strategii przez graczy
i
. Jeśli gracz 
wybierze wiersz i, to wygra co najmniej
Ponieważ gracz 
wybiera numer wiersza, więc może wybrać takie i, które maksymalizuje jego wygraną:
Stosując powyższą strategię gracz 
może wygrać co najmniej

Jeśli gracz  wybierze strategię j, to w najgorszym przypadku może przegrać Ale gracz 
może wybrać taką strategię j, która minimalizuje jego przegraną:
Stosując taką strategię, gracz 
może nie dopuścić, aby gracz 
wygrał więcej niż

w grach macierzowych mówimy, że gracz
jest graczem maksymalizującym (wygraną) a gracz
graczem minimalizującym (przegraną). Można wykazać, że zawsze zachodzi nierówność

.

Zad. 3.1. Wyznaczyć optymalne strategie czyste graczy dla gry macierzowej o następującej macierzy wypłat

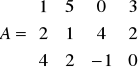
3.2. Strategie mieszane

Przez strategię mieszaną gracza 
rozumiemy wektor

,

taki, że .

Przez strategię mieszaną gracza 
rozumiemy wektor

taki, że .

Elementy oraz można interpretować jako częstości z jakimi gracz
wybiera i-ty wiersz a gracz
j-tą kolumnę w serii rozgrywek gry macierzowej.

Wielkość wygranej gracza
określa funkcja wypłaty (nadzieja matematyczna)

 .

Rozwiązaniem gry macierzowej nazywamy parę strategii mieszanych

,  ,

i taką liczbę rzeczywistą v, że

dla wszystkich strategii czystych j=1,2,...,n ,

dla wszystkich strategii czystych i=1,2,...,m .

Strategie nazywamy strategiami optymalnymi a v wartością gry.

Zasadnicze twierdzenie gier macierzowych

Dla każdej gry macierzowej istnieją i są sobie równe. Innymi słowy każda gra macierzowa ma rozwiązanie.

Uwaga. Za pomocą modelu programowania liniowego można wyznaczyć rozwiązanie gry macierzowej.

Zad. 3.2. Znaleźć rozwiązanie gry macierzowej o następującej macierzy wypłat

.

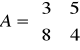
Zad. 3.3. Znaleźć rozwiązanie gry macierzowej o następującej macierzy wypłat

.

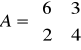
Zad. 3.4. Znaleźć rozwiązanie gry macierzowej o następującej macierzy wypłat

.

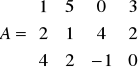
3.3. Gry z naturą

Gry z naturą są grami dwuosobowymi o sumie zero, w których przeciwnik (natura) nie podejmuje decyzji w trakcie gry.

Przykład 3.1. Rolnik ma wybrać jeden z trzech możliwych terminów t1, t2, t3 zasiewu zbóż. Wielkość plonów z hektara zależy od terminu zasiewu i stanu pogody. Zostały one zestawione w poniższej tabeli (w której wyróżniono 4 stany pogody S1, S2, S3, S4).

Terminy	Stany pogody
zasiewów	S1	S2	S3	S4
t1	21	15	32	16
t2	28	20	10	20
t3	13	27	25	15

Należy wspomóc rolnika w podjęciu decyzji o wyborze terminu zasiewu zbóż.

Wyboru można dokonać w oparciu o jedno z poniższych kryteriów.

• Kryterium Walda

Zakładamy, że zajdą warunki najbardziej niekorzystne dla podejmującego decyzję.     Dlatego optymalna decyzja i jest wybierana według reguły minmax. Odnośnie przykładu 1:

Następnie wybieramy

.

Ostatecznie wybieramy termin pierwszy (t1) gwarantując sobie wydajność z hektara      co najmniej 15 kwintali.

• Kryterium Hurwicza

Określa się arbitralnie współczynnik ostrożności a następnie wybiera się      strategię i, dla której największa jest wartość

Przyjmując w przykładzie 1 kolejno mamy:

Następnie wybieramy

.

Ostatecznie wybieramy termin pierwszy (t1) spodziewając się osiągnięcia wydajności      18.4 kwintali z hektara..

• Kryterium Bayesa

Zakładamy, że wszystkie stany z natury są jednakowo prawdopodobne. Zatem najlepszą      strategią jest ta strategia i, która daje największą średnią arytmetyczną wygranych, tzn.

.

Dla przykładu 1 mamy

Następnie wybieramy

.

Ostatecznie wybieramy termin pierwszy (t1) oczekując wydajności 21.0 kwintali z hektara.

Zad. 3.5. Trzy typy hamulców
,
,
podawano próbom w czterech rodzajach warunków drogowych
,
,
,
. Procent zadowalających prób podano w poniższej tabeli

	Rodzaj warunków drogowych
Rodzaj hamulców
	85	77	85	74
	88	70	90	78
	81	65	92	80

Wybrać do produkcji jeden z trzech rodzajów hamulców

1. przyjmując, że w trakcie eksploatacji będą występowały warunki zbliżone do najbardziej niekorzystnych,

2. przyjmując, że w trakcie eksploatacji wystąpienie każdego rodzaju warunków drogowych jest jednakowo prawdopodobne.

Skomentować podane rozwiązania.

13

---