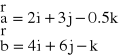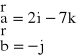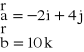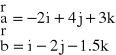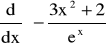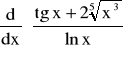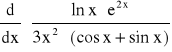ZESTAW 1
WEKTORY I POCHODNE
W0. Rozłóż na składowe wektor o długości a=5, nachylony pod kątem /3 do osi OX.
W1. Wykaż, że wektory
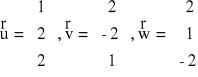
są wzajemnie prostopadłe oraz że każdy ma długość równą 3 jednostkom.
W2. Wykaż , że wektor
jest jednocześnie prostopadły do wektorów
W3. Składowa danego wektora ![]()
w kierunku dowolnego innego wektora ![]()
jest równa iloczynowi skalarnemu ![]()
, gdzie ![]()
jest wektorem jednostkowym o kierunku ![]()
.
Wektor jednostkowy ![]()
można uzyskać z wektora ![]()
poprzez znormalizowanie tego ostatniego ( normalizacja polega na podzieleniu wektora ![]()
przez jego długość).
Mając to na uwadze proszę znaleźć składową siły ![]()
w kierunku wektora
![]()
.
W4.Wyznacz iloczyn wektorowy i iloczyn skalarny dla wektorów ![]()
w czterech różnych przypadkach:
W6. W równaniu ![]()
przyjmij q=2, ![]()
i ![]()
. Ile wynosi wektor ![]()
, jeśli ![]()
?
W7. Stałe siły ![]()
działają równocześnie na cząstkę w czasie przesunięcia z punktu A(20,15,0) [m] do punktu B(0,0,7) [m]. Jak praca W została wykonana przez siłę wypadkową ![]()
przy przesunięciu cząstki (![]()
, gdzie ![]()
jest wektorem przemieszczenia cząsteczki)?
POCHODNE
WSKAZÓWKI:
e=2,718281828459
![]()
ln e = 1
Oblicz:
Oblicz:
Oblicz:
IV. Oblicz pochodną funkcji złożonej:
1. ![]()
2. ![]()
3. ![]()
4. 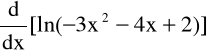
CAŁKI
V. Obliczyć całkę nieoznaczoną :
VI. Obliczyć całkę nieoznaczoną ( wykorzystujac metodę całkowania przez części ):
3
Wyszukiwarka
Podobne podstrony:
sciaga 4 mechanika, Zaawansowane materiały i nanotechnologia UJ, Fizyka, Mechanika
sciaga 5 mechanika, Zaawansowane materiały i nanotechnologia UJ, Fizyka, Mechanika
sciaga 1 mechanika, Zaawansowane materiały i nanotechnologia UJ, Fizyka, Mechanika
sciaga 2 mechanika, Zaawansowane materiały i nanotechnologia UJ, Fizyka, Mechanika
sciaga 3 mechanika, Zaawansowane materiały i nanotechnologia UJ, Fizyka, Mechanika
ruch, Zaawansowane materiały i nanotechnologia UJ, Fizyka, fizyka wyrównawcza
1.Drugie zajęcia wyrównawcze KONSPEKT DS, Zaawansowane materiały i nanotechnologia UJ, CHEMIA, Chemi
1.Trzecie zajęcia wyrównawcze KONSPEKT DS, Zaawansowane materiały i nanotechnologia UJ, CHEMIA, Chem
2.dla studentów, Zaawansowane materiały i nanotechnologia UJ, CHEMIA, Chemia nieorganiczna
autorskie prawo z lexa, Zaawansowane materiały i nanotechnologia UJ, Podstawy zarządzania i ochrony
sprawozdanie3, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały
lab4, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na labora
Materiały izolacyjne, SZKOŁA, fizyka
materiałoznawstwo, Studia - Budownictwo, Fizyka
sciaga fizyka wykl kolo 2, MATERIAŁY NA STUDIA, FIZYKA, fizykawyklegz, brak tematu
materialy sem1 A Karpio fizyka
Laboratorium Podstaw Fizyki, PWR, MATERIAŁY PWR, LABOLATORIA, FIZYKA 2
więcej podobnych podstron