Wykład 1

Literatura:

• Z. Pawłowski „Statystyka”

• Z. Hellwig „Wstęp do rachunku prawdopodobieństwa i statystyki matematycznej”

• M. Krzyśko „Statystyka matematyczna”

• Rao „Modele liniowe statystyki matematycznej”

• Aczel „Statystyka w zarządzaniu”

• Kończak, Trzpiot „Analizy statystyczne z arkuszem kalkulacyjnym Excel”

• Ostasiewicz (red.) „Statystyka

• A. Zeliasz „Statystyka”

• Sobczyk „Statystyka”

• J. Greń „Modele statystyki matematycznej” (z.z.)

• Domański „Statystyka” (z.z.)

• Zieliński „7 wykładów ze statystyki matematycznej”

Funkcja gęstości n-wymiarowej zmiennej losowej
o nieosobliwym rozkładzie normalnym:

,

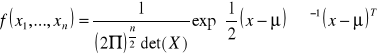
gdzie
jest
wymiarowym ............................... wartości oczekiwanych.

Tw.: Jeżeli wektor losowy
ma n-wymiarowy rozkład normalny
,
jest wektorem wielowymiarowym, oraz
jest stała, to rozkład zmiennej losowej
ma rozkład normalny
.

Niech
bezie wierszowym wektorem jednostkowym o wymiarze
oraz
macierzą jednostkową stopnia n. Wtedy z powyższego twierdzenia wynika, że jeżeli w szczególności:

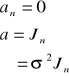
, to
.

Ponadto, gdy:

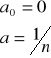
, to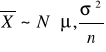
, gdzie

W końcu łatwo wykazujemy na podstawie podanego wyżej twierdzenia, że zmienna losowa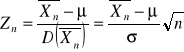
ma rozkład normalny standardowy, czyli
.

Ważne znaczenie ma rozkład chi-kwadrat

Def.: Gdy składowe ciągu
są niezależne i
dla i=1...k, to zmienna losowa
ma niecentralny rozkład
z k stopniami swobody i parametrem niecentralności
.

Gdy
dla każdego i=1,...,n , co oznacza, że
, to mówimy, że zmienna
ma centralny rozkład
z ka stopniami swobody i oznaczamy ją
.

Wartość oczekiwaną i wariancję zmiennej
o rozkładzie
określa wyrażenie
.

Tw.: Jeżeli liczba stopni swobody
to dystrybuanta zmiennej losowej
o rozkładzie
zmierza do dystrybuanty rozkładu normalnego
.

W praktyce dystrybuanta zmiennej
jest dostatecznie dobrze przybliżoną dystrybuantą rozkładu normalnego, gdy
.

Niech macierz H stopnia n i rzędu
będzie macierzą idempotentną, czyli
.

Tw.: Jeżeli
, czyli X jest n-elementową próbą pochodzącą z populacji o rozkładzie normalnym standardowym, to zmienna losowa
ma rozkład niecentralny
, gdzie
.

W szczególności, gdy
to
i
.

Tw.: Jeżeli zmienna losowa ma nieosobliwy k-wymiarowy rozkład normalny
(czyli,
jest macierzą dodatnio określoną - ma dodatni wyznacznik) to zmienna losowa
ma rozkład
.

Rozkład Studenta (Goset pseudonim Student)

Def.: Niech zmienna losowa
i
będą niezależne.

Wtedy zmienna losowa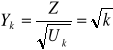
ma niecentralny rozkład studenta
z k stopniami swobody

i parametrem niecentralności
.

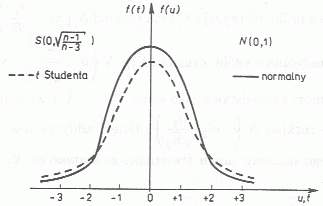
Jeżeli
to mówimy, że
ma rozkład studenta (centralny).

Gdy
to:

Rozkład studenta ma tłustszy ogon (skrzydło) rozkładu.

Tw.: Jeżeli liczba stopni swobody
to dystrybuanta rozkładu Studenta zmierza do dystrybuanty rozkładu normalnego standardowego
.

W praktyce dystrybuanta rozkładu Studenta może przybliżać dystrybuantę rozkładu normalnego przy
.

Rozkład Fischera

Def.: Jeżeli zmienna losowe
i
są niezależne i
i
, to zmienna losowa
ma niecentralny rozkład Fischera
z k₁ i k₂ stopniami swobody.

W szczególności, gdy
to zmienna losowa F ma centralny rozkład Fischera
z k₁ i k₂ stopniami swobody.

Gdy
to ..........................

Jeżeli liczba
i
to zmienna o rozkładzie Fischera ma rozkład normalny.

Definicja próby:

Niech zmienne losowe
są niezależne i każda z nich ma ten sam rozkład prawdopodobieństwa.

Wówczas ten ciąg nazywany jest prostą próbą statystyczną.

Np.

Rozważmy

przy czym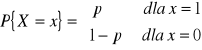

Realizacja (wartość) próby
to ciąg liczb
.

Estymacja punktowa parametryczna

Szacujemy parametr Θ, który na możliwe wartości θ.

/Każda rzeczywista funkcja próby statystycznej nazywana jest statystyką/

Szacujemy parametr Θ za pomocą statystyki, jeżeli przyjmuje wartość ze zbioru Θ to nazywamy ją estymatorem.

Błąd estymacji:

Przeciętny (średniokwadratowy) błąd estymatora
:

Zatem parametr
określa przeciętny poziom kwadratu błędu estymacji. Jego pierwiastek wskazuje, o ile średnio rzecz biorąc wartości estymatora
odchylają się (±) od wartości szacowanego parametru Θ.

Gdy
jest zmienną skokową, to:

Dekompozycja błędu:

, gdzie

- wariancja estymatora

- kwadrat obciążenia

Względny błąd estymacji:

..........................................................................

Def.: Statystyka
jest nieobciążonym estymatorem parametru Θ jeżeli
.

Jeżeli
to mówimy, że używając do oceny parametru Θ estymatora
popełniamy błąd systematyczny.

Różnicę
nazywamy obciążeniem estymatora.

a)

b)

c)

d)

Średnia z próby prostej jest nieobciążonym estymatorem.

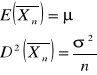
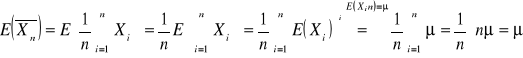
Wykład 2

W przypadku estymacji
i
wariancji w populacji
można wykazać, że jeśli
, to:

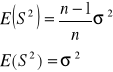
zatem statystyka
daje nieobciążone oceny parametru
.

jest granicznie nieobciążonym estymatorem wariancji.

Estymator powinien być:

1. nieobciążony

2. zgodny

3. efektywny

Względny średni błąd estymacji wyznacza wyrażenie:

,

które wskazuje jaki procent wartości szacowanego parametru stanowi pierwiastek z błędu średniokwadratowego estymacji.

Wyrażenie

definiuje względny, średni błąd szacunku estymatora
.

Gdy estymator
jest nieobciążony to
. Za pomocą zdefiniowanego wskaźnika można określić dopuszczalny poziom niedokładności estymacji. Zwykle postuluje się, aby
.

Gdy próba pochodzi z populacji, gdzie badana zmienna ma rozkład normalny to wariancja mierzonej próby
wynosi :

, gdzie:

jest stałą rzędu
, co oznacza, że wielkość
maleje do zera tak jak ciąg
.

Θ - parametr, który ma estymator

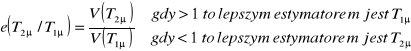
Jeśli
, to:

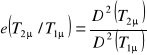
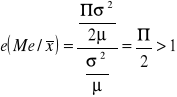
czyli precyzyjniejsza jest średnia z próby.

.... jest odpornym estymatorem średniej populacji ..................................................................[?]

Mówimy, że estymator jest zgodny, jeśli zachodzi

prawdopodobieństwo, że błąd estymacji nie przekroczy pewnego poziomu

W praktyce oznacza to, że opłaca się zwiększać liczebność próby bo rośnie wiarygodność estymacji mierzona prawdopodobieństwem nieprzekroczenia dopuszczalnego poziomu błędu estymacji.

Tw.: Statystyka
jest zgodnym estymatorem parametru θ, jeżeli
jest asymptotycznie nieobciążonym estymatorem parametru θ i
.

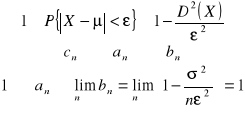
czyli
.

Efektywność

Def.: Estymator
jest efektywny w klasie nieobciążonych estymatorów K parametru θ, jeżeli dla każdej wartości parametru
i każdego estymatora
z klasy K istnieje taki estymator
, że:

Do oceny stopnia przewagi (w sensie precyzji estymacji) estymatora efektywnego nad innymi z klasy K wyznacza się współczynnik efektywności:

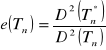
Mówi się, że statystyka
jest asymptotycznie efektywnym estymatorem parametru θ jeżeli:

Estymacja punktowa momentów i ich funkcji

gdy m - moment zwykły, to
, a we wzorach na wariancję i kowariancję znika składnik
.

Niech
będzie funkcją rzeczywistą k momentów.

Załóżmy, że:

1. funkcja H jest ograniczona w następujący sposób:

, przy czym A jest stałą, a

2. istnieją wszystkie pochodne cząstkowe funkcji H przynajmniej do drugiego rzędu włacznie. Wtedy oznaczając przez
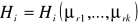
   pochodną cząstkową funkcji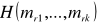
   , względnie argumentu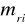
   w punkcie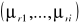
   

mamy:

Tw.: Utrzymajmy oznaczenia i założenia wprowadzone w powyższym twierdzeniu z możliwością niespełnienia założenia 1). Wtedy, jeżeli liczebność próby prostej
to rozkład funkcji momentów
zmierza do rozkładu normalnego z parametrami
przy czym wariancję
określa wzór:

Współczynnik korelacji z próby określa wzór:

,

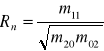
gdzie:
.

jest zgodnym estymatorem współczynnika korelacji zmiennej losowej (X,Y) który określa wzór:

Wariancję statystyki
podaje np. Cranor [?]

W szczególności, gdy zmienna (X,Y) ma e............................... rozkład normalny, to

Podobnie jak klasycznym zagadnieniu estymacji punktowej, celem estymacji przedziałowej jest ocena nielosowego parametru
zmiennej losowej X.

Na podstawie próby prostej
wyznaczamy zależne od parametru
dwie takie statystyki
i
, że
oraz:

Dla zmiennej ciągłej powyższa słaba nierówność redukuje się do równości.

Prawdopodobieństwo
jest nazywane poziomem ufności przedziału.

Przykład:

Wyznaczamy przedział ufności dla wartości przeciętnej rozkładu normalnego ze znaną wariancją
.

Średnią z n-elementowej próby prostej oznaczamy przez
, natomiast jej standardową postać przez:

.

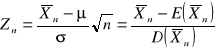
Wiadomo, że
a rozkład statystyki
nie zależy od parametru
.

Ponadto wartości statystyki
są monotonicznie malejącą funkcją wartości oczekiwanej
przy ustalonej średniej z próby.

otrzymujemy

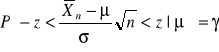
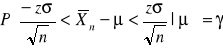
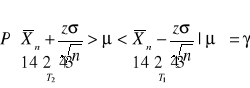
, gdzie: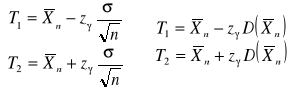

- częstość występowania przedziałów

które obejmują Θ.

Wykład 3

lub

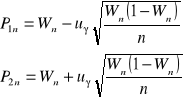
- częstość występowania cech

z tablic

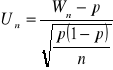
Zadanie estymacja Θ, dysponujemy
:

1)
- asymptotycznie nieobciążony

2) zgodny

3) dysponujemy wariancją

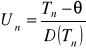
(dla wcześniejszych wzorów)

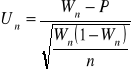
Dla mediany:

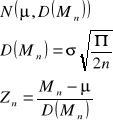
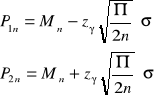
- połowa długości przedziału

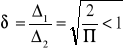
teraz nie znamy
, rozkład N(0,1) dla dowolnego rozkładu też jest dobrze, ale n>100.

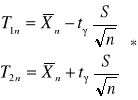
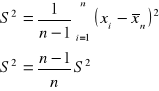
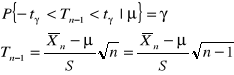
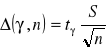
postulowana ufność
i dokładność

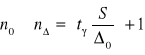
gdzie [ ] część całkowita

- wektor wartości oczekiwanych

- estymacja kombinacji liniowej

- nielosowy wektor współczynników kombinacji

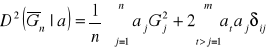
teraz nie znamy elementów wektora a, ale wiemy, że

więc

wynika, że:

- maksymalna wartość własna macierzy wariancji i kowariancji

Dla wariancji N(0,1)

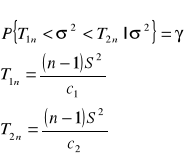
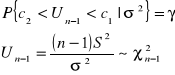
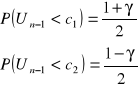
dopełnienie do dystrybuanty

Dla

Współczynnik korelacji

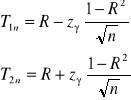
Wykład 4

Estymowany parametr:

Mamy 2 przypadki:

1) {(x_1i,x_2i); i=1,...,n} //w tym przypadku jest to jedna zmienna 2-wymiarowa

czyli wartość oczekiwana i wariancja jest jedna//

np. x_1i - praca i-tego pracownika przed podwyżką

x_2i - praca i-tego pracownika po podwyżce

d_i = x_1i - x_2i

gdzie:

- współczynnik korelacji [ro]

gdzie:

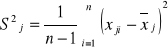
j=1,2

ostatecznie:

~

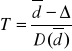
gdzie
wyznaczamy:

1. z tablic rozkładu Studenta - dla małej liczebności n,

2. z tablic dystrybuanty rozkładu normalnego dla liczebności n>100.

2) {x_1i ; i=1,2,...,n₁};{x_2i ; i=1,2,...,n₂} //tu mamy 2 zmienne o różnych wart. oczekiwanych//

x₁ ~

x₂ ~

np. zarobki w województwie śląskim i warmińsko-mazurskim

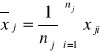
j=1,2

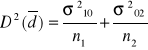
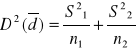
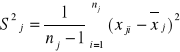
j=1,2

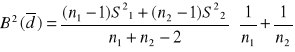
ostatecznie:

~

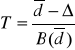
Wykład 5

Hipoteza sprawdzana i alternatywna do niej.

Hipoteza
- hipoteza sprawdzana

Hipoteza
- hipoteza alternatywna do
.

Prawdziwa jest hipoteza	Podjęto decyzję o przyjęciu hipotezy:
		Błąd pierwszego rodzaju
	Błąd drugiego rodzaju

Decyzję o przyjęciu, bądź odrzuceniu hipotezy
podejmuje się na podstawie wartości sprawdzianu testu, który nazywany jest również statystyką testową.

Rozmiar testu - prawdopodobieństwo popełnienia błędu pierwszego rodzaju poziom istotności testu

ustalany przez statystykę;

Prawdopodobieństwo niepopełnienia błędu drugiego rodzaju nazywane jest mocą testu.

Założenie:

Zmniejszenie poziomu istotności powoduje zwiększenie prawdopodobieństwa popełnienia błędu drugiego rodzaju.

Przykład:

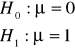
Rozważmy weryfikację prostej hipotezy sprawozdawczej:

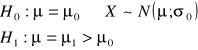
lub

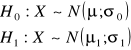
- przedział krytyczny

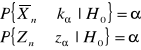
Stąd wynika, że:

- kwantyl rzędu
zmiennej losowej o rozkładzie normalnym standardowym, ponieważ
.

Zarówno statystyka
, jak i
nazywana jest sprawdzianem testu dla hipotezy sprawdzanej

względem
.

Prawdopodobieństwo popełnienia błędu drugiego rodzaju:

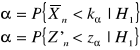
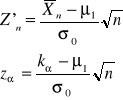
stąd wynika

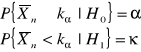
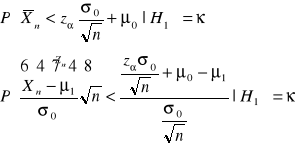
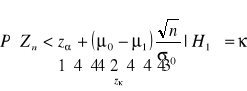
Prof. Janusz Wywiał - wykłady - Statystyka matematyczna

Str. 16

Dopuszczalny błąd

Moduł błędu estymacji

Θ

Odpowiedni kwantyl zmiennej

Odchylenie standardowe w zadaniach

Z tego wyliczamy *

---