Równowaga I₂+aromat metodą spektrofotometryczną

Oddziaływanie między promieniowaniem elektromagnetycznym a substancją, polegające na pochłanianiu części promieniowania przez substancję (absorpcja) lub oddawaniu części energii w postaci promieniowania elektromagnetycznego (emisja) jest domeną spektroskopii. Jedną z metod spektroskopowych jest spektrofotometria. Polega ona na badaniu absorpcji zachodzącej podczas przechodzenia światła przez próbkę badanej substancji (gazowej, ciekłej, stałej w roztworze lub w zawiesinie).

Spektrofotometria obejmuje trzy zakresy promieniowania elektromagnetycznego:

- promieniowanie nadfioletowe UV (ultrafiolet), λ=(200-400 nm)

- promieniowanie widzialne VIS (visible) λ=(400-800 nm )

- promieniowanie podczerwone IR (infrared) λ=(2000-25000 nm)

Wiązka światła monochromatycznego przechodząca przez ośrodek jednorodny optycznie może być pochłaniana. Równocześnie jednak część padającego promieniowania ulega odbiciu na granicy faz oraz rozproszeniu na cząsteczkach ośrodka. Przy odpowiednio dobranych warunkach pomiaru straty spowodowane odbiciem i rozproszeniem promieniowania są bardzo małe. W celu wyeliminowania poprawek na promieniowanie odbite należało by stosować pomiary porównawcze polegające na przepuszczeniu wiązki światła raz przez roztwór badany umieszczony w kuwecie, drugi raz natomiast przez odnośnik, którym jest czysty rozpuszczalnik umieszczony w takiej samej kuwecie. Możemy wówczas przyjąć, że straty spowodowane odbiciem światła na granicy faz są w obu przypadkach jednakowe. Zależność natężenia światła przepuszczonego (I) od natężenia światła padającego (I0) i grubości warstwy (b) ośrodka pochłaniającego jest ujęte prawem Lamberta:

gdzie k jest współczynnikiem zależnym od rodzaju substancji.

Stosunek
nosi nazwę przepuszczalności. Natomiast wyrażenie
nosi nazwę absorpcji. Wartość absorpcji jest oczywiście zależna od długości fali światła padającego. W przypadku roztworów absorpcja światła zależy nie tylko od grubości warstwy i specyficznych własności składników, ale również od ich stężeń.

Zgodnie z prawem Beera, absorpcja składnika rozpuszczonego w rozpuszczal-niku, który sam nie absorbuje światła o danej długości fali, jest wprost propor-cjonalna do stężenia tego składnika w roztworze (przy stałej grubości warstwy ).

Połączone prawo Lamberta Beera ma więc następującą postać :

gdzie:

a - molowy współczynnik absorpcji

b - grubość warstwy

c - stężenie molowe składnika absorbującego.

Reakcja jodu z pierścieniem aromatycznym:

Cząsteczka jodu tworzy chętnie kompleksy z donorami elektronów, którymi na przykład są pierścienie aromatyczne czy też alkohole. Pod wpływem kwantu promieniowania elektromagnetycznego z układu aromatycznego wybijany jest elektron, który „lokuje” się w pustym orbitalu jodu. Związki kompleksowe tego typu nazywamy związkami z przeniesieniem ładunku. Powstający kompleks wykazuje maksimum absorbcji w paśmie bliskiego nadfioletu przy ok. 320 nm. Zarówno jod jak i etylobenzen przy tej długości fali wykazuje znikomą absorbcję. Na tej podstawie można spektrofotometrycznie ilościowo określić stężenie powstałego kompleksu.

Wyliczamy molową absorbancję dla czystego jodu a_I oraz aromatu a_ar z równania Lamberta-Beera:

a =

gdzie:

A - absorbancja

b - szerokość kuwety [ b = 1 cm ]

c - stężenie molowe

Napięcie powierzchniowe

Cząsteczki znajdujące się na powierzchni faz skondensowanych ,posiadają pewien nadmiar energii swobodnej w stosunku do cząsteczek znajdujących się we wnętrzu tych faz. Miarą tej energii jest powierzchniowa energia swobodna przypadająca na jednostkową powierzchnię ,zwana właściwą powierzchniową energią swobodną lub napięciem powierzchniowym fazy
:

Jednostką napięcia powierzchniowego jest [
] .

Działanie energii powierzchniowej możemy zaobserwować jako siłę dążącą do zmniejszenia powierzchni rozdzielającej fazy. Metody wyznaczania napięcia powierzchniowego są oparte na pomiarze tej siły. W ćwiczeniu zastosowano dwie metody pomiaru napięcia powierzchniowego: stalagmometryczną i pęcherzykową.

.

Metoda stalagmometryczna polega na pomiarze wielkości kropli badanej substancji odrywającej się od powierzchni przyrządu .

Metoda pęcherzykowa polega na pomiarze maksymalnego ciśnienia potrzebnego do wytworzenia pęcherzyka powietrza na końcu kapilary zanurzonej w badanej cieczy , w momencie jego uwolnienia.

W obu przypadkach celem doświadczenia jest zmierzenie statycznego napięcia powierzchniowego.

Napięcie powierzchniowe czystych cieczy zmniejsza się wraz ze wzrostem temperatury, w temperaturze krytycznej osiągając wartość zerową, co opisuje równanie
:

V^2/3

Lub z wprowadzoną poprawką Ramsaya-Shieldsa:

V^2/3

gdzie V oznacza objętość molową , T_kr temperaturę krytyczna a k jest stałą dla wielu substancji przyjmującą wartość około 2.1 erg * mol^-3/2 * K^-1

Skład warstwy powierzchniowej jest odmienny od składu jego wnętrza . W najczęściej spotykanym przypadku , gdy cząsteczki rozpuszczalnika i substancji rozpuszczonej przyciągają się słabiej od cząsteczek rozpuszczalnika między sobą , cząsteczki substancji rozpuszczonej są wypychane na zewnątrz fazy i warstwa powierzchniowa zawiera ich więcej .

Różnica moli substancji rozpuszczonej w jednostkowej ilości moli rozpuszczalnika w próbce pobranej z wnętrza roztworu i jej powierzchni, podzielona przez wielkość tej powierzchni nazywa się nadmiarem powierzchniowym Gibbsa:

2. Metody pomiaru napięcia powierzchniowego:

* Metoda stalagmometryczna:

Ciecz wypływająca ze stalagmometru tworzy kroplę, która zwiększa się stopniowo i odrywa dopiero, gdy ciężar jej przezwycięży napięcie powierzchniowe.

G=

gdzie: V- objętość cieczy

- gęstość cieczy

g- przyspieszenie ziemskie

n- ilość kropli

G- ciężar kropli

Siła napięcia powierzchniowego wynosi:

F= 2 л r

gdzie r- promień kropli. W stanie równowagi:

F=G

Z tego wynika, że

2 л r
=

i na podstawie równania:

=

Obliczamy napięcie powierzchniowe po liczeniu ilości kropli. Objętości i gęstość są znane.

* Metoda pęcherzykowa:

Ta metoda polega na pomiarze ciśnienia niezbędnego do przerwania błonki powierzchniowej cieczy przez pęcherzyki powietrza. Wymagane do tego ciśnienie p na końcu kapilary równa się sumie ciśnieniu hydrostatycznemu i ciśnieniu kapilarnemu. Ciśnienie cieczy poniżej menisku jest mniejsze od ciśnienia atmosferycznego o około
, gdzie r jest promieniem rurki oraz ciśnienie wywierane przez słup cieczy wynosi:
, gdzie h_k jest wysokością kapilary zanurzonej w cieczy. Czyli manometr wskazuje ciśnienie:

P_m=
+

Czyli:

= P_m -

Porównując ciecz badaną do cieczy wzorcowej otrzymujemy:

=

=

Jak wynika z uzyskanych przez nas wyników napięcie powierzchniowe i-propanolu maleje wraz ze wzrostem temperatury. Na podstawie uzyskanych wyników można zauważyć, że dodatek alkoholu do wody obniża napięcie powierzchniowe, co świadczy o tym, że alkohol jest substancją powierzchniowo czynną.

Równowaga I₂+KI=KI₃

W układzie składającym się z dwóch niemieszających się cieczy A i B oraz z trzeciej substancji C rozpuszczalnej zarówno w jednej jak i w drugiej cieczy zachodzi ustalenie stanu równowagi ilościowo opisanego równaniem Nernsta:

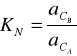
gdzie:

,
- aktywność składnika C w fazie A i B.

W stałej temperaturze lewa strona wyrażenia jest wielkością stałą. Wielkość ta oznacza zazwyczaj K_N, nazywana jest współczynnikiem podziału.

Równanie może być stosowane jako przybliżone jedynie w przypadku roztworów bardzo rozcieńczonych, szczególnie ostrożnie w odniesieniu do roztworów elektrolitów, których współczynniki aktywności różnią się wyraźnie od jedności już dla stężeń rzędu 10^-2. Poważne odchylenia od prawa podziału wystąpią także w przypadku substancji asocjujących. Dodanie trzeciej substancji B do dwóch praktycznie nie mieszających się rozpuszczalników spowoduje wzrost ich wzajemnej rozpuszczalności, a więc współistniejące fazy są roztworami trójskładnikowymi o zmieniających się zawartościach A i C .

Prawo podziału nie będzie również zachowane, gdy w jednej z faz stężenie substancji rozpuszczonej określane jest dodatkowo reakcjami równowagowymi przebiegającymi w tej fazie. Odchylenia te mogą być podstawą do wyznaczenia stałej równowagi takiej reakcji. Reakcja:

przebiega jedynie w roztworze wodnym, nie zachodzi natomiast w fazie organicznej. Stałe równowagi powyższej reakcji wyraża się wzorem:

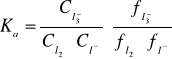
W przypadku gdy roztwór jest rozcieńczony, można przyjąć że współczynnik aktywności f_i≅1

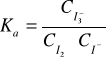
, zatem K_a≅K_c.

Jeżeli faza wodna, w której ustala się powyższa równowaga znajduje się w kontakcie z fazą organiczną np. CCl₄, wówczas stężenie równowagowe I₂ określone jest również współczynnikiem podziału:

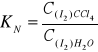
Prężność pary

Prężność pary jest to ciśnienie, pod którym ciecz i para współistnieją w stanie równowagi dynamicznej stanowiąc wówczas układ jednoskładnikowy dwufazowy, który zgodnie z regułą faz Gibbsa posiada         1 stopień swobody (F=C-P Oznacza to, że spośród ekstensywnych parametrów stanu jakimi są np. T,P tylko jeden stanowi zmienną niezależną drugi pozostaje jej funkcją.

Zależność funkcyjna T(P) lub P(T) nazywana jest krzywą równowagi fazowej, a jej opis przedstawia równanie Clapeyrona, które dla omawianego układu równowagowego ciecz-para przybiera postać:

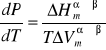
Gdzie:

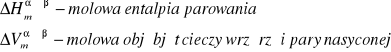
Wymienione wyżej wielkości są, indywidualnymi dla każdej substancji, funkcjami ciśnienia i temperatury, co praktycznie wyklucza scałkowanie równania Clapeyrona w sposób ogólny. Z tego powodu całkuje się, przyjmując następujące założenia upraszczające:

 zakłada się, że objętość molowa cieczy jest znacznie mniejsza od objętości molowej pary nasyconej

 przyjmuje się ze para nasycona jest gazem doskonałym

 pomija się wpływ temperatury i ciśnienia na entalpię parowania i zastępuje ją wartością średnią

 

Przy takich założeniach równanie Clapeyrona przybiera postać:

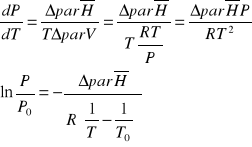
Powyższe równanie można przekształcić do postaci opisującej wpływ ciśnienia na temperaturę wrzenia cieczy

 

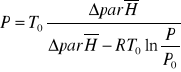
Jak również podać jego ogólną postać

Analiza powyższych zależności wskazuje na istnienie dwóch prawidłowości:

 prężność pary nasyconej cieczy jest monotonicznie rosnącą funkcją temperatury (temperatura wrzenia jest monotonicznie rosnącą funkcją ciśnienia)



 jest praktycznie funkcją liniową o współczynniku nachylenia równym -

Destylacja

Destylacja

 Destylacją nazywamy proces przeprowadzenia cieczy w stan pary i następnie skroplenie tej pary. Proces ten wykorzystywany jest do oczyszczania cieczy. Proces destylacji ze względu na swą prostotę jest najczęściej stosowanym sposobem oczyszczania cieczy o dużej lotności. W procesie destylacji wykorzystujemy fakt, że para na roztworem, w stosunku do składu roztworu, jest zawsze bogatsza w składnik bardziej lotny.

Prawo Raoulta.

Cząstkowe ciśnienie pary składnika roztworu (p) jest proporcjonalne do ułamka molowego tego składnika w roztworze (x) i do ciśnienia pary nad czystym składnikiem (p*):

p = x p*

Jeżeli roztwór jest idealny to spełnia prawo Raoulta.

Prawo Henry'ego.

Cząstkowe ciśnienie pary lotnego składnika B roztworu jest proporcjonalne do jego ułamka molowego w roztworze:

PB = xB KB

KB - to stałą charakterystyczna dla B.

Odchylenia od prawa Raoulta.

Jeżeli ciśnienie pary nasyconej jest wyższe niż przewidywane przez prawo Raoulta, mówi się o dodatnim odchyleniu od prawa Raoulta. Jeśli ciśnienia pary nasyconej są mniejsze, wówczas mówi się o odchyleniach ujemnych. Jeżeli odchylenia są tak duże, że na wykresie P(x) pojawia się ekstremum (maksimum lub minimum) mówi się o azeotropach.

Zastosowanie destylacji.

Jak już na początku było wspomniane destylacja może służyć do oczyszczania substancji ale nie tylko. Różnica składu fazy ciekłej i gazowej umożliwia stosowanie procesu destylacji do rozdzielania mieszanin ciekłych. W procesie tym faza gazowa (para) jest wzbogacana w składnik lotniejszy, a faza ciekła jest wzbogacana w składnik mniej lotny. Niestety, mieszaniny ciekłe posiadające punkt azeotropowy nie mogą być całkowicie rozdzielone na składniki w procesie destylacji.

KRIOSKOPIA

Po rozpuszczeniu w cieczy substancji trudno lotnej, prężność pary nasyconej nad daną cieczą obniża się. Z tego względu prężność pary nasyconej nad roztworem substancji nielotnej jest zawsze niższa nad czystym rozpuszczalnikiem, przy czym tym niższa, im roztwór jest bardziej stężony. Oznaczając prężność pary nasyconej nad czystym rozpuszczalnikiem przez p₀, a prężność pary nasyconej nad roztworem przez p, obniżenie prężności pary nad roztworem można określić z zależności:

Raoult wykazał, że tzw. względne obniżenie prężności pary nasyconej nad roztworem czyli
równe jest ułamkowi molowemu substancji rozpuszczonej, czyli:

m - liczba moli substancji rozpuszczonej,

N₀ - liczba moli rozpuszczalnika

Przekształcając równanie i odejmując jedność z obu stron równania otrzymuje się:

Oznaczając ułamek molowy rozpuszczalnika
przez X₀ otrzymamy ostatecznie:

Powyższe równanie stanowi treść prawa Raoulta: prężność pary nasyconej nad roztworem równa się prężności pary nasyconej nad czystym rozpuszczalnikiem, pomnożonej przez ułamek molowy rozpuszczalnika.

Ponieważ ciecz wrze w temperaturze, w której prężność pary nasyconej nad cieczą równa się prężności pary nasyconej nad jej fazą stałą obserwujemy zmiany temperatury wrzenia i krzepnięcia. Z tego wynikają następujące zależności: podwyższenie temperatury wrzenia jest proporcjonalne są stężenia molalnego substancji rozpuszczonej

gdzie: Δt_wrz - podwyższenie temperatury wrzenia, c_m - stężenie molalne, E - stała ebulioskopowa

Stężenie molalne wyraża się wzorem:

gdzie: m - masa substancji rozpuszczonej, M - masa molowa substancji rozpuszczonej, m_o - masa rozpuszczalnika

Podstawiając ostatecznie równanie do poprzedniego wzoru otrzymamy:

Z równania wynika, że gdy m = M, a m_o = 1000, Δt_w = E.

Współczynnik proporcjonalności E wyrażony w stopniach nazywa się stałą ebulioskopową. Stała ebulioskopowa E stanowi przyrost temperatury wrzenia w stosunku do temperatury wrzenia rozpuszczalnika, gdy stężenie roztworu jest jednomolalne, czyli innymi słowy stała E jest molalnym podwyższeniem temperatury wrzenia roztworu.

Obniżenie temperatury krzepnięcia roztworu jest proporcjonalne do stężenia molalnego substancji rozpuszczonej

gdzie: Δt_krz - obniżenie temperatury krzepnięcia, c_m - stężenie molalne, K - stała krioskopowa

W podobny sposób jak przy temperaturze wrzenia, możemy wyprowadzić równanie

w którym współczynnik K oznacza tzw. stałą krioskopową.

Stała krioskopowa K wyrażona w stopniach stanowi obniżenie temperatury krzepnięcia roztworu w stosunku do temperatury krzepnięcia czystego rozpuszczalnika, zawierającego jeden mol substancji rozpuszczonej w 1000 g rozpuszczalnika czyli jest molalnym obniżeniem temperatury krzepnięcia.

Wartośc stałej K można także wyliczy z równania:

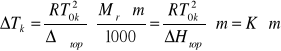
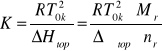
gdzie: ΔH_top jest entalpią topnienia 1 kg rozpuszczalnika, natomiast
jest jego entalpią molową

Zależność opisująca stałą kriometryczną K stanowi podstawę kriometrycznej metody wyznaczania masy molowej składnika roztworu idealnego. W metodzie tej wyznacza się wartość ΔT_k dla roztworu o znanej molalności (roztworu wzorcowego), a następnie znając wartość stałej K rozpuszczalnika wyznacza się maloalnośc badanego roztworu, a z niej poszukiwaną masę molową badanej substancji.

Istotnym warunkiem poprawności oznaczenia masy molowej metodą kriometryczną jest, aby roztwór, jaki tworzy badana substancja, był roztworem idealnym. W przypadku roztworów rzeczywistych wzór kriometryczny przybiera postać
gdzie g jest współczynnikiem osmotycznym Bjerruma. Wzór w tej postaci nie nadaje się do wyznaczania masy molowej substancji rozpuszczonej, co więcej ani substancja rozpuszczona, ani rozpuszczalnik nie mogą ulega w roztworze dysocjacji.

Pomiary ebulioskopowe i krioskopowe prowadzi się w celu wyznaczenia mas cząsteczkowych M substancji rozpuszczonych w rozpuszczalnikach o znanych wartościach stałych E albo K.

Wraz ze wzrostem stężenia wzrasta temperatura krzepnięcia. Im niższe stężenie próbki roztworu, tym mniejsze wychylenie pisaka na wykresie.

TRÓJKĄT STĘŻEŃ GIBBSA

Diagram Gibbsa, zwany też trójkątem Gibbsa - Roozebooma stosuje się do graficznego przedstawienia składu mieszanin maksymalnie trójskładnikowych.

Jest to trójkąt równoboczny, którego wierzchołki A, B, C odpowiadają 100% danego składnika. Każdy punkt leżący na boku odpowiada zawartości 2 składników (układ dwuskładnikowy). Każdy punkt wewnątrz trójkąta odpowiada zawartości 3 składników w układzie. Aby znaleźć zawartość dla dowolnego punktu przeprowadzamy przez niego 3 proste równoległe do boków trójkąta. Odległości miejsc przecięcia tych prostych z bokami od wierzchołka trójkąta wyznaczają udział procentowy składników A, B, C w mieszaninie. Odcinek równoległy do boku trójkąta zawiera punkty o jednakowym stężeniu danego składnika (wierzchołek naprzeciw tego boku). Odcinek przechodzący przez jeden z wierzchołków odpowiada stałemu stosunkowi stężeń dwu pozostałych składników. Jeżeli jest podany skład mieszaniny i chcemy znaleźć punkt na płaszczyźnie trójkąta - należy dane odłożyć na odpowiednich bokach trójkąta i przeprowadzić równoległe do boków - w miejscu ich przecięcia leży poszukiwany punkt.

Układ dwuskładnikowy i dwufazowy A-B po dodaniu pewnej ilości składnika C staje się jednofazowy; mieszanina staje się roztworem jednorodnym. Aby w założonej temperaturze określić stężenia, przy których tworzy się układ jednofazowy trójskładnikowy, miesza się A, B i C, jeżeli po osiągnięciu stanu równowagi uzyskamy układ wielofazowy - fazy rozdzielamy i określamy ich skład. Skład faz współistniejących ze sobą nanosimy na trójkąt Gibbsa i odpowiadające im punkty łączymy ze sobą odcinkami tzw. konodami. Krzywa binodalna powstaje po połączeniu punktów końcowych konod i wyznacza ona skład roztworów nasyconych. Punkt krytyczny odpowiada roztworowi nasyconemu, gdy dwie fazy mają identyczny skład. W miarę wzrostu temperatury rozpuszczalność cieczy z reguły rośnie i zmniejsza się zakres dwufazowy na trójkącie stężeń, aż do całkowitego zaniknięcia powyżej górnej temperatury krytycznej mieszalności. Istnieją też układy, w których dwie lub trzy pary składników wykazują ograniczoną rozpuszczalność.

Reguła faz określa liczbę stopni swobody układu zawierającego S składników i F faz. Odkrywcą tej reguły był twórca trójkąta stężeń J. Willard Gibbs, wyraża ją równanie:

S - liczba składników, F - liczba faz

Do ilościowego określenia składu fazy potrzebnych jest S-1 wyrazów stężeniowych. Ogólna liczba zmiennych stężeniowych wynosi F(S-1). Określa się ciśnienie i temperaturę, ogółem mamy F(S-1)+2, jeżeli uwzględnia się wszystkie fazy układu. Wyznacza się liczbę zmiennych określonych przez warunki równowagi układu. Składnik S₁ rozdzielony jest między fazy F₁ i F_2. W stanie równowagi spełniona jest pewna zależność, którą w sposób uproszczony można przedstawić za pomocą wzoru:

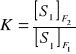
Jeżeli jest ustalone stężenie S₁ w fazie F₁ powyższe równanie określi jednoznacznie jego stężenie w fazie F₂. Dla S składników zależności równowagowe określają jednoznacznie ogółem S(F-1) parametrów intensywnych. Liczba stopni swobody (tj. liczba parametrów intensywnych, które można zmieniać) będzie równa:

Jeżeli jakiś składnik nie występuje lub występuje w znikomo małej ilości w jednej z faz układu, to liczba parametrów intensywnych odpowiadających tej fazie będzie o jeden mniejsza.

Reguła faz dotyczy wszystkich układów, niezależnie od tego, czy ich fazy zawierają jednakowe liczby składników.

---