Politechnika Warszawska Wydział Geodezji i Kartografii Katedra Geodezji i Astronomii Geodezyjnej
Ćwiczenie 7 Redukcje obserwacji geodezyjnych na geoidę i elipsoidę odniesienia (w polu siły ciężkości Ziemi)
Geodezja fizyczna i grawimetria geodezyjna II stopień studiów
Wojtek Sadowski	Grupa 2B Rok akademicki 2011/2012

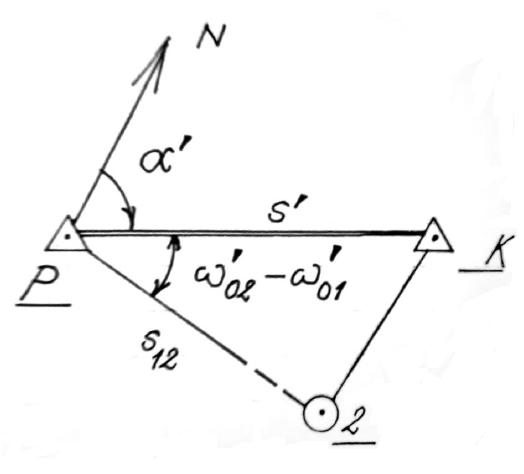
Dane do zadania:

φ'P=	49°	27'	17,062''
λ'P=	20°	3'	57,642''
α'PK=	96°	34'	6,15''
ω'01=	0°	0'	0''
ω'02=	102°	22'	36,47''
s'=	17043,117		m

Temat nr 322

Pkt	H^ort	N	ξ	η	s12	∂A/∂x	∂A/∂y
		[m]	[m]	1"	1"	[km]	[s^-2*10^-8]
P	606,92	15,42	-6,88	0,02		8,64	-0,555
K	609,21	14,93	-5,77	0,19
2	609,88	12,16	-5,08	2,07	19,699
φ2=	49°	18'	24''
λ2=	19°	57'	3''

1. Redukcja współrzędnych

Redukcje współrzędnych na geoidę:

∂φ^ort=	-1,2053”
∂λ^ort=	0,1090”

Współrzędne astronomiczne punktu P po redukcji na geoidę

Φ0=	49°	27'	15,8567”
Λ0=	20°	3'	57,7510”

Redukcja współrzędnych astronomicznych punktu P z geoidy na elipsoidę:

BP=	49°	27'	22,7367”
LP=	20°	3'	57,7202”

2. Redukcja odległości skośnej s' na elipsoidę odniesienia

Średnie współrzędne odcinka s'

Bśr =	49°	22'	53,9197''
Lśr =	20°	0'	30,3056''

Promień średniej krzywizny elipsoidy w azymucie boku:

RPK=

6390229,119

m

Obliczenie cięciwy elipsoidy ze skośnego odcinka:

HP^el=	622,340	m
HK^el=	624,140	m
H2^el=	622,040	m

s1=

17041,495

m

Długość łuku elipsoidy:

s0=

17041,500

m

Sprawdzenie istotności redukcji:

s' - s1=	1,622	m
s0 - s1=	0,005	m

Różnica długości łuku elipsoidy w stosunku do długości odcinka pomierzonego w terenie jest istotna i powinna zostać uwzględniona w dalszych etapach obliczeń.

Redukcja bazy liniowej ze względu na odchylenia pionu:

PK=	0,807	"
KP=	0,849	"

Należy zatem uwzględnić powyższą redukcję

ΔSP=	0,002	m
ΔSK=	-0,002	m

Redukcja ze względu na wzniesienie bazy nad poziomem geoidy i nad elipsoidę:

L'=	17039,838	m
L0=	17038,181	m

Powyższa redukcja jest isotna.

3. Redukcje kątów poziomych

Wpływ skręcenia płaszczyzny południka i wertykału celu ze względu na krzywiznę linii pionu z powierzchni Ziemi do geoidy:

Δp=	0,1274	"
ΔH^poz=	-0,0002	"

ΔH^poz jest mniejsze niż 0,001 zatem możliwe jest pominięcie w obliczeniach.

Wpływ odchylenia pionu na położenie wertykału:

Δα=

0,0009

"

Wpływ odchylenia pionu na kierunek południka:

p=

0,023

"

Wpływ wichrowatości normalnych do elipsoidy na położenie wertykału celu:

NSNC =	-71,839	m
δαst =	-0,006	"

Należy uwzględnić wpływ wichrowatości normalnych do elipsoidy

Wpływ odchylenia pionu w celu na kierunek wertykału:

c =

-0,2041

"

Należy uwzględnić wpływ odchylenia pionu.

Skręcenie wertykału względem przekroju normalnego:

δαcel=

-0,0002

Należy uwzględnić wpływ skręcenia wertykału.

Redukcja kierunku z powierzchni Ziemi na elipsoidę:

δ-δ'01=	-0,0066	"
δ-δ'02=	-0,0064	"

Redukcja kierunków jest istotna.

Różnica kierunków zredukowanych na elipsoidę:

δω02-δω01=

0,0002

"

Otrzymana różnica jest istotna.

Kierunki ω₀₁ i ω₀₂ po zredukowaniu na elipsoidę:

ω01^popr=	0°	0'	0,000''
ω02^popr=	102°	22'	36,4702''

---