Sygnały zdeterminowane: okresowe
Wartość skuteczna

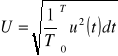
Dla przebiegu sinusoidalnego:
Wartość średnia sygnału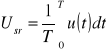
Dla sygnału sinusoidalnego:
inne sygnały:
symetryczny: U2=-U1=-U0 mamy:
Wartość skuteczna: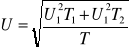

Napięcie piłokształtne
wartość skuteczna

Wykorzystanie sygnału analogowego do przenoszenia informacji: Modulacja amplitudowa (AM)
Modulacja częstotliwościowa (FM)
Modulacja fazowa (PM)

Sygnał okresowy: u(t+T)=u(t) Szereg Fouriera:
gdzie



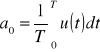
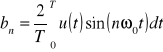
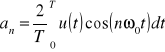
Wygodną reprezentacją sygnału jest postać: cosinusoidalna:
bądź sinusoidalna:
Postać zespolona szeregu Fouriera
gdzie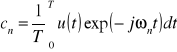
Widmem amplitudowym nazywamy wykres 2|cn(ωn)| a wykres φn(ωn) nazywamy wykresem fazowym. Dla sygnałów okresowych zarówno wykres amplitudy jak i fazy jest określony tylko w punktach ωn. Takie widmo nazywamy widmem prążkowym

Widmo amplitudowe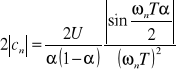
Rezystancja R pręta o długości L, przekroju S i przewodności ၳ wynosi:
izolatory ၳ < półprzewodniki ၳ < przewodniki ၳ

Sygnał zmodulowany amplitudowo u(t)=U0(1+mcosၗt)cosၷ0t Sygnały nieokresowe Transformata Fouriera: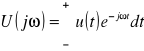
Transformata odwrotna: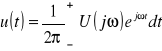
Widmo fazowe
Sygnały cyfrowe Przekształcenie sygnału analogowego u(t) dzieli się na trzy etapy: próbkowanie, kwantyzacja, kodowanie. Próbkowanie polega na pomnożeniu sygnału analogowego u(T) przez sygnał próbkujący p(t). Sygnałem próbkującym p(t) jest ciąg impulsów

prostokątnych o amplitudzie 1, okresie T i współczynniku wypełnienia α. Proces kodowania Korzystamy z kodu binarnego reprezentując liczbę za pomocą 0 i 1. Przyjmując, że zero odpowiada stanowi niskiemu, a 1 stanowi wysokiemu otrzymujemy ciąg impulsów.

Szumy cieplne wywołane chaotycznym ruchem elektronów Szumy śrutowe wynikają z ziarnistości strumienia ładunków zarówno w półprzewodnikach jak i w przyrządach próżniowych z katodą. Szumy typu 1/f wywołane generacją i rekombinacją nośników w obszarze bariery potencjału bądź na powierzchni półprzewodnika. Dla oceny wielkości szumów występujących w urządzeniach elektronicznych stosuje się tzw. współczynnik szumów F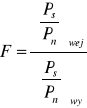
Uporządkowany ruch ładunków elektrycznych nazywamy prądem elektrycznym i opisujemy za pomocą natężenia prądu i(t). Jednostką natężenia prądu jest amper - A Prawo Ohma u(t)=Ri(t) Prądowe prawo Kirchhoffa lub I prawo Kirchhoffa:
Napięciowe prawo Kirchhoffa lub II prawo Kirchhoffa:
Jeżeli w obwodzie mamy g - niezależnych gałęzi. w których płyną nieznane prądy, to dla ich określenia pozostałe g-(w-1)=g-w+1 - równań musimy zbudować z drugiego prawa Kirchhoffa. Oznacza to, że musimy wyznaczyć g-w+1 oczek niezależnych, dla których piszemy bilans napięć.

Szeregowe połączenie rezystancji:

Jeżeli mamy K szeregowo połączonych rezystancji Ri to możemy je zastąpić rezystancją zastępczą Rzast o wartości:

Szeregowe połączenie indukcyjności: Jeżeli mamy K szeregowo połączonych indukcyjności Li, to możemy je zastąpić jedną indukcyjnością zastępczą Lzast o wartości:
Szeregowe połączenie pojemności:
Połączenie równoległe rezystancji:
Dla dwóch mamy:
Obwód prądu stałego: prąd I obliczamy dla prostego obwodu z zależności:
Moc tracona w rezystancji:
W obwodzie musi być spełniony bilans mocy jest to twierdzenie Tellegena i stwierdza ono, że: Suma mocy dostarczona przez źródła jest równa sumie mocy traconej w rezystorach znajdujących się w obwodzie. Pźr=Ptr

Obwody prądu zmiennego: Siła elektromotoryczna sinusoidalnie zmienna e(t)=Emsin(ၷt+ၪ) gdzie: Em - amplituda, ၷ - pulsacja, ၪ - faza

Indukcyjność:

Pojemność: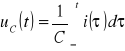

Siła Lorentza:

---