Ćwiczenia audytoryjne :Wyznaczanie krytycznej wartości prędkości przepływu płuczki wiertniczej w przestrzeni pierścieniowej

Zadanie 1:Wyznaczyć krytyczną prędkość przepływu cieczy binghamowskiej w przestrzeni pierścieniowej dla następujących danych:

• gęstość ρ = 1200 kg/m³,

• średnica zewnętrzna rur płuczkowych d_zrp = 0,127 m,

• średnica wewnętrzna rur okładzinowych D_wro = 0,2244 m,

• lepkość plastyczna η = 0,015 Pas,

• granica płynięcia τ_y = 2,5 Pa.

Rozwiązanie

Metoda pierwsza:

Z porównania wzorów na opory przepływu laminarnego i burzliwego

dla liczby Saint Venanta s ≤ 14

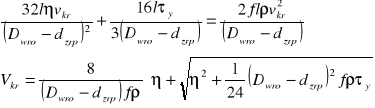
(1)

dla liczby Saint Venanta s > 14

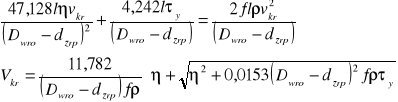
(2)

Wartość współczynnika f wyznacza się z zależności

Wstawiając dane do równań (1) oraz (2) otrzymuje się

V_kr1= 0,86 m/s

V_kr2= 0,85 m/s

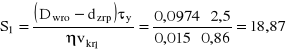
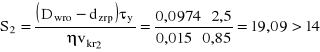
Ponieważ S₂>14 krytyczna wartość prędkości przepływu wynosi

V_kr2 = 0,85 m/s

Metoda druga

W metodzie drugiej zakłada się, że krytyczność przepływu zaistnieje gdy uogólniona liczba Reynoldsa będzie równa 2100.

Wartość krytycznej wartości przepływu wyznacza się ze wzoru

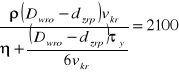
dla S ≤ 14

oraz

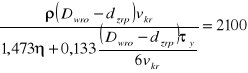
dla S > 14

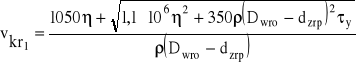
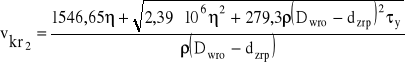
Wstawiając dane otrzymuje się

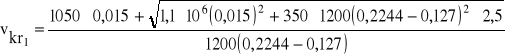
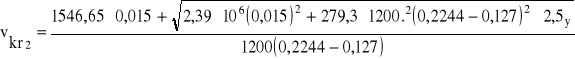
V_kr1≅1 m/s S₁=

V_kr2=0,99 m/s S₂=

prędkość krytyczna wynosi V_kr2=0,99 m/s

Metoda trzecia

W metodzie trzeciej określa się krytyczną wartość licz nie ma takiej potrzebyby Reynoldsa dla cieczy binghanowskiej.

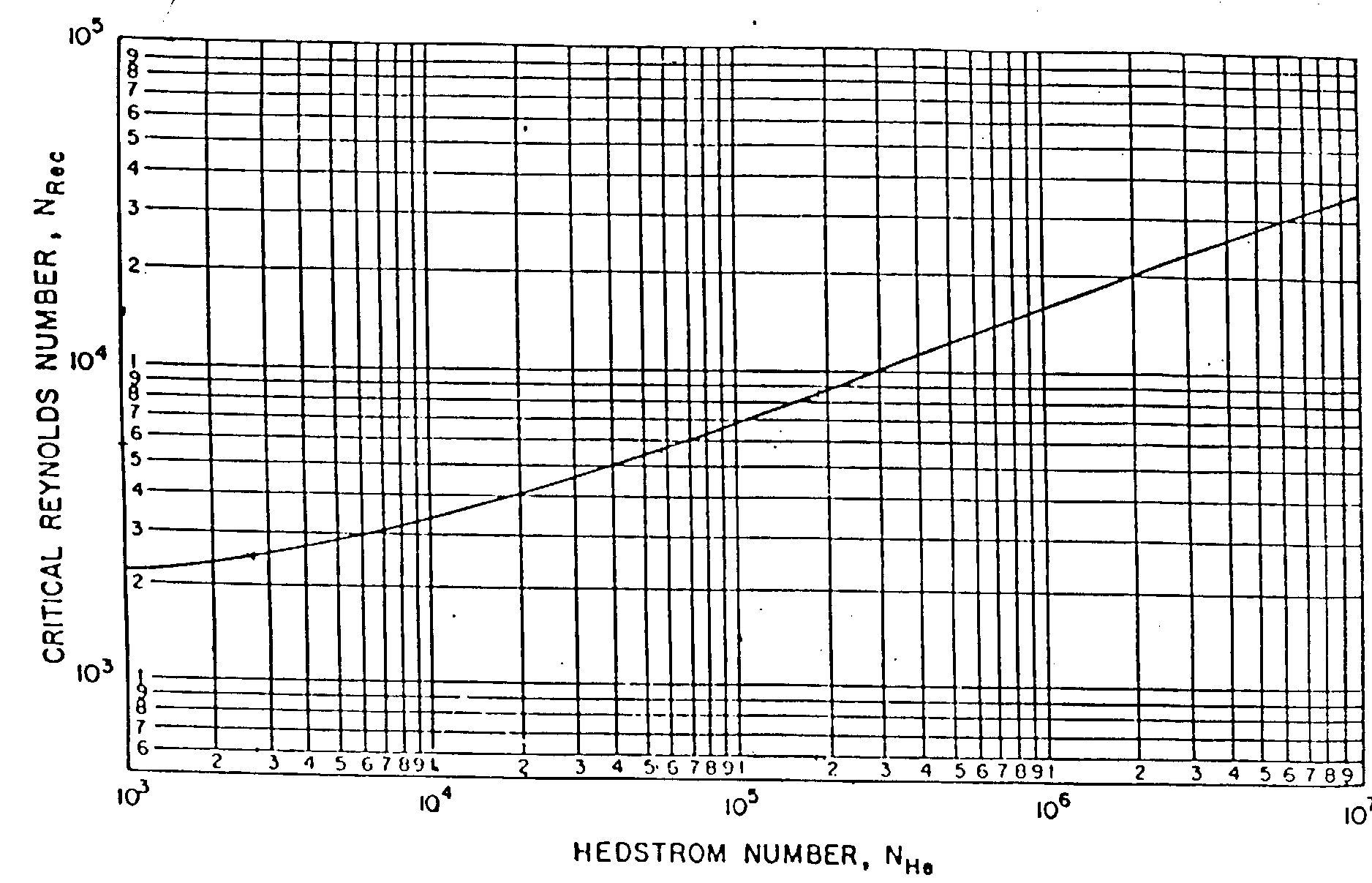
R_ekr jest funkcją liczby Hedstroma

He=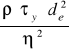

Liczba He dla danych w zadaniu warunków wynosi

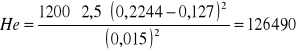
Z wykresu Re_kr=Re_kr(He) otrzymuje się

Re_kr=7100

Znając wartość krytycznej liczby Reynoldsa określić można prędkość krytyczną

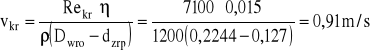
Prędkość krytyczna wynosi więc V_kr=0,91 m/s.

Zadanie 2.Określić prędkość krytyczną cieczy Ostwalda de Walde dla danych:

• Gęstość ρ = 1200 kg/ m³

• Srednica zewnętrzna rur płuczkowych d_zrp = 0,127 m

• Srednica wewnętrzna rur okładzinowych D_wro= 0,2244 m

• Współczynnik konsystencji k =0,04 Ns²/m²

• Parametr kształtu n = 0,5

Rozwiązanie:

Uogólniona liczba Reynoldsa

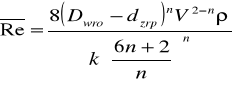
Zatem

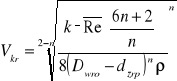
Krytyczna uogólniona liczba Reynoldsa wyznaczana jest ze wzoru

Re_kr=3470 -1370 n = 3470 - 1370 0,5 =2785