Pyanie 1
Pojęcie transmitancji widmowej odnosi się do układu dynamicznego o następujących właściwościach:
- jednowymiarowy (o jednym wejściu u(t) i jednym wyjściu y(t)),
- liniowy,
- ciągły,
- stacjonarny,
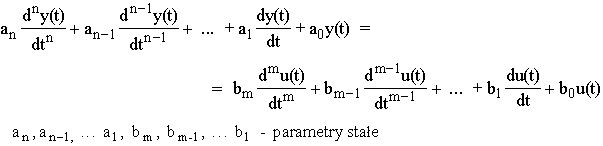
- o stałych skupionych.
Układ taki opisuje zwykłe, liniowe równanie różniczkowe o stałych parametrach:
Interpretacja tego równania jest następująca:
Obiekt dynamiczny (bez oddziaływania zakłóceń) zostaje pobudzony wymuszeniem u(t) dla t>0, a w wyniku wymuszenia powstaje odpowiedź: y(t).
Transmitancja operatorowa takiego obiektu wyraża się wzorami (patrz wykład 4.):
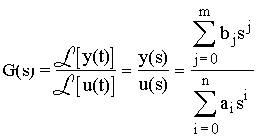
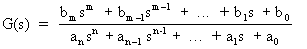
Jeśli na wejście obiektu o powyższej transmitancji wprowadzane jest wymuszenie harmoniczne czyli okresowe
![]()
np.: to otrzymuje się rozwiązanie o postaci:
![]()

co w wyniku szeregu przekształceń prowadzi do następujących wzorów na transmitancję widmową:
![]()
Postać zespolona transmitancji widmowej:
![]()
Postać zespolona transmitancji widmowej jako suma składników: rzeczywistego i urojonego:
Postać wykładnicza transmitancji widmowej:
![]()
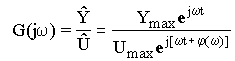
Postać transmitancji widmowej w zapisie symbolicznym (sygnały wejściowy i wyjściowy są przedstawione w zapisie symbolicznym):
![]()
Między transmitancjami: operatorową i widmową występują relacje:
![]()
Transformaty Fouriera umożliwiają bezpośrednie przejście z dziedziny czasu do dziedziny j. W tym przypadku transmitancja widmowa wyraża się wzorem
Transmitancja widmowa jest podstawą określania i wyznaczania m. in. charakterystyk częstotliwościowych obiektów dynamicznych.
Pytanie 2
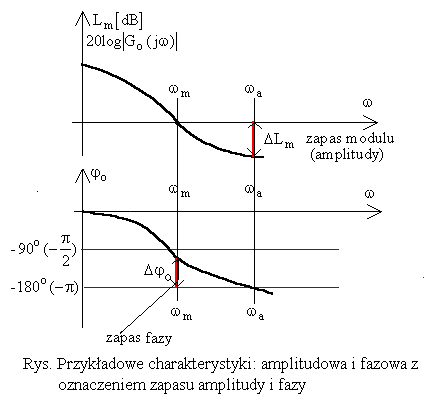
Układ zamknięty jest stabilny, jeżeli logarytmiczna charakterystyka amplitudowa układu otwartego posiada wartość ujemną dla pulsacji odpowiadajacej przesunięciu fazowemu -π. Na podstawie przebiegu charakterystyk logarytmicznych modułu i fazy można nie tylko ocenić stabilność układu, lecz również podać tzw.”zapas stabilności”. Jest to pewien margines bezpieczeństwa, dający projektantowi układu regulacji określoną pewność, że układ pozostanie stabilny, pomimo pewnych niewielkich zmian jego parametrów bądź też nieuwzględnienia niektórych parametrów przy jego obliczaniu. W języku charakterystyk częstotliwościowych dla układów stabilnych zapas stabilności określa się za pomocą zapasu modułu ΔLm0[dB] i zapasu fazy Δϕ0.
Pytanie 3
Macierze b oraz c Rów. Stanu
x(t)=Ax(t)+bu(t)
y(t)=cx(t)
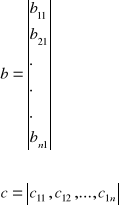
Wyszukiwarka
Podobne podstrony:
Z2, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
Z9, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
ZESTAW 1, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
156, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolos
Sciaga234, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolo
konop, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolos
ZESTAW 6, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
WNIOSKI UZUPEŁNIENIE, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty,
Z6, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
przekazniki automaty 5 wojto, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Podstawy Automat
234, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Kolos, Kolos
Z10, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
miszczu zejsc Elementy logiczne, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab,
ĆW3#DK, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty laborka, automatyka lab, Auto
Z1, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty, Zestawy
Elemety log-konspekt, Szkoła, Semestr 5, Podstawy Automatyki - laboratoria, Automaty lab, Automaty,
więcej podobnych podstron